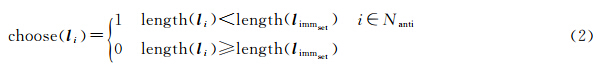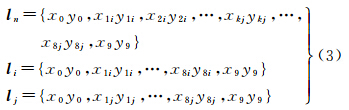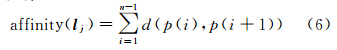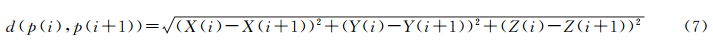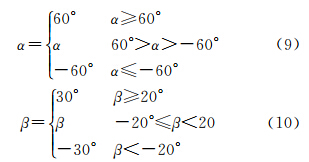2. 中国科学院地理科学与资源研究所,北京 100101;
3. 中国科学院东北地理与农业生态研究所,吉林 长春 130102
2. Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China;
3. Northeast Institute of Geography and Agroecology, Chinese Academy of Sciences, Changchun 130102, China
地形跟踪、地形回避和威胁回避(TF/TA2)对巡航导弹的军事行动和飞机导航有重要意义[1]。本文主要研究飞机参考航线规划问题。常用的航线规划算法有:粒子群算法,由初始解追随最优粒子搜索最优解,该算法有易陷入局部最优解的不足[2];遗传算法通过仿效生物界的进化规律(适者生存,优胜劣汰遗传机制)进行随机化搜索,然而该算法局部搜索能力差、易于早熟收敛,且难以保持优良个体和群体多样性[3, 4];模糊逻辑指在多值逻辑的基础上,运用模糊集合研究模糊性思维等规律的科学,但该算法的模糊规则提取困难[5];A*搜索算法通过启发函数估计搜索点和目标点间的距离,但有搜索速度慢、难以得到全局最优解的缺陷[6];Voronoi 图方法是由一组相邻点的垂直平分线构成连续多边形,但此算法在三维航线规划中复杂度较高,从而降低其实用性[7];模拟煺火方法[8]通过模拟固体退火过程实现,然而有运算效率低、速度慢的弊端;禁忌搜索利用禁忌准则和藐视准则避免迂回搜索并保证解的多样性,但结果依赖于初始解的选择[9, 10];进化算法通过模拟自然进化过程进行随机搜索的方法,该方法有保持群体的多样性及收敛性差的不足[11, 12];人工神经网络算法由大量加权节点(或称神经元)相互连接构成,缺陷有收敛速度慢、易于限于局部最优解[13, 14];GIS空间查询代数能实现最短路径查询,但空间计算较复杂[15];文献[16]研究出租车司机选择道路的经验及规律,由此建立道路寻径模型,但又受限于司机的经验; 文献[17]将时间因子引入启发式评价函数,提出了基于路段标号的时间依赖A*最短路径算法以及上述算法的混合算法[18, 19]。电势理论属于梯度寻优算法,选取惩罚函数最小的梯度方向逼近目标点,该算法结构简单速度快,但容易陷入局部最优[20]。以上算法在大范围内搜索时都存在信息存储、处理量巨大与全局最优的矛盾。因此,本文针对该问题研究飞机在复杂环境下安全、实用航线的规划问题。
针对遗传算法(GA)的缺点,文献[21]利用BP神经网络提高GA实时性和解决非线性问题的能力;文献[22]将知识规则和GA相结合实现多目标优化。目前,人工免疫算法(AIA)多用于机器人路径规划领域,而在飞机航线规划领域较少[23, 24]。文献[25]提出混合Memetic算法—GA神经免疫网络用于静态环境下的次优无碰撞路径规划。本文探讨利用AIA规划复杂环境下三维TF/TA2航线[26, 27]。
2 利用AIA的航线规划 2.1 问题提出
本文利用人工免疫算法计算在复杂环境下满足飞机性能等要求的三维飞行航线。本研究中将航线规划分为单机和双机两类。在双机规划问题中需考虑:①多机合作问题;②多机协同问题。双机系统的重点是双机间的合作问题,包括到达时间、攻击方向以及任务分配方面的协调。
飞机TF/TA2路径规划的特点有:
(1) 隐蔽性。飞行路径优先选择威胁最小的区域,例如雷达盲区、距障碍最小安全距离、最大飞行高度以及距地面最小距离。
(2) 可飞性。飞行航线需满足飞机的性能有:爬升/下降率、航线角、航程、空速以及最小转弯半径。
(3) 协同性。对于多机规划来说,要求飞机同时到达目的地。
(4) 实时性。要求下一航段规划时间小于当前航段的飞行时间。
2.2 利用AIA规划飞行路径过程
人工免疫算法(AIA)是借鉴人工免疫系统的概念和理论,将计算模型与工程应用相结合的方法。该方法将待求问题作为抗原,问题的解视为抗体。本研究利用AIA能并行计算及保持解多样性优点,结合飞机特性设计飞行航线。AIA飞行路径规划过程包括:种群特征初始化、选择技术、交叉操作、变异操作、接种、种群更新技术、进化技术和收敛条件。
2.2.1 种群特征
种群包括一定数目的抗体,抗体代表待选航线;在本试验中每条待选航线包括10个航迹点,其中,起、止点(第1点和10点,)为任务的出发点和目标点,航迹点2—9坐标在空域范围内随机产生(xmin≤xij≤xmax,ymin≤yij≤ymax,xminymin指空域左下角坐标,xmax、ymax为空域右上角坐标),即“开始点→x1y1→x2y2…x8y8→结束点”,xji、yji指第i条航线li(式(1))的第j个航迹点的x、y坐标。Nanti为抗体总数,x0y0和x9y9分别为起始点和目标点的x、y坐标
2.2.2 选择技术
利用轮盘赌方法选择抗体进行交叉操作。轮盘赌方法根据航线长度大小选择疫苗,长度小于设定的阈值length(limmset)即被选作疫苗(choose(li)=1)。其中, length(li)、length(limmset)分别为航线li和limmset的长度,见式(2)
2.2.3 复制和变异操作当抗体未达到终止条件时,抗体需要执行变异操作。由于“1-1选择概率”能为抗体提供高变异概率,因此本研究中复制全部父抗体用于变异操作;若变异后新抗体的亲和力值小于原抗体则取代之,否则,保留原抗体不变。变异分为两种模式:①交叉后变异,此方式适用于交叉操作不满足终止条件的情形;②不交叉直接变异,此方式的主要操作对象为疫苗。
变异方式1的步骤如下:
(1) 复制全部父代抗体;
(2) 按照选择的交叉方式对复制的抗体执行交叉操作,生成新抗体;
(3) 将抗体二值化,并随机选出变异位置执行变异操作,即将变异位置的值变异,若变异位置的值为“0”则变为“1”,反之亦然;
(4) 计算新抗体的亲和力值,若亲和力值小于原抗体亲和力值,则取代原抗体,否则,保留原抗体。
变异方式2的具体步骤为:
(1) 复制全部父代抗体;
(2) 将抗体二值化,并随机选择变异位置进行变异,操作同变异方式1。
2.2.4交叉和接种
本文采用3种选择抗体模式进行点交叉操作,计算过程见式(3),其中i,j ∈(1,Nanti),为提高抗体的多样性,随机选择交叉点位置k,k∈(1,8),ln指新生成的抗体:
(1) 随机选择抗体i、j执行交叉操作。
(2) 任意选择抗体i,计算抗体j执行交叉操作,其中j=Nanti+1-i。
(3) 随机选择第i个抗体,计算出抗体j的位置,其中j=[Nimm/2]+i,[]指向下取整
计算抗体亲和力函数值。抗体亲和力函数值小于疫苗阈值即为疫苗,加入疫苗池。再通过以下3种选择方法,选出抗体和疫苗执行接种操作:
(1) 随机地选择抗体i和疫苗j接种(见式(4)),其中i∈(1~Nanti)。
(2) 每个抗体i和随机选出的疫苗j接种,见式(4)
式中,i∈(1,Nanti),j∈(1,Nimm);k、q为0~9之间的随机数,且q>k;lni表示第i个新抗体;Nimm指疫苗总数。上述两种方式中,随机选择接种位置k进行接种,接种位置与航线段中航迹点的顺序、长度和疫苗一致,设疫苗段起始位置为m,即k=m、q=n。(3) 每个抗体i都接种,接种位置p和疫苗段起始位置m都是随机选择的,但接种抗体段和疫苗段的长度相同,见式(5)
式中,p=k+(n-m);k∈{0,1,2,…,9},p∈{0,1,2,…,9};p≠m;i∈{1~Nanti}。2.2.5 构建亲和函数(惩罚函数)
亲和力函数指抗体总威胁代价值见式(6)。本文中亲和力函数定义为抗体的3D综合路径长度。为统一计算各威胁值,本文中将其他威胁转化为地形威胁,因此该函数不但能反映地形威胁,还能表达不确定性威胁以及不可飞区域对飞行安全的影响
式中,affinity(lj)是路径(抗体)lj的亲和力函数值(j=1,2,…,Nanti);d(p(i)、p(i+1)) 是航线lj中航线段p(i)p(i+1) 距离;X(i)、Y(i)、Z(i)和X(i+1)、Y(i+1)、Z(i+1)分别为航迹点i、航迹点i+1的三维坐标,其中i∈(1,n),n表示航迹点总数,n=10。
2.2.6种群更新技术
抗体群由疫苗和复制的部分父抗体组成。计算种群中全部抗体的亲和力函数值,亲和值大于阈值或不满足可飞性条件的抗体将由疫苗取代,疫苗也按照亲和力值小的优先选出,且保证抗体总数Nanti不变
式中,affinityset为设定的亲和力阈值;Nchooseanti指小于affinityset的抗体数。ldeimmk指亲和力函数值较小的(Nanti-Nchooseanti)个疫苗;j∈Nanti;i∈Nanti。2.3 进化技术和收敛条件
通过上述操作可以得到新抗体群(路径解)。计算本代最优抗体与抗原比较,如果满足要求程序结束;若不满足收敛条件时,程序继续循环,否则,需要调整初始参数,例如增加种群个数、提高变异概率等,实现种群更新进化。在本试验中,为保证航线的实时性和实用性,在收敛条件结合了迭代代数和时间因素。itationset为设定的迭代次数,ldest指抗原(即最优航线)。
| while itation(i)〈itationset or lbest(i-1)〉ldest |
| perform copy,corss,immunity and variation operation |
| population update |
| i=i+1; |
| end |
利用AIA设计的初步飞行路径由条折线段连接而成,实用性受到限制;为提高飞行航线的实用性和安全性,需要对航线光滑处理。在本文中,航线光滑处理步骤包括:首先,在水平方向上,按照最大转弯角对航迹点检查,若航迹点转弯角超限,则需按坡度和曲率限制对其坐标值调整(见式(9)),否则,航迹点位置不变;其次,在垂直方向上,要求航迹点满足法向过载和最大爬升角限制;法向过载在-g~2g之间(g为重力加速度),最大爬升角限制的计算见式(10);最后,利用三次B样条曲线对航线作光滑处理
航线规划流程图中说明了人工免疫算航线规划的具体步骤(见图 1)。
 |
| 图 1 航线规划流程 Fig. 1 Path planning flow diagram |
本试验中,空域设为60 km×60 km,飞行条件中,俯仰角为-20°~20°,最大转弯角为-60°~60°,最小航线段长度为5 km,飞行速度为61~77 m/s。计算机环境为Pentium (R) 2 CPU 2.2 GHz。在单机航线规划中,起始点和目标点的坐标分别为(1 km,1 km,0.3 km)和(60 km,60 km,0.3 km)。在双机航线规划中,甲、乙起始点坐标为(1 km,8 km,0.3 km)和(10 km,1 km,0.3 km);双机的目标点和单机相同(60 km,60 km,0.3 km)。为了测试该算法的有效性和鲁棒性,在虚拟战场中假设了3种想定,对动态变化复杂环境进行仿真试验,包括飞机数量和威胁种类或/及数量变化,并与相同条件下的遗传算法(GA)进行了对比分析。
在本研究中,试验环境分为两类:简单威胁环境(简称简单环境)和复杂威胁环境(简称复杂环境)。在简单威胁环境中,仅包括考虑地形威胁,对应于TF/TA2任务的起飞阶段(即起始点进入敌方空域段)。复杂威胁环境指在敌方空域飞行阶段,威胁包括不可飞区域和突发威胁。
3.1 测试想定1
本想定的威胁环境包括:起始点处4座山峰(影响安全航线产生)及目标点前方1座山峰(阻碍航线收敛)。在图 2(a)中,威胁区域由一组等高线表示,山峰的高程见图 2(b)右侧高程表;图 2(a)中曲线表示AIA航线(三维路径在水平面上的投影)选择了纵轴附近安全、低空区域。图 2(b)中为AIA规划的三维飞行路径,飞行通过区域为威胁度最小的地区。图 3 表示利用遗传算法(GA)规划的航线,与AIA相比规划时间较短(GA 4.344 s,AIA 5.88 s),但航线长度稍长。此试验表明,GA在简单环境下能快速设计出飞行航线。表 2体现了在简单威胁环境下,遗传算法在规划时间及标准差方面都优于人工免疫算法。
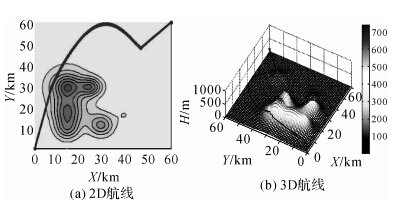 |
| 图 2 简单环境下AIA规划的飞行航线 Fig. 2 Flight path by AIA under a simple environment |
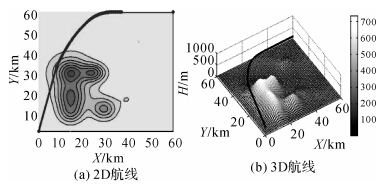 |
| 图 3 简单环境下GA规划的飞行航线 Fig. 3 Flight path by GA under a simple environment |
由于飞机视域及飞行速度的限制,在复杂环境下飞行需具有快速应对突发威胁能力。想定2的规划环境为:在想定1中加入4个不可飞区域,安全区域仅为靠近纵轴狭窄通道(见图 4(a))。不可飞区指航线不能飞越的区域,在图 4(a)和图 4(b)分别中由一组圆环和圆柱体表示。
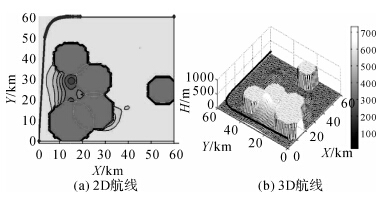 |
| 图 4 复杂环境下AIA规划的飞行航线 Fig. 4 Flight path by AIA on a complex environment |
图 4证实了在复杂环境下AIA解决飞行航线规划问题的可行性和有效性。在图 5中,GA能设计出满足要求的航线,但航线规划的迭代代数(196代)及失败次数较多(>95%)。原因在于GA中航线评价标准是唯一的,即个体对目标的适应度,而AIA中评价标准包括个体的适应度及自身的浓度,要求满足以上2个条件(即不但适应度高且个体浓度不高)的抗体才能被选择,这有利于保持群体多样性。另外,GA在交叉和变异时,以交叉为主变异为辅,在复杂环境下,若陷入局部最优解时仅仅通过交叉操作很难找到可行解;而AIA则相反,以变异为主,交叉为辅,抗体则可以通过变异改善解群取值找到可行解。通过该试验得到如下结论:在复杂环境下单机航线规划,相同条件下AIA比GA算法寻优能力更强。因此,在复杂环境下较易搜索到可行航线。
 |
| 图 5 复杂环境下GA规划的飞行航线 Fig. 5 Flight path by GA on a complex environment |
想定3为双机航线规划情景:两机从异地飞向相同目标点,要求两机的航线差最小(通过速度调整可以实现同时到达)。规划环境包括:①与想定1相同;②在想定1出现突发威胁;③在想定1内加入了4个不可飞区域。
(1) 在该规划环境下,AIA和GA规划航线见图 6、图 7。图 6(b)显示了GA仅能为甲机规划飞行航线,而不能为乙机规划出的可行航线;图 7(b)表明AIA能为双机规划出可行航线,且满足航程短、航线差小、飞行安全的要求。在图 7中,甲机航线航程64.658 km,乙机航线63.704 km,航线差为0.955 km,可以通过速度调整实现同时到。图 7(c)显示了双机都有多条备选路径,其中左侧浅色椭圆内的航线为甲机待选航线,右侧深色椭圆内的航线为乙机待选航线。待选航线生成提高了该算法的实用性,即当威胁环境变化时,飞机能够快速调用备选航线。
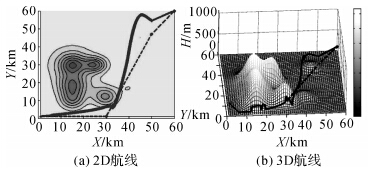 |
| 图 6 复杂环境下用GA规划的双机飞行航线 Fig. 6 Flight paths planning for dual aircrafts by GA under a complex environment |
 |
| 图 7 复杂环境下AIA规划的双机飞行航线及待选航线 Fig. 7 Flight and candidate paths planning for dual aircrafts by AIA under a complex environment |
该试验说明:在较复杂环境下的双机航线规划,AIA比GA更有效;源于GA以获得全局最优解为目的,而AIA则能搜索多极值函数的多个极值点,该算法自身特点决定了AIA在双机航线规划中具有GA不具备的优势。 (2) 在该规划环境中,设定突发威胁出现在图 4中参考航线附近(即参考航线位于突发威胁的影响范围内),重新规划后的航线见图 8。图 8(a)和8(b)表示规划出的双机安全航线,甲机航线采取低空地形回避策略,乙机航线则选择地形跟随策略,8(c)显示了甲乙两机规划的待选航线。
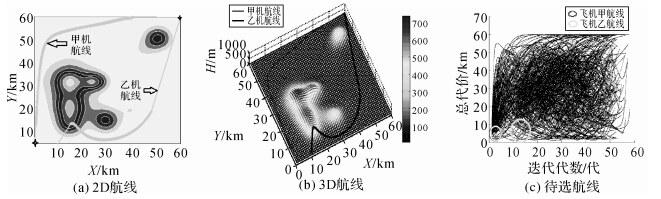 |
| 图 8 复杂环境下有突发威胁时AIA规划的飞行航线及待选航线 Fig. 8 Flight and candidate paths with unexpected threats for dual aircrafts by AIA under a complex environment |
(3) 在该规划环境中,在想定1中加入4个不可飞区域,规划结果见图 9。从图 9(a)和9(b)中表明双机航线都位于安全且地势较低的区域,9(c)则显示了由于环境复杂度提高,迭代代数的极大增加,也得到更多次优航线。AIA规划的航线通过低空威胁度最小的区域,且充分地利用了地形的隐蔽作用,因此能提高飞机TF/TA2的成功率。
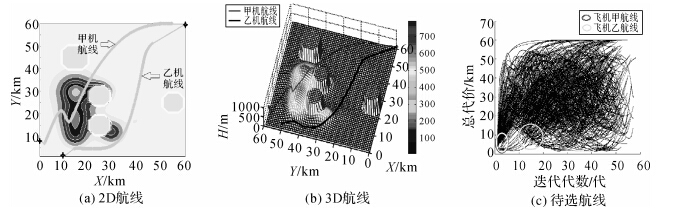 |
| 图 9 复杂环境下有不可飞区域时AIA规划的飞行航线及待选航线 Fig. 9 Flight and candidate paths with unexpected threats for dual aircrafts by AIA under a complex environment |
对于GA和AIA的性能进行评价,表 2和表 3为AIA和GA算法在计算复杂度、实时性、鲁棒性方面对比,图 10显示了AIA和GA算法在收敛性方面比较。表 2显示了在简单环境下,两种算法规划的航线实时性都较强,GA规划时间和计算复杂度比人工免疫算法(增加了接种操作)较优,但在离线航线规划中由于地面计算资源和规划时间充足而影响极小。另外,AIA能规划出多条备选航线,可以应对突发状况的出现,从而提高了该算法的鲁棒性和适应性。
 |
| 图 10 人工免疫算法和遗传算法的收敛曲线 Fig. 10 The convergence curves of AIA and GA |
| 交叉方式 | 最短时间 | 遗传算法 | 人工免疫算法 | ||||
| 最短时间 | 标准差 | 平均时间 | 最短时间 | 标准差 | 平均时间 | ||
| 1 | 3.616 | 3.616 | 0.118 | 3.747 | 5.071 | 0.100 | 5.201 |
| 2 | 3.459 | 3.459 | 0.059 | 3.523 | 4.772 | 0.272 | 5.019 | 3 | 3.448 | 3.448 | 0.048 | 3.495 | 4.831 | 0.089 | 4.941 |
| 两种规划算法 | 实时性 | 抗差性 | 计算复杂度 |
| 遗传算法 | 差 | 较差 | 较高 |
| 人工免疫算法 | 好 | 高 | 低 |
由表 2可知,算法计算复杂度与抗差性成反比,在计算复杂度和抗差性方面AIA优于GA。这在复杂环境下遗传算法未能为双机规划出飞行航线中体现出来。图 10是在地形威胁环境下两种算法收敛时间的比较:AIA(180代)收敛速度比GA(大于200代)快,因此实时性也较好。在迭代的初始阶段,AIA的航线代价(87.5)大于GA(74.6),随着迭代代数的增加,航线代价不断地减小,在146代时小于GA,这体现了该算法在航线安全性方面的优势(总代价与安全性成反比)。
4 结论与讨论
本文研究利用人工免疫算法规划单、双机TF/TA 2飞行路径。在基本人工免疫算法基础上,加入威胁环境、飞行任务及可飞性和安全性约束条件,对算法进行初步改进。另外,通过设计综合安全性能评价函数(亲和力函数)和三次样条曲线光滑处理方法对该算法进一步优化,提高其实用性。仿真试验结果表明,在复杂环境下,人工免疫算法能够为飞机规划出一条最优或多条待选次优飞行航线。本算法在出发点处障碍率为94.25%的环境下规划出多条安全飞行航线。平均规划时间5.49 s远小于最小航线段飞行时间60 s,迭代代数160,且标准差小于0.7,说明该算法具有较强的搜索能力、抗差性和实时性。
本研究分别在简单环境和复杂环境下的AIA单双机航线规划,并与相同条件下GA规划结果比较:在复杂环境下的航线规划中,AIA比GA收敛性更强,成功率更高。这是由于免疫算法具有以下特点:①提取一部分亲和力较低的抗体作为疫苗,并将疫苗与复制扩增参的父代抗体接种,提高算法收敛性;②交叉、变异操作能够有效地保持抗体的多样性,使其更适应于复杂环境下的航线规划;③复制过程是抗体自身复制过程,抗体之间没有交叉;④疫苗池能够较好地保持优良抗体及其信息。因此,AIA具有全局搜索能力较强,且局部搜索能力快的优点。另外,AIA自身的模式识别能力,也能够生成适应复杂环境下不同任务的抗体,使其特别适用于复杂环境下最优解和多解的问题。由于在复杂环境下的航线规划中AIA比GA的成功率提高了175%,也说明该算法在复杂环境下优越性更强。
| [1] | TANG Q, ZHANG X G, LIU X C. TF/TA2 Trajectory Tracking Using Nonlinear Predictive Control Approach[J]. Journal of Systems Engineering and Electronics, 2006, 17(2): 396-401. |
| [2] | LI Linyi, LI Deren. Image Texture Classification Based on Immune Particle Swarm Optimization[J]. Acta Geodaetica et Cartographica Sinica, 2008(5), 37(2): 185-195. (李林宜, 李德仁. 基于免疫粒子群优化算法的影像纹理分类[J]. 测绘学报, 2008(5), 37(2): 185-195.) |
| [3] | ALLAIRE F C J, TARBOUCHI M, LABONTÉ G, et al. FPGA Implementation of Genetic Algorithm for UAV Real-time Path Planning[J]. Journal of Intelligent and Robotic Systems, 2009, 54(1-3): 495-510. |
| [4] | FOO J L, KNUTZON J, KALIVARAPU V, et al. Path Planning of Unmanned Aerial Vehicles Using B-splines and Particle Swarm Optimization[J]. Journal of Aerospace Computing, Information, and Communication, 2009, 6: 271-290. |
| [5] | SABO C, COHEN K, KUMAR M, et al. Effectiveness of 2D Path Planning in Real Time Using Fuzzy Logic[C]//Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando: AIAA, 2010: 1-13. |
| [6] | WARREN C W. Fast Path Planning Using Modified A* Method[J]. Robotics and Automation, 1993, 2: 662-667. |
| [7] | HAMMOURI O M, MATALGAH M M. Voronoi Path Planning Technique for Recovering Communication in UAVs[C]//Proceedings of ACS International Conference on Computer Systems and Applications. Doha: ACS, 2008: 403-406. |
| [8] | ZHANG Keshi, WANG Zhengping. On Optimizing Large-scale Air-combat Formation with Simulated: Annealing GA (Genetic Algorithm)[J]. Journal of North Western Polytechnical University, 2003, 21(4): 477-480. (张科施, 王正平. 基于遗传模拟退火算法的空战编队优化研究[J]. 西北工业大学学报, 2003, 21(4): 477-480.) |
| [9] | QIU Z P, ZHANG Y. Parametric Optimization Design of Aircraft Based on Hybrid Parallel Multi-objective Tabu Search Algorithm[J]. Chinese Journal of Aeronautics, 2010, 23 (4): 430-437. |
| [10] | BAI Zhipeng, CHEN Fuji. Compound Method of Taboo Search and Genetic Algorithm to Sove Knapsack Problem[J]. Automation & Information Engineering, 2007, 28(2): 9-11. (白志鹏, 陈福集. 禁忌搜索与 GA 算法结合求解背包问题[J]. 自动化与信息工程, 2007, 28(2): 9-11.) |
| [11] | ZHANG Fuwei, LI Jun, MENG Pinchao, et al. Survey of Multi-objective Evolutionary Algorithms[J]. Journal of Changchun University of Science and Technology: Natural Science Edition, 2012, 35(3): 102-105. (张福威,李军,孟品超, 等. 多目标进化算法综述[J]. 长春理工大学学报: 自然科学版, 2012, 35(3): 102-105.) |
| [12] | PONGPUNWATTANA A, RYSDYK R. Evolution-based Dynamic Path Planning for Autonomous Vehicles[J]. Studies in Computational Intelligence, 2007, 70: 113-145. |
| [13] | DONG Z, YUAN J. A Formulation for Collision Identification and Distance Calculation in Motion Planning Using Neural Networks[J]. The International Journal of Advanced Manufacturing Technology, 1993, 8(4): 227-234. |
| [14] | YOU Shucheng, YAN Tailai. A Study on Artificial Neural Net Work Based Surface Interpolation[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(1): 30-34. (尤淑撑, 严泰来. 基于人工神经网络面插值的方法研究[J]. 测绘学报, 2000, 29(1): 30-34.) |
| [15] | LI Lin. Variable Query Algebra and Shortest Path Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(1): 59-63. (李霖. 变量查询代数及最短路径分析[J]. 测绘学报, 2000, 29(1): 59-63.) |
| [16] | TANG Luliang, CHANG Xiaomeng, LI Qingquan. The Knowledge Modeling and Route Planning Based on Taxi' Experience[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 404-409. (唐炉亮,常晓猛,李清泉. 出租车经验知识建模与路径规划算法[J]. 测绘学报, 2010(8), 39(4): 404-409.) |
| [17] | ZHENG Nianbo, LU Feng, LI Qingquan, et al. The Adaption of A* Algorithm for Least-time Path in Time-dependent Transportation Networks with Turn Delays[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 404-409. (郑年波, 陆锋, 李清泉, 等. 顾及转向延误的时间依赖A*最短路径算法[J]. 测绘学报, 2010, 39(5): 404-409.) |
| [18] | JIANG Y, WANG H G, FANG L J, et al. 2006. Motion Planning for Climbing Robot Based on Hybrid Navigation[J]. Advance in Machine Learning and Computing, 2006, 3930: 91-100. |
| [19] | KURNAZ S, KAYNAK O, KONAKO L U E. Adaptive Neuro-fuzzy Inference System Based Autonomous Flight Control of Unmanned Air Vehicles[J]. Expert Systems with Applications, 2007, 37(2): 14-21. |
| [20] | XIN Y, ZHU Q D, YAN Y J. Collision Avoidance Planning in Multi-robot System Based on Improved Artificial Potential Field and Rules[J]. Journal of Harbin Institute of Technology, 2009, 16(3): 413-418. |
| [21] | LIU Hanli, ZHOU Chenghu, ZHU Axin, et al. Multi-Population Genetic Neural Network Model for Short-term Traffic Flow Prediction at Intersections[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 363-368. (刘汉丽, 周成虎, 朱阿兴, 等. 多子群遗传神经网络模型用于路口短时交通流量预测[J]. 测绘学报, 2009, 38(4): 363-368.) |
| [22] | ZHAI Renjian, WU Fang, DENG Hongyan, et al. An Automated Selection Model of Ditch Based on Multi-objective Optimization by Genetic Algorithm[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 108-113. (翟仁健, 武芳, 邓红艳, 等. 基于遗传多目标优化的人工河网自动选取模型[J]. 测绘学报, 2008, 37(1): 108-113.) |
| [23] | MAYORGA R V, WONG A K C. A Robust Method for the Concurrent Motion Planning of Multi-manipulators Systems[J]. Journal of Intelligent and Robotic Systems, 1997, 19(1): 73-88. |
| [24] | YU Z G, SONG S M, DUAN G R. A New Artificial Immune Algorithm and Its Application for Optimization Problems[J]. Journal of Harbin Institute of Technology, 2006, 13(2), 129-133. |
| [25] | BHADURI A. University Time Table Scheduling Using Genetic Artificial Immune Network[C]//International Conference on Advances in Recent Technologies in Communication and Computing. Los Alamos: IEEE Computer Society, 2009: 289-292. |
| [26] | MALIM M R, KHADER A T, MUSTAFA A. Artificial Immune Algorithms for University Timetabling[C]//Proceedings of the 6th International Conference on Practice and Theory of Automated Timetabling. Brno:[s. n.], 2006: 234-245. |
| [27] | OBERHEID H, SÖFFKER D. Cooperative Arrival Management in Air Traffic Control: A Coloured Petri Net Model of Sequence Planning[J]. Applications and Theory of Petri Nets, 2008, 5062: 348-367. |