2. 国家基础地理信息中心， 北京 100036
2. National Geomatics Center of China, Beijing 100036, China
线/面实体间存在多种拓扑关系，这些关系在空间数据建模、分析、查询、更新与质量控制中起着重要作用。如图 1所示的线状道路与面状河流间的冲突检测中，一般认为道路与河流应为分离关系，如果相交，则可能存在冲突。图 1(a)中弯曲河流(灰色面)与道路(黑色线)间存在4个交，各个交的细分情况又彼此不同：图 1(b)道路穿越河流，图 1(c) 道路完全落入河流，图 1(d) 道路部分落入河流，图 1(e) 道路接触河流。上述4种线面拓扑关系细分情况对应着不同的处理方法：图 1(b)所示的冲突一般将穿越路段用桥梁替代；图 1(c)可能是由于该道路目标位置信息或编码信息存在错误；图 1(d)在数据质量控制时，要对落入河流的路段进行检测，如果该路段在容差允许范围内应该将其剪切掉；图 1(e)可能是测量误差所致，一般对接触路段简单移位即可。
 |
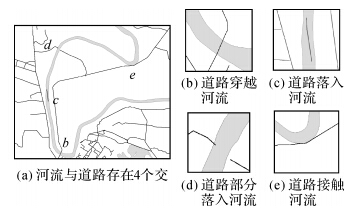| 图 1 线状道路与面状河流间的细分拓扑关系 Fig. 1 Examples of the refined topological intersection types between lines (roads) and polygons (rivers) |
从图 1可看出，一条河流可能与多条道路有交，也可能与一条道路存在多个不同的交。在空间数据冲突检测与处理中，需要检测出每一个线/面交，并区分交的细分类型，然后根据细分类型采取不同的处理方法。
近年来，多位学者在二维空间目标拓扑关系的描述与计算方面开展了大量的研究工作，取得了丰富的研究成果，主要包括基本拓扑关系模型和细分拓扑关系模型两大类。基本拓扑关系模型用若干个特定变量的不同取值来区分二元目标间的相离、相接、相交、包含、相等基本拓扑关系类型，代表性模型包括四元组模型[1]，九元组模型[2]，基于维数扩展的九元组模型[3, 4]，基于Voronoi图的V9I模型[5, 6]，使用目标整体及其Voronoi区域的VW 方法[7]，基于目标整体交、差结果的欧拉数的E-WID方法[8, 9, 10, 11, 12]，基于目标整体的空间逻辑的RCC 方法[13, 14, 15]等。上述基本拓扑关系模型无法精确区分如图 1所示的线/面目标间存在多个交的细分类型，难以满足数据质量检查与处理的应用需求。
为此，多位学者发展了通过交的顺序、类型等分量表达目标间精确拓扑关系的细分拓扑关系模型。在面/面细分拓扑关系方面，文献[16—17]提出基于边界/边界交的细分模型；文献[8]提出基于目标整体交、差结果的欧拉数的E-WID模型；文献[18]提出一种空间拓扑关系进行定量描述的方法。在线/线细分拓扑关系方面，文献[4]提出一种基于线目标整体交的顺序、共线性、类型、连接方向的细分方法。另外，多位学者探索了不确定线/面目标间的拓扑关系问题[20, 21]等，但在线/面细分拓扑关系模型研究方面成果有限。
在现有文献中线/面细分拓扑关系的研究成果主要包括文献[22]提出的一种通过线目标整体与面目标边界交的基本拓扑关系来区分线/面目标间细分拓扑关系的方法。该方法将线/面基本拓扑关系定义为“一条线和一个面边界相交为0或1次的关系”。根据该定义他们通过枚举方法得到了16种基本拓扑关系(包括相离，2种交点类型和13种交线类型，交线类型中又包括3种对称交线类型，因此实质为10种交线类型)。但是上述16种线/面基本拓扑关系不包括最常见的穿越关系(即一条线和一个面的边界交于两个点的关系，如图 1(b)所示)，不符合人们的认知习惯。且根据上述定义，基本交线的划分不具有唯一性，如图 2中的P1—P2、P3—P4必须被打断，其基本交线可划为P1—A1、A1—P2、P2—P3、P3—A2、A2—P4、P4—P5、P5—P6，也可分为P1—A1、A1—B1、B1—A2、A2—B2、B2—P6，或P1—A1、A1—P3、P3—A2、A2—P5、P5—P6等。此外，文献[19]提出一种线/面拓扑关系的组合推理方法，推导出了97种线/面拓扑关系组合类型；文献[23]提出了一种用拓扑和度量分量矩阵对线/面关系进行细分描述和计算的方法；这些方法没有明确定义包含多个交的线面关系中每个交的细分类型与描述方法，因此难以指导线/面目标间的冲突检测与处理。
 |
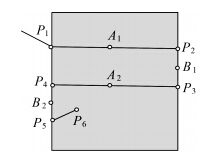| 图 2 现有线/面基本交线划分非唯一性 Fig. 2 An example of non-uniqueness of the line/polygon intersection segment |
空间目标间的拓扑关系是客观存在的，理论上线/面目标间可存在无数个交，各个交的类型又可能不一样，因此具有多个交的线/面拓扑关系的组合类型可能是无穷的。人们对拓扑关系的认识是由粗到细、由宏观到微观、由浅入深，具有层次性。在宏观层面对拓扑关系的描述往往包括两目标是否有交、有几个交、交的维数如何、交集对两目标的作用效果如何等；而微观层次对拓扑关系的描述则详细到每个交的具体情况，但目前尚缺少符合认知习惯的线/面拓扑关系层次模型。
本文在基于目标整体交、差结果的欧拉数的E-WID层次模型[8, 9, 10]的基础上，引入结点度来区分线/面交的细分拓扑关系类型，提出一种基于结点度的线/面拓扑关系细分方法。
2 结点度的引入
E-WID层次模型如式(1)、式(2)所示，能够计算基础拓扑关系和部分细分拓扑关系。在粗分层次采用式(1)所示目标整体交、差结果的维数和欧拉数来描述两目标是否有交、交的个数、维数及交对两目标的分割效果；在细分层次上，则通过式(2)所示每个交的维数、类型及顺序来表达目标间拓扑关系的细分情况
式(1)中，A、B分别表示面和线，符号“∩”、“\”分别表示交、差运算，A∩B、A＼B、B＼A分别表示A与B的3种集合运算；fDi与fE分别表示运算结果的维数与欧拉数，其中A∩B的运算结果可能包括空、纯点、纯线和点/线混合情况；B＼A的运算结果可能为空集或线集，A＼B的运算结果一般为面集。因此fDi的取值范围为{ -1、0、1、2、3}，分别表示结果为空(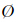
)、0维(点)、1维(线)、2维(面)、0维点和1维线组合情况等。fE表示结果的欧拉数。
式(2)中，Ni(N1，N2，…,Nm)表示交的编号；Di(D1,D2,…,Dm)表示交的维数；Ti(T1，T2，…,Tm)表示交的类型[8]。式(2)通过单元交的顺序与类型来区分两者的细分拓扑关系。
在拓扑学中，两个闭集的差可能为开集。一般认为GIS中的拓扑为应用拓扑，空间目标为封闭目标(闭集)，其交、差运算结果集合中的目标仍为封闭目标(闭集)。图 3说明本文线/面目标整体交、差运算操作的结果。设图 3(a)为面目标A与线目标B的拓扑关系，则A∩B、A＼B、B＼A的结果分别如图 3(b)、图 3(c)、图 3(d)所示。
 |
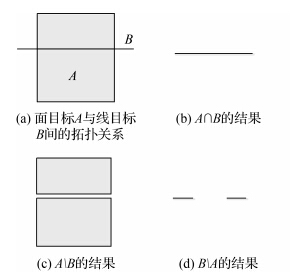| 图 3 面目标A与线目标B间交、差集合操作的定义 Fig. 3 The definitions of the two set operations(intersection and difference) between polygon A and line B |
式(2)中的0维交点的类型易于区分。如图 4所示，设A、B为待求拓扑关系的面和线目标，IP表示A、B的交点。IP仅包括在端点相交和在中间点相交两种类型，通过fE(B＼IP)的值即可区分。fE(B＼IP)=1，交点为B的端点；fE(B＼IP)=2，交点为B的中间点。
 |
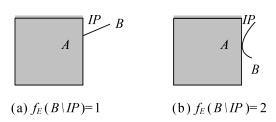| 图 4 线/面交点类型定义 Fig. 4 The definition of the topological intersection point types |
交线的情况则复杂得多，当交线多次穿越面时(图 2)，单元交线的定义就存在异议。图 2中，设A为一湖泊，B为志愿者的行车轨迹。若将行车轨迹绘制为道路，根据经验，P1—P2、P3—P4可能为跨湖桥梁；P2—P3、P4—P5可能为沿湖道路，P5—P6可能为码头等，都可能为独立单元。可将A、B的交集打断为P1—P2、P2—P3、P3—P4、P4—P5、P5—P65段单元交线。这些单元交线或完全位于面的内部，或完全位于面的边界上，或端点位于面的边界上、其余点全位于面的内部。为了保障基本交线的唯一性，本文对线/面单元交线定义如下：
定义：线/面单元交线为完全位于面的内部，或完全位于面的边界上，或仅有1—2个端点位于面的边界上其余点全在面的内部的连续线段，线/面交线与面目标边界的交点必为单元交线的端点。
此外，即使参照面/面二维交细分类型区分方法，采用两目标与某个交的差的欧拉数来区分该交的细分类型[8]，即如IL为A、B的某个单元交线，则可通过A、B与该交线IL的差的欧拉数，即fE(A＼IL)和fE(B＼IL)的取值来区分该交线的细分类型。但该方法不能区分如图 5所示的两对单元交线图 5(a)和图 5(b)及图 5(c)和图 5(d)的类型。
 |
| 图 5 fE(A＼IL)和fE(B＼IL)的取值不能区分的单元交线类型 Fig. 5 The undistinguishable units intersection segment using fE(A＼IL) and fE(B＼IL) |
仔细分析图 5中的(a)与(b)及(c)与(d)这两对单元交线，发现尽管交线对A、B的分割效果完全相同，即fE(A＼IL)和fE(B＼IL)的取值完全相同，但其端点连通状况完全不同。在拓扑学和图论中有一个反映结点连通状况的指标——结点的度(或次)。
拓扑学将平面图定义为：图G是由点集V和边集E构成的集合，记为G =(V，E)，其中点集和边集分别表示为：V={v1,v1,…,vn},vi也称为顶点、端点或结点；E={e1,e1 ,…,en},ei可以是边(没有方向)，也可以是弧(有方向)。
与点vi关联的边数称为该点的度(或次)，记为deg(v)。其中度为0(deg(v)=0)的点为孤立点；度为1(deg(v)=1)的点为悬挂点(即线段端点)；度为2(deg(v)=2)的点为线段中间点；度大于或等于3(deg(v)≥3)的点为结点[24, 25]。如图 6所示，图 6(a)中的交线端点P1、P2的度分别为1和3；图 6(b)中的交线端点P1、P2的度均为2；图 6(c)中的交线端点P1、P2的度分别为2和3；图 6(d)中的交线端点P1、P2的度分别为1和4。
 |
| 图 6 用结点度区分图 5所示的单元交线类型 Fig. 6 Discriminating the unit intersection segment using node-degree |
由此可见，在线/面交中引入结点的度(或次)有助于判断线/面单元交线的细分类型。另外，引入结点度后不难发现，尽管线/面交点类型可通过fE(B＼IP)的值来区分，但用交点度来区分更为简单、直接，设交点为P，deg(P)=3,则P为B的端点；deg(P)=4，P为B的中间点。因此，本文采用结点度来区分线/面交点、交线的细分类型。在E-WID模型的式(2)中引入结点度来区分线/面交的细分类型：设交线的两个端点为P1、P2，则交线类型ti可用(deg(P1)，deg(P2))来区分；设交点为P，交点的类型ti可用(deg(P))来区分。
3 基于结点度的线/面单元交线类型细分
引入结点度后，线/面单元交线的两个端点P1、P2的度分别包括{1,2,3,4}4种可能取值，共包括16种可能组合情况。剔除其中无意义及对称的取值，可得到8种有意义的端点度组合情况，即单元交线端点度分别为(1,1)、(1,3)、(1,4)、(2,2)、(2,3)、(3,3)、(3,4)、(4,4)。
这一方法可以完全区分端点度组合为(1,1)、(2,2)的基本交线，而端点度包含3与4的基本交线仍然不能被详细区分。例如，端点度为(1,3)、(2,3)、(1,4)的基本交线包含图 7(a)与图 7(b)、图 7(c)与图 7(d)、图 7(e)与图 7(f) 3组不同的细分拓扑类型。观察分析得出3组之间的差异，主要是由度为3或4的端点引起的。图 7(a)与图 7(b)的差异是交线端点P2是否是线目标B的端点，图 7(c)与图 7(d)、图 7(e)与图 7(f)中的差异是与P2相连的线段在多边形A的内部还是外部。究其原因，度为3或4的端点既可能是线的端点，又可能存在相连线段，而相连线段与面的拓扑关系又存在多种情况，这些都导致了端点度包含3与4的基本交线更加复杂，而度为1或2的端点通常都是线目标的端点，不存在相连线段，所以度为(1,1)、(2,2)的基本交线具有唯一性。
 |
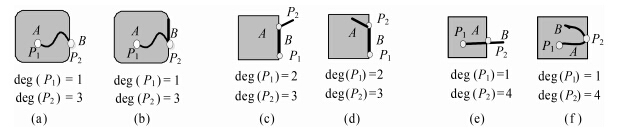| 图 7 用结点度仍不能区分的单元交线类型举例 Fig. 7 Examples of the undistinguishable unit intersection segment using node-degree |
因此，为了进一步区分采用端点度仍不能区分的基本交线类型，需要对存在度大于等于3的端点的交线类型进一步细分。本文根据此类交线是为线目标的端点还是中间点来进一步细分。如该点为线目标端点，则B中不存在与之相连的线段，用“null”表示；如该点为线目标中间点，则B中存在相连线段，相连线段与面目标A的拓扑关系仍存在在内部(interior)、在外部(exterior)或在边界上(on-boundary) 3种类型。
因此本文在8种有意义的交线端点度组合情况的基础上，对度为3和4的交线端点再次细分，用null、on-boundary、interior、exterior分别表示不存在相连线段、相连线段位于面的边界、内部和外部4种情况，组合得到有实际意义的21种线/面单元交线类型，如图 8所示。
 |
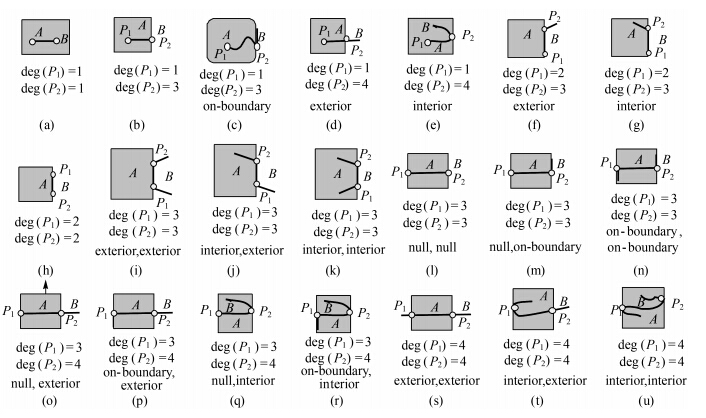| 图 8 21种有意义的线/面单元交线类型 Fig. 8 21 refined topological intersection types between lines and polygons |
将图 8所示的21种有意义的线/面单元交线类型与文献[22]的定义线/面基本拓扑关系(后文称为现有方法)比较不难发现，两种方法主要存在如下3点区别：
(1) 基本拓扑关系(单元交线)定义不同：现有方法将线/面基本拓扑关系定义为“一条线和一个面边界相交为0或1次的关系”；本文将线/面单元交线定义为“完全位于面的内部，或完全位于面的边界上，或仅有端点位于面的边界上其余点全在面内部的连续线段”。根据上述定义，前一种方法的基本拓扑关系不包含最常见的穿越关系，且基本交线划分具有非唯一性。本文单元交线包含穿越交线，且单元交线划分具有唯一性，符合人们的认知习惯。
(2) 在区分能力方面，本文基于结点度的线/面单元交线包括图 8所示的21种类型，其中包含了现有方法所定义的10种基本交线类型，更丰富了两端点都在面的边界上的穿越交线类型。
(3) 在描述方法方面，基于结点度的线/面单元交线可通过交线端点的结点度和null、 on-boundary、interior、exterior 4个谓词来区分，现有方法通过定义基本交线顺序号来区分，不便于交流。
从上述分析可看出，本文方法与现有方法相比，在基本交线类型的定义、区分能力与描述方法方面都具有明显优势。下面举例说明含多个交的复杂线/面拓扑关系的层次描述方法。
采用式(1)、式(2)所示的E-WID层次模型、图 8所示的21种线/面单元交线类型和上述交点类型可以详细表达出简单线/面目标之间的任意复杂拓扑关系。下面以图 9为例来说明详细描述方法。图 9(a)、图 9(b)都包含5个交，交的维数都包含0维点和1维线，A＼B和B＼A的维数和欧拉数都相同，因此R1所示的6元组完全相同。但图 9(a)、(b)中的2、3、4所示3个交的类型却不一样，用结点度和“null、 on-boundary、interior、exterior”(分别简写为N,D,I,E)4个谓词可将这些交点、交线类型完全区分开来。
 |
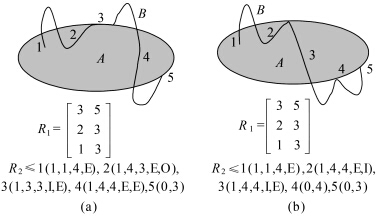| 图 9 本文方法区分复杂线/面细分拓扑关系示例 Fig. 9 21 Examples of refined complex line/polygon topological relations distinguished by the proposed model |
为了验证本文线/面拓扑关系细分模型与方法的有效性，以线状道路与面状河流为例分析了21种线/面单元交线与2种交点类型的可能冲突类型及相应处理方法(可包含多种)，发展了一套基于细分拓扑关系的冲突检测与自动(半自动)化处理规则。采用自动检测冲突类型、根据冲突类型提供人机交互选择自动修正处理方法的模式，在课题组已开发出的增量采编原型系统上，用Visual Studio 2008的C#编程开发了线/面拓扑关系的细分计算与基于细分关系的道路、面状河流冲突检测与处理原型系统，并用如图 10所示的实际数据验证了其有效性。
图 10是一幅从OpenStreetMap(OSM)上下载的老挝万象地区的道路与水系地形图(图 1(a)为图 10红色方框的局部放大图)。图中紫色线状实体为道路，蓝色面状实体为面状水体。用本文方法检测出两个图层存在的图 8中的a类交4个、c类交1个、d类交15个、g类交1个、 j类交1个、 o类交9个、 p类交12个、 t类交2个。试验证明本文方法能够提高冲突检测与处理效率。
 |
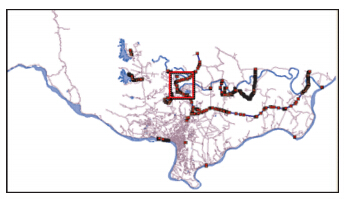| 图 10 基于结点度的线/面细分拓扑关系应用 Fig. 10 21 An applied example of node-degree based line/polygon topological relationship refinement model |
线/面细分拓扑关系在空间数据更新、质量检查与分析应用中具有重要作用，但现有的线/面细分拓扑关系模型在基本交线定义、区分能力与描述方法等方面都存在不足。本文针对上述问题，在基于目标整体交、差结果的欧拉数的E-WID层次模型的基础上，引入结点度来区分线/面交的细分拓扑关系类型，提出了一种基于结点度的线/面拓扑关系细分方法。该方法以单元交线的端点度为基础，结合线目标在度为3和4的交线端点处是否有相连线段、相连线段位于多边形的边界上、内部和外部(分别用null、 on-boundary、interior、exterior表示)4个谓词，推导出21种线/面单元交线类型。通过比较分析本文方法与现有方法，阐明了本文方法在单元交线划分、区分能力与描述方法等方面都优于现有方法。举例说明了在E-WID层次模型下用21种线/面单元交线类型和基于结点度的交点类型详细描述简单线/面目标之间任意复杂拓扑关系的方法，最后以实际数据验证了本文方法在空间数据质量检查与处理中的有效性。
应该说明的是，本文基于结点度的线/面拓扑关系细分方法是对基于目标整体交、差结果的欧拉数的E-WID层次模型的补充和发展。另外，交线端点的度同样可用来描述线目标间单元交线的细分类型。由于E-WID层次模型和本文基于结点度的交线细分方法中所用的集合操作(交、差)和拓扑不变量(欧拉数和结点度)都可用于三维空间，因此基于目标整体交、差结果的欧拉数和结点度的三维拓扑关系模型将是本文的后续研究工作。
| [1] | EGENHOFER M J, FRANZOSA R D. Point-set Topological Spatial Relations[J]. International Journal of Geographical Information System, 1991, 5(2): 161-174. |
| [2] | EGENHOFER M J, SHARMA J, MARK D M. A Critical Comparison of the 4-intersection and 9-intersection Models for Spatial Relations: Formal Analysis[C]//Auto Carto11: Proceedings of the Eleventh International Symposium on Computer-assisted Cartography Autocarto Conference. [S. l.]: American Society for Photogrammetry and Remote Sensing, 1993: 1. |
| [3] | CLEMENTINI E, FELICE P D. A Comparison of Methods for Representing Topological Relationships[J]. Information Sciences: Applications, 1995, 3(3): 149-178. |
| [4] | CLEMENTINI E, DI FELICE P D. Topological Invariants for Lines[J]. IEEE Transactions on Knowledge and Data Engineering, 1998, 10(1): 38-54. |
| [5] | CHEN Jun, ZHAO Renliang, QIAO Chaofei. Voronoi Diagram_Based GIS Spatial Analysis[J].Geomatics and Information Science of Wuhan University, 2003,28(sup1):32-37. (陈军,赵仁亮,乔朝飞. 基于Voronoi图的GIS空间分析研究[J].武汉大学学报: 信息科学版, 2003,28(sup1):32-37.) |
| [6] | CHEN J, LI C M, LI Z L, et al. A Voronoi-based 9-in-tersection Model for Spatial Relations[J]. International Journal of Geographical Information Science, 2001, 15(3): 201-220. |
| [7] | LIZL,ZHAO RL,CHEN J. A Voronoi-based Spatial Algebra for Spatial Relations[J]. Progress in Natural Science, 2002, 12(7): 528-536. |
| [8] | ZHOU X G, CHEN J,ZHAN F, et al. A Euler-number-based Topological Computation Model for Land Parcel Database Updating[J]. International Journal of Geographical Information Science, 2013, 27(10): 1983-2005. |
| [9] | ZHOU Xiaoguang, CHEN Jun. Computation of Topological Relations between Cadastral Objects Based on Euler-number[J]. Acta Geodaetica et Cartographica Sinica, 2006, 8(3): 291-298. (周晓光,陈军. 基于欧拉数的地籍拓扑关系计算[J]. 测绘学报, 2006, 35(3): 291-298.) |
| [10] | ZHOU Xiaoguang. Incremental Updating of Cadastral Database[M]. Beijing: Surveying and Mapping Press, 2007. (周晓光. 地籍数据库增量更新[M]. 北京: 测绘出版社, 2007.) |
| [11] | ZHOU Xiaoguang, YUE Guosen, WEI Jinzhan. A Computation Method of Parcels' Topological Relations Based on Oracle Spatial[J]. Journal of Central South University: Science and Technology, 2005, 36(2): 317-322. (周晓光, 岳国森, 魏金占. 基于Oracle Spatial的地籍地块空间拓扑关系判断[J]. 中南大学学报: 自然科学版, 2005, 36(2): 317-322.) |
| [12] | ZHOU Xiaoguang, CHEN Jun, JIANG Jie. Topological Relations between Parcels[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(4): 356-361. (周晓光, 陈军, 蒋捷. 地籍地块间的空间拓扑关系[J]. 测绘学报, 2003, 32(4): 356-361.) |
| [13] | RANDELL D A, CUI Z, COHN A G. A Spatiallogic-based on Regions and Connection[C]//Proceedings of the 3rd International Conference on Knowledge Representation and Reasoning. San Francisco: Morgan Kaufmann,1992: 165-176. |
| [14] | CUI Z, COHN A G, RANDELL D A. Qualitative and Topological Relationships in Spatial Databases[C]//Proceedings of the Third International Symposium on Advances in Spatial Data Bases. Singapore: Springer-Verlag, 1993: 293-315. |
| [15] | COHN A G. Exploiting Temporal Continuity in Qualitative Spatial Calculi.[C]//Spatial and Temporal Reasoning in Geographic Information Systems. New York: Oxford University Press, 1998:5-24. |
| [16] | EGENHOFER M J, FRANZOSA R. On the Equivalence of Topological Relations[J]. International Journal of Geographical Information Systems, 1995,9:133-152. |
| [17] | DENG M, CHENG T, CHEN X, et al. Multi-level Topological Relations between Spatial Regions Based upon Topological Invariants[J]. Geoinformatica, 2007, 11: 239-267. |
| [18] | GUO Qingsheng, DU Xiaochu, LIU Hao. Research on Quantitative Representation and Abstraction of Topological Relation between Two Regions[J]. Acta Geodaetica et Cartographica Sinica, 2005, 34(2): 123-128. (郭庆胜, 杜晓初, 刘浩. 空间拓扑关系定量描述与抽象方法研究[J]. 测绘学报, 2005, 34(2): 123-128.) |
| [19] | GUO Qingsheng, CHEN Yujian, LIU Hao. Combinational Reasoning of Spatial Topological Relations between a Line and an Area[J]. Geomatics and Information Science of Wuhan University, 2005, 30(6): 529-532. (郭庆胜, 陈宇箭, 刘浩. 线与面的空间拓扑关系组合推理[J]. 武汉大学学报: 信息科学版, 2005, 30(6): 529-532.) |
| [20] | DU S, WANG Q, GUO L. Modelling the Scale Dependences of Topological Relations between Lines and Regions Induced by Reduction of Attributes[J]. International Journal of Geographical Information Systems, 2010, 24: 1649-1686. |
| [21] | DU Xiaochu, HUANG Maojun. Description and Discrimination of Topological Relations between Uncertain Linear and Area Object[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 340-350. (杜晓初, 黄茂军. 不确定线-面拓扑关系的描述与判别[J]. 测绘学报, 2007, 36(3): 340-350.) |
| [22] | DENG Min, MA Hangying. The Hierarchical Representation of Topological Relations between a Line and an Area[J].Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 507-513. (邓敏, 马杭英. 线与面目标间拓扑关系的层次表达方法[J]. 测绘学报, 2008, 37(4): 507-513.) |
| [23] | WU Changbin, LÜ Guonian. Detail Representation and Calculation Method of Topological and Metric Relationships between Line and Region[J]. Journal of Computer-aided Design & Computer Graphics, 2009, 21(11): 1551-1556. (吴长彬, 闾国年. 线面拓扑和度量关系的细分描述和计算方法[J]. 计算机辅助设计与图形学学报, 2009, 21(11): 1551-1556.) |
| [24] | HU Jiaji. Operations Research[M]. Changsha: Central South University Press, 1987. (胡家骥. 运筹学[M]. 长沙: 中南工业出版社, 1987.) |
| [25] | WANG Yongxian. Operations Research: Programming Theory and Network[M]. Beijing: Tsinghua University Press, 1993. (王永县. 运筹学: 规划论及网络[M]. 北京: 清华大学出版社, 1993.) |