2. 地理信息工程国家重点实验室,陕西 西安 710054
2. State Key Laboratory of Geography Information Engineering, Xi'an 710054, China
在人们的衣食住行等日常生活中,大约有70%~80%的数据都与空间位置相关,大量空间信息的存在使得信息查询和综合成为目前GIS的基本组成部分。文献[1]总结了地球空间信息学的七大理论问题,而这七大理论问题中有4个涉及空间关系,说明空间关系在GIS基础理论研究中的重要地位。空间关系包括了拓扑关系、度量关系和距离关系,其中拓扑关系是空间关系理论中最重要的部分。复杂对象间的拓扑关系描述分析作为地理信息科学的一个基础研究问题,对完善空间关系理论体系、空间推理、人工智能等具有重要意义。
当前在GIS中,空间区域拓扑关系的描述模型主要是基于文献[2—3]提出的9-交集模型(nine-intersection model,9IM)及其一些扩展,如维扩展的9-交集模型(dimensionally extended nine-intersection model,DE-9IM)[4, 5, 6]等。它们描述了简单区域间的8种基本拓扑关系,但现实中的空间对象往往是复杂的,如一个区域包括分开的子部分、洞等。例如海南岛与中国大陆是分开的,南非的领土是带洞的,因为它完全包含莱索托,因此对于这些复合面状对象仅仅使用简单面状对象不能完全模拟现实世界。文献[7]把有洞区域分为区域整体和其包含的洞,扩展了4交集模型,但代价是对一切细节进行单调枚举;文献[8]同样通过扩展4交集模型,使其能够判断由任意多个二维区域(可能带洞)组成的复杂区域之间的拓扑关系,但没有考虑到分离的部分;文献[9—10]分别基于9-交集模型研究了复杂空间对象之间的关系;文献[11]通过计算不确定线状目标与面状目标各组成部分之间的相交程度组成的空间向量与9-交集模型确定的空间关系向量之间的相关度,确定线状目标和面状目标之间拓扑关系的描述模型,但是适用范围较小;文献[12—13]基于混合几何对象模型和维扩展9-交集模型,提出了混合几何对象拓扑关系判断模型,但是没有研究分开的区域或带洞区域;文献[14]给出了“蛋-黄”模型的邻近拓扑关系之间的动态变化图和相对应的93种拓扑关系;文献[15]针对复杂空间关系扩展9-交集模型,给出了新的语法、语义和推理规则。文献[16]通过扩展9-交集模型,将9-交集矩阵的元素扩展为二进制编码,分别研究了带双洞区域和简单区域[17]、带单洞区域和简单区域[18]及3个简单区域[19]间的拓扑关系。综合已有的研究成果可知,基于简单区域的9-交集模型表达不够简洁、明确,不能统一表达复合面状对象的拓扑关系,无法保证复合面状对象间拓扑关系的唯一性,同一9-交集矩阵可能对应多种物理解释。虽然学者们在复合面状对象拓扑关系的表达模型方面做了不少研究,但大多都是基于一种特定的面状对象,如带单洞区域和简单区域、3个简单区域等,并不能扩展到所有复合面状对象,适用范围有限。
针对目前9-交集模型表达复合面状对象拓扑关系时所存在的问题,本文采用“分解”思想,分解复合面状对象,对现有的9-交集模型进行改进,扩展到一般情况,并不只针对某一特定面状对象,增强其适用范围。方法1根据复合面状对象的结构分解成多个简单区域,用多个9-交集矩阵表示拓扑关系;方法2根据空间区域划分方法分解成点集,使9-交集矩阵的元素扩展为二进制编码。这样9-交集矩阵的表示范围变大,能够准确地区分复合面状对象间的拓扑关系。最后比较了扩展模型和9-交集模型的表达能力。
2 复合面状对象
从应用的观点出发,空间应用处理更多的是复合的几何结构,而不是当前空间数据库系统、空间查询语言和GIS中常见的简单点、线、区。开放地理信息联盟(OGC) 在OGC抽象规范[6]及地理标记语言GML中提出了称为简单要素的几何结构,对这些被称为MultiPoint、 MultiLineString和MultiPolygon的几何结构进行了非正式的描述。
复合面状对象A是由n(n≥1)个区域组成,这些区域或分离,或相交于一个或多个边界点,或带洞,即A={A1∪A2∪…∪An},如图 1所示。
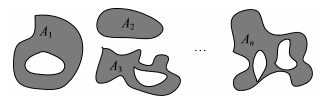 |
| 图 1 复合面状对象A Fig. 1 Complex geometric objects A |
针对复合面状对象,9-交集模型虽然也能表达区域间的拓扑关系,但是其表达不够准确,无法将区域的子集、边界、补集与另一个区域的相交情况的细节区分开,无法保证复合面状对象间拓扑关系的唯一性,同一9-交集矩阵可能对应多种物理解释。例如,图 2中的两种拓扑关系是不同的,但却对应同一个9-交集矩阵,用简单9-交集模型表示为相离。
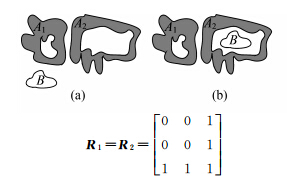 |
| 图 2 不同拓扑关系对应同一个9 Fig. 2 Different topological relations correspond to the same 9-intersection matrix |
经典9-交集模型出现这种问题的原因在于将区域划分为内部A0、边界A和外部A-3部分,而在复合面状对象中,这几部分包含了多个相离的子集,仅用这3部分的整体的相交程度无法区分各部分细节的拓扑关系。因此,研究复合面状对象间的拓扑关系的关键是如何描述复合面状对象各部分子集的拓扑关系。本文采用“分解”的思想,将复合面状对象分解,以表现复合面状对象各部分细节的拓扑关系。
3.1 分解成简单区域的9-交集模型
根据OGC抽象规范[6]中对复合几何结构的描述,复合空间对象主要通过对基本空间对象或它们的拓扑部分进行几何组合如合并和求差生成,空间对象组成部分间的拓扑关系约束对于构建对象间的拓扑起着至关重要的作用。对于区A和区B,约束条件为A包含B,集的差的闭包就形成了有着一个洞的闭合区域(图 3(a));对于区C和区D,如果C与D相离,那么将会形成一个封闭的分离区域(图 3(b));对于区E、F和G,约束条件为E包含F,且E与G相离,将会得到一个带洞区且在区外有一个分离部分(图 3(c))。
 |
| 图 3 复合面状对象的构成 Fig. 3 Constitute a complex geometric objects |
因此,根据复合面状对象的构成方法,可以将复合面状对象分解成多个简单区域,如图 4所示。图中在计算复合面状对象A与B的拓扑关系时,可以分解成简单区域A1、A2、A3、A4与B的拓扑关系。
 |
| 图 4 分解成简单区域 Fig. 4 Broken down into a simple regional |
以图 2中几何对象为例,研究图 2(a)与图 2(b)中A与B的拓扑关系。
先将几何对象A与B分解。A分解后的简单区域包括A1、A2、A3、A4,由于B是简单区域,分解后还是B,故几何对象A与B的拓扑关系可以通过A1、A2、A3、A4与B的4个9-交集矩阵表示。这样,就有R1、R2、R3、R4共4个9-交集矩阵。通过分析这4个9-交集矩阵的值就可以判断复合面状对象A与B的拓扑关系。
则图 2(A)中,4个9-交集矩阵分别为

图 2(b)中,4个9-交集矩阵分别为

通过比较可以发现,虽然图 2(a)与图 2(b)中复合面状对象A与B都对应同一个经典9-交集矩阵(相离),但通过分解表示后,R1、R2、R3相同,R4不同,也即图 2(a)与图 2(b)拓扑关系的不同点的细节通过R4反映了出来,区分了图 2(a)与图 2(b)的不同拓扑关系。
扩展到一般情况,复合面状对象A分解成p个简单区域,复合面状对象B分解成q个简单区域,则总共需要p×q个9-交集矩阵。通过比较这p×q个9-交集矩阵来判别复合面状对象A与复合面状对象B的拓扑关系细节。需要指出的是,复合面状对象分解成简单区域后,需要对每个区域设定一个标记,来指明简单区域是否是洞。
3.2 分解成点集的9-交集模型
按照空间区域划分方法[20],对任意区域A,令A0、∂inA、∂outA、A-、Ah、A(包括A和Ah)分别表示其内部、内边界(当A不带洞时为空)、外边界、外部、洞(当A不带洞时为空)、补集。根据复合面状对象的定义,复合面状对象是由n个分离的可能带洞的区域组成,因此按照复合面状对象A分离的构成部分分解成n个子集区域(可能带洞)A1、A2、…、An,然后按照空间区域划分方法分解为A10、A20、…、An0、∂inA1、∂outA1、…、∂inAn、∂outAn、A1、A1h、…、An—、Anh、A1、…、An,分别表示复合面状对象n个子集的内部、内边界、外边界、外部、洞、补集(如图 5所示)。
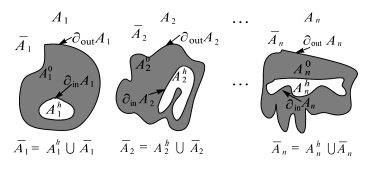 |
| 图 5 分解成点集模型 Fig. 5 Decomposed into point set model |
对于任意的复合面状对象A、B首先被分解成n、m个子集区域,并按照空间区域的划分方法,分解成其子集的内部、内边界、外边界、外部、洞、补集。
用一个4nm+1位的二进制编码Rij(i≥1、j≤3)代替9-交集矩阵中的值,用这个二进制位中的每位数值来区分子集的相交关系,最后综合表示复合面状对象A、B的拓扑关系,即
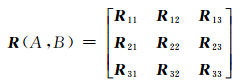
Rij的取值根据划分后的点集来确定。考虑R11,取代的是A0∩B0,因此有A10∩B10、A10∩B20、…、A10∩Bm0、A20∩B10、…、An0∩Bm0共n×m个数值,最后加上一个整体的相交情况A0∩B0。为了区分整体与细节,本文采用┐(A0∩B0),即R11需要n×m+1位来表示。同理,R12取代的是A0∩∂B。对于边界分成了内边界和外边界的情况,∂B共有2m种情况,因此R12需要2nm+1位来表示。依此类推,可以总结R11需要nm+1位(最小);R12、R13、R21、R31需要2nm+1位;R22、R23、R32、R33需要4nm+1位(最大)。
为了使9-交集矩阵各元素的数值形式相同,则二进制编码Rij(i≥1、j≤3)需要4nm+1位(最大)来表示,不足的用0来补充。Rij=X4nmX4nm-1…X2nmX2nm-1…XnmXnm-1…X1X0。Rij(i≥1,j≤3)的取值如表 1所示。
在实际情况中,根据分解后的n、m的值确定Rij元素取值表,然后根据表格确定Rij元素每位的值,形成二进制编码9-交集矩阵,为了表示方便,可以把二进制编码Rij转换成十进制数值表示。
这里同样以图 2中的几何对象为例,研究图 2(a)与图 2(b)中A与B的拓扑关系。
首先将复合面状对象A与B分解,A包括A1、A2,B分解后只有B,故这里n=2、m=1。因此,二进制编码Rij(i≥1、j≤3)需要4nm+1=4×2×1+1=9位来表示。则Rij元素取值表如表 2所示。
则图 2(a)中,二进制编码Rij(i≥1、j≤3)分别为
R11 = 000000001(二进制)=1(十进制)
R12 =000000001(二进制)=1(十进制)
R13 =000001010(二进制)=10(十进制)
R21 =000000001(二进制)=1(十进制)
R22 =000000001(二进制)=1(十进制)
R23 =010101010(二进制)=170(十进制)
R31 =000001010(二进制)=10(十进制)
R32 =000100010(二进制)=34(十进制)
R33 =010101010(二进制)=170(十进制)
即图 2(a)中的9-交集矩阵为
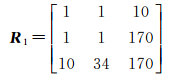
同理,图 2(b)中的9-交集矩阵为

通过比较9-交集矩阵R1与R2,可以发现R1≠R2,也即图 2(a)与图 2(b)中的拓扑关系不同,区分了图 2(a)与图 2(b)的不同拓扑关系。
| X4nm | X4nm-1 | … | X2nm | X2nm-1 | … | Xnm | Xnm-1 | … | X1 | X0 | |
| R11 | 0 | 0 | 0 | 0 | 0 | 0 | A10∩B10 | A10∩B20 | … | An0∩Bm0 | ┐(A0∩B0) |
| R12 | 0 | 0 | 0 | A10∩∂inB1 | A10∩∂outB1 | … | … | … | … | An0∩∂outBm | ┐(A0∩B) |
| R13 | 0 | 0 | 0 | A10∩B1h | A10∩B1— | … | … | … | … | An0∩Bm— | ┐(A0∩B) |
| R21 | 0 | 0 | 0 | ∂inA1∩B10 | ∂inA1∩B20 | … | … | … | … | ∂outAn∩Bm0 | ┐(A∩B0) |
| R22 | ∂inA1∩∂inB1 | ∂inA1∩∂outB1 | … | … | … | … | … | … | … | ∂outAn∩∂outBm | ┐(A∩B) |
| R23 | ∂inA1∩B1h | ∂inA1∩B1— | … | … | … | … | … | … | … | ∂outAn∩Bm— | ┐(A∩B) |
| R31 | 0 | 0 | 0 | A1h∩B10 | A1h∩B20 | … | … | … | … | An—∩Bm— | ┐(A∩B0) |
| R32 | A1h∩∂inB1 | A1h∩∂outB1 | … | … | … | … | … | … | … | An—∩∂outBm | ┐(A∩B) |
| R33 | A1h∩B1h | A1h∩B1— | … | … | … | … | … | … | … | An—∩Bm— | ┐(A∩B) |
| X8 | X7 | X6 | X5 | X4 | X3 | X2 | X1 | X0 | |
| R11 | 0 | 0 | 0 | 0 | 0 | 0 | A10∩B0 | A20∩B0 | ┐(A0∩B0) |
| R12 | 0 | 0 | 0 | 0 | A10∩∂inB | A10∩∂outB | A20∩∂inB | A20∩∂outB | ┐(A0∩B) |
| R13 | 0 | 0 | 0 | 0 | A10∩Bh | A10∩B— | A20∩Bh | A20∩B— | ┐(A0∩B) |
| R21 | 0 | 0 | 0 | 0 | ∂inA1∩B0 | ∂outA1∩B0 | ∂inA2∩B0 | ∂outA2∩B0 | ┐(A∩B0) |
| R22 | ∂inA1∩∂inB | ∂inA1∩∂outB | ∂outA1∩∂inB | ∂outA1∩∂outB | ∂inA2∩∂inB | ∂inA2∩∂outB | ∂outA2∩∂inB | ∂outA2∩∂outB | ┐(A∩B) |
| R23 | ∂inA1∩Bh | ∂inA1∩B— | ∂outA1∩Bh | ∂outA1∩B— | ∂inA2∩Bh | ∂inA3∩B— | ∂outA2∩Bh | ∂outA2∩B— | ┐(A∩B) |
| R31 | 0 | 0 | 0 | 0 | A1h∩B0 | A1—∩B0 | A2h∩B0 | A2—∩B0 | ┐(A∩B0) |
| R32 | A1h∩∂inB | A1h∩∂outB | A1—∩∂inB | A1—∩∂outB | A2h∩∂inB | A2h∩∂outB | A2—∩∂inB | A2—∩∂outB | ┐(A∩B) |
| R33 | A1h∩Bh | A1h∩B— | A1—∩Bh | A1—∩B— | A2h∩Bh | A2h∩B— | A2—∩Bh | A2—∩B— | ┐(A∩B) |
针对同一组复合面状对象,通过两种扩展交集模型及经典9-交集模型来描述8种基本的拓扑关系,显示扩展交集模型对每一个9-交集矩阵的细化,这里仍然选取图 2中所示的两个复合面状对象,讨论其8种基本的拓扑关系(由于同一拓扑关系可能的物理解释较多,只列举其中两种不同物理解释),如表 3所示。
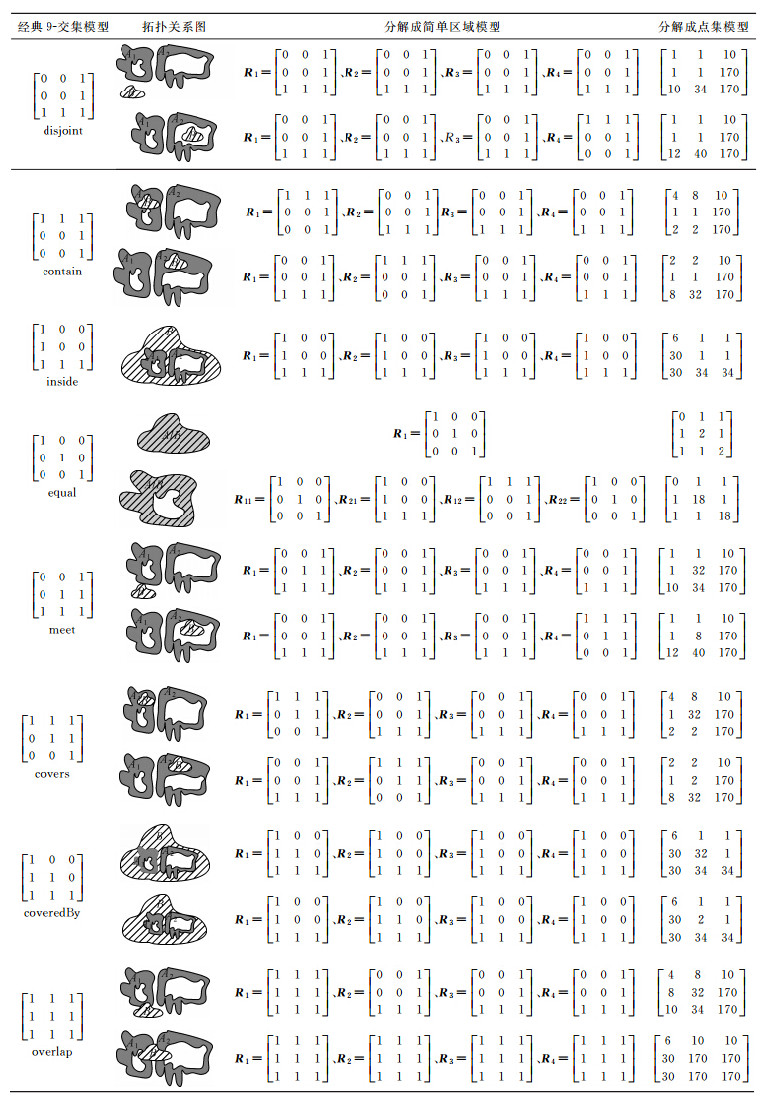 |
由于图 2中的两个几何对象不可能存在相等的拓扑,但为了表现两种扩展交集模型及经典9-交集模型的表达能力的区别,表 3的相等拓扑关系选取了简单的区域与一个带洞的区域进行比较。
由比较可知,相对于经典的9-交集模型,两种扩展的交集模型都能更加准确地表达出复合面状对象各子部分之间的拓扑关系的细节。分析可知,分解成简单区域和分解成点集两种扩展方式均采用“分解”的思想,化繁为简,但分解成简单区域是按照OGC抽象规范[6]中对复合几何结构描述分解的,简单区域是原子量;分解成点集是按照空间区域划分方法[20]分解,点集是原子量。
5 结束语
为了表达复合面状对象间的细节拓扑关系,对经典9-交集模型进行了改进,本文给出了两种基于分解思想的交集模型,并且用示例比较了两种扩展交集模型及经典9-交集模型的表达能力。结果表明,两种扩展交集模型均能准确地表达出复合面状对象各子部分之间的拓扑关系的细节。分解成简单区域的9-交集模型9-矩阵较多,表现形式不够简洁,影响存储和分析效率;分解成点集的9-交集模型需要建立Rij元素取值表,由1bit扩充为(4nm+1) bit,分析效率有待提高。因此,本研究下一步的工作主要集中于两种扩展交集模型的优化,提高分析效率,同时研究基于两种扩展模型的相似性度量。
| [1] | LI Deren,GUAN Zequn. Integration and Implementation of Spatial Information Systems[M]. Wuhan: Wuhan University Press, 2002. (李德仁,关泽群. 空间信息系统的集成与实现[M]. 武汉:武汉大学出版社,2002) |
| [2] | EGENHOFER M J, FRANZOSA R D. Point-set Topological Spatial Relations[J]. International Journal of Geographical Information Systems, 1991, 5(2): 161-174. |
| [3] | EGENHOFER M J, HERRING J R. Categorizing Binary Topological Relations between Regions, Curves and Points in Geographic Databases[R]. Orono: University of Maine, 1991. |
| [4] | CLEMENTINI E, FELICE P D. A Comparison of Methods for Representing Topological Relationships [J]. Information Science, 1994, 80: 1-34. |
| [5] | CLEMENTINI E, FELICE P D, OOSTEROM P V. A Small Set of Formal Topological Relationships Suitable for End-user Interaction[C]//Advances in Spatial Databases: Proceedings of the third International Symposium. Singapore: Springer-Verlag, 1993: 277 -295. |
| [6] | Open GIS Consortium Inc. OpenGIS Simple Features Specification for SQL[S/OL]. rev 1.1. 1999[2013-02-13]. http: //www.opengis.org1 |
| [7] | EGENHOFER M J, CLEMENTINI E, FELICE P D. Topological Relations between Regions with Holes[J]. International Journal of Geographical Information Systems, 1994, 8(2): 129 -144. |
| [8] | NGUYEN V H, PARENT C, SPACCAPIETRA S. Complex Regions in Topological Queries[C]//Proceedings of the International Conference on Spatial Information Theory: COSIT97. Laurel Highlands: Springer-Verlag, 1997. |
| [9] | SCHNEIDER M, BEHR T. Topological Relationships between Complex Spatial Objects[J]. ACM Transactions on Database Systems, 2006, 31(1): 39-81. |
| [10] | LI S J. A Complete Classification of Topological Relations Using the 9-intersection Method [J]. International Journal of Geographical Information Science, 2006,20(6): 589-610. |
| [11] | DU Xiaochu,HUANG Maojun. Description and Discrimination of Topological Relations between Uncertain Linear and Area Objects[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 340-350. (杜晓初,黄茂军.不确定线-面拓扑关系的描述与判别[J]. 测绘学报,2007, 36(3): 340-350.) |
| [12] | ZHONG Zhinong, TANG Zhengwu, ZHANG Fan, et al. A Unified Model of Distinguishing Topological Relationships[J]. Journal of National University of Defense Technology, 2004, 26(5): 57-62. (钟志农, 唐征武, 张帆, 等. 一种统一的拓扑关系判断模型[J]. 国防科技大学学报, 2004, 26(5): 57-62.) |
| [13] | XUE Dan, ZUO Huaiyu, ZHONG Zhinong, et al. Mixed Geometric Features and Their Topological Relations[J]. Advanced Manufacture and Management,2008, 27(7): 26-31. (薛丹,左怀玉,钟志农,等. 混合几何对象及其拓扑关系[J]. 先进制造与管理,2008, 27(7): 26-31.) |
| [14] | ZHOU Tao,LU Huiling,YANG Deren,et al. Popularized “Egg-folk” Model[J]. Geomatics and Information Science of Wuhan University,2012, 37(2): 242-246. (周涛,陆惠玲,杨德仁,等. “蛋-黄”模型的拓展研究[J]. 武汉大学学报:信息科学版,2012,37(2): 242-246.) |
| [15] | HUO Linlin. Research on Some Problems of Complex Spatial Relations Models and Spatial Description Logic[D]. Changchun: Jilin University, 2013. (霍林林. 复杂空间关系模型及空间描述逻辑中若干问题的研究[D]. 长春: 吉林大学,2013.) |
| [16] | OUYANG Jihong,HUO Linlin,LIU Dayou,et al. Extended 9-intersection Model for Description of Topological Relations between Regions with Holes[J]. Journal of Jilin University: Engineering and Technology Edition, 2009, 39(6): 1595-1600. (欧阳继红,霍林林,刘大有,等. 能表达带洞区域拓扑关系的扩展9-交集模型[J]. 吉林大学学报: 工学版, 2009, 39(6): 1595-1600.) |
| [17] | LI Jian,OUYANG Jihong,WANG Zhenxin. Topological Relational between a Region with Two Holes and a Simple Region[J]. Journal of Jilin University: Engineering and Technology Edition,2012, 42(5): 1214-1218. (李健,欧阳继红,王振鑫. 带双洞区域与简单区域间的拓扑关系[J].吉林大学学报: 工学版,2012,42(5): 1214-1218.) |
| [18] | LI Jian,OUYANG Jihong,WANG Guowei,et al. Representation for Topological Relations between a Region with a Hole and a Simple Region[J]. Journal of Jilin University:Science Edition,2012, 50(6): 1209-1213. (李健,欧阳继红,王国伟,等. 一个带单洞区域和一个简单区域间的拓扑关系表示[J]. 吉林大学学报: 理学版,2012, 50(6): 1209-1213.) |
| [19] | LI Jian,OUYANG Jihong,WANG Zhenxin,et al. Representation Model of Topological Relational among Three Simple Regions[J]. Journal of Jilin University: Engineering and Technology Edition,2013, 43(1): 117-122. (李健,欧阳继红,王振鑫,等. 三个简单区域间的拓扑关系的表示模型[J]. 吉林大学学报: 工学版,2013, 43(6): 117-122.) |
| [20] | EGENHOFER M J, VASARDANI M. Spatial Reasoning with a Hole[C]//Proceedings of the 8th International Conference on Spatial Information Theory. Heidelberg: Springer-Verlag, 2007: 303-320. |


