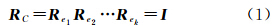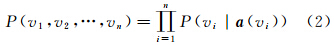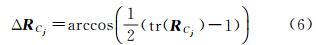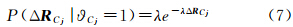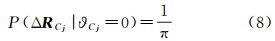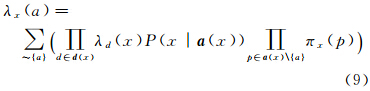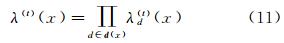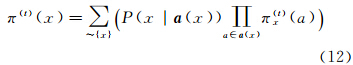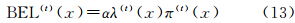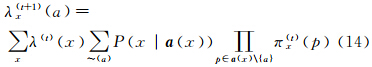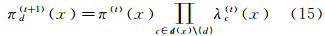1 引 言
基于无序多视影像的场景三维重建已经是摄影测量和计算机视觉领域中的一个热点问题，重建算法总体上可以分为增量法[1, 2, 3]和全局法[4, 5, 6, 7, 8]，如果没有足够的先验知识，一般情况下都需要匹配所有可能的像对，但由于场景的模糊或者不同场景中存在重复的纹理，两视匹配可能会产生错误的对极几何关系(epipolar geometry,EG)，并且误判的对极几何关系可能直接造成重建模型的变形甚至发生漂移现象[1]。
影像集中像对间的对极几何关系构成一个影像关系图G(V,E)，其中V代表顶点集，E代表边集，图中的每一个顶点代表一张影像，如果顶点i和顶点j之间存在足够多的同名像点，则i和j的连线构成G的一条边，每条边可以通过对应影像间的相对方位关系来表达(即两张影像间的旋转矩阵Rij)，误匹配会在G中产生很多误判的边(即计算得到错误的相对方位关系)。文献[9]提出一种像方特征点和物方平面元集成的多视影像密集匹配方法，利用多视影像上特征点投影范围和平面元位置的制约关系，实现特征点和平面元的同时匹配，可以有效解决影像匹配中由于重复纹理、断裂特征等引起的错误匹配，提高匹配的可靠性。文献[10] 提出一种像方和物方信息相结合的多影像匹配方法，利用分层匹配策略，对各立体像对的匹配结果进行物方融合，能剔除掉部分误匹配点，但这些算法需要利用影像间空间关系的先验信息，在没有任何先验知识的前提下并不适用。文献[11]将贝叶斯抽样一致性检验引入SIFT特征匹配，能有效提高匹配的正确率和效率，但对整体满足局部一致性的误匹配没有效果。文献[12—13]利用RANSAC引擎随机采样图G的生成树，通过遍历生成树计算对应边的全局旋转矩阵，然后利用非树边构回路，通过量测非树边的相对旋转矩阵与全局旋转矩阵的差异来检测错误边，这种算法只能确定到一个回路中是否存在误判的边，无法直接定位到回路中存在误判边的具体位置，并且它属于随机抽样算法，受制于假设样本空间的大小和G的空间结构。文献[14]首先提取G的最大生成树，然后量测非树边构成的回路中所有边对应旋转矩阵的乘积与单位阵的差异来检测环路中几何关系的一致性，但这些方法都过于依赖生成树的结构，如果生成树本身存在错误，则可能会给出错误的检测结果。
对于多视影像，利用所有的像对进行相对定向会产生很多附加信息，利用这些信息可以检验影像间几何关系的一致性，这在本质上相当于从带噪声污染的数据集中检测噪声的具体位置。本文首先将噪声检测转换成概率推论问题，通过图G中的回路约束和像对匹配过程中获得的先验信息构建概率图模型，然后利用置信传播算法(belief propagation,BP)直接确定误判相对方位关系的位置。
2 多视影像相对方位关系的概率图模型
对无序影像集V，由于缺少影像间空间关系的先验信息，本文首先利用SIFT特征匹配算法[15]匹配所有可能的像对，然后在RANSAC引擎下利用五点算法[16]计算像对间的相对方位，并剔除外点(文中外点指无法适应RANSAC假设模型的匹配点，而内点指满足RANSAC假设模型的匹配点)，如果通过RANSAC检测之后获得的匹配点对数量过少，则认为这两张影像不相关，对任意相关的两张影像vi和vj，计算出的旋转矩阵Rij构成一种估算的相对方位关系，但这种关系并不一定可靠，如图 1，两张影像分别对应公寓的左右两侧，属于不同的场景，没有重叠部分，但可以获得51对匹配像点，这可能会给出错误的相对方位关系。
 |
| 图 1 纹理重复造成场景的误匹配Fig. 1 Mismatches caused by repeated texture |
以二值变量νi表示E中第i条边ei对应两张影像间相对方位关系的正确性，将正确的相对方位关系记为νi=1，误判的相对方位关系记为νi=0。由于这种误判的相对方位关系满足局部一致性，仅仅利用两张影像本身的信息很难检测其正确性，但误判的相对方位关系不具备全局一致性，利用其他附加的信息可以对其进行检测。
2.1 基于回路约束的概率图模型
对影像集对应的关系图G(V,E)，如果边集E中存在回路，在没有误判的前提下，将回路中所有边对应的旋转矩阵顺序相乘应该等于单位阵。假设G中的某个回路为C=(e1,e2,…,ek)，则理论上存在
式中，I表示单位阵。但由于影像中噪声的存在以及数值计算中的舍入误差等影响，RC与单位阵I之间会存在一定的差异，本文以ΔRC来表示RC与I之间的差异，如果ΔRC过大，则认为回路C中至少有一条边存在误判，反之则认为C中所有的边都满足正确的相对方位关系。以变量νC表示整个回路上的相对方位关系，记νC=min(ν1,ν2,…,νk)，显然，νC=0表示回路中至少有一条边存在误判。
图 2表示4张影像构成的关系图，图中包含6条边、5个回路。
 |
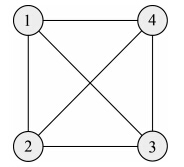| 图 2 4张影像构成的关系图Fig. 2 Relation graph composed of 4 images |
ΔRC的取值与回路中所有边对应的ν相关，以P(ΔRC|νC)表示在整个回路相对方位关系为νC的条件下ΔRC发生的概率。同样，边ei对应的旋转矩阵Rei与其对应的相对方位关系νi也存在一定的内部联系，记在相对方位关系νi的条件下Rei发生的概率为P(Rei|νi)，于是可以将关系图G(V,E)转换成贝叶斯网络，图 3表示与图 2对应的贝叶斯网络，箭头方向代表概率依赖关系，每一个回路C对应的ΔRC节点依赖于构成其回路的所有边对应的ν节点。
 |
| 图 3 贝叶斯网络Fig. 3 Bayes network |
贝叶斯网络是描述特征之间因果关系的有向无环图(DAG)，由节点和表示因果关系的有向边组成，每一条边都由父节点指向子节点，表示节点间的概率依赖关系，每一个节点都代表一个变量，对应一个条件概率表(CPT)，表示子节点在父节点取值下的条件概率，若某个节点不包含父节点，则其条件概率为其先验概率分布。记a(v)为节点v的父节点集，则贝叶斯网络可以表示为一个概率分布函数
如果a(vi)=φ(即节点vi没有父节点)，则记P(vi|φ)=P(vi)，于是图 3对应的概率分布为
式中，x为节点Re的个数；y为节点ΔRC的个数(即关系图G中的回路数)；z为节点ν的个数。由于G中每条边e对应的旋转矩阵Re只与构成该条边的两张影像相关，所以概率图中x=z。
2.2 回路构建
图G(V,E)中的每一个回路都包含一个旋转矩阵乘积闭合约束，理论上穷举G中的所有回路得出的计算结果最可靠，但在图形较为复杂的情况下很难构建所有的回路，本文利用生成树算法构建图G中的部分回路。
生成树是指图G中包含所有顶点，但没有回路的联通子图，影像关系图中一般以每条边对应两张影像的匹配点对数量作为该边的权值，最大(小)生成树为权重之和最大(小)的生成树，理论上最大生成树是关系图中最稳健的生成树[14]。本文首先对G中的每条边e赋权值w(e)。w(e)为这条边对应两幅图像的匹配点数量的倒数，于是得到一个新的带权关系图G，很明显G的最小生成树即为G的最大生成树。然后利用贪心算法[17]计算G的最小生成树：假设G中顶点数为n，T=(U,Ew)为G的最小生成树，首先置U的初值等于V(即包含有G中的全部顶点)，Ew的初值为空集，将图G中的边按权值从小到大的顺序依次选取，若选取的边未使生成树T形成回路，则加入Ew；否则舍弃，直到Ew中包含(n-1)条边为止，便获得了G的最小生成树T，而T即是G的最大生成树。
图 4是构建最大生成树的一个示意图，每条边上的数值代表其对应两个顶点间匹配点对的数量，实线部分代表生成树，G中每一条生成树之外的边与生成树中的部分边产生一个回路，并且这个回路的路径是唯一的。同时本文利用穷举法构建所有三元视图组的回路，在影像集的所有n张影像中随机取3张，如果其中任意两张影像都相关，则其构成一个回路。依据本文的方法，图 4中包含9个回路(非树边6个，三元视图组6个，减去重复的3个三元视图组回路)。
 |
| 图 4 最大生成树Fig. 4 Maximum spanning tree |
本文的目的是推导关系图G(V,E)中所有边对应相对方位关系的正确性，通过贝叶斯网络将其转换成了一个最大后验概率(maximum a posteriori,MAP)的求解问题，即确定贝叶斯网络中所有νk节点的值以最大化公式(3)，这种概率推论问题并不一定需要计算出严格的分布函数，只需要式(3)中的因式符合正确的分布趋势。
贝叶斯网络中节点νk的取值代表其对应的两张影像相对方位关系的正确性，可以取0和1，在没有任何先验信息的前提下，节点νk取0和1的概率是相等的，都为1/2。
利用影像间的点特征关系可以估算条件概率P(Rei|νi)。假设Rei和νi对应的两张影像为vl和vr，N表示这两张影像SIFT匹配点对的数量，Nl和Nr分别为两张影像上提取的SIFT特征点数，记Nlr= min(Nl,Nr)。在νi=1的前提下，理想的情况是影像vl和vr获得的匹配点数接近Nlr；然而受影像重叠度、场景结构、拍摄角度等因素的影响，实际应用中获取的匹配点数可能与Nlr有较大差异。本文将所有这些影响因素用一个变量p1表示，它表示在νi=1的前提下从影像上提取到同一特征点的概率，于是从(Nl+Nr)个特征点中提取出N对同名像点的概率模型服从二项分布B(Nlr,p1)，二项分布即n重伯努利分布，表示n个独立的是非试验中成功次数的离散概率。于是
如果这两张影像的相对方位关系存在误判，即νi=0，则在这两张影像上匹配同名像点属于偶然事件，假设这种偶然事件发生的概率为p0，同样可以认为误判的几何关系下，条件概率P(Rei|νi=0)服从二项分布B(Nlr,p0)，即
误判条件下匹配成功的概率应该远小于正确对极几何关系的匹配成功的概率，本文取经验值p1=0.1，p0=0.001。
接下来计算条件概率P(ΔRC|νC)。根据式(1)，RCj为图G中第j个回路中所有边对应旋转矩阵的乘积，所以RCj也是一个旋转矩阵。根据欧拉旋转定理，在三维空间中，旋转矩阵有一个等于单位1的实特征值，假设其对应的旋转角为θ(θ∈[0，π])，另外两个复数特征值为exp(iθ)和exp(-iθ)，存在
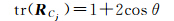
在回路Cj中所有边的相对方位都不存在误判时，理论上引起RCj与单位阵差异的因素是噪声和计算的舍入误差，这种影响不会造成ΔRCj的巨大偏移，文献[18]在大量样本统计的基础上，得出环路中的角度闭合差ΔRCj在不存在误判的条件下大致服从指数分布，即
式中，ΔRCj以度表示；参数λ取固定值0.5；文献[18]中所有环路中的边数量都限制在6条以内，而ΔRCj与回路Cj中边的数量有关，边越多，可能产生的累积误差就越大，即在回路中是否存在误判的推论与回路的长度有关。文献[14]证明在大影像集中限制环路的长度可能导致部分误判边无法被检测出来，并且回路角度闭合差与环路长度的算术平方根大致成正比关系，假设回路Cj中边的数量为L，本文试验中取经验值
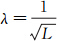，即满足概率函数的均值为
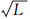。如果回路Cj中存在误判的对极几何关系，旋转矩阵的累积误差可能在[0，π]上取任意值，所以ΔRCj服从[0，π]上的均匀分布，即
3 基于置信传播的相对方位关系推论
相对方位关系检测实际上就是在贝叶斯网络中确定所有vi节点的取值，在已知先验概率分布的前提下，本文利用置信传播算法来解算贝叶斯网络中的概率推论问题。置信传播算法是20世纪80年代初提出的一种高效的消息传播推论算法[19]，文献[20]最先在编码领域建立置信传播算法与贝叶斯网络的联系，文献[21—22]在贝叶斯网络中应用置信传播算法很好地解决了“turbo编码”问题，现在联合使用置信传播和贝叶斯网络已经是解决推论问题的最重要手段之一。
与马尔科夫随机场(Markov random field,MRF)一样，贝叶斯网络是以因式分解形式来表示联合概率分布，可以将其转换成因子图。因子图是一个表示因式分解结构的二分图，对式(2)中的每一个因式P(vi|a(vi))引入一个函数节点，函数节点分别连接vi和其父节点集a(vi)，图 5就是贝叶斯网络(图 3)对应的因子图。
 |
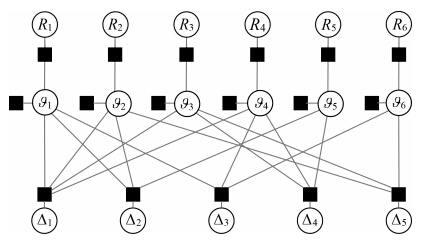| 图 5 因子图Fig. 5 Factor graph |
将因子图中的每个节点vi与其对应的函数节点P(vi|a(vi))相关联，构成一个变量节点，并考虑贝叶斯网络中的依赖关系，可以将因子图转换成为置信网络。设节点vi对应的节点变量为x，记父节点向子节点传递的消息记为πc(p)，子节点向父节点传递的消息记为λc(p)，其中p代表父节点，c代表子节点。如图 6表示置信传播中节点ν2对应的消息传递方式，图中每一个虚线框代表一个变量节点。
 |
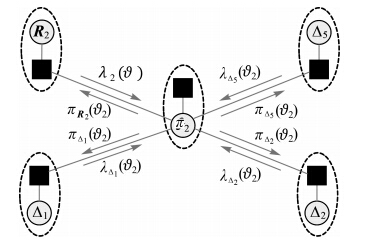| 图 6 置信传播中的消息传递Fig. 6 Messages sent in belief propagation |
节点vi向其任意一个父节点a∈a(vi)传递的消息为
vi向其任意一个子节点d∈d(vi)传递的消息为
式中，a(x)＼{a}表示集合a(x)中除a外的元素；d(x)＼{d}表示集合d(x)中除d外的元素；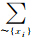
f(x1,x2,…，xn)代表函数f的第i个变量取xi时的边缘概率[23]，如
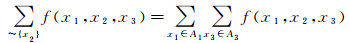
置信网络中没有有向环，但却可能包含无向环，如图 5中的ν1-Δ1-ν2-Δ2-ν1，消息可能在环路中无限传播。环路置信传播算法(loopy belief propagation,LBP)可以很好地解决这个问题[23—24]。LBP算法的主要思想是让消息在置信网络中迭代传播，直到获得稳定的置信度。在第t次迭代中，计算所有子节点向节点vi传送的消息
所有父节点向vi传送的消息
第t次迭代中x的置信度为
式中，
代表置信度的归一化参数。在第t+1次迭代中，任意节点vi向其父节点a发送的消息为
向其子节点d发送的消息为
置信网络中的消息是并行传播的，每一次迭代中节点vi发出的消息都基于上次迭代中其向所有邻域接收的消息，如果所有节点在连续两次迭代中的置信度差值都小于一个阈值，则称置信网的消息收敛，即取使节点vi置信度最大的标签值x*作为该节点变量的值。环路置信传播在绝大多数情况下都能达到收敛，不收敛时经过多次迭代之后能提供一个很好的近似[24]。
4 试验结果
本文对多组影像集进行了试验，这里选取其中的5组，图 7(a)—(e)分别为公寓、平房、天坛、Kapel、Providence影像集中的部分影像，其中公寓和平房影像集为定焦拍摄，Kapel影像集为牛津大学提供的公开测试数据，Providence影像集为美国Providence部分地区无人机影像测试数据。
 |
| 图 7 影像集Fig. 7 Image sets |
试验中首先利用SIFT特征匹配算法对影像集中所有的像对进行匹配，将匹配点对数量不少于16的像对列为相关影像，将所有的相关影像相连构建原始的影像关系图G，如图 8(a)—(e)的左一图。对任意两张相关影像(i,j)，在RANSAC引擎中利用五点算法计算像对的本质矩阵(包括旋转矩阵Rij和位移向量tij)，以影像宽或高中较大值(单位为像素)的0.5%作为内点的阈值，取内点最多的一组样本为最佳样本，如果其中内点数量少于16或者内点率小于50%(内点数量少于初始匹配点数的一半)，则认为像对不相关。在G中将所有RANSAC检测出的不相关像对的对应边剔除，构成新的影像关系图G′，如图 8(a)—(e)的左二图。然后利用本文的检测算法对G′中的相对方位关系进行检测。最后剔除G′中检测出的误判相对方位关系并对影像集进行三维场景重建，并将重建结果与部分现有的重建算法进行对比，以检验本文算法的有效性。
 |
| 图 8 相对方位关系检测中的影像关系图Fig. 8 Image relation graphs in detection of relative orientation relations |
试验中将置信网络中所有消息都初始化为1，由于理论上环路置信传播算法并不能保证收敛，本文试验中将迭代次数设置为100，迭代的置信度限差的阈值设置为10-6，如果连续两次迭代中置信度之差小于阈值便停止迭代。为了提高检测的可靠性，本文在试验中使用迭代检测方法，每次迭代中首先利用LBP算法检测误判边，然后在影像关系图中将误判边剔除，接下来在新获得的影像关系图中再次利用LBP算法进行检测，直到获得稳定的影像关系图为止。
本文的5组试验中都在2次LBP迭代内便获得了稳定的影像关系图。图 8(a)—(e)左二图中的红色部分代表第一次LBP检测出的误判边，图 8(a)—(e)左三图是剔除第一次LBP检测误判边之后新的影像关系图，其中蓝色部分为第二次LBP检测出的误判边，图 8(a)—(e)左四图是利用文献[14]中算法检测误判边后得到的最终影像关系图。
图 9(a)—(e)中的左图为增量法[1]得到的重建结果，增量法[1]没有使用误判边检测(本文中误判边指满足局部一致性，但不满足全局一致性的边)，中图为利用本文算法剔除误判边后的重建结果，右图为文献[14]算法得到的重建结果，这3种算法中都使用了RANSAC检测。从试验结果可以看出，误判的相对方位关系对重建结果产生了很大的影响。增量法[1]中公寓、平房、Kapel和Providence的重建结果都发生了明显的漂移现象，天坛影像集重建结果虽然没有明显的漂移，但有部分场景无法得到重建，原因是重建过程中每张影像的射影矩阵是在RANSAC引擎下计算的，部分误判的边能通过检测，从而得到错误的空间结构，如公寓、平房、Kapel和Providence影像集(特别是Providence影像集，其中只有少量的误判边，但对重建结果却产生了很大的影响)，但当这些通过RANSAC检测的误判边处于影像集中的弱连接处时，即使少量计算错误的空间点坐标也可能会导致新加入的影像无法通过RANSAC检测，从而大量的影像将会被排除，如天坛影像集，实际参与重建的仅仅有48张影像。文献[14]算法对部分影像集的重建结果相比增量法[1]有较大改进(如公寓、天坛和Providence影像集)，其中Providence影像集与本文的检测和重建结果几乎一致(差异可能源于计算过程中部分阈值的设定不同)，但公寓和平房影像集发生了漂移(图 9(a)和(b)的右图)，天坛和Kapel影像集只有部分场景完成重建(图 9(c)和(d)的右图，原因是其对应的影像关系图被分割成了若干个不联通的子图，如图 8(c)和(d)的左四图，而重建结果基于其中的最大联通子图)。本文算法则更加稳健，从图 9中也可以看出利用本文算法能够得到更可靠的重建结果。
 |
| 图 9 剔除误判边前后的重建结果Fig. 9 Reconstruction results without and with rejecting of false positive edges |
表 1对5组试验的结果进行了统计。
| 影像集 | 数量 | 初始边 | RANSAC检测后的边数 | 初始回路 | LBP(1) | LBP(2) | ||||
| 迭代次数 | 误判边 | 时间/s | 迭代次数 | 误判边 | 时间/s | |||||
| 公寓 | 56 | 910 | 202 | 445 | 2 | 83 | 0.09 | 2 | 2 | 0.05 |
| 平房 | 161 | 3010 | 913 | 2564 | 6 | 36 | 1.12 | 4 | 4 | 0.38 |
| 天坛 | 347 | 6710 | 2177 | 6218 | 14 | 234 | 3.30 | 5 | 80 | 0.45 |
| Kapel | 77 | 1331 | 237 | 515 | 2 | 10 | 0.33 | 2 | 1 | 0.10 |
| Providence | 103 | 1851 | 479 | 1265 | 2 | 6 | 0.59 | 0 | 0 | 0 |
通过以上试验可以发现，场景中的重复纹理可能会导致误判的相对方位关系，造成场景重建失败。增量法[1]由于没有进行误判相对方位关系检测，最容易产生错误的重建结果。文献[14]算法受影像关系图结构的影响较大，当影像集的空间关系较为简单时，该算法能有效检测出部分误判相对方位关系，改善重建结果，但算法不够稳健，当影像关系图的最大生成树中存在误判边时可能会给出错误的检测结果，从而导致重建结果发生漂移。从图 9中可以看出利用本文算法剔除误判边之后的重建结果得到明显改善，这也证明了本文算法的有效性。从表 1中也可以看出，一般情况下环路置信传播算法经过较少的迭代便能达到收敛，同时由于变量的标签空间很小(ν的取值为0或者1)，本文算法具有较高的计算效率。
5 结束语
本文利用全局一致性约束来检测影像间的相对方位关系，除了利用文献[14]中的最大生成树构建回路之外，还加入了三元视图组回路约束，极大地降低了影像关系图的结构对检测结果的影响，可以有效避免由于纹理重复或场景模糊而造成的误匹配，进而改善场景三维重建的效果。目前，直接利用影像信息来重建场景的应用需求越来越广泛，而大量场景中都存在重复纹理(特别是人工建筑物)，因此本文提出的算法在相关领域将具有较好的应用前景。
| [1] | SNAVELY N, SEITZ S M, SZELISKI R. Modeling the World from Internet Photo Collections[J]. International Journal of Computer Vision, 2008, 80(2): 189-210. |
| [2] | SNAVELY N, SEITZ S M, SZELISKI R. Skeletal Graphs for Efficient Structure from Motion[C]//IEEE Conference on Computer Vision and Pattern Recognition. Anchorage, AK: IEEE,2008:1-8. |
| [3] | AGARWAL S, FURUKAWA Y, SNAVELY N, et al. Building Rome in a Day[J]. Communications of the ACM, 2011, 54(10): 105-112. |
| [4] | KAHL F. Multiple View Geometry and the L∞-norm[C]//Tenth IEEE International Conference on Computer Vision. Beijing: IEEE, 2005, 2: 1002-1009. |
| [5] | SINHA S N, STEEDLY D, SZELISKI R. A Multi-stage Linear Approach to Structure from Motion[M]//KUTULAKOS K N ed. Trends and Topics in Computer Vision. Berlin:Springer, 2012: 267-281. |
| [6] | ARIE-NACHIMSON M, KOVALSKY S Z, KEMELMACHER-SHLIZERMAN I, et al. Global Motion Estimation from Point Matches[C]//2012 Second International Conference on 3D Imaging, Modeling, Processing, Visualization and Transmission (3DIMPVT). Zurich: IEEE, 2012: 81-88. |
| [7] | MOULON P, MONASSE P, MARLET R. Global Fusion of Relative Motions for Robust, Accurate and Scalable Structure from Motion[C]//2013 IEEE International Conference on Computer Vision (ICCV). Sydney, NSW:IEEE, 2013: 3248-3255. |
| [8] | MARTINEC D, PAJDLA T. Robust Rotation and Translation Estimation in Multiview Reconstruction[C]//IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis, MN:IEEE, 2007: 1-8. |
| [9] | WANG Jingxue, ZHU Qing, WANG Weixi. A Dense Matching Algorithm of Multi-view Image Based on the Integrated Multiple Matching Primitives [J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 691-698. (王竞雪, 朱庆, 王伟玺. 多匹配基元集成的多视影像密集匹配方法[J]. 测绘学报, 2013, 42(5): 691-698.) |
| [10] | YUAN Xiuxiao, MING Yang. A Novel Method of Multi-image Matching Using Image and Space Synthesis Information [J].Acta Geodaetica et Cartographica Sinica, 2009, 38(3): 216-222. (袁修孝, 明洋. 一种综合利用像方和物方信息的多影像匹配方法[J]. 测绘学报, 2009, 38(3): 216-222.) |
| [11] | JIA Fengman, KANG Zhizhong, YU Peng. A SIFT and Bayes Sampling Consensus Method for Image Matching [J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 877-883. (贾丰蔓, 康志忠, 于鹏. 影像同名点匹配的 SIFT 算法与贝叶斯抽样一致性检验[J]. 测绘学报, 2013, 42(6): 877-883.) |
| [12] | GOVINDU V M. Robustness in Motion Averaging[M]// NARAYANAN P J, NAYAR S K, SHUM H Y.Computer Vision:ACCV 2006. Berlin:Springer, 2006: 457-466. |
| [13] | OLSSON C, ENQVIST O. Stable Structure from Motion for Unordered Image Collections[M]//HEYDEN A, KAHL F.Image Analysis. Berlin:Springer, 2011: 524-535. |
| [14] | ENQVIST O, KAHL F, OLSSON C. Non-sequential Structure from Motion[C]//2011 IEEE International Conference on Computer Vision Workshops (ICCV Workshops). Barcelona:IEEE, 2011: 264-271. |
| [15] | LOWE D G. Distinctive Image Features from Scale-invariant Key Points[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. |
| [16] | NISTÉR D.An Efficient Solution to the Five-point Relative Pose Problem[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(6): 756-770. |
| [17] | KRUSKAL J B. On the Shortest Spanning Subtree of A Graph and the Traveling Salesman Problem[J]. Proceedings of the American Mathematical Society, 1956, 7(1): 48-50. |
| [18] | ZACH C, KLOPSCHITZ M, POLLEFEYS M. Disambiguating Visual Relations Using Loop Constraints[C]//2010 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). San Francisco, CA:IEEE, 2010: 1426-1433. |
| [19] | PEARL J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference[M]. San Francisco:Morgan Kaufmann, 1988. |
| [20] | MACKAY D J C, NEAL R M. Good Codes Based on Very Sparse Matrices[M]//BOYD C ed. Cryptography and Coding. Berlin:Springer, 1995: 100-111. |
| [21] | KSCHISCHANG F R, FREY B J. Iterative Decoding of Compound Codes by Probability Propagation in Graphical Models[J]. IEEE Journal on Selected Areas in Communications, 1998, 16(2): 219-230. |
| [22] | MCELIECE R J, MACKAY D J C, CHENG J F. Turbo Decoding as an Instance of Pearl's “Belief Propagation” Algorithm[J]. IEEE Journal on Selected Areas in Communications, 1998, 16(2): 140-152. |
| [23] | KSCHISCHANG F R, FREY B J, LOELIGER H A. Factor Graphs and the Sum-product Algorithm[J]. IEEE Transactions on Information Theory, 2001, 47(2): 498-519. |
| [24] | MURPHY K P, WEISS Y, JORDAN M I. Loopy Belief Propagation for Approximate Inference: An Empirical Study[C]//Proceedings of the Fifteenth Conference on Uncertainty in Artificial Intelligence. San Francisco:Morgan Kaufmann Publishers Inc., 1999: 467-475. |