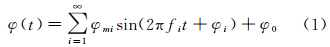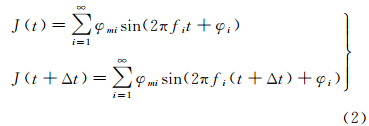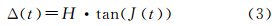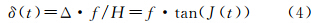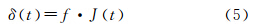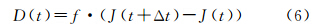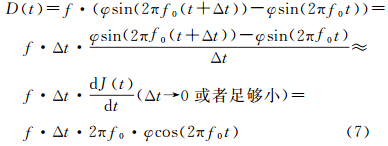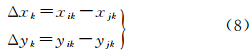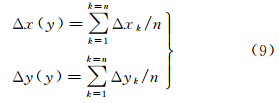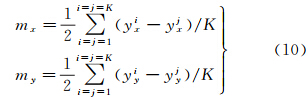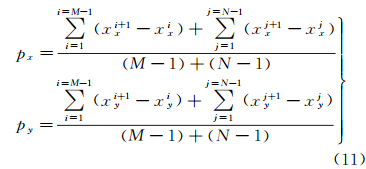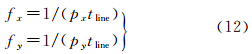2. 国家测绘地理信息局卫星测绘应用中心,北京 100830
2. Satellite Surveying and Mapping Application Center, National Administration of Surveying and Mapping and Geoinformation, Beijing 100830, China
1 引 言
卫星平台震颤,又称卫星微振动,是指卫星在轨运行期间,星上运动部件周期性运动或因变轨冷热交变等因素引发的扰动,使星体产生一种幅值较小、频率较高的颤振响应[1]。平台震颤具有微小性、固有性、难控性和敏感性等特点[2]。随着遥感卫星空间分辨率的提高,卫星平台震颤对成像质量的影响越来越受到卫星总体设计、相机设计以及地面处理与应用部门的重视。早在2001年,日本国家空间发展署(National Space Development Agency,NASDA)利用试验卫星 ETS-VI 进行了卫星振动测量试验,卫星平台角振动在 0.39 Hz 到 250 Hz范围内的径向均方根为 16.3×10-6 rad(约3.36″),其中 83.6%的振动能量集中在 0.39~10 Hz 之间,99%以上的能量在 102 Hz 以下[3]。哈尔滨工业大学通过理论分析和仿真试验研究了平台运动对星载时间延时积分(time delay integration,TDI) CCD成像质量的影响,研究结果表明平台振动会引起不同程度的图像模糊和几何变形[4]。卫星平台震颤对几何预处理中的内检校、外检校以及几何产品的生产均有不同程度的影响[5, 6, 7]。
对于卫星平台震颤,一方面需要通过动力学方法采取隔振和抑振措施,另外一方面需通过直接或者间接的方式进行平台震颤测量。考虑到平台震颤不可避免且难以控制,对平台震颤的精确测量才能保证高分辨率遥感影像的高质量、高精度处理。卫星平台震颤直接测量是利用测量频率和测量精度均较高的角度传感器进行测量,获取平台角位移、角速度和角加速度等信息。常用的角度传感器有磁流体效应(magneto-hydro-dynamics,MHD)角速度传感器和流体旋转差动感应(fluid-rotor differential induction,FDI)角位移传感器,测量精度优于0.2″,测量频率高达上千赫兹,在国外在轨卫星中已有应用[8],但目前国内暂无在轨卫星搭载这类姿态测量载荷。平台震颤间接测量是利用非姿态测量装置对平台震颤进行检测与估计。基于遥感影像的卫星平台震颤检测是进行平台震颤分析的思路之一。法国国家空间研究中心(Centre National d’Etudes Spatiales,CNES)提出基于立体像对的卫星平台微振动探测方法,分别对翻滚、俯仰和偏航3个方向的平台震颤进行识别和移除[9]。日本东京大学也发表了利用遥感影像进行卫星震颤检测和补偿的研究成果[10]。国内利用遥感影像分析卫星平台震颤的研究仍十分落后。
资源三号卫星发射于2012年1月10日,是我国首颗民用立体测图卫星。自卫星发射以来,其几何精度一直备受关注,众多学者对资源三号影像的在轨定标以及各类产品精度等展开了大量研究,验证资源三号满足测图及其他应用要求的可行性[11, 12, 13, 14, 15, 16]。本文利用资源三号多光谱影像高空间分辨率、高成像频率和内视场平行排列成像的特点,开展了利用多光谱影像检测卫星平台震颤的方法研究。首先对资源三号多光谱相机焦平面设计和成像特点分析了影响配准误差的因素,然后论述平台震颤对配准误差的影响规律,提出利用高精度影像匹配技术进行平台震颤检测的方法,最后利用不同波段组合和不同时间数据进行检测试验,初步发现资源三号卫星在轨初期存在周期性运动规律。
2 资源三号多光谱相机成像几何特点 2.1 多光谱成像设计
资源三号卫星搭载的多光谱相机采用多色TDI CCD器件的推扫式成像系统[11, 17, 18],由于TDI CCD器件的物理特性使得每个波段之间均存在一定的物理间隔,同一时刻各波段对应不同的摄影点,如图 1所示。
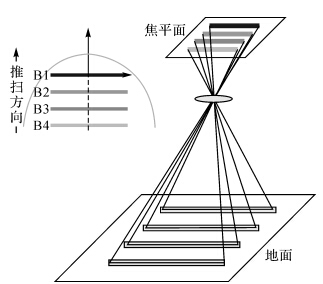 |
| 图 1 资源三号多光谱相机成像示意图Fig. 1 Multi-spectral camera imaging design |
资源三号卫星多光谱相机包含蓝、绿、红以及近红外4个波段,依次记为B1、B2、B3、B4。在相机焦平面上,4个波段线阵CCD在沿轨方向依次平行摆放,相邻CCD间距约2×10-3 m。每一扫描行成像时间约为8×10-4 s(每秒成像约1250行),在姿态平稳的情况下,4个波段将间隔Δt约0.121 6 s依次对相同地物成像(图 2)。
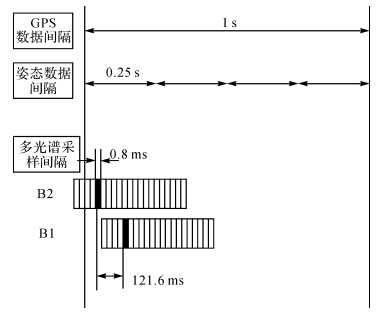 |
| 图 2 GPS数据、姿态数据与多光谱成像采样时间示意图Fig. 2 Sampling timetable of GPS,attitude data and multi-spectral imagery |
这意味着若卫星在成像间隔内存在平台震颤且震颤周期不等于Δt、nΔt或者1/nΔt(n为大于1的整数),不同波段影像会出现随平台震颤变化的配准误差,反之,对配准误差进行分析即可检测平台震颤。而资源三号卫星提供的姿态数据测量精度5″、采样频率4 Hz,从测量精度和频率上,都无法对微小的或者较高频率的平台震颤进行精确测量。因此,多光谱影像高空间分辨率、高成像频率、多波段小间隔平行成像的特点,使得利用多光谱影像检测平台震颤的方法具有可行性,补偿了姿态测量精度和频率的不足。
2.2 多光谱影像配准误差源分析
多光谱影像波段配准误差是指多光谱影像不同波段间同名像点的坐标差,包括垂直轨道方向的配准误差和沿轨道方向的配准误差。根据推扫式影像严密几何成像方程可知[19, 20],影响多光谱影像波段间配准误差的因素主要包括3个方面:平台运动状态、相机设计以及地球自转。
平台运动状态包括平台位置状态和姿态。卫星飞行轨迹一般较为平滑,对成像的影响较小,可忽略不计,但由于卫星飞行轨道高,姿态稳定度对成像的影响较大[7],轨道高度500 km的卫星,1″姿态偏差将会导致对应地面指向误差达到2 m。因此对于资源三号多光谱影像,影响配准误差的平台状态主要是姿态。姿态控制误差包含姿态指向误差和平台震颤[21]。姿态指向误差体现实际姿态与理想姿态偏差的平均值;平台震颤体现实际姿态的波动情况。
多光谱相机CCD平行排列在焦平面成像的设计使得多光谱不同波段CCD对相同地物根据其排列依次成像,是引起多光谱多波段影像间沿轨方向配准误差的主要来源。通常在卫星发射、运行稳定后,CCD之间的间隔为常定值,由此引起的配准误差较为稳定,通过在轨定标可以精确确定[13, 14, 15, 16, 17, 18, 19, 20, 21, 22]。
在不同波段成像前后成像时间间隔内,地球自转将引起垂直于轨道方向的配准误差,且时间间隔越大,配准误差越大。通常为了克服地球自转引起的成像问题,卫星控制系统会对卫星进行持续偏流角改正,以消除或者减小地球自转的影响。
通过分析可知,观测平台、成像载荷以及观测目标的特性共同决定了多光谱影像波段配准误差,但相机内方位元素属于静态因素,地球自转可以理解为偏流角控制误差,二者都可视为线性误差;而平台的震颤运动则是唯一具有时序特性的动态因素,可通过波段配准误差时序特征分析实现卫星平台的震颤检测。
3 利用多光谱影像配准误差检测平台震颤原理与方法 3.1 利用多光谱影像检测卫星平台震颤原理
多光谱影像检测卫星平台震颤的基本思想是利用平台震颤引起不同波段成像差异(即配准误差)特性进行卫星震颤运动的分析与反演。平台震颤对成像的影响主要体现在绕卫星三轴的姿态抖动,包括侧滚角抖动、俯仰角抖动以及偏流角抖动对多波段成像的差异,引起沿飞行方向的配准误差和垂直于轨道方向配准误差。卫星的姿态抖动通常是一种周期性运动或者是由多个周期和频率与姿态指向误差叠加的运动[23]
式中,φ(t)表示姿态控制系统输出的姿态角;t为卫星飞行的时间;φ0为姿态指向误差;fi、φmi和φi分别为姿态抖动第i个谐波分量的频率、幅度和初始相位。
对于多光谱影像,假设t时刻第1波段成像,那么在t+Δt时刻第2波段成像,二者受到的姿态震颤如式(2)所示
姿态角的变化直接影响卫星成像载荷的对地成像的变化,由式(2)可知,若Δt不是卫星震颤周期倍数,两个波段影像受到震颤的影响是不一样的,在经历相同时间间隔,对地成像的距离也随之变化。根据几何定位原理,在星下点成像时,姿态角对几何定位影响可用式(3)计算
对应到图像上则有
式中,H为卫星高度;f为多光谱相机焦距。当震颤角度很小时,可以近似为
那么经历Δt时间后,两个波段由于平台震颤的相对位置误差,即引起的配准误差为
考虑简单的平台震颤,仅为单一周期运动,J(t)=φsin(2πf0t),多光谱之间的成像时间间隔Δt比较短,则有
由式(7)推导可知,当Δt足够小时,平台震颤引起的配准误差是平台震颤微分量的函数,也将满足周期性变化规律,振动频率与平台震颤频率一致,振幅为平台姿态振幅的f·Δt·2πf0倍。为此,根据式(3)仿真了两个波段在不同成像时间间隔情况下,平台震颤对其定位误差的影响以及相对定位(配准误差)的影响。取平台震颤振幅φ=1″,f0=1 Hz,分别取Δt=0.2 s、0.1 s、0.01 s、0.001 s,令H为500 km,共仿真了2.5 s,50个样本(图 3)。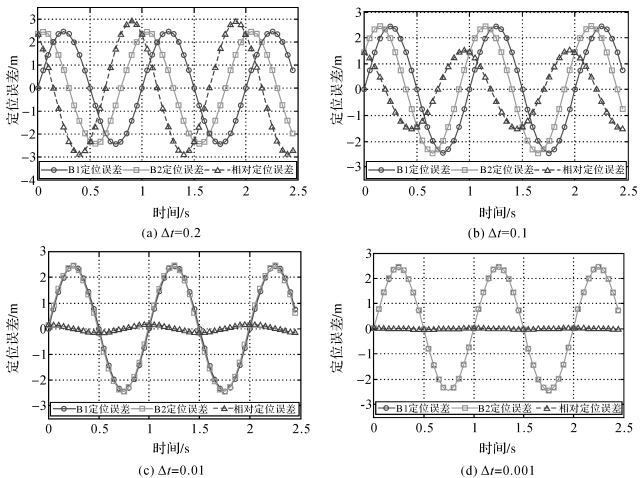 |
| 图 3 平台震颤配准误差仿真Fig. 3 Simulation of registration error caused by jitter |
仿真结果表明,在平台周期性震颤作用下,波段间配准误差也呈现周期性变化,且频率与平台震颤频率一致,而配准误差幅值随着波段间成像时间间隔的增大而增大。由此可见,可以通过检测不同波段间的配准误差频率来获取平台震颤的频率。
3.2 利用多光谱影像检测卫星平台震颤流程
由式(1)可知,在空间上,平台震颤大小是一个随时间变化的函数。为了检测平台是否存在震颤,需要得到波段配准误差随成像时间的变化规律。由2.1节可知,资源三号多光谱相机为线阵推扫式成像,成像频率可达1250行。那么对每一扫描行的配准误差进行分析,则可获得每一扫描行成像时刻对应的平台震颤情况。为了准确获取每一行的配准误差,需要在两个波段影像上的每一扫描行获取足够数据量的样本点,从而对每一成像时刻的配准误差进行有效估计,对成像序列的配准误差进行时序分析,得到配准误差随成像时间的变化规律。为此本文提出基于高精度密集点匹配的平台震颤检测方法,具体方法流程如下:
(1) 数据准备。对原始多光谱影像进行辐射校正、CCD拼接等预处理得到未配准多光谱影像。
(2) 波段选择。选取一组最优组合的两个波段,减小匹配误差对检测结果的影响。
(3) 高精度密集匹配。逐点或者以一定间隔选取样本点,保证样本点分布均匀、数量充足,然后利用影像相关匹配和最小二乘匹配[24]逐步得到子像素精度的同名像点坐标,并对匹配粗差点进行剔除。
(4) 逐行分析。对匹配的结果逐点计算配准误差
式中,Δxk、Δyk分别为沿CCD方向和沿轨道方向的配准误差;(xik,yik)、(xjk,yjk)分别为第k个同名像点在第i、j两个段影像上的坐标。
考虑到多光谱相机视场角较小,假定在同一成像时间内每一行受到的平台震颤影响具有一致性,若每一扫描行最终匹配出n个点,统计配准误差平均值,作为每一行配准误差的最优估值,即
(5) 震颤分析。通过逐行分析得到配准误差随成像行的变化,即得到了配准误差随成像时间的变化规律。震颤分析主要是对平台震颤引起的配准误差变化周期(频率)、振幅等周期性特征进行分析。
4 试验与分析
为全面分析平台震颤的规律,首先对资源三号多光谱影像不同波段组合的检测结果进行对比,然后分析不同成像日期和成像地区的卫星平台震颤情况。
4.1 不同波段组合平台震颤检测试验
试验数据为资源三号河南登封地区多光谱原始影像,影像大小8824像素×9715像素,成像日期为2012年2月3日。为了选取最优波段组合,采用本文提出的方法对多光谱影像4个波段进行6种组合试验,分析检测结果的异同。为了保证检查点的均匀分布,对每一扫描行每隔15个像素进行匹配运算,将相关系数达到0.9的同名点作为检查点;由于采用的数据是未配准的多光谱影像,将沿轨方向的配准误差减去CCD间隔设计值,并统计两两波段间匹配得到的总点数、行平均点数、配准误差的平均值、最大值和最小值如表 1所示,配准误差曲线图如图 4所示。
| 波段 | 检查点总数 | 行平均点数 | 平均值/像素 | 最大值/像素 | 最小值/像素 | |||
| 垂轨 | 沿轨 | 垂轨 | 沿轨 | 垂轨 | 沿轨 | |||
| B1-B2 | 2 156 866 | 228 | -0.372 | 0.172 | 0.144 | 0.539 | -0.919 | -0.073 |
| B2-B3 | 3 190 078 | 339 | -0.313 | 0.081 | 0.094 | 0.236 | -0.904 | -0.083 |
| B3-B4 | 1 686 299 | 181 | -0.307 | 0.083 | 0.149 | 0.342 | -0.813 | -0.243 |
| B1-B3 | 1 863 204 | 198 | -0.650 | 0.387 | 0.290 | 0.977 | -1.565 | -0.112 |
| B2-B4 | 951 943 | 102 | -0.589 | 0.257 | 0.338 | 0.843 | -1.411 | -0.219 |
| B1-B4 | 611 058 | 65 | -0.951 | 0.443 | 0.519 | 1.149 | -2.068 | -0.251 |
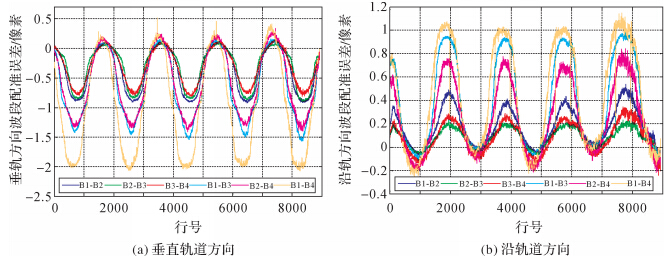 |
| 图 4 波段间配准误差曲线Fig. 4 Registration error curve |
从图 4和表 1可以明显看出,资源三号多光谱影像沿轨方向和垂轨方向配准误差均随成像行呈现十分规律的周期性变化,且不同波段间配准误差变化周期基本一致,振幅不同,相邻波段振幅小,非相邻波段振幅大。这与3.1节中的仿真结果一致,说明资源三号卫星在该成像时段存在平台震颤。另外,多光谱影像配准误差除了周期性变化外,还存在平移量,且每一组平移值也存在差异。根据2.2节中的分析可知,沿轨方向的平移值为两个CCD之间的CCD间隔误差引起的配准误差,垂轨方向的配准误差为偏流角控制未完全改正地球自转引起的配准误差。受二者影响最小的为B2-B3组合和B3-B4组合。另外,匹配误差也会影响到检测结果的精度,从表 1匹配点数可以得知,在相同匹配条件下,B2与B3的匹配点数最多,匹配精度最高。因此第2波段和第3波段为资源三号平台检测最优波段组合。 4.2 不同时间成像数据平台震颤检测试验
选取3组不同时间成像多光谱数据对第2波段和第3波段影像的配准误差进行时序分析,试验数据基本信息如表 2所示。
| 序号 | 成像日期 | 飞行轨道号 | 成像地区 | 中心经/纬度 | 数据大小/像素 | 成像阶段行积分时间/ms |
| 1 | 2012-01-24 | 229 | 河南洛阳 | 112.510°E/34.619°N | 8824×9715 | 808.6 |
| 2 | 2012-02-03 | 381 | 河南平顶山 | 112.993°E/33.857°N | 8824×9715 | 803.0 |
| 3 | 2012-02-13 | 542 | 广东化州 | 110.563°E/21.542°N | 8824×9715 | 804.2 |
采用4.1节中相同的方法对第2波段和第3波段影像进行试验,检测得到3组数据的误差曲线如图 5所示。
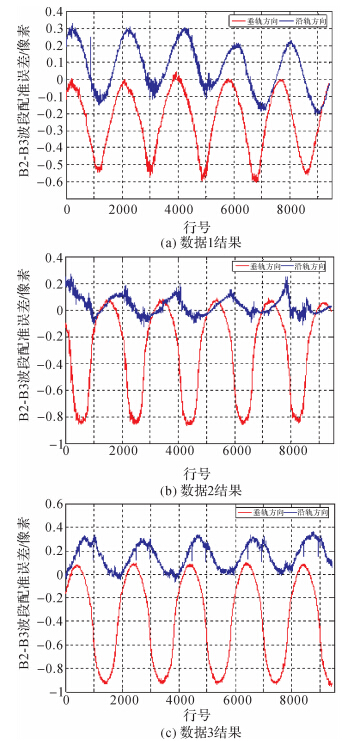 |
| 图 5 B2-B3波段间配准误差曲线Fig. 5 Registration error curve between B2-B3 |
设曲线中有M个波峰和N个波谷,以行号为x轴,配准误差为y轴,在误差曲线中测量垂轨方向波段配准误差曲线中波峰点坐标(xix,yix)和波谷点坐标(xjx,yjx),同时测量沿轨方向波段配准误差曲线中波峰点坐标(xiy,yiy)和波谷点坐标(xjy,yjy),其中i、 j为波峰和波谷的编号(i=1,2,…,M; j=1,2,…,N)。将多个周期的波峰波谷配准误差的相对误差平均值的一半作为振幅的估计值,如式(10)所示
式中,mx、my分别为垂轨和沿轨方向振幅;K为M、N中较小者。
同时,利用波峰和波谷横坐标分别可得到垂轨和沿轨方向波段配准误差曲线的周期px、py
若成像阶段每行的积分时间为tline(单位:s),则可得到对应配准误差的频率
利用式(10)—(12)对3组数据的振幅、周期、频率进行统计,如表 3所示。
| 数据序列号 | 幅值/像素 | 周期/行 | 成像阶段行积分时间/s | 频率/Hz | |||
| 垂轨 | 沿轨 | 垂轨 | 沿轨 | 垂轨 | 沿轨 | ||
| 1 | 0.30 | 0.20 | 1875 | 1950 | 0.000 808 6 | 0.659 6 | 0.634 2 |
| 2 | 0.45 | 0.10 | 1950 | 2000 | 0.000 803 0 | 0.638 6 | 0.622 7 |
| 3 | 0.50 | 0.15 | 2000 | 2000 | 0.000 804 2 | 0.621 7 | 0.621 7 |
从试验结果可以看出,3组不同成像时间和不同地区的数据检测出来的配准误差在频率上具有很强的一致性,基本保持在0.6 Hz的量级,且垂轨方向配准误差幅值大于沿轨方向。结合3.1节中分析可知,资源三号在该段成像时期内出现了0.6 Hz的平台震颤,垂轨方向震颤幅度大于沿轨方向。进一步从试验结果中可以看出,虽然卫星震颤在短时间内具有基本相同的震颤频率,但在不同成像时段卫星震颤的幅度略有不同,引起的波段间配准误差在垂轨方向约0.3~0.5像素(相对地面1.73~2.9 m),沿轨方向约0.1~0.2像素(相对地面0.58~1.16 m)。对于资源三号卫星,这种微小的波段间相对变形对目视判读的影响并不大,但随着空间分辨率的提高,若卫星存在同等振幅的震颤,那么引起的影像变形将变得明显。
5 结 论
本文从多色TDI CCD器件多光谱影像波段配准误差分析的角度对资源三号卫星平台的震颤进行了检测。文中介绍了资源三号多光谱相机的成像特点和多光谱影像配准误差源,分析了卫星平台震颤对配准误差的影响规律,提出了基于高精度密集点匹配的平台震颤检测方法和流程,并利用多波段、不同时间成像数据进行组合试验,结果表明资源三号卫星在试验数据成像阶段存在约0.6 Hz的平台震颤,且垂轨方向震颤幅度大于沿轨方向,引起波段间周期性配准误差。该方法也适用于其他搭载多色TDI CCD器件的卫星震颤分析。在下一步的研究中将分析资源三号卫星震颤时序特性和震颤源,并应用检测结果补偿卫星震颤引起的误差,进一步提高资源三号影像几何处理精度。
| [1] | JIANG Guowei, ZHOU Xubin, SHEN Junfeng et al. Study and Application of Micro-vibration Virtual Simulation of Satellite[J]. Computer Measurement & Control, 2011, 19(9): 2206-2209. (蒋国伟, 周徐斌, 申军烽, 等. 卫星微振动虚拟仿真技术研究及应用[J]. 计算机测量与控制, 2011, 19(9): 2206-2209.) |
| [2] | PANG Shiwei, YANG Lei, QU Guangji. New Development of Micro-vibration Integrated Modeling and Assessment Technology for High Performance Spacecraft[J]. Structure & Environment Engineering, 2007, 34(6): 1-9. (庞世伟, 杨雷, 曲广吉. 高精度航天器微振动建模与评估技术最近进展[J]. 强度与环境, 2007, 34(6): 1-9.) |
| [3] | TOYOSHIMA M, ARAKI K. In-orbit Measurements of Short Term Attitude and Vibrational Environment on the Engineering Test Satellite VI Using Laser Communication Equipment[J]. Optical Engineering, 2001, 40(5): 827-832. |
| [4] | ZHUANG Xuxia. The Effect Analysis and Simulation of Platform Motion on Image Quality of Spaceborne TDICCD Camera[D]. Harbin: Harbin Institute of Technology, 2011. ( 庄绪霞. 平台运动对星载TDICCD相机成像质量影响分析与仿真[D]. 哈尔滨: 哈尔滨工程大学, 2011.) |
| [5] | ZHANG L, GRUEN A. Multi-image Matching for DSM Generation from IKONOS Imagery[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 60(3): 195-211. |
| [6] | SULTAN K, GRUEN A. Orientation and Self-calibration of ALOS PRISM Imagery[J]. The Photogrammetric Record, 2008, 23(123): 323-340. |
| [7] | LIU Bin. Space-ground Integated Attitude Determination of High-resolution Satellite and Geometric Image Processing under Jitter Conditions[D]. Wuhan: Wuhan University, 2011. (刘斌. 高分辨光学卫星空地一体化定姿及姿态抖动下影像几何处理方法研究[D]. 武汉: 武汉大学,2011). |
| [8] | HUO Hongqing, MA Mianjun, LI Yunpeng, et al. High Precision Measurement Technology of Satellite's Angle Microvibration[J]. Transducer and Microsystem Technologies, 2011, 30(3): 4-6, 9. ( 霍红庆, 马勉军, 李云鹏, 等. 卫星微角颤振高精度测量技术[J]. 传感器与微系统, 2011, 30(3): 4-6, 9.) |
| [9] | ROQUES S, JAHAN L, ROUGÉ B, et al. Satellite Attitude Instability Effects on Stereo Images[C]//IEEE International Conference on Acoustics, Speech, and Signal Processing. Montreal, Que: IEEE, 2004, 3: 1520-6149. |
| [10] | IWASAKI A. Detection and Estimation of Satellite Attitude Jitter Using Remote Sensing Imagery[M]//HALL J ed. Advances in Spacecraft Technologies. Rijeka, Croatia: InTech, 2010: 257-272. |
| [11] | LI Deren. China's First Civilian Three-line-array Stereo Mapping Satellite: ZY-3[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 317-322. (李德仁. 我国第一颗民用三线阵立体测图卫星:资源三号测绘卫星[J]. 测绘学报, 2012, 41(3): 317-322.) |
| [12] | WANG Mi, YANG Bo, JIN Shuying. A Registration Method Based on Object-space Positioning Consistency for Satellite Multi-spectral Image[J]. Geomatics and Information Science of Wuhan University, 2013, 38(7): 765-769. (王密, 杨博, 金淑英. 一种利用物方定位一致性的多光谱卫星影像自动精确配准方法[J]. 武汉大学学报: 信息科学版, 2013, 38(7): 765-769.) |
| [13] | LI Deren, WANG Mi. On-orbit Geometric Calibration and Accuracy Assessment of ZY-3[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(3): 1-6. (李德仁, 王密. “资源三号”卫星在轨几何定标及精度评估[J]. 航天返回与遥感, 2012, 33(3): 1-6.) |
| [14] | JIANG Yonghua, ZHANG Guo, TANG Xinmin, et al. High Accuracy Geometric Calibration of ZY-3 Three-line Image[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 523-529, 553. (蒋永华, 张过, 唐新明, 等. 资源三号测绘卫星三线阵影像高精度几何检校[J]. 测绘学报, 2013, 42(4): 523-529, 553.) |
| [15] | D'ANGELO P. Evaluation of ZY-3 for DSM and Ortho Image Generation[C]//HEIPKE C, JACOBSEN K., ROTTENSTEINER F, SORGEL U eds. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume XL-1/W1. Germany: Hannover, 2013: 57-61. |
| [16] | WANG M, YANG B, HU F, et al. On-orbit Geometric Calibration Model and Its Applications for High-resolution Optical Satellite Imagery[J]. Remote Sensing, 2014, 6(5): 4391-4408. |
| [17] | CRESDA. Introduction to ZY-3[EB/OL].[2012-07-25]. http://www.cresda.com/n16/n1130/n175290/175676.html. (资源卫星应用中心. 资源三号卫星介绍[EB/OL].[2012-07-25]. http://www.cresda.com/n16/n1130/n175290/175676.html.) |
| [18] | FAN Bincai, WEI Jun, ZHANG Xiaohong et al. Technology of the Multi-spectral Camera of ZY-3 Satellite[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(3): 75-84. ( 范斌蔡, 伟军, 张孝弘, 等. “资源三号”卫星多光谱相机技术[J]. 航天返回与遥感, 2012, 33(3): 75-84.) |
| [19] | GAEL Consultant. SPOT 123-4-5 Geometry Handbook Issue 1Revision 4[DB/OL][2012-01-01]. http://www-igm.univ-mlv.fr/-riazano/publications/GAEL-P135-DOC-001-01-04.pdf. |
| [20] | POLI D. A Rigorous Model for Spaceborne Linear Array Sensors[J]. Photogrammetric Engineering & Remote Sensing, 2007, 73(2): 187-196. |
| [21] | NEECK S P, VENATOR T J, BOLEK J T. Jitter and Stability Calculation for the ASTER Instrument[C]//Proceedings of SPIE 2317, Platforms and Systems. Rome, Italy:[s.n.], 1995: 70-81. |
| [22] | MULAWA D. On-orbit Geometric Calibration of the OrbView-3 High Resolution Imaging Satellite[J]. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2004, 35(B1): 410. |
| [23] | CHEN Jie, ZHOU Yinqing, LI Chunsheng, et al. Relationship between Satellite Attitude Jitter and SAR Imaging Quality[J]. Journal of Beijing University of Aeronautics and Astronautics, 2001, 27(5): 518-521. (陈杰, 周荫清, 李春升, 等. 卫星姿态指向抖动与SAR 成像质量关系研究[J]. 北京航空航天大学学报, 2001, 27(5): 518-521.) |
| [24] | GRUEN A. Development and Status of Image Matching in Photogrammetry[J]. The Photogrammetric Record, 2012, 27(137): 36-57. |