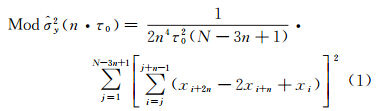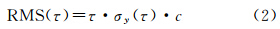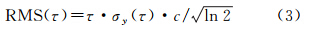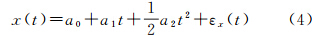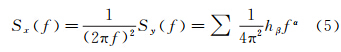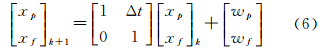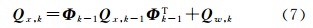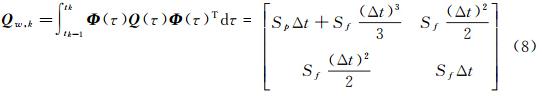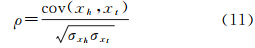近年来,精密单点定位(precise point positioning,PPP)技术的快速发展使其成为获取高精度测站坐标的一种重要技术手段,已被广泛应用于地球动力学、电离层和对流层延迟估计等诸多地学研究。但是,受卫星定位几何条件的限制,GNSS精密定位获得的测站高程精度明显次于平面位置精度(1.5~2倍)。因此,在利用GNSS跟踪站的观测资料计算地壳垂直运动量时,一些微弱的地学信号往往被淹没在测站坐标时间系列的噪声中而无法准确提取[1, 2]。造成GNSS定位高程精度偏低的主要原因是地球遮挡影响,接收机捕获的卫星信号仅来自地平线以上的可视卫星,这种几何上非对称性的观测条件使得接收机钟差、天顶对流层延迟以及测站高程参数之间存在显著的数学相关性(瞬时相关性高达80%~90%),这种强相关性使得高程方向的定位精度偏低[3, 4]。尽管引入低高度角卫星的观测数据能够在一定程度上削弱接收机钟差、测站高程以及天顶对流层延迟三者之间的相关性,但是由于低高度角卫星受到的系统误差(大气残余误差、多路径效应)和观测噪声(低信噪比)明显较大,反而可能降低水平分量的定位精度。解决这一问题的一种有效途径是引入外部约束信息。假设能够使用一些高频稳度的接收机钟,如原子钟或超稳石英钟,充分利用其短期频稳的约束条件,对接收机钟差进行建模与预报,则有望显著减少接收机钟差参数个数,降低上述3种参数的相关性,从而更加准确地分离(估计)出测站高程与天顶对流层延迟。
长期以来,国内外学者对时钟性能评估与钟差建模方面的研究主要是针对卫星端高性能的原子钟,并取得了丰硕的研究成果[5, 6, 7, 8, 9, 10]。针对地面或星载GNSS接收机端的钟差建模及其应用研究相对较少,尚处于起步阶段。近年来,随着IGS跟踪站网硬件设备的不断升级,目前已有超过130个跟踪站(接收机端)配置了高准确度和高频稳度的氢原子钟、铷原子钟或铯原子钟[11];此外,一些科学试验卫星如GRACE重力卫星上也搭载了超稳振荡器[12],其短期(1~1000 s)频稳度高达1×10-13~3×10-13(文献[13])。这些高稳定度的接收机钟使得地面或星载接收机钟差建模成为可能。
因此,本文在分析评价当前IGS跟踪站的几类原子钟性能的基础上,拟重点研究并分析钟差建模方法在精密单点定位中的应用。本文第2节将利用Allan方差法简要评估现有IGS几类原子钟的稳定性能,第3节给出了本文钟差建模的二次多项式模型,第4节重点讨论了钟差建模在精密度单点定位中的应用及效果。
2 接收机原子钟的性能评估钟差性能(频稳度)评估是接收机钟差建模与预报的前提,目前常用的GNSS接收机钟类型有石英钟、铷原子钟、铯原子钟、氢原子钟等[14],但并非所有类型的接收机钟都适合建模,特别是对于一些频稳度较差的石英钟,即便采用复杂的钟差模型也难以准确描述时钟的运行特性。此外,温度变化、空间环境(地面和星载)差异等因素也会对接收机钟的稳定性造成影响。表 1给出了当前IGS跟踪站原子钟配置统计[15],图 1为3类原子钟的全球分布图。
| 氢原子钟个数 | 铯原子钟个数 | 铷原子钟个数 |
| 69 | 43 | 24 |
Allan方差(或标准差)是目前最常用的时域频率稳定性分析方法[16],它不仅可以用于计算接收机钟的稳定度,还可用于识别接收机钟的噪声类型、计算噪声水平系数。为了克服传统的Allan方差无法识别调相白噪声和调相闪烁噪声这一缺陷[17],本文采用修正Allan方差来表征接收机钟的时域稳定度[18],其计算公式为
式中,N为钟差采样数;τ为钟差取样(平滑)间隔;xi为历元i对应的钟差值;n为钟差平滑因子,一般取为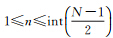 。
。噪声类型识别方面,通过修正Allan方差双对数图的斜率来区分噪声过程,相应给出了振荡器噪声的修正Allan方差在双对数图上的表现形式,如图 2所示。从图中可以得到,调相白噪声(WPM)和调相闪烁噪声(FPM)的斜率是-1,调频白噪声(WFM)的斜率是-0.5,调频闪烁噪声(FFM)的斜率是0,调频随机游走噪声(RWFM)的斜率是0.5。
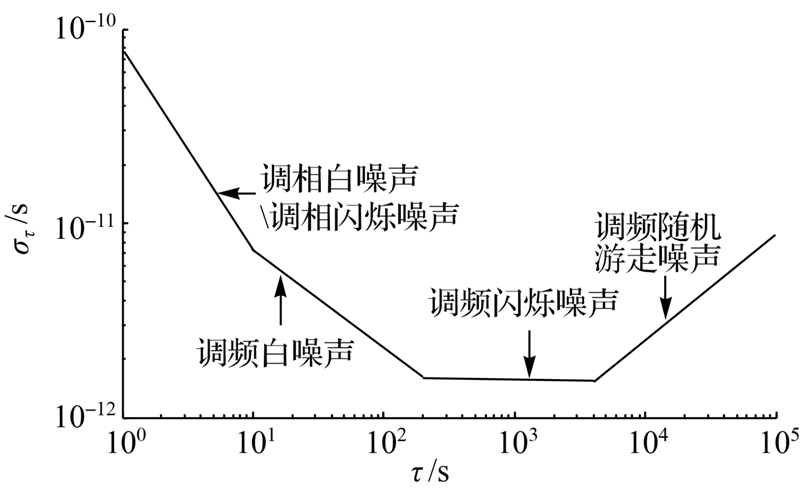 |
| 图 2 振荡器噪声类型的修正Allan方差 Fig. 2 The modified Allan variance of oscillator noise |
为了分析接收机钟的稳定性,首先采用精密单点定位获得了部分IGS跟踪站30 s 间隔的接收机钟差,然后对接收机钟差序列采用修正Allan方差计算得到部分IGS跟踪站接收机钟(H:氢原子钟; Cs:铯原子钟;Rb:铷原子钟;QUARTZ:石英钟)的半日稳定度。如图 3所示,其中横轴代表时间间隔;纵轴代表对应的Allan标准方差数值(数值越小,稳定度越高);两条黑色虚线(GPS code clock,GPS phase clock)分别代表无电离层组合伪距和载波相位观测值的等效噪声下界[19]。
从图 3中可以看出,当采样间隔在30~2000 s左右时,4款接收机钟的噪声类型主要表现为调频白噪声,当采样间隔取至2000 s甚至更长时,调频闪烁噪声占主导地位。通过比较4种类型的接收机钟差在双对数图的纵坐标值,可以明显地看出氢原子钟的稳定度比铯原子钟要好,铯原子钟比铷原子钟的稳定度高,石英钟的稳定度最差。分析图 3中无电离层组合伪距和载波相位观测值的噪声下界不难发现,石英钟的频稳度较差,即使在非常短的时间内也无法满足载波相位水平的钟差建模要求(即模型预报误差大于观测噪声);铯原子钟具有较好的短期稳定度,但是当平滑间隔在超过300 s时,其预报误差也将超出载波相位观测值的噪声水平;而氢原子钟的稳定度最高,可以满足1~2 h以内的钟差建模精度要求。
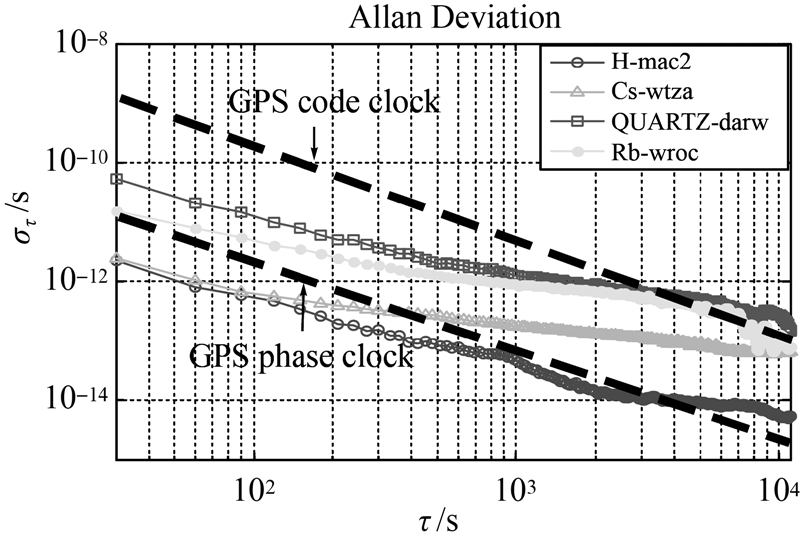 |
| 图 3 4款接收机钟差的修正Allan方差 Fig. 3 The modified Allan variance of four types of receiver clock offset |
根据Allan方差原理,钟差随机项中不同噪声分量引起的模型预报误差RMSx(τ)存在所示的对应关系,见表 2[16]。给定预报误差的阈值RMSmax,利用表 2中的模型预报误差计算公式(RMSx(τ)≤RMSmax),即可以确定钟差建模(模型参数)的有效时长。以图 3中氢原子钟差建模为例,设定预报误差的阈值RMSmax为0.006 m,平滑间隔2000 s以内的噪声类型表现为调频白噪声,其预报误差的计算公式为
式中,RMS(τ)为预报误差;τ为预报的时间间隔;σy(τ)为平滑间隔为τ时的修正Allan标准差;c为光速。| 噪声类型 | 预报误差 |
| WPM | τ·σy(τ)/√ 3 |
| FPM | τ·σy(τ)/ln τ/√ ln 2 |
| WFM | τ·σy(τ) |
| FFM | τ·σy(τ)/√ ln 2 |
| RWFM | τ·σy(τ) |
当τ取最大值2000 s时,由图 3知σy(τ)为10-14,根据式(2)计算得到的预报误差为0.006 m,满足RMS(τ)≤RMSmax的条件,可以在30~2000 s内任取采样间隔进行钟差建模。当采样间隔超过2000 s时,调频闪烁噪声占主导地位,调频闪烁噪声的预报误差计算公式为
由图 3知,采样间隔为2000~8000 s以内的σy(τ)基本在10-14左右,根据式(3)算得的τ为1665 s。综合以上分析,得到跟踪站mac2钟差建模的有效时长取为2000 s。
3 接收机钟差模型接收机钟差可以用确定性变化分量和随机性变化分量来描述[8],即
式中,右边前3项为钟的确定性时间分量;a0、a1和a2依次代表接收机的钟差、钟速与钟漂;εx(t)为接收机钟差的随机变化分量。接收机钟差的系统性变化部分(确定性分量)可采用线性方程或二阶多项式等确定性函数模型来表达[20],而其随机性变化分量只能从统计意义上来分析,其统计特性由噪声幂律谱模型(式5)确定[21]。瞬时时间偏差x(t)的功率谱密度可表示为
式中,fα(α=-4,-3,-2,-1,0)代表5种噪声类型的傅氏频率;hβ(β=-2,-1,0,1,2)为噪声强度系数[22]。对于给定的原子钟,随着取样时间的变化将表现出不同的随机噪声分量,但在较短的时间内,一般只有1~2种噪声起主导作用。 4 钟差建模在精密单点中的应用 4.1 附有钟差约束的精密单点定位方法在传统的精密单点定位[23]中,采用Kalman滤波作为参数估计器,一般将接收机钟差视作独立的白噪声(过程噪声非常大),忽视了钟差参数之间可能存在的短期相关性。因此,本文采用钟差-钟速二维状态模型描述接收机钟的动态过程[24],其状态一步预测方程可表示为
式中,xp和xf分别代表接收机钟差、钟速;Δt为历元间隔;wp和wf为状态的过程噪声。根据误差传播定律[25],得到状态一步预测的协因数矩阵Qx,k为
式中,Φ为状态转移矩阵;Qw,k为系统过程噪声,取决于钟的稳定度,可根据Allan方差或谱密度系数确定[26] 式中,Sp、Sf分别代表引起时差和频差的噪声谱振幅。采用Kalman滤波算法即可获得所有历元的递推解,为了确保所有历元滤波解的精度和可靠性,本文采用双向平滑滤波算法[27]对其结果进行优化。设前向滤波和后向滤波的解分别为Xk,f、Xk,b,对应的估值协因数矩阵为Qk,f、Qk,b,则平滑滤波的估值Qk及其协因数矩阵Xk为
4.2 试验结果与分析利用2010年4月18日WTRZ跟踪站(配备氢原子钟)的观测数据(30 s采样率)和CODE分析中心提供的精密星历和精密钟差产品,依次采用以下两种方案进行动态PPP解算:
方案1:采用传统的逐历元估计一维钟差参数的方法,过程噪声设置为3×105;
方案2:采用本文的钟差建模方法估计钟差-钟速二维状态[28],过程噪声由谱密度系数(本文根据氢原子钟的特性设置了h0=1×10-24;h-1=4×10-29)确定。
基于上述两种方案获得的测站高程分量偏差、接收机钟差参数以及测站高程分量与接收机钟差参数之间的相关系数时序,如图 4—6所示。利用PPP逐历元解算的方差协方差阵中的相关数据,计算得到各个历元的相关系数ρ
式中,cov(xh,xt)代表高程分量与接收机钟差参数的协方差;σxh代表高程分量的方差;Qσxt代表接收机钟差参数的方差。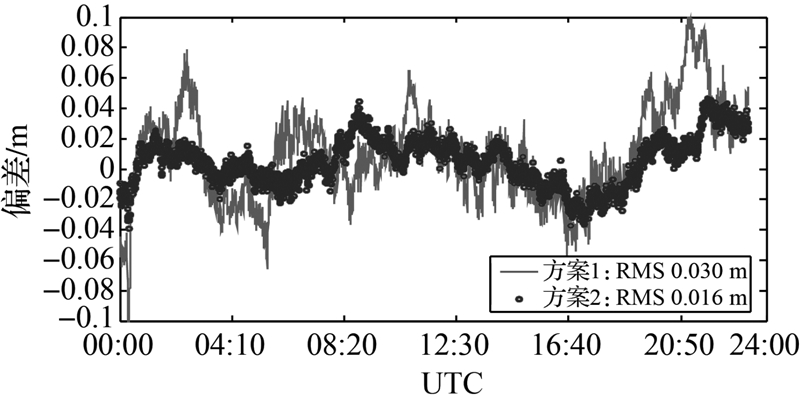 |
| 图 4 两种方案解算的高程方向偏差 (WTRZ) Fig. 4 Time series of height errors (WTRZ) |
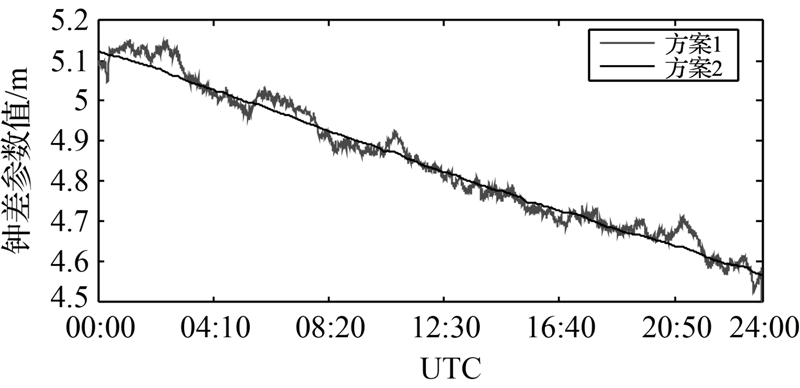 |
| 图 5 两种方案解算的接收机钟差参数 (WTRZ) Fig. 5 Time series of receiver clock errors (WTRZ) |
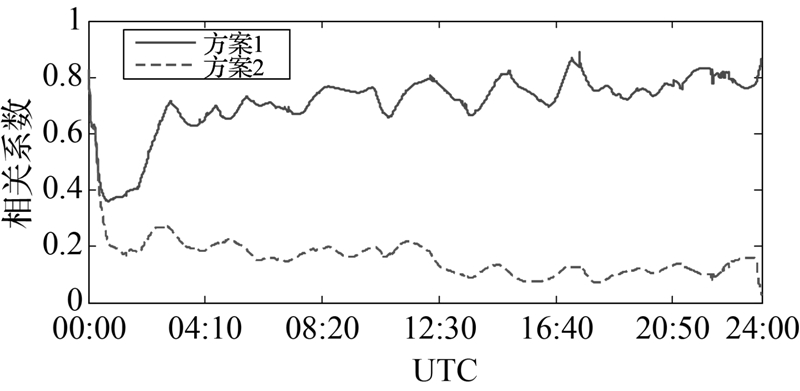 |
| 图 6 高程分量与接收机钟差参数的相关系数时序 (WTRZ)Fig. 6 Correlation coefficients between height component and receiver clock offset (WTRZ) |
类似的,根据2010年4月18日WAB2跟踪站(配备氢原子钟)的观测数据(30 s采样率)和CODE分析中心提供的精密星历和精密钟差产品采用上述两种方案进行动态PPP解算,得到测站的高程分量偏差、高程分量与接收机钟差参数之间相关系数如图 7和图 8所示。
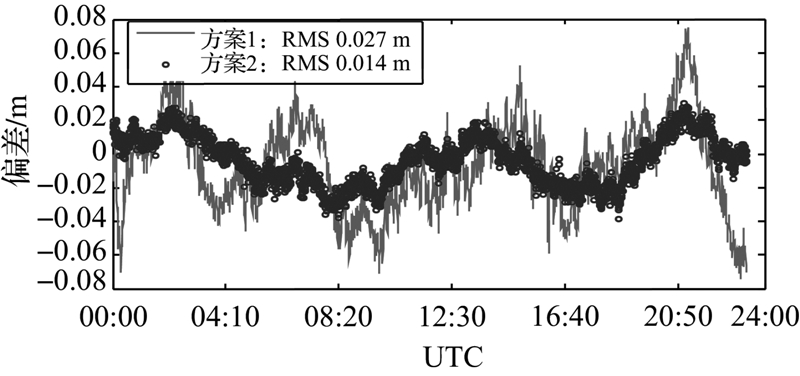 |
| 图 7 两种方案解算的高程方向偏差 (WAB2) Fig. 7 Time series of height errors (WAB2) |
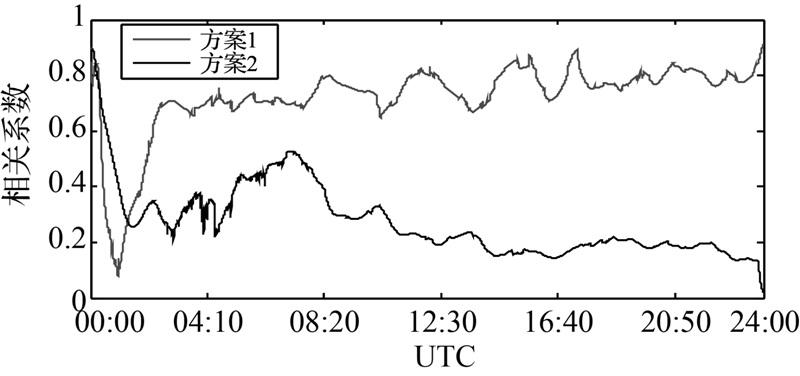 |
| 图 8 高程分量与接收机钟差参数的相关系数时序 (WAB2)Fig. 8 Correlation coefficient between height component and receiver clock offset (WAB2) |
本文采用正反向平滑滤波算法(后处理),而不是单向滤波处理,即后处理PPP正反向平滑滤波算法消除了PPP单向滤波的收敛过程。分析上述结果不难发现,采用将接收机钟差视为白噪声的钟差逐历元估计方案,由其得到的测站高程分量、天顶对流层延迟与接收机钟差参数之间存在显著的相关性(特别是测站高程分量与接收机钟差参数之间的相关性高达80%~90%),由此导致动态PPP高程方向的定位精度偏低,且波动较大,这就使得一些微弱的地学信号往往被淹没在测站坐标时间系列的噪声中而无法准确拾取。方案二则充分利用了接收机钟差参数之间的短期稳定性,通过钟差建模在一定程度上削弱了测站高程分量、天顶对流层延迟与接收机钟差参数之间数学相关性,进而改善了动态PPP高程方向的定位精度,相应的RMS提高了50%左右。
此外,本文还对比分析了上述两种方案估计的天顶对流层延迟精度。利用2010年4月18日AMC2、TWTF、WAB2、WDC3、WTZR 5个测站(配备氢原子钟)的GPS观测数据进行动态PPP解算获得了各观测站的天顶对流层延迟参数(ZPD),并与IGS分析中心提供的ZPD参考值进行比较,统计两种方案解算的天顶对流层延迟参数的外符合精度,见表 3。结果表明,基于接收机钟差建模的精密单点定位对各测站的ZPD参数估计均有不同程度的改善,尤其是WTZR和TWTF站的ZPD精度提高了近20%。
| 测站名 | 方案1 RMS/m | 方案2 RMS/m | 精度提高程度/(%) |
| AMC2 | 5.802 | 5.408 | 6.79 |
| TWTF | 5.034 | 3.885 | 22.8 |
| WAB2 | 5.743 | 5.396 | 6.04 |
| WDC3 | 3.974 | 3.837 | 3.45 |
| WTZR | 3.577 | 2.982 | 16.6 |
对比前文高程分量的改善程度,接收机钟差建模的方法对ZPD参数估值精度的改善幅度不及测站高程分量。这主要是因为ZPD参数与接收机钟差参数之间的相关性次于测站高程分量与接收机钟差参数之间的相关性。图 9给出了接收机钟差参数与测站高程分量、ZPD参数的相关系数,虚线代表接收机钟差参数与测站高程分量之间的相关系数,实线代表接收机钟差参数与ZPD参数之间的相关系数,4条黑色虚线是判断相关性强弱程度的临界,接收机钟差参数与ZPD参数的相关系数的绝对值基本维持在0.3~0.5之间;接收机钟差参数与测站高程分量之间的相关系数的绝对值却大于0.5。
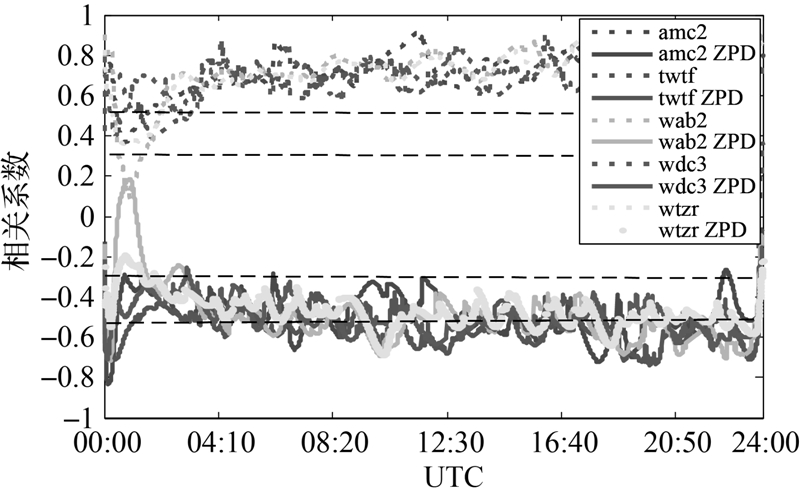 |
| 图 9 接收机钟差参数与测站高程分量、ZPD参数的相关系数结果Fig. 9 Correlation coefficients among the receiver clock offset,height coordinate and zenith path delay |
针对当前许多IGS跟踪站均配置有高性能原子钟的这一现状,本文首先采用修正Allan方差评估了不同类型接收机钟的短期频稳度及钟差建模的可行性,结果表明,不同类型接收机钟的稳定性有所差异,在给定模型预报误差限值条件下(预报误差小于观测噪声水平),铯原子钟仅能满足较短时间(数分钟)内的建模精度要求,氢原子钟具有良好的短期稳定度,能够满足1~2 h内的钟差建模精度要求。实例说明本文方法能有效改善动态PPP高程方向的定位精度,对天顶对流层延迟参数的估计也有一定改善。
| [1] | CRYER J D, CHAN K S. Time Series Analysis:with Applications in R[M].2nd ed.Berlin:Springer, 2008. |
| [2] | GU Guohua. Recent Progress in Researches on Crustal Movement through GNSS(GPS) Observations[J]. Recent Developments in World Seismology, 2007, 343(7): 9-15.(顾国华. GNSS(GPS)观测研究地壳运动的新进展[J]. 国际地震动态,2007(7): 9-15.) |
| [3] | ROTHACHER M,BEUTLER G. The Role of GPS in the Study of Global Change [J]. Physics and Chemistry of the Earth, 1998, 23(9): 1029-1040. |
| [4] | DACH R, BEUTLER G, HUGENTOBLER U. Time Transfer Using GPS Carrier Phase: Error Propagation and Results[J].Journal of Geodesy, 2003,77(1):1-14. |
| [5] | HESSELBARTH A,WANNINGER L. Short-term Stability of GNSS Satellite Clocks and Its Effects on Precise Point Positioning [C]//Proceedings of ION GNSS 2008. Savannah,GA:[s.n.]:1885-1863. |
| [6] | HUANG Guanwen, ZHANG Qin,WANG Jigang. Research on Estimation and Prediction of GPS Satellite Clock Error [J]. Journal of Geodesy and Geodynamics, 2009, 29(6): 118-122.(黄观文,张勤,王继刚. GPS卫星钟差的估计与预报研究[J]. 大地测量与地球动力学,2009, 29(6): 118-122.) |
| [7] | GUO Hairong, YANG Yuaxi, HE Haibo, et al. Determination of Covariance Matrix of Kalman Filter Used for Time Prediction of Atomic Clocks of Navigation Satellites [J]. Acta Geodaetica et Cartographica Sinica, 2010,39(2):147-149.(郭海荣,杨元喜,何海波,等. 导航卫星原子钟Kalman滤波中噪声方差-协方差的确定[J].测绘学报,2010,39(2):147-149.) |
| [8] | DELPORTE J, BOULANGER C, MERCIER F. Short-term Stability of GNSS On-board Clocks Using the Polynomial Method [C]//European Frequency and Time Forum (EFTF).[S.l.]:IEEE,2012, 117-121. |
| [9] | GONG Hang, YANG Wenke, LIU Zengjun,et al. Estimation Method of BDS On-board Clock Short-term Stability Combining Satellite Two-way with One-way Carrier Ranging [J]. Journal of National University of Defense Technology, 2013, 35(3): 158-163.(龚航,杨文可,刘增军,等. 卫星双向与单向载波联合的北斗星载钟短稳评估方法[J]. 国防科技大学学报,2013, 35(3): 158-163.) |
| [10] | HAUSCHILD A, MONTENBRUCK O,STEIGENBERGER P. Short-term Analysis of GNSS Clocks[J]. GPS Solutions, 2013,17(3): 295-307. |
| [11] | WANG K, ROTHACHER M. Stochastic Modeling of High-stability Ground Clocks in GPS Analysis [J]. Journal of Geodesy, 2013, 87(5): 427-437. |
| [12] | DUNN C, BERTIGER W, BAR-SEVER Y, et al. Application Challenge-instrument of Grace-GPS Augments Gravity Measurements: Twin Satellites Trail Each Other in Earth Orbit. As They Pass over Contours in the Gravity Field, They First[J]. GPS World, 2003, 14(2): 16-29. |
| [13] | WEINBACH U, SCHON S. GNSS Receiver Clock Modeling when Using High-precision Oscillators and Its Impact on PPP [J]. Advances in Space Research, 2011, 47(2): 229-238. |
| [14] | ALLAN D W. Statistics of Atomic Frequency Standards [J]. Proceedings of the IEEE,1966,54(2):221-230. |
| [15] | CLKLOG. A Summary File of the Deployment History for GPS Receiver, Antenna, Frequency Standards, and Other Equipment at IGS Stations[EB/OL].2010-01-20[2014-05-30]ftp://igsws.unavco.org/igscb/station/general/loghist.txt. |
| [16] | ALLAN D W. Time and Frequency (Time-domain) Characterization,Estimation, and Prediction of Precision Clocks and Oscillators [J]. IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control, 1987, 34(6): 647-654. |
| [17] | ALLAN D W, WEISS M A. A Frequency-domain View of Time-domain Characterization of Clocks and Time and Frequency Distribution Systems [C]//Proceedings of the 45th Annual Symposium on Frequency Control:667-678. |
| [18] | ALLAN D W, HOWE D A,WALLS F L.Characterization of Clocks and Oscillators[M].Gaithersburg:US Department of Commerce,National Institute of Standards and Technology,1990. |
| [19] | WEINBACH U, SCHÖN S. Improved GRACE Kinematic Orbit Determination Using GPS Receiver Clock Modeling [J]. GPS Solutions, 2013,17(4): 511-520. |
| [20] | GUO Hairong. Research on Theory and Method about Time-frequency Characteristic of Atomic Clocks of Navigation Satellites [D].Zhengzhou:Information Engineering University,2006:30-33.(郭海荣.导航卫星原子钟时频特性分析理论与方法研究[D]. 郑州:解放军信息工程大学,2006:30-33.) |
| [21] | BROWN R G, HWANG P Y. Introduction to Random Signals and Applied Kalman Filtering:with MATLAB Exercise and Solutions [J]. Wiley Global Education, 2012(1):1-10. |
| [22] | BARNES J A, CHI A R, CUTLER L S,et al. Characterization of Frequency Stability [J]. IEEE Transactions on Instrumentation and Measurement, 1971, 1001(2): 105-120. |
| [23] | KOUBA J. A Guide to Using International GNSS Service (IGS)Products [J].International GNSS,2009,13(8):1-10. |
| [24] | STRANG G, BORRE K. Linear Algebra, Geodesy, and GPS [M]. Siam:Wellesley-Cambridge Press, 1997. |
| [25] | ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks [J]. Journal of Geophysical Research,1997,102(B3): 5005-5017. |
| [26] | HERRING T A, DAVIS J L, SHAPIRO I I. Geodesy by Radio Interferometry: The Application of Kalman Filtering to the Analysis of Very Long Baseline Interferometry Data [J]. Journal of Geophysical Research, 1990, 95(B8): 12561-12581. |
| [27] | GELB A. Applied Optimal Estimation [M]. Cambridge:MIT Press,1974. |
| [28] | SEEBER G. Satellite Geodesy:Foundations,Methods and Applications[M].2nd ed. New York:Walter de Gruyter, 2003. |