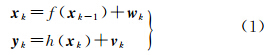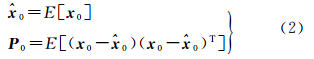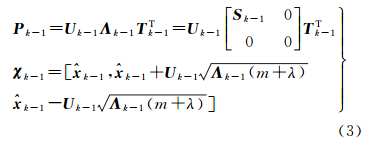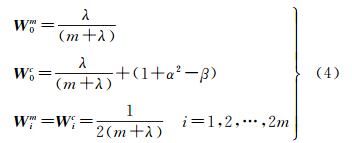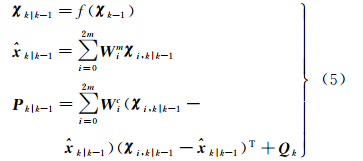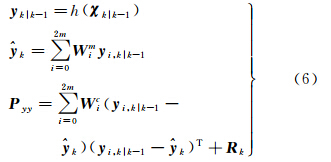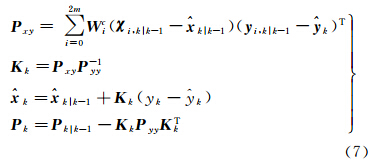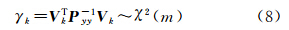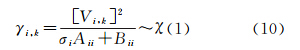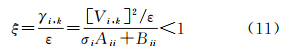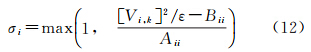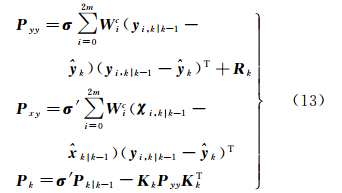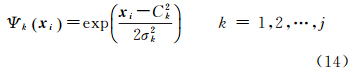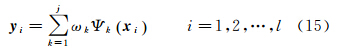2. 中国矿业大学环境与测绘学院,江苏 徐州 221116
2. Environment and Spatial Informatics, China University of Mining and Technology, Xuzhou 221116, China
由于难以得到GPS/INS组合系统中目标状态后验概率密度函数的完整描述,为实现最优非线性滤波,常采用次优近似的估计方法[1, 2, 3, 4, 5]。扩展卡尔曼滤波(extended Kalman filter,EKF)是一种函数近似法。其基本思想是围绕状态估值对非线性模型进行一阶Taylor展开,再结合经典的卡尔曼滤波进行估计,算法简单易实现[6, 7, 8]。但线性化引起的高阶项截断误差会降低滤波器的精度,且需要计算非线性函数的雅克比矩阵。不敏卡尔曼滤波(unscented Kalman filter,UKF)和粒子滤波(particle filter,PF)属于基于采样的近似估计算法。其中PF会随机产生大量粒子,计算量庞大、实时性较差[9]。UKF采用确定的样本点,通过样本点逼近状态向量后验概率密度函数的均值和协方差,避免了由线性化导致的跟踪误差,滤波解精度较高,实时性优于前者[10, 11]。
GPS/INS组合导航非线性系统中,系统噪声相关信息的不确定性以及状态模型扰动异常等都会影响UKF滤波解的精度。为此,文献[12]提出采用预测残差向量协方差矩阵构造最优自适应因子算法;文献[13,14]采用方差膨胀的原则将自适应因子引入卡尔曼滤波;文献[15]基于部分状态不符值来构造自适应因子,降低状态异常的权值。但每一个状态的异常程度不同,单一的自适应因子不能精确地修正所有状态异常。文献[16]采用整体异常检验判断是否存在异常,利用支持向量回归算法预测次优观测值辅助自适应滤波算法。文献[17]基于假设检验构造多重渐消卡尔曼滤波。文献[18]提出多重衰减因子自适应估计卡尔曼滤波方法,对系统每个误差状态估计进行控制,提高滤波器的估计性能。文献[19, 20]基于相关观测值的双因子抗差估计理论提出多因子自适应估计算法。文献[21]利用开窗法计算新息序列协方差的无偏估计获得渐消因子矩阵,对不同的滤波通道提供不同的渐消速率。文献[22]利用卡尔曼滤波取得最佳增益时残差序列互不相关,在线自适应地调整多个渐消因子,提高滤波性能。
以上多渐消因子自适应滤波大都基于假设检验和数理统计,其理论前提是残差向量符合高斯白噪声的数字特征分布。而实际导航中,残差向量常受到粗差或系统误差影响失去其高斯白噪声的数字特征分布。基于此,本文在标准UKF算法的基础上,结合径向基神经网络(radial basis function neural network,RBFNN)算法、多重渐消因子(multiple fading factors,MF)和奇异值分解(singular value decomposition,SVD),提出一种基于神经网络辅助的多重渐消因子自适应SVD-UKF算法。
2 基于多重渐消因子的GPS/INS组合系统自适应SVD-UKF算法以北东地(north-east-down,NED)为导航坐标系,取GPS/INS组合导航系统状态参数15维,分别为位置、速度、姿态误差以及陀螺仪和加速度计分别在三轴上的漂移。根据INS误差方程,结合GPS和INS在导航系下的位置和速度差,构造GPS/INS组合系统的状态方程和观测方程[23]
式中,xk和xk-1分别为k和k-1时刻的状态向量;yk为观测向量;f(·)为状态模型;h(·)为观测模型;wk为系统噪声向量;vk观测噪声向量;wk、vk为高斯白噪声且对应方差分别为Qk、Rk。则SVD-UKF算法计算步骤如下。 2.1 SVD-UKF算法 2.1.1 状态参数初始化2.1.2 计算Sigma点
Sigma点采样策略是UKF算法的关键,要求其在抓住输入变量x的分布特征的同时,又能使逼近输出性能指标的代价函数达到最小。受观测条件和模型扰动影响,当方差矩阵失去对称正定性时,传统UT变换中的Cholesky分解算法无法对Sigma点进行取样,导致程序中断,稳定性差,而SVD算法则可解决上述难点,性能优于前者。为抑制方差矩阵负定性变化,采用基于SVD分解的对称采样策略,即对于均值为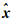 k-1,方差为Pk-1∈Rm×m的m维随机变量xk-1,产生的2m+1个列向量χk-1(Sigma点)为
式中,Sk-1=diag(s1,s2,…,sr),s1≥s2≥…≥sr≥0,s1、s2、…、sr为矩阵Pk-1的奇异值;r为Pk-1的秩;Uk-1、Tk-1的列向量分别为Pk-1的左右奇异向量;χk-1∈Rm×(2m+1)为Sigma点;m为状态参数个数;λ=α2(m+k)-m为尺度因子;κ为常数,设置为0或3-m;α为Sigma点到
k-1,方差为Pk-1∈Rm×m的m维随机变量xk-1,产生的2m+1个列向量χk-1(Sigma点)为
式中,Sk-1=diag(s1,s2,…,sr),s1≥s2≥…≥sr≥0,s1、s2、…、sr为矩阵Pk-1的奇异值;r为Pk-1的秩;Uk-1、Tk-1的列向量分别为Pk-1的左右奇异向量;χk-1∈Rm×(2m+1)为Sigma点;m为状态参数个数;λ=α2(m+k)-m为尺度因子;κ为常数,设置为0或3-m;α为Sigma点到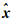 k-1的距离,一般取10-4≤α≤1。各个Sigma点权值为
式中,Wim、Wic分别为均值和方差的权值;β用于融于随机变量的先验信息,对于高斯分布取β=2。
k-1的距离,一般取10-4≤α≤1。各个Sigma点权值为
式中,Wim、Wic分别为均值和方差的权值;β用于融于随机变量的先验信息,对于高斯分布取β=2。
式中,
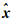 k|k-1为预测状态值;Pk|k-1为预测状态向量协方差矩阵。
2.1.4 测量更新
k|k-1为预测状态值;Pk|k-1为预测状态向量协方差矩阵。
2.1.4 测量更新式中,
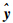 k为预测观测值;Pyy为预测观测向量协方差矩阵。
2.1.5 滤波更新
k为预测观测值;Pyy为预测观测向量协方差矩阵。
2.1.5 滤波更新式中,Kk为增益矩阵;
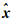 k为估计状态;Pk为估计状态协方差矩阵。
2.2 多重渐消因子
k为估计状态;Pk为估计状态协方差矩阵。
2.2 多重渐消因子
根据式(1)和式(6),预测残差向量为Vk=Yk-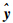 k,在滤波器稳定状态条件下Vk~N(0,Pyy),因此有
k,在滤波器稳定状态条件下Vk~N(0,Pyy),因此有
若判决函数被拒绝,则认为滤波器存在异常,采用多重渐消因子σi控制残差向量中的异常值。令Vi,k为残差向量Vk中的第i个元素,Aii为矩阵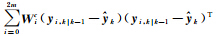 对角线中第i个元素,Bii为矩阵Rk对角线中第i个元素,此时根据式(6)和式(8)有
对角线中第i个元素,Bii为矩阵Rk对角线中第i个元素,此时根据式(6)和式(8)有
令多重渐消因子σ=diag(σ1,σ2,…,σn),σ′=diag(σ1,σ2,…,σn,1,1,…,1),n为观测值个数。此时,SVD-UKF算法中Pyy、Pxy、Pk更新如式(13)所示
需要指出的是,基于多重渐消因子的自适应滤波算法的理论前提是预测残差向量符合均值为零的高斯白噪声。而当GPS观测向量中含有观测粗差或系统误差时,会严重影响预测残差向量的数字分布特征,导致算法失效。
3 RBFNN辅助多重渐消因子自适应滤波 3.1 径向基神经网络原理RBFNN为两层的前馈网络,输入层和输出层由线性神经元组成,通过隐层节点核函数对输入矢量产生局部响应,输出层对隐层节点的输出线性加权,从而实现输入空间到输出空间的映射,使整个网络实现函数逼近和回归[24]。本文中RBFNN的隐层节点中的基函数采用高斯核函数,则有
式中,Ψk(xi)为隐层的第k个隐节点的输出,xi为第i个输入矢量;Ck为第k个隐节点的中心;σk为第k个隐节点的宽度;j为隐节点个数。则径向基神经网络的输出为 式中,yi为第i个输入矢量;ωk为输出层与隐层第k个节点间的连接权值;l为总样本数。值得注意的是模型参数选取决定拟合效果,文中采用最近邻聚类学习算法确定隐节点个数及核函数中心,基于最小二乘算法求解网络的连接权值,采用遗传算法计算最优核函数隐节点的宽度。
3.2 RBFNN辅助自适应算法模型鉴于RBFNN具有较强的非线性映射能力,能以任意精度全局逼近一个非线性函数,且运算速度快,文中采用RBFNN算法削弱观测向量中的粗差或系统误差对预测残差向量的影响。由于等历元时间间隔内GPS观测值的位移和速度增量与前一时刻系统速度、姿态、INS系统在该时间间隔内的加速度和角速度增量存在某种非线性关系[25],基于RBFNN算法建立这种非线性模型的映射关系。当组合系统存在异常时,利用训练好的映射模型预测出下一时刻的近似观测值,削弱可能存在的观测异常,再基于多重渐消因子的自适应SVD-UKF算法消除潜在的状态异常,达到提高组合系统导航解可靠性和精度的目的。技术路线如图 1所示,具体步骤如下:
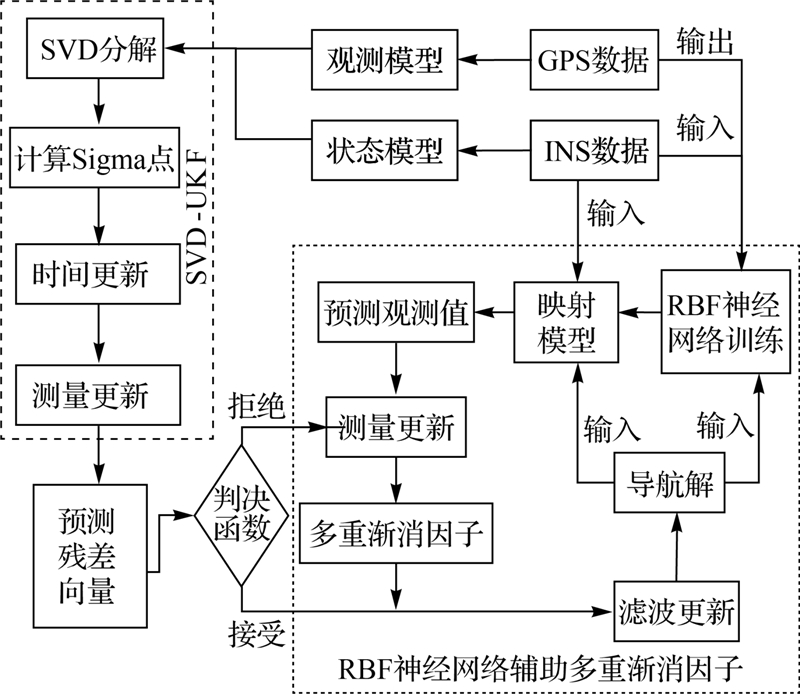 |
| 图 1 RBFNN辅助多重渐消自适应SVD-UKF算法 Fig. 1 RBFNN aided multiple fading factors in adaptive SVD-UKF algorithm |
步骤1:基于SVD-UKF算法对k时刻的输入的GPS/INS数据进行时间和测量更新,通过判决函数判断预测残差向量是否存在异常。
步骤2:若判决函数被接受,则认为系统无异常,滤波更新后计算导航解。
步骤3:将k-1时刻导航解中的速度、姿态、k时刻加速度和角速度增量作为输入,k时刻观测值的位移和速度增量作输出,进行RBFNN训练后,转到步骤1计算k+1时刻。
步骤4:若判决函数被拒绝,则认为系统存在异常,则认为观测异常或动力学异常至少存在一项,基于已训练出的映射模型和k-1时刻导航解中的速度、姿态、k时刻加速度和角速度增量作为输入,预测出k时刻观测值代替原观测值进行测量更新(削弱潜在的观测异常),计算多重渐消因子(削弱潜在的状态异常),进行滤波更新计算出k时刻的导航解,转到步骤3。
4 计算与分析仪器采用Leica 1200 Base & Rover GPS System和SPAN-CPT,采集2166 s GPS-RKT(1 Hz)和IMU(200 Hz)实测数据。设GPS-RTK测量值在纬度、经度和高程方向位置中误差分别为0.1 m、0.1 m和0.3 m,速度中误差分别为0.04 m/s、0.04 m/s和0.08 m/s;INS北东地初始位置误差分别为1 m、1 m和2 m;北东地初始速度为0.5 m/s;俯仰翻滚和航向初始姿态误差分别为1°、1°和3°;陀螺漂移和加速度偏置误差分别为5°/h和50 μg;陀螺仪和加速度相关时间分别为100 s和60 s。采用后处理计算导航解验证提出的算法。
4.1 预测残差向量数字特征分析预测残差向量为均值等于零的高斯白噪声,是构建文中多渐消因子的前提条件。基于SVD-UKF算法,图 2为位置和速度预测残差向量的自相关函数(非偏估计)及其对应的概率密度函数。结果显示:①预测残差序列的自相关函数中,延迟为零时,纬度、经度和高程方向的残差自相关系数分别0.01 m2/s、0.01 m2/s、0.1 m2/s,速度北东地方向的残差自相关系数分别0.001 m2/s3、0.001 m2/s3、0.003 m2/s3,数值上约为预设GPS观测中误差的二次方,与实际相符;②从预测残差向量的概率密度函数中可以看出,预测残差随机变量符合高斯分布;③二者皆服从本文多重渐消因子自适应SVD-UKF滤波的理论前提。
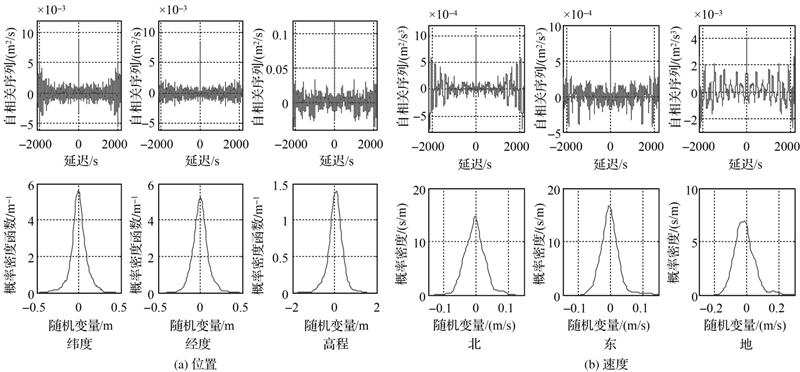 |
| 图 2 预测残差向量自相关函数与概率密度函数 Fig. 2 Autocorrelation functions and probability density functions of the predicted residual vectors |
为验证观测值含粗差时预测残差向量的数字特征,选取观测质量较好的600~800 s实测数据进行分析,在GPS观测值纬度方向每间隔20 s加入均值为3 m、中误差0.1 m的观测粗差;在速度东方向每间隔20 s加入均值为0.3 m/s、中误差0.01 m/s的观测粗差。图 3为加入观测粗差后,采用SVD-UKF算法,纬度和速度东方向预测残差向量的自相关函数(非偏估计)与概率密度函数。从图中可以看出:①观测值含有粗差或系统误差时,观测新息的预测残差向量的具有较强的相关性,不符合白噪声的特征分布;②纬度方向和速度东方向上的预测残差向量分别在3 m、0.3 m/s处存在较突出的概率密度分布(箭头处),与所加观测粗差一致,不符合高斯白噪声的零均值正态分布。
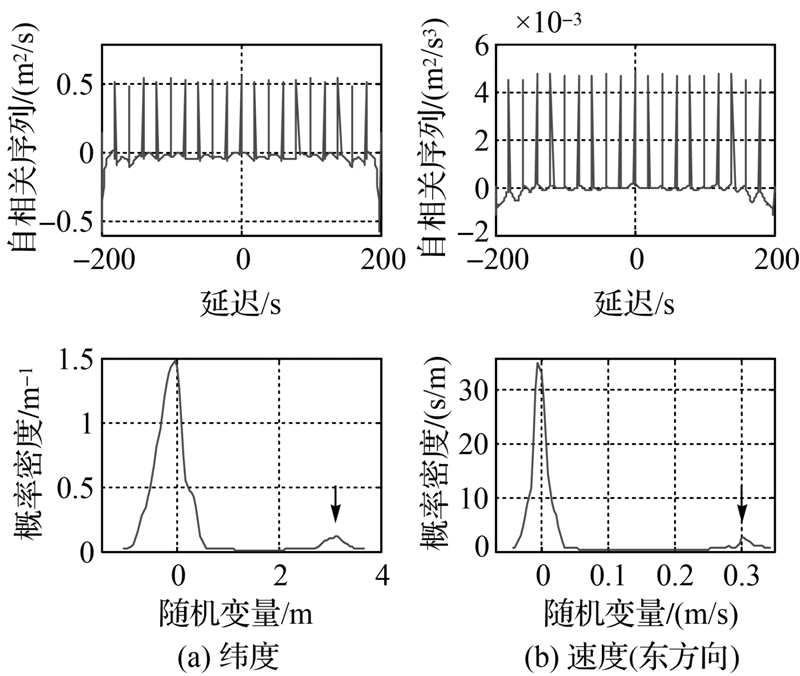 |
| 图 3 预测残差自相关函数与概率密度函数(含观测粗差)Fig. 3 Autocorrelation functions and probability density (observation abnormalities contained) |
为验证多重渐消因子自适应效果,在上述的试验样本中,载体坐标系Z方向上INS输出比力再加入N (0,2)的随机误差。图 4为速度地方向加入状态异常、纬度和速度东方向加入观测粗差后的多重渐消因子。图中可以看出:①速度地方向的渐消因子由所加入的状态异常导致,该渐消因子可以合理调节该处的状态方差,削弱此异常状态对导航解的贡献;②纬度和速度北方向未出现异常,高程方向存在较小的异常由GPS高程方向精度较弱导致;③纬度和速度东方向的渐消因子由观测粗差导致,该渐消因子错误地将观测粗差归结到状态异常,进一步放大了观测粗差对导航解的影响。
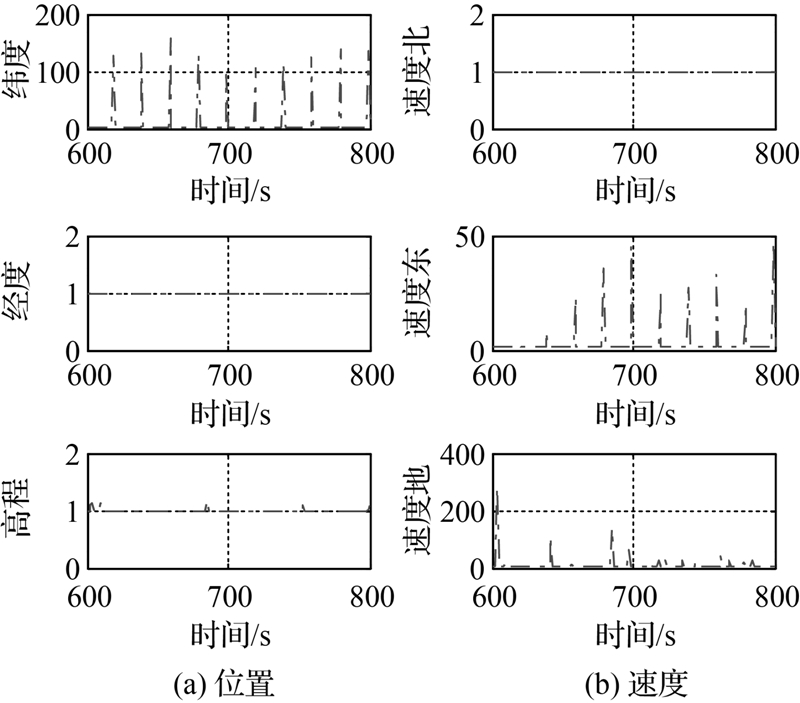 |
| 图 4 多重渐消因子(含观测粗差和状态异常) Fig. 4 Multiple fading factors (observation and state abnormalities contained) |
当观测值含有粗差或系统误差时,预测残差向量为有色噪声,多渐消因子自适应算法失去了应用的理论前提。为削弱观测向量中有色噪声的影响,采用径向基神经网络算法预测次优观测值代替观测粗差。以200~600 s数据作为训练样本(INS速度、姿态、加速度增量、姿态增量为训练输入,GPS位置增量为训练输出),构建回归模型。图 5为采用径向基神经网络算法对纬度坐标增量和速度东方向增量的训练及预测结果。其中,纬度方向训练、预测中误差分别为0.068 m、0.16 m;速度东方向训练、预测中误差分别为1.48 e-4 m/s、2.43 e-4 m/s。可以看出该算法在位置和速度上预测误差约为训练误差的2倍,位置和速度都可以获得较高精度。
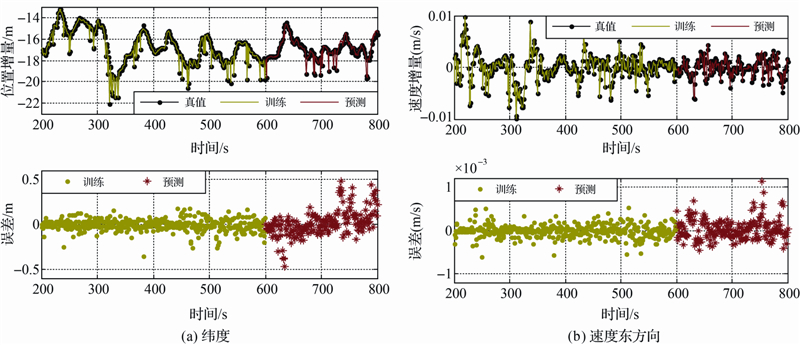 |
| 图 5 RBFNN训练及预测结果 Fig. 5 Results of RBFNN trained and predicted data |
利用SVD-UKF算法解算不含观测粗差和状态异常原始观测值,以解算出的车载组合系统的导航解作为真值。图 6为采用标准SVD-UKF算法(SVD-UKF)、多重渐消因子自适应SVD-UKF算法(MFUKF)、神经网络辅助的多重渐消因子自适应SVD-UKF算法(NNMFUKF),对速度地方向含状态异常、纬度和速度东方向含观测粗差的600~800 s数据进行解算的误差图。表 1为图 6的统计结果。可以看出:①对标准SVD-UKF算法而言,由于INS短时精度高,INS结果在滤波器中对导航解的贡献较大,因而高程方向上存在的状态异常引起导航解误差较大,纬度和速度东方向存在观测粗差对导航解影响较小;②多重渐消因子自适应算法可以单独调整每个滤波通道,较好地消除了高程方向状态异常,但当观测值含粗差时会扩大观测粗差对导航解的贡献;③神经网络辅助的多重渐消因子自适应SVD-UKF算法即能同时消除观测粗差和状态异常对导航解的贡献。
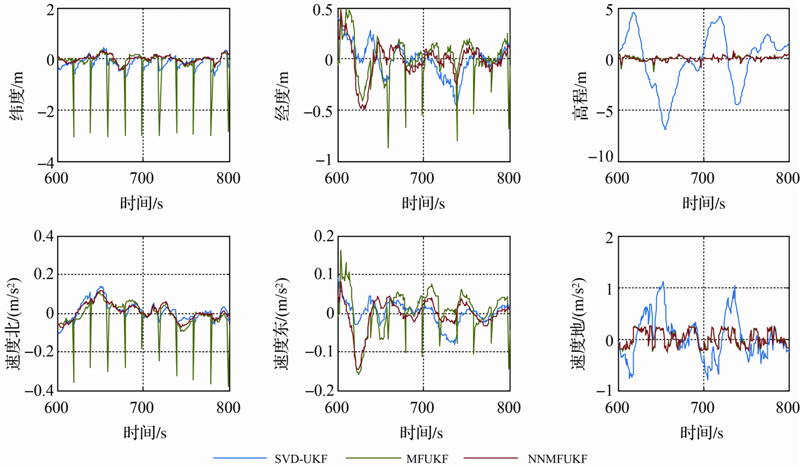 |
| 图 6 3种方案误差对比(含观测粗差和状态异常) Fig. 6 Errors comparison of SVD-UKF,MFUKF and NNMFUKF(observation and state abnormalities contained) |
| 算法 | 位置误差/m | 速度误差/(m/s) | ||||
| 纬度 | 经度 | 高程 | 北 | 东 | 地 | |
| SVD-UKF | 0.288 | 0.160 | 2.758 | 0.050 | 0.040 | 0.425 |
| MFUKF | 0.680 | 0.205 | 0.240 | 0.084 | 0.056 | 0.157 |
| NNMFUKF | 0.153 | 0.165 | 0.222 | 0.045 | 0.030 | 0.155 |
分析上述结果可以看出:①当观测向量不受粗差或系统误差影响时,预测残差向量符合高斯白噪声的数字特征分布,将渐消因子引入SVD-UKF算法中,能够准确消除各状态中不同幅度的异常,提高了导航解精度;②当观测向量受粗差或系统误差影响时,基于径向基神经网络的多重渐消因子自适应SVD-UKF算法可以同时削弱观测粗差、消除系统状态异常,提高了滤波器导航解的可靠性。
5 结 论UKF算法采用确定性采样策略逼近非线性分布,具有精度高、计算简单、不需计算雅可比矩阵等优点,将其引入GPS/INS组合导航非线性系统计算导航解,采用SVD分解代替传统的UT算法,抑制先验协方差矩阵负定性变化,提高了滤波算法中的数值稳定性。通过理论推导和实测数据预测残差向量的数字特征分析,验证了多重渐消因子用于SVD-UKF自适应算法的可行性。引入径向基神经网络算法削弱观测异常对预测残差向量高斯白噪声分布特性的影响,拓展了多重渐消自适应算法应用范围。使得该算法能在观测值存在异常的情况下,实现每个滤波通道下不同幅度的自适应效果,为GPS/INS组合导航非线性系统次优估计算法提供了一种解决思路。
| [1] | MOHAMED A H, SCHWARZ K P. Adaptive Kalman Filtering for INS/GPS[J]. Journal of Geodesy, 1999, 73(4): 193-203. |
| [2] | YANG Y, HE H, XU G. Adaptively Robust Filtering for Kinematic Geodetic Positioning[J]. Journal of Geodesy, 2001, 75(2-3): 109-116. |
| [3] | YANG Y, GAO W, ZHANG X. Robust Kalman Filtering with Constraints: A Case Study for Integrated Navigation[J]. Journal of Geodesy, 2010, 84(6): 373-381. |
| [4] | LI Bofeng, SHEN Yunzhong. Equivalent Residual Product Based Outlier Detection for Variance and Covariance Component Estimation[J]. Acta Geodaetica et Cartographic Sinica, 2011, 40(1): 10-14. (李博峰, 沈云中. 基于等效残差积探测粗差的方差-协方差分量估计[J]. 测绘学报, 2011, 40(1): 10-14.) |
| [5] | QIN Yongyuan, ZHANG Houyue, WANG Shuhua. Kalman Filter and Integrated Navigation Principle [M]. Xi'an: Northwest Industry University Press, 2012: 25-48. (秦永元, 张洪钺, 汪叔华.卡尔曼滤波与组合导航原理[M]. 西安: 西北工业大学出版社, 2012: 25-48.) |
| [6] | DING W, WANG J, RIZOS C, et al. Improving Adaptive Kalman Estimation in GPS/INS Integration[J]. Journal of Navigation, 2007, 60(3): 517-529. |
| [7] | SHI Xingxi, WANG Tiesheng, HUANG Bo. Integrated Localization Algorithm for DGPS/DR Based on SUT-EKF [J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 528-533. (石杏喜, 王铁生, 黄波, 等. 基于SUT-EKF的 DGPS/DR 组合定位算法[J]. 测绘学报, 2010, 39(5): 528-533.) |
| [8] | HIDE C, MOORE T, SMITH M. Adaptive Kalman Filtering for Low-cost INS/GPS[J]. Journal of Navigation, 2003, 56(1): 143-152. |
| [9] | ARULAMPALAM M S, MASKELL S, GORDON N, et al. A Tutorial on Particle Filters for Online Nonlinear/non-Gaussian Bayesian Tracking[J]. IEEE Transactions on Signal Processing, 2002, 50(2): 174-188. |
| [10] | JULIER S J, UHLMANN J K. New Extension of the Kalman Filter to Nonlinear Systems[C]//Aero Sense'97. [S. l.]: International Society for Optics and Photonics, 1997: 182-193. |
| [11] | JULIER S J, UHLMANN J K. Reduced Sigma Point Filters for the Propagation of Means and Covariances through Nonlinear Transformations[C]//Proceedings of the American Control Conference. Anchorage: IEEE, 2002: 887-892. |
| [12] | YANG Y, GAO W. An Optimal Adaptive Kalman Filter[J]. Journal of Geodesy, 2006, 80(4): 177-183. |
| [13] | GAO Weiguang, HE Haibo, CHEN Jinping. An Adaptive UKF Algorithm and Its Application for GPS/INS Integrated Navigation System[J]. Transactions of Beijing Institute of Technology, 2008, 28(6):505-509. (高为广, 何海波, 陈金平. 自适应UKF算法及其在GPS/INS组合导航中的应用[J].北京理工大学学报, 2008, 28(6): 505-509.) |
| [14] | GAO Weiguang, YANG Yuanxi, ZHANG Ting. Neural Network Aided Adaptive Filtering for GPS/INS Integrated Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 26-30. (高为广, 杨元喜, 张婷. 神经网络辅助的GPS/INS组合导航自适应滤波算法[J]. 测绘学报, 2007, 36(1): 26-30.) |
| [15] | WU Fumei. Error Compensation and Extension of Adaptive Filtering Theory in GNSS/INS Integrated Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(3): 401-401. (吴富梅. GNSS/INS 组合导航误差补偿与自适应滤波理论的拓展[J]. 测绘学报, 2010, 40(3): 401-401.) |
| [16] | TAN Xinglong, WANG Jian, HAN Houzeng. SVR Aided Adaptive Robust Filtering Algorithm for GPS/INS Integrated Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(6): 590-606. (谭兴龙, 王坚, 韩厚增. 支持向量回归辅助的 GPS/INS 组合导航抗差自适应算法[J]. 测绘学报, 2014, 43(6): 590-606.) |
| [17] | ZHANG Chaowei, FU Li, FAN Yuezu. Multiple Fading Kalman Filter Based on Hypothesis Testing[J]. Journal of Beijing University of Aeronautics and Astronautics, 2004, 30(1): 18-22. (庄朝文, 富立, 范跃祖. 一种基于假设检验的多重渐消卡尔曼滤波[J]. 北京航空航天大学学报, 2004, 30(1): 18-22.) |
| [18] | GENG Yanrui, GUO Wei, CUI Zhongxing. Comparative Research on Multiple Fading Kalman Filter in Integrated Navigation System[J]. Journal of Chinese Inertial Technology, 2004, 12(2): 18-22. (耿延睿, 郭伟, 崔中兴. 组合导航系统多重衰减因子自适应估计算法比较研究[J]. 中国惯性技术学报, 2004, 12(2):18-22.) |
| [19] | CUI X, YANG Y. Adaptively Robust Filtering with Classified Adaptive Factors[J]. Progress in Natural Science, 2006, 16(8): 846-851. |
| [20] | YANG Y, CUI X. Adaptively Robust Filter with Multi Adaptive Factors[J]. Survey Review, 2008, 40(309): 260-270. |
| [21] | GAO W, MIAO L, NI M. Multiple Fading Factors Kalman Filter for SINS Static Alignment Application [J]. Chinese Journal of Aeronautics, 2011, 24:476-483. |
| [22] | QIAN Minghua, GE Lei, PENG Yu. Multiple Fading Factors Kalman Filter and Its Application in SINS Initial Alignment[J]. Journal of Chinese Inertial Technology, 2012, 20(3): 287-291. (钱华明, 葛磊, 彭宇. 多渐消因子卡尔曼滤波及其在SINS初始对准中的应用[J]. 中国惯性技术学报, 2012, 20(3): 287-291.) |
| [23] | KAYGISIZ B H, ERKMEN A M, ERKMEN I. Enhancing Positioning Accuracy of GPS/INS System during GPS Outages Utilizing Artificial Neural Network[J]. Neural Processing Letters, 2007, 25(3): 171-186. |
| [24] | SESHAGIRI S, KHALIL H K. Output Feedback Control of Nonlinear Systems Using RBF Neural Networks[J]. IEEE Transactions on Neural Networks, 2000, 11(1): 69-79. |
| [25] | XU Z, LI Y, RIZOS C, et al. Novel Hybrid of LS-SVM and Kalman Filter for GPS/INS Integration[J]. Journal of Navigation, 2010, 63(2): 289-299. |