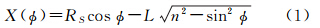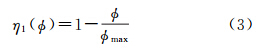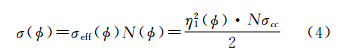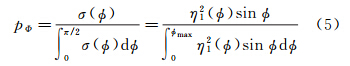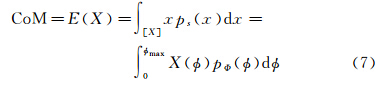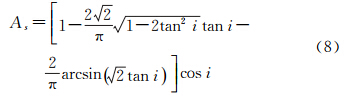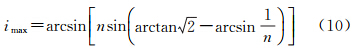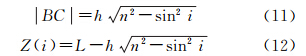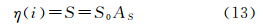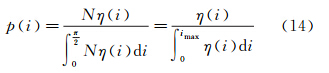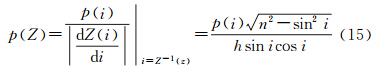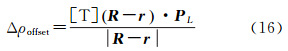2. 中国科学院研究生院, 北京 100049；
3. 宇航动力学国家重点实验室，陕西 西安 710043；
4. 上海微小卫星工程中心，上海 201203
2. Graduate University of Chinese Academy of Sciences, Beijing 100049, China;
3. State Key Laboratory of Aerospace Dynamics, Xi'an 710043, China;
4. Shanghai Engineering Center for Microsatellites, Shanghai 201203, China
卫星激光测距(satellite laser ranging，SLR)利用人卫激光测距仪测得的激光脉冲往返于测站和卫星之间的时间换算为两者之间的距离[1]。SLR数据处理涉及卫星的状态(位置和速度)、观测站在空间的位置以及激光在大气中的传播[2]。在利用SLR数据进行卫星精密定轨过程中，需要高精度模型来进行星-地距离归算修正，卫星质心改正就是其中一个重要因素。从SLR实测的激光脉冲往返时间间隔换算得到的是地面测站与卫星表面激光反射点之间的距离，而在计算卫星精密星历、确定地球参考架或其他SLR技术应用中，需要的是卫星质心与测站之间的距离。因此，必须在实测距离中加入卫星有效反射面至卫星质心的距离补偿改正，这就是卫星的质心改正(center-of-mass，CoM)。卫星质心改正与星载角反射器的大小、几何构型、材料等有关，可通过相关的理论计算和卫星发射前的地面光学检验等手段确定[3]。
目前，各种科学应用也对SLR数据分析与评估提出更高要求。与测站发射的激光脉冲相比，经过星载角反射器阵列反射的激光脉冲不仅被展宽，而且脉冲轮廓发生改变，这种由于卫星的表面反射器的分布引起的激光回波波形的变化称为卫星形状效应(satellite signature effect)[4]。数值模拟和模型分析表明，卫星形状效应将给激光卫星的观测数据带来至少几毫米的偏差[5]。在不考虑地球大气的影响下，这一效应导致卫星质心改正需要考虑以下3类因素：一是地面发射系统的发射激光波长、脉冲能量与波形，这类因素决定了发射光束中光子在时间和空间上的分布；二是卫星角反射器阵列的光学特性及几何分布，这类因素确定了发射光束中同一波阵面的光子被反射器阵列中不同反射器反射的时间差，即确定了脉冲波形的展宽程度，再结合第一类因素，可以确定返回激光脉冲中光子能量在时间上的分布；三是地面接收系统探测器的光电响应特性，这类因素确定了回波光子从到达探测器到转化为光电流而被记录的时间[6]。3类因素的综合确定了激光脉冲往返时间的修正值，最终可换算得到卫星质心改正[7]。
质心改正需要精确标定，以提高卫星测距精度。在诸多激光测距卫星中，卫星的各项几何、物理参量较为完善，而且其质心改正值也在发射前通过试验测定[8]。美国NASA/GSFC和德国地学中心的研究人员以LAGEOS卫星为例，提出了计算质心改正的方法和模型[9]，他们讨论主要反映在对物理现象的解释，给出的表达式主要针对具体的物理现象[10]。上海天文台研究人员从物理过程分析了激光测距脉冲波形的变化，给出了完整的数学描述，并讨论不同脉冲强度对卫星质心改正值和测距精度的影响可达10 mm以上[11]。对于激光测距卫星，其质心改正值主要由角反射器分布效应引入，其真实值为角反射器阵列的能量反射中心到卫星质心的距离，与几何光学中心不同[12, 13, 14]。本文对以LAGEOS为代表的球形卫星和以北斗为代表的导航卫星的激光反射器分别进行建模，对角反射器的有效雷达截面面积进行拟合，通过以入射角为随机变量的概率模型，计算了LAGEOS-1球形激光测距卫星的质心改正值，并对BeiDou M3卫星的多个角反射器组成的激光反射器平面阵列的情况进行了探讨。
2 基于概率密度函数的测地卫星质心改正模型的建立因卫星形状效应是一种平均效应，可使用概率模型模拟，即假设质心改正值是某一随机变量的平均值，而角反射器的物理特性决定了质心改正值可由某一分布函数确定，且该分布函数由卫星及其反射器的雷达反射特性确定[15]。
2.1 随机变量的选取及其分布函数
以LAGEOS-1卫星为例，首先确定函数随机变量，这里选激光束入射角为随机变量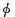
，以LAGEOS-1卫星的几何中心为零点，建立极坐标系，X轴为零角度，如图 1所示，有
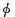是角坐标值；Rs为卫星球体的半径；L为角反射器的正高；n是角反射器的折射率。显然，X(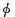)的平均值就是质心改正的值[8]。
 |
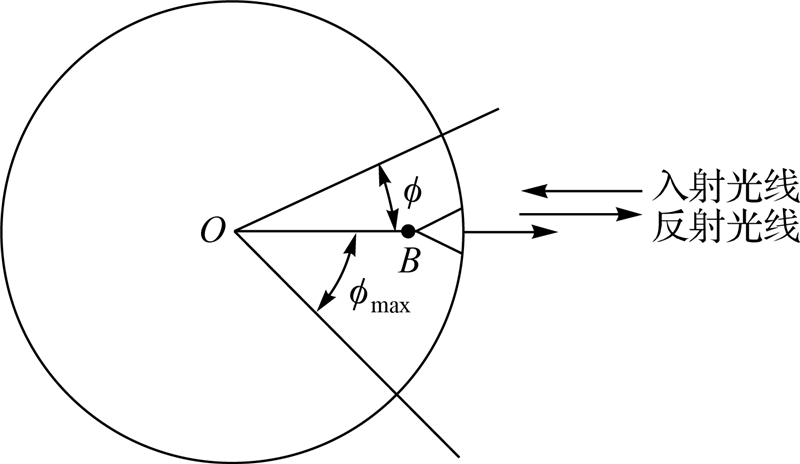| 图 1 LAGEOS-1/2卫星的质心改正模型坐标示意图 Fig. 1 Coordinate for the CoM model of LAGEOS-1/2 |
根据雷达反射特性，激光测距卫星类似于雷达目标，其反射的能量与有效截面积成正比。因此，激光测距卫星的有效雷达光学面积的分布函数就是随机变量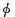的概率密度函数[8]。
对于激光测距卫星上的每个角反射器，在入射角为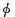时的相对有效几何面积[16]为
文献[9]研究中将式(2)用式(3)拟合有效反射面积
式中，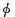
max为入射截止角(Cut-off-Angle，CoA)，即光线入射到角反射器的最大入射角。不同的截止角在拟合前后的相对有效反射面积[η(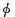)]2与[η1(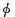)]2的比较如图 2所示。
 |
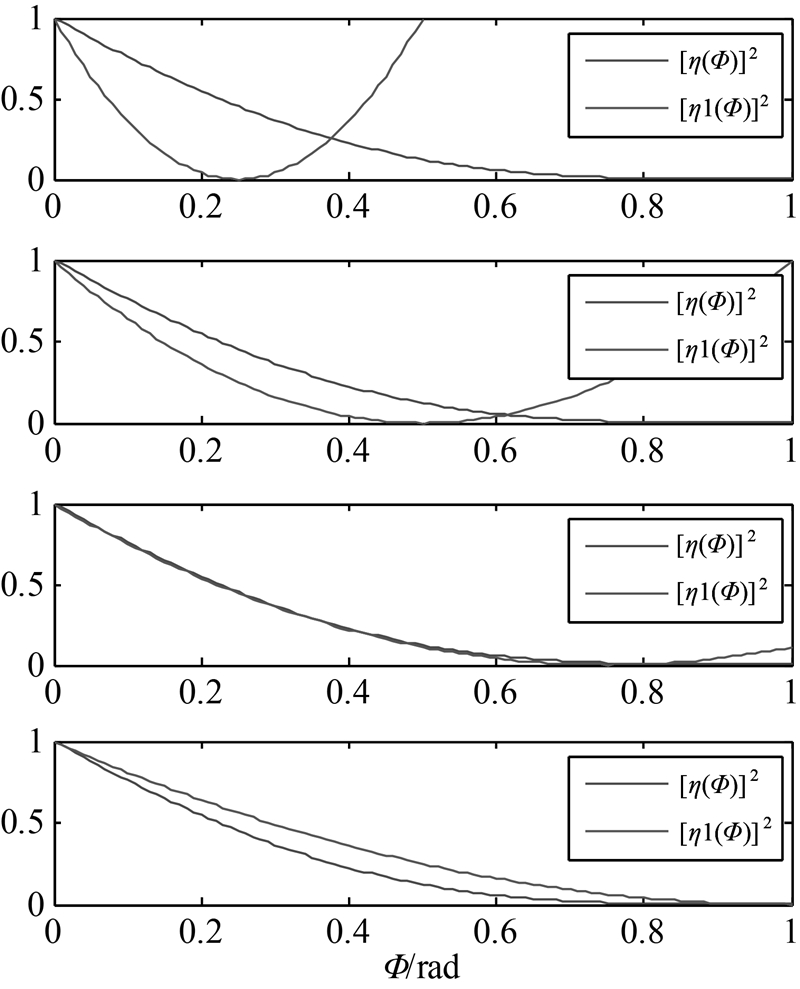| 图 2 相对有效几何面积比较(n=1.46，从上到下CoA依次为0.25、0.5、0.75、1)Fig. 2 Comparison of relative effective area,n=1.46,CoA is 0.25,0.5,0.75,1 corresponding |
由图 2的结果显示可知，CoA为0.75时拟合程度最好，而在CoA取其他值时，拟合结果和原式的结果差别很大，所以式(3)在满足条件下才能使用。
角反射器一般均匀分布在卫星表面，设总数为N，假设每个角反射器在光线零角度入射时的峰值光学截面为σcc，在入射角为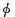时的光学截面为σeff(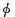)，整个卫星的光学截面分布函数为
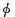的概率密度函数
由概率模型
得到X的概率密度函数
推导得质心改正的计算公式
利用Matlab软件，采用牛顿-科特斯法积分，所需积分步数少，效率高，积分精度可达10-6，用拟合方法计算得LAGEOS卫星的质心改正为242.3 mm，用原始推导式计算LAGEOS卫星的质心改正为240.4 mm。
3 BeiDou-M3卫星角反射器的质心改正模型在我国自主研发的北斗卫星导航系统的卫星星座中，BeiDou-M3卫星除了可以主动地发播导航定位信息外，还由于在它的对地一侧安装了后向激光反射器，便可被动地实施激光测距观测。考虑热效应的影响，BeiDou-M3和LAGEOS卫星的角反射器底部都是采用内接圆切割[16]。但与LAGEOS卫星不同的是，BeiDou-M3卫星上的激光反射器是由42个角反射器组成的平板阵列[17]，如图 3所示，两种卫星的角反射器的参数见表 1。
 |
| 图 3 BeiDou-M3上的激光反射器阵列 Fig. 3 The laser reflector array of BeiDou-M3 |
| 卫星 | LAGEOS-1/2 | BeiDou-M3 |
| 内接圆直径/mm | 38.1 | 33 |
| 高/mm | 27.8 | 24.0 |
| 折射率n | 1.455 | 1.46 |
当光线垂直入射，即入射角i=0时的有效面积记为S0=πr2，其中r为内接圆的半径。相对有效面积[16]为
式(8)是对空心角体合作目标而言的，如果是实心的话，必须考虑材料的折射率n，此时将相对有效面积公式中的tan i换成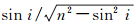
(文献[18])，那么实际有效面积S为
对于入射角i的范围，尚须考虑角反射器的接收角，即光线在非镀层角反射器的全反射而不受破坏的最大入射角，根据光学折射定律和几何关系得到[16]
在BeiDou-M3中角反射器的材质为熔石英，其折射率n =1.46，计算得到imax为16.8°。实际中需要考虑能量中心的位置，由于其角反射器阵列设计的对称性，阵列所在平面的几何中心位置即能量中心的水平分量所在位置，那么能量中心在厚度方向的位置由于无法直接测量成为难题。本文定义角反射器底面的法线方向为Z轴方向，即讨论Z轴方向的能量中心位置，详细的卫星激光反射器的简化结构剖面图如图 4所示。
 |
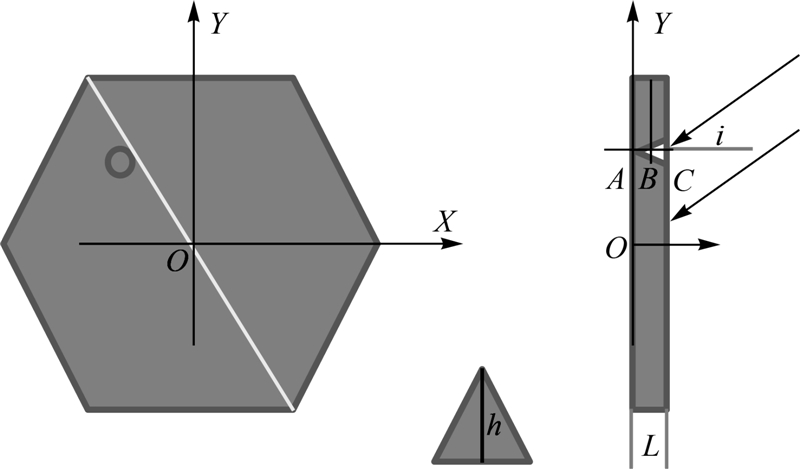| 图 4 BeiDou-M3的激光反射器示意图 Fig. 4 Coordinate for the CoM model for BeiDou-M3 |
式中，i为光线入射角。令能量中心到O-XY平面的距离为CoM′，按几何关系有
角反射器阵列有N个角反射器，对于每个角反射器，在入射角度为i时的实际有效面积为
角反射器的相对有效面积和实际有效面积均随入射角度减小也逐渐减小。
整个激光反射器阵列的光学截面分布为Nη(i)，将其归一化，即得i的概率密度函数
进一步，得到Z的概率密度函数 类比LAGEOS卫星，Z方向的改正值为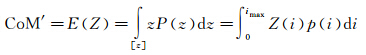
ILRS官方公布的BeiDou-M3的数据中，L=30 mm，h=24 mm，N=42，n=1.46，没有镀膜，仿真给出的质心改正，体现为反射中心在星固坐标系中的坐标为(-0.432 1 m，-0.562 1 m，1.133 8 m)[19]。通过计算，CoM′值为-4.8 mm(Z轴方向)。根据几何信息，计算得到新的质心改正值，其能量反射中心点在星固坐标系中为(-0.432 1 m，-0.562 1 m，1.112 5 m)。由此可见，能量中心与几何中心、质心理论值不在同一处。
4 LAGEOS-1和BeiDou-M3卫星质心改正模型精度的评估 4.1 卫星精密定轨的统计动力学方法卫星精密定轨计算采用基于线性估计技术的统计动力学方法。本文选择LAGEOS-1和BeiDou-M3共2颗卫星作为研究对象。LAGEOS卫星处于中轨道，是专用测地卫星，被ILRS列为优先观测目标[20]，而BeiDou-M3轨道较高，观测数据少，适当延长定轨弧长。利用上海天文台SHORDER软件，遵照轨道统计学原理[21]，对上述卫星进行精密定轨，测站坐标采用ITRF2000，采用IAU1976岁差模型和IAU1980+IERS章动模型改正，对观测量进行潮汐改正(固体潮、极潮、海潮负荷形变造成的台站位移改正)、对流层折射改正、广义相对论引力时延改正和卫星质心改正。由ILRS公布的LAGEOS-1原质心改正为0.251 m，本文计算的质心改正为0.242 7 m；BeiDou-M3原质心改正为(-0.432 1 m，-0.562 1 m，1.133 8 m)，各测站的现质心改正为(-0.432 1 m，-0.562 1 m，1.112 5 m)。轨道高度的差别导致地球重力场模型GGM01C阶数不同，LAGEOS采用30×30阶，而BeiDou-M3采用15×15阶；选取LAGEOS数值积分步长为150 s，定轨弧长为3 d，而BeiDou-M3数值积分步长为300 s，定轨弧长为10 d；均选取1 mm作为它的收敛标准[7]。在解算卫星轨道参数时，将部分运动学参数和动力学参数作为待估量一起解算，保证观测法方程求解精度，使各待估参数之间的相关性尽量减弱。这两颗卫星的待估参数包括类阻力系数、横向和法向经验加速度、太阳辐射压系数和地球自转参数。
4.2 BeiDou-M3卫星的质心补偿修正对于LAGEOS-1/2等球形激光测距卫星，质心修正只需要在原始测距上加上质心改正值。但是，BeiDou-M3卫星上的激光反射器与卫星质心不重合，需要把测距数据修正到卫星质心上。一般投影到卫星测距方向，卫星质心补偿修正为
式中，[T]是J2000.0地心惯性坐标系到星固坐标系的转换矩阵；R、r分别为观测时刻测站和卫星在J2000.0地心惯性坐标系中的位置矢量；PL即前面计算得到的质心改正，是卫星激光反射器在星固坐标系中的位置矢量[14]。 4.3 结果与分析
LAGEOS-1轨道低，观测数据多，本文选择了2011年4月—2012年12月的SLR数据，采用本文获得的质心改正模型和ILRS建议的参数进行精密轨道确定，来评估模型的精度和效果。由于6月观测比较多，本文用SLR资料解算了2013年6月BeiDou-M3卫星的SLR轨道。内符合精度通常以轨道拟合残差的均方根误差(root-mean-square error，RMSE)表示，其大小受测量数据的数量和误差、定轨弧段的长短、定轨过程中待估参数的数目和分段方法、数据剔除标准以及轨道数值积分的精度和收敛标准等因素的影响[21]。利用SLR数据进行精密轨道确定，本文质心改正模型对LAGEOS卫星进行SLR精密定轨的轨道残差约为1.7 cm，与ILRS公布值计算结果精度相当，相差在亚毫米级，如图 5所示。
 |
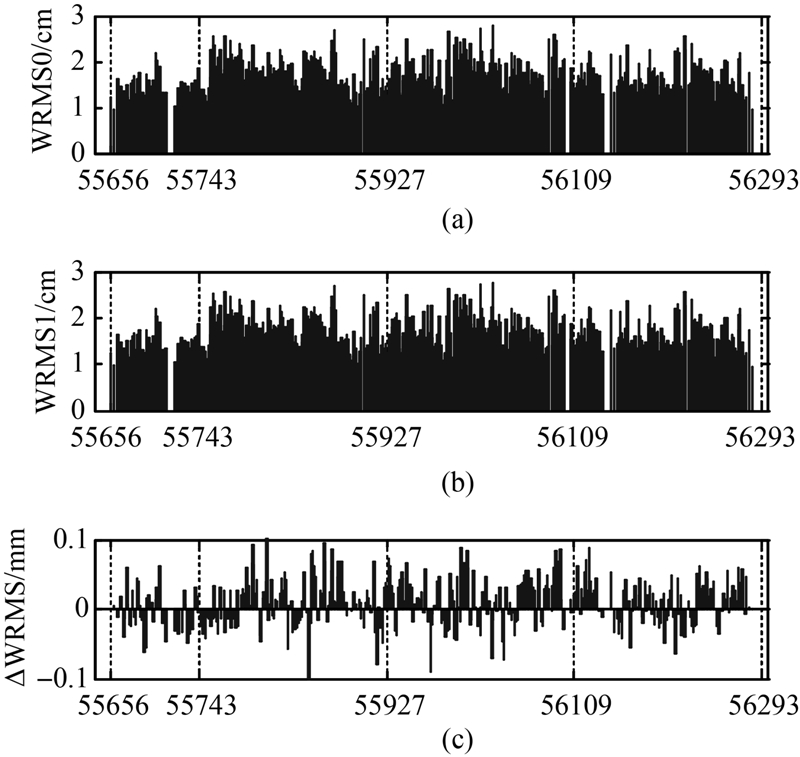| 图 5 对LAGEOS-1，采用原质心改正时的定轨精度(a)、采用现质心改正后的精度(b)以及二者之差(WRMS1-WRMS0)(c)Fig. 5 Difference between WRMS1 and WRMS0,using ILRS CoM,new CoM and the difference |
同时，采用两种质心改正值对BeiDou-M3卫星进行了精密定轨，弧段长度为10 d，并且重叠5 d。统计发现，两种质心改正值的内符合精度均约为1.9 cm，相差在亚毫米级。对重叠弧段进行轨道作差，并转换到RTN方向，结果表明，在数据比较充足时R方向的轨道精度相差不超过1 m，但是在T方向和N方向轨道差别达到几十米或两三百米左右，导致这一现象的原因主要是因为数据稀少，测站少且分布不均。同时，图 6给出了两种质心改正值计算的轨道在RTN方向的差，表明反射能量中心与几何中心的区别引起的CoM值的变化对卫星轨道的径向方向影响很小，在切向和法向引起轨道2~4 m的波动，引起这种现象的原因主要是受非球形卫星姿态的影响。
 |
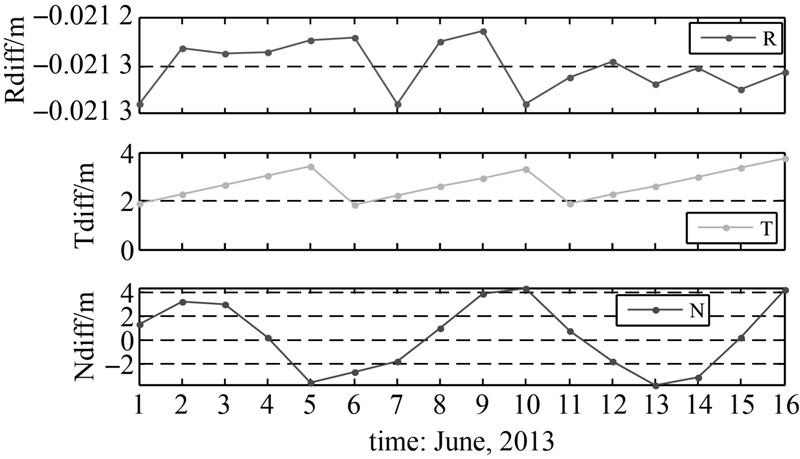| 图 6 两种CoM值分别确定的轨道在RTN方向的差(NewCoM - ILRSCoM)Fig. 6 The difference of the satellite’s orbit using 2 kinds of CoM value |
本文将球形LAGEOS卫星和“盒翼”形状的卫星BeiDou-M3的卫星质心改正概率模型用于SLR精密定轨，定轨内符精度均优于2 cm，证明概率模型的理论正确性。对LAGEOS卫星的长期观测数据进行统计发现，使用ILRS公布的质心改正值和概率模型计算的质心改正值进行SLR精密定轨，轨道精度相差为亚毫米。在对BeiDou-M3计算分析发现，轨道重叠弧段的R方向(径向)的相对误差保持在亚米级，而T方向、N方向的相对误差在几十米甚至更高；利用两种不同的质心改正值进行SLR定轨，对轨道精度的影响达到2 m。
因此，对于激光测距的反射中心的位置改正，并非是发射前标定的质量中心改正值，而应该是由卫星几何形状等因素决定的能量反射中心改正值，概率模型利用统计平均理论从球型卫星移植到非球形卫星，结合物理参数，讨论其质心改正与ILRS公布值对定轨精度的影响，结果符合较好。因此，可以利用概率模型计算其他卫星的激光反射器的能量反射中心，即质心改正值。
| [1] | SEEBER G. Satellite Geodesy[M]. Berlin: Walter de Gruyter, 2003: 424-436. |
| [2] | GURTNER W, NOOMEN R, PEARLMAN M R. The International Laser Ranging Service: Current Status and Future Developments[J]. Advances in Space Research, 2005, 36(3): 327-332. |
| [3] | WAN Qiang, GUO Yanlong, WANG Xiaobing, et al. Present Status and Progress of Laser Cooperative Targets for SLR[J]. Laser & Optoelectronics Progress, 2005, 42(5): 20-23, 29. (万强, 郭延龙, 王小兵, 等. 卫星激光测距合作目标技术现状和进展[J]. 激光与光电子学进展, 2005, 42(5): 20-23, 29.) |
| [4] | APPLEBY G M. Satellite Signatures in SLR Observations[C]//Proceedings of the 8th International Workshop on Laser Ranging Instrumentation. Annapolis: NASA, 1993: 3-19. |
| [5] | FAN Jianxing, YANG Fumin, CHEN Qixiu. Theoretical Analysis and Numerical Solution of Laser Pulse Transformation for Satellite Laser Ranging[J]. Science in China Series A: Mathematics,2001, 44(7): 915-922. |
| [6] | OTSUBO T, APPLEBY G M. System-dependent Center-of-mass Correction for Spherical Geodetic Satellites[J]. Journal of Geophysical Research, 2003, 108(B4): 2201-2210. |
| [7] | ZHAO Gang, WANG Xiaoya, WU Bing. Effect Analysis of System-dependent Center-of-mass Correction on Precision of SLR Orbit Determination[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 165-170. (赵罡, 王小亚, 吴斌. 不同测站卫星质心不同改正对卫星激光测距定轨精度的影响分析[J]. 测绘学报, 2012, 41(2): 165-170.) |
| [8] | FAN Jianxing, YANG Fuming, CHEN Qixiu. Center-of-mass Model of Satellites Used for Laser Ranging[J]. Acta Photonica Sinica, 2000, 29(11): 1012-1016. (范建兴, 杨福民, 陈启秀. 激光测距卫星的质心改正模型[J]. 光子学报, 2000, 29(11): 1012-1016.) |
| [9] | NEUBERT R. An Analytical Model of Satellite Signature Effects[C]//9th International Workshop on Laser Ranging Instrumentation.Canberra, Australia: Australia Government Publishing Service, 1994: 82-91.) |
| [10] | VARGHESE T K, SELDEN M, OLDHAM T, et al. Test Results from LAGEOS-2 Optical Characterization Using Pulsed Lasers[C]//Proceedings of the 8th International Workshop on Laser Ranging Instrumentation.1992.) |
| [11] | FAN Jianxing, YANG Fuming, CHEN Qixiu. Theoretical Analysis and Numerical Calculation of Laser Pulse Waveform Changes in the Satellite Laser Ranging[J]. Science in China(Series A), 2001, 31(1): 63-69. (范建兴, 杨福民, 陈启秀. 卫星激光测距中激光脉冲波形变化的理论分析及数值计算[J]. 中国科学(A辑), 2001, 31(1): 63-69.) |
| [12] | QU Feng, WANG Tanqiang, CHEN Xianjun, et al. Precise Orbit Determination of GPS35 Satellite Using SLR Data[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(3): 224-228. (瞿锋, 王谭强, 陈现军, 等. 用SLR资料精密确定GPS35卫星轨道[J]. 测绘学报, 2003, 32(3): 224-228.) |
| [13] | QU Feng, WANG Tanqiang, CHEN Xianjun, et al. The Comparison of SLR Orbit with IGS Orbit for GPS35 Satellite[J]. Bulletin of Surveying and Mapping, 2002(2): 14-16. (瞿锋, 王谭强, 陈现军,等. GPS35卫星的SLR轨道与IGS轨道的联合比较[J]. 测绘通报, 2002(2): 14-16.) |
| [14] | LIU Yuqiong, ZHANG Yaowen, WU Jixian. Evaluation of GPS35 Satellite Precise Orbit with SLR Measurements[J]. Engineering of Surveying and Mapping, 2007, 16(2): 36-38, 50. (刘宇琼, 张耀文, 吴吉贤. 利用SLR检核GPS35卫星精密轨道[J]. 测绘工程, 2007, 16(2): 36-38, 50.) |
| [15] | APPLEBY G M, OTSUBO T, PAVL1S E C. Cannonbal Spacecraft Center of Mass Offset Modeling[C]//International Laser Ranging Service 2007-2008 Report. Greenbelt: NASA, 2009: 3-5. |
| [16] | SHENG Yuan. The Theoretical Calculation about the Properties of Angle of Body Cooperation Target[J]. Laser & Infrared, 1973(12): 1-15. (声远. 关于角体合作目标性质的理论计算[J]. 激光与红外, 1973, (12): 1-15.) |
| [17] | FENG Chugang, ZHU Yuanlan, ZHANG Feipeng. Determination of LAGEOS Satellite's Precise Orbits and Residual Analysis[J]. Acta Astronomica Sinica, 2003, 44(1): 55-64.(冯初刚, 朱元兰, 张飞鹏, 等. LAGEOS卫星精密定轨及残差分析[J]. 天文学报, 2003, 44(1): 55-64.) |
| [18] | TAPLEY B D. Statistical Orbit Determination Theory[C]//Proceedings of the NATO Advanced Study Institute. Dordrecht: Reidel, 1973:396-425. |
| [19] | Satellite Missions Infomation[Z]. http://edc.dgfi.badw.de:8080/satellite_missions/list_of_satellites/cmi3_reflector.html. |
| [20] | SHEN Xiumei. Using SLR to Determine Satellite LAGEOS's Precisely Orbit[D]. Qingdao: Shandong University of Science and Technology, 2011. (申秀梅. 基于SLR技术的LAGEOS卫星精密定轨[D]. 青岛: 山东科技大学, 2011.) |
| [21] | QIN Xianping. The Precise Orbit Determination of Satellite Laser Ranging[D]. Zhengzhou: PLA Information Engineering University, 2003. (秦显平. 基于SLR技术的卫星精密定轨[D]. 郑州: 中国人民解放军信息工程大学, 2003. )" |