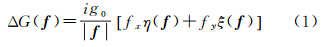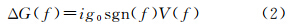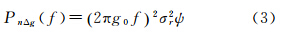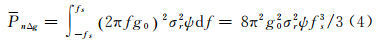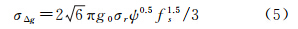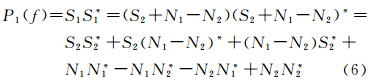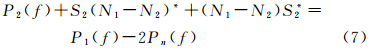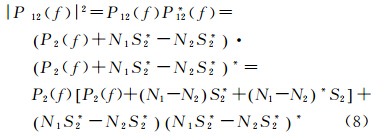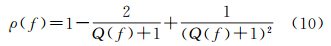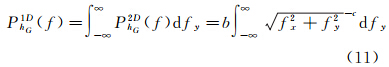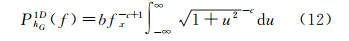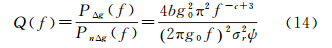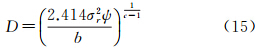重力异常反演精度和空间分辨率是衡量重力场模型的重要参数，数据源的精度和反演方法是影响重力异常反演精度和空间分辨率的两大因素。从目前的研究现状来看，由卫星测高数据反演重力场的方法可分为两类。一类是以大地水准面高为数据源[1,2]，另一类以大地水准面梯度，即垂线偏差为数据源[3,4,5]，此类方法对长波误差的影响不敏感，且能够有效地检测短波信号，较前一类方法具有明显的数值稳定性[6,7]。其中，文献[3]发展起来的沿轨迹垂线偏差法是求解沿轨迹重力异常的常用方法，其基本思想是，根据大地水准面高、重力异常和垂线偏差等扰动场元的定义以及Laplace方程，推导出频率域(波数域)内沿轨迹垂线偏差与重力异常的线性关系式[4,9]。在求解沿轨迹重力异常的基础上，通常采用交叉谱分析法求解沿轨迹空间分辨率[8,10,11]。
除反演方法的影响，海面高确定精度是影响沿轨迹重力异常反演的另一重要因素，文献[12—13]分别采用不同的方法推导了海面高与重力异常的误差传播公式，但仅讨论了海面高中随机误差对重力异常反演精度的影响，未涉及海面高测量过程中的关键载荷雷达高度计测距精度对反演的影响。基于垂线偏差的反演方法，微分运算时有效地削弱了长波误差，例如卫星轨道高度观测量、干湿对流层和电离层校正项、逆气压校正项以及深海区域的海面地形和潮汐，能量主要集中在长波部分[3,14,15,16]，进行微分运算时，在相邻采样点几千米的间隔内，上述物理量的梯度信息可以忽略，而高度计的测距误差可认为是高斯白噪声，微分后噪声幅度增大，因此，定量分析高度计精度对沿轨迹重力异常反演的影响是十分必要的。
2 沿轨迹重力异常和空间分辨率的求解方法 2.1 求解沿轨迹重力异常的垂线偏差法
根据物理大地测量理论，大地水准面高hG的x轴(西向)分量η和y轴(北向)分量ξ与重力异常Δg的关系可表示为
式中，f(fx,fy)为二维频率点，fx=1/λx、fy=1/λy，λx、λy为波长，
ΔG(f)、η(f)和ξ(f)分别为Δg、η和ξ的二维傅里叶变换，g0为平均重力加速度(9.81ms-2)，i为复数虚部。实际测量中，雷达高度计采集沿星下点轨迹的一维数据，为此，需将式(1)转换为一维表达式，以用于沿轨迹重力异常的计算，具体过程见文献[4]和[9]，即
式中，sgn( )为符号函数；V(f)为沿轨迹垂线偏差v的傅里叶变换，v=∂hG/∂ψ，ψ为沿轨迹的空间采样间隔。式(2)表明，1×10－6rad的垂线偏差误差对应1×10－5ms-2的重力异常误差。
2.2 求解空间分辨率的交叉谱分析法
式(2)描述了采样间隔为ψ尺度上的沿轨迹重力异常计算式，根据奈奎斯特准则得，所能确定的最短重力场波长为2ψ。然而，由于噪声的影响，最短波长将大于2ψ，即空间分辨率大于ψ。通常采用交叉谱分析法求解空间分辨率。
对于同一地面轨迹地球重力场信号的两次采样s1和s2，S1和S2分别为s1和s2傅里叶变换，则各自的功率谱密度P1(f)和P2(f)以及交叉功率谱密度P12(f)表示为：P1(f)=S1S1*、P2(f)=S2S2*、P12(f)=S1S2*，*为复数共轭运算，则交叉谱分析中一致性系数ρ(f)定义为：ρ(f)=P12(f)2/P1(f)P2(f)。地球重力场包含丰富的波长信息，将采样序列分解成一系列代表固定波长的频率点，一致性系数评估了两次采样序列在不同波长处的相关程度。若在两次采样过程中，均没有引入噪声，即两序列完全相同，ρ(f)在频域内处处为1，则能够确定的最短重力场波长为采样间隔的2倍，即空间分辨率等于采样间隔。在实际的采样过程中，噪声的引入使得各频率点处的信号相关程度下降，ρ(f)界于0与1之间，由于地球重力场的功率谱密度随着频率的增大而减小，因此信号的相关程度在高频部分比低频部分下降明显，ρ(f)随着频率的增加逐渐减小到0，当ρ(f)=0.5时，将此处的1/f作为空间分辨率的估计[8,10,11]。
3 高度计测距精度对沿轨迹重力异常反演精度的影响
由式(2)知，分析高度计测距误差对沿轨迹重力异常的影响，需先分析高度计误差对垂线偏差的影响。根据卫星测高的基本原理，在计算沿轨迹垂线偏差时，对高度计的测距值r进行微分，测距噪声同样进行微分运算，微分后功率谱密度为2πf2Pnr(f)，其中Pnr(f)为高度计测距噪声的功率谱密度，因此可以认为，垂线偏差中由高度计测距噪声引入的噪声功率谱密度为Pnv(f)=2πf2Pnr(f)。高度计测距噪声可认为是高斯白噪声。根据随机信号理论，高斯白噪声的功率谱密度Pnr(f)=n0，n0为正常数。当采样频率为Fs，功率谱密度在频域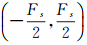
内积分得平均功率，而平均功率等于方差，即
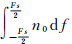=n0Fs=σr2，其中σr2为高度计测距噪声的方差，所以Pnr(f)=n0=σr2/Fs，而Fs=1/ψ，因此，垂线偏差中由高度计测距噪声引入的噪声功率谱密度为Pnv(f)=2πf2σr2ψ，再联合式(2)得，沿轨迹重力异常中由高度计测距噪声引入的噪声功率谱密度为
4 高度计测距精度对沿轨迹空间分辨率的影响
首先推导交叉谱分析中一致性系数与信噪比的数学表达式，再以此为基础，理论分析高度计测距精度对空间分辨率的影响。
对同一信号s的两次采样序列s1=s+n1、s2=s+n2，n1、n2为均值为零、方差相同、互不相关的噪声，且均与s不相关，设S、S1、S2、N1、N2分别为以上空域序列的傅里叶变换，s、s1和s2的功率谱密度分别为：Ps(f)=SS*、P1(f)=S1S1*、P2(f)=S2S2*，n1、n2的功率谱密度为Pn(f)=N1N1*=N2N2*。有s1=s2+n1－n2，s1的功率谱密度为
n1和n2互不相关，有N1N2*=N2N1*=0，式(6)变为P1(f)=P2(f)+S2(N1－N2)*+(N1－N2)S2*+2Pn(f)，得 交叉功率谱密度P12(f)=S1S2*=P2(f)+N1S2*－N2S2*，则 将式(7)代入式(8)得P12(f)2=P2(f)[P1(f)－2Pn(f)]+(N1S2*－N2S2*)(N1S2*－N2S2*)*。因n1、n2、s两两互不相关，有N1S2*=N1(S+N2)=0，N2S2*=N2(S*+N2*)=Pn(f)，则|P12(f)|2=P2(f)P1(f)－2Pn(f)+Pn2(f)，得一致性系数 式中，P1(f)=Ps(f)+SN1*+N1S*+Pn(f)=Ps(f)+Pn(f)，同理P2(f)=Ps(f)+Pn(f)，频率点f处的信噪比Q(f)=Ps(f)/Pn(f)，代入式(9)得一致性系数ρ(f)与Q(f)的关系为 式中，频率点f处信噪比Q(f)=Ps(f)/Pn(f)，其具体含义为：在频率点f附近很小的领域内，分别对信号和噪声的功率谱密度Ps(f)和Pn(f)进行积分，得出信号功率和噪声功率，两者相除得到在频率点f处的信噪比，由于在频率点f附近很小的领域内积分，信噪比可表示为Q(f)=Ps(f)/Pn(f)。由式(10)知，当ρ(f)=0.5时，Q(f)=2.414。
若已知沿轨迹重力异常与其噪声的功率谱密度，则可求得信噪比为2.414所对应的频率点f0.5，从而计算1/f0.5为空间分辨率。大地水准面高短波部分的功率谱密度为[17]：PhG2D(f)=b|f|－c。其中b、c为大于零的常数，与区域地质结构相关。f(fx,fy)为二维频率点，|f|=
。在沿地面轨迹的一维方向[18]
由式(3)知沿轨迹重力异常的噪声功率谱密度，在频率点f处信噪比Q(f)为
当Q(f)=2.414时，得空间分辨率D=1/f为
上式表明，高度计测距精度σr提高m倍，相应的空间分辨率D提高m2c－1倍。因常数b和c与区域地质结构密切相关，所以空间分辨率因区域的不同而不同。对于全球平均空间分辨率的估计，可利用大地水准面高短波部分的全球平均功率谱密度函数，通过上述推导过程得出。例如EGM2008模型短波部分的功率谱密度函数中的常数b=1.611×10－19，c=5.306(文献[19])，则全球平均空间分辨率为
上式表明，高度计测距精度提高m倍，全球平均空间分辨率提高m0.4644倍。 5 数值仿真及结果分析
考虑到仿真结果的验证，选取文献[8]和[10]中均涉及的两个区域以及Geosat卫星的精密重复轨道模式为例，分析高度计测距精度对沿轨迹重力异常精度和空间分辨率的影响。两区域的地理位置为：大西洋赤道附近区域A，30°S—30°N，0°W—50°W；南太平洋区域B，65°S—40°S，90°W—165°W。
具体仿真框图见图 1，将Geosat GDR(geophysical data record)中0.1s间隔的海面高测量数据平均为0.5s的数据，则空间采样间隔为3.37km，将其中1s间隔的地面轨迹位置数据插值成0.5s的位置数据[20]，并采用EGM2008重力场模型根据文献[21]中的相关公式计算沿卫星地面轨迹的大地水准面高和重力异常，并将此重力异常值作为参考值，依据卫星测高数学模型和沿轨迹重力异常的垂线偏差反演方法，对加入高度计噪声的沿轨迹大地水准面高进行微分、滤波，截至频率fs取1/16cyc/km，将处理后得到的重力异常估计值与重力异常参考值进行比较，得到沿轨迹重力异常的估计精度。采用交叉谱分析法计算空间分辨率的估计值，最后将仿真结果与文献[8]和[10]中Geosat卫星的实际测高数据处理结果比较，从而验证仿真模拟以及理论分析的正确性。
 |
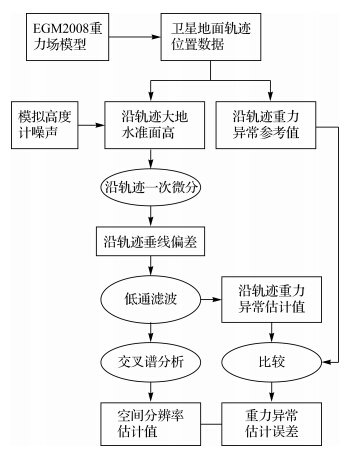| 图 1 沿轨迹重力异常精度和空间分辨率仿真框图 Fig. 1 Simulation scheme for accuracy and spatial resolution of along-track gravity anomaly |
在区域A和B内，Geosat卫星高度计的实际精度分别为3.2cm和4.9cm(文献[20])。当区域A加入的高度计测距噪声为3.2cm时，沿轨迹重力异常精度的仿真结果为4.63×10－5ms-2，与文献[8]中对实际测高数据的处理结果4.68×10－5ms-2基本一致。当区域B加入的高度计噪声为4.9cm时，沿轨迹重力异常精度的仿真结果为7.08×10－5ms-2，略小于文献[8]中的处理结果7.36×10－5ms-2，是因为实际测高数据中包含了海洋现象中短波成分引入的噪声。数值仿真结果与实际测高数据处理结果基本一致，证明了沿轨迹重力异常精度数值仿真设计的正确性。
图 2为两区域内不同高度计测距精度对应的沿轨迹重力异常精度仿真结果，理论值由式(5)得出。仿真结果表明：当加入的高度计噪声相同时，沿轨迹重力异常精度的仿真结果相同；重力异常精度与高度计测距精度成正比关系；两区域沿轨迹重力异常精度与理论值基本一致，证明了沿轨迹重力异常误差分析的正确性。
 |
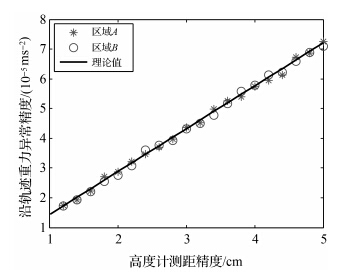| 图 2 沿轨迹重力异常精度随高度计测距精度的变化 Fig. 2 Accuracy of along-track gravity anomalies versus altimeter noise |
当区域A加入的高度计噪声为3.2cm时，其空间分辨率的仿真结果见图 3。其中，图 3(a)为沿轨迹重力异常和其噪声的功率谱密度，图 3(b)中虚线为一致性系数曲线，实线为其多项式拟合趋势线。从中可以看出，重力异常的功率谱密度随着频率增加而下降。噪声的功率谱密度先随着频率的增加而增大，是由微分运算引起的，之后下降是低通滤波器作用的结果。当一致性系数下降到0.5处时，信噪比为2.414，空间分辨率为31.9km，与文献[10]中实际空间分辨率估计结果33km基本一致。当区域B加入的高度计噪声为4.9cm时，空间分辨率的仿真结果为49.5km，见图 4，略小于文献[10]中实际空间分辨率估计结果52km，因为实际数据中包含了海洋现象中短波成分引入的噪声。两区域空间分辨率的数值仿真结果与文献[10]中实际空间分辨率的估计结果基本一致，证明了空间分辨率数值仿真设计的正确性。从图 3和图 4中可以看出信噪比与一致性系数的对应关系，当一致性系数下降到0.5时，信噪比均为2.414，证明了一致性系数与信噪比的表达式(式(10))理论推导的正确性。
 |
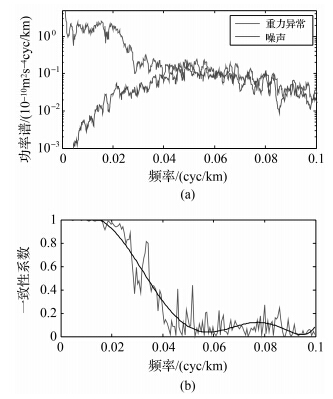| 图 3 区域A功率谱密度和一致性系数 Fig. 3 Power spectral density and coherence versus frequency(1/wavelength) for area A |
 |
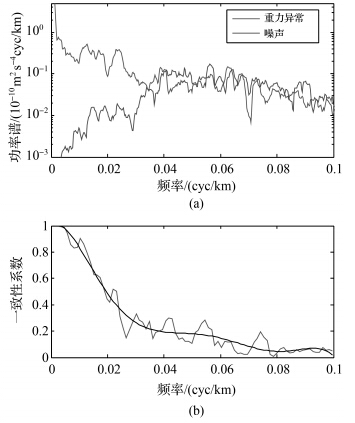| 图 4 区域B功率谱密度和一致性系数 Fig. 4 Power spectral density and coherence versus frequency(1/wavelength) for area B |
当高度计测距精度从5cm提高到1cm时，图 5和图 6分别为区域A和区域B的一致性系数多项式拟合曲线。比较两图，共同点：空间分辨率随着高度计测距精度的提高而提高；不同点：高度计测距精度相同时，区域A和区域B的空间分辨率存在明显差异。因为区域地质结构是影响短波重力场功率谱密度的主要因素，相比于区域A，区域B的断裂破碎带较少，海底地形较为平缓，所以，两区域的重力异常功率谱密度不同，可以从图 3(a)和图 4(a)中看出。当高度计测距精度相同时，重力异常噪声的功率谱密度相同，由于两区域的重力异常功率谱密度不同，则对应于信噪比为2.414的频率点不同，即空间分辨率不同，因此，高度计测距精度对区域A和区域B空间分辨率的影响存在差异。
 |
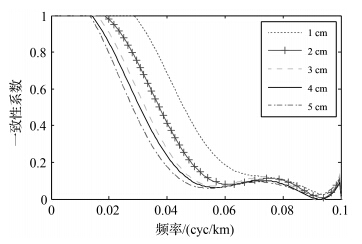| 图 5 不同高度计测距精度下区域A的一致性系数 Fig. 5 Comparison of smoothed coherence between different altimeter noise for area A |
 |
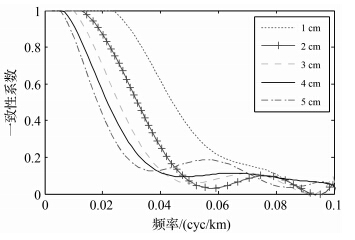| 图 6 不同高度计测距精度下区域B的一致性系数 Fig. 6 Comparison of smoothed coherence between different altimeter noise for area B |
图 7为两区域在不同高度计测距精度下，空间分辨率的变化图，对数据进行幂函数拟合得出，两区域空间分辨率DA、DB与高度计测距精度σr的关系为：DA=1.329×105σr0.4238，DB=2.221×105σr0.4891，拟合相关系数分别为0.9894和0.9937，说明空间分辨率与高度计测距精度成幂函数的关系，验证了式(15)的正确性。将拟合表达式中的参数代入式(15)得：bA=5.358×10-21、cA=5.720、bB=1.120×10-18、cB=5.089。当高度计测距精度提高m倍，区域A和区域B的空间分辨率分别提高m0.4238和m0.4891倍。采用式(16)对全球平均空间分辨率进行估计，如图 7所示，即高度计测距精度提高m倍，全球平均空间分辨率提高m0.4644倍。
 |
| 图 7 空间分辨率随高度计测距精度的变化 Fig. 7 Spatial resolution versus altimeter noise |
基于卫星测高的数学模型和沿轨迹重力异常的反演方法，本文开展了高度计测距精度与沿轨迹重力异常反演精度以及空间分辨率的关联性研究，以Geosat卫星的高度计数据为对象进行仿真，并通过与相关文献中实测数据的处理结果比较，验证了理论分析的正确性，得到如下主要结论：
(1) 根据求解沿轨迹重力异常的垂线偏差法，给出沿轨迹重力异常的误差传播方程，得出沿轨迹重力异常的反演精度与高度计测距精度成正比关系。
(2) 推导出交叉谱分析法中一致性系数与信噪比的解析关系，得出当一致性系数为0.5时信噪比为2.414的结论，为沿轨迹空间分辨率的估计提供了新的解决思路。
(3) 以上述结论为基础，建立了空间分辨率与高度计测距精度的关联性模型，表明空间分辨率与高度计测距精度成幂函数的关系，即高度计测距精度提高m倍，全球平均空间分辨率提高m0.4644倍。
| [1] | GOPALAPILLAI S. Non-global Recovery of Gravity Anomalies from a Combination of Terrestrial and Satellite Altimetry Data [D]. Columbus: Ohio State University, 1974. |
| [2] | RAPP R H. Gravity Anomaly Recovery from Satellite Altimetry Data Using Least Squares Collocation Techniques[D].Columbus: Ohio State University, 1974. |
| [3] | SANDWELL D T, SMITH W H F. Marine Gravity Anomaly from Geosat and ERS-1 Satellite Altimetry[J].Journal of Geophysical Research,1997,102(B5): 10039-10054. |
| [4] | WANG Haiying, WANG Guangyun. Inversion of Gravity Anomalies from Along-track Vertical Deflections with Satellite Altimeter Data and Its Applications[J]. Acta Geodaetica et Cartographica Sinica, 2001, 30(1): 21-26. (王海英,王广运. 卫星测高数据的沿轨迹重力异常反演法及其应用[J]. 测绘学报,2001, 30(1): 21-26.) |
| [5] | HWANG C. Inverse Vening Meinesz Formula and Deflection-geoid Formula: Applications to the Predictions of Gravity and Geoid over the South China Sea[J]. Journal of Geodesy, 1998,72(5):304-312. |
| [6] | HUANG Motao, ZHAI Guojun, GUAN Zheng, et al. On the Recovery of Gravity Anomalies from Altimeter Data[J]. Acta Geodaetica et Cartographica Sinica, 2001,30(5):179-184.(黄漠涛,翟国君,管铮,等. 利用卫星测高数据反演海洋重力异常研究[J].测绘学报, 2001,30(5):179-184.) |
| [7] | OLGIATI A, BALMINO G, SARRAILH M, et al. Gravity Anomalies from Satellite Altimetry: Comparison between Computation via Geoid Heights and via Deflections of the Vertical[J]. Bulletin Géodésique, 1995, 69(4): 252-260. |
| [8] | SANDWELL D T, MCADOO D C. High-accuracy, High-resolution Gravity Profiles from 2 Years of the Geosat Exact Repeat Mission[J]. Journal of Geophysical Research, 1999,95(C3): 3049-3060. |
| [9] | FU L L, CAZANAVE A. Satellite Altimetry and Earth Sciences [M]. San Diego:Academic Press, 2001. |
| [10] | SANDWELL D T, YALE M M, SMITH W H F. Comparison of Along-track Resolution of Stacked Geosat, ERS-1 and TOPEX Satellite Altimeters [J]. Journal of Geophysical Research, 1995, 100(B8): 15117-15127. |
| [11] | SANDWELL D T, SMITH W H F. Global Marine Gravity from Retracked Geosat and ERS-1 Altimetry: Ridge Segmentation Versus Spreading Rate [J]. Journal of Geophysical Research, 2009, DOI: 10.1029/2008JB006008. |
| [12] | ZHAI Zhenhe, SUN Zhongmiao. Spherical Harmonic Analysis of Error Propagation between Mean Gravity Anomaly and Sea Surface Height Data [J]. Journal of Geodesy and Geodynamics, 2010, 30(2): 137-140. (翟振和,孙中苗. 海面高数据与平均重力异常误差传播的球谐分析[J]. 大地测量与地球动力学,2010, 30(2): 137-140.) |
| [13] | PENG Fuqing, CHEN Shuangjun, JIN Qunfeng. Influence of Altimetry Errors on Marine Geopotential Recovery [J]. Journal of Geodesy and Geodynamics, 2014, 43(4): 337-340. (彭富清,陈双军,金群峰. 卫星测高误差对海洋重力场反演的影响[J]. 测绘学报, 2014, 43(4): 337-340.) |
| [14] | SANDWELL D T, SMITH W H F, GILLE S, et al. Bathymetry from Space: White Paper in Support of a High-resolution, Ocean Altimeter Mission[C]//Proceedings of High-resolution Ocean Topography Science Working Group Meeting.[S.l.]: CEOAS, 2001. |
| [15] | BAO L, XU H, LI Z. Towards a 1 mGal Accuracy and 1 min Resolution Altimetry Gravity Field[J]. Journal of Geodesy, 2013, 87(10-12): 961-969. |
| [16] | SANDWELL D, GARCIA E, SOOFI K, et al. Toward 1-mGal Accuracy in Global Marine Gravity from CryoSat-2, Envisat, and Jason-1[J]. The Leading Edge, 2013, 32(8): 892-899. |
| [17] | TURCOTTE D L. A Fractal Interpretation of Topography and Geoid Spectra on the Earth, Moon, Venus, and Mars[J].Journal of Geophysical Research, 1987, 92(B4): 597-601. |
| [18] | MAUS S, DIMRI V. Depth Estimation from the Scaling Power Spectrum of Potential Fields[J].Geophysical Journal International, 1996, 124(1): 113-120. |
| [19] | JEKELI C. Omission Error, Data Requirements, and the Fractal Dimension of the Geoid[C]//VII Hotine-Marussi Symposium on Mathematical Geodesy. Berlin: Springer, 2012: 181-187. |
| [20] | LILLIBRIDGE J, CHENEY R. The Geosat Altimeter JGM-3 GDRs on CD-ROM[R]. Silver Spring: National Oceanographic Data Center,1997. |
| [21] | NING Jingsheng, LIU Jingnan, CHEN Junyong, et al. Theory and Technology of Modern Geodesy[M]. Wuhan: Wuhan University Press, 2006.(宁津生,刘经南,陈俊勇,等. 现代大地测量理论与技术[M]. 武汉:武汉大学出版社,2006.) |