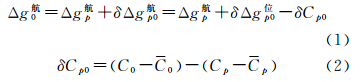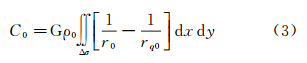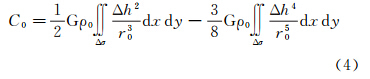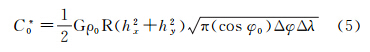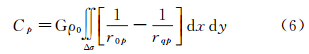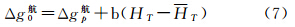2. 海军工程大学导航工程系,湖北 武汉 430033;
3. 武汉大学测绘学院,湖北 武汉 430079
2. Department of Navigation, Naval University of Engineering, Wuhan 430033, China;
3. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
自20世纪80年代末由于高精度卫星定位系统的发展,使得航空重力测量技术取得实质性突破以来,航空重力测量数据向下延拓问题一直受到极大的关注,国内外学者为此开展了深入研究并提出了许多不同类型的解算方法,具有代表性的主要有梯度法、最小二乘配置法、FFT法、点质量方法等[1, 2, 3],但目前在实际应用中,大多仍沿用传统的球面Poisson积分方法解决此问题,即求逆Poisson积分方法,包括不同形式的迭代求解和非迭代求解法[4, 5]。文献[6]研究了航空重力测量数据向不规则面(包括地面)延拓的可能性,提出了顾及地形高度但无密度假设的向下延拓方法。文献[7—9]先后提出直接代表法和球内Dirichlet法。但由于重力场向下延拓计算在数学上属于不适定反问题,其解算过程存在不稳定性是该问题本身固有的一种属性,即很小的观测噪声也可能引起模型解严重偏离真解[10, 11]。因此,无论是早期的逆Poisson积分迭代求解法,还是后期的最小二乘配置法和FFT法,都无法确保向下延拓解算结果是绝对稳定有效的。针对此问题,自20世纪末以来,国内外学者的注意力一致投向将正则化方法引入到航空重力测量向下延拓这个典型的不适定反问题解算中来,其研究成果可谓层出不穷[12, 13, 14, 15, 16, 17, 18, 19]。但必须指出的是,航空重力测量向下延拓计算结果的有效性不仅取决于解算方法的稳定性,同时取决于航空重力观测数据的噪声特性[20]。从已有研究成果看,在3km计算高度上,即使采用有针对性的正则化处理方法,向下延拓解算精度一般也只能达到±(3~5)mGal(mGal=10-5m/s2)的水平[3, 9, 15, 20]。而要想取得这样的精度,还需要在观测高度归一化、观测数据网格化、边缘效应处理和模型参数选择等多个方面作出不懈的努力。总之,现有的航空重力测量向下延拓方法仍需要作进一步的改进和完善。为此,笔者曾从另一角度出发,提出了一种基于外部数据源、独立于观测数据的向下延拓方案[20]。针对海域重力场的变化特点,文献[20]提出了直接利用超高阶重力场模型计算延拓改正数的实用方法,其解算结果的稳定性不再受到航空重力观测噪声的干扰,突破了向下延拓不适定问题的技术瓶颈,同时显著简化了其计算过程和解算难度,取得了较好的解算效果[20]。本文继续沿用这种“差分”思路将该方法拓展应用到陆部,提出联合使用超高阶位模型和地形高数据,实施陆部航空重力向下延拓总改正数的计算,以飞行高度面与地面对应点的位模型差分信息表征总改正数的中长波分量,以相对应的局部地形改正差分修正量表征总改正数的中高频成分,从而实现航空重力数据点对点向地面的全频段延拓。在地形变化不同区域,联合使用EGM2008位模型、地面实测重力和高分辨率高程数据进行了实际数值计算、精度评估和对比分析,证明该方法是可行有效的,具有推广应用价值。
2 计算模型与适用性分析 2.1 利用位模型和地形信息计算延拓改正数 2.1.1 问题的提出
如引言所述,针对海域重力场的变化特点,笔者已在文献[20]中提出了直接利用超高阶重力场模型计算海域延拓改正数的实用方法。由于EGM2008模型在建模时已经充分利用了当时最好的卫星测高数据集[21],因此在海域使用该模型计算航空重力测量向下延拓改正数,能够取得较高精度的归算结果[20]。但在地形变化比较复杂的陆部,EGM2008模型的适用性如何还不得而知。文献[22]利用我国大陆GPS水准高程异常和地面平均空间重力异常数据,对EGM2008模型在我国陆部的符合度进行了评估,本文利用多个部门在我国及邻近海域测量获得的1500多万个船测重力数据,对EGM2008位模型进行了外部检核,现将两部分比对结果汇总于表 1。
| mGal | ||||||
| 参量 | 最小值 | 最大值 | 平均值 | 标准差 | 均方根 | 点数 |
| EGM2008-船测点值 | -42.6 | 40.6 | -0.0 | 5.9 | 5.9 | 15226669 |
| EGM2008-5′×5′平均值 | -141.3 | 170.8 | 1.2 | 10.6 | 10.7 | 覆盖中国大陆 |
| EGM96-5′×5′平均值 | -183.6 | 203.8 | 1.8 | 24.9 | 30.0 | 覆盖中国大陆 |
从表 1比对结果可以看出,EGM2008模型对我国海域重力场的逼近度较高,已接近于我国现役航空重力仪的测量精度水平(±(3~5)mGal)[23, 24],而在表征我国大陆地区5′×5′重力异常方面,尽管与EGM96相比,EGM2008模型的逼近度已经有了较大幅度的提高,但比对误差仍超过±10mGal。此结果说明,在我国陆部单纯使用位模型计算延拓改正数,不会取得理想的结果,在地形变化比较剧烈的山区,情况更是如此。为了改善位模型延拓改正数的计算精度,必须考虑在原有基础上增加陆部重力场高频信息的作用。地形是一种可见的重力场高频信息,在局部范围内,空间重力异常与地形的相关度可达0.95以上[8]。因此,联合利用位模型和地形信息确定延拓改正数,成为本文研究思路的基本出发点。
2.1.2 基于差分局部地形改正的延拓归算模型
由高等物理大地测量学得知[5],Molodensky边值问题解是通过计算G1、G2、G3、…各项改正来顾及地球表面形态变化的。在Bjerhammar边值理论中,地形质量影响则是通过解析延拓手段间接转移到等效重力异常或虚拟点质量上来的。文献[4—5]将G1分解为两项G1=G11+G12,同时证明了G11正好是将地面重力异常“延拓”到海平面的空间改正,而G12的Stokes积分又相当于从海平面“回到”地面的高程异常改正[25]。当重力异常与地形高度呈线性相关时,可证明局部地形改正C和G1项改正是近似等价的。以上情况说明,局部地形改正是表征地球重力场高频信息的一类关键参量,在局部重力场逼近计算中具有非常重要的作用。重力位模型由于受空间分辨率的限制,高频含量明显不足,因此很难在表示地球重力场局部特征方面有所作为,局部地形改正参量正好能够弥补这方面的缺陷。空中一点重力异常的高频分量随高度增大而衰减,空中测点与对应地面投影点局部地形改正数之差异,正是这种高频信号衰减的量化体现。据此,本文提出陆部航空重力测量向下延拓计算模型,见式(1)和式(2)
式(1)和式(2)中,Δg航0代表待求的地面重力异常;Δg航p代表空中观测重力异常;δΔg航p0代表实际的航空重力测量向下延拓改正数;δΔg位p0代表由位模型计算得到的延拓改正数;δCp0代表由地形信息计算得到的延拓改正数;Cp代表空中测点P的局部地形改正数;Cp代表一定网格大小范围内Cp的平均值;C0为与空中测点相对应的地面投影点O的局部地形改正数;C0代表一定网格大小范围内C0的平均值。式(1)右端δCp0前面为减号,是因为这里要求恢复地形效应的影响,与传统的去除地形效应正好相反。需要指出的是,在式(2)中分别扣除p和0的影响,是因为在式(1)的计算模型中已经考虑了位模型中长波信息的作用。为了顾及δCp0和δΔg位p0两部分改正数频谱特征的匹配问题,在实际应用中,Cp和C0平均值的计算网格大小可取为5′×5′,即与EGM2008位模型的空间分辨率保持一致。局部地形改正可按照文献[26]提出的球面公式进行严密计算,但考虑到叙述方便起见,这里仍采用平面近似方式给出相应的计算模型。计算O点处的局部地形改正数C0时,不管是高出计算点部分(h-h0>0),还是低于计算点部分(h-h0<0),其地形改正数均为正值。C0的统一计算式为[25]
或写为 式中,Δh=h-h0;r20=(x-x0)2+(y-y0)2;r2q0=(x-x0)2+(y-y0)2+(h-h0)2;G为引力常数;ρ0=2.67g/cm3为地壳密度;h0和h分别代表地面计算点O和积分流动点Q的高程;(x0,y0)和(x,y)分别代表O点和Q点的平面坐标。为了避免奇异积分问题,计算点中心方块的地形改正量由式(5)计算 式中,R为地球平均半径;hx和hy分别代表计算点在经圈和纬圈方向上的地形梯度。
计算空中测点P的局部地形改正数Cp时,仍然选择与其相对应的地面投影点O作为地形高程面,此时高出O点高程面部分的地形改正数为负值(h0-hp>h-hp),低于O点高程面部分的地形改正数为正值(h0-hp
在实际应用中,一般使用数值积分完成式(3)和式(6)的计算,式(4)更适合使用FFT技术进行解算,但当使用特别高分辨率的地形数据(如3″×3″甚至1″×1″)时,由于不能确保Δh/r0≤1,式(3)无法近似过渡到式(4),此时需对核函数作非奇变换[27],因此必须注意,使用式(4)是有前提条件的。空中测点和地面点局部地形改正计算各参量之间的几何关系见图 1。
不难看出,本文提出的延拓计算模型即式(1),同样适用于陆海交界区域的重力向下延拓解算。当计算点从陆区向海域延伸时,局部地形差分改正数δCp0将逐步减小;当计算点距离陆地地形超出局部地形改正积分半径时,差分改正数δCp0为零。2.2 基于差分层间地形改正的延拓归算模型
文献[7]曾依据空中一点重力异常主要与其相应地面一定区域内的重力异常大小相关联这一事实,提出直接使用空中测点重力异常代替相应地面方块平均重力异常的延拓归算方案,简称直接代表法。文献[8]在此基础上,提出了利用地形信息改善直接代表法的改进型延拓归算方案,其基本思想是:首先通过使用空中测点重力异常代表相应地面方块平均重力异常的方法,确定地面投影点重力异常的主项,然后利用地形信息补充该主项的高频分量,最终按式(7)完成延拓归算[8]
文献[8]的数值试验结果表明,利用式(7)作为延拓归算模型的主要缺陷是,延拓计算值与地面观测值之间存在一个比较明显的系统性偏差。这显然跟直接使用空中测点重力异常作为地面点重力异常的主项存在不确定性有关。实际上,随着飞行高度的增大,空中测点重力异常不仅高频分量在衰减,中低频分量也在衰减。因此,在Δg航0和Δg航p之间,除了由地形质量引起的高频分量差异外,还应包括由高度差引起的中低频分量差异。本文在式(1)中特别引入位模型延拓改正数项δΔg位p0,其作用就是为了补偿由高度差引起的中低频分量衰减。为了对比分析不同方法的计算效果,这里特意列出现行国家军用标准选用的直接代表法模型即式(7)[28],并在后面的数值检核中一同给出其计算结果。因式(7)右端第二项实为地面投影点与平均高程点的层间改正互差,故将式(7)称为基于差分层间地形改正的延拓归算模型。
2.3 新方法特点分析
本文方法的最大特点是,向下延拓改正数计算过程完全独立于航空重力测量观测数据,不受观测噪声的影响,更重要的是,不受向下延拓不适定反问题解算过程固有的不稳定性影响。如前所述,由于空中一点重力异常的高频分量随高度增大而衰减,因此相比较而言,空中重力场变化要比地面重力场平缓是不言而喻的。而从理论上讲,要想通过求解传统的逆Poisson积分方程,单纯由变化相对平缓的空中重力异常信息恢复包含更多高频分量的地面重力异常,几乎是不可能的。即使能够获取一部分高频信息,那也是观测噪声被放大后的虚假的重力异常信息。因此从这个角度上讲,传统延拓方法一直存在理论上的缺陷。本文方法的独特之处正是完全避开了传统方法的弊端,首先利用超高阶地球位模型恢复延拓改正数的中长波部分,然后利用地形信息恢复地面重力场的高频分量,从而实现航空重力测量数据向地面的全频延拓。
3 精度分析与数值检核
3.1 精度分析
由式(1)知,本文提出的陆部航空重力测量向下延拓计算模型精度,主要取决于位模型延拓改正数δΔg位p0和局部地形差分改正数δCp0的计算精度。笔者曾对位模型延拓改正数δΔg位p0的计算精度做过理论估算[20],其中,在5km延拓高度上,由位模型系数误差引起的延拓改正数计算误差不超过2.5mGal,由位模型阶次截断引起的延拓改正数计算误差不超过2.8mGal。因在式(1)中已经引入局部地形差分改正数,来补偿位模型缺失的高频分量,故在新模型中不需考虑后一项位模型截断误差的影响。又由文献[25—27] 分析结果知,在具备高精度和高分辨率数字地形模型条件下,局部地形差分改正数的计算误差完全可以控制在1mGal以内。因此,从理论上讲,新模型中两项延拓改正数的总体估算精度应优于3mGal。但必须指出的是,新模型的实际计算精度还受多种不确定因素的影响,包括位模型在陆部逼近度的非均匀性及数字地形模型精度和分辨率水平的不一致性等。
3.2 数值检核
3.2.1 检核方法与试验数据
检验向下延拓计算模型精度最有效的方法是,直接使用航空和地面实际重力观测数据求互差作为基准值,将由新模型计算得到的延拓改正数与基准值进行比较,由此可得到新模型计算精度的评价指标。遗憾的是,陆部同时拥有高精度航空和地面实际重力观测数据的区域并不多见,目前笔者还缺乏这方面的可靠资料。为此,本文改用向上与向下延拓比对方法对新模型计算精度进行外部检核,即首先利用地面网格重力和地形高数据,通过向上延拓方法计算一定高度面上的空间重力异常,进而求取地面与计算高度面重力异常的互差,将此互差值分别与单独由位模型计算得到的改正数(即文献[20]中的式(8))及由式(1)、式(7)计算得到的延拓改正数进行逐一比较,即可获得相应延拓归算模型的精度评价。由于向上延拓过程是稳定可靠的,因此其解算结果可作为检核向下延拓计算结果的基准值。这里考虑到向上延拓的Poisson积分方程是球面公式,当地形起伏较大时,利用球面向上延拓公式推算低空重力异常精度难以得到保证[4]。为此,本文改用虚拟点质量方法进行地面重力异常向上延拓计算,具体解算模型可参见文献[25]和[27]。因点质量模型以最简单的方式顾及了地形效应,故向上延拓解算结果更接近实际[27]。
本文选用的试验区包括两个区块,一个位于我国大陆中部,区块大小为3°×3°(称为区块1),属于地形变化相对比较平缓的中等山区;另一个位于美国大陆南部,区块大小为4°×4°(称为区块2),属于地形变化比较剧烈的大山区。区块1和2分别拥有1′×1′和2′×2′网格地面重力异常数据,同时拥有30″×30″地形高数据。两个区块所对应的重力和地形数据变化特征如表 2统计结果所示。
试验区块1的平均地形高为358m,最大高程为1698m。据此,这里取飞行高度(相对椭球面高)hp=3km,进行地面重力异常Δg地向上延拓计算,首先解算得到3km高度面上的空间重力异常Δgh,进而计算相对应的延拓改正数基准值δΔg地=Δg地-Δgh。又利用EGM2008位模型和地面30″×30″地形高数据,分别按文献[20]中的式(8)计算位模型延拓改正数δΔg位,按式(1)计算位模型和差分局部地形改正的延拓总改正数δΔg位局=δΔg位-δC,按式(7)计算差分层间地形改正的延拓改正数δΔg层=b(HT-T)。将基准值δΔg地分别同以上3组计算值δΔg位、δΔg位局和δΔg层作比较,可得到相应的精度评估信息。表 3为地面和3km高度面局部地形改正计算值统计结果,具体比对结果见表 4。
为了说明单独使用位模型计算延拓改正数的精度并不完全取决于位模型自身的绝对精度[20],表 4第2行同时给出了同一区域位模型重力异常与地面实测网格重力的比对结果。从表 4可以看出,位模型重力异常与地面观测重力比对的系统性偏差超过1mGal、均方根误差超过9mGal,但由位模型计算延拓改正数的精度仍达到了6mGal,加上局部地形改正差分延拓改正数后的比对精度则提升到了3mGal,系统性偏差减小到0.5mGal。而利用层间地形改正模型进行延拓计算的比对效果并不十分理想,均方根误差接近6mGal。这个结果说明,将本文提出的差分模式应用于陆部航空重力测量数据延拓处理,能够取得较高精度的延拓解算结果。
3.2.3 区块2检核结果
为了进一步了解各种计算方案在地形变化剧烈山区的适用性,这里继续在表 2所示的区块2进行与表 4相类同的数值检核。其中,考虑到区块2的平均地形高为1987m,最大高程为4116m,实施地面重力异常向上延拓计算时,特别把飞行平均高度改取为hp=5km,其他参量保持不变。表 5为地面和5km高度面局部地形改正计算值统计结果,具体比对结果见表 6。图 2同时给出了(δΔg地-δΔg位)和(δΔg地-δΔg位局)的等值线图,从图 2可清晰看出,单独由位模型计算得到的延拓改正数误差(见图 2(a))明显与地形变化幅度大小有关;由位模型和局部地形改正差分得到的延拓改正数与地面实测数据解算结果则具有很好的一致性(见图 2(b)),误差分布比较均匀,不存在明显的边缘效应。
从表 6结果可以看出,即使在地形变化剧烈的大山区,由位模型计算延拓改正数的精度仍达到了5.71mGal,加上局部地形改正差分延拓改正数后的比对精度则提升到了2.97mGal,系统性偏差很小。而利用层间地形改正模型计算延拓改正数的效果明显失效。对比表 4和表 6计算结果不难看出,地形变化剧烈大山区(即区块2)的比对效果还略好于地形变化相对平缓的区块1,这个结果也从另一个侧面说明,EGM2008模型在美国本土的符合度要明显高于在我国的符合度,与该模型在建模时已经使用了美国本土比较高精度和高分辨率重力及地形数据这一事实相符。
为了从另一个侧面说明本文新方法的有效性,这里进一步采用文献[19]介绍的逆Poisson积分正则化方法,将由点质量模型向上延拓计算得到的3km高度(对应区块1)和5km高度(对应区块2)上的重力异常,分别向下延拓到两个区块的平均地形高度,然后将向下延拓计算结果与地面已知重力异常作比较,可得到向下延拓计算模型的精度评价指标,其结果见表 7。
由于这里采用的空中重力异常是由点质量模型向上延拓计算得到的,因此它与地面已知重力异常之间形成闭环关系,即相当于不存在通常意义下的观测误差,向下延拓计算结果与已知值互差所反映的应当是纯粹的计算模型误差。对比表 7和表 4、表 6计算结果可以看出,即使没有观测噪声的干扰,逆Poisson积分正则化方法的延拓计算比对效果,无论是系统偏差还是均方根误差指标,都不及本文提出的新方法。此外,从计算过程看,新方法不需要对观测重力做网格化处理,能够实现点对点延拓计算也是传统逆积分方法无法比拟的。
4 结论与建议
前面的理论分析和数值检核结果表明,利用EGM2008模型和地形信息计算延拓总改正数,将陆部航空重力数据向地面延拓是可行有效的,具有很好的推广应用价值。
(1) 联合使用超高阶位模型和地形信息进行陆部航空重力数据向下延拓解算,在5km高度下,其理论估计精度优于±3mGal;在地形变化剧烈的大山区,实际比对精度达±3mGal。此结果与当前国际航空重力测量精度水平相当,因此使用新方法不会显著降低航空重力测量成果质量。
(2) 利用本文方法计算向下延拓改正数,不仅简化了向下延拓计算过程,更重要的是可获得稳定可靠的解算结果。同时相对降低了航空重力测量测线布设要求,不需要对观测数据作高度归一化和网格化处理,可直接对不同高度的测点进行点对点计算。
(3) 本文方法计算效果优于传统的直接代表法和逆积分正则化方法,建议尽早对现行的国家军用标准相关内容作必要的修改。
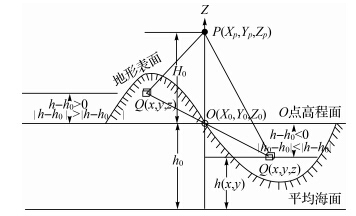
图 1 局部地形改正参量几何关系
Fig. 1 Geometry relations of parameters in topographic correction computations
参量 最小值 最大值 平均值 标准差 均方根
区块 重力/mGal -43.1 104.5 -8.7 17.6 19.6
1 高程/m 27.0 1698.0 358.5 241.9 432.5 区块 重力/mGal -96.2 167.2 5.5 40.1 40.5
2 高程/m 1056.0 4116.0 1987.3 436.1 2034.5
mGal 高度/km 最小值 最大值 平均值 标准差 均方根
0 0.06 17.20 1.10 1.20 1.63
3 -19.29 51.16 -0.02 7.24 7.24
mGal 参量 最小值 最大值 平均值 标准差 均方差
Δg地-Δg地 -49.98 63.70 -1.13 9.47 9.54
δΔg地-δΔg位 -29.81 31.63 -0.52 6.29 6.31
δΔg地-δΔg位局 -15.35 21.11 -0.52 3.13 3.17
δΔg地-δΔg层 -30.96 37.46 -0.84 5.70 5.76
mGal 高度/km 最小值 最大值 平均值 标准差 均方根
0 0.13 28.73 2.06 2.17 2.99
5 -61.92 87.15 -0.05 10.38 10.38
mGal 参量 最小值 最大值 平均值 标准差 均方差
Δg地-Δg地 -53.43 87.89 0.09 9.90 9.90
δΔg地-δΔg位 -34.67 39.61 -0.38 5.69 5.71
δΔg地-δΔg位局 -24.64 17.38 -0.38 2.95 2.97
δΔg地-δΔg层 -87.38 48.57 -1.65 9.06 9.21 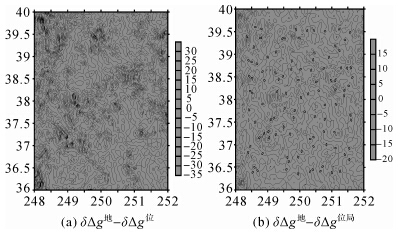
图 2 地面数据延拓改正数与模型计算值互差等值线图
Fig. 2 Maps of continuation correction differences between the true and model values
mGal 参量 最小值 最大值 平均值 标准差 均方差
区块1 -54.38 9.81 -0.75 3.32 3.41
区块2 -66.53 12.07 -1.52 3.92 4.21
| [1] | MUELLER F, MAYER-GUERR T. Comparison of Downward Continuation Methods of Airborne Gravimetry Data[C]//International Association of Geodesy Symposia Volume 128: A Window on the Future of Geodesy. Berlin: Springer, 2003: 254-258. |
| [2] | TZIAVOS I N, ANDRITSANOS V D, FORSBERG R, et al. Numerical Investigation of Downward Continuation Methods for Airborne Gravity Data[C]//International Association of Geodesy Symposia Volume 129: Gravity, Geoid and Space Missions. Berlin: Springer, 2005: 119-124. |
| [3] | WANG Xingtao, XIA Zheren, SHI Pan, et al. A Comparison of Different Downward Continuation Methods for Airborne Gravity Data[J]. Chinese Journal of Geophysics, 2004, 47(6): 1017-1022. (王兴涛, 夏哲仁, 石磐, 等. 航空重力测量数据向下延拓方法比较[J]. 地球物理学报, 2004, 47(6): 1017-1022.) |
| [4] | HEISKANEN W A, MORITZ H. Physical Geodesy[M]. San Francisco: Freeman W H and Company, 1967. |
| [5] | MORITZ H. Advanced Physical Geodesy[M]. Karlsruhe: Herbert Wichmann Verlag, 1980. |
| [6] | JEKELI C. The Downward Continuation of Aerial Gravimetric Data without Density Hypothesis [J]. Bulletin Géodésique, 1987, 61(4): 319-329. |
| [7] | SHI Pan, WANG Xingtao. The Frequence Domain Analysis for the Determination of Terrestrial Mean Gravity Anomaly Using Airborne Gravimetry[J]. Acta Geodaetica et Cartographica Sinica, 1995, 24(4): 301-308. (石磐, 王兴涛. 空中测量地面平均重力异常的频域分析[J]. 测绘学报, 1995, 24(4): 301-308.) |
| [8] | SHI Pan, WANG Xingtao. Determination of the Terrain Surface Gravity Field Using Airborne Gravimetry and DEM[J]. Acta Geodaetica et Cartographica Sinica, 1997, 26(2): 117-121. (石磐, 王兴涛. 利用航空重力测量和DEM确定地面重力场[J]. 测绘学报, 1997, 26(2): 117-121.) |
| [9] | SHI Pan, SUN Zhongmiao. The Solution to the Problem of the Spherical Interior Dirichlet and Its Application[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(3): 195-198. (石磐, 孙中苗. 球内Dirichlet问题解及其应用[J]. 测绘学报, 1999, 28(3): 195-198.) |
| [10] | KELLER W, HIRSCH M. Downward Continuation versus Free-air Reduction in Airborne Gravimetry [C]//International Association of Geodesy Symposium Volume 112: Geodesy and Physics of the Earth. Heidelberg, Berlin: Springer Verlag, 1992, 266-270. |
| [11] | WANG Yanfei. Computational Methods for Inverse Problems and Their Applications[M]. Beijing: Higher Education Press, 2007. (王彦飞. 反演问题的计算方法及其应用[M]. 北京: 高等教育出版社, 2007.) |
| [12] | KERN M. An Analysis of the Combination and Downward Continuation of Satellite, Airborne and Terrestrial Gravity Data [D]. Calgary: University of Calgary, 2003. |
| [13] | HWANG C, HSIAO Y S, SHIH H C, et al. Geodetic and Geophysical Results from a Taiwan Airborne Gravity Survey: Data Reduction and Accuracy Assessment [J]. Journal of Geophysical Research, 2007, 112(B4), DOI: 10.1029/2005JB004220. |
| [14] | ALBERTS B. Regional Gravity Field Modeling Using Airborne Gravimetry Data[C]//Publications on Geodesy 70. Delft: Netherlands Geodetic Commission, 2009. |
| [15] | WANG Xingtao, SHI Pan, ZHU Feizhou. Regularization Methods and Spectral Decomposition for the Downward Continuation of Airborne Gravity Data[J]. Acta Geodaetica et Cartographica Sinica, 2004, 33(1): 33-38. (王兴涛, 石磐, 朱非洲. 航空重力测量数据向下延拓的正则化算法及其谱分解[J]. 测绘学报, 2004, 33(1): 33-38.) |
| [16] | GU Yongwei, GUI Qingming. Study of Regularization Based on Signal-to-noise Index in Airborne Gravity Downward to the Earth Surface[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 458-464. (顾勇为, 归庆明. 航空重力测量数据向下延拓基于信噪比的正则化方法的研究[J]. 测绘学报, 2010, 39(5): 458-464.) |
| [17] | JIANG Tao, LI Jiancheng, WANG Zhengtao, et al. Solution of Ill-posed Problem in Downward Continuation of Airborne Gravity[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 684-689. (蒋涛, 李建成, 王正涛, 等. 航空重力向下延拓病态问题的求解[J]. 测绘学报, 2011, 40(6): 684-689.) |
| [18] | DENG Kailiang, HUANG Motao, BAO Jingyang, et al. Tikhonov Two-parameter Regulation Algorithm in Downward Continuation of Airborne Gravity Data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 690-696. (邓凯亮, 黄谟涛, 暴景阳, 等. 向下延拓航空重力数据的Tikhonov双参数正则化法[J]. 测绘学报, 2011, 40(6): 690-696.) |
| [19] | WU Taiqi, DENG Kailiang, HUANG Motao, et al. An Improved Singular Values Decomposition Method for Ill-posed Problem[J]. Geomatics and Information Science of Wuhan University, 2011, 36(8): 900-903. (吴太旗, 邓凯亮, 黄谟涛, 等. 一种改进的不适定问题奇异值分解法[J]. 武汉大学学报: 信息科学版, 2011, 36(8): 900-903.) |
| [20] | HUANG Motao, OUYANG Yongzhong, LIU Min, et al. Practical Methods for the Downward Continuation of Airborne Gravity Data in the Sea Area[J]. Geomatics and Information Science of Wuhan University, 2014, 39(10): 1147-1152. (黄谟涛, 欧阳永忠, 刘敏, 等. 海域航空重力测量数据向下延拓的实用方法[J]. 武汉大学学报: 信息科学版, 2014, 39(10): 1147-1152.) |
| [21] | PAVLIS N K, HOLMES S A, KENYON S C, et al. The Development and Evaluation of the Earth Gravitational Model 2008 (EGM2008)[J]. Journal of Geophysical Research, 2012, 117(B4), DOI: 10.1029/2011JB008916. |
| [22] | ZHANG Chuanyin, GUO Chunxi, CHEN Junyong, et al. EGM 2008 and Its Application Analysis in Chinese Mainland[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4): 283-289. (章传银, 郭春喜, 陈俊勇, 等. EGM2008地球重力场模型在中国大陆适用性分析[J]. 测绘学报, 2009, 38(4): 283-289.) |
| [23] | SUN Zhongmiao, ZHAI Zhenhe, LI Yingchun, et al. Concurrent Flight Test of LaCoste & Romberg (LCR) Airborne Gravimeter Ⅱ and Ⅰ System [J]. Journal of Geodesy and Geodynamics, 2012, 32(2): 24-27. (孙中苗, 翟振和, 李迎春, 等. LCRⅡ型和Ⅰ型航空重力仪的同机飞行试验[J]. 大地测量与地球动力学, 2012, 32(2): 24-27.) |
| [24] | OUYANG Yongzhong, DENG Kailiang, LU Xiuping, et al. Tests of Multi-type Airborne Gravimeters and Data Analysis[J]. Hydrographic Surveying and Charting, 2013, 33(4): 6-11. (欧阳永忠, 邓凯亮, 陆秀平, 等. 多型航空重力仪同机测试及其数据分析[J]. .海洋测绘, 2013, 33(4): 6-11) |
| [25] | LI Jiancheng, CHEN Junyong, NING Jinsheng, et al. Theory of the Earth's Gravity Field Approximation and Determination of China Quasi-geoid 2000[M]. Wuhan: Wuhan University Press, 2003. (李建成, 陈俊勇, 宁津生, 等. 地球重力场逼近理论与中国2000似大地水准面的确定[M]. 武汉: 武汉大学出版社, 2003.) |
| [26] | ZHANG Chuanyin, CHAO Dingbo, DING Jian, et al. Precision Topographical Effects for any Kond of Field Quantities for any Altitude[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(1): 28-34. (章传银, 晁定波, 丁剑, 等. 球近似下地球外空间任意类型场元的地形影响[J]. 测绘学报, 2009, 38(1): 28-34.) |
| [27] | HUANG Motao, ZHAI Guojun, GUAN Zheng, et al. The Determination and Application of Marine Gravity Field[M]. Beijing: Surveying and Mapping Press, 2005. (黄谟涛, 翟国君, 管铮, 等. 海洋重力场测定及其应用[M]. 北京: 测绘出版社, 2005.) |
| [28] | HEADQUARTERS OF GENERAL EQUIPMENT OF PLA. GJB 6561—2008, Rules for Operations of Airborne Gravimetry[S]. Beijing: Military Standard Press of the Headquarters of General Equipment, 2008. (中国人民解放军总装备部. GJB 6561—2008, 航空重力测量作业规范[S]. 北京: 总装备部, 2008.) |