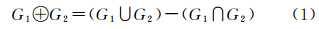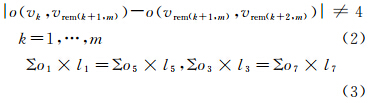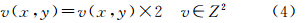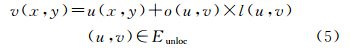网络示意性地图(network schematic map)使用抽象的图形符号来表示物体,着重展示网络自身结构,而忽略其他信息。在地图服务领域,示意图被广泛应用于公交线路、地铁线路等公共交通系统。不同于一般地图,示意性地图模糊了地理精度,当地理精度的重要性低于连接、邻接和相对位置关系时,这种灵活变通的制图方法是可行且有效的[1]。
地图示意化具有不同的几何和美学准则,其共同的目标是简化图形、保留网络信息以及易于理解。绘制网络示意图不仅耗费时间而且需要专业的制图人员。当网络规模较大或是需要经常更新时,手工绘制或者使用绘图软件就显得不切实际。针对示意图的自动生成,存在相关研究工作,整体思路是“化简+匹配”。文献[2]使用迭代的方法简化路径并将其离散为线段,根据线段转角及相邻线段长度建立价值函数,以判定形状的适度性;文献[3, 4, 5, 6, 7]采用Douglas-Peucher算法对路径进行化简,并通过基于梯度下降的优化算法迭代移位约束网络路径线段的方位;近似的还有文献[8, 9]中的研究;文献[10]基于动态分段,将延续性好的道路合并为一条路径,依据重要度由高到低以路径为单元对道路网进行示意化,生成图形具有良好的路径延续性且更加简化。以上算法以路径为单位对网络进行示意化,提出一系列约束优化路径线段位置,并不能严格限定输出路径方向,同时在移动顶点方位时要对相关路径上所有顶点的坐标值进行修正,需进行大量的计算来维持网络拓扑一致性。文献[11, 12]提出了一种相对简单且有效的示意图生成算法,将顶点定位在其原始位置,并以两段或三段限制方向的线段替代输入路段,然后依照连接顺序自上而下依次排列各线段。然而其未提供处理路径冲突的方法,如果输入路径不符合设定的示意化条件将不会被示意化,且生成图形不够简化。
路网规模较大情况之下,路径的相互交错会形成诸多闭合多边形(道路网眼)。从拓扑上来讲,闭合多边形相较于非闭合的线段(悬垂路段)要重要得多,因为悬垂路段并不会对网络的连通性造成影响[13, 14]。与此同时,闭合多边形具有相对独立性,以闭合多边形为单位划分网络,那么对于单个多边形来说,其余多边形均在其外部。鉴于此,本文以闭合多边形为基本单位,通过依次将其示意化图形映射至当前映射图形的外部空间,对网络空间进行再分配生成规范的网络示意图。本算法简化了拓扑检查过程,对于一般复杂道路网络示意图生成具有较强实用性。 2 理论基础与约束过程 2.1 基本概念
多边形[15]:平面上一条非自相交的有向封闭曲线形成的图形为多边形。将曲线分割成线段a1、a2、...、an,分割点位于多边形的邻接点。线段a=(u,v)是顶点u与v的有序偶对,称u与v是边a的端点,u为起点,v为终点,a是u和v的关联线段。
多边形图[15, 16]:多边形图G由一系列简单多边形路径构成,这些多边形互不相交,除非享有共同边。多边形图不包含任何未成回路线段,多边形间具有邻接、相离与内含3种拓扑关系。
度[17]:图G中与顶点v关联的线段的数目称为v在G中的度(degree),记作deg(v)。度为0的顶点为孤立点,度为1的顶点为悬挂点,与悬挂点关联的线段为悬挂边。
多边形和:多边形图G1与多边形图G2的并集中去掉G1与G2的交集,所得到的图称作G1与G2的多边形和,记作G1 ⊕ G2,即
2.2 约束过程参照建立网络示意图的一般约束[18, 19],建立本算法示意化的约束条件:①拓扑一致,目标网络应与输入网络保持拓扑一致;②方向规范,示意化路径方向应仅包含水平、垂直或对角线方向;③路径长度适宜,目标网络路径长度应大于某个最小限制以使图形清晰;④路径无重叠,非相交路径间距应大于某个最小距离限制以使图形清晰;⑤示意化后的路径方向应尽可能地接近其原始方向。
本文使用规则网格空间来存放目标网络示意图,将示意化问题描述为:如何满足以上约束条件将原始网络图形映射至规则网格空间(R2→Z2)。定义顶点的位置为网格,每个顶点占据一个网格,同一网格只能被一个顶点占据;路径为直线,且只能平行于网格线,即路径方向固定为90°及其倍数(仅在处理重复路径时使用45°线);路径之间不能出现交叉或重叠,间距最小为一个网格。
图 1展示了原始网络向目标网格空间映射的整个流程。其主要思路即分离原始网络非闭合线段得到多边形图,通过多边形生长算法将多边形图映射至网格空间,然后恢复分离点线得到完整的网络示意图。上述过程中,重点在于如何将多边形图依照约束映射至规则网格空间。多边形图的映射过程就像起始多边形这颗种子不断地聚合相邻的多边形,因此,将这种算法称为“多边形生长算法”。
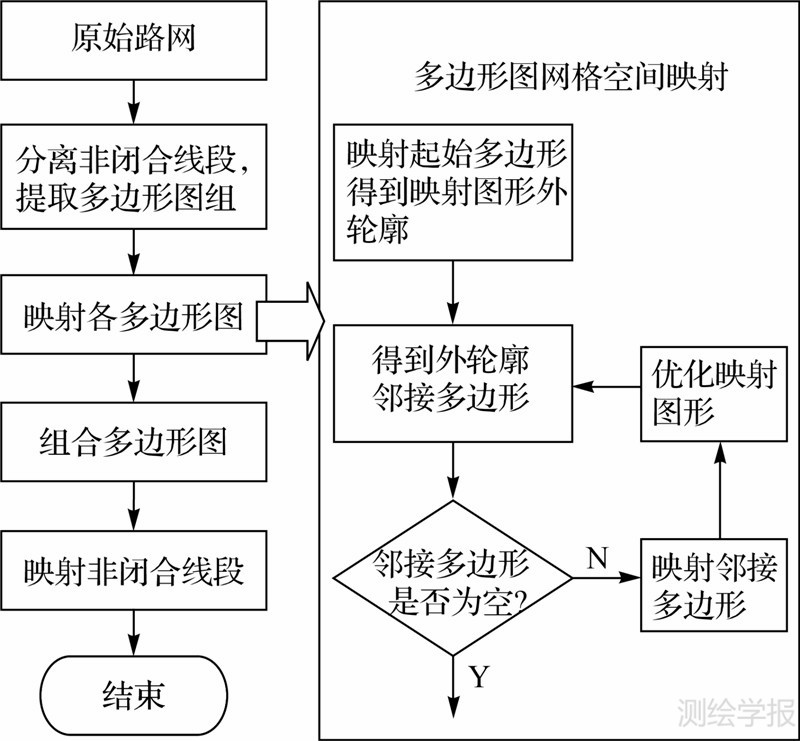 |
| 图 1 网络映射流程图Fig. 1 Flow chart of network mapping |
原始地理数据中不存在多边形这种几何类型,首先对数据进行处理,提取得到多边形图。
(1) 将网络看作图结构G=(V,E),建立顶点-顶点、顶点-线段、线段-线段关联矩阵。
(2) 简化对拓扑关系无影响的图形结构。若一对顶点连接几条不同的线段则将其简化为一条,若线段的两个端点是同一个顶点,则删除此线段。
(3) 分离悬挂点和线段。迭代分离图中deg(v)=1的点及其关联线段分别记入链表结构SprtPointList与SprtLineList。
(4)分离非相邻多边形组。若存在空间关系上分离或包含的多边形(组),则需将其分离为独立多边形组分别进行映射。通过查找无法构成多边形的线段来分离多边形组,如图 2所示,若多边形(组)A与B非相邻,则连接线段序列(v1,v2)不存在于任何多边形中。分离后的多边形组去除连接线段序列后得到的图形即为多边形图。
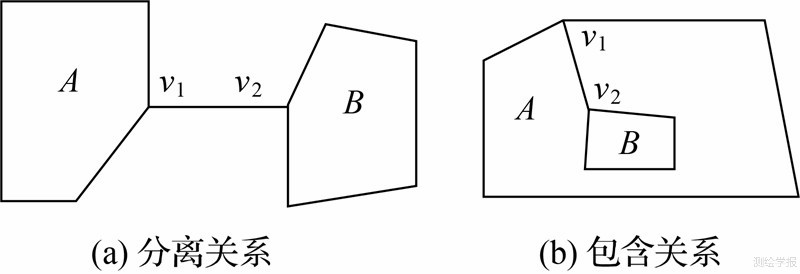 |
| 图 2 非相邻多边形组Fig. 2 Non-adjacent polygons |
(5) 依次遍历多边形图中的顶点提取图中所有多边形。使用左转算法[20]提取多边形,简单描述为以任意顶点o为坐标原点,自o起,选择与点相通的任意一条相邻线段(o,a),然后,以a为原点,获得a点所有关联线段的方位角,记方位角的最大值为αmax,最小值为αmin。如果αao为最小方位角,则取αmax的边为下一搜索线段;如果αao不是最小方位角,取次小于αao的边为下一搜索线段。依次向下搜索直到回到o点,得到一个多边形,这个构成顺序是逆时针的。剔除无效的多边形(顶点构成顺序是顺时针)、删除重复多边形,将无重复的多边形组放入BaseDList链表。 3.2 多边形闭合
记多边形Dd中已映射顶点集为Vloc(v1,v2,…,vi),已映射线段集合为Eloc((v1,v2),…,(vi-1,vi)),Dd中未映射顶点集为Vunloc(vj,…,vm),未映射线段集合为Eunloc((vi,vj),…,(vm,v1)),则Dd={Eloc,Eunloc}=((v1,v2),…,(vi,vj),…,(vm,v1))。Dd映射至目标空间即调节Vunloc各点以使映射图形满足约束并闭合。定义规则网格空间Z2方向集合为O={oi,i=1,…,8},其中1-8分别表示右、右上、上、左上、左、左下、下、右下8个方向。若线段(u,v)的实际方向or为u指向v,则其在Z2的方向oz为与or偏差最小的规范方位,即oz={oi,min| or-oi|}。初始化线段(u,v)的长度l(u,v)=1。由于各线段的方向长度在Z2中均发生了改变,初始化的映射图形显然不能闭合。为了使多边形在Z2闭合同时满足约束,须使各边方向在顺序上可行(如向上的线段后不能是向下的线段),同时对应方向线段总长度相等,即
式(2)中rem表示求余数,将式(3)展开,得
Σo1(loc) l1(loc) +Σo1(unloc)l1(unloc)=Σo5(loc)l5(loc) +Σo5(unloc)l5(unloc)
Σo3(loc)l3(loc)+Σo3(unloc)l3(unloc)=Σo7(loc)l7(loc)+Σo7(unloc)l7(unloc)
Vloc中各点位置是不能改变的,因此需要调节Eunloc各线段长度,以适应Eloc。一般原则是扩大总长度较小方向各线段长度使其与相对方向长度相等,有两种特例:
(1) 由于s方向不具有未映射线段而导致其对应t方向各待映射边长度均为初始值1时,总长度仍大于s方向总长度。采取整体放大Z2所有已定位点坐标来使图形满足映射要求,即
(2) 由于s方向上没有线段而导致图形无法闭合。通过自起始点(vi,vj)逐个检索未映映射线的方式,依照逆时针顺序(右-上-左-下),添加辅助线段。
自vi起,依次定位Vunloc各点
需要注意的是,若原始网络拓扑出现自交叉或者多边形结构过于复杂(如某条边呈锯齿状)则无法得到正确的映射图形。 3.3 网络网格空间映射
选取BaseDList中任意多边形作为起始多边形Dstart。此时目标空间为空,设置Dstart上一点v0位于坐标原点,Dstart(v0,v1,…,vn)为顶点自v0逆时针顺序组成矢量。依照3.2节所述映射Dstart中各点。矩阵NS记录网格空间状态,若网格(i,j)被占据则NS(i,j)=1,否则为0。记录当前网格空间映射图形的外轮廓线,outline=Dstart,逆时针顺序。
在现有图形的基础上完成其余多边形的映射。将BaseDList中所有与outline接壤且未被映射的多边形记入AdjDList,依照其与outline最后交点的顺序逆时针方向(图 3)依次定位每个多边形Dd。Dd与outline的交集(已确定位置顶点集)为Vloc,Dd中未确定位置顶点集为Vunloc,在完成每个多边形的映射后都需要更新outline,outline=outline ⊕ Dd。直至AdjDList中所有多边形都完成映射,清空AdjDList,将此时BaseDList中所有与outline接壤且未被映射的多边形记入AdjDList,重复上述过程直至BaseDList中所有多边形完成映射。
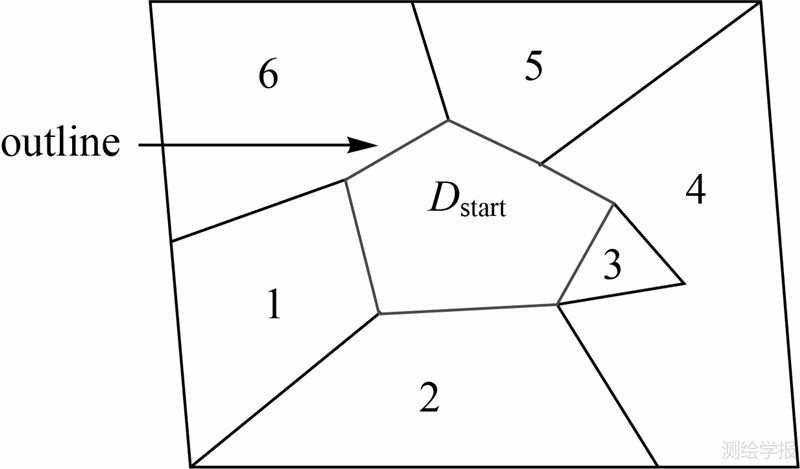 |
| 图 3 相邻多边形映射顺序(图中数字)Fig. 3 Adjacent polygons mapping order (the numbers in the figure) |
图形自R2映射至Z2,线段方向固定为水平竖直必然会出现重叠。对映射后重叠的线段,通过平行偏移的方法来避免重叠。为了保证有足够的空间进行平移,首先将Z2进行整体放大(式(4))。水平方向重叠:将a向上平移一格,若平移后与其他线段产生交叉,则恢复a原位置并将a向下平移一格。竖直方向重叠:将a向左平移一格,若平移后与其他线段产生交叉,则恢复a原位置并将a向右平移一格。如果重复线段a中含有已定位点(a=(vi,vj)或a=(vm,v1)),通过添加辅助点来避免移动已定位点(图 4)。
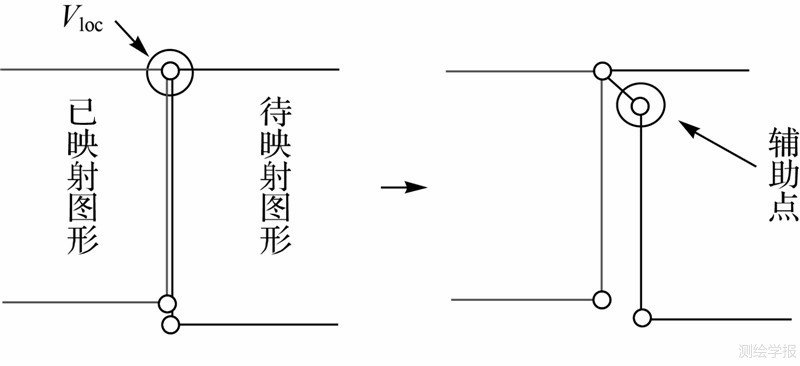 |
| 图 4 线段重叠处理Fig. 4 Segments overlapping |
在处理重叠线段时添加的单位长度45°线会随目标空间一同放大,为了维持目标图形的简化与美观,尝试将45°线转化为90°线。45°线的产生是由于在处理线段重叠时添加了辅助顶点va,va有且仅有两个相邻顶点vb和vc。尝试移动va,使其与vb、vc的连线成水平竖直,若目标网格未被占据则将va移动至目标点,见图 5(a);若目标网格被占据,直接移动会产生重复,则依重复线段方法处理,处理后的45°线最多占用一个网格,见图 5(b)。
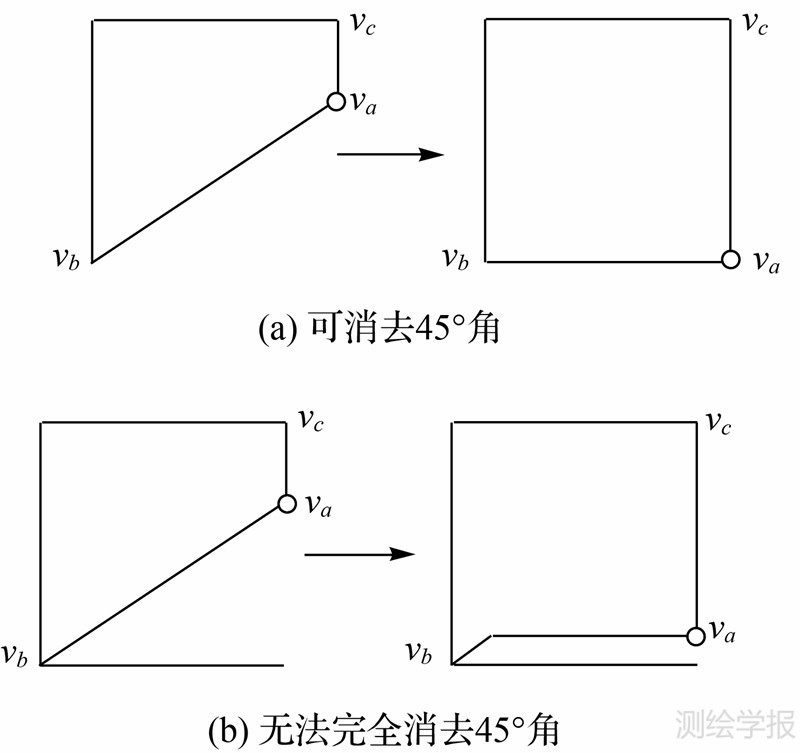 |
| 图 5 45°线转化为90°线Fig. 5 Convert 45° into 90° |
为了满足映射的需要对映射空间进行整体放大会带来空间浪费,并影响图形美观。在不影响拓扑结构的情况下,以行、列为单位删除未使用空间以收缩图形,如图 6中同时向左平移节点C、D、E以避免AC、BE过长。
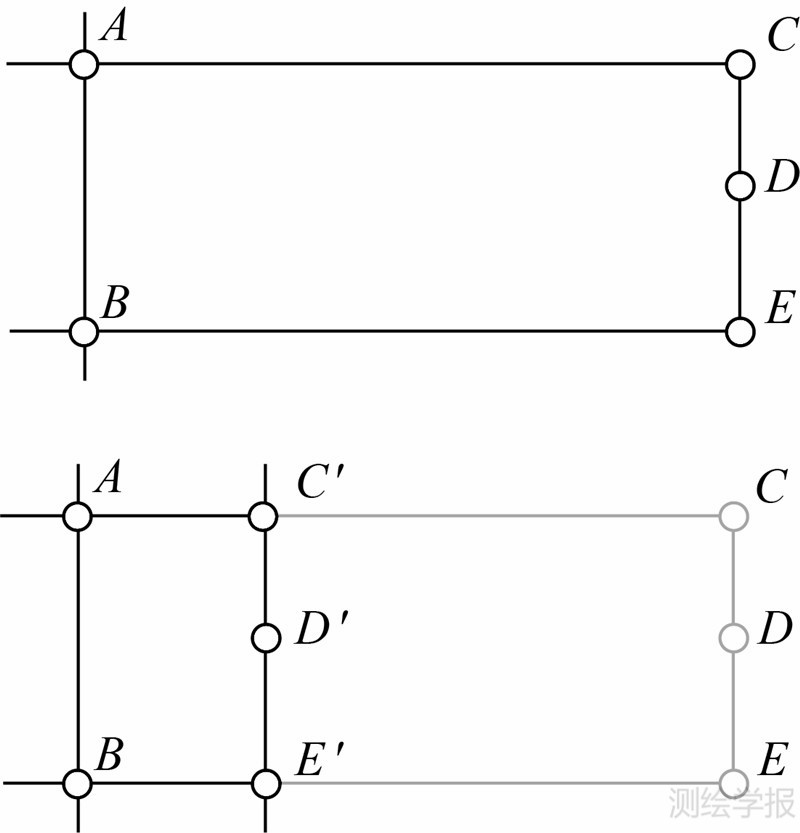 |
| 图 6 收缩图形优化空间分布Fig. 6 Shrinking graph to optimize spatial distribution |
分别对多边形图进行映射后,组合各多边形图。选取复杂度(∑deg(v),v (G)最高的多边形图作为主图Gmain,将其他多边形图G镶嵌至Gmain。多边形图G镶嵌过程如下:①映射连接线段,依照拓扑连接依次映射连接线段组A={a1,a2,...,an}中各线段至Gmain映射空间Zmain2,线段方向为真实的方向近似,长度为1,线段映射空间被占用则放大Zmain2;②镶嵌多边形图,因为已对映射空间进行优化,所以此时G的映射空间即为放置其映射图形的最小空间。将G的映射空间ZG2镶嵌至连接线段an,若Zmain2中空间不足以放置ZG2则放大Zmain2(图 7)。依照原始方位将SprtLineList中分离的非闭合线段映射至目标图形,至此,得到完整的网络示意图表示。
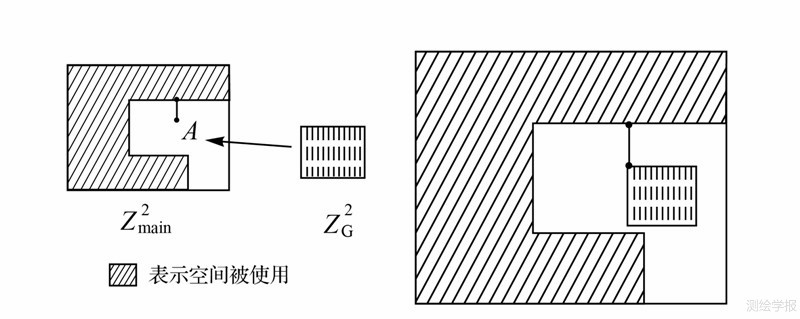 |
| 图 7 组合图结构Fig. 7 Graph structure combination |
开发环境为Matlab2012b,试验数据为美国锡安国家公园部分道路数据(图 9(a)),共计239个顶点,309条边。
经分离悬挂点71个,得到图 8(b)所示结构,图中存在非相邻的多边形组(图 8(b)中灰色线条与黑色线条),故将其分离为两个独立的多边形组。图 8 (c)为主图Gmain提取得到的多边形图,图 8 (d)为经生长算法得到的主图映射图形。经过组合图及非闭合线段映射后的最终图形如图 9(b)所示。
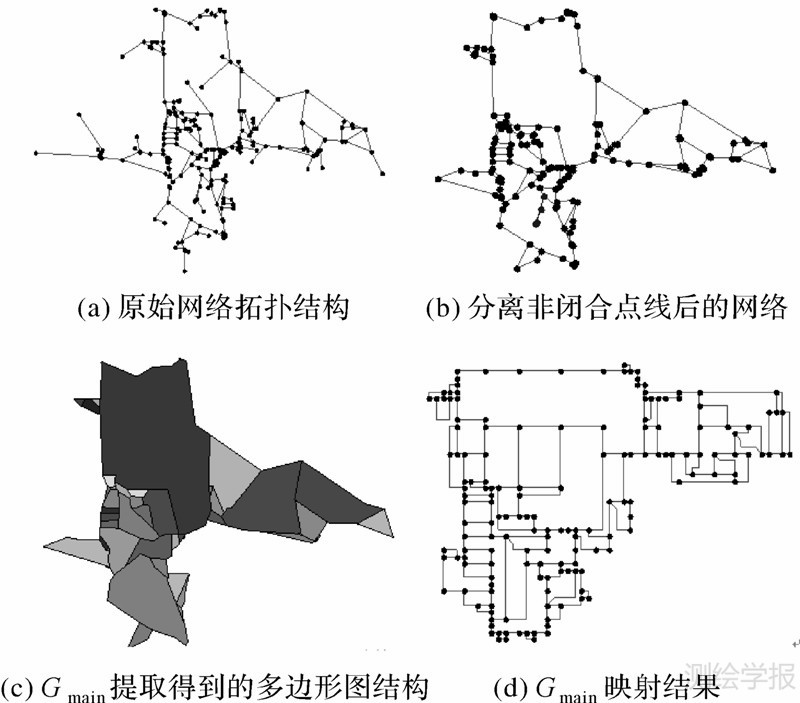 |
| 图 8 算法过程Fig. 8 Algorithm process |
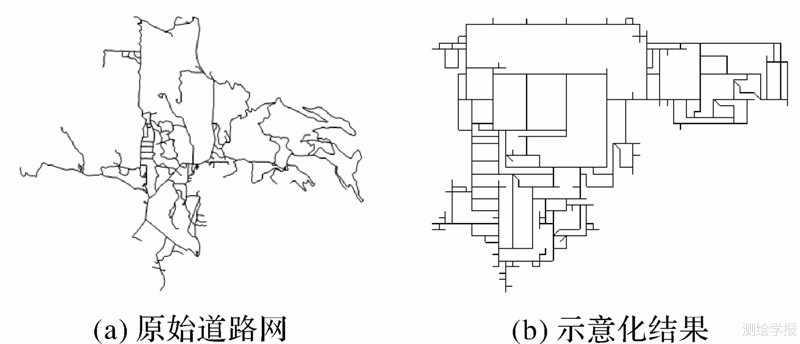 |
| 图 9 试验结果Fig. 9 Experiment result |
图 9(b)中所有路段方向都被示意化为水平、垂直或对角线方向,且与原始网络保持拓扑一致。图 10展示了原始网络以及映射图形中路段长度分布情况:①映射图形路段长度分布总体上与原始地图呈现相似性;②原始地图中相邻顶点间最大最小距离(直线距离)相差249倍,而在映射图形中路段长度最大仅为13个单位网格;③相较于原始路段长度,映射图形路段长度更加集中于较小长度。示意化结果保持了网络的拓扑结构,简化了图形,使网络表达清晰,提高了易读性。
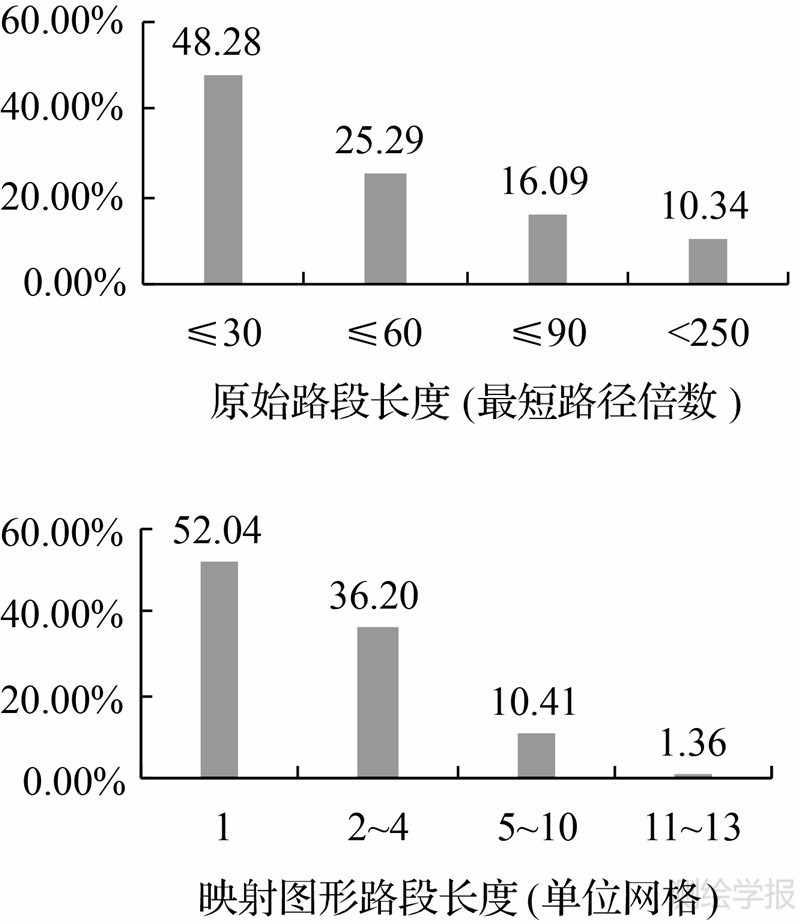 |
| 图 10 映射前后网络路段长度分布Fig. 10 The distribution of network paths length before and after mapping |
将网络空间横竖20等分,计算每部分节点个数,结果如图 11所示。原始网络节点集中在中间,而在映射图形中节点分布则较为均匀,可在一定程度上缓解局部节点集中趋势,增加网络的易读性。
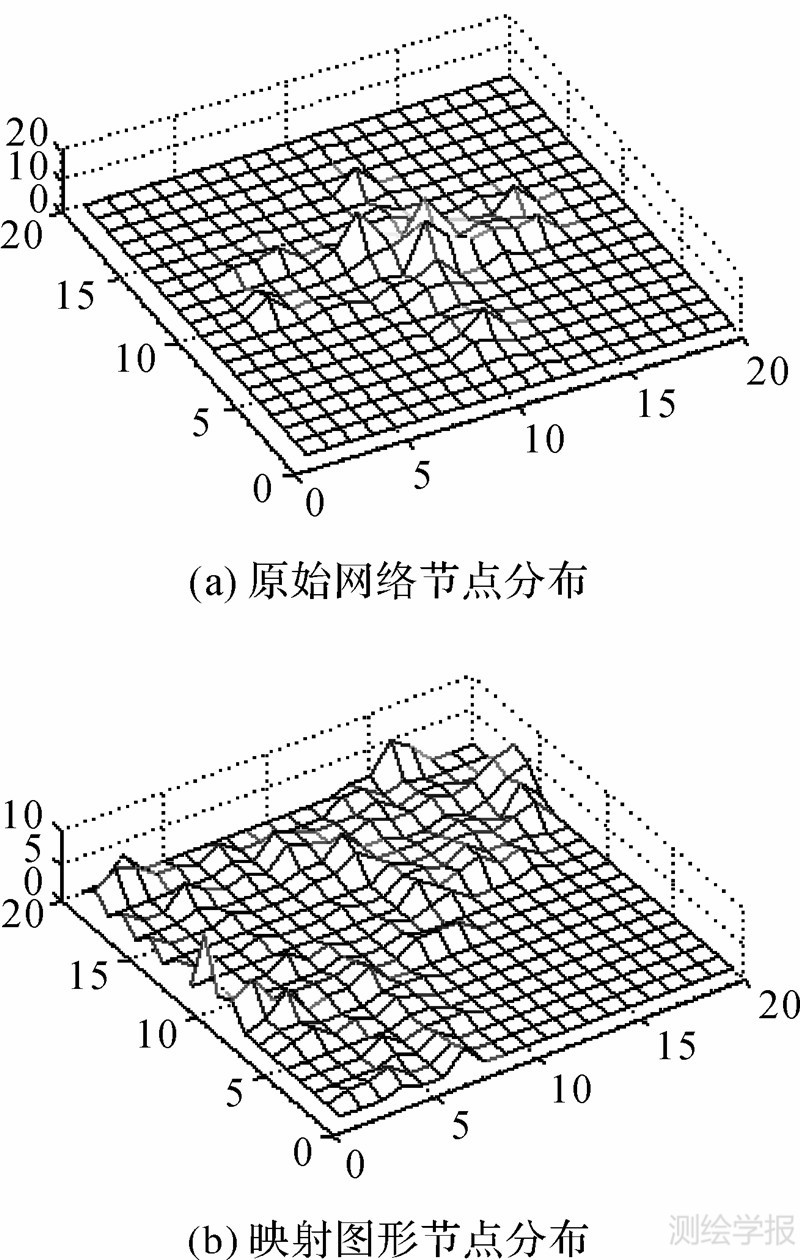 |
| 图 11 映射前后网络节点分布Fig. 11 The distribution of network nodes before and after mapping |
将文献[11]试验数据进行矢量化,并使用本文算法进行示意化,与文献[11, 12]提出的两段替代路径算法的对比试验见图 12。文献[11, 12]的算法以路段为单位进行示意化,限定顶点位于其原始位置,本文以闭合多边形为单位进行示意化,使顶点位置自适应,得到的示意化图形更为简化,拓扑结构更加清晰;由于限定顶点位置,文献[11, 12]的算法在局部点线密集区域不能有效处理路径冲突,如图 12(b)中灰色线段未能被示意化。而本文使用45°线及扩大映射空间处理局部映射区域路径重叠,使符合闭合规则的所有多边形均能被有效示意化。
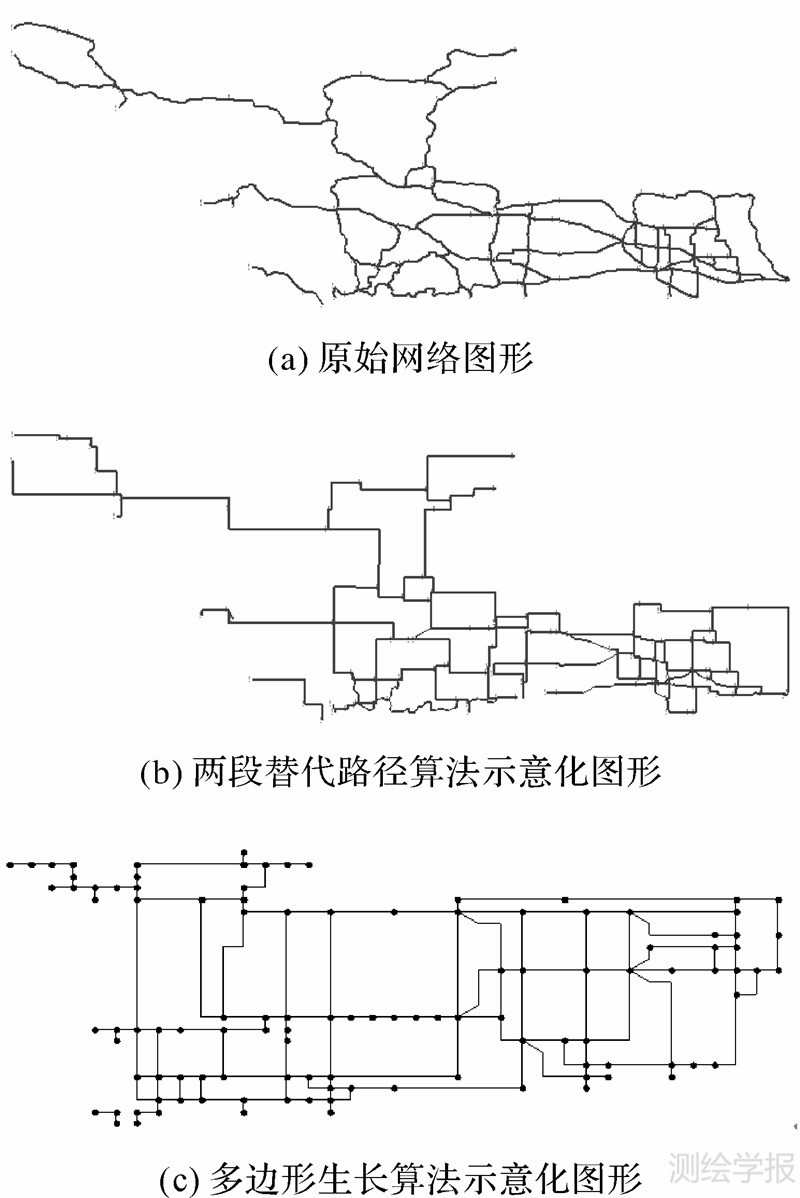 |
| 图 12 与Cabello的两段替代路径算法的对比Fig. 12 The comparison of our algorithm and Cabello’s |
针对附有地理信息的复杂网络拓扑示意图的生成,本文提出了一种基于多边形生长的算法。较之于以前的方法,本算法并非使用迭代移位的方法来优化图形而是基于拓扑关系直接定位点线,避免部分解决拓扑关系冲突的计算,同时这种定位(而非优化)的规则严格地限定了示意图的路径方向。试验结果表明,本算法能够均衡网络路径长度及节点分布,对网络空间分布进行一定优化,使生成的图形更加清晰、易读。
本算法仍有许多可改进的地方。目前算法仅考虑了节点之间的部分方向信息,而没有参考图形的长度信息,可以看出示意化图形在形状上存在较大变形,如何在尽量简化图形的同时更好地维持图形相似性,是下一步研究的重点。
| [1] | MONMONIER M S. How to Lie with Maps[M]. Chicago: The University of Chicago Press, 1996. |
| [2] | BARKOWSKY T, LATECKI L J, RICHTER K F. Schematizing Maps: Simplification of Geographic Shape by Discrete Curve Evolution[C]//Proceedings of Spatial Cognition II. Berlin: Springer, 2000: 41-53. |
| [3] | AVELAR S, MÜLLER M. Generating Topologically Correct Schematic Maps[C]//Proceedings of the 9th International Symposium on Spatial Data Handling. [S.l.]: Springer, 2000: 28-35. |
| [4] | AVELAR S. Schematic Maps on Demand: Design, Modeling and Visualization[D]. Zurich: Swiss Federal Institute of Technology, 2002. |
| [5] | AVELAR S. Convergence Analysis and Quality Criteria for a Iterative Schematization of Networks[J]. Geoinformatica, 2007, 11(4): 497-513. |
| [6] | AVELAR S, HURNI L. On the Design of Schematic Transport Maps[J]. Cartographica: The International Journal for Geographic Information and Geovisualization, 2006, 41(3):217-228. |
| [7] | AVELAR S, HUBER R. Modeling a Public Transport Network for Generation of Schematic Maps and Location Queries[C]//Proceedings of the 20th International Cartographic Conference. Beijing: Surveying and Mapping Press, 2001: 1472-1480. |
| [8] | STOTT J M, RODGERS P, MARTINEZ-OVANDO J C, et al. Automatic Metro Map Layout Using Multicriteria Optimization[J]. IEEE Transaction on Visualization and Computer Graphics, 2011, 17(1): 101-114. |
| [9] | STOTT J M. Automatic Layout of Metro Maps Using Multicriteria Optimisation[D]. Canterbury: University of Kent, 2008. |
| [10] | DONG Weihua, LI Zhilin, GUO Qingsheng. Automated Model Generalization of Schematic Networl Maps Based on Dynamic Segmentation[J]. Geomatics and Information Science of Wuhan University, 2010, 35(8): 892-895.(董卫华, 李志林, 郭庆胜. 基于动态分段的道路网示意性地图模型综合[J]. 武汉大学学报:信息科学版, 2010, 35(8): 892-895.) |
| [11] | CABELLO S, DE BERG M, VAN KREVELD M. Schematization of Networks[J]. Computational Geometry, 2005, 30(3): 223-238. |
| [12] | CABELLO S, VAN KREVELD M. Schematic Networks: an Algorithm and Its Implementation[C]//Proceedings of the 10th International Symposium on Spatial Data Handling. Ottawa: Springer, 2002: 475-486. |
| [13] | HU Yungang, CHEN Jun, LI Zhilin, et al. Selective Omission of Road Features Based on Mesh Density for Digital Map Generalization[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 351-357.(胡云岗, 陈军, 李志林, 等. 基于网眼密度的道路选取方法[J]. 测绘学报, 2007, 36(3): 351-357.) |
| [14] | DENG Hongyan, WU Fang, WANG Huilian, et al. A Generalization of Road Networks Based on Topological Similarity[J]. Journal of Geomatics Science and Technology, 2008,25(3):183-187.(邓红艳, 武芳, 王辉连, 等. 基于拓扑相似性的道路网综合模型[J]. 测绘科学技术学报, 2008, 25(3): 183-187.) |
| [15] | CHEN Chun, ZHANG Shuwen, XU Guifen. The Basis for Generation of Topologic Information of Polygons in GIS[J]. Acta Geodaetica et Cartographica Sinica, 1996, 25(4): 266-271.(陈春, 张树文, 徐桂芬. GIS中多边形图拓扑信息生成的数学基础[J]. 测绘学报, 1996, 25(4): 266-271.) |
| [16] | DU Qingyun. Automatic Organization of Polygon Data in Cartographic Database[J]. Acta Geodaetica et Cartographica Sinica, 1989, 18(3): 204-212.(杜清运. 地图数据库中多边形数据的自动组织[J]. 测绘学报, 1989, 18(3): 204-212.) |
| [17] | WANG Zhaorui. Graph Theory[M].3rd Edition. Beijing: Beijing Institute of Technology Press, 2001.(王朝瑞. 图论[M]. 3版. 北京: 北京理工大学出版社, 2005.) |
| [18] | AWARE J M, ANAND S, TAYLOR G E, et al. Automated Production of Schematic Maps for Mobile Applications[J]. Transactions in GIS, 2006, 10(1): 25-42. |
| [19] | DONG Weihua, GUO Qingsheng, LIU Jiping, et al. Progressive Generalization Research of Schematic Road Network Maps[J]. Geomatics and Information Science of Wuhan University, 2007, 32(9): 829-832.(董卫华, 郭庆胜, 刘纪平, 等. 道路网示意性地图的渐进式综合研究[J]. 武汉大学学报:信息科学板, 2007, 32(9): 829-832.) |
| [20] | LIANG Xiaowen, LIU Zongqi, CHEN Yijin. An algorithm of Polygon Auto-Construction Based on Angle Changing Tendence[J]. Journal of Image and Graphics, 2005, 10(6): 785-789.(梁晓文, 刘宗岐, 陈宜金. 基于夹角变化趋势的多边形自动搜索和生成算法[J].中国图象图形学报, 2005, 10(6): 785-789.) |