2. 中国科学院地理科学与资源研究所资源与环境信息系统国家重点实验室,北京 100101;
3. 山东科技大学测绘科学与工程学院,山东 青岛 266590
2. State Key Laboratory of Resources and Environmental Information System, Institute of Geographic and Nature Resources Research, Chinese Academy of Sciences, Beijing 100101, China;
3. College of Geomatics, Shandong University of Science and Technology, Qingdao 266590, China
1 引 言
多边形叠加分析是地理信息系统常用的空间分析工具之一,具有典型的高算法复杂度和计算时间密集性特征[1],在空间分析算法体系中占有重要地位,是地理数据处理领域所面临的核心且困难的基础问题之一[2, 3]。简单多边形的相交测试是线性时间且可以变换为线段求交问题采用Shamos-Hoey算法[4]或Bentley-Ottmann算法[5]实现快速求解,而对于复杂多边形的叠置分析问题,最坏情况下则需要O(N2)的时间[6]。简单要素模型条件下的任意多边形叠加分析问题通常基于多边形裁剪算法解决,目前公认的既支持任意形状多边形裁剪又能在有限时间内获得正确计算结果的算法包括Weiler算法[7]、Vatti算法[8]和Greiner-Hormann算法[9, 10]。其中后两者所采用的双线性链表数据结构和计算速度均优于前者[11]。尽管Greiner-Hormann算法被认为比Vatti算法具有更简单的原理和实现过程,也声称拥有更高的执行效率,但在某些情况下其计算效率却低于Vatti算法[12, 13]。文献[14]实现了对Vatti算法的改进,解决了输入多边形中不允许出现水平边的问题,增强了算法稳定性,但其依靠递归实现的交点求解在处理大数据时易出现资源消耗过大的问题[15]。尽管上述多边形裁剪算法具有精度高的优点,但是在数据结构复杂度和计算量等多个方面却表现出了一定的不足。根据文献[16]的试验结果,基于平面扫描和线段求交等算法实现的多边形裁剪算法的时间开销随多边形顶点数量的增加几乎均呈上升趋势,以Vatti算法为例,其计算时间随多边形顶点数量的增加表现出近似O(N2)的快速增长特征[17],这对处理包含大量顶点的多边形叠加分析问题非常不利。
与矢量数据相比,栅格数据更适用于空间建模、尺度分析和叠加分析操作[18, 19],且栅格数据分辨率越精细,越能更加细致地表现地理特征[20],栅格化处理是扩展矢量数据共享范围的常用手段[21]。矢量数据的栅格化处理是克服矢量数据计算复杂、效率低且实现困难的有效途径。文献[22]将栅格化的思想应用于矢量电子地图的更新变化检测中,在大幅提高计算速度的同时保证了计算结果的可靠性。而多边形栅格化的过程是有损过程,涉及多边形面积、周长、形状以及拓扑结构等多方面信息,因此必须对栅格化处理后的计算结果的面积误差进行分析并加以控制[23, 24],栅格化处理过程产生的误差受网格单元大小、图形形状和结构等多个因素的影响[25]。本文尝试将离散化处理思想引入多边形裁剪过程中,提出了一种基于栅格化处理思想的多边形裁剪算法——RaPC算法,来解决传统多边形裁剪算法在处理包含大量顶点的多边形叠加时的低效问题。
本文组织结构为:首先阐述RaPC算法原理,重点描述边界搜索追踪方法和顶点构环方法;其次分析RaPC算法计算结果的面积误差特征;再开展试验比较其与Vatti算法的计算效率及算法复杂度差异;最后得出结论。
2 RaPC算法原理
2.1 算法基本思想及流程
RaPC算法的基本思想是将空间范围进行离散化,按照离散化后网格与叠加多边形间的包含关系将空间区域定义为4种类型:目标多边形区域、裁剪多边形区域、重叠区域、空白区。与之对应,离散网格同样包含4种类型:SUBJP(1)、CLIPP(2)、SUBJP_CLIPP(3)、NONE_SUBJP_CLIPP(0)。完成网格离散化过程后,按照计算需求搜索特定类型的网格进行输出,即完成了多边形裁剪过程。
RaPC算法由多边形离散化、网格填充、结果输出3个核心步骤构成。多边形离散化的实质是将空间区域划分为规则网格,可采用矩阵结构来存储。初始化矩阵需要3个参数,分别是多边形几何对象P、网格单元大小cellsize和多边形类型type(目标多边形或裁剪多边形)。矩阵的元素代表空间区域内的网格单元,元素取值的不同代表所属空间区域的不同。叠加操作算子支持求交(INTSEC)、求差(DIFF)、合并(MERGE)3种类型。
网格填充的过程是遍历矩阵并对每个元素进行多边形包含测试的过程,每个网格根据其特征点与目标或裁剪多边形的包含关系的不同被赋予不同的值,本文采用射线法进行点在多边形内探测[26]。
RaPC算法支持两种不同的结果输出形式:离散网格输出和单一多边形整体输出,前者指将每个网格作为单一的裁剪结果进行输出,后者则是将裁剪完成的所有网格进行聚合,形成单一的几何对象并输出。
2.2 边界网格环绕追踪算法
不失一般性,考虑简单多边形的情形,如图 1所示,假设多边形P1是两个多边形叠加分析的计算结果,与之相对应,RaPC算法的计算结果如图 1中8×8的格网所示,环绕边界追踪算法的目标是在该矩阵中进行搜索追踪,找出所有外环的入口,在每个入口定义出1个外环和若干个内环,构造出最接近于多边形P1的图斑。
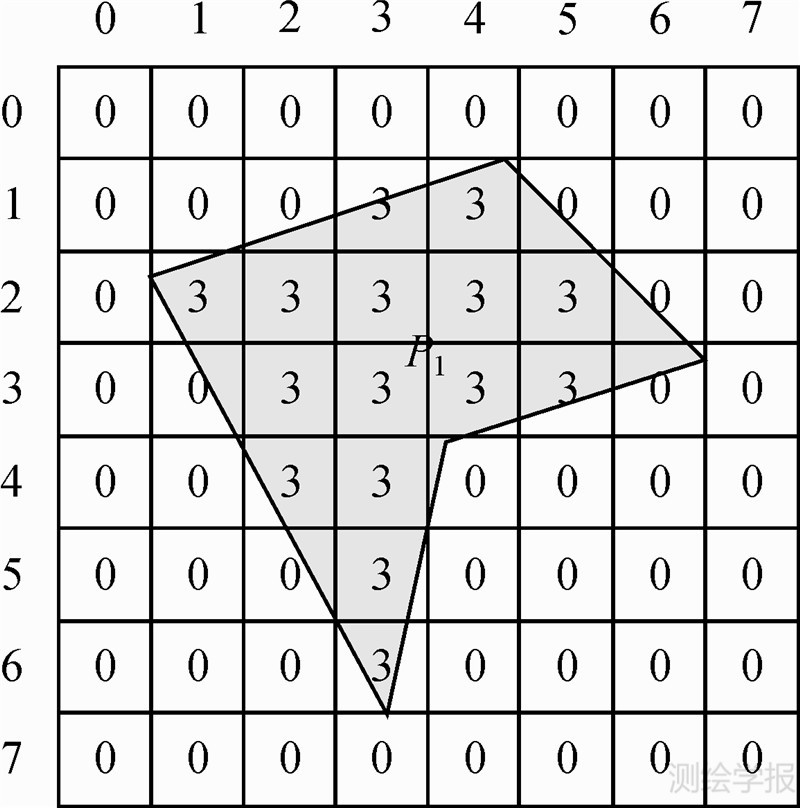 |
| 图 1 简单多边形图斑示意图Fig. 1 Patch of simple polygon |
边界环绕追踪算法的具体流程如下:
(1) 按照从上至下、从左至右的规则遍历网格,遍历过的网格标记为已访问状态。
(2) 将首个未被访问且为期望类型的网格标记为入口网格,如图 1中第2行第4列的网格,记为g(1,3),同时创建一个新的外环对象RE(采用双向链表实现)并将g(1,3)作为头节点加入RE,此时头节点的前驱和后继节点都为空,开始环绕追踪构环的过程。
(3) 以g(1,3)为中心,采用图 2(a)所示3×3窗口进行扫描,基于图 2所示行程规则搜索下一新网格节点并加入RE末尾,标记当前网格为已访问状态同时设置当前节点为新节点的前驱,新节点为当前节点的后继,移动窗口至新网格节点继续上述扫描过程。
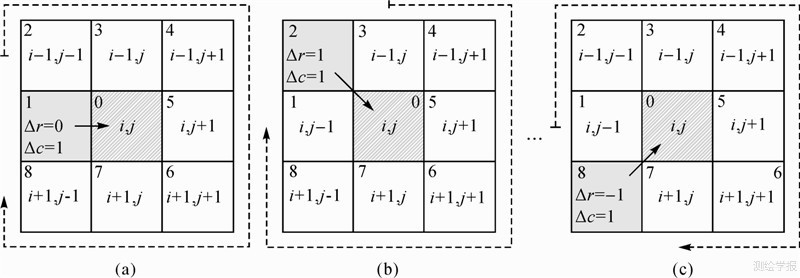 |
| 图 2 窗口扫描追踪的行程规则Fig. 2 Route rules for window-based scanning and tracking |
(4) 当寻找得到的节点为RE的头节点时,标志环RE发生闭合,以该头节点为入口的追踪构环过程完成。
(5) 在环RE内部执行内环的搜索追踪过程,搜索到的内环加入RE的holes容器并输出。
(6) 从上一入口网格处的下一(右侧)网格开始,继续遍历剩余网格单元,直至完成所有网格的遍历,找出所有的外环及每个外环所包含的内环,算法结束。
上述窗口扫描的规则决定了追踪构环为顺时针进行,窗口扫描起始位置判定、窗口网格遍历的详细规则如图 2所示。图 2(a)—(c)中,3×3的窗口中心网格为当前节点,编号为0,从0节点左侧网格开始顺时针编码依次为1—8,从网格1—8至网格0的实线箭头表示从前一节点至当前节点的前进方向(也即边界网格的走向),包围窗口的虚线箭头表示在当前前进方向条件下窗口扫描的行程(或环绕追踪顺序),Δr和Δc分别为当前网格与前一网格的行列号之差,为搜索辅助变量。窗口扫描过程中存在特殊情况,如图 1中遍历至g(6,3)网格时,采用上述窗口扫描方法无法找到期望网格,此时需将当前网格的前一网格作为下一节点加入环的末尾,而此时当前网格成为“前一”网格,网格g(5,3)将会被记录两次,这与图斑的真实情况相符。完成搜索后,将结果转为GIS矢量数据结构。
2.3 岛、洞处理规则
洞是多边形内环的表现形式,RaPC算法支持包含洞、岛的任意多边形之间的叠加裁剪。当完成了一个外环的搜索过程之后即开始在该外环内部搜索内环,本文采用外环边界跨越数统计的方式判断扫描窗口网格是否位于当前外环内。边界跨越计数方法类似于经典的用于解决点面包含问题的射线算法,它通过统计某一点沿某一方向(如水平方向)与多边形边界的交点个数来判断该点是否被多边形包围。本文中的边界跨越计数方法操作的点是离散网格,而边界对应于由离散网格按照一定次序构成的环。RaPC算法中内环的搜索算法过程如图 3所示。
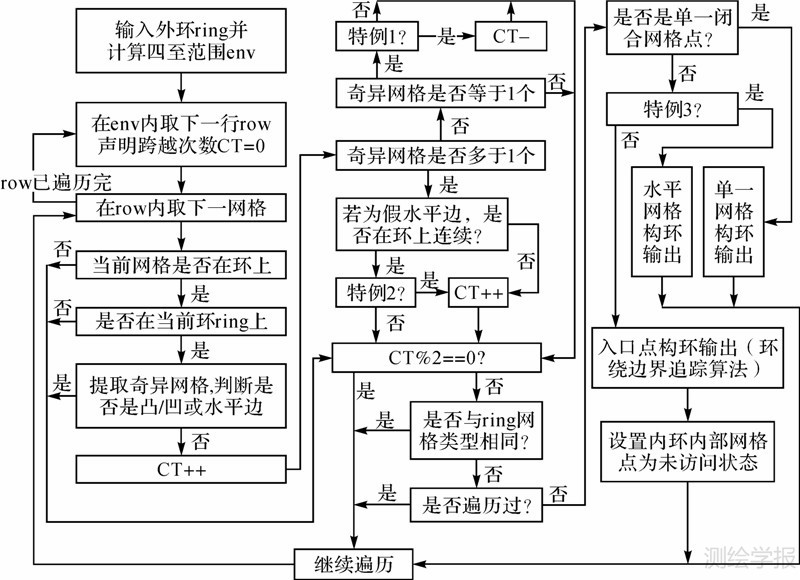 |
| 图 3 内环搜索流程Fig. 3 Flow for interior ring searching |
图 3中,CT是扫描窗口网格在网格矩阵的每一行中从左至右对外环ring的边界跨越次数(crossing time),根据其奇偶性的不同确定网格点与外环的包围关系;“网格在环上”指的是某网格是构成环边界的网格单元,如图 1中网格g(1,3)在环上,而g(2,3)不在环上;奇异网格特指3种不构成边跨越条件的网格组合,如图 4(a)、(b)、(c)所示,假水平边指在环上但不连续的水平相邻网格组合,如图 4(d)所示。
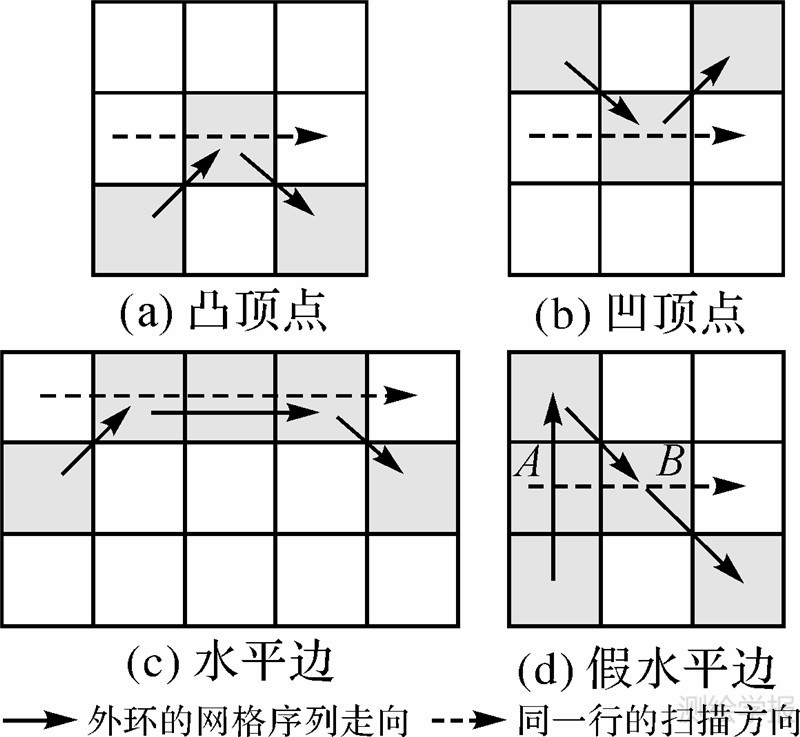 |
| 图 4 3种类型的奇异网格组合与假水平边Fig. 4 Three odd combination types of grids and fake horizontal edge |
如图 5所示,3个特例分别是单网格非跨越特例、在环上连续的水平边构成边界跨越特例和同一行水平分布的相邻网格单独构环特例。
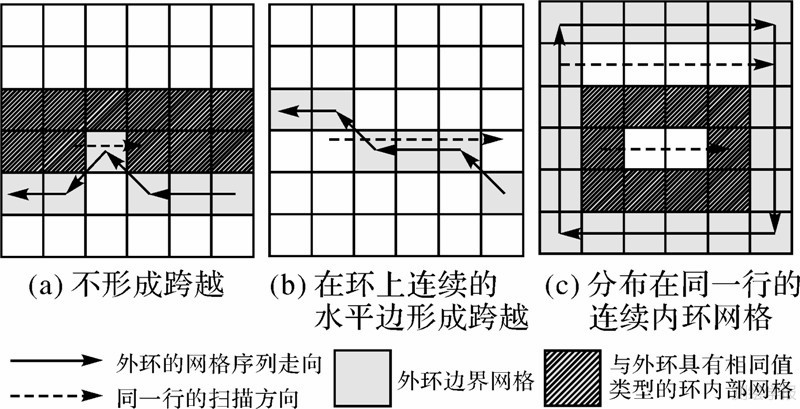 |
| 图 5 内环搜索过程中的3种特例情况Fig. 5 Three exceptions during searching of interior ring |
按照上述算法步骤寻找到满足条件的内环入口网格后,采用2.2节所述算法构造顺时针的环。由于目标是生成内环,因此在构环完毕后须进行点的逆序操作。生成内环后,对内环所包含的所有网格点进行遍历,设置为未访问状态,目的是继续在其内部搜索岛屿多边形。岛的探测、边界提取方法与之前所述外环的边界网格环绕追踪算法完全相同。然而,按照前述方法完成岛屿多边形的边界追踪之后,必须在其内部再次探测是否存在内环,若存在则依据本节所述方法提取内环的边界,这说明RaPC方法可对多层洞、岛嵌套的多边形提供递归探测支持。
3 RaPC算法误差分析
Vatti算法是公认的经典任意多边形裁剪算法[11],被开源及商业GIS软件广泛采用[14],本文选择Vatti算法进行对比。根据前人的研究成果,栅格化处理是一个有损转化过程,且误差不可避免[21],这些误差来自多方面,例如网格取舍策略、栅格化算法和所采用的数据结构等。目前对此类误差产生的原因、控制模型和误差分析方法等均有了较为详尽的研究[25],出现了一些能够确保栅格化转换结果面积精度和稳定性的模型和分析方法[23, 24]。由于RaPC算法在多边形栅格化过程中采用网格中心点与多边形的包含关系作为网格取舍依据,未涉及复杂的网格内部面积计算和统计,因此本节针对此种处理方式下RaPC算法所得到的多边形裁剪计算结果的相对面积误差的变化规律进行分析。相对面积误差e定义如下
式中,ARaPC为采用RaPC算法得到的裁剪结果面积值;AVector为采用Vatti算法得到的裁剪结果面积值。试验所采用的数据如图 6(a)所示(试验区长宽分别约为840 km和562 km),多边形求差的计算结果如图 6(b)所示,而图 6(b-1)为Vatti算法的计算结果细节,图 6(b-2)为RaPC算法的计算结果细节。
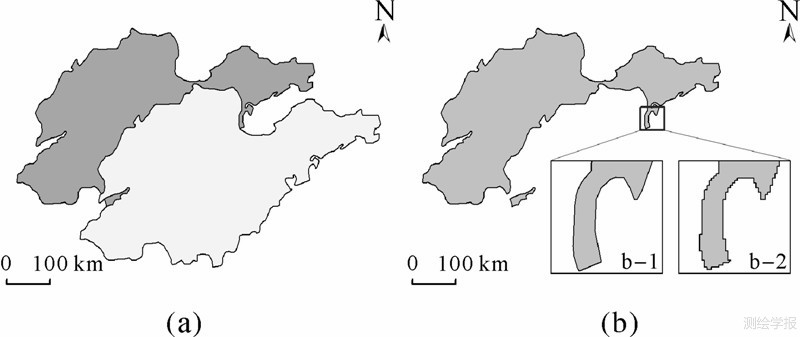 |
| 图 6 面积误差统计试验数据与矢量算法计算结果Fig. 6 Experimental data for statistics of area error and calculation result of vector algorithm |
Vatti算法得到的结果多边形面积为102 331 740 839.384 m2,当网格大小为10 km时,RaPC算法计算结果的相对面积误差为-0.324%,而当网格尺寸缩小至1 km(图 6(b-2))时,误差仅为-0.012%,误差随网格大小的增加整体上呈现出增大的趋势,同时具有强烈的不稳定性,这与边界网格单元的取舍策略存在直接关系。当采用网格中心点与多边形的包围关系作为网格取舍依据时,边界网格单元的取舍更多地表现出了一种随机性特征,可采用EAC模型[24]进行误差控制和约束。因此,RaPC算法误差总体处于较低水平且可以通过调整网格大小进行控制。
4 RaPC算法效率分析
本文采用长春市居民地多边形数据(两图层均包含3959个多边形,试验区长宽分别约为9.4 km和7.8 km)作为试验数据比较Vatti算法与RaPC算法在计算多边形图层求交时的效率差异。在相同硬件试验条件下的试验结果如表 1所示。其中,基于Vatti算法的计算时间约为1.060 s,计算结果图层内的多边形图形面积为11 206 600 m2。
| 网格大小/m | |||||||
| 2 | 5 | 10 | 15 | 20 | 25 | 30 | |
| 计算时间/s | 17.544 | 3.735 | 1.519 | 1.061 | 0.842 | 0.733 | 0.652 |
| 相对面积误差/(%) | -0.007 | -0.129 | 0.553 | -0.922 | -1.065 | 0.967 | 0.516 |
上述结果表明,随网格单元的增大,RaPC算法的计算效率迅速提高,同时误差也随之增大,当网格单元为15 m时,得到了与Vatti算法相当的计算效率。因此,RaPC算法能够通过调整网格大小获得精度与效率的平衡。Vatti算法的计算效率对多边形顶点数量高度敏感[17]。本文通过比较具有相同形状但不同顶点数量的多边形间的求交计算时间来观察两种算法的效率差异。多边形顶点数量从1000至30 000递增时,试验结果如图 7所示。
 |
| 图 7 不同网格大小和多边形顶点数量条件下RaPC算法与Vatti算法的时间开销对比Fig. 7 Time costs comparison of the RaPC algorithm and the Vatti algorithm with different grid sizes and polygon vertex amounts |
图 7表明,与Vatti算法类似,多边形顶点数量同样影响RaPC算法的计算效率。当多边形所包含的顶点数量较少时,Vatti算法具有较高的计算效率,随着多边形顶点数量的增加,Vatti算法的计算效率快速降低。而RaPC算法的时间开销则表现出了较为平稳的线性增长模式,且随网格增大,线性增长模型的斜率降低,说明增长变慢。因此,尽管当采用较小的网格时RaPC算法的时间开销要高于Vatti算法,但是在处理包含大量顶点的多边形的叠加操作时,RaPC算法更有优势。实际上,RaPC算法的计算效率更多地受网格大小的影响。
从时间复杂度角度比较,最差情况下,Vatti算法的时间复杂度为O((p-2)2),其中p为单次叠置操作中两个多边形多具有的顶点数量[9]。RaPC算法的原子操作为点在多边形内的判断过程,该过程所需要的浮点数计算次数是多边形顶点数量的线性函数,而点在多边形内的判断次数为2N,其中N为网格单元数量,它是网格单元大小的二次函数。因此,当网格单元大小恒定时,RaPC算法的时间复杂度为O(2N),这与本文的试验结果相符。
从空间复杂度角度比较,RaPC算法的栅格化处理过程具有典型的高空间复杂度特征。Vatti算法仅通过定义一组边界线来存储多边形的所有顶点,通过自底向上的“扫描束”实现交点结算,同时仅为每个扫描束维护一个活动边表。因此Vatti算法的内存开销仅与多边形顶点数量线性相关,其空间复杂度为O(n),n为多边形顶点数量。而RaPC算法并不存储多边形顶点,它存储的是多边形所包围的离散化空间范围,因此每次叠加计算所占用的存储空间与多边形空间范围和网格大小的比例系数密切相关。当空间范围确定时,RaPC算法的空间复杂度为O(p2),即RaPC算法的空间复杂度随网格单元边长减小呈平方增长,其中p为比例系数,可由公式(2)计算
式中,L、W分别为离散化空间范围的长和宽;l为网格单元边长;N为网格单元数量。尽管存在上述不足,但在当今计算机硬件技术进步的背景下,内存限制已不再是算法面临的主要瓶颈,RaPC算法以空间换时间的处理方式能获得可期待的计算效率改进,同时也有望在GPU等新型计算架构下进一步提高计算效率。
5 结 论
本文针对传统矢量多边形裁剪算法在处理包含大量顶点的多边形叠加分析时所面临的效率下降问题,提出了一种基于栅格化处理思想的多边形裁剪算法——RaPC算法,并对其计算结果的面积误差进行分析和讨论,与经典的Vatti算法进行了对比。试验结果表明,RaPC算法的计算效率受网格单元大小和多边形顶点数量双重因素的影响,其时间开销随多边形顶点数量呈线性增长,随网格大小增大呈幂函数规律快速下降,通过控制网格大小能实现对时间开销和面积误差的控制和调整。Vatti算法在处理小数据时较为高效,而RaPC算法在处理包含大量顶点的多边形数据时更有优势。因此,RaPC算法为在一定精度水平下大规模多边形间的裁剪问题提供了一个潜在的求解方法。
此外,多边形裁剪过程具有典型的高计算密集性特征,传统的多边形裁剪算法计算过程与数据结构紧密耦合,难以实现细粒度并行化,而基于RaPC算法的多边形裁剪问题的细粒度并行加速求解是下一步的研究方向。
| [1] | DOWERS S, GITTINGS B M, MINETER M J. Towards a Framework for High-performance Geocomputation: Handling Vector-topology within a Distributed Service Environment[J]. Computers, Environment and Urban Systems,2000, 24(5): 471-486. |
| [2] | GOODCHILD M F. Statistical Aspects of the Polygon Overlay Problem[M]//DUTTON G. Harvard Papers on Geographic Information Systems. Reading, MA:Addison-Wesley Publishing Company, 1977. |
| [3] | AGARWAL D, PURI S, HE Xi, et al. A System for GIS Polygonal Overlay Computation on Linux Cluster: An Experience and Performance Report[C]//Proceedings of the 2012 IEEE 26th International Parallel and Distributed Processing Symposium Workshops & PhD Forum.Shanghai: IEEE, 2012: 1433-1439. |
| [4] | SHAMOS M I, HOEY D.Geometric Intersection Problems[C]//Proceedings of the 17th Annual Symposium on Foundations of Computer Science.Washington DC: IEEE, 1976:208-215. |
| [5] | BENTLEY J L, OTTMANN T A. Algorithms for Reporting and Counting Geometric Intersections[J].IEEE Transactions on Computers,1979, C-28(9): 643-647. |
| [6] | PREPARATA F P, SHAMOS M I. Computational Geometry: An Introduction[M]. Translated by Zhuang Xingu.Beijing: Science Press, 1990. (PREPARATA F P, SHAMOS M I. 计算几何导论[M]. 庄心谷, 译. 北京: 科学出版社, 1990). |
| [7] | WEILER K, ATHERTON P. Hidden Surface Removal Using Polygon Area Sorting[C]//Proceedings of the 4th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press, 1977:214-222. |
| [8] | VATTI BR. A Generic Solution to Polygon Clipping[J]. Communications of the ACM, 1992, 35(7): 56-63. |
| [9] | GREINER G, HORMANN K. Efficient Clipping of Arbitrary Polygons[J]. ACM Transactions on Graphics, 1998, 17(2): 71-83. |
| [10] | CHEN Zhanlong, WU Xincai, WU Liang. Polygon Overlay Analysis Algorithm Based on Monotone Chain and STR Tree in the Simple Feature Mode[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 102-108. (陈占龙, 吴信才, 吴亮. 基于单调链和STR树的简单要素模型多边形叠置分析算法[J]. 测绘学报, 2010, 39(1): 102-108). |
| [11] | LIU Yongkui, GAO Yun, HUANG Youqun. An Efficient Algorithm for Polygon Clipping[J]. Journal of Software, 2003, 14(4): 845-856. (刘勇奎, 高云, 黄有群. 一个有效的多边形裁剪算法[J]. 软件学报, 2003, 14(4): 845-856). |
| [12] | KUI Liuyong, QIANG Wangxiao, ZHE Baoshu, et al. An Algorithm for Polygon Clipping, and for Determining Polygon Intersections and Unions[J]. Computers & Geosciences, 2007, 33(5): 589-598. |
| [13] | MARTNEZ F, RUEDA A J, FEITO F R. A New Algorithm for Computing Boolean Operations on Polygons[J]. Computers & Geosciences, 2009, 35(6): 1177-1185. |
| [14] | MURTA A.A General Polygon Clipping Library[EB/OL].[2013-11-01].http://www.cs.man.ac.uk/-toby/alan/software/gpc.html. |
| [15] | XIE Zhong, WEI Dongqi, WU Liang, et al. Graph Model of Polygon Clipping Using Simple Vector Data[J]. Acta Geodaetica et CartographicaSinica, 2009, 38(4): 369-374. (谢忠, 魏东琦, 吴亮, 等. 简单矢量数据多边形裁剪问题的图模型[J]. 测绘学报, 2009, 38(4): 369-374). |
| [16] | LEONOV M. Comparison of the Different Algorithms for Polygon Boolean Operations[EB/OL]. [2013-11-02]. http://www.complex-a5.ru/polyboolean/comp.html. |
| [17] | FAN Junfu, MA Ting, JI Min, et al. Implementation and Optimization of Eight Parallel Polygon Overlapping Tools with OpenMP at the Feature Layer Level in GIS[J]. Progressin Geography, 2013, 32(12): 1835-1844. (范俊甫, 马廷, 季民, 等. GIS中8种图层级多核并行多边形叠置分析工具的实现及优化方法[J]. 地理科学进展, 2013, 32(12): 1835-1844). |
| [18] | BATES P D, DEROO A P J. A Simple Raster-based Model for Flood Inundation Simulation[J]. Journal of Hydrology, 2000, 236(1-2): 54-77. |
| [19] | YANG Cunjian, ZHANG Zengxiang. Models of Accuracy Loss During Rasterizing LanduseVector Data with Multi-scale Grid Size[J]. Geographical Research, 2001, 20(4): 416-422. (杨存建, 张增祥. 矢量数据在多尺度栅格化中的精度损失模型探讨[J]. 地理研究, 2001, 20(4): 416-422). |
| [20] | CHEN Shupeng, LU Xuejun, ZHOU Chenghu. Introduction to Geographic Information Systems[M]. Beijing: Science Press, 1999. (陈述彭, 鲁学军, 周成虎. 地理信息系统导论[M]. 北京: 科学出版社, 1999). |
| [21] | BAI Yan, LIAO Shunbao, SUN Jiulin. Scale Effect and Methods for Accuracy Evaluation of Attribute Information Loss in Rasterization[J]. Journal of Geographical Sciences, 2011, 21(6): 1089-1100. |
| [22] | LI Yuguang, LI Lianying, LI Qingquan, et al. Vector Map Geometric Data Change Detection Based on Grid Method[J]. Geospatial Information, 2010, 8(1): 142-146. (李宇光, 李莲营, 李清泉, 等. 基于栅格化思想的矢量电子地图几何变化检测[J]. 地理空间信息, 2010, 8(1): 142-146). |
| [23] | CHEN Jianjun, ZHOU Chenghu, CHENG Weiming. Area Error Analysis of Vector to Raster Conversion of Areal Feature in GIS[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 344-350. (陈建军, 周成虎, 程维明. GIS中面状要素矢量栅格化的面积误差分析[J]. 测绘学报, 2007, 36(3): 344-350). |
| [24] | ZHOU Chenghu, OU Yang, YANG Liao, et al. An Equal Area Conversion Model for Rasterization of Vector Polygons[J]. Science in China: Series D: Earth Sciences, 2007, 50(S1): 169-175. (周成虎, 欧阳, 杨辽, 等. 矢量多边形栅格化的保积优化模型[J]. 中国科学D辑: 地球科学, 2006, 36(增刊Ⅱ): 157-163). |
| [25] | SHORTRIDGE A M. Geometric Variability of Raster Cell Class Assignment[J]. International Journal of Geographical Information Science, 2004, 18(6): 539-558. |
| [26] | ZHOU Peide. Computational Geometry Algorithm Design and Analysis(Fourth Edition)[M]. Beijing: Tsinghua University Press, 2011. (周培德. 计算几何:算法设计与分析(第4版)[M]. 北京: 清华大学出版社, 2011). |