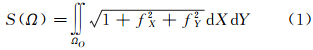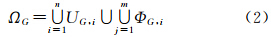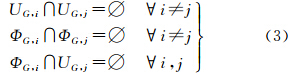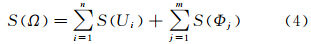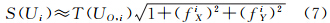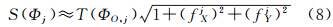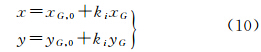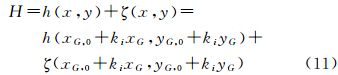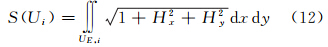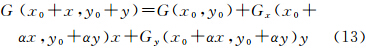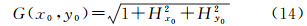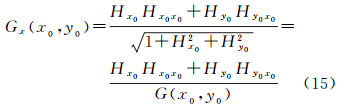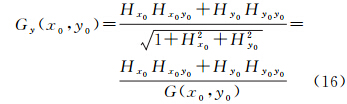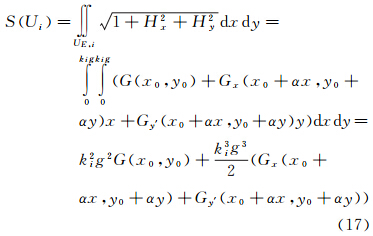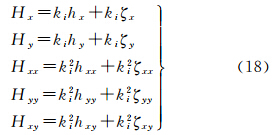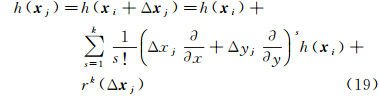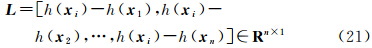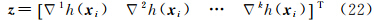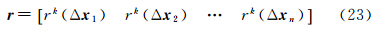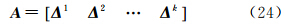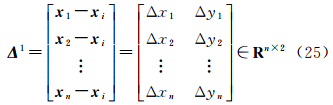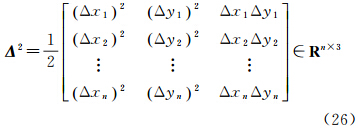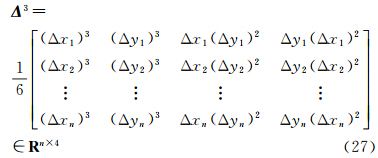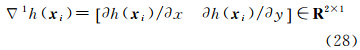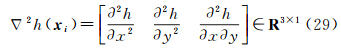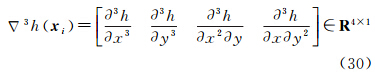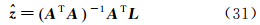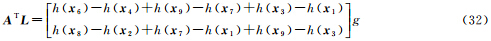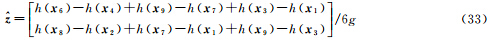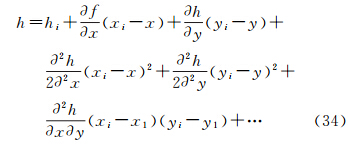2. 长安大学地质工程与测绘学院，陕西 西安 710054
2. School of Geology Engineering and Geomatics, Chang'an University, Xi'an 710054, China
1 引 言
地理国情监测是新时期空间信息科学的重要使命[1]，是地理信息更深层次的应用。地理国情包括3种信息：感知信息、统计信息和分析信息。许多国家和组织都开展了地理国情监测方面的项目或工程，以便更好地服务于本国或地区的资源、环境、能源、社会等领域[2, 3, 4]。
数字高程模型(digital elevation model，DEM)是表示地面高程的一种实体地面模型[5]，在测绘、水文、气象、地貌、地质等科学领域应用广泛。地表高斯投影面积、椭球面积和地表面积是3类常用统计量[6, 7]。文献[8]讨论了高斯投影中央子午线变化和投影面高程变化引起的面积变形，以及椭球面面积与高斯面上面积的差异。地球旋转椭球和地球三轴椭球是两种常用的地球形状简化模型。已有文献讨论多边形区域的旋转椭球或三轴椭球面积计算的严密公式[3, 9, 10]。在许多应用中，地表面积比投影面积或椭球面积更具有参考价值[11, 12]。构造地表三角网并建立地表面积栅格数据是地表面积统计的常用方法[11]。
对于相同的投影面积，地表面积会因地形因子不同而异。利用DEM提取地形因子可分为数值分析方法和局部曲面拟合方法[14, 15, 16, 30]。坡度和坡向的常用数值分析方法主要包括简单差分、二阶差分、三阶差分、Frame算法等[28]。应用表明，三阶不带权差分算法具有较高精度[28]；局部曲面拟合方法则通过最小二乘曲面拟合再进行求导获取地形的坡度和坡向等信息[30]。基于数值积分的复化公式法则需要高分辨率的微观地形因子数据[13]。文献[17]基于二维小波的多分辨分析理论，提出并证明了不同分辨率下地面坡度的面积与复杂地貌形态复杂度及尺度之间的变化关系。对于具有特定分辨率的DEM数据，提高地形因子计算精度需根据地形起伏情况设计合适的窗口，最大限度消除随机观测误差的影响。利用准确的地形因子及其变化率信息构造地表三角网可提高地表面积的统计精度。
本文研究地表面积的理论面积及其近似方法，讨论影响地表面积统计精度的主要因素，提出了一种顾及任意地形因子的地表面积统计方法。该方法首先利用泰勒级数逼近原理对地形因子进行最小二乘估计，然后利用这些地形因子对DEM进行加密，最后利用加密后的DEM构建地表三角网统计地表面积。试验表明，在局部地形因子显著的山区或丘陵地区，不同分辨率下地表面积统计结果存在较大的差异，而利用本文提出的顾及地形局部地形因子的地表面积统计方法可明显提高低分辨率DEM地表面积统计精度。
2 地表面积统计原理与精度分析 2.1 地表的理论面积及其近似
数字高程模型是一种采用二维高斯投影坐标附加正(常)高实现的一种三维空间地理信息，是反映离散地表曲面模型。如图 1所示，对于地表封闭区域Ω，设投影区域ΩG的边界线为A1、A2、…、Ap。由于(似)大地水准面和参考椭球面均为曲面参考基准，且高斯投影变换存在面积变形，当利用DEM数据计算地表面积时，可将DEM据中恢复为地形表面的三维空间模型[23, 24]。
 |
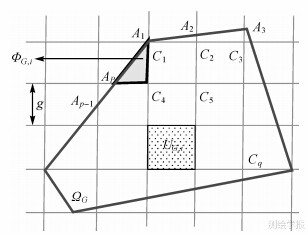| 图 1 投影DEM格网划分Fig. 1 Projection DEM grid division |
对于在地固地心坐标系中给出的地表曲面(X,Y,Z)，其尺度来自于地心坐标系基准的定义。将地表曲面(X,Y,Z)表示为函数式Z=f(X,Y)，并设其为分段光滑曲面，地表区域Ω在XOY平面上的投影为ΩO，则地表区域Ω的面积由以下曲面积分给出[13, 22]
式中，fX、fY为曲面函数Z=f(X,Y)的一阶偏导数。如图 1所示，对于给定的高斯投影边界区域ΩG，则分别率为g的DEM格网对ΩG的划分为
式中，UG,i和ΦG,i分别为完整单元格和破碎单元格。
基于高斯投影划分式(2)，地表区域Ω的面积可由表示为
式中
表示高斯投影区域UG,i和ΦG,i映射为地表区域(由坐标变换公式和基准定义给出)。若子区域内地表为平面或起伏不大，则式(4)中子区域的面积可近似为
式中，T(UO,i)和T(ΦO,j)分别为子区域Ui和Φj在XOY平面上的投影面积，fX、fY在相应子区域内的一阶偏导数。可见，利用式(1)计算地形表面积需要地形表面的严格曲面方程，而利用式(4)近似地表面积则需要高分辨率DEM数据。
2.2 局部地形因子对地表面积计算的影响
以高斯投影子区域UG,i边界上的任意DEM格网点(xG,0,yG,0)按高斯投影逆变换映射至椭球面的o点，并将该映射点o为原点在椭球面上建立地平空间直角坐标系o-xyH，则在o-xyH系下，地表曲面方程为
式中
式中，x、y为高斯投影坐标。顾及大地高和正(常)高的转换关系，可得 式中，h(x,y)为正常高或正高；ζ(x,y)为高程异常或大地水准面差距；ki为高斯投影长度变形比。在空间直角坐标系o-xyH下，类似于式(3)，地表区域Ui的地表面积为
式中，积分区域UE,i为地表区域Ui在地平面上的投影区域。
为便于讨论，设G(x,y)=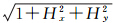
，由泰勒级数展开定理将函数G(x,y)在点(x0,y0)展开至一阶偏导数可得
式中，Hx0、Hy0、Hx0x0、Hy0y0、Hx0y0为式(9)中地表函数H=f(x,y)的一阶、二阶在点(x0,y0)处的取值。
对于边长为kig的高斯投影正方形区域UG,i，结合式(3)和式(13)，其表面积为
式(17)第1项为顾及地形函数一阶偏导数的地表区域Ui的近似面积，第2项为地形函数H=f(x,y)二阶偏导数对地表面积计算的影响，即利用线性地形因子(如坡度或地表函数一阶偏导数)计算地表面积的截断误差。由第2项可知，当且仅当DEM分辨率足够高，即g足够小，或者Hx0x0、Hy0y0、Hx0y0足够小，即地表函数二阶偏导数足够小时，利用式(4)计算地表面积才是严格的。为此，本文将地表曲面在地平坐标系下的各偏导数统称为局部地形因子，以便讨论和揭示地形起伏对地表面积统计的影响。
3 局部地形因子的最小二乘估计
对于给定的DEM数据，提高地表面积统计精度需提取DEM数据中所蕴含的局部地形因子。由式(11)可得以下微分关系
式中，Hx、Hy，Hxx、Hyy、Hxy分别为函数式(9)的一阶、二阶。在小区域内，ζx和ζy的几何意义为大地水准面相对于椭球面的夹角正切值。
由式(18)可知，曲面(x,y,H)的偏导数信息可由DEM曲面(xG,yG,h)的偏导数间接计算。局部地形因子空间函数近似服从Tobler定理，即距离较近的点比距离较远的点其特征值具有更大的相似性[21, 25]。使用窗口大小为N×N实测数据构建观测方程，利用最小二乘原理计算窗口中心DEM格网点处的各阶偏导数。下面基于DEM数据讨论地形函数h=h(x)(x:=[xGyG]∈R2为高斯投影坐标)在已知点处的各阶偏导数计算方法。在已知DEM点xi处，利用窗口内的其他已知点可构造以下观测方程[26]
式中，j=1,2,…,n，j≠i，Δxj:=Δxj,Δyj=xj－xi，xj为已知DEM点xi处的邻近已知点；rk(Δxj)为泰勒级数展开残余项，n=N×(N-1)为窗口内可构造的虚拟观测方程数目，k为泰勒级数展开的阶数。将方程(19)简记为
式中 类似的，可继续写出h(x)在xi处的高阶偏导数。将方程(20)中的残余项r视为随机误差，则该问题的最小二乘解为
采用局部地形因子信号的最小二乘估计，可平滑DEM量测误差，提高局部地形因子信号估值的精度和可靠性。当N=3，方程(20)存在8个方程，即n=8。若令k=1，即仅估计式(28)给出的两个地形参数，此时
则由式(31)可得
式(33)即为坡度坡向计算数学模型之三阶不带权差分公式[28]。事实上，若对虚拟观测量Δyi赋予适当权重，则可导出其他配权坡度坡向计算数学模型，如使用反距离配权模型。值得注意的是，文献[28]在坡度坡向算法精度分析中指出，在实际生产中，因DEM误差占主导因素，三阶不带权差分算法精度最高，推荐使用三阶不带权差分坡度计算模型。文献[26]指出：若平差模型式(20)仅估计空间函数的一阶偏导数，将空间函数非线性信号的高阶偏导数信息归为平差随机模型是有条件的。
4 DEM加密与地表面积统计
当DEM分辨率不够高或地表非线性起伏显著时，可利用地表函数的高阶偏导数信息提高地表面积统计精度。如前所述，利用式(4)计算地表面积则需要地表离散数据，且DEM数据的分辨率越高，式(4)近似地表理论面积的精度越高。下面给出利用式(31)所得地表函数偏导数估值对DEM进行加密方法，在通过提高DEM分辨率和地面三角网的分辨率，进而提高地表面积统计精度。
地表区域边界一般由高斯投影坐标给出，且区域边界的顶点一般为非整数格网点，需要推估这些多边形边界区域的高程。当利用低分辨率DEM数据统计地表面积时，可利用局部地形因子对DEM进行加密，以提高地表面积统计的精度。设距离待估点x处最近的整数格网点为xi，顾及整数格网点xi处的各阶偏导数，则待估点x的高程推估模型可表示为
式中，各阶偏导数由式(31)给出。
当整数格网点xi处的各阶偏导数为0时，则式(34)给出的高程推估退化为邻近点插值法。式(34)是一种顾及局部地形因子的邻近点高程插值法，因其使用一个已知点进行高程推估，可将该模型称为单点推估模型。基于空间函数高阶偏导数的多点推估方法可参考文献[26]。
如图 1所示，根据加密DEM数据的分辨率，依次计算统计封闭多边形区域边界与整数格网的交点，并利用式(34)计算这些交点的高程值。对封闭多边形边界点和区域内单元格网按DEM等间距格网线逐行逐列构建地表规则三角网(保证每个三角形的顶点坐标互差均小于等于1倍的整数格网间距)。地表三角网构造方法并不唯一，地表不规则三角网构建方法可参考文献[27]。将地表三角网点坐标转化为大地空间直角坐标后，累加地表三角网中三角形的面积，可得地表面积的三角网近似为
式中，Ti为第i个地表三角形的面积。
5 算 例 5.1 算例1：DEM分辨率对地表面积统计精度的影响
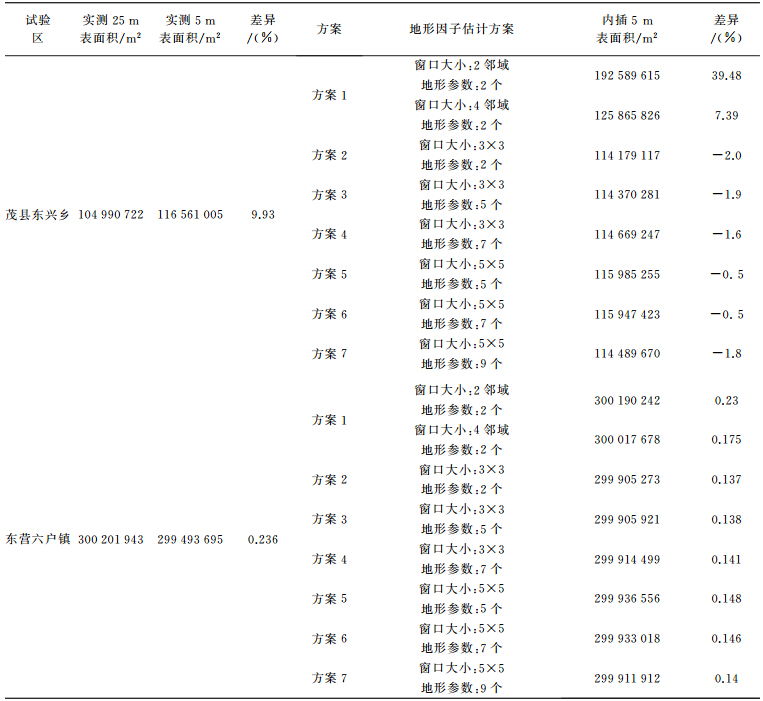
为验证DEM分辨率对地表面积统计精度的影响，在5 m分辨率实测DEM数据的基础上，提取了25 m分辨率DEM数据，使用这两种分辨率DEM构造地表三角网计算地表面积。四川茂县东兴乡(山区)和山东东营六户镇(平原地区)的地表面积计算结果表明，对于山区，地表面积和椭球面积之间的差异明显，不同DEM分辨率计算地表面积结果差异也较大，例如，利用5 m分辨率DEM计算四川茂县东兴乡地表面积比利用25 m分辨率DEM计算所得表面大9.93%。在平原地区，地表面积和椭球面积相差不大，不同DEM分辨率统计所得地表面积差异也较小，例如，不同DEM统计山东东营六户镇地表面积差异仅为0.236%。
5.2 算例2：实测DEM与内插DEM统计地表面积精度对比
DEM分辨率和地形起伏程度共同决定了地表三角网的地表面积统计精度。为验证本文的方法，采用式(31)提取区域地形因子，并采用式(34)将实测25 m分辨率DEM内插为5 m分辨率DEM后，构建地表三角网并统计地表面积，即按式(35)计算地表面积。本算例采用以下7种方案(表 1)。
以实测5 m分辨率DEM计算所得地表面积为参考，评价内插5 m分辨率DEM对地表面积统计的精度。结果表明，在地形起伏较大的茂县，上述7种DEM加密方案中，当考虑地表函数的二阶或三阶偏导数时，地表面积统计精度最高，其25 m内插5 m计算结果和实测5 m DEM统计结果相差仅为0.5%，相比于9.93%，地表面积计算精度提高显著。然而，若仅提取线性地形因子，采用三阶差分算法具有最高的地表面积统计精度，而简单差分算法精度最低(其差异高达39.48%)，二阶差分算法次之，这与文献[28]讨论坡度信息提取算法时的结论一致。而在局部地形起伏较小的平原，各种方法对地表面积统计结果均有改进，其中基于简单差分算法提取地形因子对地表面积几乎没有改进，而基于三阶差分算法提取地形因子对地表面积的改进最为显著。可见，地形因子的提取精度及其分辨率是最终决定地表面积计算精度的两个重要因素。对于特定分辨率的DEM，将本文给出的公式(31)作为局部地形因子的统一计算模型，对于山区或丘陵地带，可采用相对大的窗口提取非线性地形因(如二阶偏导数)，而对于平原地区，可直接小窗口使用三阶差分算法仅提取线性地形因子。 6 结 论
地表理论面积计算由地表曲面积分给出，其计算需要附加地表曲面函数假设。在实践中，可利用基于局部地形因子的最小二乘估计，对地表曲面进行剖分和面积近似。影响地形表面区域面积计算精度的因素由局部地形因子、DEM精度和分辨率。当仅利用坡度信息计算地表面积时，其截断误差与DEM分辨率的三次方成正比，而与地表空间函数的二次阶偏导数成正比。在实际应用中，可利用DEM格网点的对称性导出地形因子的实用计算公式，避免复杂的矩阵求逆运算。利用DEM提取所得地形因子有望提高地表面积的统计精度。当仅考虑地形线性地形因子时，本文建议采用三阶差分算法提取地形因子。在地形起伏显著的地区，窗口不应小于5×5，地形参数不应少于5个，即应考虑坡度变率对地表面积计算的影响。鉴于我国5 m分辨率DEM覆盖率不足50%，建议采用非线性插值对低分辨率DEM数据进行加密或根据需要重新采集生产高分辨率DEM数据，以提高地表面积统计精度。
| [1] | LI Deren,SUI Haigang, SHAN Jie.Discussion on Key Technologies of Geographic National Conditions Monitoring[J]. Geomatics and Information Science of Wuhan University, 2012(5):505-512. (李德仁,眭海刚,单杰.论地理国情监测的技术支撑[J]. 武汉大学学报:信息科学版, 2012(5): 505-512.) |
| [2] | CHEN Junyong. Study Notes on National Condition Monitoring[J]. Acta Geodaetica et Cartographica Sinica, 2012,41(5):633-635. (陈俊勇.地理国情监测的学习札记[J]. 测绘学报, 2012,41(5):633-635.) |
| [3] | CAO Zhenyu, TAN Mingjian, SHEN Yanmin. Study on Polygon Area Calculation Methods in Geodetic Coordinate System[J]. Bulletin of Surveying and Mapping, 2012(S1): 570-572. (曹振宇, 谭明建,沈艳敏.大地坐标系中多边形面积计算方法研究[J]. 测绘通报, 2012(S1): 570-572.) |
| [4] | QIAO Chaofei. Review of Overseas National Condition Monitoring[J]. Bulletin of Surveying and Mapping, 2011(11): 81-83. (乔朝飞.国外地理国情监测概况与启示[J]. 测绘通报, 2011(11): 81-83.) |
| [5] | American Society for Photogrammetry and Remote Sensing.Digital Elevation Model Technologies and Applications: The DEM Users Manual[M]. Bethesda ASPRS Publications,2007. |
| [6] | SJöBERG L E. Determination of Areas on the Plane, Sphere and Ellipsoid[J]. Survey Review, 2006. 38(301): 583-593. |
| [7] | GILLISSEN I. Area Computation of a Polygon on an Ellipsoid[J]. Survey Review,1993,32(248): 92-98. |
| [8] | WANG Jiexian, YU Zhenwu. Area Calculation Error Caused by Gauss Projection[J]. Bulletin of Surveying and Mapping, 2003(4): 5-6. (王解先,俞振武.高斯投影引起的面积计算误差[J]. 测绘通报, 2003(4): 5-6.) |
| [9] | PEDZICH P, KUZ＇MA M. Application of Methods for Area Calculation of Geodesic Polygons on Polish Administrative Units[J]. Geodesy and Cartography, 2012, 61(2): 105-115. |
| [10] | JI Bing, BIAN Shaofeng.Calculation of Surface Area of Triaxial Ellipsoid[J]. Journal of Naval University of Engineering, 2008(4): 21-24.(纪兵,边少锋.三轴椭球表面积的计算[J]. 海军工程大学学报, 2008(4): 21-24.) |
| [11] | ZHANG Y. Surface Area Processing in GIS for Different Mountain Regions[J]. Forestry Studies in China, 2011,13(4): 311-314. |
| [12] | JENNESS J S. Calculating Landscape Surface Area from Digital Elevation Models[J]. Wildlife Society Bulletin, 2004,32(3): 829-839. |
| [13] | JIANG Fan, LU Xiaohua, WANG Zhonglan. The Analysis of DEM Surface Area Based on Composed Calculus Algorithms[J]. Journal of Institute of Surveying and Mapping, 2005(4): 263-265. (江帆, 吕晓华, 王仲兰.基于复化公式的DEM表面积算法分析[J]. 测绘学院学报, 2005(4): 263-265.) |
| [14] | JENSON S, DOMINGUE J.Extracting Topographic Structure from Digital Elevation Data for Geographic Information System Analysis[J]. Photogrammetric Engineering and Remote Sensing, 1988,54(11): 1593-1600. |
| [15] | HOECHSTETTER S.Effects of Topography and Surface Roughness in Analyses of Landscape Structure—a Proposal to Modify the Existing Set of Landscape Metrics[J]. Landscape Online, 2008,3: 1-14. |
| [16] | BEASOM S L, WIGGERS E P, GIARDINO J R. A Technique for Assessing Land Surface Ruggedness[J]. The Journal of Wildlife Management, 1983,47(4): 1163-1166. |
| [17] | QIN Yanhong, LU Lin, WU Jitao.A Study on the Multi-resolution Representation of the Areas Based on Two-dimension Wavelet Transformation[J]. Mathematical Theory and Applications, 2005(2): 43-48. (秦艳红, 卢林, 吴纪桃.地形坡度面积的二维多分辨分析研究[J]. 数学理论与应用, 2005(2): 43-48.) |
| [18] | AGUILAR F J.Effects of Terrain Morphology, Sampling Density, and Interpolation Methods on Grid DEM Accuracy[J]. Photogrammetric Engineering and Remote Sensing, 2005,71(7): 805. |
| [19] | WISE S M. The Effect of GIS Interpolation Errors on the Use of Digital Elevation Models in Geomorphology[J]. Landform Monitoring, Modelling and Analysis, 1998,99: 139-164. |
| [20] | CHILDS C. Interpolating Surfaces in ArcGIS Spatial Analyst[R].[S.l.]:ESRI Education Services, 2004. |
| [21] | LI Xin, CHENG Guodong, LU Ling. Comparison of Spatial Interpolation Methods[J]. Advance in Earth Sciences, 2000, 15(3): 260-265. (李新, 程国栋, 卢玲.空间内插方法比较[J]. 地球科学进展, 2000, 15(3): 260-265.) |
| [22] | THOMAS G B, FINNEY R L. Thomas' Calculus[M].[S.l.]:Addison Wesley Publishing Company,2002. |
| [23] | DANG Yamin, CHENG Yingyan, XUE Shuqiang.Geodetic Coordinate System and Its Applications[M]. Beijing:Surveying and Mapping Press, 2010. (党亚民, 成英燕,薛树强.大地坐标系统及其应用[M]. 北京:测绘出版社, 2010.) |
| [24] | ZHU Huatong. Establishment of Geodetic Coordinate System[M]Beijing:Surveying and Mapping Press, 1986. (朱华统.大地坐标系的建立[M].北京:测绘出版社, 1986.) |
| [25] | ZHU Huiyi,LIU Shulin,JIA Shaofeng.Problems of the Spatial Interpolation of Physical Geographical Elements[J]. Geographical Research, 2004, 23(4): 425-432. (朱会义, 刘述林, 贾绍凤. 自然地理要素空间插值的几个问题[J]. 地理研究, 2004, 23 (4): 425-432.) |
| [26] | XUE Shuqiang, YANG Yuanxi. Generalized Inverse Distance Weighting Method for Spatial Interpolation[J]. Geomatics and Information Science of Wuhan University, 2013,38(12):1435-1439.(薛树强,杨元喜. 广义反距离加权空间推估法[J]. 武汉大学学报:信息科学版,2013,38(12):1435-1439.) |
| [27] | ZHU Qing, CHEN Chujiang. Quick Generation of TIN and Its Dynamic Updating[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1998(3): 18-21. (朱庆,陈楚江.不规则三角网的快速建立及其动态更新[J]. 武汉测绘科技大学学报, 1998(3): 18-21.) |
| [28] | LIU Xuejun, GONG Jianya, ZHOU Qiming, et al. A Study of Accuracy and Algorithms for Calculating Slope and Aspect Based on Grid Digital Elevation Model(DEM)[J]. Acta Geodaetica et Cartographica Sinica, 2004,33(3):258-263. (刘学军,龚健雅,周启鸣,等. 基于DEM坡度坡向算法精度的分析研究[J]. 测绘学报,2004,33(3):258-263). |
| [29] | LIU Xuejin, REN Zhifeng, WANG Yanfang, et al. Slope Model at Arbitrary Direction Derived from Grid-based DEM[J]. Areal Research and Development,2009(4):139-141. (刘学军,任志峰,王彦芳,等. 基于DEM的任意方向坡度计算方法[J]. 地域研究与开发,2009(4):139-141.) |
| [30] | HE Dan. Window Analysis for Extraction of Terrain Factors from Different Resolution DEM[D]. Xi'an:Northwest University,2012. (贺丹. 不同分辨率DEM提取地形因子的适宜分析窗口研究[D].西安:西北大学,2012.) |