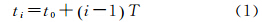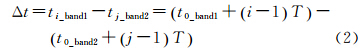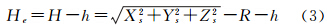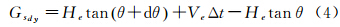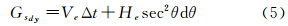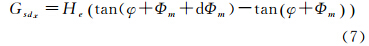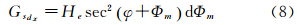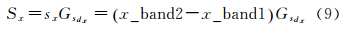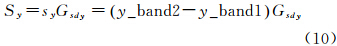2. 北京大学地球与空间科学学院,北京 100871
2. School of Earth and Space Science, Peking University, Beijing 100871, China
1 引 言
近年来,高分辨率卫星遥感成像与应用技术飞速发展。自20世纪70年代美国发射80 m空间分辨率的地球观测卫星Landsat-1以来,卫星遥感影像的空间分辨率一直不断提高,如今,WorldView、GeoEye等卫星已实现亚米级空间分辨率遥感影像获取。2012年1月,我国成功发射资源三号测绘卫星,空间分辨率达到2.1 m,实现了我国高分辨率民用立体测绘卫星零的突破。高分辨率卫星遥感成像为遥感影像应用与信息提取提供了更丰富的数据源。遥感成像模型的不断完善也为卫星遥感影像处理和地理空间信息的提取奠定了理论基础;基于高分辨率卫星遥感影像的运动目标的检测与运动信息提取是卫星遥感应用的重要方面[1, 2]。
传统的航空航天遥感成像都被视为静止成像,即一景影像近似是同一时刻拍摄,在一景遥感影像内目标地物的空间、时间、光谱等属性保持不变[3]。大量研究利用高分辨率卫星遥感影像开展运动目标识别与运动信息检测,并广泛应用于民用和军事领域[4, 5, 6, 7, 8, 9, 10]。利用光学遥感成像方法检测运动目标速度的方法主要有以下两种基本方式:一是利用两台或多台遥感器在两个或多个摄站点、在一定时间内获取运动目标影像;二是利用一台遥感器在两个或多个摄站点、在一定时间内获得两次或多次运动目标影像,进而提取目标运动信息。上述方法都是利用两景或多景遥感影像中运动目标的差异,通过复杂的特征匹配和变化检测方法,来提取目标运动信息。一方面增加了遥感影像数据获取的难度和所需遥感影像的数据量,另一方面增加了目标运动信息提取的复杂性[11, 12, 13, 14, 15]。
随着卫星遥感影像的分辨率不断提高,运动目标在极短的成像时间(例如资源三号卫星多光谱影像行积分成像时间约为0.000 8 s)发生的微小空间位移将导致影像空间、光谱属性的变化,即动态遥感成像的时空移变成像[14, 15, 16]。相关研究表明,利用两景或多景成像时间间隔很短的航空航天遥感影像,不仅可实现对运动目标的提取,而且可以提取目标的运动信息[17]。相关文献利用QuickBird卫星同一景的全色和多光谱影像,提取运动目标的速度信息,而不是利用多景遥感影像或者立体像对[4]。该方法虽减少了提取运动目标所需的遥感影像数量及获取难度,但其思路仍是采用精化的几何成像模型,在地面控制点辅助条件下,经过复杂坐标系转换,计算得到运动目标在地心坐标系下的地理坐标,进而求解目标运动的绝对距离与运动速度。
2 基于单景卫星影像的目标运动信息提取原理 2.1 多波段线阵推扫成像影像数据
卫星遥感成像普遍采用线阵CCD推扫成像方式。以资源三号测绘卫星多光谱成像传感为例,蓝(band1)、绿(band2)、红(band3)、近红外(band4)。四波段成像传感器相互平行布设在成像焦平面内,间距分别是152个像素、128个像素和128个像素,如图 1所示。在卫星推扫成像过程中,每个波段对同一目标地物的成像存在微小的时间间隔,为目标运动信息提取提供了可能。
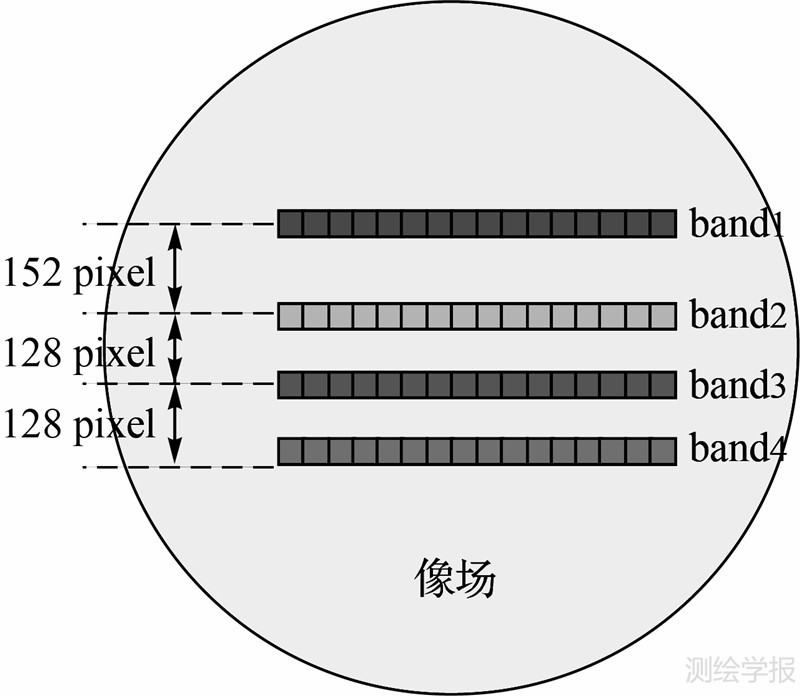 |
| 图 1 资源三号卫星多光谱传感器布设示意图Fig. 1 ZY-3 multi-spectral sensor’s arrangement |
光学遥感数字成像是对地物时间和空间信息的动态记录,其信息记录能力有限,且包含了复杂的时间和空间信息转换问题[18]。数字遥感成像系统是严格意义的时空移变系统,由光电积分过程中的物像移动、多CCD拼接的多中心投影以及多传感器曝光时间不同步等都导致时空移变效应的信息混淆[19, 20, 21, 22]。
以一维运动情况为例,如图 2所示。S0、S1、S2为3个摄站点,成像时刻分别为t0、t1、t2。band1和band2两个波段间距为d,遥感器平台运动速度为Vs,目标运动速度为Va。
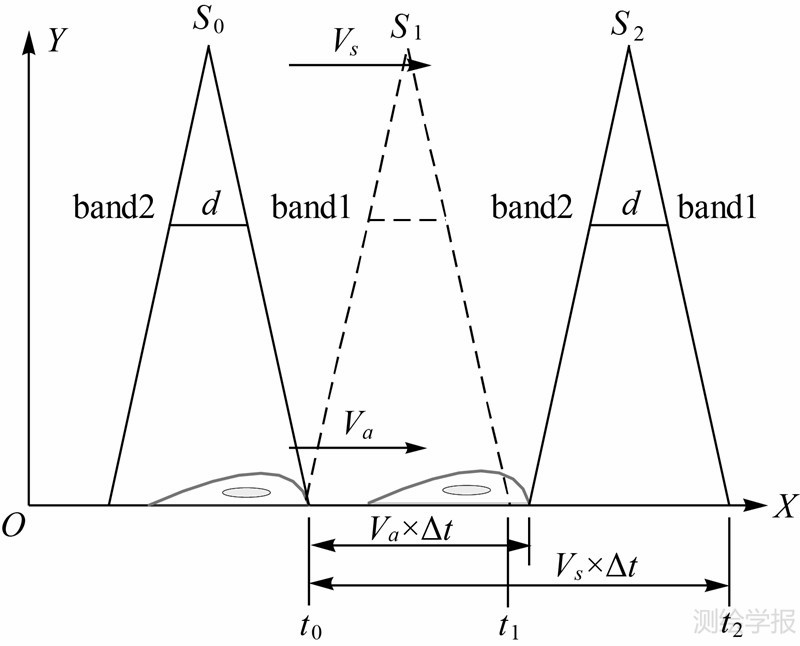 |
| 图 2 运动目标遥感成像的时空移变特性原理Fig. 2 Moving target’s space variant principle in remote sensing imaging |
在t0时刻,band1传感器对地物目标成像,若地物目标静止,则在t1时刻,band2传感器对同一地物目标成像,两波段成像时间间隔为t1-t0;若地物目标运动速度为Va,则在t2时刻,band2传感器对同一地物目标成像,两波段成像时间间隔为t2-t0。因此,目标与遥感器平台的相对运动,引起同一运动目标在两波段影像上微小位置差异S。在精确获取微小位置差异S和微小成像时间间隔t2-t0的情况下,可以计算得到目标的运动速度Va=S/(t2-t0)。
3 时空移变成像模型与目标运动信息求解
基于单景卫星遥感影像的目标运动信息提取,要解决两个方面的问题:一是对运动目标的精确识别;二是遥感成像对运动目标成像的时间-空间移变成像模型的建立与微小位置、时间间隔的精确计算。本文研究重点在于第2个方面。
3.1 卫星成像时空移变参数
3.1.1 卫星遥感成像涉及的坐标系
图 3表示卫星线阵推扫成像示意图。在WGS-84地球固定参考坐标系O-XearthYearthZearth下,线阵CCD影像像主点M的星下点为M′,成像点为N;卫星平台的侧摆角为φ;卫星平台的俯仰角为θ;运动目标点(例如飞机)的高程为h;卫星距椭球面距离为H;椭球面点与地心的距离为R;卫星遥感器摄站点坐标为(Xs,Ys,Zs),运行速度为Vs;运动目标点坐标为(Xa,Ya,Za),运行速度为Va。
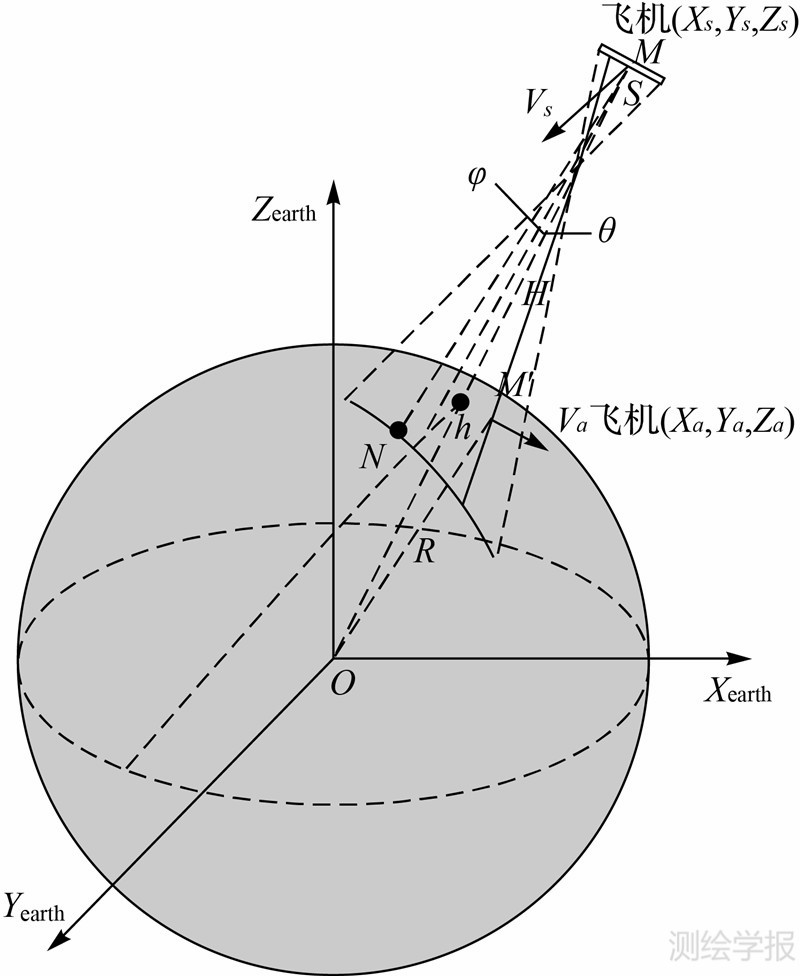 |
| 图 3 卫星线阵CCD推扫成像几何关系示意图Fig. 3 Geometric schematic of satellite linear scanning imaging |
卫星成像传感器一般采用多线阵CCD推扫成像方式,线阵CCD传感器的基本参数包括像元尺寸δ以及像元数N。多线阵CCD推扫成像严格记录了起始行的成像时间,成像传感器具有固定的扫描频率f。由此可推知CCD线阵推扫成像每行影像的成像时间ti。
3.1.3 卫星运行位置、速度与姿态参数
卫星平台的位置、速度与姿态参数在卫星数据的辅助文件中进行周期性记录,可以通过适当的插值方法计算得到CCD线阵传感器每行影像成像时刻的卫星平台位置、速度和姿态信息。
3.2 时空移变成像模型与精确解算 3.2.1 线阵推扫成像时变参数精确求解
线阵推扫成像的时变参数是建立线阵CCD时空移变成像模型的基础,必须准确获取线阵CCD传感器对目标地物的扫描成像时间。根据线阵CCD推扫式成像原理,第i行影像成像时间可表示为
式中,t0是起始行的成像时间;T是每一行的积分时间。
以资源三号卫星为例,多光谱各波段传感器对同一目标地物成像时间差可表示为
式中,t0_band1为band1影像的起始成像时间;t0_band2是band2影像的起始成像时间;i为目标物在band1影像中的所在行;j为目标物在band2影像中的所在行。3.2.2 线阵推扫成像空变参数精确求解
线阵推扫成像的空变参数主要表现为遥感影像空间采样距离(ground sample distance,GSD)。卫星平台的内外方位元素极大的影响遥感器对地观测的地面分辨率Gsd,必须精确求解卫星遥感器在沿轨和垂轨方向上Gsd。
在沿轨方向上,如图 4所示,Si和Si+1分别代表第i行和第i+1行成像时的摄站点位置;Ve是卫星平台飞行速度Vs在成像面上投影的速度;He是卫星遥感器摄站点与成像面的垂直距离;θ是第i行成像时遥感器在沿轨方向的俯仰角(pitch);θ+dθ是第i+1行成像时遥感器在沿轨方向的俯仰角;Δt是第i行和第i+1行成像的时间间隔。卫星线阵推扫成像方式的每行影像扫描成像时间很短,例如资源三号测绘卫星多光谱传感器每行扫描成像时间一般为0.000 8 s。因此,卫星平台可视为匀速直线运动且卫星姿态dθ变化很小。
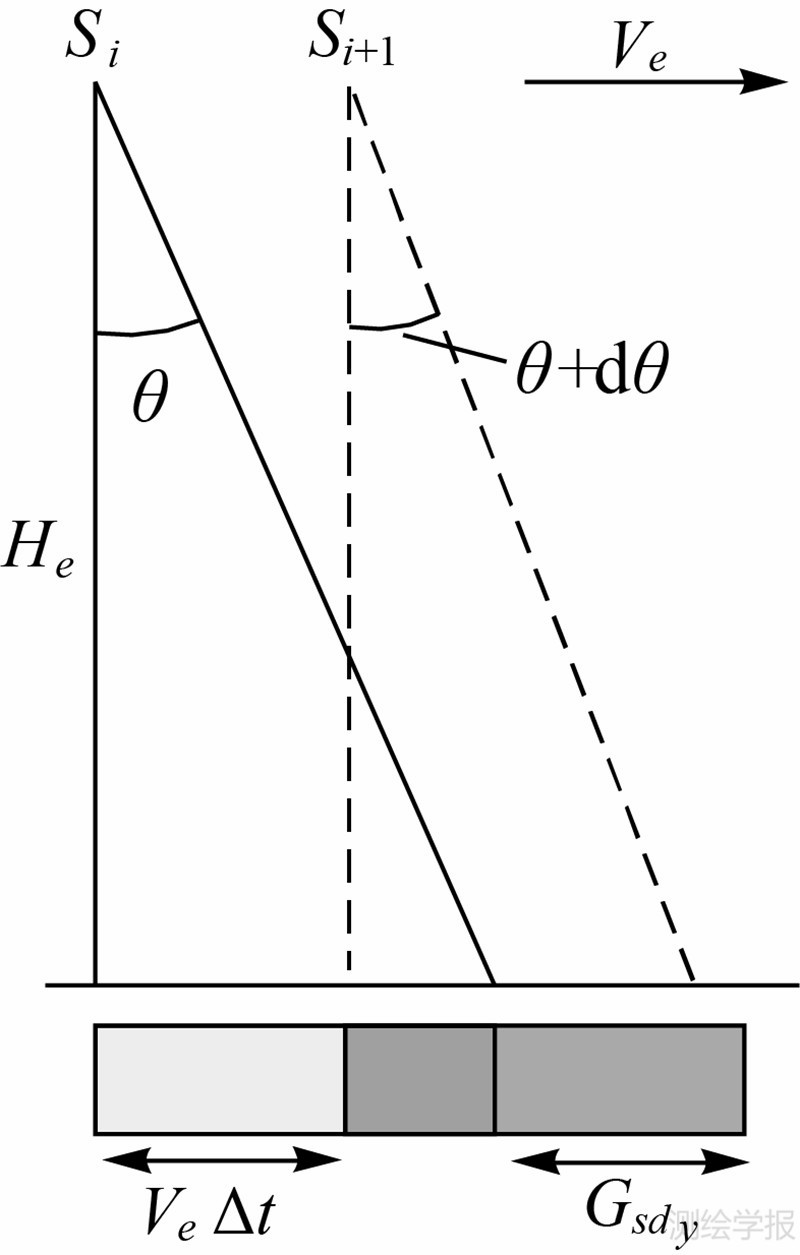 |
| 图 4 沿轨向GSD几何关系Fig. 4 GSD geometry in along-track direction |
由此,推扫成像在沿轨方向上的分辨率Gsdy可表示为
在dθ很小的情况下,上式可化简为
式中
线阵CCD传感器在垂轨方向上的分辨率Gsd,如图 5所示。CCD像元尺寸为δ;φ是成像时的卫星遥感器的侧视角;Φ是成像方向与主光轴的夹角;光学系统成像焦距为f。焦距f在S-YZ平面的投影SM′为fcos θcos φ。
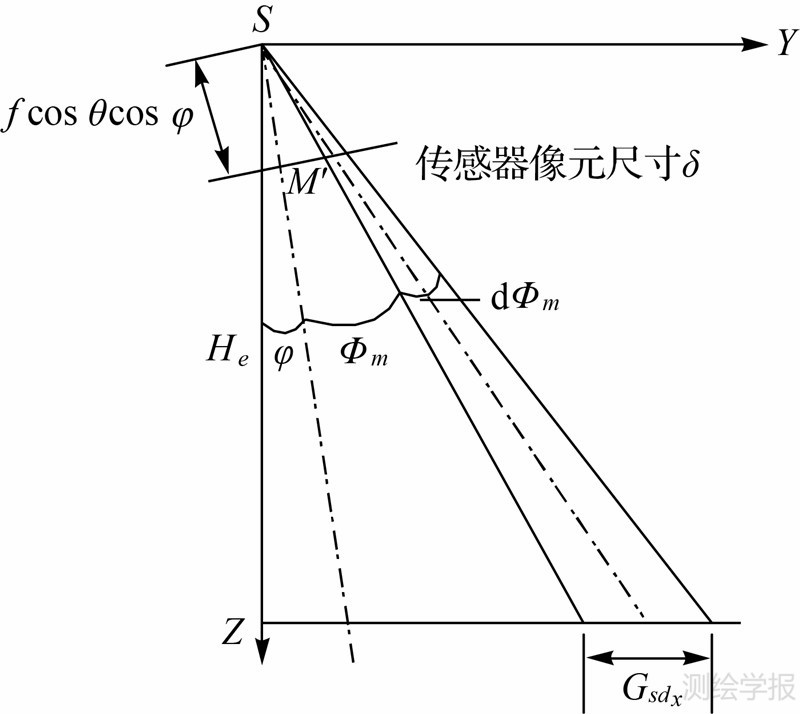 |
| 图 5 垂轨向GSD几何关系Fig. 5 GSD geometry in across-track direction |
垂轨方向上的分辨率Gsd可表示为
在dΦm很小的情况下,式(7)可化简为
3.2.3 目标运动速度与方向解算
在不同波段两幅影像精确配准后,如图 6所示。目标物点在不同波段影像上的坐标分别为(x_band1,y_band1)、(x_band2,y_band2),可以计算得到运动目标在不同波段影像上像平面位置差异sx和sy,通过线阵推扫成像地面分辨率参数,计算实际地面距离。可表示为
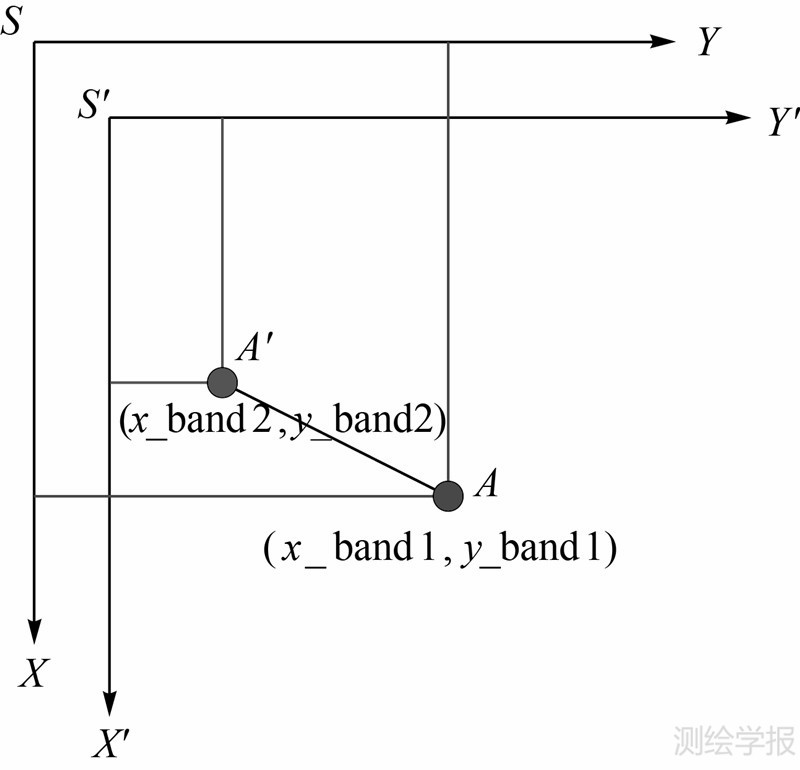 |
| 图 6 运动目标像面距离示意图Fig. 6 Moving target’s geometric schematic in image plane |
运动目标在扫描成像时间差内运动的距离为
根据不同波段影像上同一目标成像时间差Δt,获得目标的运动速度Va和方向α。
4 目标运动信息提取试验与分析 4.1 资源三号卫星多光谱影像数据与辅助参数信息
本文采用资源三号测绘卫星一景多光谱影像数据,在该景影像内有两架高速飞行的飞机经过,在多光谱影像中的成像效果如图 7所示,两架飞机分别命名为airplane_A和airplane_B。其中,3个飞机影像分别是该景影像红、绿、蓝波段扫描成像时间内所获取的飞机影像。
 |
| 图 7 资源三号测绘卫星多光谱影像数据Fig. 7 ZY3’s multi-spectral remote sensing image |
资源三号卫星多光谱成像传感器参数如表 1所示。
| 多光谱影像谱段 | 蓝/绿/红/近红 | |
| 传感器像元尺寸δ/mm | 20×10-3 | |
| 谱段间距/像素 | band1—band2 | 152 |
| band2—band3 | 128 | |
| band3—band4 | 128 | |
根据该景遥感影像的辅助参数,经插值后得到在该景影像中目标飞机所在扫描行成像时刻的卫星平台在WGS-84坐标下的位置(Xs,Ys,Zs)、速度(Vsx,Vsx,Vsx)以及在本体坐标系坐标下的姿态(俯仰角pitch、横滚角roll、旋偏角yaw)数据如表 2所列。
| 指标 | 数值 | 指标 | 数值 | 指标 | 数值 |
| Xs/m | -2 410.465 6 | Ys/m | 4 724.078 7 | Zs/m | 4 373.179 0 |
| Vsx/(m/s) | -686.66 | Vsy/(m/s) | 5 020.52 | Vsz/(m/s) | -5 787.4 |
| pitch/弧度 | 0.000 006 7 | roll/(弧度) | -0.000 062 94 | yaw/(弧度) | 0.049 504 7 |
两架飞机airplane_A和airplane_B经人工精确选取飞机机头特征点在各波段影像中的位置行列数如表 3所示。
| 坐标 | 波段 | ||||
| band1 | band2 | band3 | band4 | ||
| airplane_A | Ximage/像素 | 5 863.774 05 | 5 860.860 71 | 5 857.761 41 | 5 855.591 90 |
| Yimage/像素 | 384.587 73 | 377.769 27 | 371.694 65 | 365.805 98 | |
| airplane_B | Ximage/像素 | 5 780.041 98 | 5 776.816 251 | 5 773.871 02 | 5 771.447 741 |
| Yimage/像素 | 150.863 842 | 147.918 61 | 144.833 13 | 141.696 962 | |
充分利用airplane_A和airplane_B的飞机机型、飞行高度、飞行速度等不同的特点,本文分别开展了两架飞机的运动信息提取的试验,从两个方面验证了所建立的时空移变成像模型的有效性以及运动信息提取算法的稳定性。一是分别将所提取的airplane_A和airplane_B运动信息与相应机型的飞行技术指标相比较,计算所提取的飞行速度与理论飞行速度的误差,验证本文所提出模型及算法的有效性;二是通过卫星影像不同波段之间所提取的airplane_A和airplane_B运动信息进行相互比较,计算所提取各个飞行速度结果的均方根误差,验证本文所提出模型及算法的稳定性。具体试验结果如下:
由于飞机的准确飞行高度未知,根据规定民航飞机巡航高度在8000 m至12 000 m之间,与遥感卫星的轨道高度(约480 km)相比甚小,因此,不妨假设airplane_A和airplane_B的飞行高度分别为12 000 m和9000 m。依据卫星成像时空移变成像模型,由band1与band2、band2与band3、band3与band4分别计算得到airplane_A和airplane_B的飞行速度平均值为1210 km/h和770 km/h,如表 4所示。
从影像上估算,airplane_A和airplane_B机型长度约为60 m和40 m。根据飞机机型尺寸参数判断[23],airplane_A和airplane_B可能为空客A330和空客A320。根据空客飞机技术指标参数可知,空客A330和A320机型的巡航速度(相对于风速)约为920 km/h和850 km/h。由于无法获取该景影像获取时刻飞机所在位置风速的准确数值,因此,由本文提取的飞机速度结果无法进行准确衡量。但与上述飞机的巡航速度相比,通过本方法提取的airplane_A和airplane_B飞机速度平均值(见表 4)的误差分别约为30%和90%。在不考虑飞机飞行状态瞬时风速环境影响条件下,所提取的飞机运动信息与飞机额定巡航速度基本吻合。
| 解算参数及结果 | 解算对象 | |||||
| airplane_A | airplane_B | |||||
| band1-2 | band2-3 | band3-4 | band1-2 | band2-3 | band3-4 | |
| 垂轨方向距离SX/m | 16.933 5 | 18.014 4 | 12.610 1 | 18.749 3 | 17.118 9 | 14.085 1 |
| 沿轨方向距离SY /m | 38.408 0 | 34.218 1 | 33.170 6 | 16.590 3 | 17.380 39 | 17.665 9 |
| 合成距离S/m | 41.975 3 | 38.670 3 | 35.486 6 | 25.035 5 | 24.395 4 | 22.593 7 |
| 成像时间差Δt/s | 0.128 8 | 0.108 7 | 0.108 5 | 0.125 6 | 0.106 1 | 0.106 1 |
| 垂轨方向速度VX/(km/h) | 473.292 0 | 596.424 9 | 418.077 1 | 537.141 4 | 580.321 5 | 477.477 3 |
| 沿轨方向速度VY/(km/h) | 1 073.503 5 | 1 132.899 0 | 1 099.743 9 | 475.291 1 | 589.184 7 | 598.863 8 |
| 合成速度Vairplane /(km/h) | 1 173.207 2 | 1 280.305 8 | 1 176.531 0 | 717.232 6 | 826.989 6 | 765.912 8 |
| 平均值Vaverage/(km/h) | 1 210.014 6 | 770.045 04 | ||||
通过对卫星影像band1与band2、band2与band3、band3与band4等4个谱段间时空移变特性差异所提取的飞行运动信息结果(见表 4)进行相互比较验证,所提取的airplane_A和airplane_B飞行速度的均方根误差分别为49.805 1 km/h和43.099 0 km/h,约为airplane_A和airplane_B飞机飞行速度平均值的4%和5%,证明本文所建立的时空移变成像模型与运动信息提取算法的稳定性。
5 结 论
本文建立了高分辨率卫星遥感成像时空移变成像模型,提出了一种基于单景卫星影像的目标运动信息提取方法,并在资源三号多光谱成像中开展了飞机运动信息提取验证试验。所提取的两架飞机飞行速度分别为1210 km/h和770 km/h,与相应飞机机型的巡航速度相比,所提取的airplane_A飞机速度误差约为30%,airplane_B飞机速度误差约为9%;通过各谱段间影像时空移变特性差异提取的airplane_A和airplane_B飞行速度的均方根误差分别为49.8051 km/h和43.0990 km/h,约为airplane_A和airplane_B飞机飞行速度平均值的4%和5%。在无法准确获知飞机飞行时的飞行高度、风速等参数情况下,上述试验结果基本验证了基于单景卫星影像提取速度信息的有效性和稳定性。随着卫星影像地面分辨率的不断提高,本研究成果将可进一步用于更小尺度的运动目标(例如汽车、火车等)的检测与运动信息提取。
| [1] | LI Deren, LI Qingquan, YANG Bisheng. Techniques of GIS, GPS and RS for the Development of Intelligent Transportation[J]. Geomatics and Information Science of Wuhan University, 2008, 33(4): 331-336. (李德仁, 李清泉, 杨必胜. 3S技术与智能交通[J]. 武汉大学学报: 信息科学版, 2008, 33(4): 331-336.) |
| [2] | GONG Peng, LI Xia, XU Bing. Interpretation Theory and Application Method Development for Information Extraction from High Resolution Remotely Sensed Data[J]. Journal of Remote Sensing, 2006, 10(1): 1-5. (宫鹏, 黎夏, 徐冰. 高分辨率影像解译理论与应用方法中的一些研究问题[J]. 遥感学报, 2006, 10(1): 1-5.) |
| [3] | CHENG Liang, GONG Jianya, SONG Xiaogang, et al. A Method for Affine Invariant Feature Extraction with High Quality for Wide Baseline Stero Image Matching[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 77-82. (程亮, 龚健雅, 宋小刚, 等. 面向宽基线立体影像匹配的高质量仿射变换不变特征提取方法[J]. 测绘学报, 2008, 37(1): 77-82.) |
| [4] | EASSON G, DELOZIER S, MOMM H G.Estimating Speed and Direction of Small Dynamic Targets through Optical Satellite Imaging[J]. Remote Sensing, 2010, 2(5): 1331-1347. |
| [5] | ZHANG Y, HONG G. A Wavelet Integrated Image Fusion Approach for Target Detection in Very High Resolution Satellite Imagery[C]//Proceedings of SPIE Signal Processing, Sensor Fusion and Target Recognition. [S.l.]: SPIE, 2005. |
| [6] | YAMAZAKI F, LIU Wen, VU T T. Speed Detection for Moving Objects from Digital Aerial Camera and Quickbird Sensors[C]//Proceedings of the 5th International Workshop on Remote Sensing Applications to Natural Hazards. Washington DC: [s.n.], 2007. |
| [7] | GERHARDINGER A, EHRLICH D, PESARESI M. Vehicle Detection from Very High Resolution Satellite Imagery[J]. The International Archives of Photogrammetric & Remote Sensing Spatial Information Science, 2005, 36(3): 83-88. |
| [8] | JIN X, DAVIS C H. Vehicle Detection from High-resolution Satellite Imagery Using Morphological Shared-weight Neural Networks[J]. Image and Vision Computing, 2007, 25(9): 1422-1431. |
| [9] | LEITLOFF J, HINZ S, STILLA U. Vehicle Detection in Very High Resolution Satellite Images of City Areas[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(7): 2795-2806. |
| [10] | LIU W, YAMAZAKI F, VU T M. Automated Vehicle Extraction and Speed Determination from Quickbird Satellite Images[J]. Selected Topics in Appliced Earth Observations and Remote Sensing, 2011, 4(1): 75-82. |
| [11] | VOLLMERHAUSEN R H, DRIGGERS R G, WILSON D L. Predicting Range Performance of Sampled Imagers by Treating Aliased Signal as Target-dependent Noise[J]. Journal of the Optical Society of America A, 2008, 25(8): 2055-2065. |
| [12] | GONG Peng. Some Frontiers of Remote Sensing Science and Technology[J]. Journal of Remote Sensing, 2009, 13(1): 13-24. (宫鹏. 遥感科学与技术中的一些前沿问题[J]. 遥感学报, 2009, 13(1): 13-24.) |
| [13] | TAO Xiaoping, FENG Huajun, LEI Hua, et al. A Splicing Method of Sectioned Restoration Algorithm for Images with Space-variant Point Spread Function[J]. Acta Optica Sinica, 2009, 29(3): 648-654. (陶小平, 冯华君, 雷华, 等. 一种空间变化PSF图像分块复原的拼接方法[J]. 光学学报, 2009, 29(3): 648-654.) |
| [14] | ZHANG Chunsen. 3D Motion Object Location Tracking Based on Binocular Sequence Images[J]. Acta Geodaetica et. Cartographica Sinica. 2006, 35(4): 347-354. (张春森. 双目序列影像3维运动物体定位跟踪[J]. 测绘学报, 2006, 35(4): 347-352.) |
| [15] | ZHANG Ka, SHENG Yehua, YE Chun. Digital Close-range Stereo Image Matching Based on Digital Parallax Model and Improved SIFT Feature[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(6): 624-630. (张卡, 盛业华, 叶春. 基于数字视差模型和改进SIFT特征的数字近景立体影像匹配[J]. 测绘学报, 2010, 39(6): 624-630.) |
| [16] | VOLLERHAUSEN R H. Representing the Observer in Electro-optical Target Acquisition Models[J]. Optics Express, 2009,17(20): 17253-17268. |
| [17] | ZHANG Y, XIONG Z. Moving Vehicle Detection Using a Single Set of Quickbird Imaging[C]//Proceedings of ISPRS Commission VII Mid-term Symposium: Remote Sensing: From Pixels to Processes. Enschede: ISPRS, 2006. |
| [18] | ZHAO Shihu, YIN Dan. Simulation and Analysis of Digital Remote Sensing Camera's Space Variant Effect[J]. Geography and Geo-Information Science. 2013, 29(4): 122-129. (赵世湖, 尹丹. 光学遥感数字成像系统空间移变效应仿真与分析[J]. 地理与地理信息科学, 2013, 29(4): 122-129.) |
| [19] | VOLLERHAUSEN R H, REAGO J D A, DRIGGERS R G. Analysis and Evaluation of Sampled Imaging Systems[M]. Washington: SPIE Press, 2010. |
| [20] | BHAKTA V R, SOMAYAJI M J, CHRISTENSEN M P. Applications of the Phase Transfer Function of Digital Incoherent Imaging Systems[J]. Applied Optics, 2012, 51(4): 17-26. |
| [21] | ZHANG Y Y, WANG X W, WANG C X. Restoration of Space-variant Blurred Image Based on Motion-blurred Target Segmentation[J]. Journal of Systems Engineering and Electronics, 2010, 21(2): 191-196. |
| [22] | QI Huaichuan, HUANG Qiaolin, HU Yongli. The Study about the Means of Simulation for the Motion Blurred of Space Optical Remote Sensing[J]. Spacecraft Recovery & Remote Sensing, 2010, 31(2): 51-57. (齐怀川, 黄巧林, 胡永力. 空间光学遥感运动模糊仿真方法研究[J]. 航天返回与遥感, 2010, 31(2): 51-57.) |
| [23] | WIKIPEDIA. Airbus A330 and Airbus A320[EB/OL].2012-10-20[2012-10-12]. http://en.wikipedia.org/wiki/Airbus_A330. |