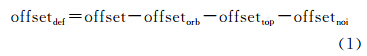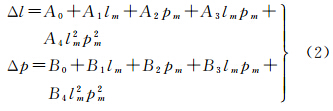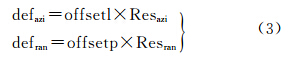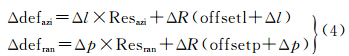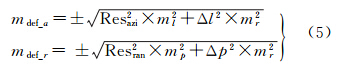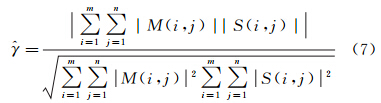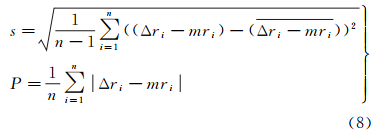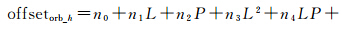强震地表形变场的准确观测对于正确认识震源机制、反演断层滑动与分析断裂活动状态具有重要意义。合成孔径雷达干涉测量(interferometric synthetic aperture radar,InSAR)具有覆盖范围广、全天候、分辨率高等独特的技术优势,正成为同震形变场提取的有效手段[1, 2]。InSAR技术是对同一地区地震前后的两幅或多幅SAR影像进行干涉处理获得同震位移,然而,InSAR直接测量的位移是地表沿雷达视线方向(line of sight,LOS)上的一维形变,且地震前后获取的SAR信号可能受强震引发过大的地表形变梯度、地表破坏以及轨道位置差异导致干涉失相关现象,极大阻碍了地表形变场的准确提取[3, 4]。
SAR影像配准过程中的像素偏移量可提取地表沿雷达方位向(近南北向)和距离向(近东西向)的二维形变场,与InSAR提取的LOS方向一维形变形成优势互补。像素偏移量是从覆盖同一地区的两幅或多幅SAR影像中搜索大量同名像点进行精确配准,计算同名点在方位向与距离向的坐标偏移量,扣除轨道位置差异和地形起伏引起的系统偏差后,提取成像期间发生的强震地表位移[5]。像素偏移量技术的显著特点是适用于地表发生大位移的形变场监测,如观测强震同震形变、检测冰川运动、监测沙丘迁移等[6, 7, 8, 9, 10],无须进行相位解缠,提取地表沿近似南北向与东西向的二维完整形变场,可弥补强震地表形变使得InSAR干涉图条纹过于密集、相位梯度过大而导致的解缠失败问题以及InSAR仅能提取沿LOS一维方向位移的不足。
随着当前高分辨率SAR卫星的发射升空(如TerraSAR-X、COSMO-SkyMed、Sentinel-1和ALOS-2),影像配准偏移法应用于地表形变提取具有较好的前景,SAR影像空间分辨率的提高将显著改善像素配准偏移量提取地表形变场的精度与可靠性。目前已有的探索多侧重于偏移量方法提取形变场的应用研究,而对于系统分析该方法提取形变场的误差源、精度模型以及系统性验证还有待进一步研究。因此,本文在分析该方法提取形变场的理论基础上,推导建立了像素偏移量提取地表位移的误差模型,并使用Bam地震的ASAR影像和玉树地震的PALSAR影像开展了精度验证与误差影响规律分析。 2 像素偏移量提取形变的方法与误差 2.1 计算模型
SAR影像配准得到的同名像素坐标偏移量主要由4个分量贡献组成:地表形变引起的偏移量,两次成像卫星轨道位置与姿态差异引起的像素偏移量(简称轨道系统偏移量),地形起伏引起的偏移量以及噪声等引起的偏移量[5]。从总偏移量中扣除轨道分量、地形分量和噪声偏移量后,可获得地表形变偏移分量,如下式
式中,offset为主、从影像同名点配准后的坐标偏移量;offsetorb为轨道引起的偏移分量,一般呈现为系统性的偏移量;offsettop为地形引起的偏移分量;offsetdef为形变偏移量;offsetnoi为噪声引起的偏移量。影像配准偏移量方法提取形变场主要分为以下几个步骤。
2.1.1 影像配准,获取大量同名像点的坐标偏移量
首先,基于卫星轨道参数进行影像中心像元的粗配准[11]。以主影像中心作为目标点,利用主、从影像的卫星轨道参数及SAR成像几何,计算主影像中心点在从影像上的同名像点,获得粗配准坐标偏移参数。
其次,SAR影像像元级的配准。在粗配准基础上,采用窗口搜索法寻找主、从影像中的同名像点[12, 13],并以主影像行、列坐标为自变量,在最小二乘准则下建立两幅影像同名像点的偏移模型(式(2)),基于此模型计算得到主影像像点的配准偏移量,精度为像元级
最后,为进一步提高配准精度,需要进行亚像元级配准[14]。首先依据像元级配准偏移模型获得主、从影像同名像点的初始坐标,然后选取一定大小的搜索窗口计算互相关系数;为达到亚像元级的配准精度,此处可采取两种匹配策略:一种是对SAR影像本身进行内插过采样处理,再进行互相干系数计算,进而在搜索窗口内寻找互相干系数峰值位置作为亚像元级的配准结果;另一种方法无需对SAR影像直接进行内插采样,而是对搜索窗口内计算得到的互相关系数进行内插过采样,选择内插后的互相关系数峰值作为亚像元级的配准结果。基于互相关系数过采样的精配准方法具有较高的计算效率,因此本文采用了基于互相关系数过采样的方法进行亚像元级的配准,获得密集分布的同名像点坐标偏移量。
2.1.2 去除轨道和地形偏移量
上述精配准后获得的像素偏移量主要包括地表形变引起的偏移分量、轨道差异和地形起伏引起的偏移分量(忽略噪声影响),为分离出地表形变信号,必须去除轨道和地形偏移分量。轨道偏移量的建模需选取无形变区域的偏移数据,这样可有效避免地表形变本身对轨道偏移模型的影响,然后联合研究地区的地形起伏数据(如DEM),采用最小二乘准则构建系统偏移模型,扣除轨道和地形引起的偏移分量,获得由于地表形变引起的像素偏移分量。将配准得到的方位向和距离向形变偏移量分别乘以对应方向上的地面分辨率,可获得二维方向上的地表位移量,然后进行地理编码完成地表形变场的获取。
2.2 误差模型
根据上述计算过程,SAR影像配准偏移量提取地表形变场的数学计算模型为
上述形变量计算模型表达了地表位移与像素偏移量、分辨率之间的函数关系,根据误差传播定律,推导获得形变量的误差模型
根据形变量误差模型及中误差公式,在影像分辨率固定情况下,形变场精度主要受像素偏移量误差影响。而像素的形变偏移量主要受影像配准过程制约,因此SAR影像的精确配准对于形变场提取非常重要。根据前述影像配准内容分析可知,形变偏移量精度主要来源于以下几个因素的影响。
2.3.1 匹配测度与窗口尺寸
基于互相关系数的匹配测度指标具有较好的稳健性[19, 20],本文采用基于强度信息的匹配策略,将像素点对应的复数值转换为强度值,其计算模型如下
窗口尺寸对匹配指标值的计算有直接影响。过大的匹配窗口严重影响计算效率,而过小的匹配窗口产生较多奇异点,匹配可靠性降低,因而选择适宜大小的匹配窗口对于形变场的准确提取较为重要。
2.3.2 互相关系数过采样因子
亚像元级的精配准需要进行过采样处理,基于SAR影像本身的过采样耗时较长,不利于高密度偏移量的快速获取。因此本文使用了基于互相关系数过采样的方法进行亚像级精配准。该方法首先在从影像上选择6像素×6像素大小的搜索窗口(因前一步的像元级配准结果可保证达到了像元级的配准精度,因此搜索窗口无需过大),基于公式(7)计算得到搜索窗口内的互相关系数,之后采用一定倍数如16倍的过采样因子,将窗口中互相关系数过采样为96像素×96像素的大小,以互相关系数峰值位置为对应的亚像元级同名像点。过采样因子直接影响着同名像点的精确位置,从理论上看,过采样因子越大,同名点位置越精确,形变场精度越高,但较大的过采样因子会增加计算负荷。
2.3.3 轨道引起的像素偏移分量计算模型
两次SAR成像轨道位置和姿态差异引起的同名像素偏移量,难以通过轨道参数直接计算。因此,不直接使用轨道姿态数据(如位置矢量和速度矢量),而是使用大量(如约600对)同名像素的配准坐标偏移量,采用多项式模型拟合由于轨道引起的系统偏移量,即:将轨道姿态误差及其他相关误差都纳入多项式模型中进行一并考虑,获得由于卫星轨道差异引起的系统性配准偏移分量(类似于有理函数建模方法)。然后,从总的配准偏移量中扣除轨道引起的偏移分量,从而获得形变分量信号。具体可采用一阶多项式offsetorb1=n0+n1L+n2P、二阶多项式offsetorb2=offsetorb1+n3L2+n4LP+n5P2或三阶多项式offsetorb3=offsetorb2+n6L3+n7P3+n8LP2+n9L2P进行计算,其中ni为模型参数,L、P为主影像点的方位向与距离向坐标。
2.3.4 地形起伏效应
对于较为平坦的地区,同名像点的偏移量主要来自于两次成像的轨道偏离影响,而对于地形起伏较大的区域,像素偏移量除了轨道影响之外,还包括由于地形起伏引起的偏移量。因此,采用像素偏移量方法提取地形起伏较大区域的形变场时,必须考虑地形起伏对SAR像素位置的影响[21],引入SAR影像区域对应的DEM联合建立系统偏移量模型。
3 试验结果与分析
3.1 Bam试验数据
为验证分析上述误差模型和精度规律,采用2003年Bam地震的ASAR影像开展试验,具体参数见表 1。由于Bam地震发震断层主要以南北方向的走滑量为主,距离向(与断层近似垂直)形变场不显著,因此本文主要分析地表沿方位向的形变场。
为验证影像配准偏移量方法提取形变场的精度,评价不同计算条件下获取的形变场,根据文献[22]反演的Bam地震断层参数,采用Okada模型正演计算方位向的形变场[23],如图 1所示。
根据前述推导的误差模型,计算Bam地震ASAR影像提取方位向形变场的理论误差。ASAR影像的方位向分辨率取值为Resazi=7.8 m,方位向形变像素偏移量offsetl=0.05,方位向地表形变defazi=0.4 m,Bam地震ASAR影像数据相干性较好,配准精度较高,取偏移量误差Δl=0.01,分辨率舍入误差ΔR=0.000 1,则形变量误差Δdefazi=7.8 cm。
3.2 匹配窗口尺寸
为分析匹配窗口尺寸对形变场提取精度的影响,采用了4种大小的匹配窗口:32像素×32像素、64像素×64像素、128像素×128像素和256像素×256像素窗口,采用相同的Oversample匹配方法及32倍过采样因子。基于4种不同窗口尺寸提取的方位向形变场,如图 2所示。
从图 2可以看出,窗口尺寸越小,形变场的噪声奇异值(可认为是误匹配点)越多;窗口尺寸越大,形变场的奇异值越少,但同时形变场呈现出渐变性的条纹状,在最大的256像素×256像素窗口提取的形变场中表现最显著。针对图中剖面线上的形变场,定量分析不同尺寸匹配窗口提取的形变差异。
根据图 2中的直线剖面位置,对像素偏移算法提取的形变场与正演的参考形变场进行定量统计分析,如图 3所示,其中,标准差s和差异绝对均值P采用如下公式计算
对上述两个评价指标及形变差异进行分析,采用128尺寸窗口提取的形变场与参考形变场的吻合程度最好,32尺寸窗口提取的形变场奇异点较多,标准差、差异绝对均值两项评价指标都较大,64尺寸窗口次之。256窗口提取的形变场无明显突变点,呈一定的梯度性过渡,整体走势与128窗口相似,但两项评价却没有得到显著的改善,且标准差大于128尺寸窗口。
3.3 过采样因子
对SAR影像精配准过程采用不同的过采样因子进行验证,匹配窗口尺寸固定为128像素×128像素,分别采用了16倍、32倍、64倍、128倍的过采样因子,获得如下图 4所示的4种形变场。
从图 4中可以看出,过采样因子越大,提取出的形变场越平滑。在固定128像素×128像素匹配窗口条件下,16倍过采样因子提取的形变场具有明显的突变条纹,与实际地震形变场不符,说明过小的过采样因子会严重降低形变场精度。对局部剖面线上形变场定量分析表明,过采样因子越大,形变量越平滑,评价指标值越好。从16倍到64倍过采样因子提取的形变场中各项评价指标都有明显提高,但128倍相比64倍过采样因子提取的形变量没有显著改善。
3.5 地形起伏影响
由于Bam地震所处区域的地形较为平坦,其地形起伏引起的像素偏移效应不显著。而玉树地震发震区所在区域地形起伏较大[24, 25],适用于探索其对偏移量方法提取地表形变的精度影响。玉树地震试验影像参数如表 2所示,采用偏移量方法提取玉树地震沿方位向和距离向形变场时,采用了128像素×128像素搜索窗口尺寸及64倍过采样因子。
在不考虑地形起伏对像素偏移量提取影响的情况下,根据前文所述方法,精确配准获取约17万对同名像点,计算其像素偏移量,再利用600个分布于稳定无形变区域的偏移量拟合轨道多项式模型,去除轨道偏移量,获得同震形变场,如图 5(a)为方位向形变场、图 5(b)为距离向形变场。
分析图 5(a)方位向形变场可发现,地震破裂线的几何位置清晰,可明显判别地表形变趋势;而位于纬度33.3°N以上形变场(椭圆形区域)具有类似山脊线走向的趋势,且形变场中存在较多奇异值,位移量超过1 m。分析图 5(b)的距离向形变场,存在更为明显的地形效应,基本掩盖了地震本身造成的形变,导致无法分辨出真实的地表位移信息,图 5(b)距离向形变场分布与DEM走势非常相似,表明地形起伏对于像素偏移量影响较为显著。
从上述分析可知,为准确提取其可靠的形变场,必须去除地形起伏对像素偏移量的影响。因此,引入该地区的DEM数据进行联合建模,采用顾及轨道因素、地形起伏效应的系统偏移量模型,如公式(9)。依据此多项式模型可达到同时去除这两种系统偏移量的目的,再经后续处理,则得到如图 6所示的方位向和距离向形变场。
上式中系统偏移模型主要包括两部分,即轨道偏移模型与地形起伏偏移模型,offsetorb_h为轨道偏移量及地形偏移量总和,公式(9)中的前6项为轨道偏移量二阶多项式模型,以主影像的方位向和距离向坐标为自变量,其中ni为轨道偏移量模型系数;公式中的后两项为地形效应偏移模型,其中h为主影像(L、P)像元对应的高程值,mi为地形偏移量模型系数。
分析图 6(a)可以发现,沿方位向形变场的奇异点明显减少,对比于图 5(a),其系统性的效应得到较好去除,且形变场较为平滑,地震破裂线更加清晰。而对于距离向形变场,在去除地形效应后,图 6(b)可以清晰分辨出地表沿距离向位移分布的趋势,可清楚解译出地表破裂线几何位置,相比图 5(b),去除地形起伏影响后获取的距离向形变场可靠性得以显著改善。
4 结 论
本文分析了SAR影像配准方法提取方位向与距离向地表形变的误差因素,探索了使用像素偏移量提取地表形变的主要误差源及其影响规律,分别采用ASAR影像和PALSAR影像开展了同震地表形变场的提取与误差分析试验,得到如下结论:
(1) 根据误差模型分析出SAR像素偏移量方法提取地表形变的精度主要受到影像分辨率与配准误差影响。影像分辨率越高,形变场误差越小;SAR影像配准精度主要受到匹配窗口与过采样因子的显著影响。
(2) 匹配窗口越大,形变场误差越小,但计算耗时增加;匹配窗口越小,计算效率越高,但同名像点误匹配率增大。因此,对于相干性较好的 SAR影像对,如地表变形较小,植被稀疏等,可选用较小的匹配窗口;对于相干性较差的SAR影像对,如地形起伏大、植被覆盖密集、地表变形大等区域,可选用较大的匹配窗口,避免形变场出现过多奇异点。适当增大过采样因子有助于提高影像配准和形变场提取精度。
(3) 对于地形起伏较大的区域,地形效应对距离向形变场的影响较为显著,构建系统偏移量模型时必须考虑地形效应影响才能获得可靠的距离向形变场;对于方位向的形变,地形效应影响相对较弱,去除地形偏移量后精度也有所提高。因此,采用SAR影像配准偏移量提取地形起伏较大区域的距离向和方位向形变场时,必须顾及地形起伏对像素偏移量的影响。
影像名称 影像获取时间 传感器 波段 时间基线/d 影像中心坐标纬度 影像中心坐标经度 数据类型 垂直基线/m
主影像 2003-12-03 ASAR C波段
69 29.138 5°N 58.521 9°E 降轨 8.4 从影像 2004-02-11 ASAR C波段 28.964 9°N 58.480 5°E 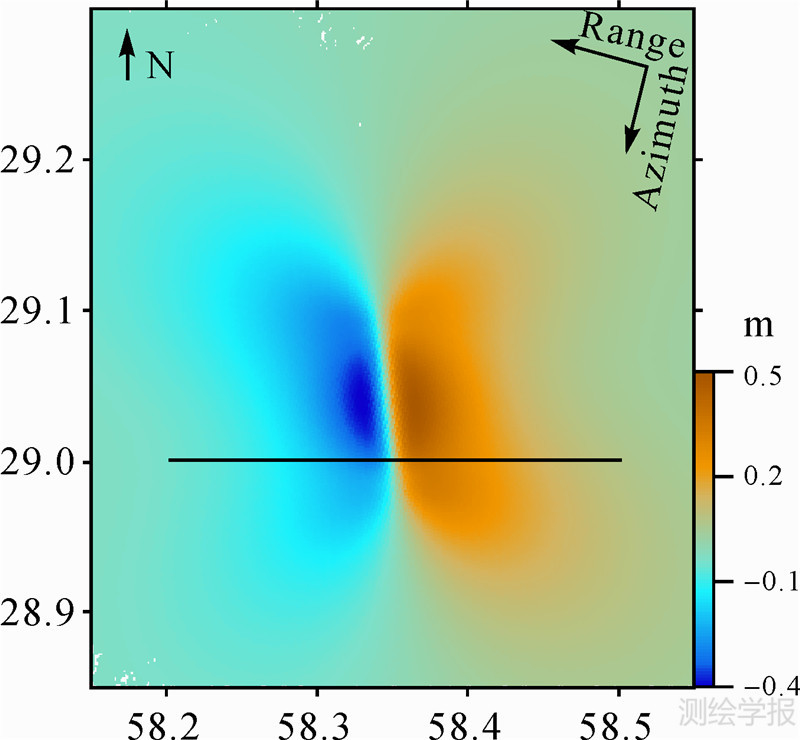
图 1 Bam地震沿方位向的形变场Fig. 1 Azimuthal deformation field associated with Bam earthquake 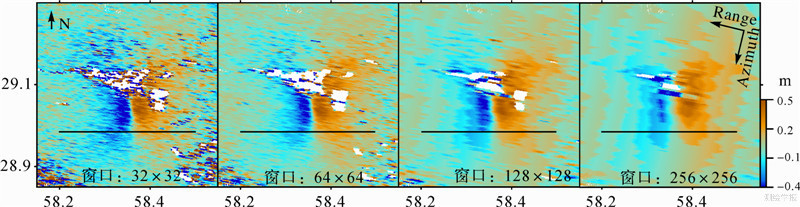
图 2 不同窗口尺寸提取的形变场Fig. 2 Extracted deformation field from different windows sizes
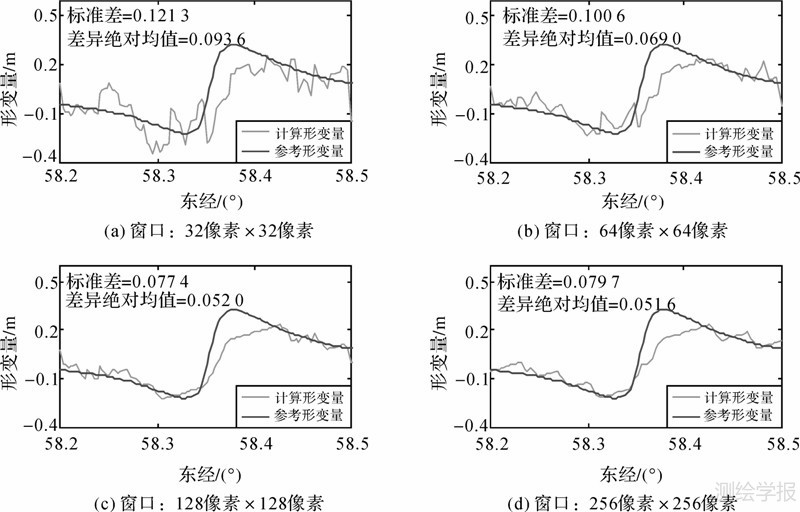
图 3 沿剖面的形变量Fig. 3 Comparison of extracted deformation at the cross-section 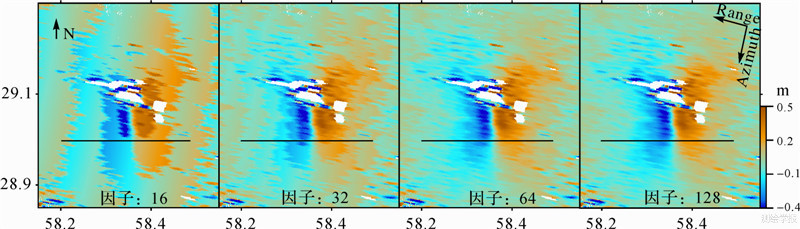
图 4 不同过采样因子提取的形变场Fig. 4 Extracted deformation field from different oversampling factors
影像名称 影像获取时间 传感器 波段 时间基线/d 影像中心坐标纬度 影像中心坐标经度 数据类型 垂直基线/m
主影像 2010-04-17 PALSAR L波段
92 33.195 8°N 96.693 6°E 升轨 28.2 从影像 2010-01-15 PALSAR L波段 33.195 1°N 96.690 1°E 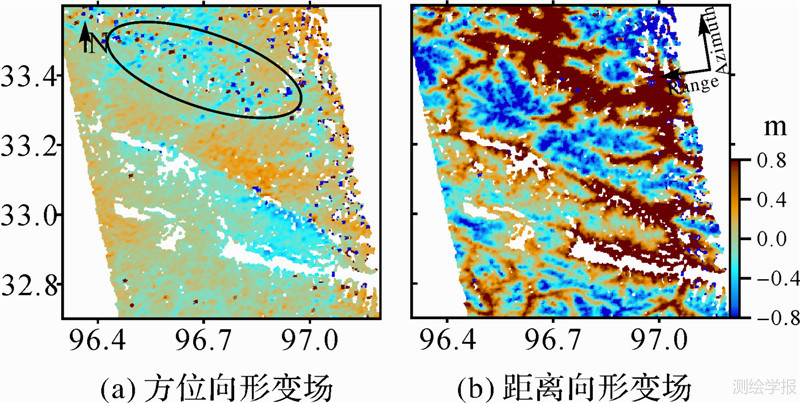
图 5 未顾及地形起伏影响的形变场Fig. 5 Deformation field without considering terrain effects 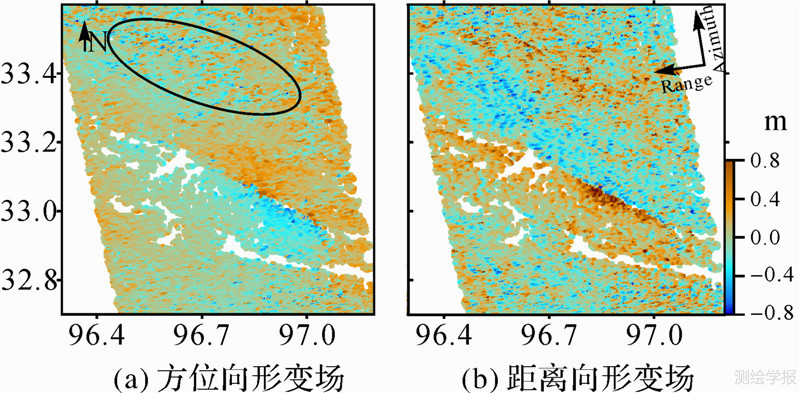
图 6 去除地形起伏影响的形变场Fig. 6 Deformation field after removing terrain effects
| [1] | SHAN Xinjian, MA Jin, WANG Changlin, et al. Extraction Coseismic Deformation of the 1997 Mani Earthquake with Differential Interferometric SAR[J]. Acta Seismologica Sinica, 2002, 24(4): 413-420. (单新建,马瑾,王长林,等.利用差分干涉雷达测量技术(D-InSAR)提取同震形变场[J]. 地震学报, 2002, 24(4): 413-420.) |
| [2] | HAMIEL Y, FIALKO Y. Structure and Mechanical Properties of Faults in the North Anatolian Fault System from InSAR Observations of Coseismic Deformation due to the 1999 Lzmit (Turkey) Earthquake[J]. Journal of Geophysical Research, 2007, DOI: 10.1029/2006JB004777. |
| [3] | WANG Lucai, WANG Yaonan, MAO Jianxu. Registration of InSAR Image Based on Integrating Correlation-registration and Max-spectrum Image Registration[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(4): 320-324. (汪鲁才,王耀南,毛建旭.基于相关匹配和最大谱图像配准相结合的InSAR复图像配准方法[J]. 测绘学报, 2003, 32(4): 320-324.) |
| [4] | TAO Qiuxiang, LIU Guolin. A New Method for Fine Registration of SAR Images in PSInSAR[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 69-73. (陶秋香,刘国林.永久散射体差分干涉测量技术中SAR影像精配准的一种新方法[J]. 测绘学报, 2012,41(1): 69-73.) |
| [5] | MICHEL R, AVOUAC J P, TABOURY J. Measuring Near Field Coseismic Displacements from SAR Images: Application to the Landers Earthquake[J]. Geophysical Research Letters, 1999, 26(19): 3017-3020. |
| [6] | LIU Yunhua, QU Chunyan, SHAN Xinjian. Two-dimensional Displacement Field of the Wenchuan Earthquake Inferred from SAR Intensity Offset-Tracking[J]. Chinese Journal of Geophysics, 2012, 55(10): 3296-3306. (刘云华,屈春燕,单新建.基于SAR影像偏移量获取汶川地震二维形变场[J]. 地球物理学报, 2012, 55(10): 3296-3306.) |
| [7] | FIALKO Y, SANDWELL D, SIMONS M, et al. Three-dimensional Deformation Caused by the Bam, Iran, Earthquake and the Origin of Shallow Slip Deficit[J]. Nature, 2005, 435(19): 295-299. |
| [8] | STROZZI T, LUCKMAN A, MURRAY T, et al. Glacier Motion Estimation using SAR Offset-tracking Procedures[J].IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(11): 2384-2391. |
| [9] | JI Lingyun, XU Jiandong. Acquring 3D Coseismic Deformation Field of Bam Earthquake by Using D-InSAR and AZO Techniques[J]. Journal of Geodesy and Geodynamics, 2009, 29(6): 40-44. (季灵运,许建东.利用D-InSAR和AZO技术获取Bam地震同震三维形变场[J]. 大地测量与地球动力学, 2009, 29(6): 40-44.) |
| [10] | CASU F, MANCONI A, PEPE A, et al. Deformation Time-series Generation in Areas Characterized by Large Displacement Dynamics: the SAR Amplitude Pixel-Offset SBAS Technique[J]. IEEE Transaction on Geoscience and Remote Sensing, 2011, 49(7): 2752-2763. |
| [11] | WANG Chao, ZHANG Hong, LIU Zhi. Spaceborne Synthetic Aperture Radar Interferometry[M]. Beijing: Science Press, 2002:72. (王超,张红,刘智.星载合成孔径雷达干涉测量[M]. 北京: 科学出版社, 2002:72.) |
| [12] | HUANG Shiqi, LIU Daizhi. Analysis of Some Uncertain Factors in Spaceborne SAR Imaging and SAR Image[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(2): 152-157. (黄世奇,刘代志.星载SAR成像与SAR图像中一些不确定性因素分析[J]. 测绘学报,2007,36(2):152-157.) |
| [13] | LUO Xiaojun, LIU Guoxiang, HUANG Dingfa, et al. Comparison of Algorithms for Co-registration of Satellite Synthetic Aperture Radar Images[J]. Sicence of Surveying and Mapping, 2006, 31(1): 19-21. (罗小军,刘国祥,黄丁发,等.几种卫星合成孔径雷达影像配准算法的比较研究[J]. 测绘科学, 2006, 31(1):19-21.) |
| [14] | LIU Lei, WANG Zhiyong, ZHOU Xingdong. The InSAR High Precision Registration Method Based on the DEOS Precise Orbit Data and Interpolation[J]. Journal of ShangDong University of Science and Technology, 2008, 27(6): 9-15. (刘磊,王志勇,周兴东.基于DEOS精密轨道数据和插值的InSAR高精度配准方法[J]. 山东科技大学学报, 2008,27(6):9-15.) |
| [15] | JIAO Minglian, JIANG Tingchen. Discussion on Registration Procedure for InSAR Complex Image[J]. Geomatics and Spatial Information Technology, 2008, 31(6): 21-23. (焦明连,蒋廷臣.InSAR复数影像配准方法探讨[J]. 测绘与空间地理信息, 2008,31(6): 21-23.) |
| [16] | ABDELFATTAH R, NICOLAS J M. Sub-pixelic Image Registration for SAR Interferometry Coherence Optimization[C]//Congress of the International Society for Photogrammetry and Remote Sensing. Istanbul: ISPRS, 2004:273-276. |
| [17] | LI Z, BETHEL J. Image Co-registration in SAR Interferometry[C]//The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences .Beijing: ISPRS, 2008: 433-438. |
| [18] | SCHEIBER R, MOREIRA A. Coregistration of Interferometric SAR Images Using Spectral Diversity[J]. Geoscience and Remote Sensing, IEEE Transactions on, 2000, 38(5): 2179-2191. |
| [19] | ZOU W, Li Y, Li Z, et al. Improvement of the Accuracy of InSAR Image Co-registration Based on Tie Points-a Review[J]. Sensors, 2009, 9: 1259-1281. |
| [20] | WANG Qingsong, QU Jishuang, HUANG Haifeng, et al. A Method Based on Integrating Real and Complex Correlation Function for InSAR Image Coregistraion[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(4): 563-569. (王青松,瞿继双,黄海风,等.联合实、复相关函数的干涉SAR图像配准方法[J]. 测绘学报, 2012, 41(4):563-569.) |
| [21] | LIU Xiufang, HONG Wen. Analysis of Spaceborne SAR Pixel Location Influenced by Terrain Variation[J]. Journal of Telemetry, Tracking and Command, 2005, 26(6): 28-32. (刘秀芳,洪文.地形起伏对星载 SAR 像素定位影响的仿真分析[J]. 遥测遥控, 2005,26(6): 28-32.) |
| [22] | FUNNING G J, PARSONS B, WRIGHT T J, et al. Surface Displacements and Source Parameters of the 2003 Bam(Iran) Earthquake from Envisat Advanced Synthetic Aperture Radar Imagery[J]. Journal of Geophysical Research, 2005, 110: 1-23. |
| [23] | OKADA Y. Surface Deformation due to Shear and Tensile Faults in a Half-space[J]. Seismological Society of America, 1985,75(4): 1135-1154. |
| [24] | ZHANG G, SHAN X, DELOUIS B, et al. Rupture History of the 2010 Ms 7.1 Yushu Earthquake by Joint Inversion of Teleseismic Data and InSAR Measurements[J]. Tectonophysics, 2013, 584: 129-137. |
| [25] | LI Z, ELLIOTT J R, FENG W. The 2010 MW 6.8 Yushu (Qinghai, China) Earthquake: Constraints Provided by InSAR and Body Wave Seismology[J]. Journal of Geophysical Research: Solid Earth, 2011, 116(B10), DOI: 10.1029/2011JB008358. |