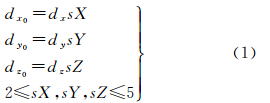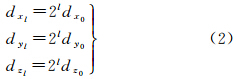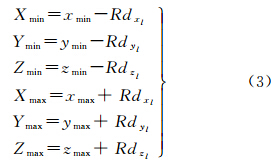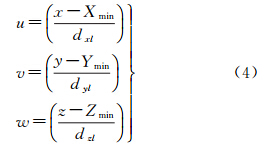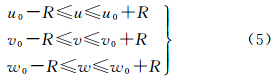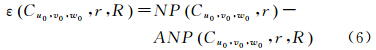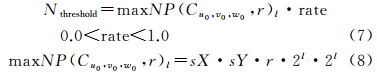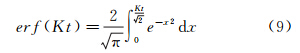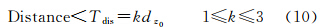2. 武汉大学遥感信息工程学院, 湖北 武汉 430079
2. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China
点云数据的处理一直是数字摄影测量与计算机视觉的重要研究内容。当前获取密集的三维点云主要有两种方式:①采用LiDAR激光扫描系统直接得到三维点云;②利用影像密集匹配得到密集的点云。但两种来源的点云数据都存在一定数量的噪声点。噪声的存在对点云数据的处理产生很多影响。如LiDAR点云滤波处理过程中,很多算法假设地面点为局部最低点[1, 2, 3],而在点云中存在局部低噪声的情况下,这种假设则是不适用的。另外噪声点对后续的大规模点云分层渲染、地物识别提取、建筑物建模及密集匹配所得同名点云的后续处理精度(如影像匹配、地物识别等)都会造成较大影响[4, 5, 6]。因此,噪声点的检测和剔除是获取准确密集点云数据的重要环节。
从空间分布特性来看,噪声可归纳出两大特点:①典型的高程异常的孤立点,表现为局部高噪声点和局部低噪声点;②非典型的簇状噪声点(数量不多的噪声点的聚类)——在一定局部范围内不能明显高出邻近地面点和地物点的高程异常点,表现为低矮噪声,形态呈点簇状或块簇状[7, 8, 9]。许多学者对点云噪声处理进行过研究,现有的点云去噪的算法可大致概括为以下3类:①分析、利用高程值的分布进行去噪[8, 9, 10, 11];②利用数学形态学的方法进行去噪[12, 13, 14];③根据点云密度进行去噪[15, 16, 17]。方法①和方法②都是通过局部或是全局的高程值比较,并判断阈值来检测噪声,这类方法通过选取合适的阈值可以对孤立噪声有效检测,但对簇状噪声的检测结果并不理想[8]。方法③基于密度的方法是将噪声假设为位于低密度区域(相对于正常的点云密度)的单一物体或物体聚类,因此检测噪声的过程也就是检测低密度区域的过程[17]。但现有的一些基于密度的去噪方法中,往往不能兼顾处理多种点云数据的不同类噪声,如文献[15]提出基于密度检测噪声的算法来检测孤立点,但该方法对簇状噪声不能有效处理。文献[16]提出利用最小生成树的方法去除簇状噪声,但该方法只能适应地面激光雷达的数据处理,对于机载激光雷达获得的数据,由于复杂性更高不能够处理。通常密度分析的方法存在着处理簇状噪声失败的问题,主要是因为簇状噪声在局部小范围内其密度和分布表现都与非噪声点类似,因而需要找到一种既可以检测出孤立点,又可有效检测出簇状噪声点的算法。
点云中的噪声可以认为是其高程偏离“邻域”范围内的点“较远”的点,因此点云噪声检测的关键就在于邻域的确定和阈值的选择。本文利用多尺度的网格划分三维空间来确定点与点之间的领域关系,并通过逐级进行密度分析来区分噪声的算法,最后结合三角网面距离约束实现检测算法的错判纠正。基于网格去噪的方法在逆向工程邻域已有较多研究,如各向同性的方法[18],各向异性的方法[19, 20],这些方法针对的目标较小,针对的噪声多为偏离正常模型较近的小噪声。而本文算法针对的是机载激光雷达数据获取的点云,以及影像密集匹配得到的点云,这两种点云的噪声种类相对复杂,既有偏离正常点较近的低矮噪声,也有离散的孤立点噪声,以及簇状噪声。文献[7]也是针对这两种数据进行处理的多尺度网格划分空间进行去噪的方法,该方法是利用有限元进行去噪。本文与该方法的区别在于判断噪声的方法上。本文方法不仅仅依据局部网格内点的数量,还依据局部点的密度情况进行区分噪声。另外本文的算法第2步,利用三角网将第1步中误检测为噪声的点重新归为正常点,也是上述提到的算法中未曾涉及的。试验表明本文算法适用于LiDAR点云数据和密集匹配点云数据中的孤立点和簇状噪声两种噪声的检测。通过真实数据进行剔噪试验表明本文提出的基于密度分析的多尺度噪声检测算法对孤立噪声和簇状噪声都较为有效,对噪声的检测率达到97%以上,且对于质量较差的影像匹配点云的检测也能有效处理。 2 噪声检测算法 2.1 算法思想和流程
本文提出的基于密度分析的多尺度噪声检测算法设计的基本思想如图 1所示。
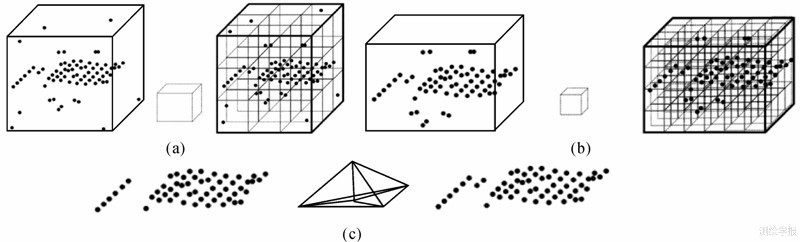 |
| 图 1 多尺度的局部密度分析点云噪声检测算法流程示意图Fig. 1 Schematic diagram of proposed hierarchical outlier detection method |
图 1中,(a) 为采用空间六面体进行点云数据的三维分割,建立离散点云三维网格和最大范围包围盒,通过局部密度分析方法标记噪声点为0并剔除,得到新的非噪声包围盒;(b) 是在(a)得到的非噪声包围盒基础上,降低一级尺度层级,以1/2的三维网格大小逐个进行邻域的局部密度分析,进一步剔除较小的噪声点或噪声点聚类并标记为0,获得新的非噪声包围盒,迭代进行,直到完成最小尺度层级噪声点检测;(c)为完成尺度层级迭代后,需要检测标记为0的噪声是否为真正的噪声点(利用非噪声点构建狄罗妮三角网,检测标记为0的噪声点到对应三角面的距离,当距离小于给定的阈值时则认定为非噪声点)。
下面将详细描述算法的细节和局部密度算法的判据。 2.2 逐尺度层级分割点云数据
首先定义原始点云中X、Y、Z 3个方向的点间距大小为dx、dy、dz,即以dx、dy、dz构成的三维网格中包含的点数应约为1。本文根据文献[21]中的方法计算原始点云数据X—Y方向间距离Dxy,且令dx=dy=Dxy。对于Z方向间距dz,理想设置应为点云自身的高程精度,但是如果输入点云的高程精度是未知的,本文的方法中对于未知的点云数据本文算法dz的取值范围为Dxy/3≤dz≤Dxy。由于自动计算的dx、dy、dz较为粗糙,在实际操作中可能无法保证每个三维网格都大致包含一个点。为增强算法的稳定性,本文将最小尺度层级level 0级(本文定义不同尺度层级用level l 表示,其中l=0~L,L为间距最大的最大尺度层级)的三维网格大小的计算作一定适应性增强,如式(1)
式中,sX、sY、sZ为放大因子。增加放大因子之后,可以认为在level 0的dx0、dy0、dz0三维网格中约包含sX·sY个点。对于其他尺度层级level l的3个方向的间距为dxl=dyl=dzl,根据式(2)计算得到各尺度层级的三维包围盒范围将从大尺度层级以较大的网格间距首先建立,逐级剔除噪声点,对剩余的点云以小尺度层级、直到level 0级的最小网格间距建立。对于每一个尺度层级l的三维盒范围都以两个点来确定:Pminl(xmin,ymin,zmin)、Pmaxl(xmax,ymax,zmax)。同样,为在实际操作中能够处理边界的点云数据,用式(3)将三维包络范围坐标往外拓展两个边界点的坐标变为Pminl(Xmin,Ymin,Zmin)、Pmaxl(Xmax,Ymax,Zmax)
式中,R为正整数,代表向外拓展的程度,数值上等同2.3.2 小节中的R。本文中将每一个分割而成的三维网格命名为单元体。在某一尺度层级l下的某一单元体的位置坐标可用C(u,v,w)l表示,其中u、v、w可以通过式(4)确定 2.3 基于邻域的局部密度分析的噪声检测 2.3.1 噪声点的标记假设输入的点云数据集为W={Wi},其中包含的噪声点集为P={pi | xi,yi,zi},P ⊂ W、i=0~n-1,n为点云总个数。噪声点的检测按从大尺度层级到小尺度层级逐级地进行。设第l级的点集为Nl={Ni | xi,yi,zi}l,即为点云数据集W={Wi}减去已经检测到的噪声点后的数据集。点集W={Wi}中的检测出的噪声点将被标记为0,而得到的非噪声点Nl将被标记为1。在检测初始时所有的点都标记为1。 2.3.2 r窗口范围和R搜索空间
对特定尺度层级下,文本方法对噪声点的检测以某一单元体为中心一定邻域范围形成空间范围作为一个单位,在一个指定的搜索空间内进行遍历,计算该邻域范围内的密度,并以此来判断在此三维网格内的点是否为噪声点。单位体的邻域范围本文称之为r窗口范围,指定的搜索空间本文称之为R搜索空间。
本文定义r窗口范围为:以某个单元体C(u0,v0,w0)为中心,并以r为半径的三维窗口范围(即该三维窗口的边长为2r+1)作为其邻域的空间范围。R搜索空间为以C(u0,v0,w0)为中心,定义一个以更大的半径R定义的三维搜索空间(即该三维窗口的直径为2R+1)。注意:此处的R与式(3)中的R在数值上是相等的。如图 2以二维和三维形式展示R搜索空间与r窗口范围的定义,其中图 2(a)中r=1且R=2,图 2(b)中r=1,R为大于2的某一正整数。对于处于level l层级的某一个单元体C(u0,v0,w0),所有满足式(5)的单元体C(u,v,w)都在R搜索范围内。此处,R为整数,与式(3)中的R数值相等
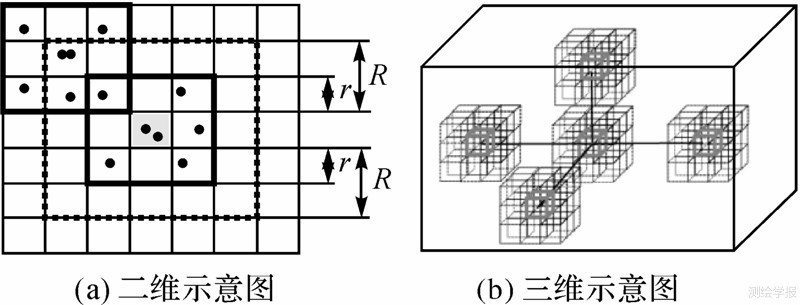 |
| 图 2 r窗口范围与R搜索空间的概念示意图 Fig. 2 Schematic diagram of r window and R search space |
表 1定义下面将会使用到的概念。
以某一尺度层级level l的某一个单元体C(u0,v0,w0)为中心,需要执行4个步骤来判断该单元体内的点是否为噪声点。
步骤1:对单元体C(u0,v0,w0),计算NP(Cu0,v0,w0,r),如果NP(Cu0,v0,w0,r)=0,则不处理该单元体,开始计算下一个单元体;若NP(Cu0,v0,w0,r)>0,则进入步骤2。
步骤2:遍历获得R范围内的每一个有效单元体C(u,v,w)的NP(Cu,v,w,r)计算ANP(Cu0,v0,w0,r,R),并以此利用式(6)计算C(u0,v0,w0)的局部密度δ(Cu0,v0,w0,r,R)
步骤3:本文提出的算法同时使用两个条件判定C(u0,v0,w0)内的点是否为噪声点,两个条件只要有一个被满足时即接受为噪声点,并标记为0;非噪声点则标记为1。
条件1:满足NP(Cu0,v0,w0,r)<Nthreshold。阈值定义如式(7)、式(8)所示
式中,rate无法检测出很多噪声,过高则容易将非噪声判定为噪声。maxNP(Cu0,v0,w0,r)l为level l 层级下C(u0,v0,w0)的r邻域范围内包含的点数的最大估算值。条件2:满足ε(Cu0,v0,w0,r,R)<-Ktδ(Cu0,v0,w0,r,R)
Kt的取值依据正常分布的概率密度函数[22],如果数据分布是正常的,则位于均值Kt倍的标准差范围内的数据的比例称为误差函数(error function,ERF),具体形式如式(9)
文献[23]指出99.7%的正常分布的数据位于高于或低于均值3倍标准差的范围内。故Kt=3且满足条件2时,C(u0,v0,w0)内包含的点可以被认定为噪声点。
步骤4:重复步骤1—3,直到该尺度层级下的包围盒中所有的单元体都被处理。
本文噪声的检测是按照尺度层级从大到小进行迭代,在完成以上4个步骤后,需要按下一尺度层级,将标记为1的点重新建立新的包围盒,以新的三维网格大小,重复步骤1—4,直到完成level 0下各单元体的噪声检测。 2.4 误判噪声点的检测
虽然以上步骤能够去除大量噪声但是可能还是会出现一些非噪声点因分布过于稀疏而满足上述2.3.3 节步骤3中两个判定条件之一而被认定为噪声点。为将这些误检测为噪声点重新判定为非噪声点,本文首先利用已经判定为非噪声点的点(标记为1的点)构建一个狄罗妮三角网,然后对已经判定为噪声的点(标记为0的点)进行检测,如果满足以下条件则重新标记为非噪声点
式中,Distance为待判定点到其所在的三角形面的距离;Tdis为阈值参数。满足此条件的点将重新标记为非噪声点1,并将参与到下一次构建三角网。此过程将不断迭代,创建新的三角网,直到没有点再被判定为非噪声点。 3 试验与评价此节将讨论本文提出的算法应用到激光扫描与影像匹配得到的点云试验结果,并评估算法的效果。试验中算法涉及的参数设置全部使用默认参数,即令dz=Dxy/2,sX和sY设置为3,sZ设置为2,最大的尺度层级level L为3,rate默认设置为0.2,Kt=3、k=1、R=2、r=1。通过大量试验验证,这些参数的选择即可实现较好的检测效果。 3.1 算法应用于密集匹配得到的点云的效果评估
由于匹配点云的噪声情况相对较复杂,很多点从目视解译都无法区分是否为噪声点(例如相对平的表面上存在的起伏,无法判断是物体自身的形状还是由于匹配质量不高造成),所以对于匹配点云的算法评估,本文只给出定性的结果。 3.1.1 匹配点云噪声检测实例分析
图 3所示试验数据来自于两张建筑物墙面的影像,通过密集匹配得到的点云,包含一些由于误匹配造成的孤立的噪声点。数据中噪声的形式较为简单,多为高程异常的离散孤立噪声点。从图 3的结果可见,本文的算法可有效地去除密集匹配获得的孤立噪声点。
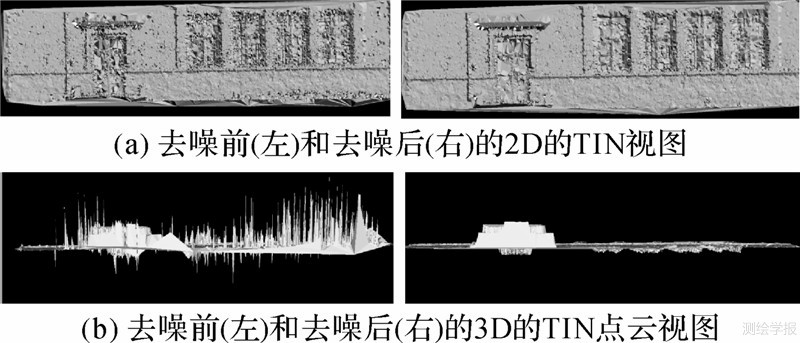 |
| 图 3 本文提出的算法应用于密集匹配得到的点云去噪结果Fig. 3 The result of outlier detection applying our method to the data set from dense match algorithm |
为体现本文算法中第2步,利用三角网将第1步中误检测为噪声的点重新归为正常点的作用,本文进行另一组试验。试验数据为来自以陡峭地形的匹配点云数据,此数据较为复杂,既包含有稀疏的噪声点,也有稀疏的坡面点。
如图 4(a)、4(b)所示,图 4(b)黄色圈内标记了该数据中的噪声点,其中白色圈内为位于坡面上的稀疏的非噪声点,这些坡面上的点的密度相较于顶部与底部的点云都较稀疏,且其密度与噪声点的密度较接近。从图 4(c)、4(d)对比结果上看,本文算法的第1步在去除了噪声的同时也将坡面上的大量的稀疏的非噪声点去除了,而第2步利用三角网将第1步中误检测为噪声的点重新归为正常点。从图 4中可以看出本文的算法在去除噪声点的同时也能有效保存住稀疏的非噪声点。
 |
| 图 4 本文提出的算法应用于密集匹配得到的复杂点云去噪结果Fig. 4 The result of outlier detection applying our method to the complicated point clond from dense match algorithm |
为进一步验证本文算法的性能,将本文提出的算法与开源点云数据处理库(point cloud library(PCL))中的基于距离的算法以及基于统计的算法[24]进行处理效果的对比。基于距离和基于统计这两种算法同属于引言中归类的第1类算法。本文进行两组对比试验,分别在匹配点云和LiDAR点云两套数据上进行。 3.1.2.1 对比试验1
匹配点云去噪对比试验。数据来自立体像对密集匹配生成的一个复杂场景点云,如图 5(a)所示。本文选取图 5(a)中白框范围内的点云作为对比,如图 5(c)、5(d)、5(e)所示。
 |
| 图 5 不同算法的噪声去除结果Fig. 5 Comparison results from the white rectangle |
从图 5的试验结果比对可以看出:对于处理相对比较杂乱的低质量匹配点云,3种算法都能去除绝大部分的明显噪声点。但相比于图 5(c)和图 5 (d)的结果,经过本文的处理结果图 5(e),更好地还原目标物体的轮廓,对于局部低噪声和簇状噪声,即在一定局部范围内不能明显高出邻近点的噪声点,也都能有效地处理,而PCL库中提供的两种算法对于此两类噪声的处理结果并不理想。 3.1.2.2 对比试验2
本试验使用ISPRS网站中提供的4组数据[24](“samp12”、“samp22”、“samp31”、“samp41”)对本文算法以及PCL中的两种算法进行评估。4组数据的点云情况如图 6所示,从图 6中可以看到,4组数据都包含不同种类的噪声点。
 |
| 图 6 各组试验数据的二维与三维点云图Fig. 6 Raw LiDAR point cloud data chosen as the comparison |
本文首先对比“samp41”的处理结果。“samp41”为德国斯图加特地区的一个较平坦区域的大型建筑点云数据,共有11 231个点,点间距在1.0~1.5 m。从图 7(a)中可以看到此数据中同时包含小的簇状噪声和孤立噪声(图 7(a)中方框所示)。图 7对比展示了3种算法的去除噪声的效果。从图 7中可以看到本文算法能够同时有效地处理孤立噪声点和簇状噪声点,而对比的两种算法则在不同程度上都未能有效去除噪声。
 |
| 图 7 利用本文提出的算法进行LiDAR点云噪声检测的结果与其他算法的比较Fig. 7 Comparison result of outlier detection applying our method to the data set from LiDAR |
为定量评估3种算法的性能,4组数据中所有的噪声点均由人工标记出,并使用统计学中的第1类错误和第2类错误来对3种算法进行评估:第1类错误指的是将噪声点认定为非噪声的百分比;第2类错误指的是将非噪声点误分为噪声点的百分比。
表 2展示了对比结果,图 8展示了3种算法对4组数据不同错误类型的比较结果。PCL的两种算法需要人工输入参数,文中的结果是对这两种算法多次尝试不同参数后得到的最优结果。从以上试验结果可以看出:
| 数据集名称 | 点数 | 本文算法/(%) | 基于统计的方法/(%) | 基于距离的方法/(%) | ||||||
| 第1类错误 | 第2类错误 | 总错误 | 第1类错误 | 第2类错误 | 总错误 | 第1类错误 | 第2类错误 | 总错误 | ||
| samp12 | 52 119 | 5.26 | 2.53 | 2.53 | 7.89 | 6.67 | 6.67 | 7.89 | 5.05 | 5.05 |
| samp22 | 32 706 | 5.26 | 2.95 | 2.95 | 0.00 | 7.05 | 7.05 | 0.00 | 8.73 | 8.72 |
| samp31 | 28 862 | 3.84 | 1.91 | 1.91 | 7.69 | 5.40 | 5.41 | 3.85 | 7.14 | 7.13 |
| samp41 | 11 231 | 1.45 | 1.06 | 1.07 | 20.29 | 5.72 | 5.81 | 20.29 | 9.25 | 9.31 |
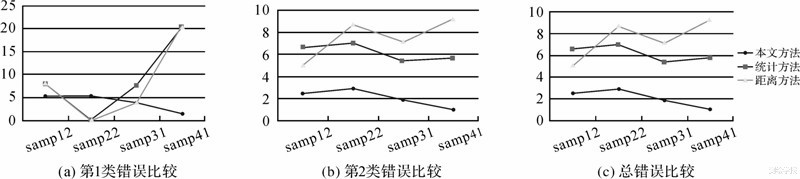 |
| 图 8 3种算法对4组测试数据处理结果的比较Fig. 8 Comparison results from ISPRS datasets |
(1) 本文提出的算法能够有效地检测、剔除LiDAR点云中的孤立噪声和簇状噪声。从samp41数据的处理结果中可以看到,PCL中的两种算法不能很好地应对簇状噪声,两类错误明显增大,虽然也能去除大量噪声,但是结果中残余簇状噪声,总体的错误率也高于本文的算法。
(2) 本文提出的算法在4组数据上的检测率都达到97%以上。
(3) 本文提出的算法相对于PCL中的两种算法第2类错误和总的错误都相对低。虽然第1类错误的比较中,本文的算法对samp22的第1类错误略高于其他两种算法,但是起伏平缓,更加稳定。而在其他3组数据中,本文算法的第1类错误都比另外两种方法更低。
本文算法对4组数据处理的结果都未能达到100%的原因,主要在于本文的算法是基于局部密度分析的算法,如果非噪声点在某一局部范围过于稀疏(如LiDAR透过树叶获取的稀疏的地面点)或者离其他周围点所表达的表面较远(如稀疏的离地面较远的树木或其他地面的点),容易将这些非噪声点误判为噪声点。但总的来说本文的算法能够有效去除明显的孤立噪声点和簇状噪声,综合检测率也达到了97%,优于PCL中提供的两种算法。 3.2 参数对算法的影响分析
本文所有的试验都使用默认参数,但算法参数的改变必然影响试验结果。本文算法中,参数改变对结果会产生较大的影响的参数包括式(7)中的rate值,以及dz的设置。rate值过低将会漏判部分噪声,即增大第1类错误;反之,过高则增大第2类错误。rate值的意义就在于理论上在第l层级上r范围内包含的非噪声点的数量与格网数量的比例。从多次试验中得出经验值rate=0.2时综合的效果最佳。对于dz,设置过小则增大第2类错误,过大则增大第1类错误,对于机载LiDAR点云可以将dz直接设置为0.25将满足需要。另外,通常在处理数据量较大的点云时,建立三维外包进行剖分的做法所占用的内存将会极具增加,本文算法则可以通过增加点云的总尺度层级level L来解决这个问题。本文给出参数默认值是本文从大量数据的试验结果中得到的综合结果较好的经验值,本文中所有的试验结果均来自于此参数配比。 4 结论与展望
点云噪声检测与去除是点云处理中的关键步骤。本文提出一个基于多尺度的局部密度点云噪声检测算法,并结合三角网面距离约束实现检测算法的错判纠正。通过使用影像匹配得到的点云与机载LiDAR点云进行多组试验表明,本文提出的算法就能够有效地检测出两种数据源中的孤立噪声和小的簇状噪声,定量试验结果表明检测率超过97%。本文采取的多尺度的方式是一种从粗到精的策略,采取这一方式的原因是因为如果从一开始就细分三维格网,在噪声分布散乱、分布跨度大的时候,精细的三维格网需要占用的内存会非常大,常规的计算机将无法承受此开销,使得算法的实用性降低。为了提高算法的实用性,本文引入多尺度的方式,降低部分效率,换取算法的稳定性和实用性。另一方面,多尺度的方式,在较粗的尺度上可以去除簇状噪声,而如果只使用最精细的三维网格,在精细的尺度上往往将无法区分簇状噪声。但本文的方法是通过检测低密度区域来确定噪声,这需要假设噪声为点云数据中的低密度区域。此假设存在一些例外,例如密林地区的LiDAR点云数据,由于树木过于密集,能够穿过树木打到地面的点较少,在点云数据的表现即为孤立的离散点,或者稀疏的簇状点,这种情况下,假设低密度区域为噪声点就是错误的。虽然本文算法中的第2步利用三角网弥补了这一缺陷但不能解决所有问题,而文中提到的其他算法在处理这种情况时也会失效。因为,无论是噪声的密度表现还是空间上的分布表现都是噪声的一个属性,是判定具备此类特性的点是否为噪声的必要条件,但不是充分条件,若遇到符合这些特性的非噪声点时,基于此特性的算法都会失败。解决此类问题一种可能的途径是加入模式识别,区分真正的噪声点和稀疏的非噪声点,这也是本文未来努力的方向。
| [1] | AXELSSON P. DEM Generation from Laser Scanner Data Using Adaptive TIN Models[C]//Proceedings of International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Amsterdam: [s.n.], 2000: 110-117. |
| [2] | SUI Lichun,YANG Yun. Filtering of Airborne LiDAR Point Cloud Data Based on car(p,q) Model and Mathematical Morphology[J]. Acta Geodaetica et Cartographica Sinica, 2012,41(2): 219-224. (隋立春,杨耕. 基于car(p,q)模型和数学形态学理论的LiDAR点云数据滤波[J]. 测绘学报, 2012, 41(2): 219-224.) |
| [3] | SUI Lichun, ZHANG Yibin, LIU Yan, et al.Filtering of Airborne LiDAR Point Cloud Data Based on Adaptive Mathematical Morphology[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4); 390-396. (隋立春,张熠斌,柳艳, 等. 基于改进的数学形态学算法的LiDAR点云数据滤波[J]. 测绘学报, 2010, 39(4): 390-396.) |
| [4] | ZHANG Yi, YAN Li. 3D Diffusion Filtering Method of Intensity Noise for Terrestrial Laser Scanning Point Cloud[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 568-573. (张毅,闫利. 地面激光点云强度噪声的三维扩散滤波方法[J].测绘学报, 2010, 39(4); 219-224.) |
| [5] | CHENG Liang, GONG Jianya. Building Boundary Extraction Using Very High Resolution Images and LiDAR[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3):391-393. (程亮,龚健雅. LiDAR辅助下利用超高分辨率影像提取建筑物轮廓方法[J]. 测绘学报, 2008, 37(3): 391-393.) |
| [6] | HASLER D, SBAIZ L, SVSSTRUNK S, et al. Outlier Modeling in Image Matching[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(3): 301-315. |
| [7] | SITHOLE G, VOSSELMAN G. Experimental Comparison of Filter Algorithms for Bare-Earth Extraction from Airborne Laser Scanning Point Clouds[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2004, 59 (1-2): 85-101. |
| [8] | ZUO Zhiquan, ZHANG Zuxun, ZHANG Jianqing. Noise Removal Algorithm of LIDAR Point Clouds Based on 3D Finite-element[J]. Journal of Remote Sensing, 2012, 16(2): 297-309.(左志权,张祖勋,张剑清.三维有限元分析的LIDAR点云噪声剔除算法[J].遥感学报,2012, 16(2): 297-309.) |
| [9] | HAN Wenjun,ZUO Zhiquan. Noise Removing Algorithm of LiDAR Point Clouds Based on TIN Smoothing Rules[J]. Journal of Surveying and Mapping, 2012, 37(6): 153-154. (韩文军,左志权. 基于三角网光滑规则的LiDAR 点云噪声剔除算法[J]. 测绘科学, 2012, 37(6): 153-154.) |
| [10] | SILVÁN-CÁRDENAS J L, WANG L. A Multi-resolution Approach for Filtering LiDAR Altimetry Data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 61(1): 11-22. |
| [11] | MENG X, WANG L, SILVÁN-CÁRDENAS J L, et al. A Multidirectional Ground Filtering Algorithm for Airborne LiDAR[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2009, 64(1): 117-124. |
| [12] | ZHANG K Q, CHEN S, WHITMAN D, et al. A Progressive Morphological Filter for Removing Nonground Measurements from Airborne LiDAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(4): 872-882. |
| [13] | MONGUS D, ZALIK B. Parameter-free Ground Filtering of LiDAR Data for Automatic DTM Generation[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2012, 67: 1-12. |
| [14] | KOBLER A, PFEIFER N, OGRINC P, et al. Repetitive Interpolation: A Robust Algorithm for DTM Generation from Aerial Laser Scanner Data in Forested Terrain[J]. Remote Sensing of Environment, 2007, 108(1): 9-23. |
| [15] | SOTOODEH S. Outlier Detection in Laser Scanner Point Clouds[C]//Proceedings of the ISPRS Commission V Symposium, Image Engineering and Vision Metrology, Commission V: 36. Dresden: ISPRS, 2006: 297-302. |
| [16] | SOTOODEH S. Hierarchical Clustered Outlier Detection in Laser Scanner Point Clouds[C]//Proceedings of ISPRS Commission V Symposium Image Enginerring and Vision Metrology. Deresden: ISPRS, 2007: 383-387. |
| [17] | ALMEIDA J A S, BARBOSA L M S, PAIS A, et al. Improving Hierarchical Cluster Analysis: A New Method with Outlier Detection and Automatic Clustering[J]. Chemometrics and Intelligent Laboratory Systems, 2007, 87(2): 208-217. |
| [18] | DESBRUN M, MEYER M, SCHROBDER P, et al. Implicit Fairing of Irregular Meshes Using Diffusion and Curvature Flow[C]//Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques. Los Angeles: [s.n.], 1999: 317-324. |
| [19] | BAJAJ C L, XU G. Anisotropic Diffusion of Surfaces and Functions on Surfaces[J]. ACM Transactions on Graphics, 2003, 22(1): 4-32. |
| [20] | CLARENZ U, DIEWALD U, RUMPF M. Anisotropic Geometric Diffusion in Surface Processing[C]//Proceedings of IEEE Visualization 2000. Salt Lake City: IEEE, 2000: 397-412. |
| [21] | YE Aifen, GONG Shengrong, WANG Zhaohui, et al. Point Cloud Density Extraction Based on Stochastic Distribution Estimation[J]. Computer Engineering, 2009, 35(4): 183-186. (叶爱芬,龚声蓉,王朝晖,等.基于随机分布估计的点云密度提取[J]. 计算机工程, 2009, 35(4): 183-186.) |
| [22] | PATEL J K, READ C B. Handbook of the Normal Distribution[M]. 2nd ed. London: CRC Press, 1996. |
| [23] | MANN P S. Introductory Statistics[M]. 7th ed. New York: John Wiley and Sons Inc, 2010. |
| [24] | PCL. Point Cloud Library(PCL) Module Filters[EB/OL]. [2013-06-12]. http://docs.pointclouds.org/trunk/group_filters.html. |
| [25] | ISPRS. ISPRS Test on Extracting DEMS from Point Clouds: A Comparison of Existing Automatic Filters[EB/OL].2006[2013-08-06]. http://www.itc.nl/isprswgiii-3/filtertest. |