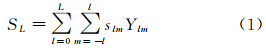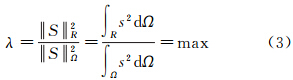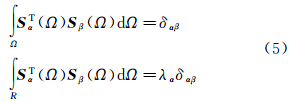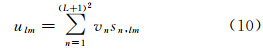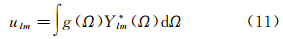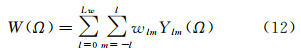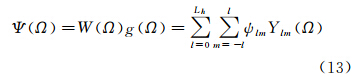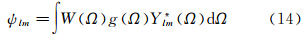2. 武汉大学中国南极测绘研究中心,湖北 武汉 430079;
3. 常州市测绘院,江苏 常州 213000
2. Chine Antarctic Center of Surveying and Mapping, Wuhan 430079, China;
3. Changzhou Surveying and Mapping Institute, Changzhou 213000, China
1 引 言
月球重力场的研究始于前苏联1966年发射的第一颗绕月航天器Luna 10,随后的Apollo系列、Clementine、Lunar Prospector、SELENE、嫦娥、GRAIL等多种多代绕月探测器极大丰富了月球重力场信息,提高了月球重力场模型的精度和分辨率。月球重力场谱分析不仅可以辅助评判重力场模型的优劣,也有助于月球岩石圈弹性厚度、内部结构、热演化史等的分析[1, 2, 3, 4]。球谐模型是目前月球重力场的主要表示形式,它联系重力场的空间特征和频谱特征,利于重力场谱分析和绕月卫星的轨道研究[5]。但月球表面地形复杂,高差起伏较大,由质量瘤和撞击坑引起的月球重力异常的不均匀分布影响重力场球谐系数的收敛性。高阶球谐重力场模型大多是利用低阶模型作为先验信息反复迭代得到的高阶结果,模型系数之间相关性强。同时球谐函数的全球正交特性也无法适用于局部重力场的研究。
随着月球观测数据的不断丰富,人们对月球的关注点逐渐从全球发展为局部研究,月球局部重力场、局部构造、局部区域岩石圈厚度变化等日益成为月球科学的研究热点,常用的球谐模型和谱分析方法已经无法满足月球局部特征分析的需求,需要寻求局部分析方法来满足日益深入的月球科学研究。目前局部重力场主要有两种表达:一是点质量法,20世纪60年代探月初期,文献[6]利用差分Doppler观测数据,基于点质量法绘制了月球近区的重力异常大致分布图,文献[7—8]也采用同样的方法利用Lunar Prospector扩展任务段的跟踪数据精化了LP100J模型,该方法可以弥补远区重力数据缺失,精化月球局部重力场,但在谱分析方面略有不足;二是局部基函数支持,在局部区域内寻找一组局部正交、紧支撑的正交函数,利用这组正交函数联系重力场的空间特征和频域特征,以此方便进行谱分析,常用的方法有小波分析[9]、Slepian函数[10]等。Slepian函数具有局部最优特性,可以作为局部正交基解算局部重力场,文献[11]利用Slepian函数将GRACE全球重力数据局部化,解算2004年苏门答腊地震对该地区的重力影响;文献[12]将Slepian函数应用到冰川消融领域,利用重力卫星跟踪数据反演格林兰岛冰盖消融;文献[13]利用球带Slepian函数解算地球重力场,解决了CHAMP、GRACE等绕地卫星的极区数据空白问题。加窗是实现局部谱分析的主要方法,文献[14—15]等利用单窗口加窗局部化重力场实现局部谱分析,但受限于窗口函数,局部优化效果并不理想。依据重力场Slepian模型系数和球谐系数之间的相互转换关系,Slepian模型也可用于计算局部重力场谱特征;Slepian函数的局部最优特性还可用于局部最优的窗口函数的构造,对重力场全球球谐模型加窗实现局部重力场谱分析[16, 17]。
鉴于Slepian函数的局部正交特性在地球物理领域应用较广,本文在分析Slepian函数数学特性的基础上,研究Slepian函数进行局部重力场解算和局部谱分析的原理和方法。考虑到目前对月球局部重力场Slepian模型的研究较少,还没有利用 Slepian模型和Slepian窗口两种方法在局部功率谱分析上进行比较分析。因此本文结合月球局部特征,将Slepian函数应用到月球上,分析月球局部重力场Slepian模型的特点和Slepian局部谱分析方法的优缺点及适用范围。同时利用不同重力场模型,分析局部月球-地形导纳及相关性。
2 Slepian函数分析 2.1 Slepian函数原理
Slepian问题最早由Slepian提出,主要解决一维连续情况下的时域和频域能量集中问题[18],由此解算出的Slepian函数在局部时间域内正交,将Slepian问题引入到三维空间内,也可以解算出一组在局部空间正交的基函数,进而可以表示三维空间内的局部物理场量。在单位球Ω上引入Slepian函数S[19, 20]
式中,Ylm为面球谐函数;slm为球谐系数;L为Slepian函数的最大阶数。
将重力场分别用球谐函数和Slepian函数表达
上式是分别利用球谐函数和Slepian正交基函数表示的重力场,Ω=(θ,λ)为空间点在行星固定坐标系中的大地坐标;ulm、vn,为相应的球谐系数和Slepian系数。
当计算区域为全球Ω时,依据式(1)及球谐函数的全球正交特性可知,球谐函数和Slepian函数在表征全球重力场信号时是等价的;当计算区域为局部R时,球谐函数无法适用,若选用的正交基函数在局部区域内也具有正交性,局部重力场就可以由这组正交基函数表示。Sn(θ,λ)在局部区域适用即是要求Sn(θ,λ)的能量尽可能集中在区域R内,空间内实现局部最优化。
为保证Sn(θ,λ)的能量尽可能集中在区域R内,引入能量集中度λ
结合式(1)、式(3)可以转为
式中,
 ,矩阵中的元素
,矩阵中的元素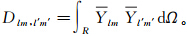
由式(4)可知,Slepian问题归结为特征方程的求解,λ是上述特征方程的特征值;s是特征方程的特征向量。式(4)可以解算得到(L+1)2个特征值和特征向量
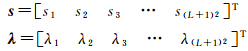
将特征向量s代入式(1),获得相应的带限基函数S(Ω)即是Slepian函数,具有局部正交特性
以球冠局部区域为例,图 1给出了L=18,球冠半径θ=40°时解算出来的前4个Sαm(θ)(m=0,1,2,3,4,5)在球面纬向上的分布图,选取纬向点数为128。
 |
| 图 1 不同m下前4个特征向量在纬度上分布(L=18,球冠半径θ=40°,纬向上选取128个点)Fig. 1 The distribution of first 4 eigenvectors in latitude of different orders where L=18,the spherical cap θ=40°and 128 points are calculated |
从图 1可以看出,当解算出来的特征值λ接近于1时,Smα(θ)的能量绝大部分集中在40°的球冠范围内,随着特征值λ的减小,泄漏在余纬40°~180°间的能量越来越多,但能量在球冠内分布越来越平均。当λ接近于0.1或更小时,Smα(θ)能量泄漏严重,能量绝大部分都分布在球冠外 40°~180°的范围内。因此利用Slepian函数表示局部重力场时需要选取合适的特征值,保证重力信号能量集中在球冠内且能量分布均匀,球冠外信号尽可能被抑制。
2.2 局部重力场Slepian模型
结合重力场的球谐表达,月球表面局部重力场Slepian模型可表示为[21]
式中,vn为Slepian系数;sn,lm为特征向量;N为选取的特征值个数。
球谐系数与Slepian系数间存在相互转换关系[22]
联合式(10)、(11)易求得局部重力场功率谱,结合地形可以计算局部重力-地形导纳及相关性。
2.3 Slepian窗口
常见的局部谱分析方法是对重力场球谐模型加窗,获得只在局部区域有物理意义的球谐模型。
由式(2)可得球谐系数ulm
式中,L和Lw分别表示重力信号和窗口函数的最大阶次;Ylm(Ω)为球谐函数。
对重力信号g(Ω)加窗可得
式中,Lh为加窗后信号的最大有效阶次,依据傅里叶变换有
由2.1节分析可知,具有局部最优特性的Slepian函数是球谐函数的线性组合,因此Slepian函数也可以构造局部窗口,实际应用时可将多个Slepian函数叠加组成多窗口函数,各Slepian函数称之为taper[23]。根据各taper能量分布特征和集中性,在进行taper叠加时可以给各taper赋予不同的权值[16]。不同权值的taper叠加获得的多窗口不仅能保证空间能量集中性,还能使窗口范围内能量分布均匀,使得加窗后的信号更准确地反映原始信号的特征[24]。空间域窗口函数与原始信号相乘、频域窗口函数与原始信号卷积的加窗过程,等价于在频域内窗口函数对原始信号频谱进行“平滑”,从而获得的局部谱不仅可以表征计算区域内的信号特征,还能反映全球信号对该区域的影响程度[23]。
3 Slepian函数表达的月球局部重力场及其谱分析 3.1 局部重力场Slepian模型表达
Slepian函数的局部最优特性可用于局部重力场解算,利用绕月卫星轨道摄动建立观测方程组,基于最小二乘原理解算重力场Slepian系数。相比于球谐模型,同阶次的Slepian模型需要解算的参数较少,应用范围也更为灵活。本文以月球重力场球谐模型作为数据源,建立局部重力场Slepian模型,以由球谐模型计算得到的月球重力异常分布作为检核,研究Slepian模型在局部区域内精度是否与原球谐模型相当,以及区域外对重力信号的抑制效果,从而验证Slepian函数表达月球局部重力场的可靠性。CEGM02模型是目前精度、分辨率都较高的模型之一[25],其精度与SGM100h相当,且嫦娥一号的高轨道数据对月球重力场的长波项有明显改善,因此本文以CEGM02模型为参考,计算相应的Slepian重力场模型和功率谱。
图 2是分别利用Slepian模型、CEGM02模型就不同带宽计算的月球北半球表面自由空气重力异常分布图,图 2(a)上方是球冠半径为40°、带宽L=18的Slepian模型和球谐模型,下方是Slepian模型与球谐模型差值统计,图 2(b)为球冠半径为40°、L=60的Slepian、球谐模型分析图,图 2(c)是半径为20°的球冠区域分析图。
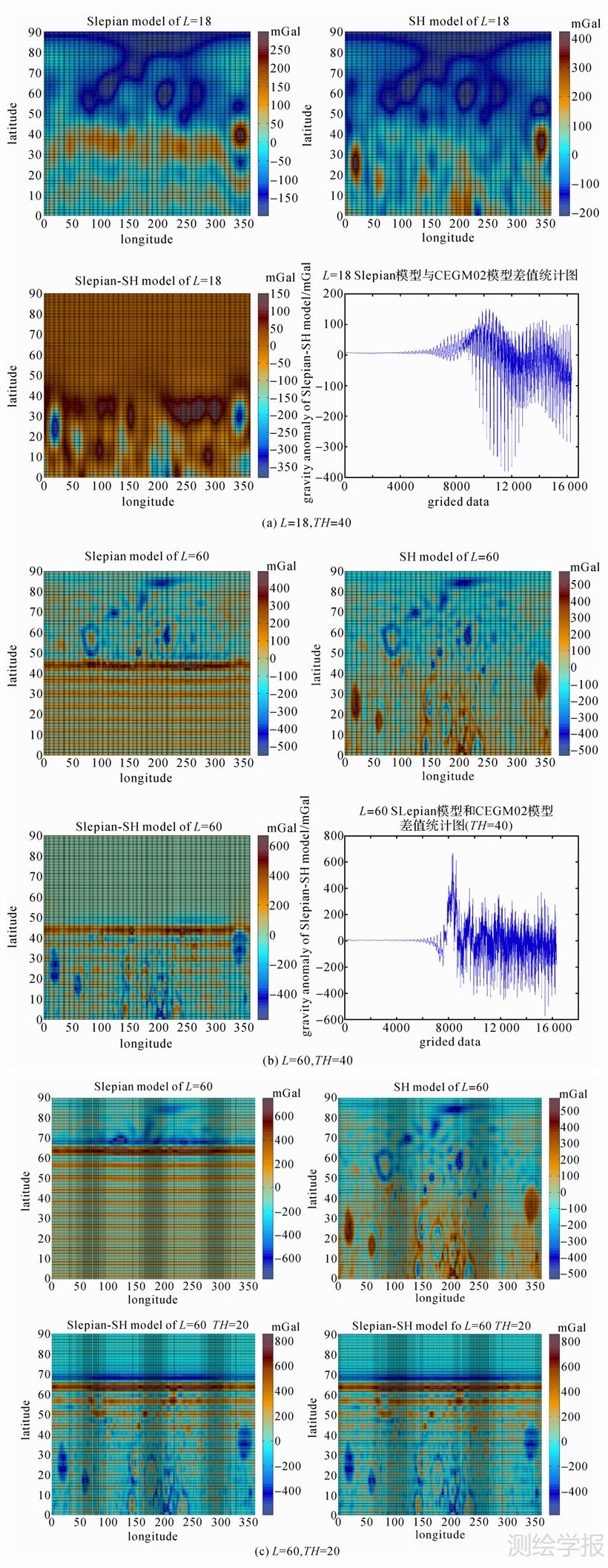 |
| 图 2 L=18、60时Slepian模型与CEGM02重力场模型比较图(0°—90°N,180°W—180°E,TH表示球冠半径)Fig. 2 The comparison of the lunar gravity between Slepian model and CEGM02 where L=18,60(0°—90°N,180°W—180°E,TH is the radius of sphere cap with the unit of degree) |
分析图 2(a)、2(b)可以看出:在以北极点为中心的40°的球冠范围内,重力场Slepian模型与球谐模型分布相同,差值大部分在10 mGal左右,与文献[21]差值统计结果接近;在(0°—50°N,180°W—180°E)的球冠外,重力信号在Slepian模型中得到了很好抑制。50°N纬度圈是理想局部模型的分界线,由于不存在绝对的能量局部集中,50°N纬度圈处存在明显信号异常。分析比较图 2(a)、(b)的重力异常分布图可以看出:当Slepian模型带宽L较小时,球冠的边缘骤变区域大于高带宽的Slepian模型,低带宽的Slepian模型球冠边缘异常变化更为缓慢。异常差值统计图中50°N边缘附近,低带宽的Slepian模型与球谐模型的异常差值点数多于高带宽模型,能量在低带宽边缘地区外泄较为严重,低带宽的Slepian模型在球冠边缘处的信号抑制效果不如高带宽模型。
比较图 2(b)和2(c)可以看出球冠大小对Slepian模型效果也有较大影响。不同球冠半径的Slepian模型重力异常在球冠内与球谐模型分布大致相同,20°半径的Slepian模型与球谐模型差值分布在20 mGal左右,大于40°的球冠模型(10 mGal);球冠边缘处,20°的球冠 Slepian模型表现出范围更广、峰值更大的信号异常,异常变化也更为缓慢,边缘区域的信号可靠性不如40°球冠。因此,Slepian模型在局部区域越大时效果越好,当区域覆盖全球时,Slepian模型表现出完全的能量集中,与球谐模型相当。
3.2 Slepian函数在局部谱分析上的应用
直接利用局部重力场的Slepian模型、利用Slepian函数构建局部最优窗口均能实现月球局部区域重力场谱分析。图 3是利用重力场Slepian模型计算得到的局部功率谱与CEGM02模型功率谱的比较图,红色线是CEGM02模型的功率谱;黑色、蓝色、紫色线是以CEGM02模型为数据源、半径为40°的月球北极球冠区域重力场Slepian模型功率谱,模型阶次分别为40、60、100。图 3中重力信号局部功率谱走向与全球功率谱相同,细部抖动更为明显,低阶部分与全球功率谱相差较小,中高阶部分差距明显,Slepian局部模型表现出了该区域更为细致的高频信号能量特征。月球北极40°范围的球冠内,不存在明显质量瘤痕迹,因而在高频部分能量偏小,与图 3一致。由重力场Slepian模型空间分布图可知球冠区域边缘重力异常值存在剧烈的抖动变化情况,数值远大于区域内部平均值,在频谱图上会带来类似于质量瘤的效果,给频谱分析带来较大的不确定性,推断图 3中功率谱曲线边缘部分Slepian模型高于CEGM02即是由区域边缘的异常信号引起。
 |
| 图 3 月球北极球冠区域重力场Slepian正交基模型及CEGM02模型功率谱图Fig. 3 The comparison of power spectrum of the Lunar gravity field on the Arctic spherical cap between the Slepian model and CEGM02 model |
图 4是利用Slepian窗口获得的月球北极40°球冠区域重力场与CEGM02功率谱比较图,2 tapers较1 taper的窗口在10阶附近有略微改进,9 tapers的窗口表现出明显的能量均匀分布特点。与CEGM02模型的功率谱图相比,可以看出:在40≤l≤60阶部分,采用Slepian窗口加窗后的局部重力场功率谱分布与CEGM02模型相差很小,但在0≤l≤40部分,由于窗口函数本身的限制,二者相差较大,这与文献[16]的研究结果相符。由于窗口的平滑作用,加窗后的重力场的功率谱图平滑程度大大增加,不利于分析频谱变化。本例中利用Slepian加窗的方法获得的重力场功率谱在40≤l≤60阶次部分可信可靠度较高。若需要提高可信可靠频域带宽,可以降低Slepian窗口带宽L,但窗口带宽的降低会导致窗口频域分辨率的降低,造成合适的Slepian taper减少,导致窗口能量分布不均匀,最终使得加窗后的重力场功率谱可信可靠度降低。加窗可靠带宽范围与窗口性能不能兼得。
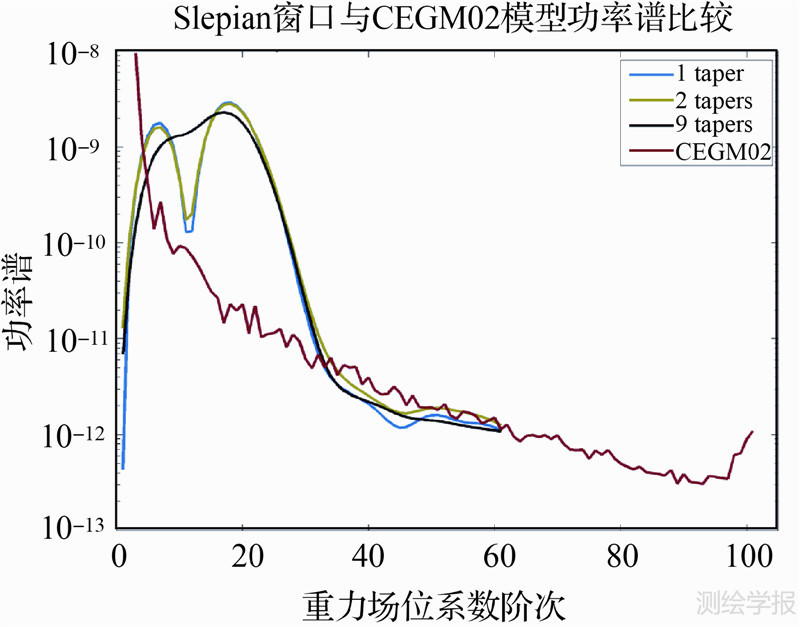 |
| 图 4 Slepian局部窗口及CEGM02模型功率谱图(计算区域为北极球冠区域,Slepian窗口半径为40°,带宽L=60)Fig. 4 The comparison of power spectrum of the Lunar gravity field on the Arctic spherical cap between the local Slepian window and CEGM02 model where the Slepian window’s radius is 40°and its bandwidth is 60 |
为进一步分析Slepian函数在局部重力场-地形导纳及相关性上的应用,选取CEGM02、SGM150j、LP150Q、GRAIL660为输入重力重立场模型,CLTM-S01为地形模型,以莫斯科海为例,计算区域重力场-地形导纳及相关性,结果如图 5(a)、(b)、(c)分别为1、3、5个Slepian特征值分析结果图。
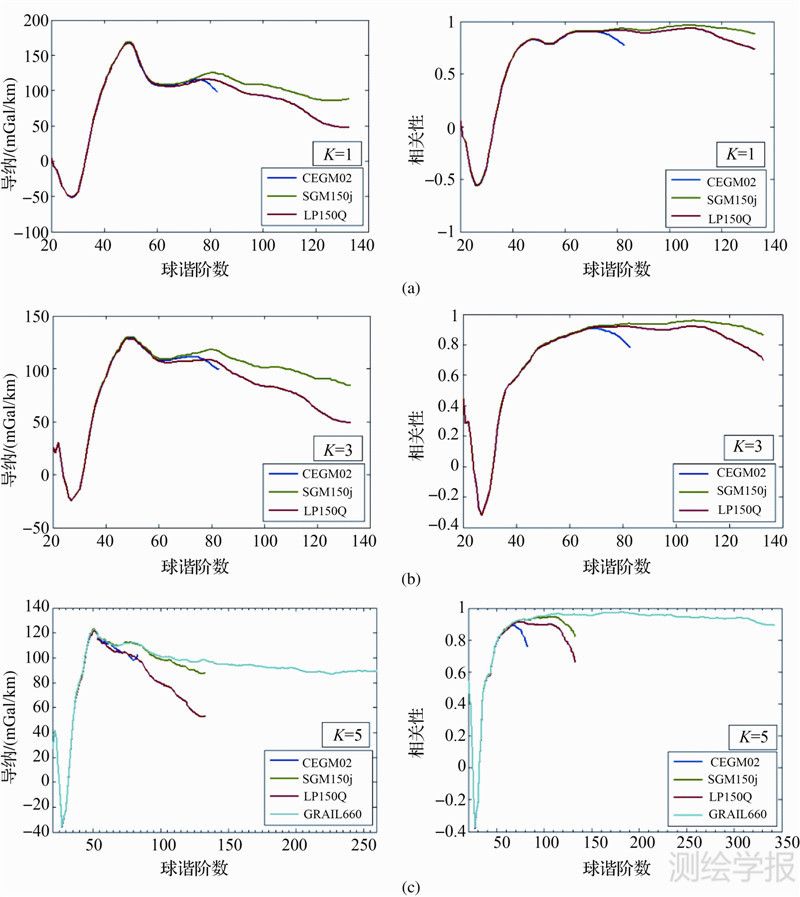 |
| 图 5 莫斯科海不同重力场模型局部重力-地形导纳及相关性分布,K选取的特征值数Fig. 5 The distribution of local admittance and correlation of gravity and topography of Mare Moscoviense based on different gravity models,K is the number of proper eigenvectors |
随着选取的合适特征值个数的增多,重力、地形局部模型能量集中度越大,图 5中解算出局部重力-地形导纳及相关性分布中低阶细部结构有显著改善,反映出更精确的局部物理场量情况。莫斯科海局部区域的重力-地形相关性在20~30阶附近负相关,相应的重力-地形导纳也为负值,验证莫斯科海处存在明显质量瘤,满足均衡补偿出现在中低阶的假设,可以利用弹性板区域均衡模型基于局部重力-地形导纳分析莫斯科海重力异常深度信息和内部构造[26]。
比较分析图 5(a)、(b)、(c)可以看出:60阶前CEGM02、SGM150j及LP150Q三模型导纳及相关性曲线分布接近;60~80阶 CEGM02与SGM150j及110~130阶SGM150j与GRAIL导纳值与相关性差值增大,这主要是由CEGM02模型高阶截断误差及模型噪声导致;而从60阶起,SGM150j和LP150Q模型的导纳、相关性差值随着球谐阶次的增大而增大,表明由于远区数据缺失及卫星轨道高度等因素导致LP150Q在高阶部分导纳及相关性可靠性降低;图 5(c)中,110阶前,SGM150j和GRAIL660的导纳及相关性分布图走向基本一致,表明在忽略高阶误差的情况下,同阶次的SGM150j和GRAIL在计算莫斯科海局部重力-地形导纳及相关性时可靠性相当,同阶次模型精度接近。
4 结 论
本文在分析Slepian函数的数学特性的基础上,将之应用到月球局部重力场解算、局部谱分析领域,得出以下结论:
(1) Slepian函数的局部最优、正交特性在月球局部重力场表示中有较大优势。与球谐模型相比,Slepian模型解算的参数较少,计算效率较高。在计算区域内,Slepian模型与球谐模型相差很小,而在区域边缘Slepian模型表现出明显的信号异常,因此Slepian模型在区域内部可信可靠度较高。Slepian模型阶数越高、计算区域越大,模型边缘抖动峰值越小,抖动范围也越小,因此高阶、大球冠半径的Slepian模型有更为优异的重力场表达效果。
(2) 对于基于月球局部重力场Slepian模型和直接利用Slepian函数构造局部窗口,这两种方法均可用于局部重力场功率谱计算,但二者适用性略有不同。
局部重力场Slepian模型法分析结果具有显著的地球物理意义,模型可信可靠的带宽范围较大;缺点是忽略了计算区域外部对区域内部重力场的影响,理论上有失严密,且球冠边缘的异常信号表现出的质量瘤效应使得功率谱曲线的高频部分可靠性降低。
Slepian加窗局部谱分析方法具有较为明显的信号处理意义,计算的功率谱能反映全球重力场功率谱变化,可以分析局部区域与全球的能量关系,且加窗信号在中高频部分可信度较高;缺点是在低阶段误差较大,可靠带宽较窄,且由于窗口的平滑效果,计算出来的局部功率谱平滑程度大大增加,不利于频谱细部结构的分析。
(3) 莫斯科海20~30阶处重力-地形导纳、相关性为负值,可利用区域均衡模型分析月海内部构造。
(4) CEGM02、LP150Q、SGM150j三模型中低阶部分导纳相关性值接近,高阶部分受截断误差及模型噪声影响可靠性均有所降低;LP150Q模型受远区数据缺失影响中高阶导纳、相关性可靠性不足;SGM150j和GRAIL的同阶次导纳相关性分析结果相当,模型精度接近。
| [1] | MCKENZIE D, NIMMO F. Elastic Thickness Estimates for Venus from Line of Sight Accelerations[J]. ICARUS, 1997, 130(1): 198-216. |
| [2] | FORSYTH D W. Subsurface Loading and Estimates of the Flexural Rigidity of Continental Lithosphere[J]. Journal of Geophysical Research, 1985, 90(B14): 12623-12632. |
| [3] | PARSONS B, SCLATER J G. An Analysis of the Variation of Ocean Floor Bathymetry and Heat Flow with Age[J]. Journal of Geophysical Research, 1977, 82(5): 802-827. |
| [4] | SUGANO T, HEKI K. Isostasy of the Moon from High-resolution Gravity and Topography Data: Implication for Its Thermal History[J]. Geophysical Research Letters, 2004, 31(24): L24703. |
| [5] | LI Fei, YAN Jianguo, PING Jingsong. Lunar Exploration and Lunar Gravity Field Determination[J]. Progress in Geophysics,2006, 21(1): 31-37. (李斐, 鄢建国, 平劲松. 月球探测及月球重力场的确定[J]. 地球物理学进展, 2006, 21(1): 31-37.) |
| [6] | MULLER P M, SJOGREN W L. Mascons: Lunar Mass Concentrations [J]. Science, 1968, 161(3842): 680-684. |
| [7] | SUGANO T, HEKI K. High Resolution Lunar Gravity Anomaly Map from the Lunar Prospector Line-of-sight Acceleration Data [J]. Earth Planets Space, 2004, 56(1): 81-86. |
| [8] | SHEN Fei, SUI Mingming, Li Jiancheng. Research on the Recovery of The Lunar Nearside Gravity Field from Line-of-sight Acceleration Data[J]. Progress in Geophysics,2008, 23(6): 1758-1763. (沈飞, 隋铭明, 李建成. 利用视线加速度数据恢复月球近区重力异常的研究[J]. 地球物理学进展, 2008, 23(6): 1758-1763.) |
| [9] | FREEDEN W, SCHNEIDER F. An Integrated Wavelet Concept of Physical Geodesy[J]. Journal of Geodesy, 1998, 72(5): 259-281. |
| [10] | PAIL R, PLANK G, SCHUH W D. Spatially Restricted Data Distributions on the Sphere: the Method of Orthonormalized Functions and Applications[J]. Journal of Geodesy, 2001, 75(1): 44-56. |
| [11] | HAN S C, SIMONS F J. Spatiospectral Localization of Global Geopotential Fields from the Gravity Recovery and Climate Experiment (GRACE) Reveals the Coseismic Gravity Change owing to the 2004 Sumatra-Andaman Earthquake[J]. Journal of Geophysical Research, 2008, 113(B1),doi:10.1029/2007JB004927. |
| [12] | HARIG C, SIMONS F J. Mapping Greenland's Mass Loss in Space and Time[J]. Proceedings of the National Academy of Sciences, 2012, 109(49): 19934-19937. |
| [13] | ZHU Guangbin, LI Jiancheng, WEN hanjiang, et al. Slepian Localized Spectral Analysis of the Determination of the Earth's Gravity Field Using Satellite Gravity Gradiometry Data[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 1-7. (朱广彬, 李建成, 文汉江, 等. 卫星重力梯度数据确定地球重力场的 Slepian 局部谱分析方法[J]. 测绘学报, 2012, 41(1): 1-7.) |
| [14] | SIMONS M, SOLOMON S C, HAGER B H. Localization of Gravity and Topography: Constraints on the Tectonics and Mantle Dynamics of Venus[J]. Geophysical Journal International, 1997, 131(1): 24-44. |
| [15] | MCGOVENRN P J, SOLOMON S C, SMITH D E et al. Localized Gravity/Topography Admittance and Correlation Spectra on Mars: Implications for Regional and Global Evolution[J]. Journal of Geophysical Research, 2002, 107(E12),doi: 10.1029/2002JE001854. |
| [16] | WIECZOREK M A, SIMONS F J. Localized Spectral Analysis on the Sphere[J]. Geophysical Journal International, 2005, 162(3): 655-675. |
| [17] | LI Fei, KE Baogui, WANG Wenrui, et al. Estimation of the Ancient Lunar Crust Thickness from the Admittance[J]. Chinese Journal of Geophysics, 2009, 52(8): 2001-2007. (李斐, 柯宝贵, 王文睿, 等. 利用重力地形导纳估计月壳厚度[J]. 地球物理学报, 2009, 52(8): 2001-2007.) |
| [18] | SLEPIAN D. Some Comments on Fourier-analysis, Uncertainty and Modeling [J]. SIAM Review, 1983, 25(3):379-393. |
| [19] | SIMONS F J, DAHLEN F A, WIECZOREK M A. Spatiospectral Concentration on a Sphere[J]. SIAM Review, 2006, 48(3): 504-536. |
| [20] | DAHLEN F A, SIMONS F J. Spectral Estimation on a Sphere in Geophysics and Cosmology[J]. Geophysical Journal International, 2008, 174(3): 774-807. |
| [21] | HAN S C. Improved Regional Gravity Fields on the Moon from Lunar Prospector Tracking Data by Means of Localized Spherical Harmonical Functions[J]. Journal of Geophysical Research, 2008, 113(E11),doi: 10.1029/2008JE003166. |
| [22] | SIMONS F J, DAHLEN F A. Spherical Slepian Functions and the Polar Gap in Geodesy[J]. Geophysical Journal International, 2006, 166(3): 1039-1061. |
| [23] | WIECZOREK M A, SIMONS F J. Minimum-variance Multitaper Spectral Estimation on the Sphere[J]. Journal of Fourier Analysis and Applications, 2007, 13(6): 665-692. |
| [24] | SIMONS F J, ZUBER M T, KORENAGA J. Isostatic Response of the Australia Lithosphere: Estimation of Effective Elastic Thickness and Anisotropy Using Multitaper Spectral Analysis[J]. Journal of Geophysical Research,2000,105(B8):19163-19184. |
| [25] | YAN J, GOOSSENS S, MATSUMOTO K, et al. CEGM02: An Improved Lunar Gravity Model Using Chang'E-1 Orbital Tracking Data[J]. Planetary and Space Science, 2012, 62(1): 1-9. |
| [26] | CHEN Bo. The Effective Elastic Thickness over China and Surroundings and Its Lithosphere Dynamic Implication[D]. Wuhan: China University of Geosciences, 2013. (陈波. 中国及邻区岩石圈有效弹性厚度及其动力学意义[D]. 武汉:中国地质大学, 2013.) |