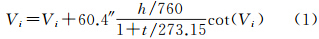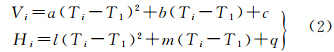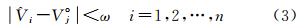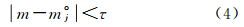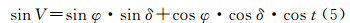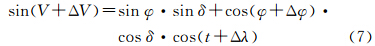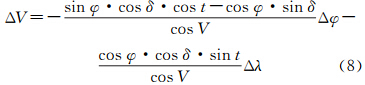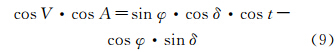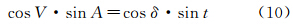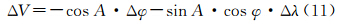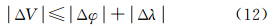1 引 言
天文定向是天文大地测量的一项重要内容,是通过观测自然天体确定地面目标方位的一种技术,具有精度高、隐蔽性强、可靠性好等优点,在大地控制网的布设、靶场测量、测控雷达标较、航天器发射保障等军事领域有着广泛的应用[1, 2, 3]。
甚长基线干涉测量技术(very long baseline interferometry,VLBI)是一种高精度的天文大地测量方法,能够精确测定基线矢量,但因其复杂的地面观测设备及较长的事后处理时间,无法实现小型化、实时、快速定向[4]。基于天顶筒的天文大地测量技术,通常只用来精确测定测站的地心位置和垂线偏差,不提供定向结果[5]。脉冲星导航是一种性能优越、有强大发展潜力的新型天文导航技术,其在航天器自主导航中具有很高的应用价值,在天文大地测量中也具有一定的应用前景,但目前的研究大多还处于理论研究阶段,距离应用还有一定的差距[6, 7]。
目前,夜间天文定向多采用全站仪(或经纬仪),利用人的肉眼观测北极星、特征星和行星、月球进行。这种方法具有实时、精确、快速等优点,但也存在诸多局限性。观测北极星是精度最高的定向方法,精度可达0.5″。但北极星只能在北半球进行观测,而且在高纬度地区,北极星过高,测站位置误差、计时误差等因素对定向影响较大;在低纬度地区,北极星过低,受大气折射的影响严重,且易被遮挡[8, 9]。特征星是指构成恒星星座的明亮恒星,全球的观测者均可利用其进行定向,一般要求天气状况良好、星座清晰可辨,且观测者具备专业的识星知识[10]。但在多云、雾霾等天气状况下,天空往往只有数颗可见亮星时,星座无法完整呈现,利用肉眼进行特征星的识别容易出错。行星和月球也可被观测者用于定向。但目视星等较高的行星只有水星、金星、火星、土星和木星,数目较少[11],而月球的可见性具有周期性,在相当长的时间内无法观测[12]。
针对上述夜间天文定向的不足,文献[13]提出利用经纬仪观测两颗近似南北方向的任意恒星进行天文定向,为了实现对任意亮星的正确识别,一般要求观测时间不少于20 min,以确保恒星在此期间具有明显的视运动量。此方法的观测效率较低,大量的时间耗费在候星上。文献[14]提出利用单颗任意亮星进行天文定向,观测者只需在夜空找到一颗明亮的恒星,利用电子经纬仪连续观测其水平角和高度角2~3次,并记录下观测时刻,即可利用球面三角公式求解该恒星的概略赤经、赤纬,然后在星表中进行搜索匹配,最后实现精确定向。文献[13]和[14]均有两个问题没有得到重视和解决:①对同一颗恒星在短时间内进行多次观测,观测量之间的相关性极强,在方程求解时表现为病态,观测值中较小的误差扰动会造成解算结果的严重失真[15, 16],最终影响恒星识别的成功率,文献[13]和[14]均没有给出大量的仿真或实际观测和识别案例,以及识别成功率,回避了这一病态问题;②对任意亮星只是在恒星星表中进行匹配和识别,没有考虑行星存在的可能性,增加了识别错误的可能性。
关于恒星识别的问题,国内外诸多学者进行了广泛而深入的研究,但这些研究大多属于星图识别范畴,即通过照相观测的方法,获取某一历元多颗恒星相互之间的星对角距等几何信息与理论信息进行匹配,进行识别[17, 18]。但全站仪只能在某一历元对单个目标进行观测,无法同时获取多个星体之间的相对几何信息,因此星图识别的理论和方法并不适用。
通过全站仪对任意亮星进行连续多次采样,本文提出了一种基于高度角和方位角速率联合匹配的单颗任意亮星识别算法,避开了求解任意亮星概略赤经和赤纬时的病态问题。通过引入高精度行星视位置和地平坐标计算,该算法可正确辨别行星和恒星。
2 任意亮识别算法
2.1 观测方法
如图 1所示,采用电子经纬仪对某颗任意亮星进行连续跟踪观测,记录其每次经过望远镜十字丝中心时的UTC时刻Ti、垂直度盘读数Vi和水平度盘读数Hi,并用简便大气折射改正模型对Vi进行改正
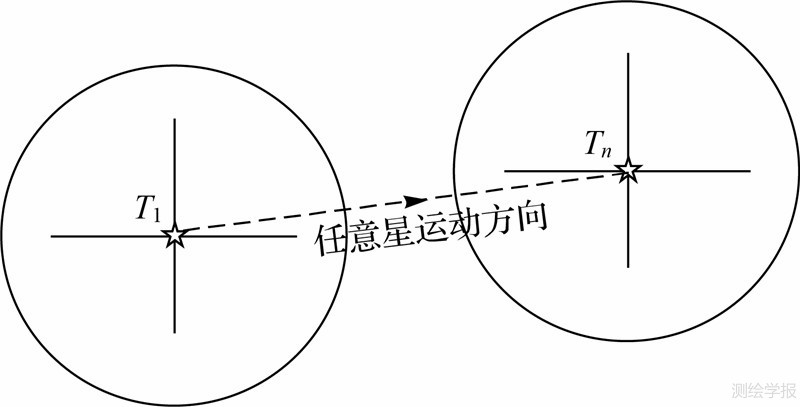 |
| 图 1 任意亮星观测方法Fig. 1 Method of observation of the random object |
一般跟踪观测时长控制在1~2 min即可,观测次数不少于10次,目的是为了减弱偶然观测误差的影响。此外,在选择任意亮星时要注意以下两点:①尽量选择明亮的星体作为观测对象,确保其目视星等高于3.0,因为在进行任意亮星匹配,星等将作为重要的阈值条件之一;②星体的高度角应当介于20°~50°之间,以减弱大气折射以及测站位置误差、计时误差等因素对定向精度的影响。
2.2 地平坐标拟合
由于对任意亮星的跟踪观测时间较短(约为1~2 min),可以认为这段时间内任意亮星的运动主要呈现为线性运动,此外还有二阶小量的非线性运动。不妨利用二次多项式模型建立水平角与观测时刻、高度角与观测时刻的函数模型
式中,T1表示第一次观测历元;V1、H1为对应的观测垂直角和水平角。根据垂直角Vi和水平角Hi的时间观测序列,不难拟合出二次多项式的系数a、b、c和l、m、q。a、l表征垂直角和水平角随时间的二阶小量变化,特征性不强;b、m表征垂直角和水平角随时间的线性变化率,具有明显的视运动特性,是很好的任意亮星识别条件;c、q表征历元T1时,任意亮星的垂直角和水平角。此外,根据上述6个拟合系数,可以计算出观测值的最或然值
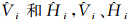 有效减弱了偶然观测误差的影响。
有效减弱了偶然观测误差的影响。2.3 全天区亮星地平坐标计算
2.1节通过仪器观测及计算,获得了任意亮星的实测水平角及其变化率、实测高度角及其变化率,还需要知道全天区所有亮星理论上的这些值,才能进行匹配和识别,即需要建立动态的全天区所有亮星的地平坐标数据库。
全天区的亮星可以分为两类,一类是最常见的恒星,另一类是太阳系的几颗大行星。恒星地平坐标计算需要恒星星表,如著名的FK5星表、依巴谷星表和第谷星表等。行星的地平坐标计算需要太阳系天体的历表,如美国喷气推进实验室研制并不断更新的DE系列历表。恒星和行星的地平坐标计算有所差异,因为恒星距离地球遥远,其在天球上的运动主要表现为运动学;而行星距离地球较近,同属太阳系内的天体,其在天球上的运动主要表现为动力学[19]。
无论是恒星还是行星的地平坐标计算,都需要提供测站的概略位置,并以时间为引数才能进行计算。目前,卫星大地测量技术已经成熟,测站概略坐标很容易获取。此外,国际天文学联合会(International Astronomy Union,IAU)提供的SOFA标准程序库,以及美国海军天文台(U. S. Naval Observatory)提供的NOVAS程序包,均实现了恒星和行星的地平坐标计算,极大地方便了天文测量工作者[20]。计算过程中涉及天球参考框架与地球参考框架的转换,需要用到地球自转参数及岁差、章动模型[21, 22]。其中地球自转参数采用国际地球自转服务(International Earth Rotation Service,IERS)定期更新的Bulletin A,岁差采用IAU2006年推荐使用的P03模型,章动采用IAU2000A模型。
本文对NOVAS的开源程序包进行改进后,研制了全天区3.0等以上亮星的地平坐标计算软件。用户只需要给定观测历元和测站的概略天文坐标,即可通过软件计算生成动态的地平坐标数据库。该数据库包含所有亮星的理论垂直角V°j和理论方位角A°j,以及通过对理论地平坐标拟合得到的二次多项式系数a°j、b°j、c°j和l°j、m°j、q°j。
需要说明的是,mj表征亮星的理论方位角的线性变化率,在没有观测误差、大气折射以及测站位置误差等因素影响的条件下,m应当与mj相等。即任意亮星的观测水平角的线性变化率应当与理论方位角的线性变化率相等。这是因为任意亮星的观测水平角与理论方位角之差为常数,这一常量即天文定向所需要求解的定向角。因此,m可作为任意亮星识别的一个条件。
2.4 匹配条件和阈值
上述6个系数并非全部能作为任意亮星识别的条件:首先,a、l反映的是二阶小量的变化,数值较小,一般不能充分反映特征星的视运动属性;其次,q与q°j之间相差固定的未知值,无法作为识别条件;再次,垂直角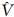 i的时间序列已包含其线性变化率b和常数项c的信息。因此,能够有效反映任意亮星视运动特征的信息可概括为垂直角时间序列
i的时间序列已包含其线性变化率b和常数项c的信息。因此,能够有效反映任意亮星视运动特征的信息可概括为垂直角时间序列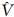 i和水平角的线性变化率m。在全天区所有亮星的地平坐标数据库中进行任意亮星的搜索和匹配时,可设定以下阈值条件
i和水平角的线性变化率m。在全天区所有亮星的地平坐标数据库中进行任意亮星的搜索和匹配时,可设定以下阈值条件
式(3)表示在每一个观测历元对任意亮星进行垂直角的匹配,需要每次匹配均成功。式(3)、(4)中,关于阈值ω和τ的设定,需要考虑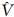 i、V°j和m、m°j的精度。此外,匹配范围应当为3.0等以上的亮星。
i、V°j和m、m°j的精度。此外,匹配范围应当为3.0等以上的亮星。
影响 i、m精度的因素主要来自仪器测角误差、偶然观测误差和大气折射模型改正误差。目前,全站仪的测角精度可达到角秒量级,通过多次测量基本可消除偶然观测误差的影响;在20°~50°内的大气折射模型精度也可达角秒量级,因此可以估计
i、m精度的因素主要来自仪器测角误差、偶然观测误差和大气折射模型改正误差。目前,全站仪的测角精度可达到角秒量级,通过多次测量基本可消除偶然观测误差的影响;在20°~50°内的大气折射模型精度也可达角秒量级,因此可以估计 i精度在角秒量级,而m的精度可能优于角秒量级。
i精度在角秒量级,而m的精度可能优于角秒量级。
影响V°j、m°j精度的主要因素为测站位置误差。快速天文定向的机动性较强,一般无法实时获取准确的测站天文坐标,最常用的办法是利用GNSS导航坐标予以代替。但GNSS卫星导航坐标是相对于参考椭球面的大地坐标,将其作为测站天文坐标时,无法顾及垂线偏差的影响,相当于测站位置存在误差,计算V°j时必然引入误差,误差的大小取决于垂线偏差的大小[23]。平原地区的垂线偏差一般较小,仅有数个角秒;山区的垂线偏差一般较大,可达数十角秒、甚至角分量级。测站位置误差对m°j的影响极小,因为对于特定的任意亮星,在1 min的观测时段内,测站位置误差对其方位角的影响为固定的系统差,因此对水平角变化率的影响可以忽略;但测站位置误差对V°j的影响一般较大,下面将给出定量的分析。
如图 2所示,Z为测站的天顶;P为北天极;O为某任意亮星。V为任意亮星的高度角;φ为测站纬度;t为任意亮星的时角;δ为任意亮星的赤纬。根据球面三角形边的余弦公式
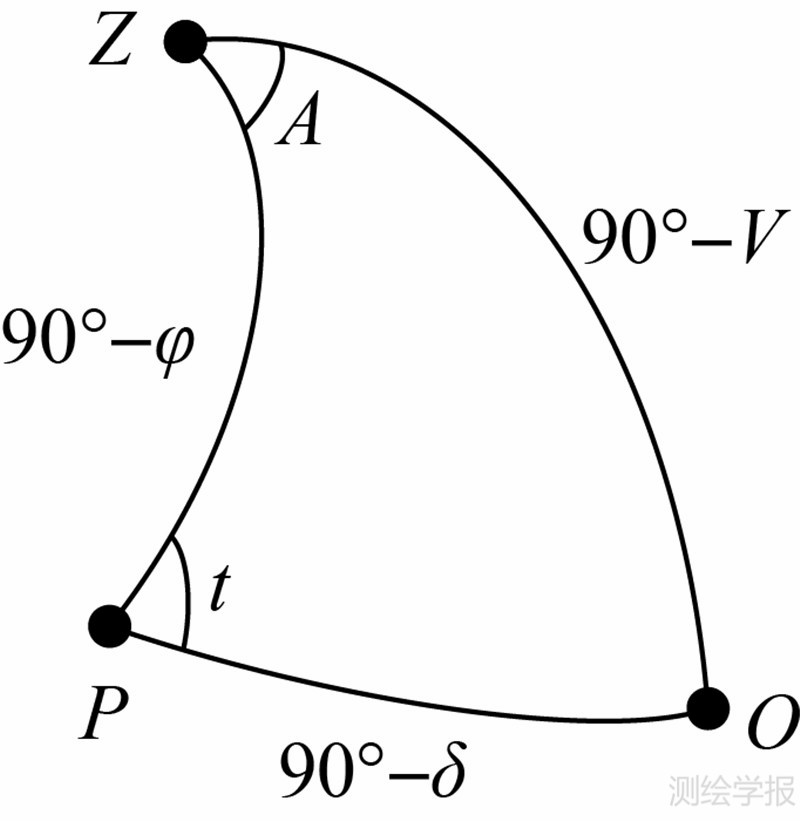 |
| 图 2 球面三角形Fig. 2 Spherical triangle |
式中,λ为测站经度;S为格林尼治恒星时;α为任意亮星的赤经。设测站经度误差为Δλ,测站纬度误差为Δφ,由此因其的高度角误差为ΔV,则式(5)变为 ΔV、Δλ和Δφ均为小量,对式(7)进行微分并化简
在图 2的球面三角形中,有五元素公式[19]
有正弦公式[24]将式(9)、 (10)代入式(8)得
顾及|cos A|≤1,|sin A·cos| φ≤1,有
由式(12)可知,任意亮星高度角受测站位置误差的影响与其方位角及测站的纬度有关。但总体来看,测站位置误差对高度角的影响量级不超过测站位置误差自身的量级。
综合上面的分析,ω的设定主要考虑V°j的精度,需要根据测站概略天文坐标的精度而定。例如,测站概略天文坐标的精度为10″时,不妨设定ω=20″;测站概略天文坐标的精度为30″时,不妨设定ω=60″。τ的设定主要考虑m的精度,需要根据实际或仿真的观测数据而定,将在下文进行讨论。
2.5 识别策略及流程
据统计,北半球的观测者能够观测到大约130颗星等高于3.0等亮星(包括行星),相距最近的两颗星为猎户座的ε星和ζ星,其角距约为0.93°。这一角距可确保两颗亮星不同时出现在经纬仪的望远镜视场。这些亮星数目较少,稀疏地分布于天球上,而任意亮星高度角的观测和计算精度可达角分甚至角秒量级,因此在任意亮星匹配识别时,可能仅利用高度角观测信息即可成功识别。为了提高识别效率、降低识别错误率,不妨先进行高度角 在实际观测中,为了进一步提高识别的可靠性,同时有效降低测站位置误差对定向精度的影响,往往会在不同的天区选择多颗任意亮星进行定向,取平均值作为最终的定向结果。若某颗任意亮星的识别出现错误,则其定向结果必然较大幅度地偏离平均值,需要将其剔除。
3 仿真识别
为验证本文提出的任意亮星识别算法的可靠性,并与文献[10]中的方法进行比较,本节进行了仿真计算,具体仿真条件如表 1所示。
测站位置设定为λ=113°、φ=34°,观测时间设定为北京时间2013-10-08 5:30:00—5:31:30,观测高度角设定为20°≤V≤50°,任意亮星的星等小于3.0。测站上空满足这些条件的任意亮星共有34颗,其中33颗为恒星,1颗为行星(火星)。对这34颗任意亮星分别进行识别,利用文献[14]的方法成功识别出21颗任意亮星,成功率仅为62%,而利用本文方法成功识别出了所有的任意亮星,成功率高达100%。
在成功识别出所有任意亮星后,对每颗任意亮星的高度角误差ΔVi(ΔVi= 由图 4可知,①任意亮星高度角误差的最大值小于30″,即小于测站位置误差,这与式(12)是相一致的。此外,注意到max(ΔVi)有趋势项的变化,这与任意亮星在星表中的排序有关;②任意亮星的水平角速率误差均小于0.3″,呈现随机性的变化,这是因为Δm误差主要来源于角度观测误差,角度观测误差为偶然误差,具有随机性。综合考虑,在实际匹配中,式(4)的阈值τ可大致设定为0.3″~0.5″。
4 定向试验
2013年10月10日夜晚,在华北某平原地区的固定天文基线上(A=186°18′48.8″),采用某天文测量系统进行了多颗任意亮星的识别及天文定向试验。该系统由卫星天文计时器、便携式计算机、高精度全站仪(Leica TS30),相应附属设备和软件系统组成。系统具有GPS、BDS卫星天文授时,计算机比时、守时和计时,全站仪主动寻星及自动观测补偿,以及数据智能解算等功能[25]。利用该系统进行任意亮星天文定向的观测纲要如下。
(1) 观测地面目标:用望远镜的纵丝连续照准地面目标3次,进行测量。
(2) 观测任意亮星:将望远镜的十字丝中心置于任意亮星运动的前方,待任意亮星通过十字丝中心时进行测量,依此重复观测10次。
(3) 设置全站仪自动翻盘,再次观测任意亮星。此时不要求任意亮星通过十字丝的中心,只要求其通过纵丝时进行测量即可,依此重复观测6次。
(4) 观测地面目标,观测方法同(1)。
重复上述步骤,进行多颗任意亮星的观测和比较,地面目标方向的解算方法和精度估计方法同北极星任意时角法相似,读者可参考文献[25],这里不再赘述。
由于天气严重雾霾且有云雾,本次试验共观测到了8颗任意亮星,这些任意亮星的观测高度角范围为20°~50°,平均分布在360°方位上。单颗任意亮星按照上述观测纲要只观测一个时段,方位角解算时采用GPS的导航坐标作为概略天文坐标,当地的天文大地垂线偏差分量约为(-5″,5″),任意亮星识别的阈值设定ω=20″、τ=0.5″。任意亮星的识别结果、解算出的地面目标天文方位角,以及与准确天文方位角的比对结果如表 2所示。
由表 2可知,所有的任意亮星均正确识别。单颗任意亮星天文定向的内符合精度普遍优于0.5″,说明测量及解算的稳定性较好;外部检核精度约为0.3″~8″,不同任意亮星之间差异较大,这与任意亮星在天球上的位置有关。任意亮星处于不同位置时,测站位置误差对其方位角计算精度的影响程度不同。对上述8颗任意亮星的定向结果取平均后,发现均值的外部检核精度为1.6″,说明因测站位置误差引入的系统性定向误差得到了很好的减弱。这是因为,对于单颗任意亮星而言,测站位置误差对定向结果存在系统误差影响;对于多颗任意亮星而言,这种系统性误差具有一定的随机性,通过取平均值的方法可以在一定程度上予以减弱。
需要说明的是,尽管第5颗任意亮星(小熊座β)定向的外部检核精度已经达到0.3″,高于8颗任意亮星定向的平均值精度,但在实际应用中,对任意亮星的选择具有随机性,且定向的真值是未知的,外部检核精度也是未知的。因此只能通过对多颗任意亮星的定向结果取平均的方法削弱测站位置误差的影响,提高绝对定向精度。
此外,在目前大量的实际观测试验中,尚未出现任意亮星识别错误的情况,但不排除在今后的观测中出现识别错误的可能性。为了降低识别错误的风险,建议在实际应用中采取如下措施:①对观测者进行判断星等大小的专业知识培训,尽量保证被选择观测的亮星的星等高于3.0;②对观测者进行观测培训,熟练仪器操作,提高高度角和方位角速率的测量精度;③进一步优化识别算法,提高识别的可靠性。考虑引入粗差探测方法,从多颗任意亮星的定向结果中发现因任意亮星识别错误而产生的定向粗差。
5 结 论
本文提出了一种基于高度角序列和水平角速率匹配的任意亮星识别算法。仿真计算及实际观测试验均表明该算法具有极高的识别成功率。将此算法成功应用于任意亮星定向,单颗任意亮星定向的内符合精度优于0.5″,外部检核精度约为0.3″~8″,多颗任意亮星定向的内符合精度约为2″,外部检核精度达到1.6″。
传统的夜间天文大地测量只能依靠北极星、特征星和行星、月球进行定向。与上述手段相比,本文提出的任意亮星定向方法具有如下优点:①在多云及雾霾天气条件下,以及低纬度和南半球等地区,当北极星可见性不好或不可见时,本文提出的方法具有很好的适用性;②较大程度上降低了对观测者识星、用星等专业知识的要求,观测者只需要大致判断星等即可;③可实现整晚观测定向,不存在测月定向中的月相周期性问题。任意亮星定向可以与陀螺定向仪进行优势互补,对惯性器件标校,实现地下、室内等特殊环境下的高精度定向。
需要说明的是,当天气状况良好、北极星可见时,不建议采用本文的方法进行天文定向,建议仍然采用北极星进行定向以取得更高精度的定向结果。此外,在不影响作业效率的情况下,建议观测的亮星数目尽可能多,且亮星要尽可能均匀分布在360°方向上,目的是有效减弱测站位置误差对定向的影响。因此,当天空只有少数几颗可见亮星且分布不均匀时,可能会出现定向误差较大的风险。
 i的匹配,当匹配到多颗亮星时,再进行水平角速率m的匹配,若仍然匹配到多颗亮星,则取m-m°j最小值对应的亮星作为匹配结果。现将任意亮星识别流程总结如图 3所示。
i的匹配,当匹配到多颗亮星时,再进行水平角速率m的匹配,若仍然匹配到多颗亮星,则取m-m°j最小值对应的亮星作为匹配结果。现将任意亮星识别流程总结如图 3所示。
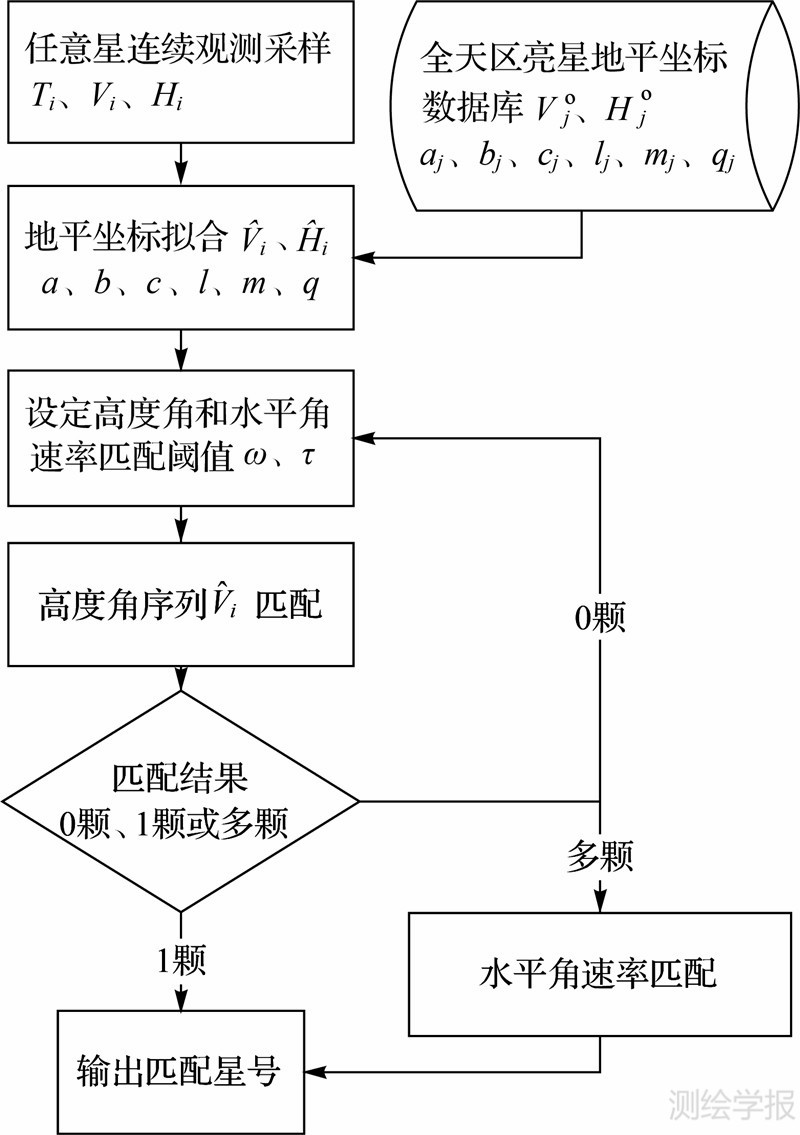
图 3 任意亮星的识别策略及流程Fig. 3 Strategy and flow chart of random stars’ identification
项目 内容指标
恒星星表 《中国大地测量星表》
行星历表 DE405
任意亮星星等 <3.0(共129颗恒星、5颗行星)
测站经度误差 Δλ=15″
测站纬度误差 Δφ=15″
测角精度 ±3″
单星观测次数 10
观测时间间隔 10 s
 i-Vj°)的最大值max(ΔVi)以及水平角速率误差Δm(Δm=m-m°j)进行统计,结果如图 4所示。
i-Vj°)的最大值max(ΔVi)以及水平角速率误差Δm(Δm=m-m°j)进行统计,结果如图 4所示。
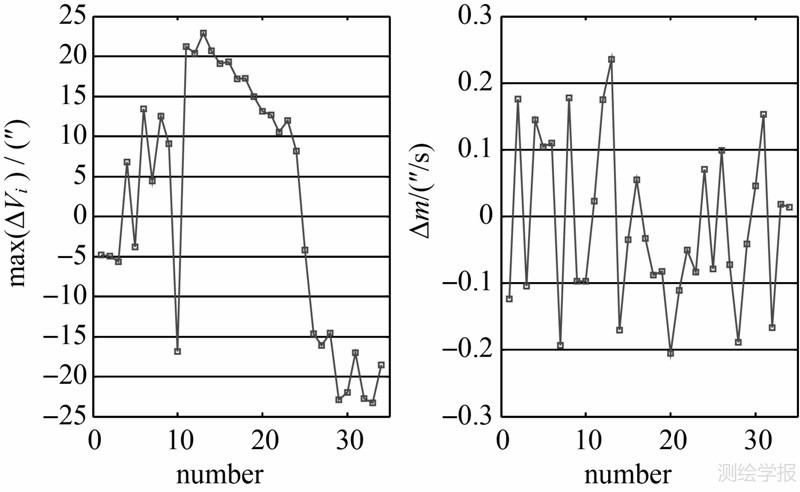
图 4 最大高度角误差及水平角速率误差Fig. 4 Errors of the maximum of vertical angles and velocity of horizontal angles
编号 识别星号 识别结果 星名 星等 概略方位/(°) 概略高度/(°) 目标方位角 中误差/(″) 与真值之差/(″)
1 3904 正确 南鱼座α 1.16 5 26 186°18′55.5″ ±0.33 +6.7
2 3326 正确 天鹰座α 0.77 70 40 186°18′57.1″ ±0.47 +8.3
3 2899 正确 蛇夫座α 2.08 77 40 186°18′56.7″ ±0.25 +7.9
4 3071 正确 天琴座α 0.03 115 38 186°18′50.8″ ±0.27 +2.0
5 2484 正确 小熊座β 2.08 161 33 186°18′48.5″ ±0.22 -0.3
6 553 正确 英仙座α 1.79 228 32 186°18′44.3″ ±0.42 -4.5
7 958 正确 御夫座α 0.08 229 23 186°18′46.8″ ±0.29 -2.0
8 330 正确 仙女座γ 2.26 241 40 186°18′43.9″ ±0.39 -4.9
平均值 186°18′50.4″ ±1.90 +1.6
| [1] | WANG Anguo.Celestial Navigation Technique in the Background of Navigation War[J].Progress in Astronomy,2001,19(2):326-330.(王安国.导航战背景下的天文导航技术[J] .天文学进展,2001,19(2):326-330.) |
| [2] | CHEN Junyong, YANG Yuanxi, WANG Min, et a1. Establishment of 2000 National Geodetic Control Network of China and It's Technological Progress[J]. ActaGeodatica et CartographiaSinica, 2007, 36(1):1-8. (陈俊勇,杨元喜,王敏,等.2000国家大地控制网的构建和它的技术进步[J].测绘学报, 2007, 36(1):1-8.) |
| [3] | SUN Xiaochang,HUANG Fukan.Precision Calibration of Moving Platform Based Radar with Stars as Reference Marks [J].Journal of Astronautics,2002,23(3):29-33.(孙晓昶,皇甫堪.以恒星位置为基准的运动平台上测控雷达精度标校技术[J].宇航学报,2002,23(3):29-33.) |
| [4] | LI Zhenghang, WEI Erhu, WANG Zhengtao.Space Geodesy[M].Wuhan: Wuhan University Press,2010.(李征航,魏二虎,王正涛.空间大地测量学[M].武汉:武汉大学出版社,2010.) |
| [5] | HIRT C, BUERKI B. The Digital Zenith Camera-A New High-precision and Economic Astrogeodetic Observation System for Real-time Measurement of Defections of the Vertical [C] //Proceedings of the 3rd Meeting of the International Gravity and Geoid Commission of the International Association of Geodesy. Thessaloniki:[s.n.], 2002:161-166. |
| [6] | WEI E, JIN S, ZHANG Q, et al. Autonomous Navigation of Mars Probe Using X-ray Pulsars: Modeling and Results[J]. Advances in Space Research, 2013, 51(5): 849-857. |
| [7] | SUN Shouming. Study on Autonomous Navigation Method of Spacecraft Based on X-ray Pulsars [D].Changsha: National University of Defense Technology, 2011.(孙守明. 基于 X 射线脉冲星的航天器自主导航方法研究[D]. 长沙: 国防科学技术大学, 2011.) |
| [8] | LAMBROU E, PANTAZIS G. Astronomical Azimuth Determination by the Hour Angle of Polaris Using Ordinary Total Stations[J]. Survey Review, 2008, 40(308): 164-172. |
| [9] | BALODIMOS D, KORAKITIS R, LAMBROU E, et al. Fast and Accurate Determination of Astronomical Coordinates Φ, Λ and Azimuth, Using a Total Station and GPS Receiver[J]. Survey Review, 2003, 37(290): 269-275. |
| [10] | ZHAN Yinhu,ZHANG Chao,WANG Yonghai.A New Method of Fast Orientation by Surveying the Constellation Stars[J].Beijing Surveying and Mapping,2012(4):11-13.(詹银虎,张超,王永海.利用特征星进行快速天文定向[J].北京测绘,2012(4):11-13.) |
| [11] | ZHAN Yinhu,ZHANG Chao,HUA Yuesheng,et a1.Research on Fast Astro-geodetic Orientation by Observing Planets [J].Journal of Geomatics Science and Technology,2011,28(5):338-341.(詹银虎,张超,华跃升,等.利用行星进行快速天文定向[J].测绘科学技术学报,2011,28(5):338-341.) |
| [12] | ZHAN Yinhu,ZHANG Chao,ZHENG Yong,et a1.A Fitting Algorithm of the Apparent Moon Center and Its Application on Fast Orientation [J].Acta Geodatica et Cartographia Sinica,2012,41(3):353-358.(詹银虎,张超,郑勇,等.月球视面中心拟合算法及其在测月快速定向中的应用[J].测绘学报,2012,41(3):353-358.) |
| [13] | BUONOCORE B, VASSALLO A. Astronomical Determination of Azimuth and Latitude by Observation of Two Unknown Stars Without Time Measurement and Knowledge of Astronomy[J]. Survey Review, 1991, 31(242): 233-237. |
| [14] | ZHANG Chao, ZHENG Yong, LI Changhui.Research of Astronomy Orientation by Using the Random Star[J].Science of Surveying and Mapping,2005,30(4): 30-32. (张超,郑勇,李长会.用任意星进行天文定向的研究[J]. 测绘科学, 2005, 30(4): 30-32.) |
| [15] | LU Xiushan,FENG Zhunde,LIU Jimin.Analysis Theory on Ill-conditioned System with Application on Surveying[M].Beijing:Surveying and Mapping Press,2007.(卢秀山,冯遵德,刘纪敏.病态系统分析理论及其在测量中的应用[M].北京:测绘出版社,2007.) |
| [16] | HANSEN P.Analysis of the Discrete Ill-posed Problems by Means of the L-curves[J].SIAM Review,1992,34:561-580. |
| [17] | ZHANG Guangjun.Star identification [M].Beijing:National Defence Industry Press,2011.(张广军.星图识别[M].北京:国防工业出版社,2011.) |
| [18] | JIANG Ming,YU Mingyan,WANG Jinxiang,et al.A Novel All-sky Autonomous Star Pattern Recognition Algorithm [J]. Journal of Astronautics, 2007, 28(4): 1020-1024.(蒋明,喻明艳,王进祥,等.一种新的全天自主星图识别算法[J]. 宇航学报, 2007, 28(4): 1020-1024.) |
| [19] | XIA Yifei,JIN Wenjing. Impacts of the New Reference System on Astrometry[J]. Progress in Astronomy, 2004, 22(3): 200-207. (夏一飞,金文敬. 新参考系的引入对天体测量学的影响[J].天文学进展, 2004, 22(3): 200-207.) |
| [20] | BANGERT J,PUATUA W, KAPLAN G, et al. User’s Guide to NOVAS Version C3.0[M].Washington:USA Naval Observatory,2009:31-32. |
| [21] | JIN Shuanggen, ZHU Wenyao. International Terrestrial Reference Frame: Current Status and Its Future[J]. Progress in Astronomy, 2003, 21(3): 241-249.(金双根,朱文耀. 国际地球参考架:现状与未来[J].天文学进展,2003, 21(3):241-249.) |
| [22] | WEI Erhu, LIU Jingnan, PAN Peijing. On Data Processing with Last Three Years of VLBI Observation[J].Geomatics and Information Science of Wuhan University, 2008,33(12):1275-1278.(魏二虎,刘经南,潘培鲸.近三年VLBI观测的数据处理及分析[J].武汉大学学报:信息科学版,2008,33(12):1275-1278.) |
| [23] | LÜ Zhiping,QIAO Shubo.Foundation of Geodesy [M].Beijing:Surveying and Mapping Press,2010.(吕志平,乔书波.大地测量学基础 [M].北京:测绘出版社,2010.) |
| [24] | XIA Yifei,HUANG Tianyi.Spherical Astronomy [M].Nanjing:Nanjing University Press,1995.(夏一飞,黄天衣.球面天文学 [M].南京:南京大学出版社,1995.) |
| [25] | ZHANG Chao.System-level Development and Application Research on Astronomic Surveying System Based on Electronic Theodolites[D].Zhengzhou:Information Engineering University,2009.(张超.基于电子经纬仪的天文测量系统及应用研究[D].郑州:信息工程大学,2009.) |
| [26] | ZHAN Yinhu.Theory and Technology Research on Fast Orientation Based on Celestial Bodies[D].Zhengzhou:Information Engineering University,2012.(詹银虎.基于自然天体的快速定向理论及技术研究[D].郑州:信息工程大学,2012.) |