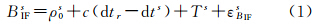1 引 言
精密单点定位技术(precise point positioning,PPP)采用单台GNSS接收机,利用国际GNSS服务组织(International GNSS Service,IGS)提供的精密星历和卫星钟差,基于载波相位观测值可实现毫米至分米级高精度定位。经过十多年的快速发展,GPS PPP的基本理论和实践问题已经得到了比较好的解决,目前已在高精度测量、低轨卫星定轨、航空测量、地表形变监测等领域取得了广泛的应用[1, 2, 3, 4, 5, 6, 7, 8]。
北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)是中国正在实施的自主发展、独立运行的全球卫星导航系统。截至2012年12月28日,BDS已有5颗GEO、5颗IGSO和4颗MEO卫星在轨运行,初步形成了亚太地区的导航定位服务能力[9]。随着北斗系统的逐步完善和发展,基于BDS的PPP技术吸引了国内外学者的广泛关注。文献[10]采用“北斗卫星观测试验网”(BETS)实测数据和我国自主研制的精密数据处理软件PANDA,实现了北斗导航卫星系统静态PPP,研究成果显示BDS静态PPP定位精度达到厘米级。文献[11]也取得了水平和垂直方向12 cm的静态北斗PPP结果,并指出该精度较低的原因是由于目前跟踪网的测站数较少,估计的北斗轨道和钟差产品精度较低所致。文献[12]利用北京和武汉站一周的观测数据进行了BDS的静态和动态PPP试验,结果表明BDS静态单天解可达1~2 cm、动态单天解可达4~6 cm。此外,文献[13]也利用2个测站3天的观测数据,初步评估了GPS、BDS、GPS/BDS双频非组合PPP的定位性能[13]。
然而,目前针对BDS PPP的试验结果大多只给出了少量单天解的结果,研究还不够全面和深入。在工程实践中,为了提高作业效率,高精度用户在很多应用场合只会观测数小时甚至更短的时间,此时BDS PPP能达到什么精度,以及为满足厘米精度的PPP定位,北斗用户最少需要观测多少时间,这些都还不是很清楚。北斗区域导航定位系统已经可向亚太地区提供被动式定位服务,PPP技术作为一种有效便捷的高精度定位技术,研究分析当前BDS PPP的定位性能,特别是其收敛速度和定位精度,具有重要的现实意义和应用价值。鉴于上述原因,本文旨在研究BDS PPP的收敛速度和短时间(数小时)的定位精度。
2 BDS精密单点定位模型与数据处理策略 2.1 观测方程
与GPS PPP类似,BDS PPP的基本观测方程采用双频无电离层组合以消除电离层一阶项误差的影响。BDS具有B1、B2、B3共3个信号频率,本文采用B1、B2频率上的相位和伪距观测值进行无电离层组合,其具体观测方程如下[14]
式中,BIFs、ΦIFs分别为无电离层组合的伪距、相位观测值;ρ0s为卫星s至接收机r之间几何距离;c是真空中光的传播速度;dtr和dts分别为接收机和卫星端的钟误差;Ts为斜路径对流层延迟;λIF为无电离层组合载波波长;NIFs是无电离层组合相位观测值的模糊度;εBIFs、εΦIFs分别表示伪距、载波测量噪声。
2.2 参数估计及误差处理策略
通过无电离层组合消除电离层延迟一阶项的影响后,PPP的待估参数包括测站坐标、接收机钟差、天顶对流层延迟,以及各卫星连续观测弧段内的模糊度参数。BDS PPP对于未知参数和各误差项的处理方式与GPS PPP类似。对于对流层延迟参数,首先使用Sasstamonion模型[15]改正其干分量,残余的湿分量则采用随机游走进行估计,并使用GMF投影函数[16]将天顶对流层延迟投影到传播路径上。使用精密的卫星轨道和卫星钟差产品来固定卫星轨道和钟差,对观测值中影响在厘米级以上的系统误差,包括相对论效应、固体潮汐、相位缠绕使用模型进行改正。值得注意的是,目前IGS只提供了粗略的BDS卫星端PCO改正,尚无机构或组织提供BDS卫星端PCV以及接收机端的PCO与PCV信息,因此无法进行精确的天线相位中心偏差及其变化改正。
本文在数据预处理阶段首先进行钟跳探测与修复,避免将接收机钟跳引起的观测值跳变误判为周跳,然后联合使用GF与MW组合探测周跳[17]。使用扩展卡尔曼滤波(EKF)进行参数估计,并通过对验后残差进行分析,采用改进的IGGIII抗差估计方案[18]进行质量控制。具体的参数估计策略如表 1所示。
| 参数 | 处理策略 | |
| 数据处理 | 观测值 | 无电离层组合伪距/载波相位 |
| 截止高度角 | 7° | |
| 误差处理 | 相位缠绕 | 模型改正,与GPS处理方式一致 |
| 固体潮汐 | 模型改正 | |
| 相对论效应、地球自转 | 模型改正 | |
| 卫星钟差、轨道 | 武汉大学卫星导航定位技术研究中心产品 | |
| 参数估计 | 坐标 | 固定,先验约束100 m(静态PPP) 白噪声,先验约束100 m(动态PPP) |
| 接收机钟差 | 白噪声,初始方差10 000 m2 | |
| 对流层延迟 | Saastamoinen模型+参数估计,随机游走,谱密度√6 mm/h,GMF投影函数 | |
| 模糊度 | 常数,浮点解 | |
为了评价BDS PPP的定位性能,本文选取了8个测站2013年DOY264—270共7 d的BDS/GPS双系统GNSS观测数据,分别进行静态和动态PPP试验。试验数据来源于IGS的MGEX(muti-GNSS experiment)观测网,所选测站信息如表 2所示,CUAA、CUBB以及CUT1-CUT3均分布在Curtin大学里面,GMSD和NNOR分别位于日本和澳大利亚,REUN站位于南非附近。作为对比,对各测站同时进行GPS PPP解算,并以其静态单天解作为各测站坐标参考真值。观测数据采样率为30 s,精密产品采用武汉大学卫星导航定位技术研究中心提供的BDS 30 s精密星历和30 s钟差产品,以及ESA分析中心提供的GPS 15 min精密星历和30 s钟差产品。使用IGS提供的ANTEX文件改正GPS卫星端和接收机端PCO和PCV,BDS仅进行卫星端PCO改正。
| 测站 | 纬度 | 经度 | 天线类型 |
| CUAA | 32.0°S | 115.9°E | TRM59800.00 SCIS |
| CUBB | 32.0°S | 115.9°E | JAV_GRANT-G3T NONE |
| CUT1 | 32.0°S | 115.9°E | TRM59800.00 SCIS |
| CUT2 | 32.0°S | 115.9°E | TRM59800.00 SCIS |
| CUT3 | 32.0°S | 115.9°E | TRM59800.00 SCIS |
| GMSD | 30.6°N | 131.0°E | TRM59800.00 SCIS |
| NNOR | 31.0°S | 116.2°E | SEPCHOKE_MC NONE |
| REUN | 21.2°S | 55.6°E | TRM55971.00 NONE |
试验将每个测站24 h观测数据切割为8个子时段,按每子时段为3 h,一共有448个子时段。将各子时段PPP解算结果与参考真值做差,获得E、N、U 3个方向上的坐标偏差以分析BDS PPP的收敛时间和定位精度。本文中的滤波收敛定义为ENU各向定位偏差均优于1 dm。为确保结果的可靠性,同时检查了首次收敛时刻后续20个历元的位置偏差,只有当连续20个历元的偏差都在限值以内时,才认为滤波在当前历元收敛[19, 20]。
3.1 收敛速度分析
对448个3 h观测时段分别进行静态、动态前向卡尔曼滤波,并统计每个数据的收敛时间,其中剔除了部分异常数据(观测质量太差或卫星数较少,约占10%)。首先以DOY264 CUT2站第1时段的定位结果为例,比较分析了BDS/GPS PPP的定位偏差序列,如图 1、图 2所示。从图 1、图 2可以看出,BDS 静态PPP经过30 min滤波可以达到收敛,动态PPP的收敛时间较长,需要约80 min才逐渐收敛。而GPS PPP的收敛时间相对较短,静态约20 min、动态30 min。图 3为该时段BDS、GPS PPP的PDOP值和可视卫星数。可以看出,尽管大部分时间BDS卫星数多于GPS,但由于目前BDS的MEO卫星数较少,总体上BDS的PDOP反而不如GPS;此外,BDS几何图形结构变化不如GPS星座显著;再者,当前由于BDS的跟踪站数量有限,BDS的精密轨道精度较低,从而导致BDS PPP的收敛时间长于GPS。滤波收敛之后,两者的静态PPP结果相差很小且比较稳定。而BDS 动态PPP由于还未充分收敛,精度及稳定性均比GPS PPP结果要差一些。
 |
| 图 1 DOY264 CUT2站第1时段BDS、GPS静态PPP定位偏差序列Fig. 1 Position bias of BDS、GPS static PPP at station CUT2-1 in DOY 264 |
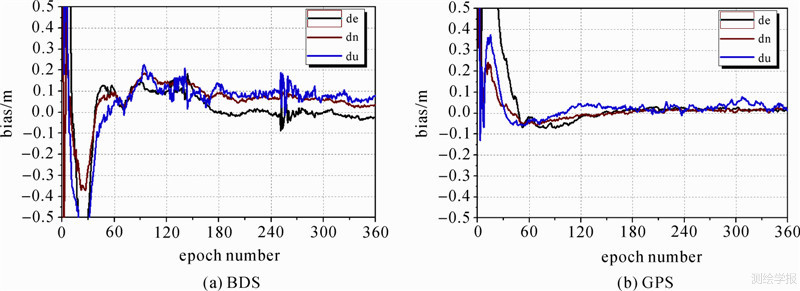 |
| 图 2 DOY264 CUT2站第1时段BDS、GPS动态PPP定位偏差序列Fig. 2 Position bias of BDS、GPS kinematic PPP at station CUT2-1 in DOY 264 |
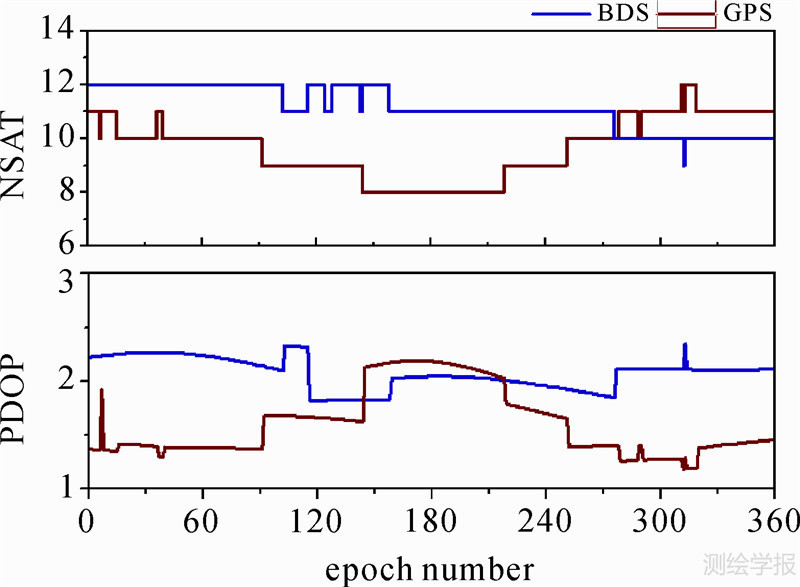 |
| 图 3 DOY264 CUT2站第1时段BDS、GPS PDOP和卫星数Fig. 3 PDOP and satellite number at station CUT2-1 in DOY 264 |
对各天数据的静态和动态PPP收敛时间进行统计,得到各天的平均收敛时间,结果如图 4所示。从中可以看出,对基于BDS和GPS系统的PPP定位,各天之间的平均收敛时间具有较好的一致性,天与天之间并无显著差异。图 5、图 6分别给出了7天所有数据静态、动态PPP的收敛时间分布统计。从图中可以看出,BDS静态PPP的收敛时间均匀分布在20~70 min、70~110 min和110~180 min 3个区间,各占约50%、20%、30%。动态PPP与静态PPP类似,收敛时间分布跨度较大,且约有10%的数据超过了180 min。GPS静态PPP收敛时间主要集中在10~30 min,动态PPP收敛时间主要集中在10~60 min,各约占80%、77%。所有数据的收敛时间统计如下:BDS静态PPP的平均收敛时间为77.4 min,动态PPP为98.3 min;GPS静态、动态PPP的平均收敛时间分别为27.6 min和49.6 min。不管是静态PPP还是动态PPP,BDS的收敛时间均比GPS长约50 min左右。
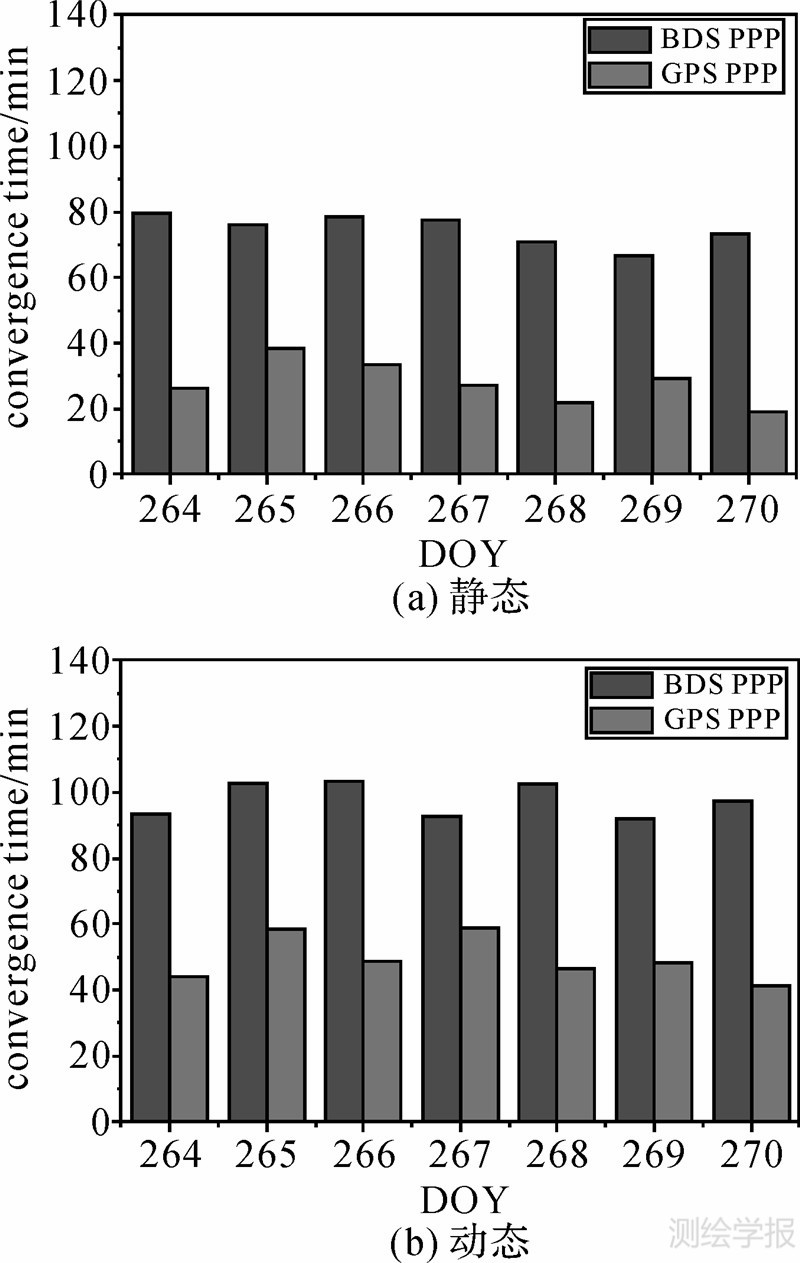 |
| 图 4 DOY264—270各天静态、动态PPP平均收敛时间Fig. 4 Average convergence time of static、kinematic PPP per day |
 |
| 图 5 BDS、GPS静态PPP收敛时间分布Fig. 5 Distribution of convergence time of BDS、GPS static PPP |
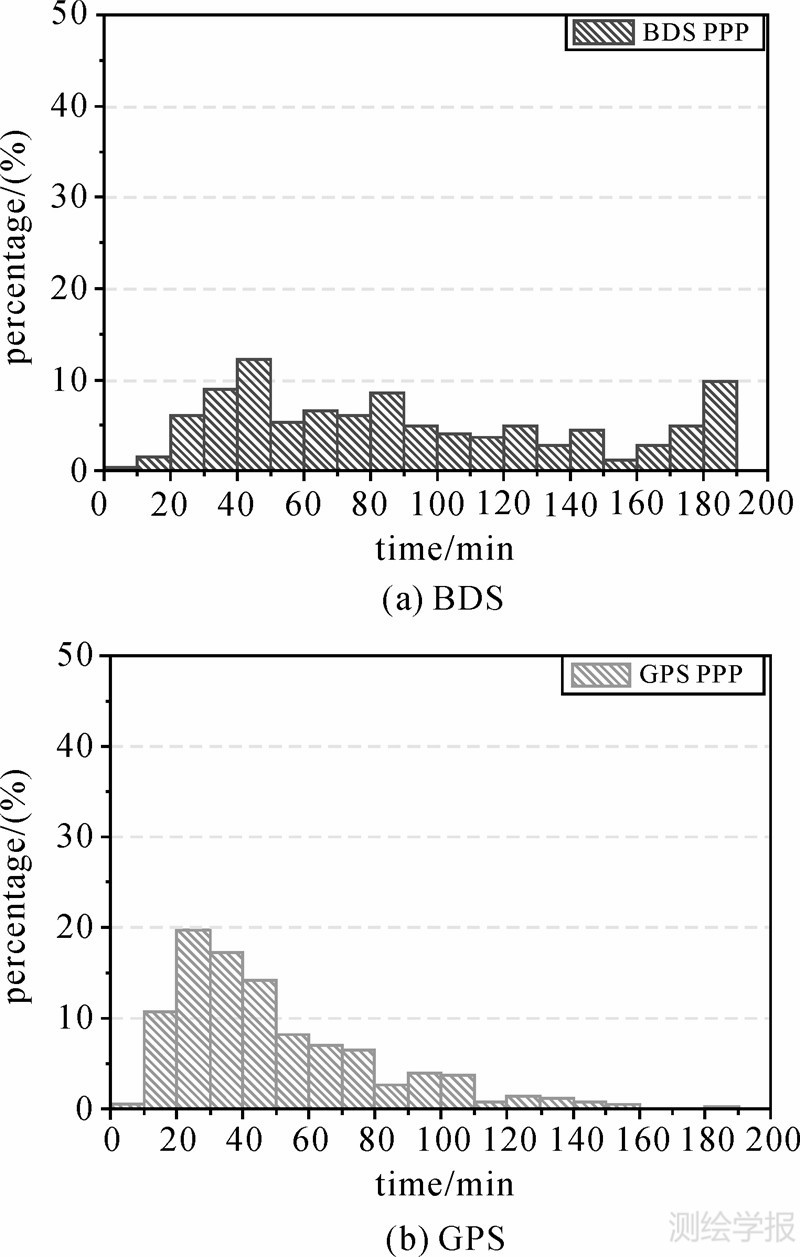 |
| 图 6 BDS、GPS动态PPP收敛时间分布Fig. 6 Distribution of convergence time of BDS、GPS kinematic PPP |
众所周知,PPP的解受卫星轨道和钟差产品精度、星座几何强度的影响较为明显。目前BDS的精密卫星产品的精度较GPS差,且无法精确改正PCO和PCV误差。而且,目前BDS的可用卫星数只有14颗,而GPS有31颗,其几何强度远比BDS要好。因此,当前条件下BDS PPP的收敛时间明显长于GPS PPP。
3.2 BDS/GPS定位精度分析
为分析滤波收敛后BDS PPP的定位精度及稳定性,对每天的解算结果进行统计。静态结果计算其定位偏差均方根RMS,对于动态结果计算平均RMS值,统计时剔除了收敛时间超过160 min的数据。以DOY264天为例,图 7、图 8分别给出了各测站静态、动态PPP定位结果统计。可以看出,对于静态解算模式,BDS PPP滤波收敛后E分量大部分优于5 cm,N分量大部分优于3 cm,U分量优于6 cm。 GPS PPP 各分量RMS约为(1.5,1,2)cm。 对于动态解算模式,BDS PPP E方向大部分优于10 cm,N方向优于8 cm,U方向约16 cm左右。GPS PPP 各方向RMS约为(3,1.5,4)cm。
 |
| 图 7 DOY264各站BDS、GPS静态PPP定位偏差RMSFig. 7 RMS of position bias of BDS、GPS static PPP per station in DOY 264 |
 |
| 图 8 DOY264各站BDS、GPS动态PPP定位偏差平均RMSFig. 8 RMS of position bias of BDS、GPS kinematic PPP per station in DOY 264 |
除了3 h的观测时段之外,笔者还分析处理了其他不同时段长度(6 h,8 h,12 h,24 h)BDS/GPS PPP的定位偏差。对所有分时段数据计算平均RMS偏差,如表 3所示。可以看出,对于3 h的观测数据,BDS 静态PPP 定位精度优于5 cm;动态PPP 水平方向定位精度优于8 cm,高程方向约12 cm。GPS 静态PPP定位精度优于2 cm,动态PPP 水平方向优于3 cm,高程方向约4 cm。随着观测时间的增加,BDS静态、动态PPP的定位精度都有不同程度的提高,静态单天解水平方向优于1 cm,高程方向约为2 cm;动态单天解可达水平方向3~4 cm,高程方向6 cm左右的精度。整体上而言,BDS PPP收敛后的定位精度要略低于GPS。这主要是由于当前BDS的MEO卫星数较少,卫星分布及定位的几何图形结构比GPS差一些,且轨道和钟差产品精度相对较低,导致其PPP定位精度要略低于GPS,动态精度的差别更为明显,这是因为静态结果统计是对各时段收敛后最后一个历元的定位偏差计算RMS,而动态结果统计是从各时段的收敛时刻开始对偏差序列计算RMS。由于BDS动态PPP收敛时间较长(约100 min),尽管在收敛时刻各方向的定位偏差已经优于1 dm,但相对于GPS结果来说大部分还未达到充分收敛。从而导致表 3中较短观测时段(如3 h、6 h)的BDS动态PPP统计结果与GPS相差较大。此外,从表中可明显看出,两种PPP北分量定位精度均优于东分量,这是由于PPP保留浮点解,未将模糊度参数固定为整数的缘故[21]。
| cm | |||||||
| 时段 | 系统 | 静态PPP | 动态PPP | ||||
| E | N | U | E | N | U | ||
| 3 h | BDS | 4.1 | 1.8 | 4.3 | 7.4 | 5.7 | 11.7 |
| GPS | 1.5 | 0.6 | 1.7 | 2.9 | 1.6 | 3.9 | |
| 6 h | BDS | 2.1 | 1.8 | 3.5 | 5.5 | 3.6 | 6.9 |
| GPS | 1.1 | 0.3 | 1.1 | 1.6 | 1.3 | 4.3 | |
| 8 h | BDS | 0.8 | 1.1 | 4.3 | 3.6 | 3.0 | 6.9 |
| GPS | 0.7 | 0.3 | 1.0 | 1.8 | 1.5 | 4.7 | |
| 12 h | BDS | 0.4 | 1.3 | 2.6 | 3.6 | 2.9 | 7.3 |
| GPS | 0.6 | 0.2 | 0.7 | 1.7 | 1.3 | 4.0 | |
| 24 h | BDS | 0.3 | 0.3 | 1.8 | 4.1 | 3.0 | 5.4 |
| GPS | 0.2 | 0.1 | 0.3 | 1.6 | 1.2 | 3.5 | |
本文利用武汉大学卫星导航定位技术研究中心发布的北斗精密卫星轨道和钟差,在TriP 2.0平台上实现了BDS PPP算法模块。并以GPS PPP为参考,基于大量实测数据进行了BDS 静态PPP、动态PPP试验。结果表明,BDS 静态PPP的收敛时间约为80 min,动态PPP的收敛时间约为100 min。对于3 h的观测数据,静态PPP收敛后定位精度优于5 cm,动态PPP收敛后水平方向优于8 cm,高程方向约12 cm。与GPS PPP类似,东分量上定位精度较北分量稍差。说明当前BDS PPP的收敛时间较长,收敛后80~100 min内可实现厘米至分米级绝对定位。将来随着北斗精密产品精度的提高及PCO、PCV模型的精化,其收敛时间和定位精度将得到进一步提高和改善。
致谢:感谢Curtin University和IGS MGEX提供的BDS/GPS观测数据;感谢武汉大学卫星导航定位技术研究中心提供的BDS精密星历和钟差产品;感谢ESA分析中心提供的GPS精密星历和钟差产品。
| [1] | ZUMBERGE J F, HEFLIN M B, JEFFERSON D C, et al. Precise Point Positioning for the Effcient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research, 1997, 102(B3): 5005-5017. |
| [2] | KOUBA J, HÉROUX P. GPS Precise Point Positioning Using IGS Orbit Products[J]. GPS Solutions,2001, 5(2): 12-28. |
| [3] | ZHANG Xiaohong, LI Pan, ZUO Xiang. Kinematic Precise Orbit Determination Based on Ambiguity-fixed PPP[J]. Geomatics and Information Science of Wuhan University, 2013,38(9): 1009-1013. (张小红,李盼,左翔. 固定模糊度的精密单点定位几何定轨方法及结果分析[J]. 武汉大学学报 :信息科学版, 2013,38(9): 1009-1013.) |
| [4] | ZHANG Xiaohong, HE Xiyang, LI Xingxing. Analysis of Undifferenced Kinematic POD for LEOs Using Trip[J]. Geomatics and Information Science of Wuhan University, 2010,35(11): 1327-1330. (张小红,何锡扬,李星星. Trip软件非差几何法精密定轨精度分析[J]. 武汉大学学报:信息科学版, 2010,35(11): 1327-1330.) |
| [5] | ZHANG Xiaohong, ANDERSEN O. Surface Ice Flow Velocity and Tide Retrieval of the Amery Ice Shelf Using Precise Point Positioning[J]. Journal of Geodesy,2006, 80(4): 171-176. |
| [6] | ZHANG Xiaohong, LIU Jingnan, FORSBERG Rene. Application of Precise Point Positioning in Airborne Survey[J]. Geomatics and Information Science of Wuhan University, 2006,31(1): 19-22. (张小红,刘经南,Forsberg Rene. 基于精密单点定位技术的航空测量应用实践[J]. 武汉大学学报:信息科学版, 2006,31(1): 19-22.) |
| [7] | ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Calibration of Slant Total Electron Content and Satellite-receiver's Differential Code Biases with Uncombined Precise Point Positioning Technique[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 447-453. (张宝成,欧吉坤,袁运斌,等. 利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J]. 测绘学报, 2011, 40(4): 447-453.) |
| [8] | YUAN Xiuxiao, FU Jianhong, LOU Yidong. GPS-supproted Aerotriangulation Based on GPS Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2007,36(3): 251-255. (袁修孝,付建红,楼益栋. 基于精密单点定位技术的GPS辅助空中三角测量[J]. 测绘学报,2007,36(3): 251-255.) |
| [9] | YANG Yuanxi. Progress, Contribution and Challenge of Compass/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010,39(1): 1-6. (杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报,2010,39(1): 1-6.) |
| [10] | SHI Chuang, ZHAO Qile, LI Min, et al. Precise Orbit Determination of Beidou Satellites with Precise Positioning[J]. Science China Earth Science, 2012,55(7):1079-1086. (施闯,赵齐乐,李敏,等. 北斗卫星导航系统的精密定轨与定位研究[J]. 中国科学: 地球科学,2012, 42(6): 854-861.) |
| [11] | MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P, et al. Initial Assessment of the COMPASS/BeiDou-2 Regional Navigation Satellite System[J]. GPS Solutions,2013(17): 2111-2122. |
| [12] | MA Rui, SHI Chuang. Precise Point Postioning Research Based on BeiDou Navigation Satellite System[J]. Journal of Navigation and Positioning, 2013,1(2): 7-10. (马瑞,施闯. 基于北斗卫星导航系统的精密单点定位研究[J]. 导航定位学报, 2013,1(2): 7-10.) |
| [13] | LI W, TEUNISSEN P, ZHANG Baocheng, et al. Precise Point Positioning Using GPS and Compass Observations[C]// Proceedings of China Satellite Navigation Conference (CSNC) 2013. [S.l.]:Springer, 2013. |
| [14] | QU Lizhong, ZHAO Qile, LI M, et al. Precise Point Positioning Using Combined Beidou and GPS Observations[C]//Proceedings of China Satellite Navigation Conference (CSNC) 2013. [S.l.]:Springer, 2013. |
| [15] | SAASTAMOINEN J H. Atmospheric Correction for the Troposphere and Stratosphere in Radio Ranging of Satellites[C]//The Use of Artificial Satellites for Geodesy. Washington D C:[s.n.], 1972. |
| [16] | BOEHM J, NIELL A, TREGONING P, et al. Global Mapping Function (GMF): A New Empirical Mapping Function Based on Numerical Weather Model Data[J]. Geophysical Research Letters,2006, 33(7): 304-307. |
| [17] | ZHANG Xiaohong, GUO Fei, LI Pan, et al. Real-time Quality Control Procedure for GNSS Precise Point Positioing[J]. Geomatics and Information Science of Wuhan University, 2012,37(8): 940-944. (张小红,郭斐,李盼,等. GNSS精密单点定位中的实时质量控制[J]. 武汉大学学报:信息科学版, 2012,37(8): 940-944.) |
| [18] | ZHOU Jiangwen. Classical Theory of Errors and Robust Estimation[J]. Acta Geodaetica et Cartographica Sinica, 1989,18(2): 115-120. (周江文. 经典误差理论与抗差估计[J]. 测绘学报, 1989,18(2): 115-120.) |
| [19] | ZHANG Xiaohong, LI Pan, GUO Fei. Ambiguity Resolution in Precise Point Positioning with Hourly Data for Global Single Receiver[J]. Advances in Space Research,2013,51(1):153-161. |
| [20] | LI Pan, ZHANG Xiaohong. Integrating GPS and GLONASS to Accelerate Convergence and Initialization Times of Precise Point Positioning[J].GPS Solutions,2014,18(3): 461-471. |
| [21] | BLEWITT G. Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baselines up to 2000 km[J]. Journal of Geophysical Research,1989, 94(B8): 187-203. |