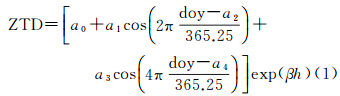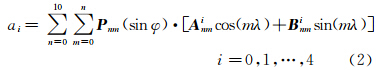2. 武汉大学地球空间环境与大地测量教育部重点实验室,湖北 武汉 430079
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China
1 引 言
无线电空间大地测量技术会受到中性大气的影响,其中电离层延迟的影响可以通过双频观测技术基本消除,而对流层延迟误差就成为该类技术中主要的误差源。在GNSS导航定位中,一般将信号传播路径上的斜延迟通过映射函数投影到天顶方向,因此通常对天顶对流层延迟(zenith tropospheric delay,ZTD)进行建模来削弱对流层对信号的影响,天顶对流层延迟可以进一步分为天顶静力学延迟(zenith hydrostatic delay,ZHD)和天顶湿延迟(zenith wet delay,ZWD)。为了能更好地适应大地测量技术的现代化发展,更可靠的对流层延迟模型将有助于改善空间大地测量技术的精度[1]。
传统的Hopfield、Saastamoinen、Black等对流层延迟模型[2, 3, 4]计算时需要已知测站实测气象参数,改正精度可达厘米或分米级,若采用标准大气气象参数则改正效果较差。Saastamoinen模型受高程的影响很小,而Hopfield模型精度随高度的增加而降低。文献[5]为美国广域增强导航系统(WAAS)的推广应用建立了UNB模型。它将美国标准大气资料沿纬度进行网格化,得到一个15°纬度间隔的大气参数表(温度、压强、水汽压、温度垂直梯度、水汽垂直变化指数)用来估算所需气象参数。经过不断发展改进,UNB目前有一系列的模型,其中比较有代表性的是UNB3、UNB4和UNB3m。在北美地区,UNB3模型估计的对流层天顶延迟平均误差为2 cm[6],UNB4改善了UNB3在高海拔地区的精度较低的缺陷[7]。UNB3m模型采用相对湿度估计湿延迟,使得平均偏差减小为-0.5 cm[8, 9]。EGNOS模型[10, 11, 12]是欧盟星基广域增强系统EGNOS采用的天顶对流层延迟改正模型,该模型对UNB3模型进行了简化,改正精度与采用实测气象参数的Hopfield和Saastamoinen模型相当[13],是国际民航组织的推荐模型[14]。文献[15]根据NECP再分析资料采用三维空间参数表构建了IGGtrop全球对流层延迟经验模型,该模型考虑了天顶对流层随经度的变化,精度有明显改善,但计算天顶对流层总延迟的过程中需要大量参数。文献[16]利用GGOS(global geodetic observing system)atmosphere提供的全球天顶对流层延迟格网数据,计算纬度、经度、高度三维网格上的对流层天顶延迟,获取其时域变化特征参数,然后基于球谐分析建立了全球非气象参数天顶对流层延迟模型GZTD(global zenith tropospheric delay)。该模型建模方法较为简单,在全球范围内的总体精度优于EGNOS、UNB系列模型且与IGGtrop模型相当,但所需参数相比IGGtrop模型大为减少。
GZTD模型以全球日平均ZTD格网数据建模,理论上其时间分辨率仅为一天。本文在GZTD模型的基础上,对其时间分辨率进行精化,利用GGOS atmosphere提供的全球天顶对流层延迟格网数据按照其6 h的时间分辨率对4个时刻(0∶00、6∶00、12∶00、18∶00UTC)的ZTD分别建模,模型应用时先计算出年积日当天4个时刻的ZTD估值,再采用三次样条插值方法计算所需任意时刻的ZTD估值,由此建立了一种改进的6 h时间分辨率的GZTD-6h模型。经过试验的检验,新模型有效提高了ZTD估值的时间分辨率。
2 GZTD-6h模型的建立
GGOS atmosphere基于ECMWF(european center for medium range weather forecasts)40年再分析资料[17]提供1979—2011年时间分辨率为6 h、空间分辨率为2.5°×2°的全球天顶对流层总延迟(包括ZHD和ZWD)格网数据。本文基于此格网数据进行建模研究。
2.1 模型建立方法
文献[16]中通过对GGOS atmosphere天顶对流层延迟数据时空分布特性的研究发现,ZTD存在年周期变化和半年周期变化,且受高度变化的影响,同时还与纬度有关。
顾及ZTD存在年周期变化和半年周期变化及高度对其的影响,任意点上的ZTD可由下式表示
式中,doy为年积日;h为高度;a0、a1、a3分别为在平均海平面(mean sea level,MSL)上的ZTD年均值、年周期变化和半年周期变化振幅;a2、a4分别为年周期变化和半年周期变化相位;β为将h高度处的ZTD改正到MSL处的改正常数,其值取-0.000 131 37。
本文采用2002—2009年GGOS atmosphere提供的全球格网ZTD时间序列按式(1)进行拟合,获取其时域变化参数,与GZTD使用全球日平均ZTD不同,按照ZTD数据的时间分辨率6 h分别拟合出4个时刻(0∶00、6∶00、12∶00、18∶00 UTC)的相应时域变化参数。
为反映全球范围内ZTD与位置(纬度和经度)的强相关性,将所有格网点对应的时域参数表示成位置的函数,从而减少模型参数数量,采用10阶10次的球谐函数将上述4组共20个参数进行球谐展开[18, 19]
式中,Pnm为勒让德多项式;φ和λ分别为格网点纬度和经度。Ainm和Binm为使用最小二乘确定的球谐函数n阶m次系数(共4×5×121个非零系数)。通过上述步骤,获得了GZTD-6h模型的基本系数。
2.2 GZTD模型时间分辨率分析
GZTD模型是基于GGOS atmospherer提供的2002—2009年全球日平均天顶对流层延迟格网时间序列建立的,模型计算只需年积日、纬度、经度和高度,总体精度为厘米级。但由于建模所采用的为全球日均值ZTD格网数据,在利用式(1)拟合时域参数时年积日为整数,所以理论上GZTD模型在应用时其分辨率也不会高过一天。本文使用GGOS atmosphere提供的2011年全球ZTD每天4次(即0∶00、6∶00、12∶00、18∶00 UTC)的格网数据进行GZTD模型时间分辨率验证,任意选取了分别位于低、中、高纬度的3个格网点((0°N,45°E,-61 m)、(28°N,60°E,1303 m)、(70°N,20°W,159 m)),计算了60、180、300年积日每天4次的GZTD模型ZTD估值,结果见图 1。
如图 1所示,在一个年积日内,GZTD模型ZTD估值变化为1 mm左右,在图中很明显表现为近乎平行于时间轴的直线,而GGOS给出的ZTD格网数据的实际变化为厘米级,模型估值比格网数据小了一个量级,这表明GZTD模型无法反映ZTD的日变化,其时间分辨率为一天,因此在模型应用时,年积日采用实数或者取当天对应的年积日整数,计算结果几乎无差别,充分说明GZTD模型在时间分辨率上有提升的空间。
 |
| 图 1 GZTD模型估计值(▲)与对应时刻GGOS格网数据(●)Fig. 1 GZTD estimates value(▲)and corresponding GGOS grid value(●) |
分析每个格网点经过式(1)拟合后MSL处ZTD年平均值a0、年周期振幅a1、半年周期振幅a3的日变化幅度情况,处理方法是对4个时刻(0∶00、6∶00、12∶00、18∶00 UTC)的a0、a1、a3依次两两求差,然后同一纬度上的差值取平均值作为对应纬圈上的差值,图 2、图 3、图 4分别为3个系数对应差值在不同纬圈上的变化情况。
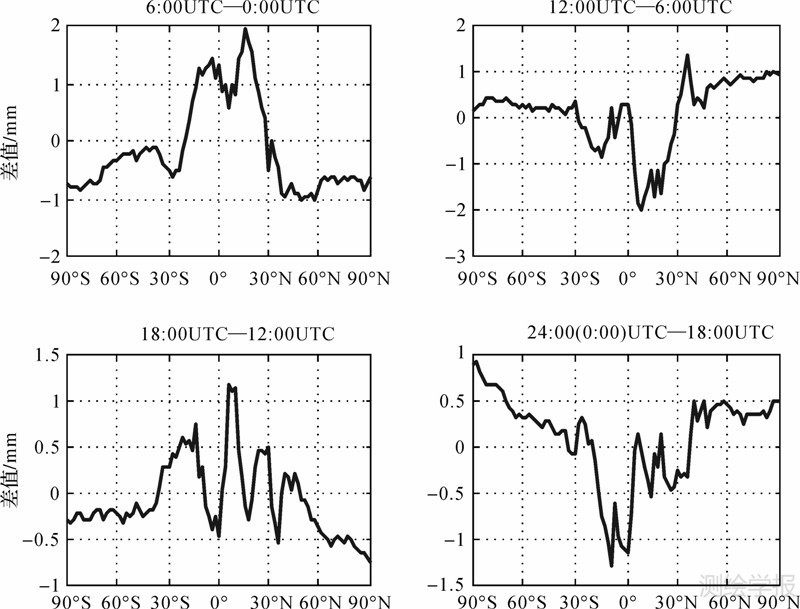 |
| 图 2 ZTD年均值a0的日变化幅度Fig. 2 Daily variation of ZTD annual mean(coefficient a0) |
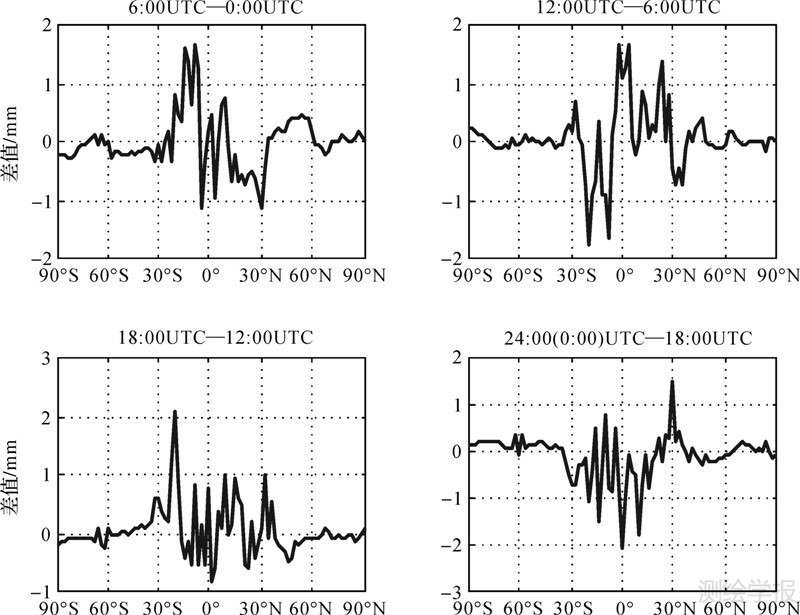 |
| 图 3 ZTD年周期振幅a1的日变化幅度Fig. 3 Daily variation of ZTD annual amplitude(coefficient a1) |
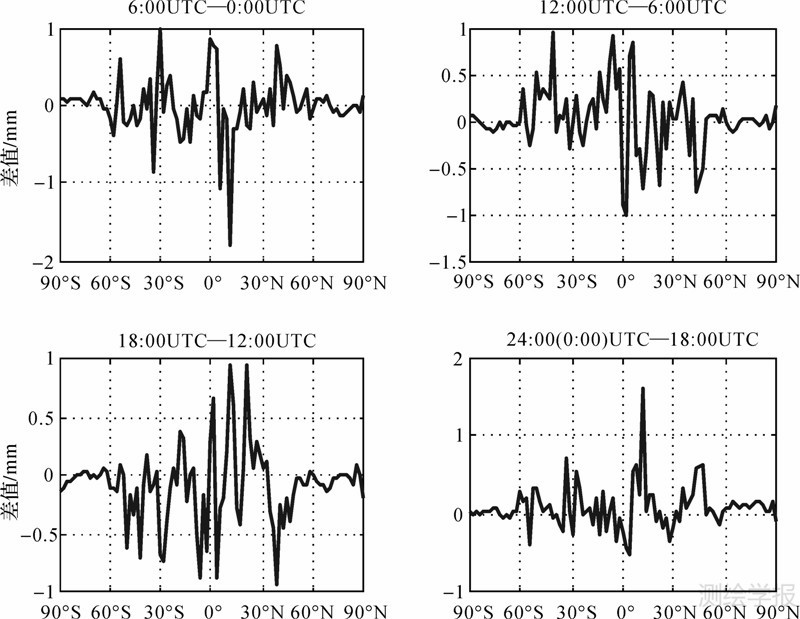 |
| 图 4 ZTD半年周期振幅a3的日变化幅度Fig. 4 Daily variation of ZTD semiannual amplitude(coefficient a3) |
如图 2所示,4组ZTD年均值差值的变化总体上呈现出南北半球对称的特征,这有可能是受南北半球洋流和赤道信风[20]的影响,而且南北纬30°之间的地区,ZTD年均值的日变化较为明显,且越靠近赤道,变化越大,最大达到2 mm;南北纬30°之外的中高纬度地区,ZTD年均值的日变化比较小,基本都在1 mm以内,说明这些地区的气候变化相对于低纬地区更稳定;此外,0∶00UTC到12∶00UTC之间的变化幅度明显较12∶00UTC和24∶00UTC之间的更大。文献[16]通过对a0的全球分布状况研究发现,a0在中低纬度地区较高,在高纬度地区相对较低,结合对ZTD年均值a0日变化分析,可以看出,中低纬度地区不仅对流层延迟整体较大,而且表现出更为显著的日变化特征,说明提高GZTD模型的时间分辨率是必要的。
ZTD年周期振幅参数a1决定ZTD的年际变化幅度。从图 3中可以看出,与ZTD年均值a0的日变化类似,ZTD年周期振幅a1的日变化在南北纬30°之间的区域较为明显,最大值达到了2 mm,而在南北纬30°之外的中高纬区域日变化幅度非常小(接近于0)。0∶00UTC至12∶00UTC,南北半球低纬度地区的ZTD年周期振幅变化呈现相反的趋势:即0∶00UTC至6∶00UTC,南半球低纬地区ZTD年周期振幅增大,北半球低纬度地区则减小,6∶00UTC至12∶00UTC年周期振幅变化情况则相反,这也许是中低纬地区海洋季风的影响。
图 4给出了ZTD半年周期振幅a3的日变化情况,从图中可以看出,相比于ZTD年周期振幅,ZTD半年周期变化振幅的日变化更小,最大值也仅在1 mm左右,此外,ZTD半年周期变化明显的区域主要在南北纬60°之间,相比于年周期变化明显区域范围扩大,而且随纬度呈现上下波动的分布变化。对ZTD年周期振幅和半年周期振幅的日变化的分析,进一步说明了精化GZTD模型的时间分辨率具有实际意义。
2.4 GZTD-6h模型估计任意时刻ZTD方法
GZTD-6h模型的计算只需年积日、纬度、经度和高度。具体计算方法是:先根据纬度和经度按式(2)计算出4组时域参数,再根据年积日和高度按式(1)反算出年积日当天4个时刻(0∶00、6∶00、12∶00、18∶00UTC)的ZTD,最后采用三次样条插值计算出年积日对应时刻的ZTD。由前述对GZTD模型时间分辨率的分析可知,GZTD模型估值分辨率为1 d,其主要原因为:在使用ZTD日均值建模过程中,拟合时的年积日均为整数,导致模型应用时年积日使用实数没有太大意义。相比较而言,GZTD-6h模型按6 h的时间分辨率建模,对ZTD采用插值法估计,理论上精化了GZTD模型的时间分辨率。
3 GZTD-6h与GZTD模型对比分析
本文采取平均偏差(bias)和均方根误差(RMS)作为模型精度评定标准。为了和与文献[16]提出的GZTD模型的内符合检验进行对比分析,使用GGOS atmosphere提供的2011年全球ZTD的格网数据的日均值进行内符合检验。全球所有2.5°×2°的网格点上的bias和RMS全球分布如图 2所示,两种模型bias和RMS结果对比见表 1。
| cm | ||
| 模型 | bias | RMS |
| GZTD-6h | 0.16[-5.5 7.9] | 3.6[1.0 9.3] |
| GZTD | 0.2[-5.4 8.0] | 3.7[1.1 9.1] |
| 注:表中方括号内为取值范围。 | ||
从表 1中可以看出两种模型的统计结果十分接近,GZTD-6h的bias和RMS略好一点,并没有明显的提高。从图 5可以看出,GZTD-6h模型的内符合检验全球分布状况与文献[16]中GZTD的十分一致,都是在太平洋以西的赤道地区出现较大误差。
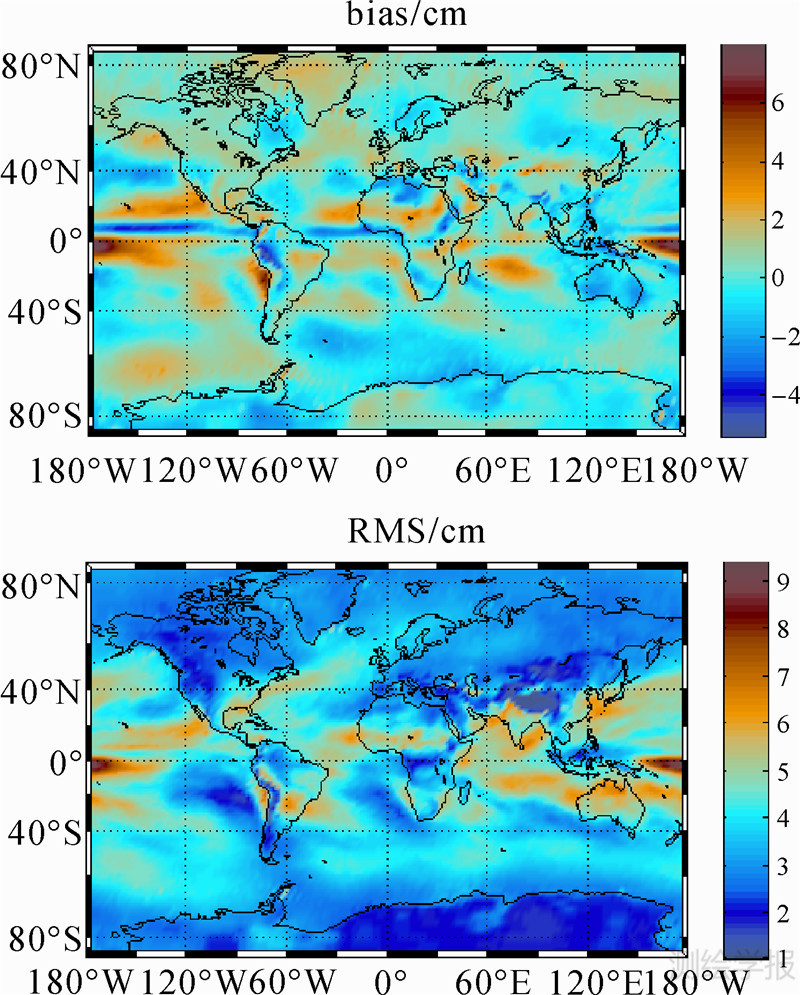 |
| 图 5 GZTD-6h模型内符合检验全球分布状况Fig. 5 Global distributionof GZTD-6h model inner coincidence |
GZTD-6h在内符合检验中没有表现出明显优势,其原因是由于内符合检验采用的是全球日平均ZTD,时间尺度为天,不能体现出改进的GZTD-6h模型在时间分辨率方面的优势。而且由第2节的分析可知,ZTD的日变化在0UTC到12UTC之间的幅度更大,因此,使用GGOS atmosphere提供的2011年全球ZTD每天4次(即0∶00、6∶00、12∶00、18∶00UTC)中6∶00UTC的格网数据进行内符合检验,分别使用改进的GZTD-6h模型和GZTD模型计算估计值,在6∶00UTC时刻两种模型的bias和RMS结果对比见表 2。
| cm | ||
| 模型 | bias | RMS |
| GZTD-6h | 0.17[-5.4 8.2] | 3.9[1.0 9.7] |
| GZTD | 0.17[-8.1 9.0] | 4.4[0.8 9.6] |
| 注:表中方括号内为取值范围。 | ||
从表中可以看出两种改正的bias都为0.17 cm,但是GZTD-6h的偏差变化范围相比GZTD小了大约4 cm,表现出更好的稳定性。GZTD-6h的RMS为3.9 cm,相比GZTD的4.4 cm减小了5 mm,有着较为明显的提高。为了更直观地分析两种模型的改正效果,对全球所有格网点在6∶00UTC时刻的bias和RMS的结果分布进行统计,相关的直方图见图 6。
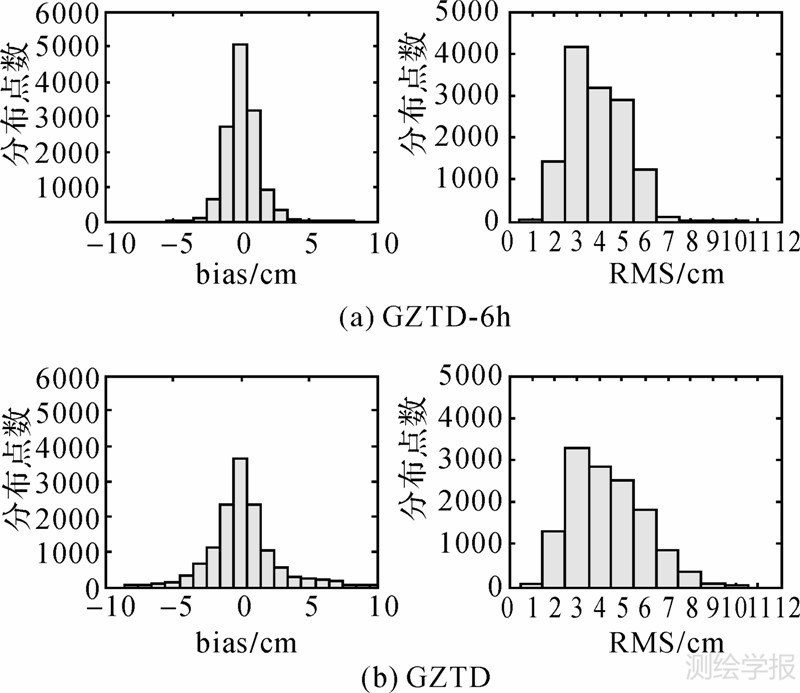 |
| 图 6 6∶00UTC时刻两种模型的误差直方图Fig. 6 Error histograms of two models at 6∶00UTC |
从两种模型的bias的直方图可以看出,GZTD-6h的bias分布更紧密,落在[-2, 2]cm区间的点更多。在RMS分布方面,GZTD-6h和GZTD均是在[3, 4]cm区间的点比其他区间更多,但前者比后者表现得更明显。结合bias的比较,说明GZTD-6h模型在比一天更高的时间分辨率下,相较于GZTD模型精度有所提高,体现出了更高的可靠性。
为了进一步对比分析两种模型在其他时刻的改正精度,本文使用2010年全球357个IGS站ZTD产品进行外符合检验。检验所用全球357个IGS站的分布见图 7,计算时刻为每天的3∶00UTC。
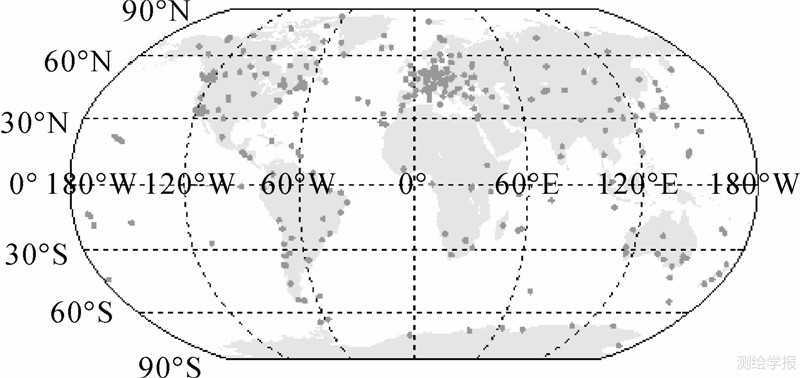 |
| 图 7 参与模型外符合检验的全球IGS站分布Fig. 7 Distribution of global International GNSS Service(IGS) sites involved in outer coincidence test |
表 3给出了两种模型使用全球IGS对流层最终产品检验的误差统计结果。可以看出GZTD-6h的全球平均偏差为-0.22 cm,只有GZTD全球平均偏差-0.45 cm的一半。GZTD-6h的全球平均RMS为4.05 cm,GZTD为4.51 cm,减少了大约5 mm,这个结果与表 2的结果比较一致,进一步说明了改进的GZTD-6h在稳定性和可靠性上的提高。
| cm | ||
| 模型 | bias | RMS |
| GZTD-6h | -0.22[-4.02 5.04] | 4.05[1.91 7.15] |
| GZTD | -0.45[-6.97 6.08] | 4.51[1.77 8.51] |
| 注:表中方括号内为取值范围。 | ||
对于延迟改正模型,模型拟合越好,其残差越表现出偶然误差的特性,残差分布更接近正态分布,通过两种模型外符合的bias分位数-理论分位数图来检验正态性。如图 8,GZTD-6h模型的分位数-理论分位数图十分近似于直线,除了在两端出现的少量异常值,而GZTD模型的分位数-理论分位数图则出现了明显的弯曲,表明前者正态性比后者更强,说明改进GZTD-6h模型更加合理。
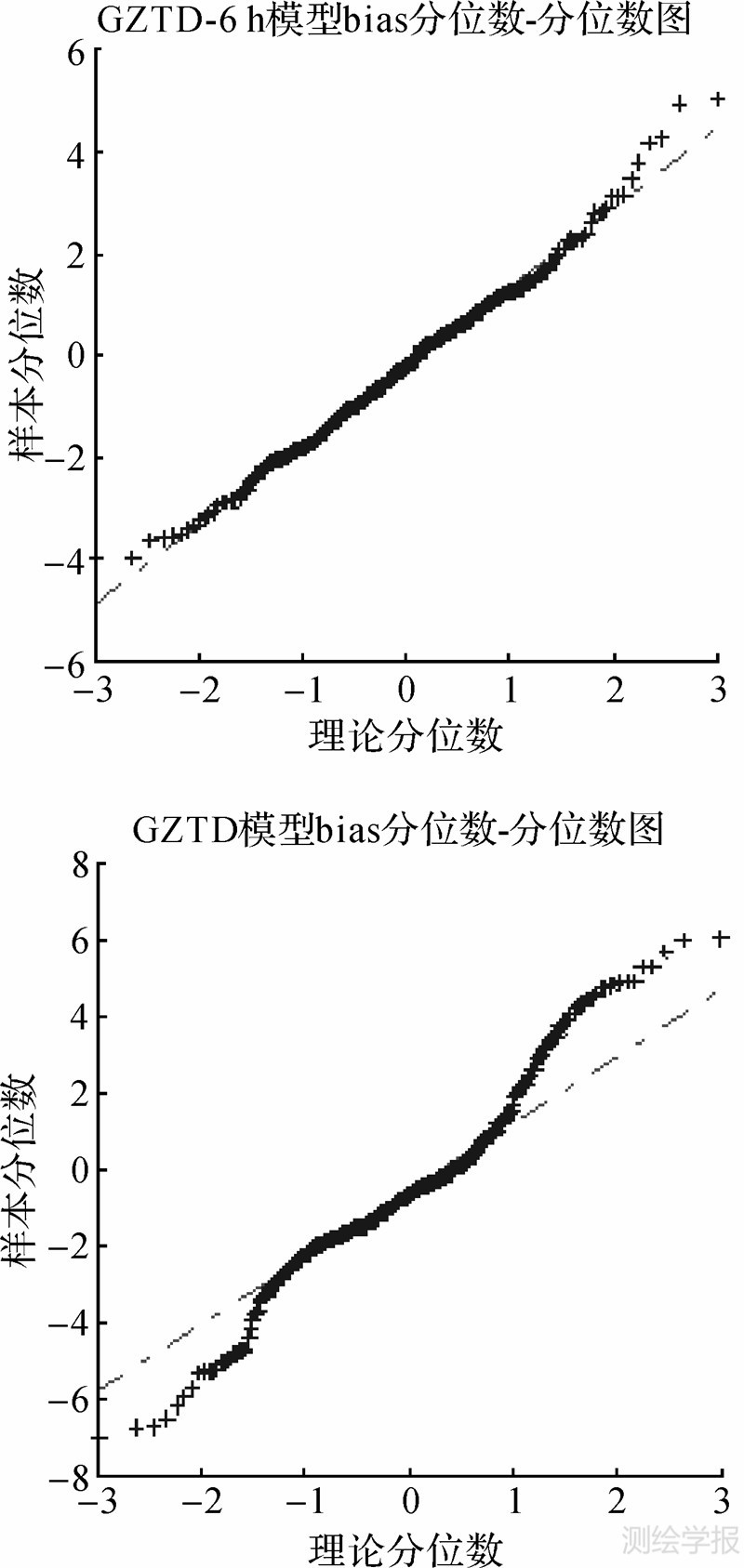 |
| 图 8 两种模型外符合bias分位数-理论分位数图Fig. 8 Quantile-quantile plot of outer coincidence bias of two models |
本文利用GGOS atmosphere提供的全球天顶对流层延迟格网时间序列,在GZTD模型的基础上,按6 h时间分辨率建模,提出了一种改进的GZTD-6h模型。首先经过试验表明GZTD模型估值不能反映ZTD的日变化,其时间分辨率为一天。在小于一天的时间分辨率下,经与GZTD模型的对比分析显示:内符合检验中,GZTD-6h模型的全球平均bias和RMS分别为0.17 cm和3.9 cm,全球平均bias与GZTD相同,全球平均RMS提高了5 mm,表明改进模型具有更好的可靠性;利用全球IGS站进行外符合检验统计,GZTD-6h模型的全球平均bias和RMS分别为-0.22 cm和4.05 cm,优于GZTD的-0.45 cm和4.51 cm,而且GZTD-6h模型的bias分布更接近于正态分布。
总体而言,改进的GZTD-6h模型相比于GZTD模型提高了ZTD估值的时间分辨率,是对后者的精化和优化。对于建立精度更高的全球对流层模型,需要更高质量、高分辨率的ZTD数据以及对ZTD日变化更精细的研究。
致谢: 感谢GGOS atmosphere机构以及IGS数据中心提供相关对流层延迟数据。
| [1] | YIN Haitao, HUANG Dingfa,XIONG Yongliang, et al. New Model for Tropospheric Delay Estimation of GPS Signal[J]. Geomatics and Information Science of Wuhan University, 2007, 32(5): 454-457. (殷海涛, 黄丁发, 熊永良, 等. GPS信号对流层延迟改正新模型研究[J]. 武汉大学学报:信息科学版, 2007, 32(5): 454-457.) |
| [2] | HOPFIELD H S. Two-quartic Tropospheric Refractivity Profile for Correcting Satellite Data[J]. Journal of Geophysical Research, 1969, 74(18): 4487-4499. |
| [3] | SAASTAMOINEN J. Contributions to the Theory of Atmospheric Refraction[J]. Bulletin Géodésique, 1972, 105(1): 279-298. |
| [4] | BLACK H D. An Easily Implemented Algorithm for the Tropospheric Range Correction[J]. Journal of Geophysical Research: Solid Earth (1978—2012), 1978, 83(B4): 1825-1828. |
| [5] | COLLINS J P, LANGLEY R B. A Tropospheric Delay Model for the User of the Wide Area Augmentation System[M]. Fredericton:Department of Geodesy and Geomatics Engineering, University of New Brunswick, 1996. |
| [6] | COLLINS J P, LANGLEY R B. The Residual Tropospheric Propagation Delay: How Bad Can it Get?[C]//Proceedings of ION GPS-98. 11 International Technical Meeting of the Satellite Division of the Institute of Navigation.Nashville,Tennessee: [s.n.], 1998: 729-738. |
| [7] | COLLINS P, LANGLEY R, LAMANCE J. Limiting Factors In Tropospheric Propagation Delay Error Modelling for GPS Airborne Navigation[C]//Proceedings of the Institute of Navigation 52nd Annual Meeting. Cambridge, MA: [s.n.], 1996: 1-10. |
| [8] | LEANDRO R, SANTOS M C, LANGLEY R B. UNB Neutral Atmosphere Models: Development and Performance[C]//Proceedings of ION NTM. Monterey, California, USA: [s.n.], 2006: 564-573. |
| [9] | LEANDRO R F, LANGLEY R B, SANTOS M C. UNB3m_pack: A Neutral Atmosphere Delay Package for Radiometric Space Techniques[J]. GPS Solutions, 2008, 12(1): 65-70. |
| [10] | DODSON A H, CHEN Wu, BAKER H C, et al. Assessment of EGNOS Tropospheric Correction Model[C]//Proceedings of the 12th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 1999). Nashville, TN: [s.n.],1999: 1401-1408. |
| [11] | PENNA N, DODSON A, CHEN Wu. Assessment of EGNOS Tropospheric Correction Model[J]. The Journal of Navigation, 2001, 54(1): 37-55. |
| [12] | UENO M, HOSHINOO K, MATSUNAGA K, et al. Assessment of Atmospheric Delay Correction Models for the Japanese MSAS[C]//Proceedings of the 14th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 2001). Salt Lake City, UT: [s.n.],2001: 2341-2350. |
| [13] | QU Weijing, ZHU Wenyao, SONG Shuli, et al. The Evaluation of Precision about Hopfield, Saastamoinen and EGNOS Tropospheric Delay Correction Model[J]. ActaAstronomica Sinica, 2008, 49(1): 113-122. (曲伟菁, 朱文耀, 宋淑丽, 等. 三种对流层延迟改正模型精度评估[J]. 天文学报, 2008, 49(1): 113-122.) |
| [14] | MOPS W. Minimum Operational Performance Standards for Global Positioning System/wide Area Augmentation System Airborne Equipment[R]. Washington DC: RTCA Inc. Documentation No. RTCA/DO-229B, 1999:6. |
| [15] | LI Wei, YUAN Yunbin, OU Jikun, et al. A New Global Zenith Tropospheric Delay Model IGGtrop for GNSS Applications[J]. Chinese Science Bulletin, 2012, 57(17): 2132-2139. (李薇, 袁运斌, 欧吉坤, 等. 全球对流层天顶延迟模型IGGtrop的建立与分析[J]. 科学通报, 2012, 57(15): 1317-1325.) |
| [16] | YAO Yibin, HE Changyong, ZHANG Bao, et al. A New Global Zenith Tropospheric Delay Model GZTD[J]. Chinese Journal of Geophysics, 2013, 56(7): 2218-2227. (姚宜斌, 何畅勇, 张豹, 等. 一种新的全球对流层天顶延迟模型 GZTD[J]. 地球物理学报, 2013, 56(7): 2218-2227.) |
| [17] | UPPALA S M, KÅLLBERG P W, SIMMONS A J, et al. The ERA-40 Re-analysis[J]. Quarterly Journal of the Royal Meteorological Society, 2005, 131(612): 2961-3012. |
| [18] | BOEHM J, HEINKELMANN R, SCHUH H. Short Note: A Global Model of Pressure and Temperature for Geodetic Applications[J]. Journal of Geodesy, 2007, 81(10): 679-683. |
| [19] | YAO Yibin, ZHU Shuang, YUE Shunqiang. A Globally Applicable, Season-specific Model for Estimating the Weighted Mean Temperature of the Atmosphere[J]. Journal of Geodesy, 2012, 86(12): 1125-1135. |
| [20] | ACKERMAN S A, KNOX J A. Meteorology: Understanding the Atmosphere[M].Pacific Grove, CA: Brooks/Cole-Thomson Learning,2002. |