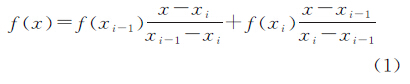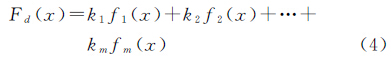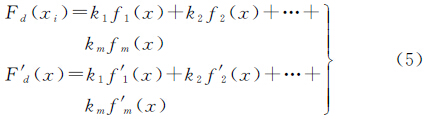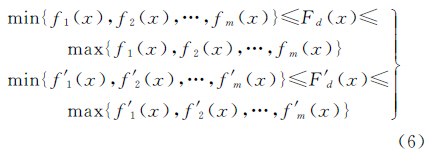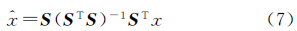1 引 言
端元提取可获得遥感图像中的基本光谱信息,它决定了混合像元解混精度的高低[1]。目前,学者们已提出了众多的端元提取算法[2, 3, 4, 5, 6, 7],而这些算法均需要较长的计算时间,海量数据的处理仍然制约着端元提取算法的有效应用[8],因此,部分学者对端元提取的加速算法进行了研究。概括来说,有两类加速思想,一类是使用并行算法进行加速[9, 10, 11, 12],另一类是减少参与端元提取的样本数以提高速度。减少样本数的方法主要有3种:基于像元空间关联下的高光谱图像分类(ECHO)的端元提取算法[13, 14] 和空间预处理算法(SPP)[15];以凸面单体边界为搜索空间的端元快速提取算法(SBA)[16];空间/光谱集成的端元提取方法(SSEE)[17]。这3种算法有着各自的优缺点: ECHO和SPP算法基于地物空间分布的连续性,从图像局部的同一类像元中提取出一条光谱作为候选端元,再进行端元提取。这种方法减少了端元提取的光谱数,具有较高的效率,对均一地表影像具有较好的效果,但对于大数据量和零碎地表加速效果不理想。SBA算法通过搜索凸面单体边界,确定候选端元,再进行端元提取,降低了运算时间。然而该算法需根据端元数进行主成分分析,而主成分分析可能会给端元提取结果带来误差[18]。 SSEE算法是一种将影像分块,对每一块选取一个光谱作为候选端元的算法,该方法有效地减少了端元计算的时间,但可能造成端元漏分的情况。因此,有必要提出一种快速、准确、稳定的端元提取加速算法。
线性混合模型广泛应用于端元提取理论当中[19]。通常认为影像光谱是一条分段曲线,端元光谱在某些波段上或者任意两个波段的差值影像上会表现为极值(最大或者最小)。由于具有极值的光谱远远少于整个影像的像元数,因此,快速筛选出具有极值的光谱,再从这些极值光谱中寻找端元,可以大大提高端元提取的速度。
基于以上原理,本文提出了一种通过光谱梯度特征搜索与识别的快速端元提取算法,简称为光谱梯度特征搜索算法(spectrum gradient feature search,SGFS)。算法包括两部分,第1部分是基于光谱不同尺度梯度特征的候选端元快速筛选,第2部分是基于迭代误差分析的端元识别。
2 光谱曲线的梯度特征
对于有 n个波段的图像,其光谱可以看作n个点拟合而成的曲线,可以采用分段线性插值拟合曲线,根据分段线性插值公式,任意两波段之间的曲线表示如下
式中,xi-1、xi为波段号(x1=1,x2=2,…,xn=n),xi-1≤x≤xi,i=2,3,…,n;f(xi)表示光谱曲线在波段i上的值。由式(1)可得f(x)的一阶导数为 式中,xi-1=i-1,xi=i,即xi-xi-1=1,则有当图像中有m条端元时,所有的像元(包括端元和混合像元)光谱由m条端元光谱组成,有
式中,k1,k2,…,km表示端元所占比重,且满足 0≤k1≤1,0≤k2≤1,…,0≤km≤1,k1+k2+…+ km=1。fm(x)表示第m条端元的曲线函数,亦可看作由n-1个式(1)组成的分段线性差值曲线,f′ m(x)表示第m条端元的曲线的导数,亦可看作由n-1个式(3)组成的分段函数;Fd(x)表示混合像元的光谱曲线函数。则有 式中,xi-1≤x≤xi,i=2,3,…,n;f′ m(x)表示第m条端元光谱曲线函数的1阶导数;F′ d(x)表示混合像元的光谱曲线函数的1阶导数。由k1+k2+…+km=1可得 式中,xi-1≤x≤xi,i=2,3,…,n,根据式(6)可以得到如下推论:(1) 节点值(波段值)最大/最小的光谱曲线为端元光谱,即具有极值(最大/最小值)的光谱为端元光谱。
(2) 任意相邻两波段的差值影像上的极值点为端元。由式(6)可知在1阶导数上具有极值的光谱曲线为端元光谱,而式(3)表明端元光谱曲线函数的一阶导数即为相邻两个波段的差值,则相邻两个波段差值影像上的极值点为端元。
如图 1所示,3条直线y1=2x,k1=2;y2=1.4x,k2=1.4;y3=x,k3=1。可以将这3条线看作有两个波段的光谱曲线。则可由y1、y3组成y2(y2=0.4y1+0.6y3),即y1、y3为端元,y2为混合像元。而在节点(x=2)处的值有如下关系
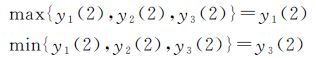
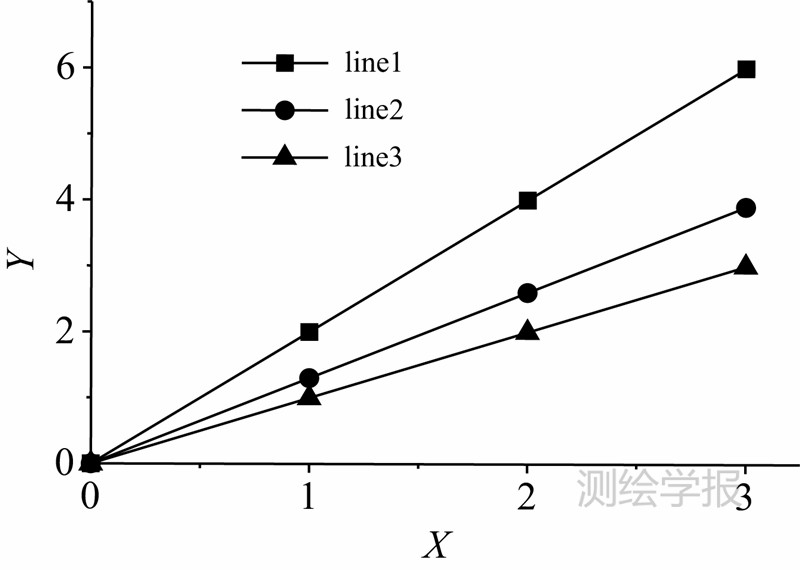 |
| 图 1 3条不同斜率的直线Fig. 1 Three lines with different gradient |
3条直线的斜率存在如下关系
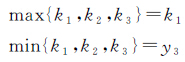
如果提取部分波段组成光谱曲线,端元点位置保持不变。混合像元的光谱曲线依然可以由端元曲线组成,即式(5)依然成立,结合式(5)可得如下推论。
(3) 影像的任意两个波段的差值影像上,具有极值(具有最大/最小值)的点为端元;在图像的任意一个波段上,极值点为端元。 3 端元快速提取的光谱梯度特征搜索法
根据上一节的推论,如果一条光谱为端元光谱,则在某一个光谱尺度上会表现为极值。找出所有的图像波段以及所有两两波段组合的差值影像的极值点集合,则所有的端元就包含在这个集合当中。根据这一结论,可以将端元识别的范围由整幅影像的像元数快速缩小为2n+2C2n=n(n+1)个(n为波段数),大大减少了端元识别的范围。
根据端元光谱的梯度特征,可以先从整幅影像中筛选出n(n+1)条光谱作为候选端元。然后再根据端元光谱进行丰度估计时的误差最小特性,迭代计算得到m个端元。为此,本文提出了基于光谱梯度特征搜索算法(SGFS算法),该算法描述如下:
步骤1 从影像中选取候选端元。
(1) 从图像中任选两个波段Bi、Bj(其中0
(2) 寻找差值影像Bc上值最大、最小的两个点,记为候选点。为保证不重复选出候选端元点,若一个点被标记为候选端元,则该点不进行下一论筛选。
(3) 对所有的波段组合进行(1)、(2)步计算处理,就可以得到总数为P1=2C2n个的候选端元点。
(4) 找出所有波段上具有最大/最小值的点,共P2=2n个候选端元点。
(5) 将(3)、(4)找到的点的并集即为所有的候选端元点,共有P=P1+P2=2n+2C2n=n(n+1)个候选端元点。
步骤2 从步骤1中提取的P个候选端元中提取最终的端元。
(1) 求得候选端元的平均光谱,构成初始端元矩阵S。
(2) 根据端元矩阵 S 用最小二乘来估计各组分(端元)的混合系数,并用混合系数计算出每个像元的最小均方差估计值[5]
(3) 计算每个像元的均方根误差RMSE
(4) 找到RMSE图像中值最大的像元,把这个像元的光谱作为新的端元光谱。
(5) 重复(2)—(4)步,进行第i次迭代,将每次迭代找到的端元光谱加入端元矩阵 S ,作为第i条端元。直到迭代次数达到上限(所需要的端元数m),或者直到第(4)步找到的端元光谱与端元矩阵 S 中光谱为同一类地物(光谱角小于给定的阈值)。
SGFS算法与IEA算法[5]的端元提取过程类似,但IEA算法从整个图像的所有像元中搜索端元,而SGFS算法仅从具有最大梯度特征的n(n+1)个像元中搜索端元,大大减少了端元搜索的像元数,因此能够大幅度提高端元提取速度。且第(1)步进行端元筛选时,由于只需要计算波段的差值和寻找最大最小值,算法简便,理论上具有较高的计算性能。
4 试验与分析
4.1 SGFS算法端元提取性能检验
为了验证SGFS端元提取算法所提取结果的准确性,将SGFS与IEA端元提取算法的结果进行比较分析。
试验数据为美国内华达州Cuprite矿区1995年 获取的AVIRIS数据,共50个波段波长范围为1.99~2.48μm,影像大小400像素×350像素,如图 2(a)所示研究区域主要有高岭石、明矾石、玉髓蛋白石、方解石、菱沸石、伊利石、布丁石等蚀变矿物[20, 21]。
图 2(b)为试验区标准矿物光谱曲线图。图 2(b)中各光谱分别为(A)明矾;(B)布丁石;(C)方解石;(D)菱沸石;(E)玉髓蛋白石;(F) 高岭石;(G) 伊利石。矿物标准光谱曲线主要用于识别算法提取结果的类别,判断端元提取结果的准确性。
由于图像主要由5种独立地物构成[21],提取过多的端元没有意义,故本试验最大提取端元数目设定为8,用SGFS与IEA这两种算法提取出的端元结果如图 3所示。
图 2(c)、(d)中,两种算法提取出的端元光谱1—7条光谱基本一致,依次为含噪声的高岭石(图 2(c)-1、2(d)-1)、高岭石(图 2(c)-2、2(d)-2)、玉髓蛋白石(图 2(c)-3、2(d)-3)、明矾石(图 2(c)-4、2(d)-4)、菱沸石(图 2(c)-5、2(d)-5)、方解石(图 2(c)-6、2(b)-6)、伊利石(图 2(c)-7、2(d)-7)。而第8条光谱(图 2(c)-8与2(d)-8)有较大差异。
通过分析,IEA提取出的第8条光谱图(2(c)-8)为混合像元光谱,SGFS第8条光谱图(2(d)-8)为布丁石光谱。图 3为布丁石标准光谱与两种算法提取出的第8条光谱对比。
对于试验区影像,IEA算法仅能识别出6种端元,而本文的SGFS算法能识别出7种端元,表明SGFS算法相比IEA算法,对端元的识别能力更强。这主要是因为在SGFS算法第1步的基于梯度特征筛选中剔除了不可能为端元的光谱,避免了非端元光谱参与第2步的端元识别。
4.2 SGFS算法的速度与影像大小的关系
本节主要测试算法从不同样本数的影像中提取端元的速度。试验数据为江苏某地区2012年12月获取的OMIS数据(共128个波段,最大光谱分辨率10nm,波长范围0.45~12.29μm),影像大小7000像素×750像素,如图 4所示。
图 5为试验区OMIS数据的局部放大图,从图中可见数据有较多种类的地物,可从中提取多种地物端元。
选取了ECHO算法和IEA算法与本文的SGFS算法进行对比。图 6是分别利用3种算法进行端元提取的时间消耗对比。其中测试波段为50,共识别5个端元。
图 6是IEA、ECHO、SGFS 3种算法从不同大小的影像中提取端元时的时间消耗。由图 6可知,3种算法消耗的时间与影像大小成正比关系。相比IEA和ECHO算法,SGFS算法所消耗的时间大幅度减少。且随着影像的像元数的增加,IEA与ECHO算法的时间消耗增长很快,而SGFS算法的时间增长较慢。
随着训练样本数的增大,SGFS算法效率的优势性越来越明显,表明SGFS算法对于大数据量的影像端元提取具有优异的性能。
4.3 SGFS算法的速度与端元数的关系
用4.2节的OMIS数据进行测试,选取的测试数据大小为7000像素×750像素,波段数为50。分别提取4、8、12、16、20、24、28个端元,统计3种算法消耗的时间。
图 7是IEA、ECHO、SGFS 3种算法提取不同端元数与消耗的时间的关系。由图 7可知,3种算法消耗的时间与影像大小成线性正比关系。随着提取端元数的增加,IEA和ECHO算法消耗时间大幅度增加,而SGFS算法消耗时间均很少。这主要是由于SGFS能够快速将候选端元减少为n(n+1)个,因此随着端元数的改变,计算消耗时间没有较大变化。
相比IEA和ECHO算法,SGFS计算所消耗的时间大幅度减少,且随着所要提取的端元数的增加,其速度优势更进一步凸显。这对于实际应用中大量端元的提取具有重要意义。
4.4 SGFS算法速度与波段数的关系
对4.2节的OMIS测试数据进行测试,选择大小7000像素×750像素的区域,共提取8个端元。分别选取影像上10、20、30、40、50、60、70、80、90、100、110、120个波段进行端元提取,测试算法处理不同波段数影像的性能。
图 8是IEA、ECHO、SGFS 3 种算法从影像中提取8条端元时的耗时与波段数的关系。由图可见,3种端元提取算法消耗的时间随着波段数的增加而增大。随着波段数的增加,IEA和ECHO算法消耗时间大幅度增加,而SGFS算法消耗时间的增长幅度很小。相比IEA和ECHO算法,对不同波段数的影像,SGFS计算只需消耗较少的时间,且随着影像波段数的增加,其性能优势性更进一步提升。
本文针对当前大数据量遥感影像端元提取算法耗时多的不足,提出了基于光谱梯度特征的快速端元提取算法,并对该算法进行了理论分析和试验验证,得出如下结论:
(1) 在端元的提取速度与效率上,基于光谱梯度特征的端元提取算法(SGFS算法)以影像的波段间梯度特征为搜索条件,能够快速大幅度减少候选端元的数量,因此可以大大提高端元提取速度。试验表明,随着影像大小、波段数、识别端元数的增加,相比IEA和ECHO算法,SGFS算法均具有较大的速度优势。
(2) 在端元提取的准确性上,SGFS算法具有较高的端元提取精度。这主要是因为在基于梯度特征筛选后,只保留了最佳特征光谱作为候选端元,避免了非端元光谱参与第2步的端元识别。因此具有更准确的端元识别能力。
(3) 在通用性与可靠性上,由于SGFS算法解决了端元提取所面临的大数据量瓶颈,可对其他端元提取算法进行大幅度加速,拓展了端元提取算法的应用范围与效率。
 为该候选端元的识别误差。
为该候选端元的识别误差。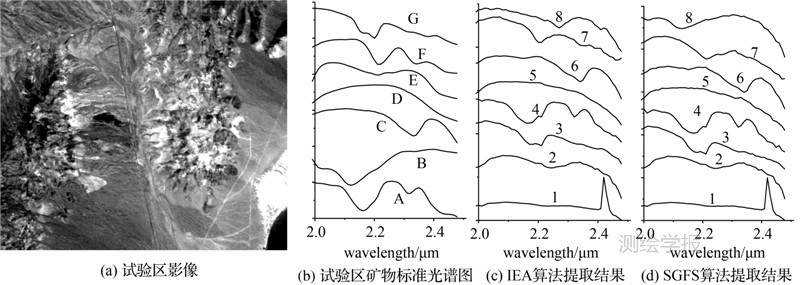
图 2 试验数据与两种算法提取出的端元结果
Fig. 2 Experimental area data and results of two algorithms 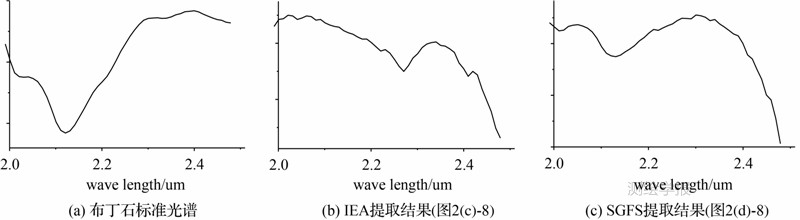
图 3 标准光谱与两种算法提取出的光谱对比
Fig. 3 Results compared with standard spectrum 
图 4 试验区OMIS数据
Fig. 4 Experimental data of OMIS 
图 5 影像局部放大图
Fig. 5 Local enlarged image of fig.4 
图 6 3种算法所耗时间与影像大小的关系
Fig. 6 Algorithm’s time consuming and image size 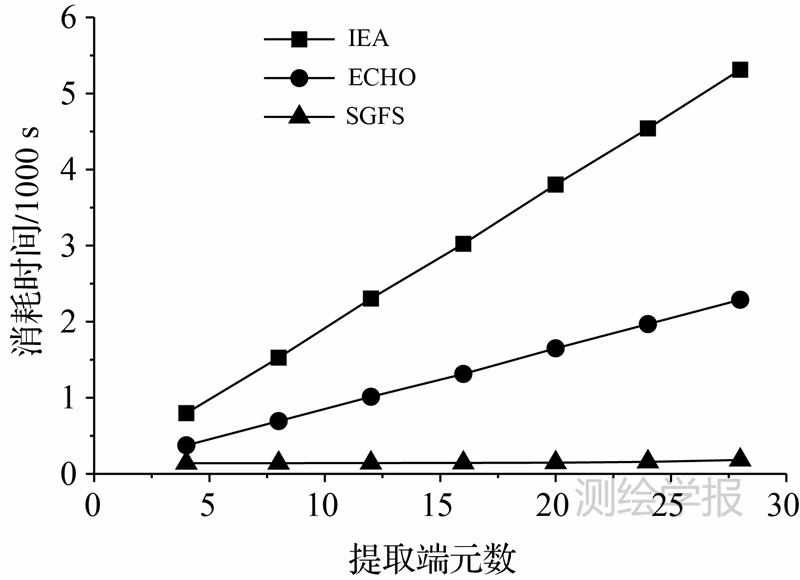
图 7 算法消耗时间与提取端元数关系
Fig. 7 Algorithm ’ s time consuming and Endmember numbers extracted 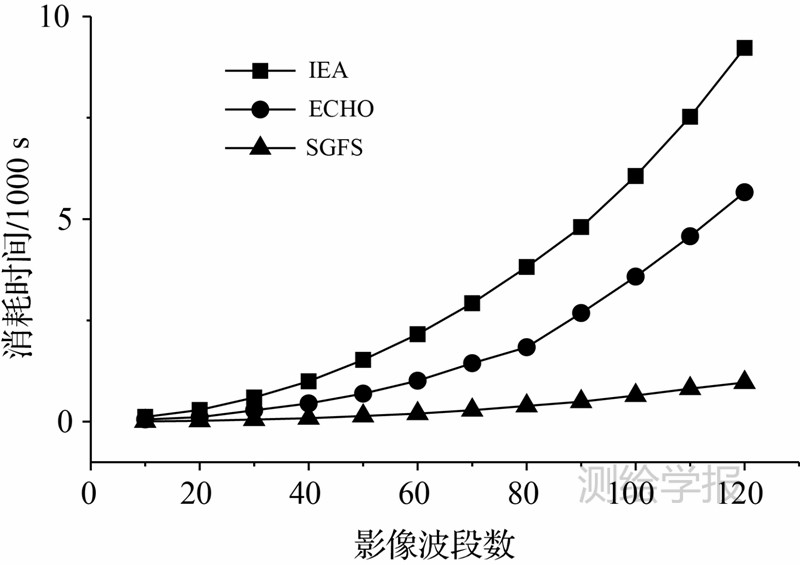
图 8 算法消耗时间与影像波段数的关系
Fig. 8 Algorithm’s time consuming and band numbers
| [1] | MIAO L D, QI H R. Endmember Extraction from Highly Mixed Data Using Minimum Volume Constrained Nonnegative Matrix Factorization [J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(3): 765-777. |
| [2] | IFARRAGUERRI A, CHANG C I. Multispectral and Hyperspectral Image Analysis with Convex Cones [J]. IEEE Transactions on Geoscience and Remote Sensing,1999, 37(2):756-770. |
| [3] | BOWLES J H , PALMADESSO P J, ANTONIADES J A, et al. Use of Filter Vectors in Hyperspectral Data Analysis[C]//Proceedings of SPIE.New York:[s.n.], 1995, 2553: 148-157. |
| [4] | BROWN M, LEWIS H G, GUNN S R. Linear Spectral Mixture Models and Support Vector Machines for Remote Sensing [J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5):2346-2360. |
| [5] | NEVILLE R A, STAENZ K, SZEREDI T, et al. Automatic Endmember Extraction from Hyperspectral Data for Mineral Exploration[C]//Proceedings of the Fourth International Air-borne Remote Sensing Conference and Exhibition/21st Canadian Symposium on Remote Sensing. Ottawa:[s.n.], 1999: 21-24. |
| [6] | PENN B S. Using Simulated Annealing to Obtain Optimal Linear Endmember Mixtures of Hyperspectral Data [J]. Computers and Geosciences, 2002, 28(7):809-817. |
| [7] | XUE Qi, KUANG Gangyao, LI Zhiyong. Endmember Extraction Algorithms from Hyperspectral Image Based on the Linear Mixing Model: An Overview [J]. Remote Sensing Technology and Application,2004,19(3):197-201. (薛绮,匡纲要,李智勇.基于线性混合模型的高光谱图像端元提取[J]. 遥感技术与应用,2004,19(3):197-201.) |
| [8] | KUMAR S MIN H A. Some Issues Related with Subpixel Classification Using Hyperion Data[C]//ISPRS XXI VII. Beijing:[s.n.], 2008:249-254. |
| [9] | ROBILA S A, MACIAK L G A. Parallel Unmixing Algorithm for Hyperspectral Images[C]//Intelligent Robots and Computer Vision XXIV.[S.l.]: SPIE Press,2006. |
| [10] | LUO Wenfei, GAO Lianru. Two-level Parallel Independent Component Analysis Endmember Extraction Algorithms [J]. Journal of Remote Sensing, 2011, 15(6): 1202-1214. (罗文斐, 高连如. 二级并行独立成分分析端元提取算法[J].遥感学报, 2011,15(6):1202-1214.) |
| [11] | PLAZA A, VALENCIA D, PLAZA J, et al. Parallel Implementation of Endmember Extraction Algorithms from Hyperspectral Data [J]. IEEE Geoscience and Remote Sensing Letters, 3(3): 334-338. |
| [12] | PLAZA A, VALENCIA D, PLAZA J, et al. Commodity Cluster-based Parallel Processing of Hyperspectral Imagery [J]. Journal of Parallel and Distributed Computing, 2005, 66(3): 345-358. |
| [13] | WANG Jie, YANG Liao, SHEN Jinxiang, et al. Two Endmember Extraction Algorithms with Combined Spatial and Spectral Domain TM Image[J]. Spectroscopy and Spectral Analysis, 2011, 31(5):1286-1290. (王杰,杨辽,沈金祥,等. 两种基于空间与光谱相结合的TM影像端元提取算法[J]. 光谱学与光谱分析, 2011, 31(5): 1286-1290.) |
| [14] | GAO Xiaohui, XIANG Libin, WEI Ruyi, et al. Research on Endmember Extraction Algorithm Based on Spectral Classification[J]. Spectroscopy and Spectral Analysis, 2011,31(7):1995-1998.(高晓惠,相里斌,魏儒义,等. 基于光谱分类的端元提取算法研究[J]. 光谱学与光谱分析, 2011, 31(7):1995-1998.) |
| [15] | ZORTEA M, PLAZA A. Spatial Preprocessing for Endmember Extraction[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009,47(8): 2679-2693. |
| [16] | ZHU Shulong, QI Jiancheng, ZHU Baoshan, et al. Fast Extraction of Endmembers from Convex Simplex's Boundary[J]. Journal of Remote Sensing, 2010,14(3): 482-492.(朱述龙, 齐建成, 朱宝山, 等.以凸面单体边界为搜索空间的端元快速提取算法[J].遥感学报,2010, 12(3):482-492.) |
| [17] | ROGGE D M, RIVARD B, ZHANG J K, et al. Iterative Spectral Unmixing for Optimizing Per-pixel Endmember Sets[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(12): 3725-3736. |
| [18] | GENG Xiurui, ZHAO Yongchao, ZHOU Guanhua. An Automatic Endmember Extraction Algorithm Using Single form Volume from Hyperspectral Image[J].Progressing Natural Science, 2006,16(9):1196-1200.(耿修瑞,赵永超,周冠华.一种利用单形体体积自动提取高光谱图像端元的算法[J].自然科学进展,2006,16(9):1196-1200.) |
| [19] | WU Bo, XIONG Zhuguo. Unmixing of Hyperspectral Mixture Pixels Based on Spectral Multiscale Segmented Features[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 205-212.(吴波,熊助国.基于光谱最佳尺度分割特征的高光谱混合像元分解[J].测绘学报,2012,41(2):205-212.) |
| [20] | RESMINI R G, KAPPUS M E, ALDRICH W S, et al. Mineral Mapping with Hyperspectral Digital Imagery Collection Experiment (HYDICE) Sensor-data at Cuprite, Nevada, USA[J]. International Journal of Remote Sensing,1997, 18(7): 1553-1570. |
| [21] | WU Bo, ZHANG Liangpei, LI Pingxiang. Automatic Extraction of Endmember from Hyperspectral Imagery by Iterative Unmixing[J]. Journal of Remote Sensing,2005, 9(3):286-293.(吴波, 张良培, 李平湘. 高光谱端元自动提取的迭代分解方法[J].遥感学报,2005,9(3):286-293.) |