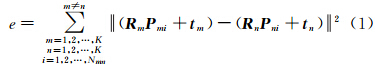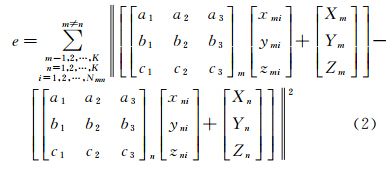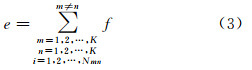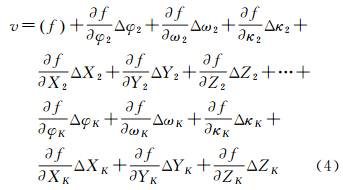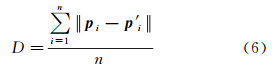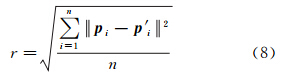2. 武汉大学 遥感信息工程学院,湖北 武汉 430079
2. School of Remote Sensing and Information Engineering, Wuhan University, Wuhan 430079, China
近年来,三维激光扫描测量技术发展迅速,在逆向工程、工业测量、文物数字化保护等方面得到了广泛的应用[1,2]。在实际应用中,为了获取物体表面完整的三维点云需要对被测物体进行多角度扫描,进而需要将多视激光点云配准到统一的坐标系中,所以配准精度会直接影响物体最终的三维重构精度[3]。因此对初始配准后的三维激光点云进行全局优化整体配准将具有十分重要的现实意义。
计算机视觉界的相关学者对点云配准领域的研究主要集中在两视点云之间的配准,大多都基于文献[4]提出的最邻近点迭代方法(iterative closest point,ICP),通过迭代选择对应点计算满足对应点之间的距离误差最小条件的旋转平移变换矩阵[5,6]。在ICP算法的基础上,很多论文对搜索最邻近点的方法进行了改进[7,8,9,10],如提出了point-point、point-to-plane、point-to-projection等方法搜索最邻近点,文献[11]采用K-D树加快了最邻近点的查找速度。此外,文献[12]提出了基于彩色三维扫描数据的配准方法,主要在ICP算法中考虑三维扫描点的纹理色彩信息进行搜索最邻近点。文献[13—14]提出了基于曲率的点云数据配准算法,并结合改进的ICP算法对点云进行精确配准。但以上这些算法都局限于两视点云之间的两两配准。
在多视三维激光点云整体配准领域的研究主要集中在依赖仪器的配准和半自动配准方面[15]。文献[16]提出一种激光扫描多视三维点云的全自动无缝镶嵌算法,应用闭合条件约束的整体平差模型,实现了激光扫描仪多视三维点云的全自动无缝镶嵌,但该方法只适用于特定硬件设备获取的360°闭合有序的多视三维点云,对于覆盖物体表面局部区域或散乱无序的多视点云全局优化不适用。文献[17]提出一种针对旋转平台获取三维 扫描点云数据的配准方法,能够实现将多视三维扫描数据自动配准到统一的坐标系中,配准精度与ICP配准或标志点配准精度相当。该方法自动化程度高,但需要借助旋转平台获取物体表面的三维点云数据,同时需要标定旋转平台与扫描仪之间的相对位置关系,因此适用性相对较低。文献[18—19]提出一种基于光束法区域网平差的地面激光扫描多站点云自动定向方法和整体定向平差模型,该方法通过标靶的布设以及标靶的自动探测和重复标靶的识别,实现全区域多站激光点云自动配准。文献[20]提出一种基于序列迭代的多视点云三维配准方法,该方法有效抑制了序列配准的累积误差,但是配准过程中人工操作比较多,因而还必须进一步研究全局性、自动化的多视点云配准方法。
本文为了提高物体表面三维模型的重构精度,提出一种多视激光点云全局优化整体配准算法。该算法是在已知多视激光点云配准初值的基础上,通过估计点云的密度,自动检测所有具有一定重叠度的两视点云,然后利用K-D树[21]搜索具有一定重叠度两视点云中的近似同名点,并将其作为观测值代入到全局优化平差模型中,通过迭代平差计算,获得多视激光点云各自最优的旋转平移变换参数,从而完成多视角三维激光点云的整体精确配准。 2 多视角三维激光点云配准全局优化平差模型的建立
假设对一个物体表面进行多视角扫描,共获取 K个视角的三维点云,并且假定这K个视角的三维点云之间具有一定的重叠区域,同时K个视角点云已经过初始配准统一到同一个坐标系中。初始配准以后,为了进一步提高三维模型整体的配准精度,需要进行多视点云全局优化整体配准。全局优化的目的是确定旋转平移参数Ri、ti(i=1,2,…,K),使得整体配准误差e最小,如式(1)所示。
式中,m、n分别表示第m个视角和第n个视角的点云,即多视点云的视角序号;K表示多视三维点云的数量,即共有K个视角的点云;Nmn表示第m个视角点云和第n个视角点云重叠区域中的近似同名点对的数量;Pmi、Pni代表第m个视角点云和第n个视角点云中第i对近似同名点;Rm、tm分别表示将第m个视角的点云转换到基准坐标系下的旋转矩阵和平移向量;Rn、tn分别表示将第n个视角的点云转换到基准坐标系下的旋转矩阵和平移向量。式(1)中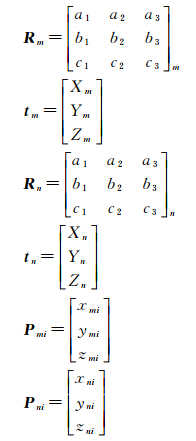
将Rm、tm、Rn、tn、Pmi、Pni代入式(1)中,得到
将式(2)简化后写成假定将第一个视角的点云所在的坐标系作为基准坐标系,那么第一个视角点云的旋转平移参数为已知量,不参与平差迭代计算,即旋转矩阵为3×3的单位矩阵,平移向量为3×1的零向量。因此对初始配准后的点云进行全局优化的过程即同时求解未知参数φi、ωi、κi、Xsi、Ysi、Zsi (i=2,3,…,K)的过程,未知参数可用近似值加相应的改正数Δφi、Δωi、Δκi、ΔXsi、ΔYsi、ΔZsi i=2,3,…,K 表示。利用泰勒公式对式(3)进行线性展开,得到线性化误差方程式如式(4)
式中,(f)是使用各未知数的近似值代入式(3)后计算得到的具有一定重叠度的两视点云中某一对近似同名点距离的平方值。对于多视点云重叠区域中的任一对近似同名点,均可列出如下误差方程 式中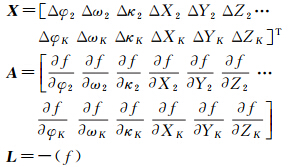
由于旋转矩阵是由3个旋转角的9个方向余弦值组成[22],结合式(2),经推导可以得到误差方程式中各偏导数的值。限于篇幅,各项偏导数的表达式从略。多视激光点云配准全局优化平差模型(式(5))为典型的间接平差模型,利用多视点云重叠区域中的近似同名点即可通过最小二乘法获得多视点云各自的旋转平移变换参数。 3 算法实现
在经过初始配准后的多视点云的基础上,本文提出一种多视点云全局优化整体配准算法。首先估计三维点云的密度,然后自动检测多视三维点云中所有具有一定重叠度的两视点云,最后采用K-D树搜索重叠区域的最邻近点对作为近似同名点对,代入到平差模型中整体解算多视点云之间的坐标系变换参数。算法的详细实现步骤如下:
(1) 对一个物体表面进行多视角扫描,假定共获取有K个视角的三维点云,并且相互之间具有一定重叠区域,对具有一定重叠区域的两视点云可以通过手工选取同名点的方式进行两两配准,直到将K个视角的三维点云都变换到同一个坐标系中,或通过配准软件将K视角三维点云初步统一到同一个坐标系中。
(2) 估计多视角三维点云的密度D。这里假定多视角三维点云是使用同一种扫描手段获取的,因此认为K个视角的点云密度基本相同,以其中一个视角点云为例来介绍点云密度估计的方法:
如果点云数量较大,则可以通过间隔采样方式在点云中获取采样点;否则可以取点云中所有的点作为采样点。遍历采样点pi,通过K-D树搜索每个采样点在点云中的最邻近点p′i,并计算两者之间的距离,最后计算所有采样点到各自最邻近点距离的平均值即为点云密度,其计算公式如式(6)
式中,n为采样点的数量。(3) 遍历经过粗配准后的K视三维点云,自动检测所有具有一定重叠度的两视三维点云,并将点云序号保存至动态数组中,具体检测方法如下:①定义一个二维动态数组I,将第一维大小设置为K-1;②从第2视角到第K视角点云中,检测与第1视角点云具有一定重叠度的三维点云,并将点云视角序号依次保存到I[0]中;③从第3视角到第K视角点云中,检测与第2视角点云具有一定重叠度的三维点云,并将点云视角序号依次保存到I[1]中;④依次类推,直到检测第K视角点云与第K-1视角点云是否具有一定重叠度,若有一定重叠度则将视角序号K保存到I[K-2]中。
本文中计算两视点云重叠度的方法定义如下:
假设两视点云中的三维点的数量分别为m和n,遍历其中一个点云中的三维点,在另外一个点云中搜索与该三维点最邻近的点,如果这两点之间的距离小于一定阈值(阈值一般为3倍点云密度)时,则定义该两点为近似同名点。利用K-D树检测该两视点云中所有的近似同名点,并假定其数量为N,则该两视点云的重叠度W计算公式如下
考虑到重叠度对配准精度的影响,本文中定义当W>0.2时,则判断该两视点云具有一定的重叠度。根据以上的描述,对于图 1所示的多视角三维点云,自动检测得到的重叠度动态数组如图 2所示。其中点云1表示第1视角的点云,以此类推,点云4表示第4视角的点云。
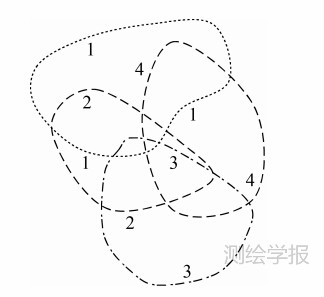 |
| 图 1 多视角点云覆盖范围分布图 Fig. 1 Coverage maps of multi-view point cloud |
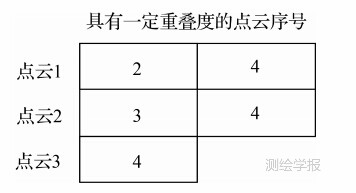 |
| 图 2 重叠度动态数组 Fig. 2 Dynamic arrays of overlap |
从重叠度动态数组中可以看出,与点云1具有一定重叠度的是点云2和点云4;与点云2具有一定重叠度的是点云3和点云4;与点云3具有一定重叠度的是点云4。实际上图 1中显示的点云3和点云1也有部分重叠区域,但由于重叠度W<0.2,不满足上述提出的具有一定重叠度的条件,所以判断点云3与点云1不具有一定的重叠度。
(4) 由步骤(3)可以检测出K视角点云中所有具有一定重叠度的两视点云,然后利用K-D树搜索这些具有一定重叠度的两视角点云中的近似同名点对,并将这些近似同名点对作为观测值代入误差方程式(4)中参与平差计算。
从第2节的分析知道,假定将第一个视角的点云所在的坐标系作为基准坐标系,则 K视点云全局优化配准的过程就是求解未知数φi、ωi、κi、Xsi、Ysi、Zsi(i=2,3,…,K)的过程。由于全局优化之前K视角点云是经过了粗配准被初步统一在同一个坐标系中,所以在第一次迭代平差时,可以将未知数φi、ωi、κi、Xsi、Ysi、Zsi(i=2,3,…,K)的初始近似值设定为0。经过第一次平差后,得到未知数的改正数Δφi、Δωi、Δκi、ΔXsi、ΔYsi、ΔZsi (i=2,3,…,K),分别加上对应未知数的近似值后作为下一次迭代新的近似值,经过循环迭代,直到迭代次数达到给定的最大值或未知数改正数小于给定限差后,整个平差过程结束。
步骤(4)中,有几点需要指出的是:
(1) 在平差过程中,对于具有一定重叠度的两视点云中近似同名点对的确定方法是,考虑到多视点云初始配准结果的精度有限,因此在前3次迭代中若两最邻近点距离小于3D(3倍点云密度)时就认为是近似同名点;经过3次迭代平差后,多视点云的配准结果整体得到优化,因此在第3次以后的迭代中,两个最邻近点之间距离满足 小于nD(1<n<2)的条件,即认为是近似同名点。其中,n为经验值,值的大小对应着搜索得到的近似同名点数量的多少,本文试验中,n取值为1.5。
(2) 由于每次循环迭代后,多视点云都会得到各自新的旋转平移参数,因此每次迭代平差过程中的观测值(即两视点云中的近似同名点)都需要重新进行计算获取,从而造成计算量较大。另外,近似同名点对数量越多即误差方程个数越多,误差方程规模也会越大。因此为了适当降低计算量以及误差方程的规模,本文采取的方法是,对于具有一定重叠度的两视点云,在其中一个点云中通过间隔采样点,利用K-D树在另一个点云中搜索该采样点的近似同名点。间隔采样的程度根据两视点云的重叠度和点的数量来确定。
(3) 迭代终止条件的确定。本文试验中迭代次数设定的最大值为50次,旋转角参数的改正数限差设定为0.1′(3×10-5弧度),平移参数的改正数限差设定为D/5。
综上所述,本文提出的多视角三维点云全局优化配准算法的具体实现流程如图 3所示。
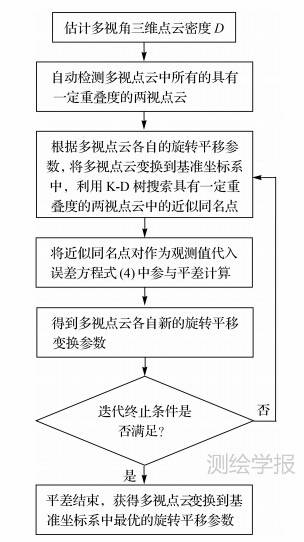 |
| 图 3 多视三维点云全局优化配准算法流程图 Fig. 3 Flow chart of global optimization registration algorithm of multi-view 3D point cloud |
为了验证本文方法的有效性,利用武汉大学数字摄影测量与计算机视觉研究中心提供的三维激光扫描仪扫描得到的一组玩偶模型数据进行试验和分析。利用激光扫描仪对玩偶模型扫描共获得8个视角的三维扫描数据,如图 4所示。
 |
| 图 4 玩偶模型多个视角的三维点云数据 Fig. 4 Multi-view 3D point cloud data of doll model |
对扫描数据进行了两组试验,并对结果进行比较分析。第1组试验,对具有一定重叠区域的两视点云手动选取3对及以上同名点,计算初始刚体变换参数,然后利用ICP算法实现两视点云的精确配准,通过这种两两配准的方法将所有扫描数据变换到同一个坐标系中。第2组试验,应用本文提出的多视点云全局优化配准算法,进行整体平差后解求出各视角三维点云的变换参数,再根据解算出的变换参数将所有扫描数据统一到同一个坐标系中,全局优化配准后的点云模型见图 5。
 |
| 图 5 全局优化整体配准后的点云模型 Fig. 5 Point cloud model after global optimization registration |
为了定量比较这两组试验结果,通过计算多视点云重叠区域的最邻近点对距离平方和的平均值的平方根,作为整体配准后的距离中误差用于评估多视点云间的配准精度[17,23]。假设近似同名点对用pi和p′i表示,近似同名点的总数量用n表示,则配准距离中误差r的计算公式为
根据距离中误差计算公式,第1组试验得到的配准中误差为0.41 mm,第2组试验得到的配准中误差为0.18 mm;经计算得到玩偶三维扫描数据的点云密度为0.28 mm。试验结果表明,全局优化整体配准精度要明显优于使用ICP算法进行两两点云配准的精度。另外从试验结果还可以看出,全局优化配准中误差近似为0.6倍点云密度,因此全局优化整体配准的精度比较理想。
在算法迭代收敛方面,为了使本文提出的整体配准算法和ICP算法的迭代收敛情况具有可比性,两种算法均采用点与点间欧氏距离最近来搜索近似同名点,同时在 两种算法中设置相同的迭代终止条件(见算法实现步骤(4)中的说明(3))。 另外考虑到ICP算法一般都应用于两视点云的精确配准中,故设计如下试验:取8个视角点云中的任意两视具有一定重叠度的点云(第1视角和第4视角点云),使用本文算法进行配准,共迭代11次满足平差终止条件,3个平移参数改正数收敛较快(第5次迭代时已收敛),3个旋转角参数的改正数迭代后期收敛相对较慢(第7次迭代时3个旋转角参数的改正数绝对值都小于5×10-5,而本文中设定的限差为3×10-5);使用ICP算法对该两视点云进行配准,同样共迭代了11次满足了迭代终止条件。从上述两视点云配准的迭代试验可以看出整体配准算法和ICP算法的迭代收敛效率基本相当。
在算法运行效率方面,由于ICP算法每次只能实现两视点云的精确配准,通过两两配准的方法将所有扫描数据变换到同一个坐标系中,因此8个视角点云的配准至少需要经过7次ICP算法的两两配准。统计这7次ICP算法运行的时间(没有统计人工选取具有重叠区域的两视角点云所需的时间),总耗时为81 s。应用本文提出的多视点云整体配准算法,共需要93 s。由于整体配准算法和ICP算法的迭代收敛效率基本相同,而前者所耗费的时间稍大于后者,究其原因在于整体配准算法需要程序自动估计多视点云中所有的具有一定重叠区域的两视点云,另外在整体平差过程中需要搜索所有具有一定重叠区域的两视点云中的近似同名点,因此对具有多度重叠区域的多视角点云来说,整体配准算法则比ICP两两配准方法相应增加了搜索近似同名点的时间。 全局优化配准过程的各项参数指标见表 1所示。
| 模型 | 视角数 | 三维点数量 | 点云密度/mm | 迭代次数 | 配准中误差/mm | 耗时/s |
| Doll | 8 | 1 347 506 | 0.28 | 13 | 0.18 | 93 |
本文介绍了一种已知多视激光点云配准初值进行自动全局优化的精确配准算法,并详细推导了多视激光点云全局优化整体平差模型,给出了算法详细的实现步骤,获得了最小二乘意义下的最优变换参数。最后通过试验证明了本文方法的可行性和有效性,实现了多视角三维激光点云的整体精确配准。文中提出的整体配准算法至少需要两视角点云,即算法适用于两视角及以上视角点云的配准,对两视点云之间的配准,整体配准算法相比于经典的ICP算法精度基本相当,对具有多度重叠区域的多视角点云,从试验结果可以看出本文方法的配准精度较ICP算法有较大的提高。
多视角三维激光点云整体配准算法相对于ICP两两精确配准算法,优点是能够自动地对散乱无序的扫描点云进行整体精确配准,配准精度较ICP算法有较大的提高,同时减少了人工搜寻具有重叠区域的两视点云的过程;缺点是整体配准算法需要自动估计所有具有一定重叠区域的两视点云,另外在整体平差过程中需要搜索所有具有一定重叠区域的两视点云中的近似同名点,因此在计算效率上稍低于ICP两两精确配准算法。未来的研究侧重于实现GPU并行化处理,进一步提高多视角三维点云全局优化整体配准算法的效率。
| [1] | ZHENG Li. 3D Measurement of Irregular Sheetmetal Parts Based on Structured Light[D]. Wuhan: Wuhan University, 2007.(郑莉. 基于结构光的不规则钣金件三维量测[D]. 武汉:武汉大学, 2007.) |
| [2] | ZHAI Ruifang, ZHANG Jianqing. Automatic Registration of Point Clouds Based on Laser Scanner[J]. Geospatial Information, 2004, 2(6): 37-39.(翟瑞芳, 张剑清. 基于激光扫描仪的点云模型的自动拼接[J]. 地理空间信息, 2004, 2(6): 37-39.) |
| [3] | LISK A C, SABLATNING R. Adaptive 3D Acquisition Using Laser Light[C]//Proceedings of Czech Pattern Recognition Workshop.Praha: [s.n.], 2000:111-116. |
| [4] | BESL P J, MCKAY N D. A Method for Registration of 3D Shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(2): 239-239. |
| [5] | NATASHA G, LESLIE I, RZYMON R, et al. Geometrically Stable Sampling for the ICP Algorithm[C]//Proceedings of International Conference on 3D Digital Imaging and Modeling. Banff: [s.n.], 2003: 260-267. |
| [6] | ZHENG Dehua, YUE Dongjie, YUE Jianping. Geometric Feature Constraint Based Algorithm for Building Scanning Point Cloud Registration[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 465-468.(郑德华, 岳东杰, 岳建平. 基于几何特征约束的建筑物点云配准算法[J]. 测绘学报, 2008, 37(4): 465-468.) |
| [7] | CHEN Y, MEDIONI G. Object Modeling by Registration of Multiple Range Images[J]. Image and Vision Computing, 1992, 10: 145-155. |
| [8] | BERGEVIN R, SOUCY M, GAGNON H, et al. Towards a General Multi-view Registration Technique[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1996, 18(5): 540-547. |
| [9] | RUSINKIEWICZ S, LEVOY M. Efficient Variants of the ICP Algorithm[C]//Proceedings of Third International Conference on 3-D Digital Imaging and Modeling. Piscataway: IEEE.2001:145-152. |
| [10] | PARK S Y, SUBBARAO M. An Accurate and Fast Point-to-plane Registration Technique[J]. Pattern Recognition Letters, 2003, 24: 2967-2976. |
| [11] | ZOU Jixiang. The Research of Point Cloud Data Registration Technique Based on KD-tree Acceleration[D]. Hefei: Anhui University, 2013.(邹际祥. 基于KD-tree加速的点云数据配准技术研究[D]. 合肥: 安徽大学, 2013.) |
| [12] | JOHNSON A E, KANG S B. Registration and Integration of Textured 3D Data[J]. Image and Vision Computing, 1999, 17: 135-147. |
| [13] | LU Yinbei, ZHANG Lei, PU Jiexin, et al. Curvature-based Registration Algorithm of Point Clouds Data[J]. Computer Applications, 2007, 27(11): 2766-2768.(路银北, 张蕾, 普杰信, 等. 基于曲率的点云数据配准算法[J]. 计算机应用, 2007, 27(11): 2766-2768.) |
| [14] | QIAN Pengpeng, ZHENG Dehua. A New Automatic Registration Method of Scanning Point Cloud[J]. Journal of Water Resources and Architectural Engineering, 2013, 11(3): 162-165.(钱鹏鹏, 郑德华. 一种新的扫描点云自动配准方法[J]. 水利与建筑工程学报, 2013, 11(3): 162-165.) |
| [15] | DAI Jinglan, CHEN Zhiyang, YE Xiuzi. The Application of ICP Algorithm in Point Cloud Alignment[J]. Journal of Image and Graphics, 2007, 12(3): 517-521.(戴静兰, 陈志杨, 叶修梓. ICP算法在点云配准中的应用[J]. 中国图象图形学报, 2007, 12(3): 517- 521.) |
| [16] | ZHANG Jianqing, ZHAI Ruifang, ZHENG Shunyi. Automatic Seamless Registration of 3D Multiple Range Views[J]. Geomatics and Information Science of Wuhan University, 2007, 32(2): 100-103. (张剑清, 翟瑞芳, 郑顺义. 激光扫描多三维视图的全自动无缝镶嵌[J]. 武汉大学学报: 信息科学版, 2007, 32(2): 100-103.) |
| [17] | ZHOU Langming, ZHENG Shunyi, HUANG Rongyong. A Registration Algorithm for Point Clouds Obtained by Scanning Objects on Turntable[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 73-79. (周朗明, 郑顺义, 黄荣永.旋转平台点云数据的配准方法[J].测绘学报, 2013, 42(1): 73-79.) |
| [18] | YAO Jili, MA Ning, JIA Xiangyang, et al. Auto-registration for Terrestrial Laser Scanning Multi-stations Point Clouds with Bundle Block Adjustment Methods[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(7): 711-716. (姚吉利, 马宁, 贾象阳, 等. 光束法区域网平差的地面激光扫描多站点云自动定向方法[J]. 测绘学报, 2014, 43(7): 711-716.) |
| [19] | YAO Jili, JIA Xiangyang, MA Ning, et al. Overall Orientation Adjustment Model of Terrestrial Laser Scanning Multi-station Point Clouds[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8): 835-841. (姚吉利, 贾象阳, 马宁, 等. 地面激光扫描多站点云整体定向平差模型[J]. 测绘学报, 2014, 43(8): 835-841.) |
| [20] | LIU Jun, GENG Guohua. Sequence Iterative 3D Registration of Multi-view Point Cloud for Archaeological Site[J]. Application Research of Computers, 2011, 28(10): 3970-3973.(刘军, 耿国华. 古遗址多视点云的渐进式三维配准[J]. 计算机应用研究, 2011, 28(10): 3970-3973.) |
| [21] | MOUNT D M, ARYA S. ANN: A Library for Approximate Nearest Neighbor Searching[EB/OL]. 2010[2013-07-25]. http://www.cs.u.md.edu/-mount/ANN/. |
| [22] | ZHANG Jianqing, PAN Li, WANG Shugen. Photogrammetry[M]. Wuhan:Wuhan University Press, 2009: 28-29. (张剑清, 潘励, 王树根. 摄影测量学[M]. 武汉:武汉大学出版社, 2009: 28-29.) |
| [23] | SEITZ S M, CURLESS B, DIEBEL J, et al. A Comparison and Evaluation of Multi-view Stereo Reconstruction Algorithms[C]//Proceedings of International Conference on 3D Digital Imaging and Modeling. Banff: IEEE Computer Society, 2003: 260-267. |