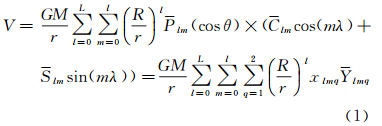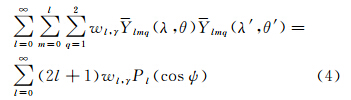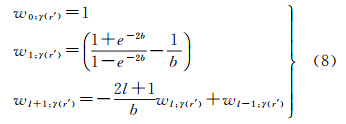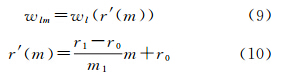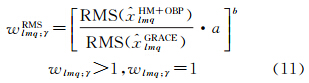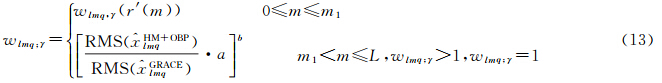2. 武汉大学 地球空间环境与大地测量教育部重点实验室，湖北 武汉 430079
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan University, Wuhan 430079, China
GRACE(gravity recovery and climate exp-eriment)[1] 卫星为地球时变重力场的研究提供了各种数据，联合其观测数据和模型数据可以量化大气圈、水圈和岩石圈之间的相互作用关系。GRACE在全球水循环及陆地水文学、两极冰盖和山岳冰川变化及质量平衡、陆地—海水质量迁移及全球海平面变化[2]、冰川均衡调整(GIA)以及地震等地球科学研究领域具有重要应用。
国内方面，文献[3]利用GRACE数据分析长江流域水储量的季节性变化，比较了水模型结果。文献[4]根据GRACE研究了全球陆地水储量的周期变化，重点分析了亚马逊流域和长江流域。文献[5]基于时变重力场反演了黑河流域的水储量变化。另外还有一些其他的流域变化GRACE探测研究结果，如文献[6,7,8]。总体上，我国目前基于GRACE反演全球或区域陆地水的周年变化，并与水模型进行比对验证的研究尚属于跟踪国际研究的水平，利用GRACE现有或可能的后续数据，精化我国主要流域水储量年际变化趋势，深化与我国水文和气象相关研究的交叉融合，提高研究水平，支持国家应对水资源和气候灾害问题，是当前我国时变重力场研究的发展趋势。
由于GRACE任务的飞行特点、传感器误差的特性以及背景模型和目前数学模型的限制，其提供的时变重力场模型球谐系数存在相关性，且随着球谐系数阶数的增加，高阶项的误差所占的比重越来越大，同时也使得GRACE模型系数误差不是简单的白噪声而是呈现“条带”噪声分布，因此采用有效的方法消除误差是最为关键的技术。
消除GRACE时变重力场模型球谐系数误差的传统经典方法是文献[9]基于文献[10]提出的各向同性高斯滤波法。但是高斯滤波存在两个主要限制：①随着平滑半径的增加，信号泄漏就越明显，从而限制了球谐系数范围的使用；②高斯平滑在空间域是各向同性的权重或者说在球谐域仅依赖于阶的权重。尽管在非常大的区域问题不是很明显，但是这些因素制约了GRACE在小区域内的应用[11]。现在也提出了很多各向异性滤波法，它们中有基于高斯滤波的思想进行改进，如文献[12]的改进高斯滤波法；也有利用给定统计准则来估计信噪比以得到最优的平滑因子，如文献[13]的RMS滤波法。文献[14—15]将GRACE月重力场解的误差协方差阵和先验信号协方差阵引入最优滤波器的设计中，通过选择不同的平滑参数得到3种不同去相关滤波方法，分别命名为DDK1、DDK2及DDK3，而最新的RL05数据又增加了DDK4和DDK5两种滤波，本文统称为DDK滤波。这些滤波方法在许多特别区域是有效的，但仍存在许多不足，如处理复杂，没有综合考虑球谐系数的误差特性，也难以联合其他不同误差结构的数据。因此，本文基于上述研究的关键技术及存在的矛盾，提出一种新的各向异性组合滤波法，不仅可以有效地去相关和滤去高阶次噪声，而且可以减少信号泄漏误差，提高信噪比及保留更多有效的地球物理信号。
本文采用CSR(Center for Space Research)、GFZ(GeoForschungsZentrum Potsdam)、JPL(Jet Propulsion Laboratory)三大机构提供的2004年1月—2010年12月，时间分辨率为1个月的RL05数据，并联合相同时间段的GLDAS(Global Land Data Assimilation System)[16]、CPC(Climate Prediction Center)[17]水文模型，及JPL提供的ECCO(estimating the circulation and climate of the ocean)模型确定海水质量变化的OBP(ocean bottom pressure)数据[18]，分析球谐系数误差特性，确定各向异性组合滤波，在此基础上利用高斯滤波、改进的高斯滤波、RMS滤波、DDK滤波及各向异性组合滤波反演水储量变化，并将这几种方法得到的结果与模型结果进行比较，结果表明，各向异性组合滤波与模型值最为接近，反演结果最优。 2 各向异性组合滤波法
地球外部任意一点( r,θ,λ)的地球引力位[15,19]，都可以用球谐展开得到
式中，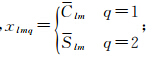
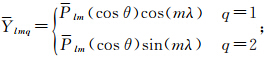
令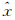
为无偏差的最小二乘估计得到的GRACE时变重力球谐系数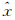；γ为平滑后的球谐系数；γ为平滑的阶数。在球谐域中，如果利用仅依赖于阶的方法平滑GEACE时变重力场模型球谐系数，可用式(2)简单地表达
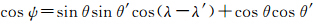；Pl为未完全规格化的Legendre多项式。
2.2 各向异性滤波法如果令权重对角矩阵Wγ既与阶有关，也与次有关，得到
得到对应于各向异性的滤波函数 在处理过程中，可以认为其为λ、θ的函数，球谐系数为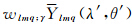
。
2.3 阶平滑-高斯滤波通常对GRACE时变重力场球谐系数处理，都是采用阶平滑-高斯滤波，其平滑函数为
式中，
为“半宽”常数，即平滑半径。高斯滤波的权重可由下面的迭代公式计算
但改变平滑函数可得到一种改进的高斯滤波，其平滑因子计算式如下[12]
式中，r0和r1为平均平滑半径。当m=0(带谐系数)，平滑半径为r0；当m=m1(非带谐系数)平滑半径为r1；当0<m<m1时，利用公式(9)进行平滑。 2.4 RMS各向异性滤波
引进陆地和海洋信噪比最大为准则的思想，可得到RMS各向异性滤波，其权重因子计算式为[13]
式中，HM为水文模型(hydrological model)；a和b为优化参数，满足准则(12)。假定GRACE测量误差在陆地和海洋上近似相同，从而得到陆地和海洋信噪比最大准则 式中，MASS为质量；Err为GRACE测量误差。当RMS_Ratio=max时，此时的a和b为最优参数。 2.5 各向异性组合滤波
本文将RMS滤波与改进的高斯滤波进行组合，即得到各向异性组合滤波法，其权重计算为公式(13)
其基本思想是将改进的高斯滤波与RMS滤波组合，在低阶项0≤m≤m1时，利用wlmq;γ=wl;γ(r′(m))进行滤波，而在高阶项m1<m≤L时，利用RMS滤波处理。
本文提出的各向异性组合滤波法，相当于分成了两次滤波。第1次，采用改进的高斯滤波，是一种近似去相关滤波，提高了低阶项的精度。第2次，高阶项采用RMS滤波，有效压制了高阶项噪声误差，保留了更多时变地球物理信号，提高了反演精度。采用不同滤波方法得到球谐系数权重因子，不同阶次对应着不同的权重因子，因此联合不同的滤波方法，可提高反演精度，但并不存在“接边”问题及由此而产生的边界效应问题。 3 时变重力场计算陆地水储量变化
基于文献[9]，得到表面质量密度变化 Δσ(θ,λ,t)为
式中，ρave为地球平均密度，等于5517 kg/m3。当以等效水高表示地球表面质量变化并进行空间平滑得到式(15)，Wlm为平滑系数，见文中第2部分。
根据式(14)，由GRACE观测误差造成的地表质量异常估计误差可表示为式(16)，其中Kl=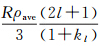 
。
由卫星观测误差引起的地表质量异常误差的全球空间方差表示为
式中，δN2是GRACE大地水准面高误差的阶方差，而且随着球谐阶数的增高而增加。由式(17)可以看出，随着球谐阶数的增高，var(σ)sat迅速增大。
利用时变重力场反演陆地水储量变化不仅受GRACE观测精度的影响，而且受其他因素影响，如冰川均衡调整(glacial isostatic adjustment,GIA)。冰川均衡调整主要指固体地球对末次盛冰期以来冰川消融及其相应海平面上升的响应[20]。相对于GRACE的运行时间(12年相比末次盛冰期12 000年)，GIA信号可以认为与时间呈线性关系[21]。在北美、北欧和极地地区，末次冰期的GIA对地球表面质量平衡的监测有重要影响。因为GRACE对质量变化的垂直方向并不敏感，很难分离由于冰盖质量变化带来重力变化信号与GIA使得质量重新分布所带来的信号(或者其他原因产生的信号)。目前，现有GIA模型及其改正均有较大的不确定性，GIA模型都是假定冰载荷历史和地幔黏度，从而产生很大的误差[22,23]，根据文献[23]可知，整个格陵兰岛的GIA改正为-8±21 km3/a，这相对于年际质量变化趋势(比GIA改正要大一个量级)几乎可以忽略不计，因此，本文给出的质量(水储量)变化速率未对GIA进行改正。 4 数值分析 4.1 数据来源和预处理
本文利用三大机构提供的2004年1月—2010年12月，总共84个月的近似月平均最高阶次为60的时变重力场模型数据，基于文献[9]确定陆地水储量变化；采用的参考场为GRACE GGM03C重力场模型，GRACE时变重力场球谐系数的低阶带谐项C20(或者J2项)的精度相对较低，这是因为GRACE的轨道几何形状对重力场的低阶项不敏感[24]，所以在本文的分析中采用卫星激光测距技术(SLR)得到的C20项替代GRACE的C20项，文献[24]表明，卫星激光测距技术得到的C20项的季节性变化比GRACE的结果要好很多，地球表面质量变化的推求需要地球重力位模型的所有球谐系数信息，但由于GRACE参考框架的原点位于地球质心，其时变重力位模型一阶项为零，为了更好地获取质量平衡信息，本文采用了ECCO海洋模型恢复的GRACE GSM-like一阶项[25]。
下文将水文模型(CPC，GLDAS)统称为HM，将CPC、GLDAS、OBP不同组合(GLDAS+OBP及CPC+OBP)统称为MODEL。本文将MODEL展开至60阶次，并与GRACE时变重力数据做相同的处理(利用SLR提供的C20项，加入一阶项，及后续的滤波处理)，进而反演以等效水高表示的水储量变化。由GRACE反演的区域陆地水储量变化值，只与HM比较。 4.2 RL05球谐系数误差特性
本文利用2004年1月—2010年12月的HM和OBP数据，联合反演得到60阶的球谐系数，计算均方差
的比值，这里RL05和MODEL都未进行任何滤波处理。
图 1表示的是不同机构(CSR、GFZ、JPL)的RL05与HM+OBP的均方差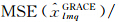
的比值。当把HM和OBP作为真值时，则最理想的情况是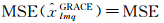
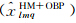，即比值为1。但由图 1得到当GRACE球谐系数大于20阶时，其比值就越来越大，表明GRACE球谐系数随着阶数的增大噪声越来越大，因此在后文研究中选取m1=15。
 |
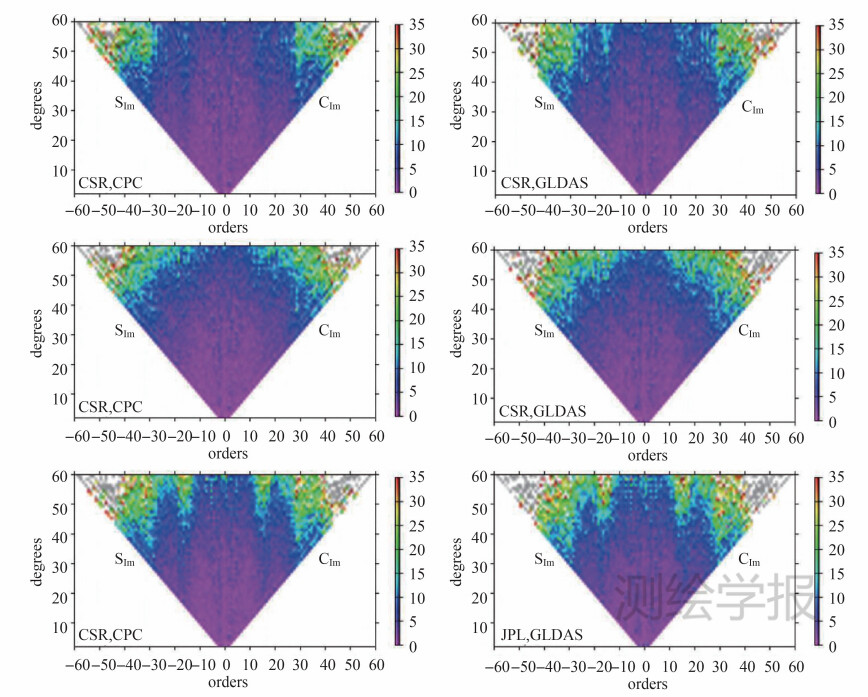| 图 1 GRACE和HM+OBP的MSE比值 Fig. 1 MSE ratios between GRACE and HM+OBP |
图 2为不同平滑半径高斯滤波作用于RL05数据后的RMS信噪比，可以得出，在平滑半径为400～1100 km时，信噪比大于1且变化很小，但当平滑半径大于1100 km时，信噪比急剧下降，说明在利用高斯平滑时平滑半径不宜过大，因此在后文研究中选取r1=1000 km。表 1为不同机构RL05数据在高斯平滑处理后的最大信噪比，得出由GFZ提供的RL05，在平滑半径为500 km时的信噪比最大，为1.339。但三大机构的信噪比差异非常小，而且最优的平滑半径为500 km(CSR的最优平滑半径为400 km，但其与500 km平滑半径所得的最大信噪比相差0.001)，因此在后文研究中选取r0=500 km。
 |
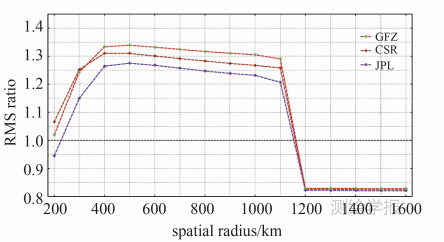| 图 2 不同平滑半径的高斯滤波信噪比 Fig. 2 RMS ratios between GRACE-observed signals over land and noise (plus signals) over the ocean as a function of the spatial radius used in Gaussian smoothing |
| 机构 | 平滑半径/km | Ratiomax |
| CSR | 400/500 | 1.311/1.310 |
| JPL | 500 | 1.275 |
| GFZ | 500 | 1.339 |
表 2为不同RL05数据与不同模型数据组合所得的各向异性组合滤波的最大信噪比。从表 2发现RL05分别与CPC+OBP、GLDAS+OBP组合，所得的最大信噪比差异很小，最大差异为0.140，其中最大信噪比为GFZ与GLDAS+OBP组合，为2.111，图 3为其不同a、b值所得的信噪比分布。
| 机构 | HM+OBP | a | b | Ratiomax |
| CSR | CPC | 1.2 | 1.6 | 2.022 |
| CSR | GLDAS | 1.6 | 1.8 | 2.019 |
| JPL | CPC | 1.2 | 1.8 | 1.976 |
| JPL | GLDAS | 1.6 | 2.0 | 1.971 |
| GFZ | CPC | 1.6 | 2.2 | 2.084 |
| GFZ | GLDAS | 1.8 | 2.2 | 2.111 |
 |
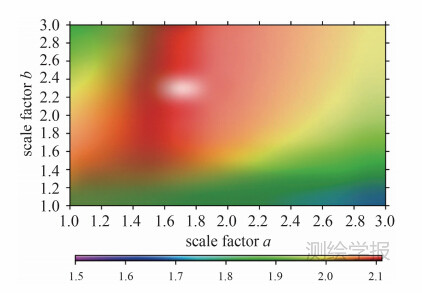| 图 3 不同a、b取值得到的信噪比值(GFZ与GLDAS+OBP组合) Fig. 3 RMS ratios by different a and b(combination the GFZ RL05 and GLDAS,OBP) |
高斯平滑所得的最大信噪比为1.339，而各向异性组合滤波所得最大信噪比为2.111，比文献[13] 得到的最大信噪比2.19略低，这是由于后者采用的数据仅为22个月，数据累积误差相对偏小。因此，各向异性组合滤波相比于高斯滤波，提高了信噪比，保留了更多有效的地球物理信号。
鉴于上述研究及文献[12]，本文最终采用各向异性组合滤波法时，选取的参数为r0=500 km，r1=1000 km和m1=15，a=1.8，b=2.2，采用GFZ与GLDAS+OBP组合。 4.4 全球变化
本文分别利用高斯滤波、改进的高斯滤波、RMS滤波、DDK滤波、各向异性组合滤波及MODEL得到1°×1°的全球水储量变化(以等效水高表示)，其中高斯滤波采用500 km的空间平滑(图 4)。
 |
| 图 4 不同滤波方法及模型得到的全球水储量变化速率 Fig. 4 The rate of global water storage change for the solutions of different filter methods注：左边：DDK(1-5)滤波；中间：RL05，(a) 平滑半径500 km的高斯滤波，(b)改进的高斯滤波，(c) RMS滤波，(d)各向异性组合滤波；右边：GLDAS+OBP，(A) 平滑半径500 km的高斯滤波，(B)改进的高斯滤波，(C) RMS滤波，(D) 组合滤波，(E) 未进行滤波处理。 |
图 4左边部分为利用DKK滤波得到的全球水储量年变化率，5种不同DKK滤波方法的效果有一定差异，从DKK1到DKK5效果是依次减弱的，而且DKK5的南北条纹仍然很明显，DKK1的效果最好。
图 4中间部分为通过不同滤波处理RL05数据后所得全球水储量年变化率，从图 4(a)可以看到经过高斯滤波处理后的结果还是存在着少许南北条纹，而图 4(b)—图 4(d)可以看到并没有南北条纹，由此可以得出，各向同性仅与阶相关的高斯滤波并不能完全去除南北条纹的误差，而需要不仅与阶相关，也与次相关的各向异性滤波，同时也说明了GRACE的误差是与其球谐系数的阶和次有关的。
比较图 4(b)、图 4(c)和图 4(d)，可以得到图 4(b)要比图 4(c)平滑，但得到海岸线的吻合度要更优；图 4(d)得到的结果要比图 4(c)平滑，海岸线的吻合度要优于图 4(b)，由此可以得出组合滤波具有改进的高斯滤波和RMS滤波的优点：有效地去相关和滤去高阶次噪声，降低信号泄漏误差。
图 4右边部分为MODEL经过不同滤波方法及未经过任何滤波方法所得的全球水储量年变化率。比较滤波图 4右边部分的(A)—(E)，发现滤波会大幅减少信号，因此如何选取最优的滤波方法尤为关键。
将模型作与GRACE相同的滤波后处理，并将模型处理后的结果作为真值进行统计分析，见表 3。由表 3得到，各向异性组合滤波得到的结果与MODEL数据结果最为吻合。因此，各向异性组合滤波法可以有效提高GRACE反演全球水储量变化的精度。
| cm/a | ||||
| 方法 | 最小值 | 最大值 | 平均值 | 中误差 |
| 高斯滤波 | -9.49 | 4.58 | -0.01 | 1.10 |
| 改进的高斯滤波 | -8.57 | 4.22 | -0.02 | 1.04 |
| RMS滤波 | -8.44 | 4.04 | -0.01 | 0.99 |
| 各向异性组合滤波 | -7.33 | 3.73 | -0.02 | 0.91 |
本文通过选取不同平滑半径的高斯滤波计算信噪比，结果表明，高斯滤波的信噪比非常小，且易受平滑半径的影响。本文利用三大机构提供的最新RL05数据与模型值组合，在最大信噪比的准则下，确定各向异性组合滤波的参数。研究表明，不同机构之间的RL05数据差异很小，该方法受水文数据的影响也很小，并得到由GFZ提供的RL05和GLDAS+OBP组合，在2004年—2010年 间的信噪比最大。
GRACE时变重力场模型存在误差，对其平滑是必不可少的，因此本文基于RL05球谐系数误差特性提出一种新的各向异性组合滤波法。这种方法不同于高斯滤波，结合了改进的高斯滤波法和RMS滤波法的特点，并具有两者的优点。
本文研究表明，利用各向异性组合滤波法相比于其他滤波方法简单，并可以有效地去除南北条带误差、减少信号泄漏误差、提高信噪比、保留更多的有效地球物理信号，进而提高GRACE反演水储量变化的精度。各向异性组合滤波法受制于先验信息，如地球物理模型、统计准则等，在参数选取上存在不确定性，对于其有效性和适应性仍需作进一步的研究。
本文提出的各向异性组合滤波法可进一步联合去相关滤波[27,28]技术，去相关滤波是处理GRACE时变大地水准面模型数据、获取地表质量变化信息的主要一环，同时可考虑比较结合扇形滤波方法[29](为另一种各向异性滤波)，这也是本文要作的后续研究。
致谢： 特别感谢美国空间研究中心CSR、德国波茨坦地学研究中心GFZ、美国喷气推进实验室JPL机构提供的GRACE时变重力数据。
| [1] | TAPLEY B D, BETTADPUR S, WATKINS M, et al. The Gravity Recovery and Climate Experiment: Mission Overview and Early Results[J].Geophysical Research Letters, 2004, 31:1-4. |
| [2] | YADU N, POKHRE L, HANASAKI N, et al. Model Estimates of Sea-level Change due to Anthropogenic Impacts on Terrestrial Water Storage[J]. Nature Geoscience, 2012(5):389-392. |
| [3] | HU Xiaogong, CHEN Jianli, ZHOU Yonghong. Monitoring Seasonal Changes in the Yangtze River Water Storage by GRACE Space Observations[J]. Science in China Series D Earth Sciences, 2006, 36(3): 225-232. (胡小工, 陈剑利, 周永宏.利用GRACE 空间重力测量监测长江流域水储量的季节性变化[J]. 中国科学D 辑, 2006, 36(3): 225-232.) |
| [4] | ZHOU Xuhua, WU Bing, PENG Bibo, et al. Detection of Global Water Storage Variation Using GRACE. Chinese[J].Chinese Journal of Geophysics, 2006, 49(6):1644-1650. (周旭华, 吴斌, 彭碧, 等. 全球水储量变化的GRACE卫星检测[J]. 地球物理学报, 2006, 49(6): 1644-1650.) |
| [5] | LUO Zhicai, LI Qiong, ZHONG Bo. Water Storage Variations in Heihe River Basin Recovered from GRACE Temporal Gravity Field[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5):676-681. (罗志才, 李琼, 钟波.利用GRACE时变重力场反演黑河流域水储量变化[J]. 测绘学报, 2012, 41(5): 676-681.) |
| [6] | DUAN Jianbin, ZHONG min, YAN Hanming, et al. Recovery of Land Water Storage Variations in Chinese Mainland by Use of GRACE Data[J]. Journal of Geodesy and Geodynamics, 2007, 27(3): 68-71. (段建宾, 钟敏, 闫昊明, 等, 利用重力卫星观测资料解算中国大陆水储量变化[J]. 大地测量与地球动力学, 2007, 27(3): 68-71.) |
| [7] | ZHU Guangbin, LI Jiancheng, WEN HanJiang, et al. Study On Variations of Global Continental Water Storage With GRACE Gravity Field Models[J]. Journal of Geodesy and Geodynamics, 2008, 28(5): 39-44. (朱广彬, 李建成, 文汉江,等. 利用GRACE时变重力位模型研究全球陆地水储量变化[J]. 大地测量与地球动力学, 2008, 28(5): 39-44.) |
| [8] | ZHAI Ning, WANG Zeming, WU Yue, et al. Recovery of Yangtze River Basin Water Storage Variations by GRACE Observations[J]. Geomatics and Information Science of Wuhan University, 2009, 34(4): 436-439.(翟宁, 王泽民, 伍岳, 等. 利用GRACE 反演长江流域水储量变化[J]. 武汉大学学报:信息科学版, 2009, 34(4): 436-439.) |
| [9] | WAHR J, MOLENAAR M, BRYAN F. Time Variability of the Earth's Gravity Field: Hydrological and Oceanic Effects and Their Possible Detection Using GRACE[J]. Journal of Geophysical Research, 1998,103:30205-30229. |
| [10] | JEKELI C. Alternative Methods to Smooth the Earth's Gravity Field[R].Columbus:Department of Geodetic Science and Surveying. Ohio State University,1981. |
| [11] | SWENSON S, WAHR J. Methods for Inferring Regional Surfacemass Anomalies from Gravity Recovery and Climate Experiment (GRACE) Measurements of Time-variable Gravity[J]. Journal of Geophysical Research, 2002, 107(B9):1-27. |
| [12] | HAN S C, SHUM C K, JEKELI C, et al. Non-isotropic Filtering of GRACE Temporal Gravity for Geophysical Signal Enhancement[J].Geophysical Journal International, 2005, 163:18-25. |
| [13] | CHEN J L, WILSON C R, SEO K. Optimized Smoothing of Gravity Recovery and Climate Experiment (GRACE) Time-variable Gravity Observations[J]. Journal of Geophysical Research, 2006,DOI:10.1029/2005JB004064. |
| [14] | KUSHE J. Approximate Decorrelation and Non-isotropic Smoothing of Time-variable GRACE-type Gravity Field Models[J].Journal of Geodesy, 2007, 81:733-749. DOI:10.1007/s00190-007-0143-3. |
| [15] | KUSHE J, SCHMIDT R, PETROVIC S,et al. Decorrelated GRACE Time-variable Gravity Solutions by GFZ, and Their Validation Using a Hydrological Model[J]. Journal of Geodesy, 2009,83(10):903-913. |
| [16] | RODELL M, HOUSER P R, JAMBOR U, et al. The Global Land Data Assimilation System[J]. Bulletin of the American Meteorological Society, 2004,85 (3):381-394. |
| [17] | FAN Y, VANDE H, MITCHELL K, et al. A 51-Year Reanalysis of the US Land-surface Hydrology [J]. GEWEX News, 2003, 13(2): 6-10. |
| [18] | FUKUMORI I, RAGHUNATH R, FU L, et al. Assimilation of TOPEX/POSEIDON Data into a Global Ocean Circulation Model: How Good are the Results?[J]. Journal of Geophysical Research, 1999, 104(C11), 25647-25665. |
| [19] | HEISKANEN W A, MORTIZ H. Physical Geodesy[M].San Francisco: Freeman and Company, 1967. |
| [20] | PELTIER W R, ANDREW J. Glatial Isostatic Adjustment. I: The forward Problem[J]. Geophy. Journal of Geophysical Research, 1976, 46, 605- 646. |
| [21] | SWENSON S, WAHR J, MILLY P. Estimated Accuracies of Regional Water Storage Variations Interfered from the Gravity Recovery and Climate Experiment (GRACE)[J]. Water Resource Research, 2003, 39(8),DOI:10.1029/2002WR001808. |
| [22] | CHEN J L, WILSON C R, BLANKENSHIP D D,et al. Antarctic Mass Rates from GRACE[J]. Geophysical. Research. Letters, 2006c, 33,DOI:10.1029/2006GL026369. |
| [23] | VELICOGNA I, WAHR J. Measurements of Time-variable Gravity Show Mass Loss in Antarctica[J]. Science, 2006, 311:1754-1756,DOI:10.1126/science.1123785. |
| [24] | CHEN J L, WILSON C R, TAPLEY B D, et al. Low Degree Gravitational Changes from GRACE: Validation and Interpretation[J]. Geophy. Res. Lett, 2004, 31, DOI: 10.1029/2004G L021670. |
| [25] | CHAMBERS D P, WAHR J, NEREM R S. Preliminary Observations of Global Ocean Mass Variations with GRACE[J]. Geophysical Research Letters, 2004, 31,DOI:10.1029/2004GL020461. |
| [26] | VELICOGNA I, WAHR J. Acceleration of Greenland Ice Mass Loss in Spring 2004[J]. Nature, 2006, 443:329-331, DOI:10.1038/nature05168. |
| [27] | SWENSON S, WAHR J. Post-processing Removal of Correlated Errors in GRACE Data[J]. Geophyscial. Research Letters, 2006,33,DOI:10.1029/2005GL025285. |
| [28] | ZHAN Jingang, WANG Yong, HAO Xiaoguang. Improved Method for Removal of Correlated Errors in GRACE Data[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4):443-446.(詹金刚, 王勇, 郝晓光. GRACE时变重力位系数误差的改进去相关算法[J]. 测绘学报, 2011, 40(4):443-446.) |
| [29] | ZHANG Z Z, CHAO B F. An Effective Filtering for GRACE Time-variable Gravity: Fan Filter[J]. Geophysical Research Letters,2009, 36,L17311, DOI: 10.1029/2009GL039459. |