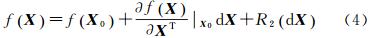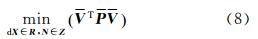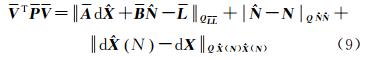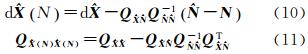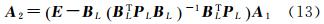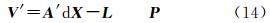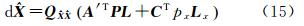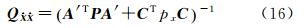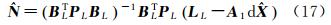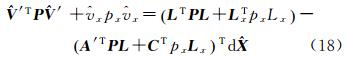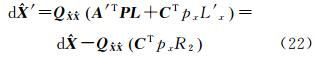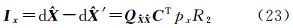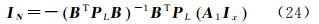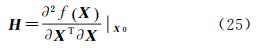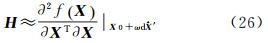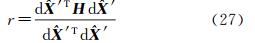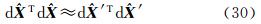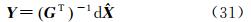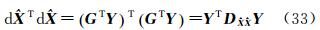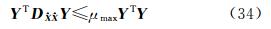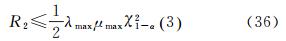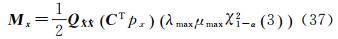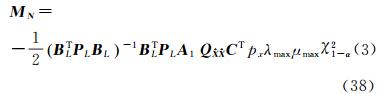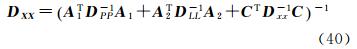2. 中国科学院 测量与地球物理研究所 大地测量与地球动力学国家重点实验室，湖北 武汉 480077
2. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy & Geophysics of CAS, Wuhan 430077, China
GNSS动态相对定位应用越来越广泛，典型的领域有姿态测量[1, 2, 3, 4]、卫星编队飞行[5, 6, 7]、变形监测[8, 9]等。对于动态相对定位，特别是单历元的动态相对定位，由于模型误差大、观测信息少以及观 测质量差之类的原因，单纯利用GNSS观测数据难以固定整周模糊度。国内外研究者常通过附加约束条件或者额外的观测量(本文中统称为约束条件)来辅助定位，基线长是常用的约束条件[1, 2, 3, 4, 10, 11]。
LAMBDA方法只能处理无约束或者线性约束的模型，而基线长是非线性约束条件，为了应用传统的LAMBDA方法进行解算，必须将非线性约束条件进行线性化近似。文献[10]将基线长约束条件线性化近似后参与模糊度浮点解的解算，同时在模糊度固定解的搜索中也将基线长作为检核条件。文献[12]在浮点解的解算中也引入了基线长线性化的约束方程，并认为对坐标的约束可以提高浮点解的精度，而对模糊度的约束可以缩小模糊度搜索空间。文献[2]发现若将基线长约束直接线性化近似参与解算，由于基线长约束条件存在固有曲率问题，只有较长的基线长约束才能提高模糊度固定成功率的效果，而且指出当GNSS伪距观测值精度提高时，基线长的限制可以更短，但文中没有给出具体的理论说明。在实践中，笔者发现有时将基线长条件线性化以后参与解算，固定模糊度成功率反而不如不加约束。原因何在？何时附加线性化的基线长约束有利于解算模糊度？本文将围绕这些问题展开探讨，首先从附加基线长约束的GNSS相对定位数学模型出发，推导了基线长约束条件线性化近似余项对浮点解的最大影响值公式，据此给出了一个基线长约束条件能否线性化近似的诊断条件，然后用算例验证了本文提出的相关结论。
1 数学模型及其解算 1.1 数学模型
GPS双差误差方程[13]
式中，V P、 V L分别为码伪距和相位伪距双差观测方程误差向量；d X∈R为基线分量改正数向量； N ∈Z为双差模糊度向量；A1、 BL为对应的系数矩阵； L P、 L L分别为码伪距和相位伪距双差观测向量。
记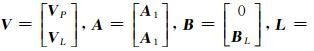 
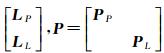，式(1)可表示为
设基线长约束条件的方程为
式中，vx为观测误差； X 为基线向量；f(·)为是基线长的函数表示；lx为基线长约束值；px为权重。
式(2)和式(3)构成了基线长约束条件下GNSS相对定位的数学模型。
1.2 模型解算
f(X)在初始值 X0处应用泰勒公式
余项表达式如下 式中，ω∈(0，1)。记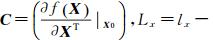
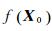，若余项可以忽略，则式(3)可表示成
记
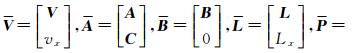
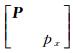，数学模型变为
在如下准则下解算
对式(8)进行正交分解[14]
式中，
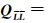
为最小二乘准则下的浮点解；
为浮点解
的协因数阵，另
为的互协因数阵，
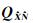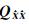为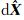
的协因数阵。显然对于任意N∈Z，式(9)右边第3项都等于0，故式(8)所述问题的求解转换为式(7)最小二乘浮点解解算和式(9)右边第2项取最小值这个准则下N整数估计这两个问题[15]。后者常采用LAMBDA方法搜索出固定解，很多文献中都已讨论[16, 17, 18]，所以本文不再赘述。式(1)中相位双差观测方程消除参数 N 的等价方程为[19]
A2可由式(13)计算
式(12)和(13)中，E为单位矩阵； UL为新的残差向量，且与式(1)中的VL有相同特性。
令 
，式(2)可转换为
综合式(6)、式(14)，可得附加约束条件的基线改正数浮点解
式中 代入原始相位双差观测方程，可得到双差模糊度的浮点解 式中，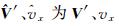
的平差值，平差以后的残差加权平方和为
单位权中误差计算式如下
r为数学模型式(7)的自由度。
估计参数协方差阵为
上述解算过程若采用Guass-Newton法，迭代停止时，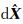
的各分量接近于0。
2 余项影响及诊断条件
令
R2为式(5)所表示的余项，将式(21)代入式(3)、式(4)，并顾及估计准则，可得到考虑余项的基线浮点解
约束条件方程线性化近似得到的基线浮点解是有偏的，偏差即基线浮点解的余项影响为
结合式(1)的相位伪距双差观测方程，可知双差模糊度浮点解的余项影响 令 当基线较长时，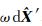
相对于X 0为一小量；而当基线较短时，X0的值本身就比较小，也可以认为 
，故
H 对应于
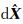'的瑞利(Rayleigh)商为
根据瑞利商的性质[20]可知
式中，λmax为H的最大特征值。
结合式(5)，可得
若采用诸如Guass-Newton等迭代法求解，迭代停止时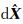，'可以认为是服从 0 向量为均值，
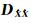为协方差阵的随机量，另
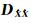的最大特征值。从式(31)可知，Y为以 0 向量为均值，单位阵为协方差阵的随机量，因此 YTY是以3为自由度的卡方分布[21]，取置信水平为1－α，有
式中，P{ ·} 为事件发生的概率。
在余项影响可以忽略的前提下，余项满足下式
则基线浮点解最大余项影响(max influence of baseline’s float solution，MIB)为
双差模糊度浮点解最大余项影响(max influence of double-difference ambiguity’s float solution，MIA)为 上式表明最大余项影响不仅与基线长、基线的方向有关，而且受GNSS观测结构和精度影响。
下面讨论什么情况下根据模糊度浮点解来固定模糊度时不受余项影响，假定采用降相关处理(Z变换)的LAMBDA方法[15, 16, 17, 18]来固定整周模糊度，令 T=Z T M N，若 T中每个元素的绝对值都小于0.1周，余项影响对模糊度取整一般就不会造成偏差，故可取诊断条件
式中，||T|| ∞表示向量 T 的无穷范数，本文称为诊断值(test value，TEV)。从上述推导过程可知，该诊断条件只是基线长约束条件可以线性化近似的一个充分条件，但它不是必要条件。
实际处理时，可以根据基线初值计算出 A1、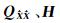
，另根据观测值和约束条件的先验精度计算出基线浮点解的精度
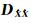。然后计算诊断值向，并测试是否满足诊断条件，如果满足，则说明假设成立；如果不满足，则说明基线长约束条件不合适通过线性化近似参与浮点解解算，此时可考虑转换参数或其他方法解算，另文再加以讨论。值得说明的是，基线初值应满足式(25)、式(26)的近似，基线较短时，应采用伪距差分解算出基线初值。3 算例分析 3.1 较长基线算例
基线GP01—GP02，长约1200 m，采样率为5 s，截取2013-5-11 2∶21∶50至2013-5-11 2∶51∶45 (GPS时间)的观测数据，该时间段内G12、G14、G18、G22、G24、G25、G31一直可见，相位观测值也没有发生周跳。选取G22(高度角最大)为参考星，利用静态解算得到的基线长1 226.009 m，L1上的双差模糊度依次为6、1、-2、-4、11、-49，L2上的双差模糊度依次为6、3、0、-4、11、44。以静态解算得到的基线长为约束条件，码伪距观测值、相位伪距观测值、基线长约束的先验精度分别取3 dm、3 mm和3 mm，根据初始值计算的双差模糊度最大余项影响随历元变化见图 1，由图可知双差模糊度最大余项影响都小于0.01周；诊断值随历元变化见图 2，显然均满足诊断条件。
 |
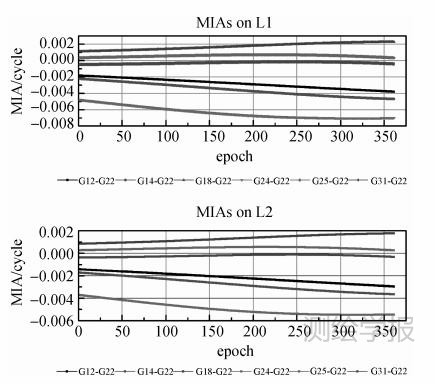| 图 1 GP01—GP02双差模糊度最大余项影响历元变化曲线Fig. 1 The change of GP01—GP02’s MIAs over epoch |
 |
| 图 2 GP01—GP02余项影响诊断值历元变化曲线Fig. 2 The change of GP01—GP02’s TEVs over epoch |
设计两种浮点解解算方案。
方案1：单纯利用GPS双频双码观测值解算。
方案2：利用GPS双频双码观测值附加基线长约束。
两种方案都采用LAMBDA方法固定模糊度，固定正确率分别为96.3%、100.0%，可见如果满足诊断条件，余项影响就可以忽略，将基线长约束条件线性化近似参与浮点解解算可以改善浮点解解算的精度，提高模糊度固定的成功率。
3.2 超短基线算例
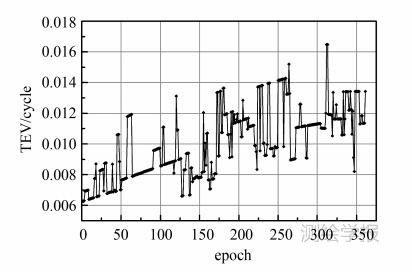
实测基线P391-P416，长约4.5 m，采样率为5 s，时间段(GPS时)：2013-3-11 7:22:40至2013-3-11 7:52:35，该时间段内可见卫星一直有G12、G14、G18、G22、G25、G31，没有发生周跳。选取G14为参考星，利用静态解算得到的基线长4.488 m，L1上的双差模糊度依次为1、-1、0、1、15，L2上的双差模糊度依次为-8、-9、-5、0、15。同样以基线长为约束条件，观测值和基线长约束的先验精度与前面一样，双差模糊度最大余项影响随历元变化见图 3，大致在周的量级，诊断值随历元变化见图 4，显然都不满足诊断条件。
 |
| 图 3 P391—P416双差模糊度最大余项影响历元变化曲线Fig. 3 The change of P391—P416 MIAs over epoch |
 |
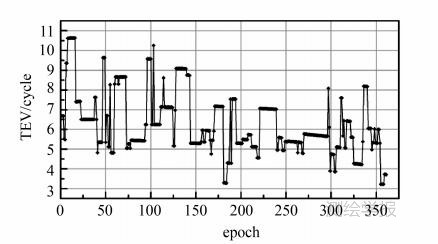| 图 4 P391—P416余项影响诊断值历元变化曲线Fig. 4 The change of P391—P416 TEVs over epoch |
采用与算例1相同的两种浮点解解算方案，模糊度固定正确率分别为100.0%、39.9%。如果诊断条件不满足时，余项影响可能会比较大，不能忽略，将基线长约束条件线性化近似参与浮点解解算会因为浮点解有偏而不能固定为正确模糊度。
3.3 基线长与诊断值的关系
为了认识双差模糊度最大余项影响及诊断值随基线长单一因素的变化情况，利用GP01—GP02第1个历元的数据算出式(38)右边除λmax之外的其他参数，固定参考站至定位站的方向(也即 C，C 实际上是参考站至定位站的单位向量，该处理旨在可以利用前面计算的参数)，用不同基线长度算出的双差模糊度最大余项影响及余项影响诊断值变化情况分别见图 5、图 6。可以看出，基线长从1 m到20 m，相应计算出来的双差模糊度最大余项影响下降很快，大约到60 m时，各双差模糊度最大余项影响都已在±0.1周以内，大致在78 m时，余项影响诊断值已满足了诊断条件。由于最大余项影响不仅与基线长、基线的方向有关，而且受GNSS观测结构和精度影响，因此其他算例中的具体数值可能会与本算例有细微差别，但总趋势应一致。
 |
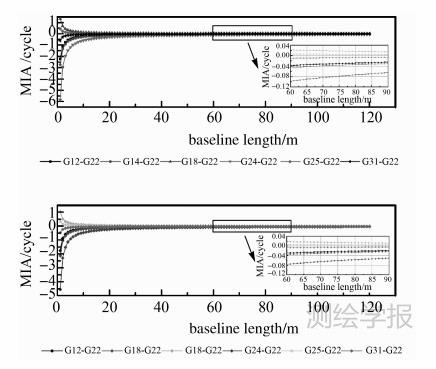| 图 5 双差模糊度最大余项影响随基线长变化曲线Fig. 5 The change of MIAs with baseline’s length |
 |
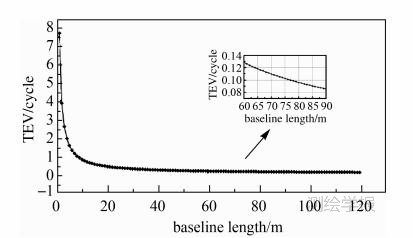| 图 6 余项影响诊断值随基线长变化曲线Fig. 6 The change of TEVs with baseline’s length |
本文基于附加基线长约束的GNSS相对定位数学模型，推导了基线长约束条件线性化近似余项对浮点解的最大影响值公式，从公式可以看出最大余项影响不仅与基线长、基线方向有关，而且受GNSS观测结构和精度影响。然后给出了一个基线长约束能否线性化近似的诊断条件，该条件是充分条件，但非必要条件。满足该条件时，线性化近似余项影响可以忽略，附加线性化近似的基线长约束可以提高浮点解解算的精度，加快模糊度的固定；若不满足，则线性化近似余项影响可能不可以忽略，附加约束会因浮点解偏差较大不能固定为正确的模糊度。文中通过相关算例验证了前述结论，此外还结合实例探究了线性化余项最大影响与基线长的变化关系，算例结果显示基线长从1 m到20 m，双差模糊度最大余项影响随之下降很快；大约到60 m时，各双差模糊度最大余项影响都已在±0.1周以内；大于78 m时均满足诊断条件，可以线性化处理基线长条件。
| [1] | WANG B, MIAO L, WANG S, et al. A Constrained LAMBDA Method for GPS Attitude Determination[J]. GPS Solutions, 2009, 13(2): 97-107. |
| [2] | TEUNISSEN P J G. Integer Least-Squares Theory for the GNSS Compass[J]. Journal of Geodesy, 2010, 84(7): 433-447. |
| [3] | TEUNISSEN P J, GIORGI G, BUIST P J. Testing of a New Single-frequency GNSS Carrier Phase Attitude Determination Method: Land, Ship and Aircraft Experiments[J]. GPS Solutions,2011, 15(1): 15-28. |
| [4] | CHEN W, QIN H. New Method for Single Epoch, Single Frequency Land Vehicle Attitude Determination Using Low-end GPS Receiver[J]. GPS Solutions, 2012, 16(3): 329-338. |
| [5] | KROES R, MONTENBRUCK O, BERTIGER W, et al. Precise GRACE Baseline Determination Using GPS[J]. GPS Solutions, 2005, 9(1): 21-31. |
| [6] | ARDAENS J S, D'AMICO S, MONTENBRUCK O. Flight Results from the PRISMA GPS-based Navigation[C]//Proceedings of the 5th ESA Workshop on Satellite Navigation Technologies. Noordwijk:[s.n.],2010:8-10. |
| [7] | MONTENBRUCK O, WERMUTH M, KAHLE R. GPS Based Relative Navigation for the TanDEM-X Mission First Fight Results[J]. Navigation, 2011, 58(4): 293-304. |
| [8] | HAN Baoming, OU Jikun. A GPS Single Epoch Phase Processing Algorithm with Constraints for Single-frequency Receivers[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(4):300-304. (韩保明, 欧吉坤. 一种附约束的单频单历元GPS双差相位解算方法[J]. 测绘学报, 2002, 31(4) : 300 - 304.) |
| [9] | YU Xuexiang,XU Shaoquan,LU Weicai.The Research of Single Epoch Algorithm for GPS Deformation Monitor Information[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(2): 123-127.(余学祥, 徐绍铨, 吕伟才. GPS 变形监测信息的单历元解算方法研究[J]. 测绘学报, 2002, 31(2): 123-127.) |
| [10] | TANG Weiming,SUN Hongxing,LIU Jingnan. Ambiguity Resolution of Single Epoch Single Frequency Data with Baseline Length Constraint Using LAMBDA Algorithm[J].Geomatics and Information Science of Wuhan University, 2005, 30(5): 444-446.(唐卫明, 孙红星, 刘经南. 附有基线长度约束的单频数据单历元LAMBDA方法整周模糊度确定[J].武汉大学学报:信息科学版, 2005, 30(5): 444-446.) |
| [11] | LI Zhenghang,LIU Wanke,LOU Yidong, et al. Heading Determination Algorithm with Single Epoch Dual-frequency GPS Data[J].Geomatics and Information Science of Wuhan University, 2007, 32(9): 753-756.(李征航, 刘万科, 楼益栋, 等. 基于双频GPS数据的单历元定向算法研究[J]. 武汉大学学报: 信息科学版, 2007, 32(9): 753-756.) |
| [12] | LI Bofeng, SHEN Yunzhong. Fast GPS Ambiguity Resolution Constraint to Available Conditions[J]. Geomatics and Information Science of Wuhan University,2009, 34(1): 117-121.(李博峰, 沈云中. 附有约束条件的GPS模糊度快速解算[J]. 武汉大学学报: 信息科学版, 2009, 34(1): 117-121.) |
| [13] | HOFMANN-WELLENHOF B, LICHTENEGGER H, WASLE E. GNSS: Global Navi-gation Satellite Systems: GPS, GLONASS, Galileo, and More[M]. Berlin:Springer, 2007. |
| [14] | SU Yucai, JIANG Cuibo, ZHANG Yuehui. Matrix Theory[M]. Beijing: Science Press, 2006. (苏育才,姜翠波,张跃辉.矩阵理论[M]. 北京: 科学出版社, 2006.) |
| [15] | TEUNISSEN P J G. The Least-squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(2): 65-82. |
| [16] | TEUNISSEN P J G, DE JONGE P J, TIBERIUS C C J M. Performance of the LAMBDA Method for Fast GPS Ambiguity Resolution[J]. Navigation, 1997,44(3): 373-383. |
| [17] | TEUNISSEN P J G. An Optimality Property of the Integer Least-squares Estimator[J]. Journal of Geodesy, 1999,73(11):587-593. |
| [18] | CHANG X W, YANG X, ZHOU T. MLAMBDA: A Modified LAMBDA Method for Integer Least-squares Estimation[J]. Journal of Geodesy, 2005, 79(9): 552-565. |
| [19] | XU Guochang. GPS Theory,Algorithms and Application[M].LI Qiang,LIU Guangjun,YU Hailiang,et al, trans. 2nd ed. Beijing: Tsinghua University Press, 2011.(许国昌.GPS理论、算法与应用[M]. 李强, 刘广军, 于海亮, 等, 译.第2版.北京: 清华大学出版社, 2011.) |
| [20] | WANG Songgui, WU Mixia, JIA Zhongzhen. Matric Inequalities[M]. 2nd ed.Beijing: Science Press, 2006. (王松桂, 吴密霞, 贾忠贞. 矩阵不等式[M]. 第2版.北京: 科学出版社, 2006.) |
| [21] | SHENG Zhou, XIE Shiqian, PAN Chengyi. Probability Theory and Mathematical Statistics[M].4th ed. Hangzhou:Zhejiang University Press, 2008. (盛骤, 谢式千, 潘承毅. 概率论与数理统计[M].第4版.杭州: 浙江大学出版社, 2008.) |