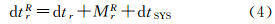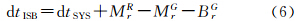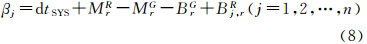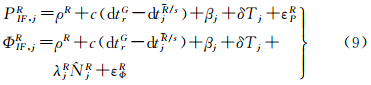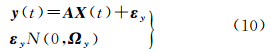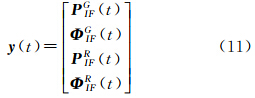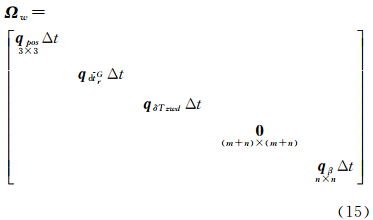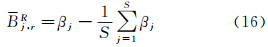2. 同济大学 测绘与地理信息学院，上海 200092
2. College of Surveying and Geo-infomatics, Tongji University, Shanghai 200092, China
1 引 言
随着GLONASS现代化进程的不断推进，截至2011年12月8日，GLONASS在轨工作卫星达24颗，已恢复系统完全运行能力。与GPS不同，当前的GLONASS系统使用频分多址(frequency division multiple access,FDMA)技术区分来自不同卫星的信号。众所周知，卫星信号在接收机内部频率通道会产生相应的硬件延迟，一般将其分为平均延迟偏差项和因通道频率而异的延迟偏差项(inter-channel bias,ICB)，后者又称为频间偏差IFB[1]。由于GLONASS采用FDMA技术，不同频率的卫星信号会进入接收机内部对应的频率通道，由此会产生不同的载波相位和码IFB。已有研究表明[2, 3, 4, 5, 6]，通过提供GLONASS相位IFB先验改正及参数估计的方法，可以提高基线解算中GLONASS整周模糊度的可靠性。近年来，基于GPS/GLONASS系统的组合PPP技术发展迅速。由于GPS与GLONASS存在系统时间基准的差异，在建立组合PPP观测方程时，一般仅估计GPS接收机钟差，同时引入一个“系统时差”(inter-system bias,ISB)参数来表征GPS和GLONASS系统时间偏差，在此称为“单参数”法[7, 8, 9, 10]。引入的“系统时差”参数将吸收接收机码平均硬件延迟，而通常在观测方程中忽略因通道频率差异引起的码IFB。在不固定整周模糊度的情况下，初始阶段PPP浮点解模糊度的收敛速度主要取决于消电离层码伪距组合观测 值，此时应考虑忽略GLONASS码IFB对伪距观测值精度的影响[11]。另外，现有的PPP模糊度固定算法一般利用Melbourne-Wübbena组合观测值估计宽巷模糊度[12, 13, 14, 15]；由于码IFB对伪距观测值的影响，GLONASS宽巷模糊度的确定变得更为困难[16, 17]。自2006年以来，越来越多的制造商进入GPS/GLONASS接收机市场。来自不同制造商的GLONASS接收机码IFB大小及变化特性如何，忽略GLONASS码IFB对组合系统PPP的收敛时间与定位精度是否有明显影响，值得进一步研究。
本文首先从GPS/GLONASS组合PPP的基本观测方程出发，分析传统“单参数”法函数模型中忽略GLONASS码IFB的不足。在此基础上，给出并推导一种基于“多参数”的GPS/GLONASS组合PPP与码IFB估计算法。通过引入多个独立的“时频偏差”参数对码IFB进行函数模型补偿，同时可实现基于单个测站的 GLONASS码IFB精确估计。最后，对来自6个GNSS设备商的11种类型GPS/GLONASS双系统接收机码IFB进行估计与相关特性分析，并探讨新算法对组合系统PPP收敛时间和定位精度的影响。
2 多参数码频间偏差估计策略 2.1 组合PPP观测方程与时频偏差卫星信号的硬件延迟偏差在卫星和接收机端都存在，且载波相位和码伪距均受其影响。若顾及卫星信号的硬件延迟，对于GPS卫星 i，其观测方程可以表示为
式中，PIF,iG、ΦIF,iG分别为码伪距和载波相位的消电离层组合观测值；dtr为接收机钟差；MrG、MiG/s、μrG及μiG/s为平均延迟偏差项；dtiG/s为GPS卫星i的钟差；BrG、BiG/s、brG及biG/s分别为GPS接收机码IFB、GPS卫星码IFB、GPS接收机相位IFB、GPS卫星相位IFB(在后续讨论中，所涉及的IFB均特指原始观测值对应IFB的消电离层线性组合值)；ρG为卫地距；δTi为对流层斜延迟；NiG为GPS卫星i对应的载波相位模糊度；εGP、εGΦ为观测噪声。
由于所有GPS卫星信号采用相同固定频率，GPS接收机码硬件延迟对所有卫星而言都是相同的，因此将被接收机钟差dtr吸收，即待估的GPS接收机钟差参数为
对应的GPS接收机相位硬件延迟扣除(MGr+ BrG)后将被相位模糊度参数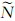
Gi吸收。在进行PPP求解时，一般采用IGS及其分析中心发布的精密卫星钟差产品，该产品由消电离层线性观测值求解得到，实际上是包含卫星码硬件延迟的卫星钟差[18]，相应的GPS卫星相位硬件延迟扣除(MG/si+BG/si)后也将由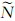Gi吸收。
对于GLONASS卫星j，其观测方程可以表示为
式(3)中与式(1)符号相同的参数含义是相同的，此处用上标R表示GLONASS系统。相应的GLONASS接收机码IFB、卫星码IFB、接收机相位IFB、卫星相位IFB分别表示为
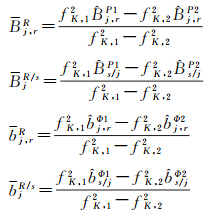
由于GLONASS接收机码IFB在不同的频率通道间存在差异，接收机钟差dtr将仅吸收GLONASS码平均硬件延迟部分。与GPS相位观测方程类似，GLONASS接收机和卫星相位硬件延迟也将由模糊度参数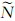Rj吸收。另外，GPS/GLONASS融合定位还必须考虑二者的系统时间偏差。它包含两方面内容：一是两个系统时间基准定义的差异；二是两个系统所采用的卫星钟差产品所对应参考时间基准的差异。若同时顾及GLONASS码平均硬件延迟和系统时间偏差，则待估的GLONASS接收机钟差参数为
式中，dtSYS为系统时间偏差项。
在以上组合PPP模型中，需估计两个接收机钟差项，即GPS接收机钟差dtGr和GLONASS接收机钟差dtrR。在实际处理中，现有文献多采用引入单个“系统时差”参数的方法[7, 8, 9, 10]，将GLONASS接收机钟差表达成GPS接收机钟差的形式，即
式中，dtISB为“系统时差”项。
比较式(2)、式(4)及式(5)，可以得到
由式(6)可知，“单参数”法引入的“系统时差”dtISB项，不仅包含系统时间偏差，还包含部分接收机通道延迟偏差。注意到式(6)中的硬件延迟偏差并未包含GLONASS接收机码IFB。对于GLONASS码伪距观测方程，BRj,r因各卫星频率间的差异而无法被接收机钟差参数吸收，最终将体现在码伪距观测值的残差中。因此，函数模型中所采用的GLONASS码伪距观测值精度要低于其实际观测精度，尤其当码IFB在数值上远大于码伪距观测值自身的噪声水平时，其对组合PPP的影响是不容忽视的。目前，一般采用在随机模型中对GLONASS伪距观测值进行降权的方法以削弱其影响[7, 8, 9, 10]。
2.2 多参数GLONASS码IFB估计针对传统“单参数”GPS/GLONASS组合PPP模型的不足，本文从函数模型角度出发，提出一种基于“多参数”组合PPP模型的GLONASS接收机码IFB补偿与估计算法。
对于GPS卫星 i，其观测方程与“单参数”法形式相同，由式(1)可得
考虑到GLONASS接收机码IFB在不同卫星间的差异性，可为每颗GLONASS卫星设置一个待估参数Bj,rR并在函数模型中对其进行估计。但是，若在式(6)中引入Bj,rR，将与系统时间偏差、平均硬件延迟偏差及GPS频间偏差线性相关，由此会造成观测方程秩亏。目前消除该秩亏较为常用的方法就是附加约束条件[11, 19]，如假定所有GLONASS卫星的码IFB之和为0，并将附加的约束条件作为虚拟观测量与各卫星观测方程一起参与求解。该方法在数值求解过程中易引起状态向量的方差-协方差阵奇异，从而导致Kalman滤波发散[19]。为避免该问题，本文采用“参数合并”策略[20, 21]消除秩亏，将GLONASS接收机码“频间偏差”与“系统时差”参数进行合并，为每颗观测的GLONASS卫星均设置一个独立“时频偏差”(inter-system and inter-frequency bias,ISFB)参数，具体可表示为
对于GLONASS卫星j，其观测方程可以表示为
式中，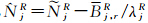
。
在GLONASS相位观测方程中，Bj,rR将由模糊度参数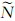jR吸收。假设在历元t，测站r同步观测到m颗GPS卫星、n颗GLONASS卫星，将所有卫星的观测方程线性化，写成矩阵形式
式中，y(t)为观测向量，其维数为2(m+n)；X(t)为待估参数向量，其维数为(m+2n+5)，包括测站位置[X Y Z]T、GPS接收机钟差
、天顶对流层湿延迟δTzwd、GPS相位模糊度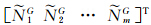
、GLONASS相位模糊度
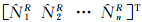及时频偏差
为设计阵。由式(10)可知，要获得逐个历元的定位解，需GPS可见卫星数m≥5。εy为测量噪声向量，且服从均值为0、协方差矩阵为Ωy的正态分布。若假设各类观测值间相互独立，则Ωy为对角矩阵，其对角线元素可表示为卫星高度角的三角函数，具体形式如下
式中，E为测站处的卫星高度角；σ0为天顶方向观测值的先验中误差。
采用扩展卡尔曼滤波模型进行参数估计，其状态方程表示如下
式(13)中，X(t)、 X(t-1)为相邻历元的系统状态向量；Ψt,t-1为状态转移矩阵；wt-1为状态噪声向量，且服从均值为0、协方差矩阵为 Ωw的正态分布。式(14)中，P为位置参数转移矩阵。式(15)中，Δt为相邻历元的时间间隔；q为各状态参数的谱密度矩阵。由于相邻历元间隔Δt通常较小，在此较短时间内可以认为ISFB参数变化是稳定的，因而可将其视为随机游走过程处理。
考察式(8)中时频偏差β的各组成项，其中dtSYS、MRr、MGr及BGr对所有GLONASS卫星的影响都是相同的。假设GPS与GLONASS系统时间偏差及接收机码平均硬件延迟在单日24 h内是稳定的，那么各GLONASS卫星所对应的ISFB解之间的差异将主要由GLONASS接收机码IFB的数值大小不同所造成。因此，在估计得到各GLONASS卫星所对应的ISFB解后，扣除所有卫星ISFB估值的平均值，则可分离出GLONASS接收机码IFB，即
式中，S为GLONASS卫星数。
3 试验与分析 3.1 数据来源
本文选取欧洲区域IGS参考站网和加拿大NRCan网共30个参考站数据进行分析，涉及6个GNSS设备商(Leica、Trimble、JAVAD、JPS、NOV、TPS)的11种GPS/GLONASS双系统机型，测站分布如图 1、图 2所示。数据采集时间为2013年DOY 91—180，采样率为30 s，观测时长为24 h。GPS和GLONASS精密卫星轨道及卫星钟差均统一采用ESA/ESOC提供的事后产品，其中轨道产品采样间隔为15 min、钟差产品为30 s。
 |
| 图 1 欧洲区域IGS参考站Fig. 1 Selected IGS sites in European area |
 |
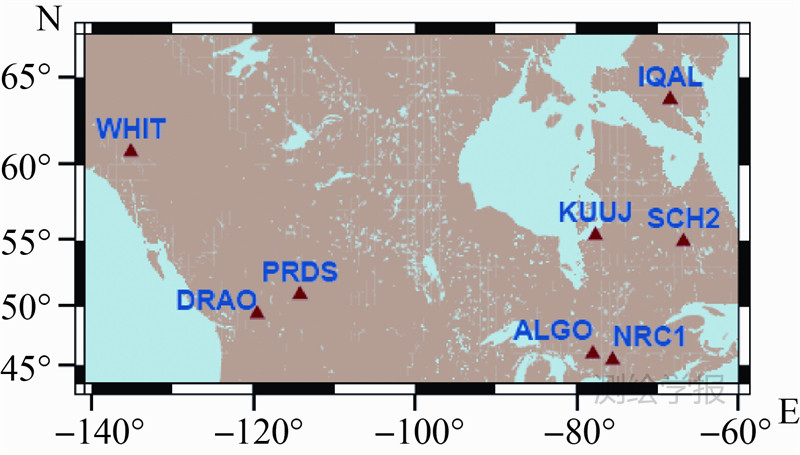| 图 2 加拿大NRCan网参考站Fig. 2 Selected IGS sites in Canada NRCan |
由于相同品牌GPS/GLONASS接收机可能配备于多个测站，限于篇幅，在此每种品牌任选一个测站对GLONASS码IFB与频率的相关性进行分析。图 3给出了6个配备不同品牌GPS/GLONASS接收机的测站在2013年DOY 91 d码IFB的估计结果。可以看出，各品牌接收机不同频率通道的GLONASS码IFB可达数米，并表现出与频率的明显相关性。多数测站的码IFB均表现出与GLONASS频率的线性相关，其中Leica、JAVAD、NOV接收机表现为正相关，Trimble、JPS接收机表现为负相关，而TPS接收机则表现为明显的二次曲线相关特征。不同品牌接收机各频率通道对应的码IFB变化范围不同，其中JPS、TPS接收机变化相对较大。注意到共用频率的GLONASS对跖卫星间的码IFB值并不一定是相同的，有的接收机其差异可达2 m以上。可见，GLONASS码IFB虽然表现出与相位IFB相似的频率相关特性[2, 3, 4]，但在共用频率的对跖卫星间可能存在较大差异，因而要通过简单函数建模(如表示为频率的线性或二次函数)为每颗GLONASS卫星对应的码IFB提供精确的先验改正值是存在一定困难的。
 |
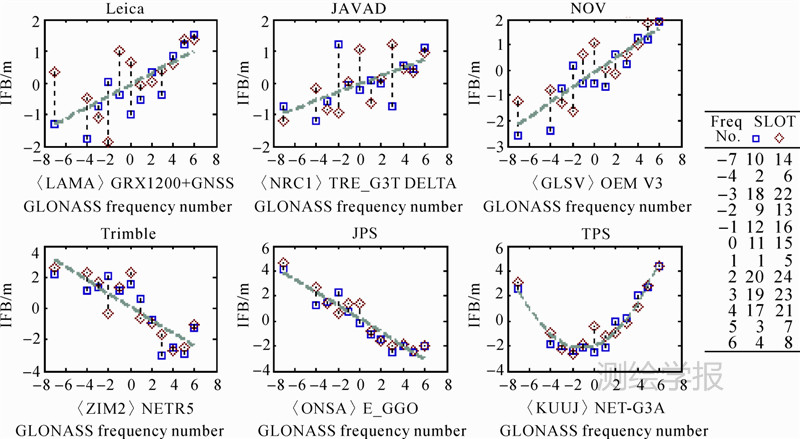| 图 3 GLONASS码IFB与频率关系Fig. 3 Relationship between GLONASS code IFB and frequency |
为分析相同品牌接收机的GLONASS码IFB特性是否相似，分别对配备Leica(频率正相关)、Trimble(频率负相关)及TPS(频率二次相关)接收机的22个测站进行处理。由2013年DOY 91的数据得到的码IFB估计结果如图 4所示。可以看出，配备相同品牌接收机测站的码IFB估值在各卫星间整体上表现出良好的聚集性；对于相同的GLONASS卫星，不同测站的码IFB估值略有不同，这与测站所采用的接收机类型、固件版本、天线类型等因素的差异有关[3, 11]。TPS品牌接收机的码IFB估值量级要明显大于Leica和Trimble品牌，其不同卫星间码IFB估值的差异最大超过15 m。值得注意的是，在配备3种品牌接收机的22个测站中，均出现个别测站码IFB估值大小及分布与其他测站明显不同的异常离群现象。其中，配备Trimble品牌的GRAS测站出现异常，可能与其采用的是ASHTECH品牌的天线有关。对于Leica品牌，出现异常的测站MATE与测站PENC的接收机类型、固件版本及天线类型是完全一致的。同样的，对于TPS品牌，出现异常的测站ALGO与测站PRDS三者也是相同的。
 |
| 图 4 相同品牌不同测站GLONASS码IFB估计结果Fig. 4 GLONASS code IFB results of different sites with the same manufacturer |
为进一步分析上述异常离群现象是否长期存在，对配备Leica、Trimble、TPS品牌接收机的6个测站2013年DOY 91—180共90 d的数据进行GLONASS码IFB估计。其中，每个品牌所对应的2个测站其接收机类型、固件版本及天线类型完全相同。每个测站任选2个不同的GLONASS卫星估计对应的码IFB，结果如图 5所示。
 |
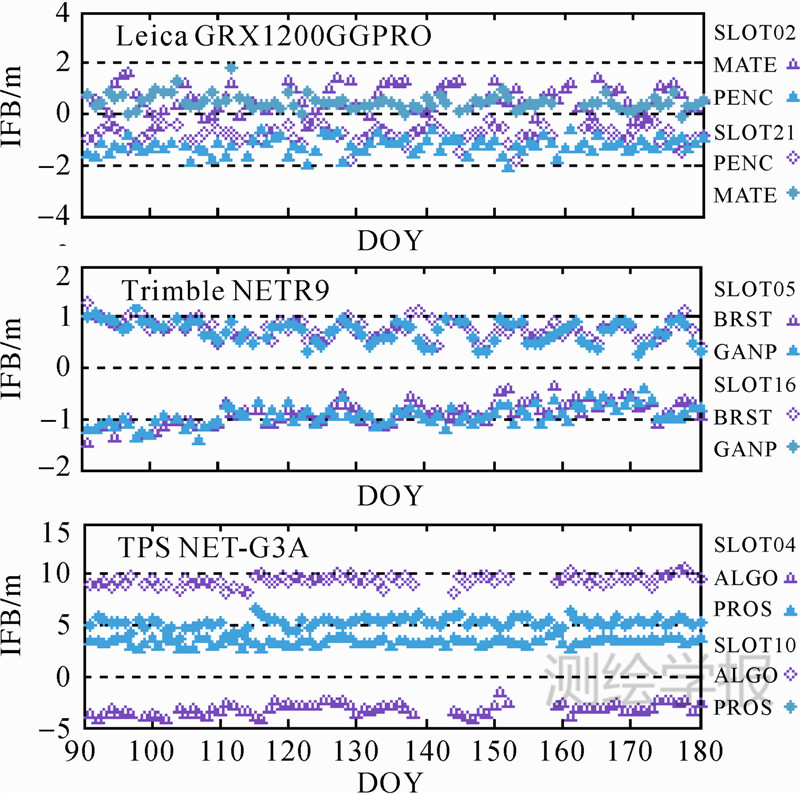| 图 5 配备相同接收机类型、固件版本、天线类型测站的码IFB长期变化Fig. 5 IFB long-term variation of sites with the same receiver type,firmware version and antenna type |
从图 5可以看出，各品牌接收机的码IFB估值在90 d时间段内是较为稳定的。对于配备Trimble NETR9接收机的测站BRST和GANP，卫星SLOT05和SLOT06对应两测站的码IFB值非常接近，其平均值差异小于0.05 m。对于配备Leica GRX1200GGPRO接收机的测站MATE和PENC，卫星SLOT02和SLOT21对应两测站的码IFB值则有明显差异，二者的平均值差异均大于1.2 m。对于配备TPS NET-G3A接收机的ALGO和PRDS测站，卫星SLOT04和SLOT10对应两测站码IFB值的差异更大，其平均值差异分别为6.58 m和4.12 m。由此可见，相同品牌接收机的码IFB值在较长时间段内表现稳定；对于接收机类型、固件版本及天线类型完全相同的测站，其码IFB值不一定就是接近的，有的测站间的差异甚至非常明显。
3.3 对GPS/GLONASS组合PPP的影响
为分析所提出“多参数”算法对PPP收敛时间和定位精度的影响，设计如下3种方案进行对比分析。
方案1：基于GPS单系统的PPP。
方案2：基于“单参数”的GPS/GLONASS组合PPP。GPS与GLONASS载波相位观测值权比按等权处理，而对GLONASS码伪距观测值进行降权处理，二者的先验中误差之比为1∶1.5。
方案3：基于“多参数”的GPS/GLONASS组合PPP。GPS与GLONASS载波相位观测值先验中误差设置与方案2相同。由于通过ISFB参数估计对码IFB进行函数补偿后，可以认为观测方程中GLONASS码伪距噪声已基本接近其在接收机内部的实际测量噪声，因此对码伪距观测值采用GLONASS与GPS等权的随机模型。
对于PPP所涉及的各项误差源如卫星位置误差、卫星钟差、潮汐效应、相对论效应、相位缠绕、天线相位偏差及变化等，3种方案的改正策略均设置为相同。
3.3.1 收敛时间为对比不同方案PPP收敛速度的差异，图 6给出了2013年DOY 91测站LAMA、ZIM2及KUUJ的3D位置偏差的收敛情况。由于PPP一般在1 h左右可收敛至厘米级，图 6中仅列出UTC 0—3 h时间段内各测站不同方案的收敛结果。
 |
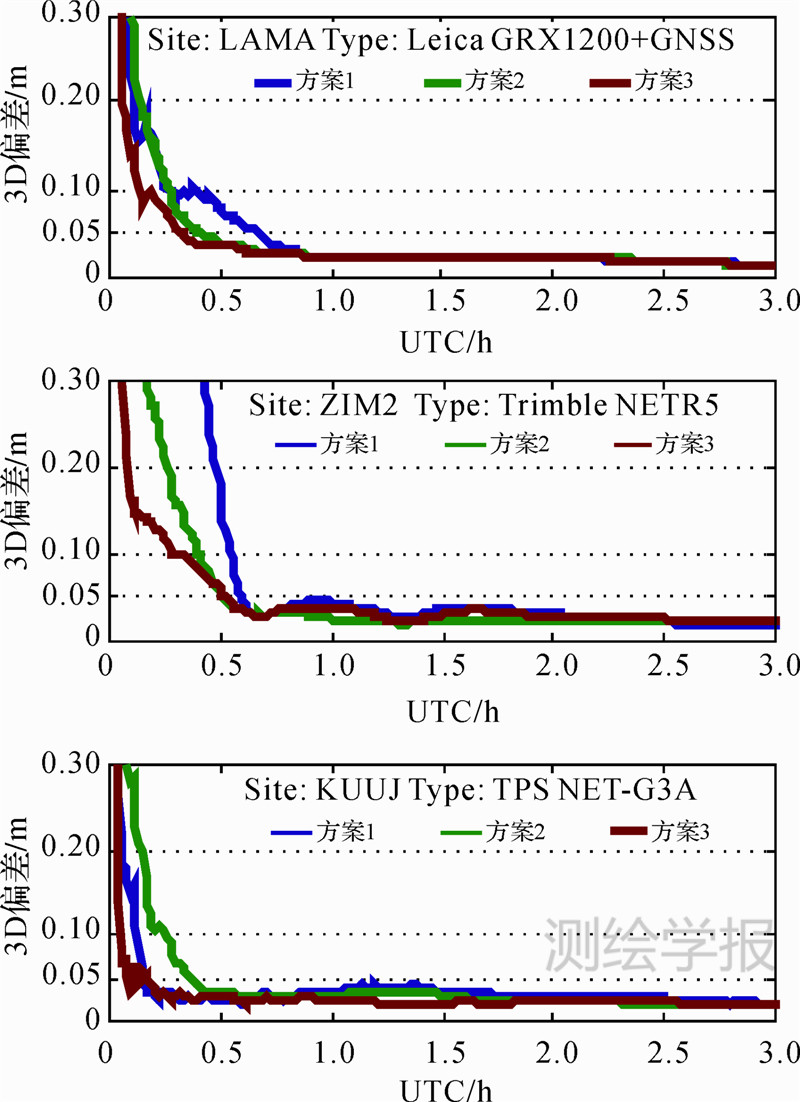| 图 6 不同方案3D位置收敛时间对比Fig. 6 Comparison of 3D bias convergence time with different cases |
从图 6可以看出，对于测站LAMA、ZIM2，方案2的收敛速度明显优于方案1，这说明GLONASS观测值的加入对PPP有明显的收敛加速效果。而对于测站KUUJ，方案2的收敛时间明显大于方案1，这意味着GLONASS观测值的加入反而不如仅使用GPS单系统观测值收敛速度快。从3.2节分析可知，TPS品牌接收机的码IFB估值范围大小及离散程度均远大于Leica和Trimble品牌。由于“单参数”法在函数模型中忽略码IFB，当码IFB量级与码伪距观测值噪声水平较为接近时(如LAMA、ZIM2)，GLONASS码伪距观测值的精度并未显著降低，此时增加GLONASS观测值可加速PPP模糊度的初始收敛。而当码IFB量级远大于GLONASS码伪距的观测噪声水平时(如KUUJ)，函数模型中所采用的GLONASS码伪距观测值实际精度要远低 于其观测精度，此时仅通过简单的降权并不能消除其不利影响。方案3通过设置多个“时频偏差”参数吸收各GLONASS卫星对应的码IFB，函数模型中GLONASS码伪距观测值实际精度可以认为与其自身的观测精度已非常接近，此时设置GPS与GLONASS观测值等权亦能取得较好效果。显然，图 6中所有3个测站方案3的收敛时间都是最短的，其中对测站KUUJ收敛速度的改善尤为明显。
为验证方案3是否对GLONASS码IFB进行了充分的函数模型补偿，图 7给出了测站KUUJ在2013年DOY 91的24 h时段内，卫星SLOT07、SLOT10所对应方案2和方案3的GLONASS码残差。从图 7可以明显地看出，方案2的码残差均值显著不为0，表现为码IFB与码伪距观测噪声的叠加。而方案3已通过多个ISFB参数吸收码IFB，码残差表现为0均值的随机观测噪声。图 8进一步给出了3个测站所有GLONASS卫星的码伪距残差统计分布。显然，方案3所得到的GLONASS码残差分布较方案2有显著改善，各测站码残差均值在0附近，且标准差约为方案2的1/2左右，符合较为理想的正态分布。这说明“多参数”法对于GLONASS码IFB的补偿是有效的。
 |
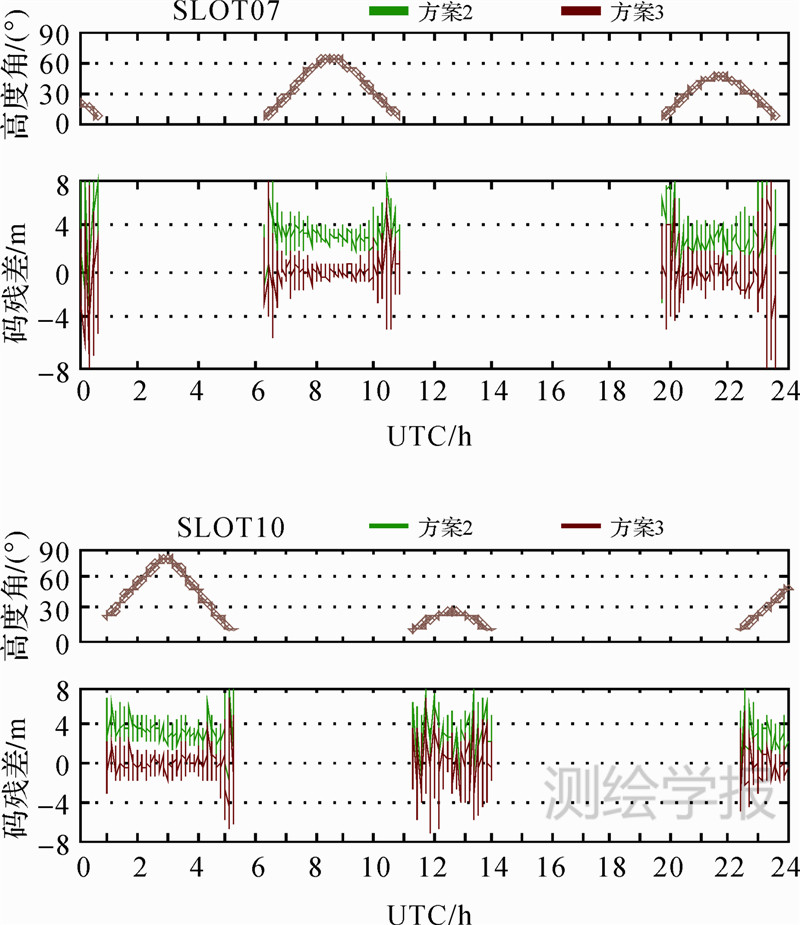| 图 7 测站KUUJ 的GLONASS 码残差方案2和方案3 对比Fig. 7 Comparison of GLONASS code residuals between case 2 and case 3 with KUUJ |
 |
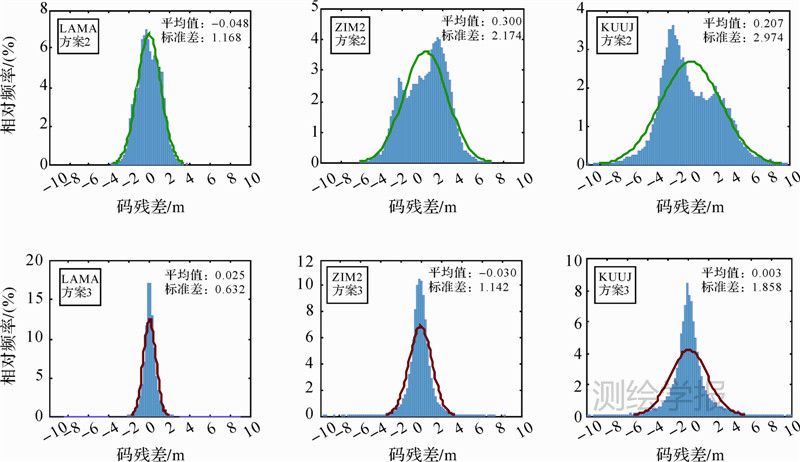| 图 8 GLONASS码残差分布方案2和方案3对比Fig. 8 Comparison of GLONASS code residual distributions between case 2 and case 3 |
为进一步验证“多参数”法对提高GPS/GLONASS组合PPP收敛速度的有效性，对每个GNSS设备品牌任选2个测站，分别采用3种方案对2013年DOY 91—180的观测数据进行处理。每3 h时段数据为一组统计各方案的收敛时间，收敛水平分别设置为10 cm和5 cm，各测站信息及收敛时间如表 1、图 9所示。
| 品牌 | 接收机类型 | 测站 |
| Leica | GRX1200+GNSS | LAMA |
| GRX1200GGPRO | NICO | |
| Trimble | NETR9 | GANP |
| NETR5 | ZIM2 | |
| JAVAD | TRE_G3T DELTA | NRC1 |
| TRE_G3TH | ZECK | |
| JPS | E_GGD | MAR6 |
| E_GGD | ONSA | |
| NOV | OEMV3 | GLSV |
| OEMV3 | KHAR | |
| TPS | NET-G3A | ALGO |
| NET-G3A | KUUJ |
 |
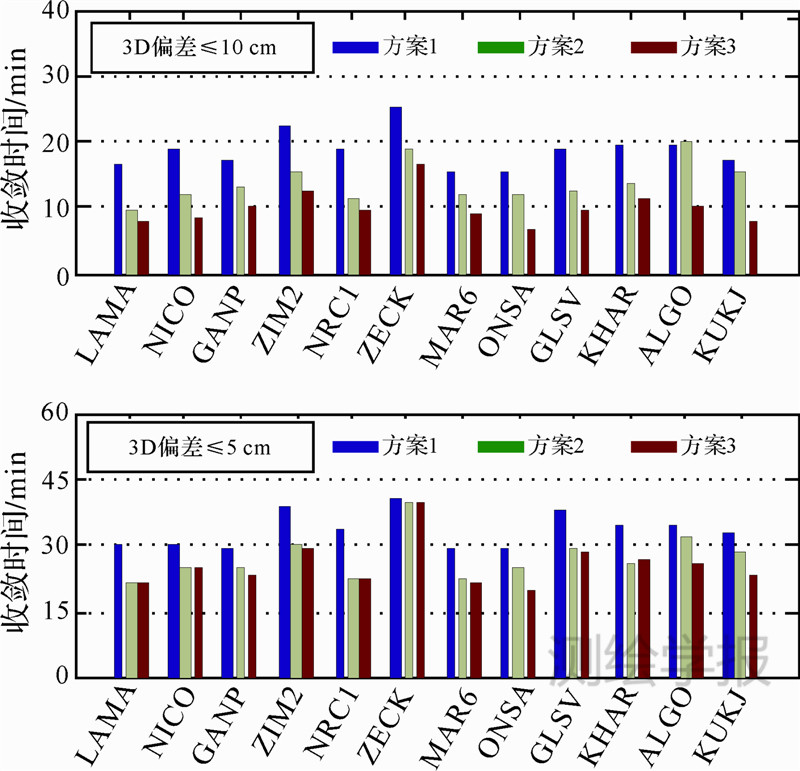| 图 9 各测站不同方案收敛时间对比Fig. 9 Comparison of convergence time with different cases |
从统计结果可以看出，在3D偏差收敛至10 cm 水平，除配备TPS品牌接收机的测站方案1和方案2的收敛时间相当外，其他5种品牌方案2相对于方案1的收敛时间可缩短30%左右。采用方案3后，所有测站收敛时间进一步明显缩短，与方案2相比，配备TPS品牌接收机测站ALGO、KUUJ及配备JPS品牌接收机测站ONSA的收敛速度均提高近50%，其他测站提高约20%。在3D偏差收敛至5 cm水平，采用方案3后，测站ALGO、KUUJ、ONSA的收敛速度相对于方案2还可进一步提高约20%，而其他测站方案3和方案2的收敛加速效果几乎相当。在5 cm收敛精度水平上，“多参数”法对多数测站的收敛加速效果不显著。这主要是由于随着模糊度收敛精度的不断提高，定位精度水平将逐渐由载波相位观测值主导，而伪距观测值的作用越来越弱。
3.3.2 定位精度为对比不同方案PPP定位精度的差异，采用3种方案分别处理得到3 h和24 h定位结果，所处理的测站及观测数据采集时间段均与3.3.1节中的相同，定位结果3D偏差RMS值如图 10所示。
 |
| 图 10 各测站不同方案定位结果对比Fig. 10 Comparison of 3D biases with different cases |
对于3 h时段，方案2、方案3的定位精度相当，二者要明显优于方案1，各测站的平均收敛精度约为2 cm。有数个测站方案3的RMS值要略大于方案2，这可能是由于“多参数”法引入多个“时频偏差”参数导致函数模型自由度减小所引起的。对于24 h时段，3种方案在不同测站的表现各有优劣，3D偏差RMS值均收敛至1～2 cm水平，整体上RMS值互差为毫米级，因而可以认为3种方案单天解精度是相当的。由此可见，方案3虽然可提高GPS/GLONASS组合PPP的收敛速度，但相对于方案2而言，其定位精度水平并未提高。方案3虽引入多个附加参数将使函数模型的自由度减小，但实际并未明显降低组合PPP的定位精度，与方案2的RMS值差异在毫米级。对于3 h时段，方案2、3均优于GPS单系统PPP的定位精度；对于24 h时段，3种方案在不固定模糊度情况下所获得的PPP单天解精度相当。
4 结 论
本文提出基于“多参数”的GPS/GLONASS组合PPP与码IFB估计算法，通过实测数据计算分析，得到如下结论：
(1) 新算法通过在函数模型中设置多个“时频偏差”参数对码IFB进行估计，弥补了传统“单参数”法组合PPP忽略码IFB的不足，且能实现基于单个测站数据的GLONASS码IFB精确估计。
(2) 各品牌接收机不同频率通道的GLONASS码IFB可达数米，且表现出与频率的明显相关性，但难以通过简单函数建模为其提供精确的先验改正值。
(3) 相同品牌接收机的GLONASS码IFB整体上具有相似的特性，但在个别测站会表现出异常特征，即使对于接收机类型、固件版本及天线类型完全相同的测站，GLONASS码IFB值也可能存在显著差异。
(4) “多参数”法能实现对GLONASS码IFB的有效补偿，明显提高组合PPP的收敛速度。在10 cm收敛精度水平上，较传统“单参数”组合PPP平均收敛时间缩短约20%，个别品牌接收机可达50%；在5 cm收敛精度水平上，一些品牌接收机仍可缩短约20%。
(5) “多参数”法与传统“单参数”进行GPS/GLONASS组合PPP的定位精度相当，引入多个附加参数虽导致函数模型自由度减小，但对定位精度的影响有限。
| [1] | ROSSBACH U. Positioning and Navigation Using Russian Satellite System GLONASS[D]. Munich: University of the Federal Armed Forces Munich, 2001. |
| [2] | WANNINGER L, WALLSTAB-FREITAG S. Combined Processing of GPS, GLONASS, and SBAS Code Phase and Carrier Phase Measurements[C]//Proceedings of ION on GNSS 2007. Fort Worth: ION, 2007: 866-875. |
| [3] | WANNINGER L. Carrier-phase Inter-frequency Biases of GLONASS Receivers[J]. Journal of Geodesy, 2012, 86(2): 139-148. |
| [4] | ZIONIEV A E, VEITSEL A V, DOLGIN D A. Renovated GLONASS: Improved Performances of GNSS Receivers[C]//Proceedings of ION on GNSS 2009. Savannah: ION, 2009: 3271-3277. |
| [5] | AL-SHAERY A, ZHANG S, RIZOS, C. An Enhanced Calibration Method of GLONASS Inter-channel Bias for GNSS RTK[J]. GPS Solutions, 2013, 17(2): 165-173. |
| [6] | YAMADA H, TAKASU T, KUBO N, et al. Evaluation and Calibration of Receiver Inter-channel Biases for RTK-GPS/GLONASS[C]//Proceedings of ION on GNSS 2010. Portland: ION, 2010: 1580-1587. |
| [7] | CAI Changsheng. Theory and Method of Combined GPS/GLONASS Precise Point Positioning[D]. Xuzhou: China University of Mining and Technology, 2008. (蔡昌盛. GPS/GLONASS组合精密单点定位理论与方法研究[D]. 徐州: 中国矿业大学, 2008.) |
| [8] | ZHANG Xiaohong, GUO Fei, Li Xingxing, et al. Study on Precise Point Positioning Based on Combined GPS and GLONASS[J]. Geomatics and Information Science of Wuhan University, 2010, 35(1): 9-12. (张小红, 郭斐, 李星星, 等. GPS/GLONASS组合精密单点定位研究[J]. 武汉大学学报: 信息科学版, 2010, 35(1): 9-12.) |
| [9] | MENG Xiangguang, GUO Jiming. GPS-GLONASS and Their Combined Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2010, 35(12): 1409-1413. (孟祥广, 郭际明. GPS/GLONASS及其组合精密单点定位研究[J]. 武汉大学学报: 信息科学版, 2010, 35(12): 1409-1413.) |
| [10] | CAI C S, GAO Y. Modeling and Assessment of Combined GPS/GLONASS Precise Point Positioning[J]. GPS Solutions, 2013, 17(2): 223-236. |
| [11] | SHI C, YI W T, SONG W W, et al. GLONASS Pseudorange Inter-channel Biases and Their Effects on Combined GPS/GLONASS Precise Point Positioning[J]. GPS Solutions, 2013, 17(4): 439-451. |
| [12] | GE M, GENT G, ROTHACHER M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations[J]. Journal of Geodesy, 2008, 82(7): 389-399. |
| [13] | LAURICHESSE D, MERCIER F, BERTHIAS J P, et al. Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and Its Application to PPP and Satellite Precise Orbit Determination[J]. Navigation, 2009, 56(2): 135-149. |
| [14] | COLLINS P, BISNATH S, LAHAYE F, et al. Undifferenced GPS Ambiguity Resolution Using the Decoupled Clock Model and Ambiguity Datum Fixing[J]. Navigation, 2010, 57(2): 123-135. |
| [15] | ZHANG Baocheng, OU Jikun. On the Different Strategies for Integer Ambiguity Resolution in Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 710-716. (张宝成, 欧吉坤. 论精密单点定位整周模糊度解算的不同策略[J]. 测绘学报, 2011, 40(6): 710-716.) |
| [16] | REUSSNER N, WANNINGER L. GLONASS Inter-frequency Biases and Their Effects on RTK and PPP Carrier-phase Ambiguity Resolution[C]//Proceedings of ION on GNSS 2011. Portland: ION, 2011: 712-716. |
| [17] | REUSSNER N, WANNINGER L. GLONASS Inter-frequency Code Biases and PPP Carrier-phase Ambiguity Resolution[C]//Proceedings of IGS Workshop 2012. Olsztyn: [s.n.], 2012. |
| [18] | SCHAER S, GURTNER W, FELTENS J. IONEX: The Ionosphere Map Exchange Format Version 1[C]//Proceedings of the IGS AC Workshop. Darmstadt:[s.n.], 1998. |
| [19] | GENG Changjiang, ZHANG Hongping, ZHAI Chuanrun. Real Time Estimation of DCB Using Kalman Filters[J]. Geomatics and Information Science of Wuhan University, 2009, 34(11): 1309-1311. (耿长江, 章红平, 翟传润. 应用Kalman 滤波实时求解硬件延迟[J]. 武汉大学学报: 信息科学版, 2009, 34(11): 1309-1311.) |
| [20] | TEUNISSEN P J G. The GPS Phase-adjusted Pseudorange[C]//Proceedings of the 2nd International Workshop on High Precision Navigation. Stuttgart: Dummlers Verlag, 1991: 115-125. |
| [21] | ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Precise Point Positioning Algorithm Based on Original Dual-frequency GPS Code and Carrier-phase Observations and Its Application[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 478-483. (张宝成, 欧吉坤, 袁运斌, 等. 基于GPS双频原始观测值的精密单点定位算法及应用[J]. 测绘学报, 2010, 39(5): 478-483.) |