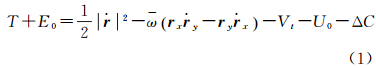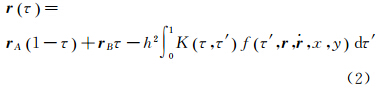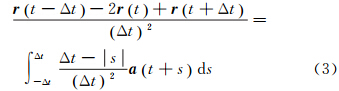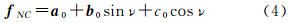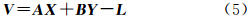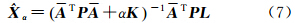1 引 言
GOCE(Gravity Field and Steady-state Ocean Circulation Explorer)于2009年3月成功发射,其任务目标是在空间分辨率优于100 km的尺度上测定重力异常的精度优于1~2 mGal,大地水准面的精度优于1 cm[1]。GOCE卫星采用卫星高低跟踪和重力梯度测量相结合的模式,可以恢复高精度高分辨率的静态全球重力场模型。利用低轨卫星跟踪数据恢复地球重力场模型的方法有很多钟,归纳起来主要有Kaula线性摄动法[2]、动力学积分法[3]、短弧积分法[4, 5, 6]、点加速度法[7, 8]、平均加速度法[9, 10]、能量守恒法[11, 12]和天体力学法[13, 14]等。
文献[15]认为基于轨道数据恢复重力场模型可以从3个层次进行分析,基于轨道的Fredholm形式的积分、基于速度的运动方程积分和基于加速度的运动方程,分别可以采用短弧积分法、能量守恒法和加速度法处理观测数据,只有轨道数据是直接观测量,速度和加速度均是对轨道数据进行数值微分而获得。需要指出的是,Kaula线性摄动法、动力学积分法和天体力学法所采用的思想与前面所述有所不同,这3种方法均是基于卫星轨道扰动原理建立位系数和卫星星历扰动的关系,需要采用先验信息,并且计算量大。本文主要分析短弧积分法、能量守恒法和平均加速度法,这3种方法均不需要先验信息,可以独立评价GOCE观测数据恢复模型的精度。短弧积分法是基于牛顿运动方程 将卫星轨道表示成Fredholm积分方程形式的边值问题,不需要初始参考信息,文献[4]对其进行了深入研究,文献[6]对短弧积分法进行力模型梯度改正,取得了较好的效果。能量守恒法是将卫星的状态矢量与受力情况同引力位系数联系起来,建立能量守恒方程来恢复位系数,文献[11]首次将该方法用于实测低轨卫星跟踪卫星的数据处理。加速度法又分为点加速度法和平均加速度法,直接利用牛顿第二定律建立卫星加速度和位系数的函数关系,该方法直观简单,但卫星加速度是通过数值微分或差分方法获得,在微分或差分的过程中会放大高频误差,本文主要对平均加速度法进行分析。文献[16, 17]对这些方法进行了简单的综合分析,均认为能量守恒法的精度最差,而加速度法的精度较高。
利用GOCE卫星实测数据恢复重力场的研究是物理大地测量学的一个热点,文献[18]利用能量守恒法处理轨道数据,结合梯度数据采用最小二乘法恢复了210阶地球重力场模型。文献[19]比较了时域法、空域法和直接法恢复重力场模型的差别,同时采用短弧积分法和能量守恒法处理轨道数据。文献[20]对短弧长积分法进行了模拟分析,并将其用于恢复GOCE重力场模型。文献[6]将其用于GOCE重力场的恢复,并联合GRACE数据分析了有无梯度改正对模型精度的影响。文献[21]研究了联合GOCE轨道和梯度数据的谱组合法,并利用实测数据进行了验证,文献[22]通过分析认为利用加速度法恢复GOCE重力场的长波部分精度最好。目前ESA(European Space Agency)公布的官方GOCE模型中,早期模型采用能量守恒法处理轨道数据,后期模型部分采用短弧积分法。
哪种方法最适合处理GOCE轨道数据,目前还没有比较完整的研究。本文利用GOCE卫星精密轨道观测数据,分别采用短弧积分法、能量守恒法和平均加速度法恢复重力场模型,分析3种方法用于恢复GOCE重力场模型的精度和特点,同时分析了GOCE轨道数据恢复重力场模型的最优正则化方法和参数的选择。
2 利用轨道数据恢复重力场模型的观测方程 2.1 能量守恒法的观测方程GOCE卫星在惯性系下的能量守恒观测方程可以表示为[12]
式中,T为扰动位;E0为能量积分常数;Vt为卫星受到的摄动位(主要包括三体引力摄动位、固体潮摄动位、海潮摄动位、固体极潮摄动位和海极潮摄动位);U0为正常重力位;ΔC为卫星受到的耗散能,r = [rx ry rz] 和
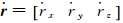 分别表示卫星在某一时刻的位置和速度向量;ω表示地球平均自转角速度;式(1)右端的第1项和第2项分别表示卫星的动能和旋转位能。
2.2 短弧积分法的观测方程
分别表示卫星在某一时刻的位置和速度向量;ω表示地球平均自转角速度;式(1)右端的第1项和第2项分别表示卫星的动能和旋转位能。
2.2 短弧积分法的观测方程基于牛顿运动方程将卫星轨道表示成Fredholm积分方程形式的边值问题,可以得到短弧积分法的观测方程[4]
式中,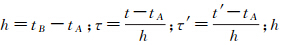 为弧段长度;τ、τ′分别表示时间变量t、t′的归一化值;K (τ,τ′) 为积分核函数。
2.3 平均加速度法的观测方程
为弧段长度;τ、τ′分别表示时间变量t、t′的归一化值;K (τ,τ′) 为积分核函数。
2.3 平均加速度法的观测方程对时间 [t-Δt,t+Δt] 内的卫星加速度进行加权平均得到卫星加速度的3点差分观测值[9]
式中,a(t) 、r(t) 分别表示卫星在t时刻的加速度向量和位置向量;Δt表示采样间隔;s表示积分变量。 2.4 误差方程建立与求解GOCE卫星主要受到保守力和非保守力的影响,进一步将卫星受到的力分解为f (ti) =fC+fNC+fNS,其中fC、fNC、fNS分别表示卫星受到的保守力(不包括非球形引力)摄动加速度、非保守力摄动加速度和非球形引力摄动加速度。非球形引力位和摄动加速度采用直角坐标系中的表达式(见文献[5]),可以简化函数模型和程序设计的复杂度。GOCE卫星受到的各种保守力可采用精确的模型计算。虽然GOCE卫星采用无阻尼推进系统对非保守力进行补偿,但是只对卫星沿轨方向进行补偿,并且由于其他各种因素的影响,不能完全补偿非保守力,还存在微小的残差[14]。残差加速度可以采用GOCE卫星梯度仪获取的共模加速度得到,但共模加速度含有大量的有色噪声,需要对其进行滤波和校正处理,并且经过补偿后残差加速度本身就已经较小,因此部分学者建议采用经验加速度吸收残差加速度[5, 20]
式中,a0、b0、c0分别表示加速度的偏差和振幅参数,文中称为局部未知参数;ν表示真近点角,本文采用ν=2πt/ta,ta=5400 s表示GOCE卫星绕地球旋转运动的周期,需要注意的是,式(4)只有在局部轨道坐标系中才成立,使用时需要将其转换至惯性系中。
最后,采用Helmert-Wolf参数估计方法建立误差方程并采用消局部参数的最小二乘法建立法方程进行求解
式中,V为观测值改正向量;X为位系数向量,称为全局未知参数;Y为残差加速度的偏差、振幅向量,称为局部未知参数;A和B为两类未知参数的系数矩阵;L为常数阵。 3 利用GOCE轨道数据恢复重力场模型 3.1 数据预处理
ESA提供了GOCE卫星的轨道数据SST_PSO_2,本文采用2009-11-01-2010-01-31共92 d的轨道数据,主要利用其中的约化动力学轨道数据(SST_PKI_2)、几何学轨道数据(SST_PRD_2) 和四元素数据(SST_PRM_2)。约化动力学轨道是通过对力模型积分得到,受到先验重力场模型的影响,而几何学轨道数据由GPS跟踪数据直接解算得到,不受先验信息的影响[23]。几何学轨道数据包含粗差,并且存在大量的数据间断,而约化动力学轨道比较平滑且一般不存在间断,因此本文采用约化动力学轨道作为参考,对几何学轨道进行粗差和间断探测。为了完全避免先验重力场的影响,对探测出来的粗差和间断只进行标记而不处理,恢复重力场模型时跳过标记数据,只利用不含粗差和间断的数据。因此本文实际用于重力场恢复的数据为几何学轨道数据和四元素数据,其中四元素数据用来获得地固系(ERF)至惯性系(IRF)的转换矩阵。
3.2 精度评定采用不同重力场模型位系数差的阶误差评定本文解算出的重力场模型精度
式中,Cnmref和 Snmref为参考模型的位系数;Cnm和 Snm为解算模型的位系数;n、m为重力场模型的阶和次。
本文采用的参考模型为EIGEN-5C,同时选取GO-CONS-GCF-2-TIM(后文简称TIM)系列模型作为对比模型,主要是原因是TIM系列模型是GOCE的官方公布的模型之一,其主要特点是该系列模型未采用先验信息,完全利用GOCE数据解算得到,该系列模型处理轨道数据时采用的方法不完全一样,其中R1至R3均采用能量守恒法,而R4采用短弧积分法。
3.3 实测数据恢复重力场模型本文的计算工作在Intel Core i7-3930K 6核12线程的计算机上进行,主频为3.20 GHz,内存为24 GB;采用Intel Fortran Compiler XE 13.1编译器和MKL 11.0(Math Kernel Library)数学函数库,并利用OpenMP对程序进行并行化处理。恢复重力场模型时,本文将92 d的数据分为若干弧段,然后将每个弧段形成的法方程累加后求解位系数,这样可以减少内存的开销。根据试验分析,能量守恒法的最佳弧段长度选择45 min;短弧积分法的最佳弧长选择20 min,多项式阶数选择9阶;平均加速度法的最佳弧段长度选择40 min,多项式阶数选择12阶。分别采用能量守恒法(文中以EBA表示)、短弧积分法(文中以SAIA表示)和平均加速度法(文中以AAA表示)各恢复120阶和130阶两组重力场模型,并比较各模型与TIM系列模型的阶方差(见图 1),在力模型提前计算完成的情况下,能量守恒法恢复重力场模型的效率最高,短弧积分法次之,平均加速度法的效率最低。
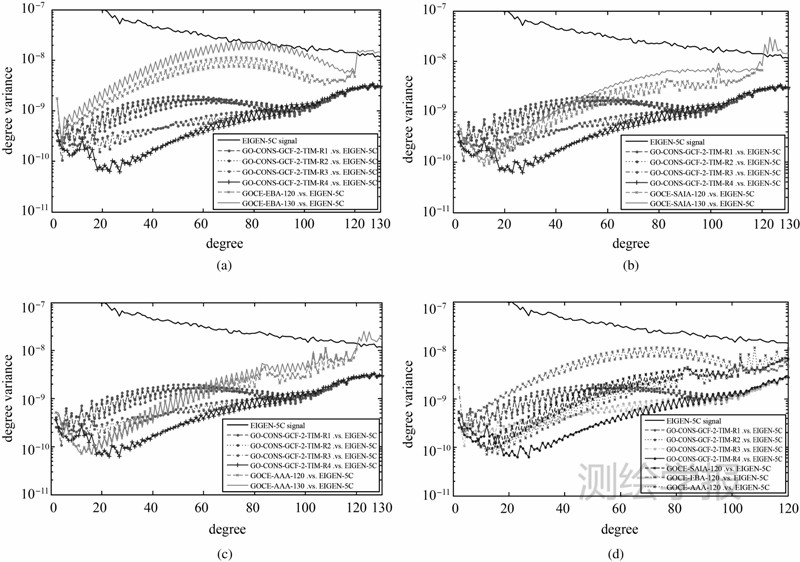 |
| 图 1 阶方差对比Fig. 1 Comparison of degree variances |
从图 1可以看出,能量守恒法恢复的模型精度最低,平均加速度法的精度最高,主要是由于能量守恒法只与卫星沿轨方向的分量有关,而不能充分利用轨道垂向和径向分量的观测信息。平均加速度法和短弧积分法在60阶以前的精度优于TIM前两代模型R1和R2,在30阶以前的精度优于R3模型,而与R4模型相比,在20阶以前部分阶次精度互有优劣。因此本文建议未来联合处理GOCE轨道和梯度数据时,最好采用平均加速度法或短弧积分法处理轨道数据。利用GOCE轨道数据恢复的重力场模型的阶方差出现锯齿状的振荡现象,主要原因是受数据极空白的影响,利用GOCE数据恢复模型的带谐项精度较低。
同时发现,利用92 d的数据恢复130阶的重力场模型,在120阶以后精度出现骤降,是否可以确定利用GOCE卫星轨道数据只能有效恢复120阶的重力场模型呢?为了说明这个问题,分别采用92 d(2009-11-01-2010-01-31)、185 d(2011-02-28-2011-08-31)和372 d(2011-02-28-2012-03-05)的GOCE轨道数据恢复130阶的重力场模型(见图 2),可以看出,在120阶以后精度均出现骤降,只是随着观测数据量的增多,位系数的精度略有提高而已,因此本文认为利用GOCE轨道数据只能有效恢复120阶左右的重力场模型,在120阶后精度骤降的原因主要是混叠误差而不是截断误差,如果是截断误差,那么随着恢复模型的阶数增加,模型的精度出现骤降的现象会不断减弱,但事实并非如此,出现此现象的具体原因还有待进一步分析。ESA官方发布的TIM系列模型的前3代利用轨道数据恢复的最大阶数均为100 阶次,而R4恢复了130阶次的模型,从本文的结果来看,联合轨道和梯度数据恢复重力场模型时,轨道数据恢复的模型阶数最好不要超过120阶次。
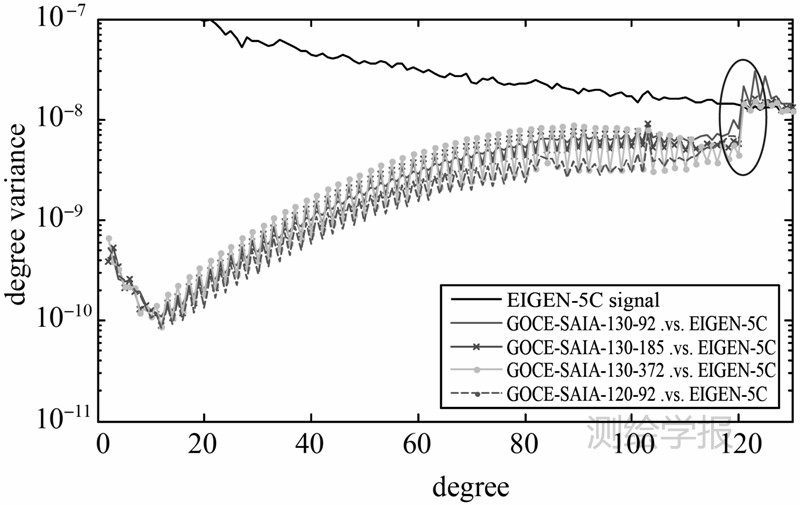 |
| 图 2 不同数据量恢复模型的阶方差对比Fig. 2 Comparison of degree variances among models by different amount of data |
由于GOCE卫星轨道为近圆形太阳同步晨昏倾斜轨道,轨道倾角约为96.7°,在两极附近各有约6.7°的轨道覆盖空白区域,利用GOCE观测数据恢复重力场模型将是一个不适定问题,采用最小二乘法解算时形成的法方程矩阵是病态的。许多学者对病态问题进行了深入研究,本文采用目前使用最广泛的Tikhonov正则化方法。根据式(5)可以得求解位系数的正则化解为
确定正则化矩阵K后还要确定合适的正则化参数α,正则化参数主要起到平衡观测误差和正则化误差对参数估计影响的作用,目前确定最优正则化参数的方法主要有L曲线法、广义交叉检验法GCV、广义不符原理和方差分量估计法等[24],但这些方法在确定最优正则化参数的过程中均需重复形成设计矩阵来计算观测值残差,计算过程相当耗时,因此本文采用文献[25]中的方法,基于恢复的大地水准面误差RMS最小的准则来确定最优正则化参数。特别指出的是,真实参考重力场模型无法获得,因此以大地水准面误差RMS最小准则来确定最优正则化参数在理论上是有缺陷的,实际处理时只能选择精度较高的模型作为参考,得到的最优正则化参数是近似值,处理高采样率的GOCE数据时采用这种解算方法是硬件条件受限制时的一种折中方案。
基于3种方法分别恢复120阶重力场模型,以全球范围内1.0°×1.0°的大地水准面格网值计算的大地水准面误差RMS作为评价正则化方法和参数优劣的标准(见图 3(a)-(c)),可以看出,平均加速度法的最优正则化方法为Kaula正则化和SOT,最优正则化参数均为1×10-1;能量守恒法的最优正则化方法为Kaula正则化和SOT,最优正则化参数分别为5×108和4×108;短弧积分法的最优正则化方法为FOT,最优正则化参数为6×107,但Kaula正则化和SOT也能达到相近的效果。总体来看,Kaula正则化和SOT处理GOCE病态问题的效果基本一样,FOT的效果次之,ZOT的效果最差。能量守恒法受极空白的影 响较大,病态性较严重,而平均加速度法和短弧积分法受极空白的影响较小,其中平均加速度法受极空白的影响最小。同时从图 3(d)可以看出经过正则化处理之后,利用3种方法恢复的模型在80阶以前的精度优于TIM前两代模型R1和R2,其中平均加速度法和短弧积分法恢复的模型在80阶以前的精度优于R3,并与R4的精度较为接近。
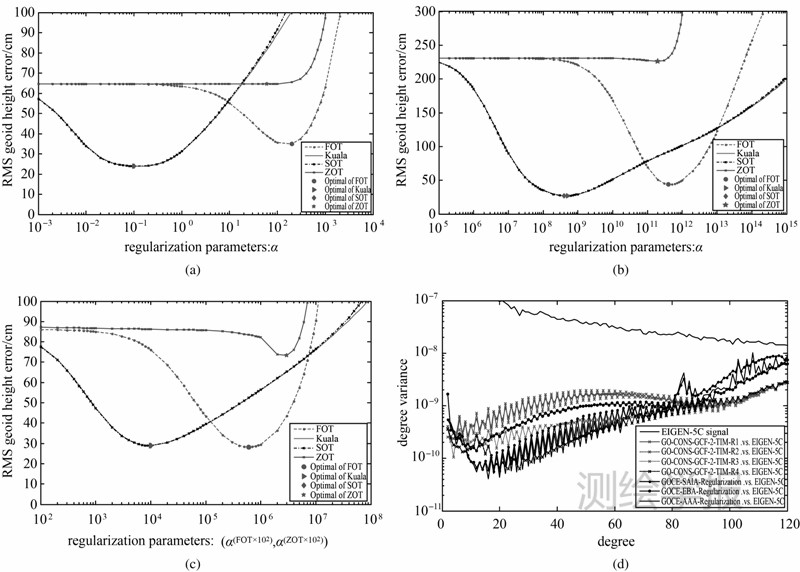 |
| 图 3 正则化方法和参数比较Fig. 3 Comparison of regularization techniques and parameters |
基于前面的分析,采用最优正则化方法和参数分别利用3种方法恢复重力场模型,并计算其在南极地区0.5°×0.5°的大地水准面误差,与未正则化模型的计算值进行比较(见图 4),图 4(a)-(c)分别表示平均加速度法、短弧积分法和能量守恒法解算的结果;图 4(d)-(f)为对应的正则化后的结果。可以看出,3种方法恢复的模型在极区的精度较差,特别是能量守恒法恢复的模型、平均加速度法和短弧积分法恢复的模型精度基本相当。经正则化处理后,3种方法恢复模型在极区的精度均有明显改善,说明正则化方法对PG问题有明显的抑制效果,但却不能完全消除PG问题带来的影响,因此为了恢复高精度、全波段的重力场信号,单独采用GOCE数据和正则化技术难以满足要求,还需要联合其他数据(如GRACE数据)进行分析处理。
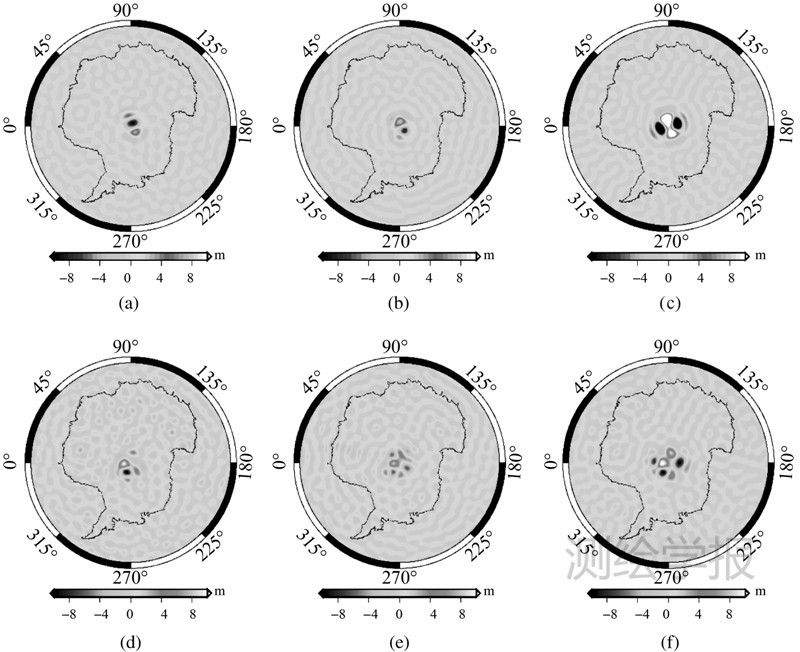 |
| 图 4 3种方法正则化前后解算的模型在南极地区的大地水准面误差比较Fig. 4 Comparison of geoid error in south pole among regularization by three methods |
本文利用GOCE卫星轨道数据,基于能量守恒法、短弧积分法和平均加速度法恢复重力场模型,比较了3种方法处理GOCE轨道数据的精度,分析了正则化方法和参数的选择问题,得出了一些有益的结论,为进一步联合GOCE轨道和梯度数据以及GRACE数据恢复高精度高分辨率重力场模型提供重要的参考和借鉴。
(1) 利用平均加速度法恢复GOCE重力场模型的精度最高,主要原因是该方法受数据极空白的影响较小,利用该方法恢复模型的精度在60阶以内优于R1和R2模型,在30阶以内优于R3模型,在20阶以内与R4模型的精度相当,短弧积分法的精度稍差于平均加速度法,能量守恒法的精度最低。因此,建议未来联合GOCE轨道和梯度数据恢复重力场模型时,最好采用平均加速度法或短弧积分法处理轨道数据。
(2) 利用GOCE卫星轨道数据可有效恢复120阶左右的模型,超过120阶以后位系数的精度较低。
(3) Kaula正则化和SOT处理GOCE病态问题的效果最好,并且两者对应的最优正则化参数基本一致,对于能量守恒法、短弧积分法和平均加速度法的最优正则化方法分别为Kaula正则化、FOT和Kaula正则化或SOT,对应的最优正则化参数分别为5×109、6×107和1×10-1,正则化技术对PG问题有明显的抑制效果,联合GRACE等其他数据可望进一步减小PG问题的影响。
致谢: 感谢ESA提供所需GOCE卫星的轨道数据。| [1] | European Space Age. GOCE Mission Requirements Document[EB/OL].[2013-05-17].http://earth.esa.int/web/guest/documeut-library. |
| [2] | HWANG C. Gravity Recovery Using COSMIC GPS Data: Application of Orbital Perturbation Theory [J]. Journal of Geodesy, 2001, 75(3): 117-136. |
| [3] | ZHU S, REIGBER C, KÖNIG R. Integrated Adjustment of CHAMP, GRACE, and GPS Data [J]. Journal of Geodesy, 2004, 78(2): 103-108. |
| [4] | MAYER-GÜRR T, ILK K H, EICKER A, et al. ITG-CHAMP01: A CHAMP Gravity Field Model from Short Kinematic Arcs over a One-year Observation Period [J]. Journal of Geodesy, 2005, 78(8): 462-480. |
| [5] | YI W Y. The Earth's Gravity Field from GOCE [D]. München: Technische Universitt München, 2011. |
| [6] | YOU W, FAN D M, HUANG Q, Analysis of Short-arc Integral Approach to Recover the Earth's Gravitational Field [J].Chinese Journal of Geophysics, 2011, 54(11): 2745-2752.(游为, 范东明, 黄强. 卫星重力反演的短弧长积分法研究[J]. 地球物理学报, 2011, 54(11): 2745-2752.) |
| [7] | REUBELT T, AUSTEN G, GRAFAREND E W. Space Gravity Spectroscopy-determination of the Earth' s Gravitational Field by Means of Newton Interpolated LEO Ephemeris Case Studies on Dynamic (CHAMP Rapid Science Orbit) and Kinematic Orbits[J]. Advances in Geosciences, 2003, 1: 127-135. |
| [8] | SHEN Y Z. Study of Recovering Gravitational Potential Model from the Ephemerides of CHAMP [D]. Wuhan: Institute of Geodesy and Geophysics, Chinese Academy of Sciences, 2000.(沈云中. 应用CHAMP卫星星历精化地球重力场模型的研究[D]. 武汉: 中国科学院测量与地球物理研究所, 2000.) |
| [9] | DITMAR P, VAN DER SLUIJS A A E. A Technique for Modeling the Earth's Gravity Field on the Basis of Satellite Accelerations [J]. Journal of Geodesy, 2004, 78(2): 12-33. |
| [10] | DITMAR P, LIU X. Dependence of the Earth's Gravity Model Derived from Satellite Accelerations on a Priori Information [J]. Journal of Geodynamics, 2007, 43(2): 189-199. |
| [11] | HAN S C, JEKELI C, SHUM C K. Efficient Gravity Field Recovery Using in Situ Disturbing Potential Observables from CHAMP [J]. Geophysical Research Letters, 2002, 29(16): 1789-1793. |
| [12] | VISSER P, SNEEUW N, GERLACH C. Energy Integral Method for Gravity Field Determination from Satellite Orbit Coordinates [J]. Journal of Geodesy, 2003, 77(3): 207-216. |
| [13] | BEUTLER G, JÄGGI A, MERVART L, et al. The Celestial Mechanics Approach: Theoretical Foundations [J]. Journal of Geodesy, 2010, 84(10): 605-624. |
| [14] | BEULTER G, JÄGGI A, MERVART L, et al. The Celestial Mechanics Approach: Application to Data of the GRACE Mission [J]. Journal of Geodesy, 2010, 84(11): 661-681. |
| [15] | ILK K H, LÖCHER A, MAYER-GÜRR T. Do We Need New Gravity Field Recovery Techniques for the New Gravity Field Satellites? [C]//VI Hotine-Marussi Symposium on Theoretical and Computational Geodesy. Berlin: Springer, 2008: 3-9. |
| [16] | MAYER-GüRR T, FEUCHTINGER M, KUSCHE J. A Comparison of Various Procedures for Global Gravity Field Recovery from CHAMP Orbits [M]. Berlin: Springer, 2005: 151-156. |
| [17] | REUBELT T, SNEEUW N, GRAFAREND E W. Comparison of Kinematic Orbit Analysis Methods for Gravity Field Recovery [C]//VII Hotine-Marussi Symposium on Mathematical Geodesy. Berlin: Springer, 2012: 259-265. |
| [18] | MIGLIACCIO F, REGUZZONI M, SANSO F, et al. GOCE Data Analysis: The Space-wise Approach and the First Space-wise Gravity Field Model[C]//Proceedings of the ESA Living Planet Symposium.Copenhagen:[s.n.], 2010. |
| [19] | PAIL R, BRUINSMA S, MIGLIACCIO F, et al. First GOCE Gravity Field Models Derived by Three Different Approaches [J]. Journal of Geodesy, 2011, 85(11): 819-843. |
| [20] | YI W Y. An Alternative Computation of a Gravity Field Model from GOCE [J]. Advances in space research, 2012, 50(3): 371-384. |
| [21] | ZHONG Bo, LUO Zhicai, LI Jiancheng, et al. Spectral Combination Method for Recovering the Earth's Gravity Field from High-low SST and SGG Data[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 735-742.(钟波, 罗志才, 李建成, 等. 联合高低卫-卫跟踪和卫星重力梯度数据恢复地球重力场的谱组合法[J]. 测绘学报, 2012, 41(5): 735-742.) |
| [22] | BAUR O, REUBELT T, WEIGELT M, et al. GOCE Orbit Analysis: Long-wavelength Gravity Field Determination Using the Acceleration Approach [J]. Advances in Space Research, 2012, 50(3): 385-396. |
| [23] | EGG-C. GOCE High Level Processing Facility:GOCE Level 2 Product Data Hand-book[EB/OL].[2012-12-25].www.iapg.bgutum.de/Projects/GOCE_HPF. |
| [24] | KUSCHE J, KLEES R. Regularization of Gravity Field Estimation from Satellite Gravity Gradients [J]. Journal of Geodesy, 2002, 76(6): 359-368. |
| [25] | DITMAR P, KUSCHE J, KLEES R. Computation of Spherical Harmonic Coefficients from Gravity Gradiometry Data to be Acquired by the GOCE Satellite: Regularization Issues [J]. Journal of Geodesy, 2003, 77(7): 465-477. |