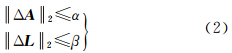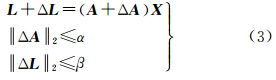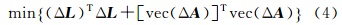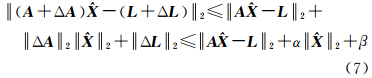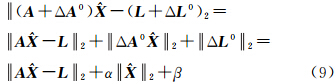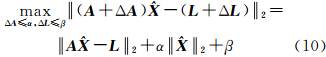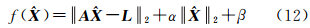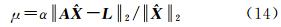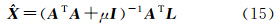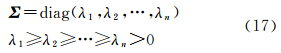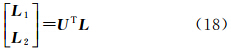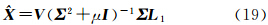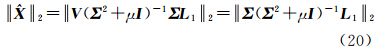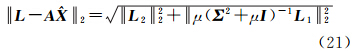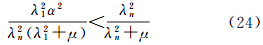1 引 言
不确定性是一种广义的误差,是不精确性、模糊性、不明确性等概念的总称,它包含数值和概念的误差,也包含可度量和不可度量误差,它比一般的误差范围要广,如属性不确定性、模糊不确定性等[1, 2, 3]。它有时具有随机性,且统计性质明显;有时没有随机性,仅是一个模糊数。不确定度是不确定性的度量,是用于表达测量结果质量优劣的一个指标,它可以用方差、均方差、误差区间、误差椭圆、误差椭球表示[4, 5]。测量数据的不确定性不再是一个具体数值,有时仅知道它们各自在一定的实数区间内变动,有时仅是一个模糊数,这给测量平差数据处理带来了困难,现有算法理论还无法抑制这些不确定性因素的影响,要提高参数估计的可靠性需要针对不确定性建立新的平差准则,研究不确定度传播规律以及观测数据中去除不确定性因素的平差方法。在测绘数据处理领域,应用不确定度理论,研究不确定度评定方法,寻找减小不确定度的算法等已成为一个研究热点[6, 7, 8, 9, 10, 11]。文献[12, 13, 14]对测量不确定度理论进行了研究,拓展了测量平差数据处理的理论与方法。整体平差算法也可以看成是对于不确定性平差算法的一种探索,它在一定程度上减弱了不确定性因素的影响[15, 16, 17, 18],然而,由于不确定性的统计信息(如均值和方差等)和概率分布函数无法确定,人为地确定它们的统计性质本身就在增加新的不确定性,从而影响状态参数估计的可靠性[19, 20]。利用先验信息来抑制不确定性是不确定性观测数据平差的有效方法,但是,测绘工程中先验信息的获取一般是比较困难的,计算也比较复杂,更重要的是,许多先验信息本身也只是一种不确定性的描述,如参数的可行区间、有界噪声、噪声方差的范围等。本文从另一个角度来研究不确定性测量数据的平差问题,直接将不确定度作为一个参数融入函数模型中,建立了一种新的针对不确定性的平差准则,在算法中对不确定度进行抑制。
2 不确定性平差模型平差模型为
式中,A为m×n(m≥n)维设计矩阵;L为n维观测向量;e 为n维随机误差向量。由于观测过程以及建立的模型中存在不确定性,假设“真实”的设计矩阵为 A +Δ A ,“真实”的观测值为 L +Δ L ,这里,Δ A = [Δaij] m×n,Δ L =[Δl1 Δl2 … Δln]T可以看成是A和L的不确定性,它们是扩展了的随机误差,可能不存在统计性质,其不确定度可用区间来评定,如
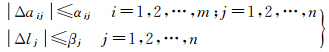
为进一步说明 A、L 的不确定性,在图 1中,分别以 A、L 为圆心,α和β为半径的圆来描述描述 A和L的不确定性,α和β可以看成是 A、L 的不确定性的一种度量,称之为 A、L 的不确定度。
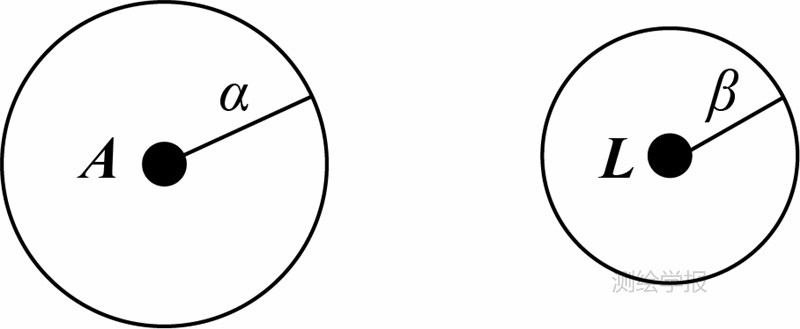 |
| 图 1 A、L 不确定性的图示Fig. 1 Diagram about uncertain of A、L |
在平差模型中融入不确定度参数α和β,可得不确定性平差模型
不确定性平差模型不同于普通的平差模型,也不同于整体平差模型。在不确定性平差模型中,设计矩阵 A 和观测向量 L 分别受到范数有界的Δ A 和Δ L 的干扰,而它们的界α和β是已知的,即设计矩阵 A 和观测向量 L 的不确定度是已知的。在整体平差模型中,A和L 的不确定性Δ A 和Δ L 是无界的,即 A和L 的不确定度是未知的。普通的平差模型中,A 没有不确定性(Δ A =0),Δ L 的不确定性未知。整体最小二乘平差的准则是
式中,vec(Δ A )为矩阵Δ A 的拉直向量。由于在这个平差准则中既要顾及观测误差又要顾及系数矩阵的误差,总体上虽然考虑了 A和L 的不确定性问题,但是,容易出现对 A 的过度校正,例如 A 的不确定度非常小,而 L 的不确定度较大时就会因为对 A 进行过度校正,从而使得 A 变成有较大的不确定性(本文后面的实例就是这一情形)。特别是在已知Δ A 和Δ L 的界的时候,在采用总体最小二乘平差时,常会出现越界的情形与先验信息不符。
利用Δ A 和Δ L 的先验信息(不确定度)进行参数估计,或者说是在有界的不确定性误差情况下,进行平差解算是测量平差数据处理的一种新的探索,在给定的有界区间内,寻找参数解更符合实际。为了寻找一种新的针对有界不确定性观测数据进行平差,笔者建立下面的min-max平差准则,即让残差中的最大不确定性达到最小,从而使得参数解中的不确定性达到最小化,即
式(5)可以称之为不确定性min-max平差准则。 3 残差中最大不确定度的几何意义
本文使用和文献[20]类似的方法来说明残差中最大不确定度的几何意义。设简单不确定性平差模型为
式中,l =[l1 l2]T不存在不确定性,只存在随机误差 e =[e1 e2]T,a =[a1 a2]T,ΔA =[Δa1 Δa2]T。令
 是模型(6)的参数估计,不妨设
是模型(6)的参数估计,不妨设 >0。在图 2中,设OA=a,OB=l,OC=a
>0。在图 2中,设OA=a,OB=l,OC=a ,圆A半径为α,它表示a的不确定性变化范围;圆C的半径为α|
,圆A半径为α,它表示a的不确定性变化范围;圆C的半径为α| |,它表示a
|,它表示a 的不确定性变化范围,OM和ON是圆A和圆C的公切线。连接B点和圆心C并延长圆周于F点,BF是圆外B点到圆C的最长的割线,对于估计值
的不确定性变化范围,OM和ON是圆A和圆C的公切线。连接B点和圆心C并延长圆周于F点,BF是圆外B点到圆C的最长的割线,对于估计值 的最大不确定度显然是B到F的距离r3,r3=max
的最大不确定度显然是B到F的距离r3,r3=max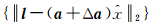 ,同样,圆A实际上可以看作是圆C在|
,同样,圆A实际上可以看作是圆C在| |=1时的一种特殊情形,BG是通过圆心A的最长的割线,因此,|
|=1时的一种特殊情形,BG是通过圆心A的最长的割线,因此,| |=1时,残差最大不确定度是B到G的距离r2,r2=
|=1时,残差最大不确定度是B到G的距离r2,r2=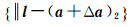 。圆C可以看成是|
。圆C可以看成是| |>1时的情形,当 |
|>1时的情形,当 | |<1时,不确定性圆会出现在圆A的左边。一般情形下,总可以从B点出发,通过圆心ax,作出半径为α|x|的最长割线求出其参数解的最大不确定度。从图 2中可以看出,r2
|<1时,不确定性圆会出现在圆A的左边。一般情形下,总可以从B点出发,通过圆心ax,作出半径为α|x|的最长割线求出其参数解的最大不确定度。从图 2中可以看出,r2 |
| 图 2 残差最大不确定度几何意义Fig. 2 Geometric meaning of the maximum possible uncertainty in residual |
从B向OM作垂线BE,交OC于D点,以D为圆心,DE为半径作圆D,同样圆D也对应模型(6)的一个参数解,这时最大的不确定度为BE的长度r1,从图形可以看出r1
在图 3中,圆H是某一参数解所对应的不确定性圆,对应| 通过上面的分析,求最小的最大不确定度过程为:① 通过B点向圆A的切线OM作垂线BE交OA于D点,E为垂足;② 以半径DE作圆,DE= a
从图 4可以看出,当OB(观测向量l)垂直于OE时,观测向量l在OE上的投影为0向量。当观测向量l与OE垂直时,AD=AE=OD,OD可以看成是向量a在向量l上的投影。因此,OD= 上面的分析中假设观测向量l中不存在不确定性,当观测向量l存在不确定性时也可以得到相应的几何解释。
利用范数的性质,有
对于给定的A的不确定度α和给定的L的不确定度β,若令
由式(7)和式(9)可知
根据式(5)和式(10),不确定性min-max平差准则可以转换成另一形式的平差准则
对于式(11),设目标函数为f(
令
利用式(22)求μ通常比较复杂,由于式(22)的右边也含有μ,可以使用迭代法进行求解,下面分析使用式(22)迭代求解μ的迭代收敛性问题。对φ(μ)求导,并顾及式(17)和式(22),有 因为上式的方括号中是一个正数,所以有
测绘工程中,由于观测值是含有误差的,因而平差模型(3)中Δ L ≠0,即β≠0。由文献[20]可知式(22)在β≠0时,当α≥λ1,
为了检验算法的有效性,笔者通过直线方程y=1.4x生成一个不含误差的数据序列,然后,在这些数据序列中加上随机误差,其中,所产生的随机误差满足
由上面产生的数据序列来生成观测向量 L =[l1 l2 l3 l4 l5 l6]T和设计矩阵 A =[a1 a2 a3 a4 a5 a6]T,其中,ai=xi-Δxi,li=yi-Δyi(见表 2),并建立不确定性平差模型 从仿真数据的产生中已经知道参数的真值为1.4,笔者用最小二乘平差方法(LS)、整体最小二乘平差方法(TLS)和不确定性平差方法(ULS)3种方法进行参数解算,并分析和比较3种方法的的效果。利用Matlab对 A 进行SVD运算,可以求得 A 的奇异值为2.891 7,因为 A 的不确定度小于 A 的奇异值,利用Matlab编程可以算得μ=1.093 2,利用式(8)可以计算出
使用文献[15]的总体最小二乘(TLS)算法,可以得到总体最小二乘平差解
由上面的计算结果可得如下结论:
(1)
(2)
(3)
在测量数据的获取过程中,经常存在着不确定性,它们影响着参数估计的可靠性。目前的测量平差方法是基于“观测值的不确定性就是随机性”这一基本假设的,实际测量工程中有许多不同于随机误差的不确定性因素,它们影响着参数估计的可靠性。扩展误差理论与测量平差方法处理测量数据中的不确定度,必须对观测中不确定性因素进行数值化、参数化,把它们融入平差模型中,这需要有理论和方法上的突破。本文通过建立不确定性平差模型,把不确定度作为参数融入函数模型中,利用残差中不确定性传播规律,建立 了一种基于残差最大不确定度达到最小的平差准则,并用迭代算法得到了不确定性平差模型的解算方法。通过实例分析了最小二乘平差、整体最小二乘平差和不确定性平差准则下的最优解的不同特点。  |<1的参数解,其圆的位置在圆D的左边,由上面的分析可知,参数解的最大不确定度为经过圆心H的割线BI的长度,设其为r4,J为直线OE与圆H相切的切点,设BJ的长度为r,BE的长度同图 1中一样为r1,由几何知识可知有r4
|<1的参数解,其圆的位置在圆D的左边,由上面的分析可知,参数解的最大不确定度为经过圆心H的割线BI的长度,设其为r4,J为直线OE与圆H相切的切点,设BJ的长度为r,BE的长度同图 1中一样为r1,由几何知识可知有r4
图 3 最小的残差最大不确定度Fig. 3 The minimized maximum possible uncertainty in residual  ,
, =1/aDE就是其最优解。
=1/aDE就是其最优解。
 ,即当不确定性圆的半径α=
,即当不确定性圆的半径α= ,l与OE是垂直的。因此模型(6)有非0的最优解,必须满足:
,l与OE是垂直的。因此模型(6)有非0的最优解,必须满足: 。
。

图 4 非0参数解的几何意义Fig. 4 Geometric meaning of non-zero-parameter solution  ,并且
,并且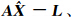
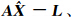 向量是共线的,由范数的运算性质,有
向量是共线的,由范数的运算性质,有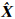 )
)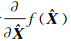 =0,可以得到参数的最优解
=0,可以得到参数的最优解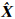 以及解向量
以及解向量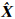 有关。要求出真正的参数解,还需要确定μ的值,下面探讨μ的计算方法,对矩阵 A 进行SVD分解
有关。要求出真正的参数解,还需要确定μ的值,下面探讨μ的计算方法,对矩阵 A 进行SVD分解 

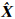 =0;而当α<λ1时,μ有唯一的正数解。由于‖Δ A‖2≤α中的α通常很小,若α满足λ1α<λn2,因为
=0;而当α<λ1时,μ有唯一的正数解。由于‖Δ A‖2≤α中的α通常很小,若α满足λ1α<λn2,因为
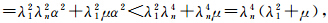 故
故 ,见表 1。
,见表 1。
xi -1.6 -0.8 -0.2 0.5 1.2 1.8
Δxi -0.071 8 0.034 4 0.145 8 0.341 2 -0.176 2 -0.231 4
yi -2.240 0 -1.120 0 -0.280 0 0.700 0 1.680 0 2.520 0 Δyi 1.739 6 1.146 7 0.928 9 0.379 0 -0.289 9 0.805 0 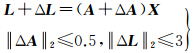
ai -1.739 9 -1.113 7 -0.211 9 0.668 3 1.165 7 1.498 0 li -1.389 3 -2.340 4 0.403 2 -0.097 1 2.072 1 3.783 7 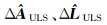
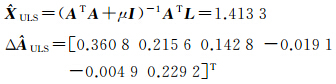



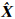 LS=1.591 5是在普通最小二乘平差准则下的最优解,其拟合直线见图 5,它没有考虑 A和L 的不确定性,其残差平方和RLS2=6.067 1,而
LS=1.591 5是在普通最小二乘平差准则下的最优解,其拟合直线见图 5,它没有考虑 A和L 的不确定性,其残差平方和RLS2=6.067 1,而 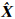 ULS和
ULS和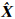 TLS在不考虑不确定性时的残差平方和为
TLS在不考虑不确定性时的残差平方和为 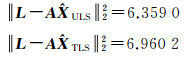
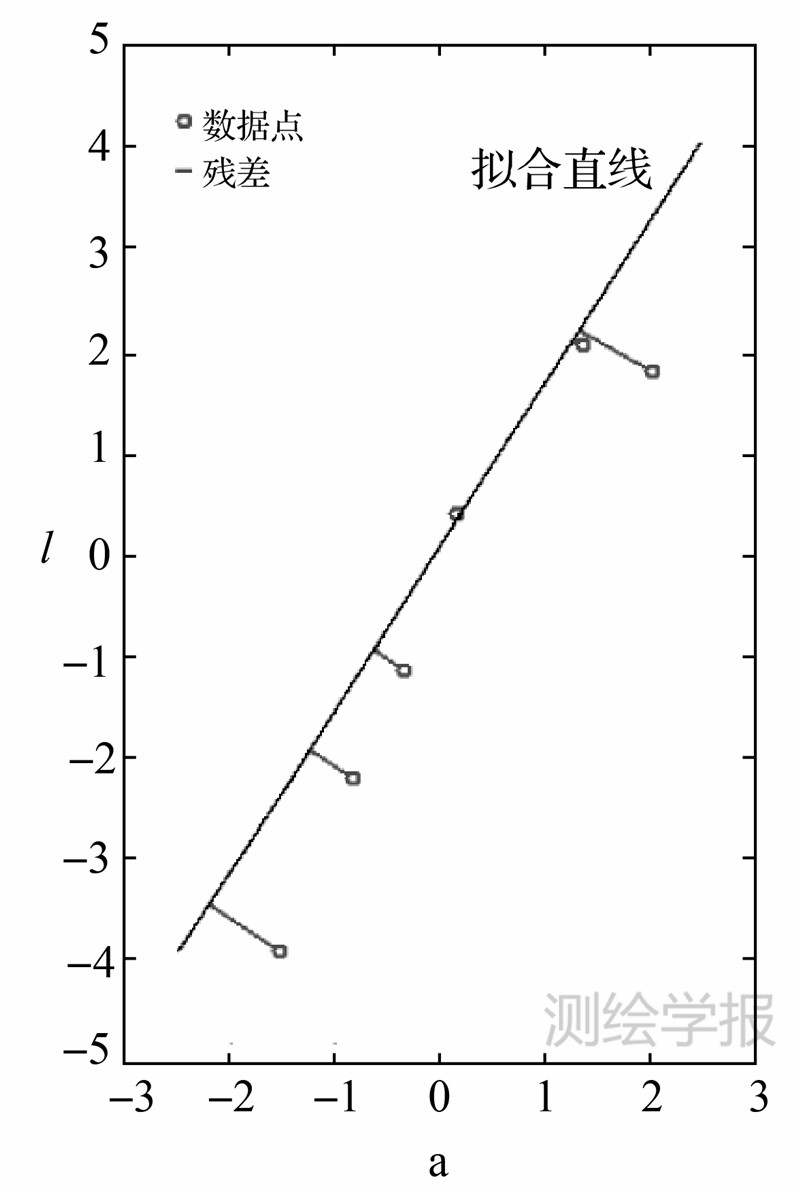
图 5 最小二乘平差方法Fig. 5 Least squares adjustment method 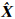 TLS=1.903 1是在整体平差准则(4)下的最优解,其拟合直线见图 6,这时目标函数值fTLS
TLS=1.903 1是在整体平差准则(4)下的最优解,其拟合直线见图 6,这时目标函数值fTLS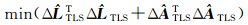

图 6 整体平差方法Fig. 6 Total least squares adjustment method 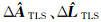 的结果已经明显地看到这些转移,这样虽然可以减少总体的不确定性,但会使得相对准确的 A 变得不够准确,从而影响解
的结果已经明显地看到这些转移,这样虽然可以减少总体的不确定性,但会使得相对准确的 A 变得不够准确,从而影响解 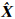 TLS的精度,这时,它甚至比普通的最小二乘平差解还要差。另外,由于
TLS的精度,这时,它甚至比普通的最小二乘平差解还要差。另外,由于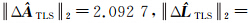 1.099 6明显地与先验信息不符,这样的解即使精度高,也会与实际情形不相符。
1.099 6明显地与先验信息不符,这样的解即使精度高,也会与实际情形不相符。 ULS=1.413 3是与真值1.4最接近的,其拟合直线见图 7,因为它是在不确定性具有先验约束 ‖Δ A ‖2≤0.5,‖Δ L‖2≤3情况下求得的,它采用的平差准则是最大不确定性的最小化原则(5)。这时,在考虑不确定性先验信息的情形下,它的残差平方和RULS2=0.320 8要小于最小二乘平差准则和整体最小二乘平差准则下的残差平方和。上面3种平差的准则各有各的侧重点,并不能说明哪一种准则更好,只是在具体的测量数据处理过程中,如果对这些不确定性有先验信息,可以选取相应的平差准则进行处理。
ULS=1.413 3是与真值1.4最接近的,其拟合直线见图 7,因为它是在不确定性具有先验约束 ‖Δ A ‖2≤0.5,‖Δ L‖2≤3情况下求得的,它采用的平差准则是最大不确定性的最小化原则(5)。这时,在考虑不确定性先验信息的情形下,它的残差平方和RULS2=0.320 8要小于最小二乘平差准则和整体最小二乘平差准则下的残差平方和。上面3种平差的准则各有各的侧重点,并不能说明哪一种准则更好,只是在具体的测量数据处理过程中,如果对这些不确定性有先验信息,可以选取相应的平差准则进行处理。
图 7 不确定性平差方法Fig. 7 Adjustment method with uncertainty
| [1] | YANG Yuanxi. Some Notes on Uncertainty, Uncertainty Measure and Accuracy in Satellite Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5): 646-650.(杨元喜. 卫星导航的不确定性、不确定度与精度若干注记[J].测绘学报, 2012, 41(5): 646-650.) |
| [2] | TAO Benzao. Basic Theory of Uncertainty of Quality Control in GIS[J]. Journal of Institute of Surveying and Mapping, 2000, 17(4): 235-238. (陶本藻. GIS质量控制中不确定度理论[J]. 测绘学院学报, 2000, 17(4): 235-238.) |
| [3] | XU Zifu, LIU Dong, RUAN Anlu. Review on Uncertainty Measure, Accuracy and Precision[J]. Measuring Technology, 2007, 27(2): 37-39.(许自富, 刘东, 阮安路.不确定度、准确度、精度辨析[J].计量技术, 2007, 27(2): 37-39.) |
| [4] | Bureau International des Poids et Mesures. JCGM 104:2009.Guide to the Expression of Uncertainty in Measurement[S]. Switzerland:[s.n.], 1993. |
| [5] | Bureau International des Poids et Mesures. JCGM 100:2008.Guide to the Expression of Uncertainty in Measurement[S].Switzerland:[s.n.], 1995. |
| [6] | ZOU Yonggang, ZHAI Jingsheng, LIU Yanchun, et al. Seabed DEM Construction Based on Uncertainty[J]. Geomatics and Information Science of Wuhan University, 2011, 36(8): 964-968. (邹永刚, 翟京生,刘雁春, 等. 利用不确定度的海底数字高程模型构建[J]. 武汉大学学报:信息科学版, 2011, 36(8): 964-968.) |
| [7] | SHI Yufeng, SHI Wenzhong, JIN Fengxiang. Hybrid Entropy Model of Spatial Data Uncertainty in GIS[J]. Geomatics and Information Science of Wuhan University, 2006, 31(1): 82-85. (史玉峰, 史文中, 靳奉祥. GIS中空间数据不确定性的混合熵模型研究[J]. 武汉大学学报:信息科学版, 2006, 31(1): 82-85.) |
| [8] | ZHANG Zhenglu, FAN Guoqing, ZHANG Songlin, et al. General Reliability of Measurement[J]. Geomatics and Information Science of Wuhan University, 2012, 37(5): 577-581. (张正禄, 范国庆, 张松林, 等. 测量的广义可靠性研究[J]. 武汉大学学报:信息科学版, 2012, 37(5): 577-581.) |
| [9] | JIA Shuaidong, ZHANG Lihua, SONG Guoda, et al. A Method for Constructing an Adaptive Grid Digital Depth Model Based on Mean Vertical Uncertaintyof Area[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 454-460. (贾帅东, 张立华, 宋国大, 等. 基于区域平均垂直不确定度的自适应网格水深建模方法[J]. 测绘学报, 2012, 41(3): 454-460.) |
| [10] | CHEN Wei. Least Uncertainty Estimation Theory With Applications[D]. Wuhan:Wuhan Univercity, 2005. (陈伟. 最小不确定度估计理论及其应用[D]. 武汉:武汉大学, 2005.) |
| [11] | CHEN Wei, WANG Xinzhou. Least Uncertainty Estimation Theory and Its Applications to Resolving Morbid Problems[J]. Geomatics and Information Science of Wuhan University, 2008,33(7): 752-754. (陈伟, 王新洲. 最小不确定度估计原理及其病态问题解法研究[J]. 武汉大学学报:信息科学版, 2008,33(7): 752-754.) |
| [12] | WANG Xinzhou. Maximum Possibility Estimation Restricted by Least Uncertainty[J]. Engineering of Surveying and Mapping, 2003(1):5-8. (王新洲. 最小不确定度约束下的极大可能性估计[J]. 测绘工程,2003(1):5-8.) |
| [13] | TAO Benzao. Estimation of Accuracy and Uncertainty and Its Application[J].Site Investigation Science and Technology,2003,5: 24-27. (陶本藻. 精确度和不确定度估计及应用[J]. 勘察科学技术, 2003,5: 24-27.) |
| [14] | YANG Yuanxi. Discussion on “A New Measure of Positional Error”[J]. Acta Geodaetica et Cartographica Sinica, 2009,38(3):280-282. (杨元喜.关于“新的点位误差度量”的讨论[J].测绘学报, 2009,38(3):280-282.) |
| [15] | SCHAFFRIN B, FELUS Y A.A Window on the Future of Geodesy[M].Berlin:Springer, 2005:417-421. |
| [16] | SCHAFFRIN B, WIESER A. On Weighted Total Least-Squares Adjustment for Linear Regression[J]. Journal of Geodesy. 2008, 82(7): 415-421. |
| [17] | QIU Weining, QI Gongyu, TIAN Fengrui. An Improved Algorithm of Total Least Squares for Linear Models[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 708-710. (邱卫宁, 齐公玉, 田丰瑞. 整体最小二乘求解线性模型的改进算法[J]. 武汉大学学报:信息科学版, 2010, 35(6): 708-710.) |
| [18] | KONG Jian, YAO Yibin WU Han. Iterative Method for Total Least-Squares[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 711-714. (孔建, 姚宜斌, 吴寒. 整体最小二乘的迭代解法[J]. 武汉大学学报:信息科学版, 2010, 35(6): 711-714.) |
| [19] | GHAOUI L E, LEBRET H. Robust Solutions to Least-Squares Problems with Uncertain Data[J].SIAM Journal on Matrix Analysis and Applications,1997,18(4): 1035-1064. |
| [20] | CHANDRASEKARAN S, GOLUB G H, GU M, et al. Parameter Estimation in the Presence of Bounded Data Uncertainties[J]. 1998, 11(4): 235-252. |