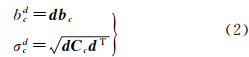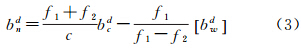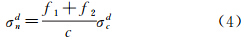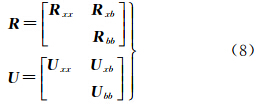2. 地理信息工程国家重点实验室，陕西 西安 710054
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054 China
1 引 言
GPS/GNSS接收机只能获得载波相位小数周的测量值，载波相位观测量总是存在一个整数周的偏差即模糊度[1]。在GPS/GNSS网解中，载波相位模糊度和其他参数(如卫星轨道、测站坐标等)一起解算，利用载波相位模糊度的整数特性，将其固定于最近的整数，从而获得高精度的大地参数解算结果[2, 3]。在过去20多年的GPS全球网数据处理实践中，模糊度解算方法得到了深入的研究和应用，每一次改进都带来网解结果的大幅改进或计算效率的大幅提升[2, 3, 4, 5, 6]。
由于卫星和接收机相位时延和初始相位的存在[7, 8, 9, 10, 11]，只有两颗卫星和两台接收机同步观测的双差模糊度才具有整数特性[1, 2, 4, 5, 12]，能够被固定到最近的整数。为了消除电离层延迟的影响，在全球GPS/GNSS网解中，采用双频消电离层组合载波相位作为主要观测量，将模糊度参数与其他参数(如：测站坐标、卫星钟差、卫星轨道等)一起作为未知参数，采用有效的线性估计方法(如最小二乘法)求得包括模糊度参数在内的所有参数的浮点解。在此基础上进行模糊度固定，将固定了的双差模糊度作为先验条件对全网解进行约束，从而改进其他参数的估计结果。由于消电离层模糊度本身不具有整数特性，模糊度固定的基本思路是先固定宽巷模糊度[2]，再基于已固定的宽巷模糊度和模糊度浮点解固定窄巷模糊度，其中固定宽巷模糊度的最常用的方法是基于双频相位和伪距的MW组合实现的。在实际数据处理中，有的采用双差数据，有的采用非差数据。对于双差数据，其模糊度参数天然就是双差的，可在其浮点解的基础上直接进行固定。对于非差数据，首先要从非差模糊度中构造出双差模糊度，从数学上讲，就是定义一个矩阵，将非差模糊度及其方差映射到双差模糊度和对应的协方差矩阵[2, 4]。人们希望得到的双差模糊度集合包含有最多的可被固定且相互独立的模糊度，但这并不是一件容易的事。在过去的20多年中，国内外学者在这方面做了许多工作，在1989年，相继提出了独立基 线选取法[3, 6]和全网Grams-Schmidt(GS)正交化独立性检验法[2]，在此后的十多年里，这方面少有进展。2005年，文献[4]吸收上述两种方法的优点，提出了分层的独立模糊度选取方法，改进了模糊度选取的标准，使得计算效率和模糊度固定的成功率都有大幅提高。尽管如此，依然有可以改进的地方。
本文将对现有的独立双差模糊度选取方法作简要的描述和分析，借鉴分层独立双差模糊度选取方法的思想提出了先星座层后网层的独立双差模糊度选取新方法，通过更新协方差阵的上三角平方根实现模糊度固定。以上方法已应用于西安测绘研究所开发的卫星定轨定位系统SPODS当中[13]。
2 现有双差模糊度选取方法当采用双差相位作为观测量时，构造(独立)双差观测量的过程就是选取独立双差模糊度的过程。尽管双差数据处理和非差数据处理在细节上有所差异，但是现有GNSS数据处理软件中独立双差模糊度选取方法可以归纳为以下3种。
方法1[6]：对所有理论上成立(对应两个测站和两颗卫星有一定时长的同步观测)的双差模糊度按照一定顺序(例如：按消电离层组合实数模糊度的方差升序)排列，采用GS正交化方法逐个判断候选双差模糊度与已入选双差模糊度的独立性，得到全网最优的独立双差模糊度集，所谓最优指包含最多可被固定的双差模糊度。
方法2[2]：以基线长度为标准采用“简易的独立性检验方法”选择独立的基线，对每一条独立基线简单地通过选取参考星确定独立双差模糊度，而参考星的选择通常以最长观测时间为标准，或采用GS方法进行独立性检验，基线中的候选双差模糊度按照消电离层组合模糊度或宽巷模糊度的方差排序。所有独立基线的独立双差模糊度构成全网独立双差模糊度集，其中“简易的独立性检验方法”就是图论中从连通图中产生最小生成树的Kruskal算法[14]。
文献[4]深入分析和评述了以上两种方法的不足，提出了一种先基线层后网层的分层独立双差模糊度选取方法。
方法3[4]：先针对每一条(小于一定长度的)基线中的双差模糊度按照固定成功概率降序排列，采用Kruskal算法确定该基线的独立双差模糊度，然后在全网范围内，将所有基线入选的双差模糊度按照固定成功概率进行排序，并逐个利用GS方法进行独立性检验，获得全网的最优独立双差模糊度集。
就独立性检验而言，方法1采用GS方法对所有理论成立的双差模糊度进行独立性检验，可以获得最优的独立双差模糊度集，但是GS算法相当耗时；方法2采用独立基线的方法，避免进行GS计算，计算效率高，但是只能获得次优的独立双差模糊度集；方法3吸取了前两种方法的优点，通过分层选取，减少在网层需要进行GS检验的双差模糊数量，提高计算的效率，且保证得到与方法1一致的最优模糊度集。此外，方法3的改进还体现在其引入模糊度固定成功概率作为候选模糊度排序的标准，这与后续模糊度固定时考察的指标一致，提高了模糊度固定成功率。该方法已经被许多研究机构的数据处理软件采用，为了便于描述和比较，下文将方法3称为传统(分层)方法。
3 新的独立双差模糊度选取方法本文提出的独立双差模糊度选取方法借鉴了传统分层方法的思想，分星座层和网层进行独立模糊度选取：①星座层，采用Kruskal方法选取每一对卫星包含的独立双差模糊度；②网层，对星座层获得的所有双差模糊度采用GS算法进行独立性检验。在这两个层级中，候选双差模糊度都按照它们的固定成功概率进行排列。舍弃在星座层中不能固定宽巷的模糊度。
3.1 星座层考察任意两颗卫星符合条件(例如被两个测站同步观测时间大于10 min)的候选双差模糊度，采用MW组合计算双差宽巷模糊度及其标准差的估值 bwd和σwd[2]，利用式(1)计算固定成功概率[3, 4]
式中，erfc(x)=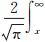
e－t2dt；[·]表示取最近的整数。式(1)同时考虑了宽巷模糊度估值和方差。对于给定的置信水平，如α=0.5%，如果pw大于1－α，则宽巷模糊度能够被固定到最近整数，否则不固定宽巷。如果在这一步无法固定宽巷，对应的窄巷模糊度也不能固定，则该双差模糊度无法固定。任意双差消电离层组合模糊度的估值bcd及其标准差σcd可表示为
式中，bc和Cc为非差消电离层组合模糊度估值及其协方差矩阵；d为对应于双差模糊度bcd的映射算子。在固定了宽巷之后，利用双差消电离层模糊度的浮点解，窄巷模糊度的估值bdn及其标准差σdn可由式(3)和式(4)计算
式中，c表示光速；f1、f2分别为两个频点的频率。
同样利用式(1)可以计算得到窄巷模糊度的固定成功概率。在序贯的模糊度固定过程中，窄巷模糊度的估值会因之前固定的模糊度而改进，这一阶段计算得到的窄巷模糊度固定成功概率并非最终值，在模糊度固定阶段需要利用更新后的估值和方差进行重新计算。
将宽巷和窄巷固定成功概率相乘得到综合固定成功概率。将该卫星对中所有固定了宽巷的双差模糊度按照综合固定成功概率的降序排列(没有固定宽巷的双差模糊度无法固定，不予考虑)，采用Kruskal算法选取独立双差模糊度。
3.2 网 层对星座层获得的所有独立双差模糊度按照综合固定成功概率的降序进行排列，采用GS正交化算法进行独立性检验，获得全网独立双差模糊度集和对应的映射矩阵。在非差数据处理中，有时为了得到可逆的转换矩阵，需要将非差模糊度也放到列表中，通过GS方法逐个检验其与已选模糊度组合(双差/非差)的独立性，直至获得的映射矩阵为满秩的方阵。
3.3 讨 论在GPS/GNSS网中，一颗卫星被多个测站观测到，测站之间或卫星之间没有直接观测量，所谓的“网”实际上是站—星观测网。通过GPS网解可以获得任意两个测站的相对位置向量，称作基线向量。这些测站和基线向量构成基线网，也称为GPS跟踪网，实际上只是该站—星观测网的子网。就独立双差模糊度选取而言，人们习惯从基线的角度来考察全网的独立双差模糊度，如方法2和方法3。然而，作为这一观测网的一个节点，测站和卫星的地位是相等的。理论上，新方法可以获得与传统方法一致的独立双差模糊度选取结果。假设某一时段有n个测站同时观测m颗卫星，则基线数量为Cn2，卫星对数为Cm2，任意一对卫星和一条基线可得到一个双差模糊度，则全网双差模糊总数为Cn2Cm2。传统方法中，每一条基线包含的独立双差模糊度个数是 (m－1) ，则网层候选双差模糊度个数为Cn2 (m－1) ，是测站数n的二次函数；新方法中，每一对卫星包含的独立双差模糊度个数是 (n－1) ，网层候选双差模糊度个数为 (n－1) Cm2，为测站数n的一次函数。采用传统方法和新方法需要在全网层进行独立性检验的双差模糊度数量比为n∶m。在全球GPS/GNSS网数据处理中，测站数量往往可以达到100～200个，要远大于卫星数量，相比而言，采用新方法将显著减少需要采用GS算法进行独立性检验的模糊度数量，从而减少计算时间。现实中，所有测站同时观测全部卫星的情况很少出现，上述数值会有所差异。如果处理多GNSS数据(暂不考虑GNSS之间的双差模糊度固定)，独立双差模糊度选取分别对不同系统的星座进行。
4 基于协方差阵上三角平方根的模糊度固定方法固定模糊度可以看作是对模糊度实数解附加(整数)先验信息约束的过程，可以基于映射后得到的双差模糊度及其协方差阵实现。对于非差数据处理而言，为了恢复模糊度以外的其他参数和计算观测值残差，需要将固定后的双差模糊度重新转化为非差模糊度，就必须要在双差模糊度选取时构建可逆的映射矩阵[2]。也可以直接基于原始法方程进行，此时不需要构造可逆的映射矩阵[4]。本文提出一种基于非差模糊度的协方差阵上三角平方根的序贯模糊度固定方法，即模糊度固定通过序贯地更新非差模糊度估值及其协方差阵的上三角平方根而实现。非特别说明时下文的“模糊度”指消电离层组合模糊度。
不妨将全球网解的法方程系统表示为
式中，
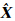为未知参数的解向量；N 为法矩阵；Z 为法方程右项。对N 进行Cholesky分解，得N=R T R，R 为上三角矩阵，式(5)的解为
式中，
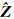=R －T Z；C 为协方差阵；U=R －1也为上三角矩阵。式(6)的求解不需要进行矩阵求逆，只需采用后向回代的方法求解[15, 16]。
将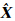表示为
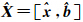，其中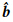
为非差模糊度参数的实数解向量；
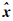为除模糊度以外的其他参数，如测站位置、卫星轨道参数、对流层、钟差等。相应的，R和U可表示为
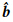的协方差阵表示为显然 Ubb为方差阵 Cb的上三角平方根。
至此已获得非差模糊度估值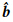及其协方差阵的上三角平方根 Ubb。下面将展示通过序贯更新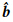和Ubb进行序贯双差模糊度固定的过程。
假设已通过3.1节和3.2节获得全网独立的双差模糊度集合，将第i个双差模糊度固定解bdd,i作为虚拟观测量，构造虚拟观测方程
式中，pi为约束权，必须显著大于观测量的权，例如取1010。则满足这一约束条件的非差模糊度参数估值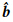
i及其方差Ubb,i的解可以通过式(12)得到[16, 17]
式中，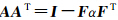
，为了保证 Ubb,i为上三角矩阵，A必须也是上三角；
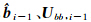表示第i个双差模糊度固定前的解，其中
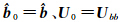。以上过程的具体算法见[15, 16]。每固定一个双差模糊度都要重新计算剩余待固定双差模糊度的估值和方差，得到新的综合固定成功率并按照降序排列，每次只固定一个“最可能”被固定的双差模糊度，直到固定所有满足条件的双差模糊度。
设得到固定模糊度后的非差模糊度参数的估值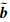
及其协方差阵的上三角平方根
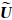bb，结合式(8)代入式(6)和式(7)有
式中
可见，只需更新
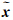和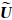xb就得到所有参数
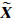及其方差阵
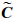的最终解。上述模糊度固定过程直接对非差模糊度协方差阵的上三角平方根进行操作，因此不需要构造可逆的映射矩阵。
5 试验及结果新的分层独立双差模糊选取方法和基于更新协方差阵上三角平方的模糊度固定方法已经应用于西安测绘研究所自主开发的SPODS软件中。为了验证新方法的有效性并评估其计算效果，收集2009年1月4—10日IGS全球观测网的数据，采用SPODS软件进行单天解算试验。试验的基本处理过程如下：在数据处理时以非差的伪距和相位消电离层组合作为观测量，采用Turboedit[18]方法进行周跳探测和修复；从IGS05.snx中选择10个测站作为基准参考站，测站坐标每个分量施加0.02 m的约束，其他测站坐标每个分量的约束为1 km；采用最小二乘法进行参数估计，估计参数包括测站坐标、卫星轨道初始状态矢量、ECOM太阳光压模型参数D0、Y0、B0、Bc、Bs[19, 20]和ERP参数，对流层天顶延迟每两小时估计一组参数，对流层水平梯度每天估计一组参数，卫星和测站钟差每个历元估计；通过验后残差分析进一步剔除粗差和周跳，以上过程迭代进行，直到没有发现新的周跳和粗差，开始模糊度固定。独立双差模糊度选取分别采用新的和传统的分层方法进行，仅考虑同步观测时长超过10 min的模糊度，固定成功概率的门限取99%。 为了更加准确地反映该方法与传统方法的差别，在以下数据处理试验中，不限制基线长度，同时无法固定宽巷的双差模糊度也作为两个层级的候选模糊度，在排序时排在固定宽巷的模糊度之后。以下试验在DELL OPTIPLEX 980 (CPU:Intel Core i5,主频：3.20 GHz,内存4 GB) 台式计算机进行。
首先，选取一个包含约64个测站的观测网，对2009年年积日4—10日的GPS数据进行单天解算。表 1是两种方法中全网双差模糊度总数、全网层候选双差模糊度数量、全网独立的双差模糊度数量，成功固定的比例和计算时间的比较。显然，全网双差模糊度的总数对两种方法是一样的。可以看出新方法与传统方法得到的全网独立双差模糊度数量也是相同的，且成功固定的比例非常接近，这说明新方法是正确的。新方法中网层候选双差模糊度的数量约为传统方法的一半，其比值约等于卫星与测站数量之比(在该试验时段GPS星座的卫星数为31)，从计算时间上看，该方法的计算时间不到传统方法的1/2。
| 年积日 | 全网双差模糊度总数 | 全网层候选双差模糊度数量 | 全网独立的双差模糊度数量 | 成功固定的比例/(%) | 计算时间/min | ||||
| 传统方法 | 本文方法 | 传统方法 | 本文方法 | 传统方法 | 本文方法 | 传统方法 | 本文方法 | ||
| 4 | 146 740 | 43 017 | 22 309 | 3364 | 3364 | 92.063 | 91.974 | 13.293 | 5.796 |
| 5 | 135 133 | 39 668 | 21 162 | 3179 | 3179 | 92.419 | 92.450 | 10.954 | 4.934 |
| 6 | 161 928 | 47 294 | 23 203 | 3474 | 3474 | 93.092 | 93.293 | 15.410 | 6.513 |
| 7 | 162 426 | 47 072 | 23 481 | 3490 | 3490 | 93.066 | 93.095 | 15.088 | 6.504 |
| 8 | 142 489 | 43 238 | 21 202 | 3291 | 3291 | 92.950 | 92.950 | 12.276 | 5.181 |
| 9 | 146 848 | 45 149 | 21 871 | 3424 | 3424 | 91.092 | 91.092 | 14.233 | 5.860 |
| 10 | 166 340 | 49 025 | 24 098 | 3608 | 3608 | 91.962 | 91.962 | 16.287 | 6.961 |
图 1给出两种方法得到的GPS卫星轨道单天解与IGS最终综合轨道比较的1D RMS。可以看出两种方法得到的GPS轨道1D RMS都在12 mm左右，仅有非常微小的差异。上文已经提到，先固定的模糊度会影响后固定的模糊度，乃至最终的参数估计结果，不同方法在实际应用时，所得到的独立双差模糊度的排序甚至具体组合都会有所差异，由此造成模糊度的固定成功比例和最终的计算结果表现出微小差异，是可以理解的。
 |
| 图 1 两种方法得到GPS卫星轨道单天解与IGS最终综合轨道比较的1D RMSFig. 1 1D RMS of the daily orbit solution with different DD-ambiguities selection approaches compared with IGS final combined orbits |
为了分析不同测站数量情况下新方法与传统方法的差别，采用2009年1月6日IGS观测网的GPS数据，针对15、31、64、93、124个测站观测网方案进行解算试验。分别考察两种方法进行独立双差模糊度选取时，网层候选双差模糊度数量和GS检验的计算时间，如图 2所示。可以看出，传统方法中，网层候选双差模糊度数量随着测站的增加呈现近似二次曲线变化，而新方法中呈现线性变化趋势，这与3.3节分析结果一致。还可以看出，随着测站数量的增加，本文方法在计算效率上的优势越明显。
 |
| 图 2 不同测站数量情况下两种方法全网层候选双差模糊度数量和GS检验计算时间的比较Fig. 2 Comparison of the number of DD-ambiguity candidates on the network level and the corresponding CPU time of GS-checking with the two different approaches for varied station numbers |
本文提出了改进的分层独立双差模糊度选取新方法。该方法和传统方法的基本思路都是通过子网分割的办法减少需要在网层进行GS独立性检验的候选模糊度数量，进而减少独立双差模糊度选取的计算时间。在全球GPS/GNSS网中，测站的数量往往是卫星数量的数倍，相比而言，本文方法在网层需要采用GS算法进行独立性检验的候选双差模糊度更少，从而显著减少计算时间。这一方法和基于更新协方差阵上三角平方的序贯模糊度固定方法已经应用于西安测绘研究所开发的SPODS软件中。本文采用IGS观测网实测的GPS数据进行计算试验，从定轨结果和模糊度选取效果两个方面，验证了本文方法的有效性；理论分析和试验结果都表明，本文方法和传统方法在网层需要采用GS算法进行独立性检验的候选双差模糊度的数量之比约为卫星与测站数量之比，测站规模越大，该方法在计算效率上的优势越明显。
| [1] | KLEUSBERG A, TEUNISSEN P J G. GPS for Geodesy [M]. Berlin: Springer-Verlag, 1996: 407. |
| [2] | BLEWITT G. Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baselines up to 2000 km [J]. Journal of Geophysical Research, 1989,94(B8): 187-203. |
| [3] | DONG D N. BOCK Y. Global Positioning System Network Analysis with Phase Ambiguity Resolution Applied to Crustal Deformation Studies in California[J]. Journal of Geophysical Research, 1989, 94(B4): 3949-3966. |
| [4] | GE M, GENDT G, DICK G, et al. Improving Carrier-phase Ambiguity Resolution in Global GPS Network Solutions[J]. Journal of Geodesy, 2005, 79(1): 103-110. |
| [5] | GE M, GENDT G, DICK G, et al. A New Data Processing Strategy for Huge GNSS Global Networks[J]. Journal of Geodesy, 2006, 80(4): 199-203. |
| [6] | MERVART L. Ambiguity Resolution Techniques in Geodetic and Geodynamic Applications of the Global Positioning System[D]. Berne: University of Berne, 1995. |
| [7] | GENG J, SHI C, GE M, et al. Improving the Estimation of Fractional-cycle Biases for Ambiguity Resolution in Precise Point Positioning[J]. Journal of Geodesy, 2012, 86(8): 579-589. |
| [8] | LOYER S, PEROSANZ F, MERCIER F, et al. Zero-difference GPS Ambiguity Resolution at CNES-CLS IGS Analysis Center [J]. Journal of Geodesy, 2012, 86(11): 991-1003. |
| [9] | ZHANG Xiaohong, LI Pan, LI Xingxing, et al. An Analysis of Time-varying Property of Widelan Carrier Phase Ambituity Fractional Bias[J]. Acta Geodaetica et Cartographica Sinica, 2013,42(6): 798-803(张小红, 李盼, 李星星, 等. 宽巷载波相位模糊度小数偏差时变特性分析[J]. 测绘学报, 2013, 42(6): 798-803). |
| [10] | COLLINS P, LAHAYE F, HEROUX P, et al. Precise Point Positioning with Ambiguity Resolution Using the Decoupled Clock Model[C]//Proceedings of the 21st International Technical Meeting of the Satellite Division of the Institute of Navigation. Savannah: ION, 2008: 1315-1322. |
| [11] | GE M, GENDT G, ROTHACHER M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations [J]. Journal of Geodesy, 2008, 82: 389-399. |
| [12] | TEUNISSEN P J G. The Least-squares Ambiguity Decorrelation Adjustment:A Method for Fast GPS Integer Ambiguity Estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65-82. |
| [13] | WEI Ziqing, RUAN Rengui, JIA Xiaolin, et al. Satellite Positioning and Orbit Determination System SPODS: Theory and Test[J]. Acta Geodaetica et Cartographica Sinica, 2014,43(1): 1-4. (魏子卿, 阮仁桂, 贾小林, 等. 卫星定位定轨系统SPODS:理论与测试 [J]. 测绘学报, 2014, 43 (1): 1-4). |
| [14] | BONDY J A, MURTY U S R. Graph Theory with Applications[M]. New York: Elsevier Science Pubblishing Co Inc, 1976. |
| [15] | BIERMAN G J. Factorization Methods for Discrete Sequential Estimation[M]. New York: Academic Press, 1977: 81-103. |
| [16] | TAPLEY B D, SCHUTZ B E, BORN G H. Statistical Orbit Determination[M]. Burlington: Elsevier Inc, 2004: 330-339. |
| [17] | FU Mengyin. Kalman Filtering Theory and Its Applications in Navigation Systems[M]. Beijing: Science Press, 2003: 199-202. (付梦印. Kalman 滤波理论及其在导航系统中的应用[M]. 北京: 科学出版社, 199-202.) |
| [18] | BLEWITT G. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letter, 1990, 17(3): 199-202. |
| [19] | BEUTLER G, MERVART L, VERDUN A. Methods of Celestial Mechanics Volume I: Physical, Mathematical, and Numerical Principles[M]. Berlin: Springer-Verlag, 2005. |
| [20] | SPRINGER T A. Modeling and Validating Orbits and Clocks Using the Global Positioning System[D]. Berne: University of Berne, 1999: 169. |