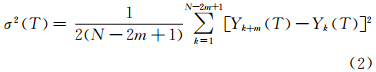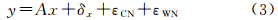1 引 言
以GPS为代表的空间大地测量技术广泛用于大规模连续地壳形变监测[1, 2, 3, 4],这些观测网的成果依赖于高精度的数据处理方法,各网基本采用GAMIT、BERNESE或GIPSY软件解算。其中,GAMIT和BERNESE采用最小二乘法估计参数[5, 6],而GIPSY采用Kalman滤波估计参数[7]。这两种估计方法均假定观测值噪声为高斯正态分布的条件下进行参数求解。然而,研究表明,卫星端误差、传播路径误差和测站环境误差等并不能用简单的白噪声来描述[8],并且未模型化误差也会污染白噪声,实际情况并不符合估计准则的假设条件,退化为次优估计,部分有色噪声可能被GPS坐标序列吸收,影响GPS监测网对有用信号的正确识别能力。GPS随机模型应包含观测数据的白噪声、有色噪声以及未模型化误差,其中的非白噪声部分将造成两方面的影响:①破坏最小二乘估计准则;②部分噪声将被状态参数吸收,影响估计的准确性。
对GPS噪声的分析,多采用零基线法[9],但该法消除了卫星端和传播路径上的误差,只能反映接收机的噪声特性。通过观测值残差分析得到的如高度角模型[10]、载噪比模型[11],本质上仍是将观测噪声当作白噪声,并未研究其成分和性质。目前,噪声分析法有很多种,在大地测量研究中主要有极大似然估计法(MLE)[12]。该法被成功应用于GPS坐标时间序列的噪声分析[13, 14],基于自相关序列(ACS)的方法被应用于惯导数据的随机模型分析[15],而由Allan提出的Allan方差已成为噪声分析的标准工具[16],不但可以识别出各类噪声,还能求出相应的噪声模型参数。文献[17]详细研究了Allan方差理论,并以此建立惯导数据的随机模型;文献[18]利用Allan方差研究了VLBI、SLR、DORIS和GPS定位结果的稳定性;文献[19]则基于Allan方差估计了GPS速度场的不确定度;文献[20, 21]同样利用Allan方差研究了GPS坐标序列的噪声特性,清晰地分离出 各噪声分量。本文利用Allan方差分析了大量PPP双频观测数据的验后残差序列,详细研究了GPS非差随机模型。正确认识GPS观测模型中的噪声成分,确定各噪声的参数,一方面可以为GPS随机模型参数提供近似的先验值,另一方面,由于观测数据不服从高斯白噪声分布,其估计准则或状态模型有待改善,通过误差成分分析,为建立新的估计准则(如贝叶斯估计)提供随机模型依据。同时,由于GPS信号穿过电离层和地球大气层,并且受到测站环境影响,GPS观测值噪声有可能携带这些影响因素的随机信号,可用来研究内部机理。
2 Allan方差理论分析Allan方差由Allan在19世纪60年代提出,是一种基于时域的噪声分析标准工具,最早用于研究精密振荡器的频率稳定性[22]。它不仅可以准确识别噪声类型,还能精确确定噪声的特性参数,广泛应用于各种噪声分析,如随机游走(RW)、白噪声(WN)、闪烁噪声(FN)和高斯-马尔科夫过程(GM)等研究。
Allan方差反映了相邻两个采样段内平均频率差的起伏,它的最大优点在于对各类噪声的幂律谱项都是收敛的。计算Allan方差前,先对长度为N,采样间隔为τ0的序列按平均因子m(即每组包含m个数据)分组,求取每组序列的平均值Yi T ,其中T=mτ0。Allan方差分组有两种方式:标准分组和交叠式分组。
从图 1中可以看出,标准分组每个数据只使用一次,当T较长时,N/m较小,估计误差较大,而交叠式分组扩展了数据集的自由度,重复多次使用了其中的数据项,相比于标准分组,稳定性更高,估计精度更好,本文使用交叠式Allan方差作为分析工具。
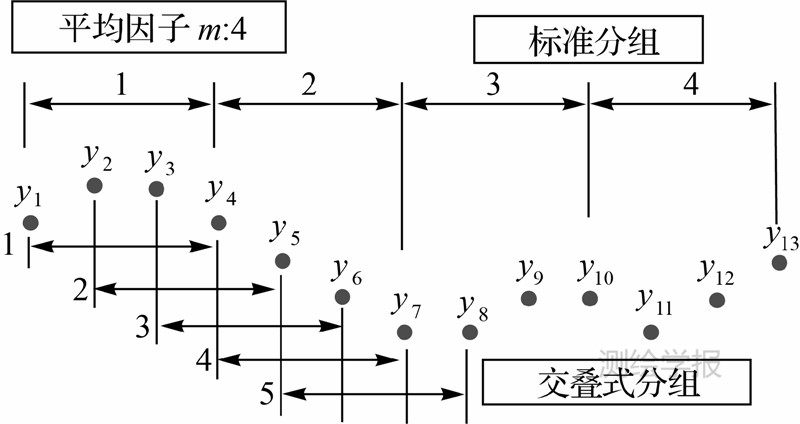 |
| 图 1 Allan方差两种分组方式Fig. 1 Two grouping mode of Allan variance |
交叠式分组的平均值Yi T 计算如下
相应的交叠式Allan方差σ2(T)为[23]
式中,分母中的2表示有两个均值样本Yk+m(T)和Yk(T)。Allan方差不同于标准方差公式,它从噪声方差的无偏估计出发推导出该公式,IEEE组织将其推荐为频率稳定度的时域表征,可用来分析各种噪声特性[24]。
得到Allan方差后,通过对数变换得到双对数图,从图中可以准确分析噪声特性,其流程如图 2所示。
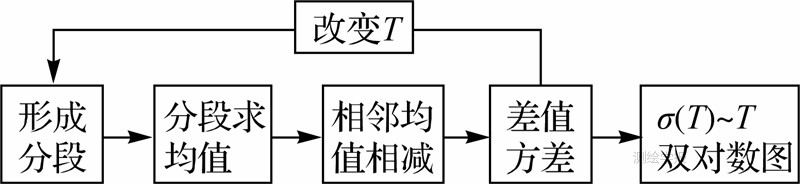 |
| 图 2 Allan方差计算流程Fig. 2 The flow chart of Allan variance calculation |
不同性质的噪声具有不同的Allan方差,其双对数曲线具有不同的斜率,如图 3所示。
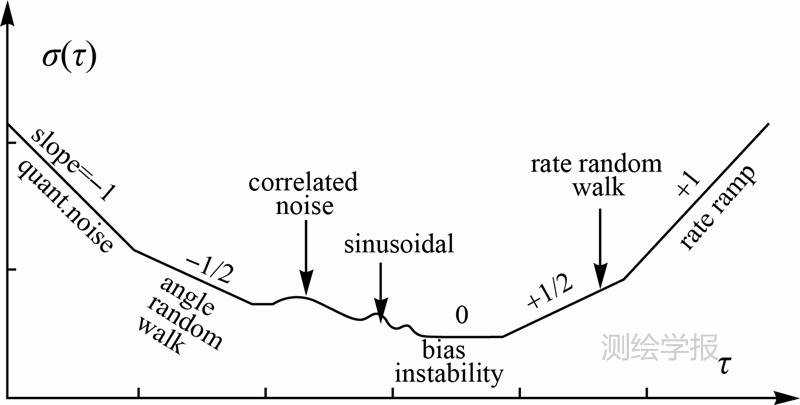 |
| 图 3 随机噪声Allan方差图Fig. 3 Plot of Allan variance analysis results |
使用Allan方差分析,一般先利用式(2)计算噪声序列的Allan方差,然后利用对数变换提取相关时间T的斜率,并得到如图 3的双对数图,根据斜率识别出对应的噪声类别,然后根据特征点提取相关参数。
3 Allan方差分析特性及策略针对不同性质的数据源,Allan方差分析的 特性不同。利用符合实际数据性质的模拟数据分析Allan方差性能是一种有效的方法。由于模拟数据的性质已事先了解,通过比较Allan方差分析 确定的参数和预设的参数,研究其分析特性。另一方面,模拟数据可以任意设置其参数,并且可以任意组合,使得数据源丰富,能够充分挖掘Allan方差的特性以及各种因素对其影响,增加Allan方差分析的经验,以便在实测数据分析中得到更准确的结果。
本文分析了大量模拟数据的Allan方差性能,得到以下结论:
(1) 不同噪声对应的Allan方差图像区别明显,因而能够准确识别噪声类型,而相应的特征点可以估计得到正确的参数。
(2) 数据长度,采样率在超过一定长度或采样频率后(即满足检测条件)以及数据不连续,不会影响Allan方差分析结果,粗差对WN、FN影响较小,但会导致RW、GM的Allan方差图像严重变形,分析前,对序列进行粗差剔除,而与序列幅值相当的小粗差不影响Allan方差图像。
(3) 只有当WN强度较大时,才能从随机序列中分离出白噪声项。
(4) GM过程与WN叠加时,不同的相关时间Tc和过程噪声Qc,Allan方差图像特征形态不一,在噪声类型的检测与相应参数的估计时,应结合模拟数据判定。
在后续GPS非差随机模型分析中,WN和GM占主要成分,两者叠加时,Allan方差具有特定的性质,这里给出相应的分析策略。
3.1 Tc较大的GM与WN叠加GM由相关时间Tc和过程噪声Qc两个参数表证,其中Qc表证了GM的强度大小;WN由噪声参数Q表证,反映了WN的强度。不同比例强度的GM和WN噪声混合时,Allan方差图具有不同形状。模拟了3组混合噪声,如图 4所示。
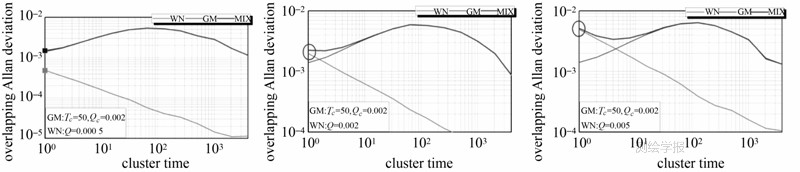 |
| 图 4 3组混合噪声的Allan方差图Fig. 4 Allan plot of three mixed noise |
模拟噪声中的GM参数为Tc=50、Qc=0.002,而WN的参数分别为Q=0.000 5、0.002和0.005。从图中可以看出,不同WN强度下的混合噪声的Allan方差线有明显区别。WN强度较小时,其-1/2斜率特性完全被掩盖,混合噪声的Allan方差图和GM的Allan方差图基本一致,此时从图中很难判断出WN的存在。当WN强度加大时,混合噪声的Allan方差线在低时间簇段开始上升,此时WN的Allan方差线位于GM的Allan方差线上方,WN开始控制低时间簇段的混合噪声,当Q=0.005,即为Qc的1.5倍时,混合噪声完全受WN控制,在T=1时,两者的纵坐标几乎相等,而WN的参数Q的数值等于此处纵坐标值。因此,当混合噪声的Allan方差线在低时间簇段非下滑,可判断有WN存在,并且其参数Q由T=1处的纵坐标值给出。另外,在曲线的最高点处,混合噪声的Allan方差图和GM的Allan方差图几乎重合,表明这段完全受GM控制。因此,GM的参数可由混合噪声Allan方差图的最高点给出,为了使估计更精确,该最高点通过高次项拟合得到。
3.2 Tc较小的GM与WN叠加从图 4中可以看出,WN在T较小时,幅值较大。当GM的Tc较小时,GM整体会向左移动,即使WN的强度很大,也会受到GM的影响。
模拟噪声中的GM参数为Tc=6、Qc=0.8,而WN的参数为Q=0.6,混合噪声的Allan方差线为Origin线。此时从图中可以得到T=1时,纵坐标大约为0.8,比WN的参数Q=0.6要大0.2,这说明从图中不能直接给出WN的参数,但是GM参数仍能从最高点给出。对于WN参数,本文采用搜索的方法来确定WN的参数,在一定范围内,以一定步长生成WN参数序列,如图 5,范围为0.3~0.9,步长为0.15,由于此时GM参数已由最高点求出,加上WN参数种子,可以模拟生成噪声序列,再得到相应的Allan方差图。从图 5中可以看出,各WN参数种子下的Allan方差线具有收敛性,如果减小步长,可逼近到原始曲线(Origin线),当模拟生成的Allan方差曲线与原始曲线符合最佳,那么相应的WN参数种子即为所要的结果,如图 5中,当Q=0.6时,模拟数据的Allan方差曲线和原始曲线符合最佳。
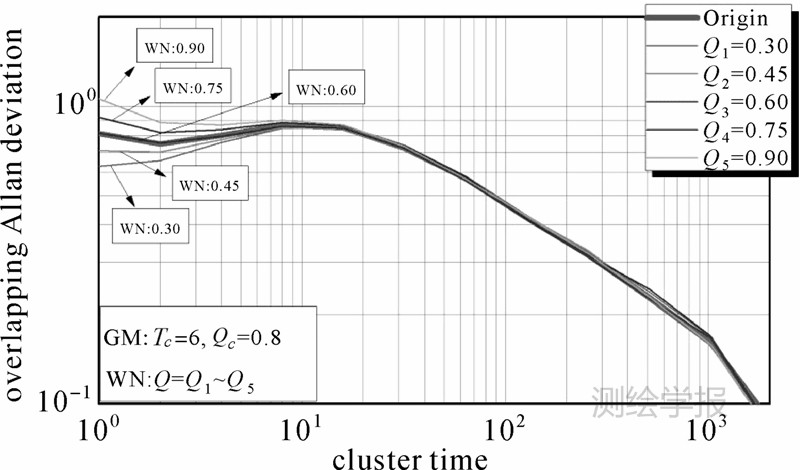 |
| 图 5 Tc较小的GM与WN叠加时的Allan方差图Fig. 5 Allan plot of mixed noise of GM with small Tc and WN |
GPS非差定位中,随机模型部分通常假设观测值为白噪声,然而,GPS观测数据受到卫星端误差、传播路径误差、测站环境误差等,并不能简单地描述成白噪声,其中还包含了各种性质的有色噪声和幂律噪声,并且由于模型考虑不充分或者建模不精确,未模型化误差也会污染白噪声,如果在随机模型中不考虑非白噪声部分,将破坏估计准则,并且部分残余噪声会被状态参数吸收,影响状态参数的准确估计。GPS非差定位方程可以简单写为
式中,y为观测值;x为估计的状态参数,包括位置、钟差、ZWD和模糊度等;A为相应的系数矩阵;δx为未模型化误差;εCN和εWN分别为观测数据的有色噪声和白色噪声,它们通称为随机模型。分析残差序列,如图 7和图 12所示,没有明显的系统项趋势,这表明未模型化误差表现为随机性,将未模型化误差纳入到随机模型中加以吸收,并建立准确的随机模型,采用合适的估计准则,有望改善GPS定位结果。
在白噪声条件下,用最小二乘可以估计得到 ,则验后残差Δ=y-A ,虽然在估计时,部分的δx和εCN被 吸收,但大部分的噪声仍包含在验后残差Δ中,因此使用验后残差序列可以来分析GPS的非差随机模型,求得近似的噪声参数。为了避免差分破坏原始观测值的噪声及动态数据引入更多的不确定因素,本文采用PPP进行单站静态解算。选取了全球均匀分布的30个IGS参考站,如图 6所示。
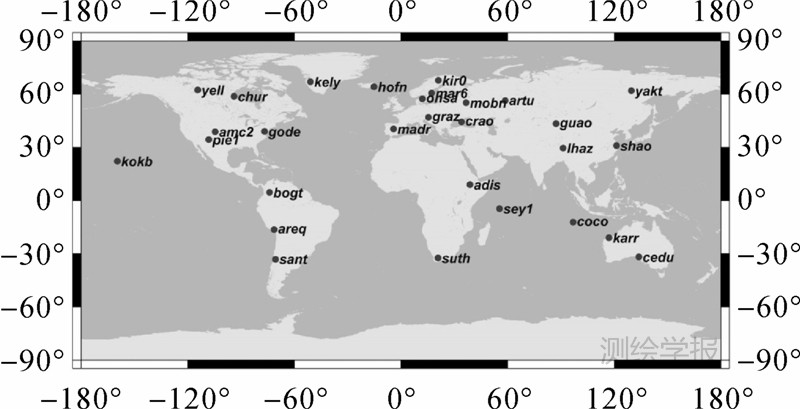 |
| 图 6 全球均匀分布的30个IGS参考站Fig. 6 30 global IGS reference stations |
从CDDIS上下载了2012年中年积日为50的1 Hz高频数据,以武汉大学测绘学院研制的精密单点定位软件TriP为数据处理平台,TriP静态定位结果精度,平面优于1 cm,高程优于2 cm。解算以后分别得到双频IF相位观测值验后残差和双频IF伪距观测值验后残差。一个测站一天内基本可以观察到所有的GPS卫星,将一天内各时段的某颗GPS卫星的所有观测值验后残差,组合形成连续的序列进行分析。为了清晰看出残差序列的变化,选取了AMC2和AREQ两个站,5种Block类型的GPS卫星为代表,给出其残差序列,相位和伪距验后残差噪声特性分析如下。
4.1 相位验后残差噪声特性分析相位验后残差部分序列如图 7所示。
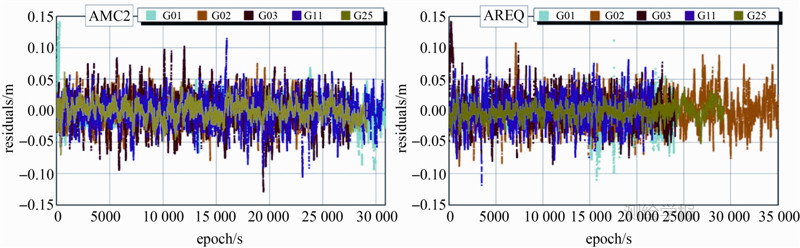 |
| 图 7 相位残差部分序列Fig. 7 Some sequences of phase residuals |
序列长度一般在25 000之上,可满足Allan方差分析的序列长度要求。相位验后残差序列变化平缓,未表现明显的系统项趋势以及随高度角变化的特征,表明未模型化误差也是一种随机噪声。残差幅值一般在50 mm左右,如果将其看作白噪声,按照3σ表示幅值,则中误差约为15 mm,而双频IF相位观测值的理论噪声约为6 mm[25],小于实际噪声值,说明实际相位噪声中还包含了其他噪声。
以AMC2站G01和G25号卫星相位验后残差序列为例,使用Allan方差分析,其双对数图如图 8所示。
 |
| 图 8 G01和G25号卫星相位残差的Allan方差Fig. 8 Allan plot of phase residuals of G01 and G25 |
图中绿色线为左右拟合直线,斜率近似为±0.5,从而判断为一阶高斯马尔科夫(GM)过程,在高频段Allan方差线趋于水平,以模拟数据分析结论为经验,此处是受到WN影响,红色线为WN虚拟线,它与高频段的绿色线相互叠加影响致使Allan方差线趋于水平(这种叠加并非图像上的直接叠加)。以G01卫星为例,GM过程参数由Allan方差线最高点给出(绿色点),可计算得到Qc=2.8 mm/ s ,Tc=74.6 s,而WN参数由横坐标为1处对应的纵坐标值读出(红色点),为Q=2.08 mm,该点处,GM过程的相关时间较小,主导作用降低,且从模拟数据分析来看,其影响可以忽略不计,因而可以直接当成WN。受到数据质量、其他次要噪声的影响,图像并非严格遵循理论形态,在拟合确定最高点时将产生一定误差,并且不能从图像单点上分离出不同噪声,因而使用Allan方差确定的噪声参数有一定偏差。这里确定的白噪声为2.08 mm和1.53 mm,比理论值小,还有可能是因为部分噪声在解算时被模糊度或其他参数吸收。从Allan方差分析来看,相位观测数据噪声组合为WN+GM,且GM成分占优,相关时间较长。
对所有测站观测到的卫星的观测验后残差进行分析,计算WN参数和GM参数,考虑到聚集程度,WN参数按测站分类,GM参数按卫星分类,如图 9和图 10所示。
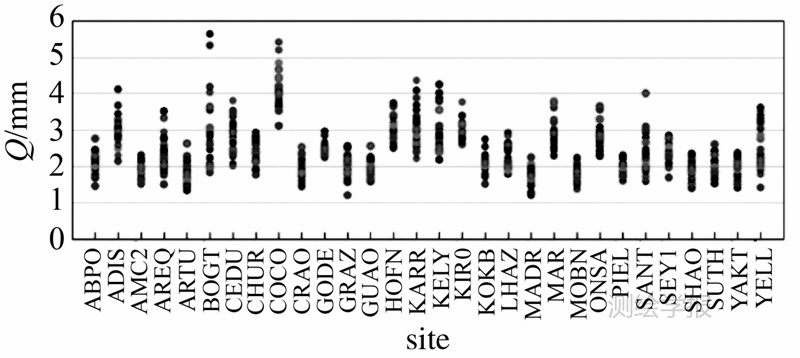 |
| 图 9 各测站WN参数Fig. 9 WN parameters of all stations |
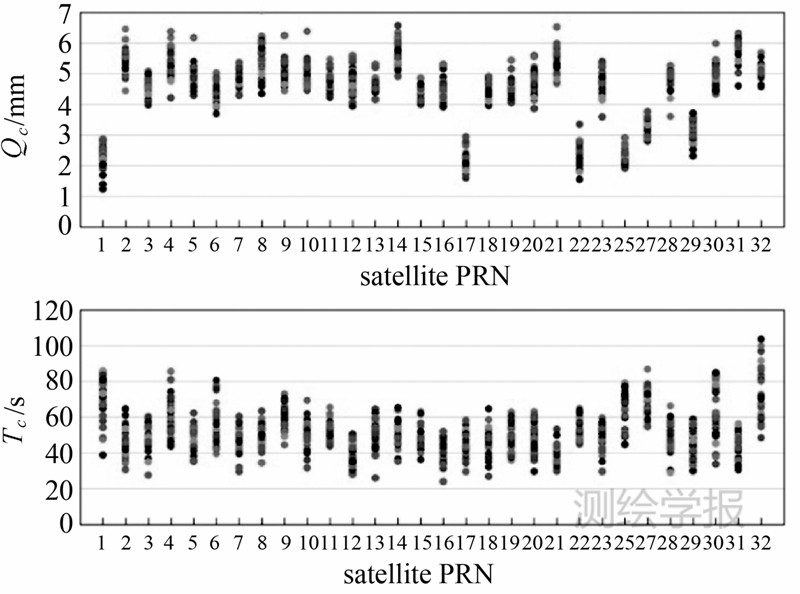 |
| 图 10 各卫星GM参数Fig. 10 GM parameters of all satellites |
各测站的相位WN参数聚集程度较高,说明对于不同卫星,同一个测站的WN相近,它与测站有较高的相关性。WN通常是接收机内部捕获观测值时引起的,主要受到接收机质量的影响,并且和测站周围环境有很大相关性。而GM按卫星分类聚集程度较高,表明与卫星端随机特性有关,具体原因有待研究。各站相位WN差异不明显,COCO站较大,对于GM噪声,G01、G17、G22和G25虽然型号不同,但它们的Qc都较小,表明这些卫星数据质量好。而相关时间基本一致。
计算均值各站或各卫星噪声参数均值,如图 11所示。
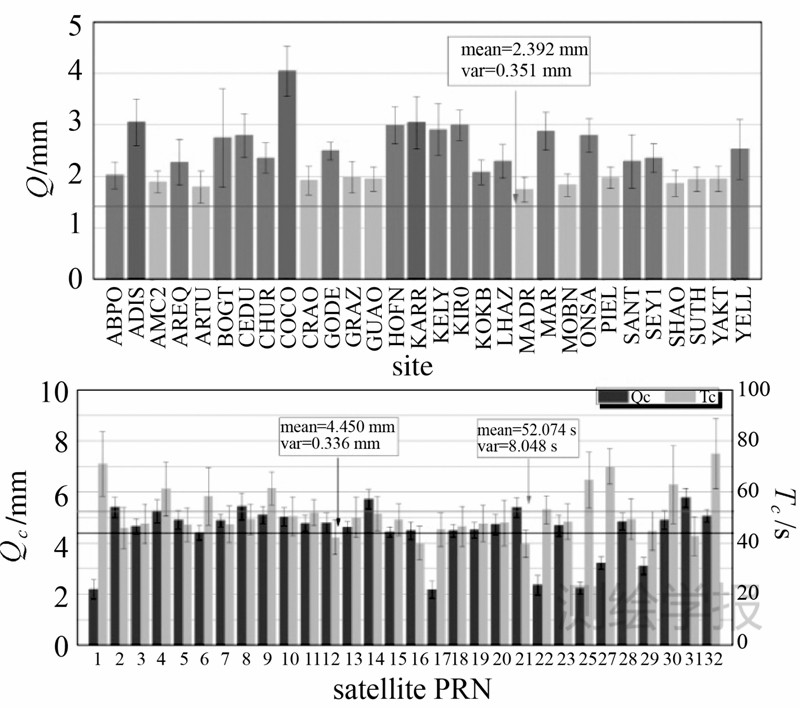 |
| 图 11 各测站WN参数和各卫星GM参数统计Fig. 11 Statistics of all WN and GM parameters |
大部分测站的相位WN在2 mm左右,方差在0.5 mm以内,coco站的相位WN最大为4 mm,而bogt站的方差最大为1 mm,所有站相位WN均值为2.392 mm,方差为0.351 mm。相应的GM参数如图 11所示。相位WN小于理论值,有可能部分噪声在解算时被模糊度或其他参数吸收。
综上分析,相位噪声组合为WN+GM,且区分度大,WN大小为2.392 mm,GM过程噪声为4.450 mm/ s ,相关时间为52.074 s,以往相位观测值噪声为白噪声的假设是不合理的。
4.2 伪距残差噪声特性分析伪距残差部分序列如图 12所示。
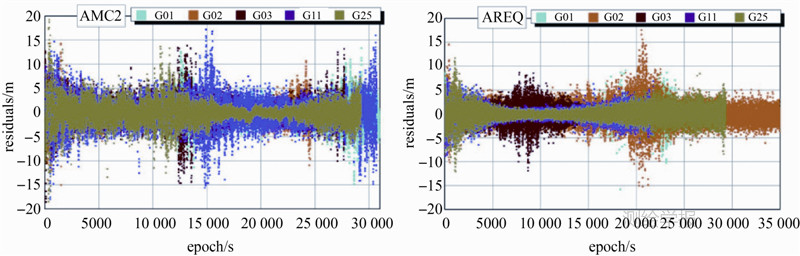 |
| 图 12 伪距残差部分序列Fig. 12 Some sequences of pseudorange residuals |
伪距残差序列也未表现出明显的系统项趋势,但有别于相位残差序列的平缓性,其图像呈现出峰谷,明显表现出随高度角变化的特性,幅值约为5 m,如果按照3σ表示幅值,其伪距噪声中误差在1.7 m左右,而双频IF伪距观测值的理论噪声约为0.9 m[25],小于实际噪声值,说明实际伪距噪声中还包含了其他噪声。
以AMC2站G01和G25号卫星伪距验后残差序列为例,使用Allan方差分析,其双对数图如图 13所示。
 |
| 图 13 G01和G25号卫星伪距残差的Allan方差Fig. 13 Allan plot of pseudorange residuals of G01 and G25 |
伪距噪声较相位噪声复杂,首先可以确定噪声组合也是WN+GM,但是两者区分度不大,主要原因是GM的相关时间较小,严重影响WN的参数判读。这里采取数据模拟的方法确定WN参数,首先GM模型参数可以通过最高点(绿色点)求得,然后与不同WN参数组合生成模拟数据,得到相应的Allan方差曲线,当某个WN参数下的Allan方差曲线与实测曲线在最高点左边所有部分及右边一定范围内拟合最佳,该WN参数即为实测数据的WN参数,这里确定得到的WN参数分别为0.68 m和0.81 m,与横坐标1 s对应的方差值相比, 分别下降了0.12 mm和0.18 mm,这也表明当GM相关时间较小时,与WN叠加后,将影响WN参数的直接判读。使用以上方法求得所有数据的噪声参数,与相位不用,伪距都按站分类,聚集程度较好,如图 14和图 15所示。
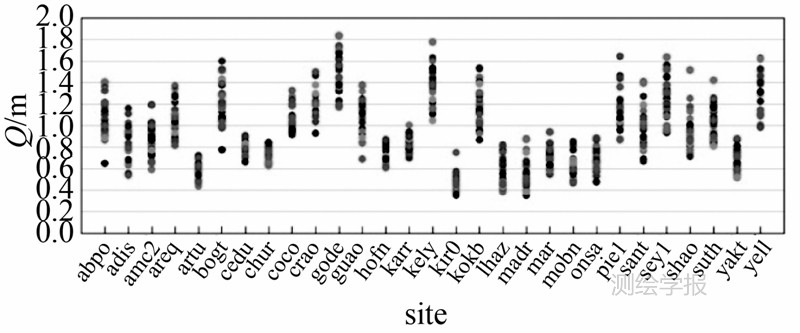 |
| 图 14 各测站WN参数Fig. 14 WN parameters of all stations |
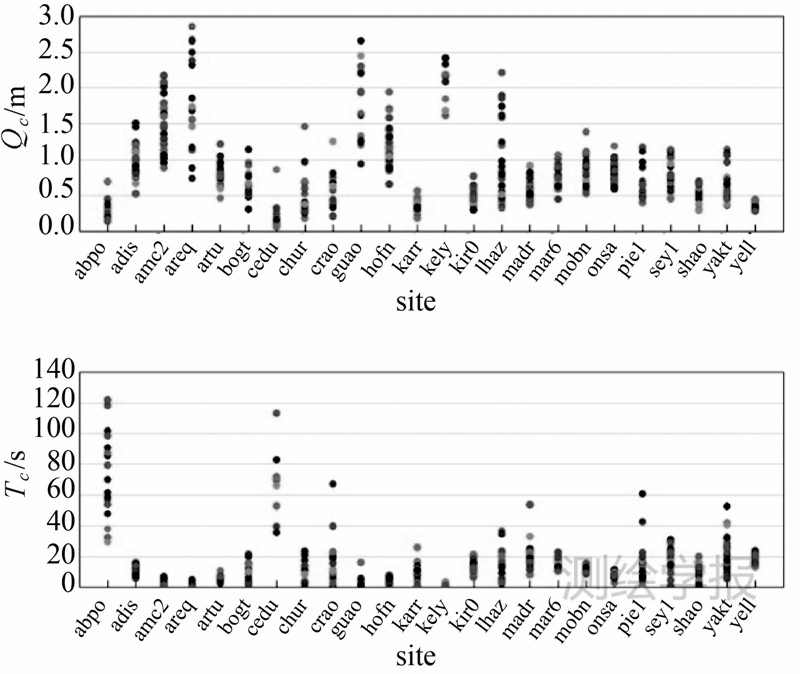 |
| 图 15 各测站GM参数Fig. 15 GM parameters of all stations |
伪距噪声容易受接收机质量和测站环境影响,与测站的相关性较大,从结果看,不同站之间的噪声差异较大,如LHAZ—ONSA站的WN约为0.6 m,而很多站在1.2 m左右,相差的幅度较大。对于GM参数,ABPO站和CEDU站的相关时间从30 s到120 s不等。不同测站和卫星的伪距噪声,稳定性相对较差。
计算均值各站或各卫星噪声参数均值,如图 16所示。
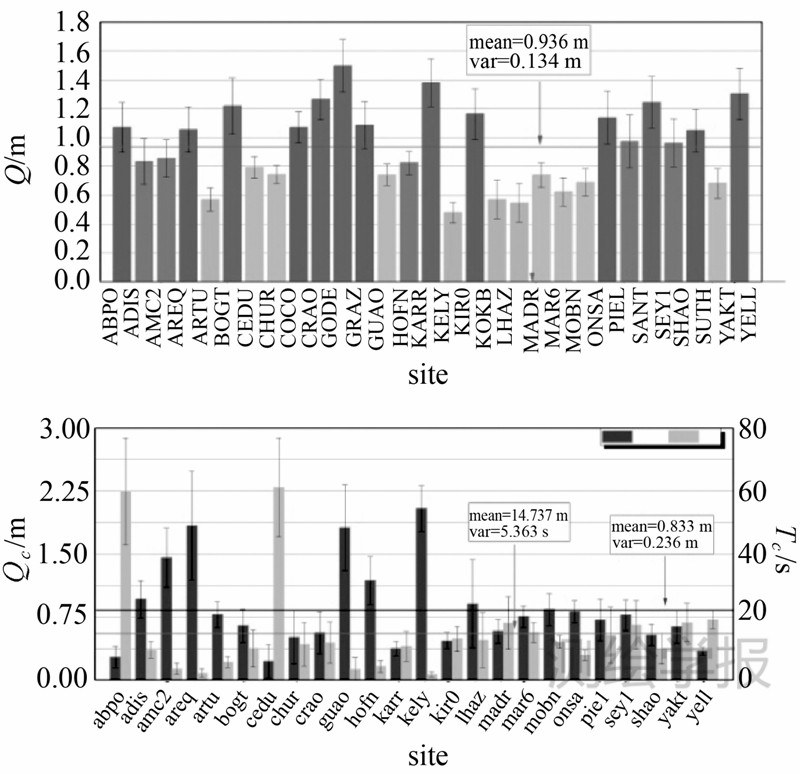 |
| 图 16 各测站WN参数和各卫星GM参数统计Fig. 16 Statistics of all WN and GM parameters |
伪距WN均值为0.936 m,与理论值十分接近,表明Allan方差提取的伪距WN参数在统计意义上具有一定可靠性。GM过程噪声为0.833 m/ s ,相关时间为14.737 s,比相位噪声的相关时间小的多。综上分析,伪距噪声组合仍为WN+GM,两者区分度小,白噪声占优。
5 结 论本文通过大量模拟数据和实测数据分析了Allan方差分析的性能,该方法能够较好地确定噪声成分和相应参数,从模拟数据中可以得到以下结论及性质:
(1) 不同噪声对应的Allan方差图像区别明显,因而能够准确识别噪声类型,而相应的特征点可以估计得到正确的参数。
(2) 数据长度,采样率在超过一定长度或采样频率后(即满足检测条件)以及数据不连续,不会影响Allan方差分析结果,粗差对WN、FN影响较小,但会导致RW、GM的Allan方差图像严重变形,分析前,对序列进行粗差剔除,而与序列幅值相当的小粗差不影响Allan方差图像。
(3) 只有当WN强度较大时,才能从随机序列中分离出白噪声项。
(4) GM过程与WN叠加时,不同的相关时间Tc和过程噪声Qc,Allan方差图像特征形态不一,在噪声类型的检测与相应参数的估计时,应结合模拟数据判定。
在以上经验结论的基础上,将Allan方差用于GPS非差随机模型特性分析,结果表明GPS数据噪声组合为WN+GM,相位白噪声为2.392 mm,GM过程噪声为4.450 mm/ s ,相关时间为52.074 s,伪距白噪声为0.936 m,GM过程噪声为0.833 m/ s ,相关时间为14.737 s,相位的GM过程与卫星相关性较大,而其余噪声则与测站相关性较大,Allan方差对于GPS观测数据的噪声分析具有很好的适用性。本文研究表明,GPS观测数据噪声为白噪声的假设是不精确的,它至少包含了GM噪声分量,因此,在估计准则或状态模型上有改善的空间。
| [1] | WILLIAMS S D P.CAST: GPS Coordinate Time Series Analysis Software[J].GPS Solution,2008,12(2):147-153. |
| [2] | BRUYNINX C, BECKER M, STANGL G. Regional Densification of the IGS in Europe Using the EUREF Permanent GPS Network (EPN)[J]. Physics and Chemistry of the Earth, Part A: Solid Earth and Geodesy, 2001, 26(6): 531-538. |
| [3] | IMAKIIRE T, KOARAI M. Wide-area Land Subsidence Caused by “the 2011 off the Pacific Coast of Tohoku Earthquake”[J]. Soils and Foundations, 2012, 52(5): 842-855. |
| [4] | WANG W, ZHAO B, WANG Q, et al. Noise Analysis of Continuous GPS Coordinate Time Series for CMONOC[J]. Advances in Space Research, 2012, 49(5): 943-956. |
| [5] | HERRING T A, KING R W, MCCLUSKY S C. GAMIT Reference Manual[EB\OL].[2010-10-28].http://www-gpsg.mit.edu/-simon/gtgk/GAMIT_Ref.pdf. |
| [6] | HUGENTOBLER R D U, MICHAEL M P F. Bernese GPS Software Version 5.0[EB\OL].[2007-01-01].http://www.bernese.unibe.ch/docs50/DOCU50.pdf. |
| [7] | GREGORIUS T. Gipsy-OasisⅡ: How it Works[M]. Newcastle: University of Newcastle Press,1996. |
| [8] | RANKIN J. An Error Model for Sensor Simulation GPS and Differential GPS[C]//Proceedings of IEEE Position Location and Navigation Symposium Record. Las Vegas:IEEE, 1994: 260-266. |
| [9] | DE JONG K. A Modular Approach to Precise GPS Positioning[J]. GPS Solutions, 1999, 2(4): 52-56. |
| [10] | HAN S. Quality-control Issues Relating to Instantaneous Ambiguity Resolution for Real-time GPS Kinematic Positioning[J]. Journal of Geodesy,1997, 71(6): 351-361. |
| [11] | HARTINGER H, BRUNNER F K. Variances of GPS Phase Observations: The SIGMA-ε Model[J]. GPS Solutions,1999, 2(4): 35-43. |
| [12] | ZHANG J, BOCK Y, JOHNSON H, et al. Southern California Permanent GPS Geodetic Array: Error Analysis of Daily Position Estimates and Site Velocities[J]. Journal of Geophysical Research, 1997, 102(B8): 18035-18055. |
| [13] | LI Zhao, JIANG Weiping, LIU Hongfei,et al. Noise Model Establishment and Analysis of IGS Reference Station Coordinate Time Series inside China[J]. Acta Geodaetica et Cartographica Sinica, 2012,41(4):496-503.(李昭,姜卫平,刘鸿飞,等.中国区域IGS基准站坐标时间序列噪声模型建立与分析[J].测绘学报,2012,41(4):496-503.) |
| [14] | LIAO Hua, XU Rui Weifeng, CHEN W F, et al. Property Variation and Statistical Analysis of Sichuan GPS Time Series before and after Wenchuan Earthquake[J]. Chinese Journal of Geophys,2013,56(4):1237-1245.(廖华,徐锐,陈维锋,等.汶川地震前后四川区域GPS时序特征演变及统计分析[J].地球物理学报,2013,56(4):1237-1245.) |
| [15] | NASSAR S. Improving the Inertial Navigation System (INS) Error Model for INS and INS/DGPS Applications[D]. Calgary:University of Calgary, 2003. |
| [16] | IEEE Aerospace and Electronic Systems Society.IEEE Standard Specification Format Guide and Test Procedure for Single-axis Interferometric Fiber Optic Gyros[S]. doi:10.1109/IEEESTD.1998.86153. |
| [17] | HOU H. Modeling Inertial Sensors Errors Using Allan Variance[D]. Calgary:University of Calgary, 2004. |
| [18] | FEISSEL-VERNIER M, DE VIRON O, LE BAIL K, et al. Stability of VLBI, SLR, DORIS, and GPS Positioning[J]. Earth, Planets, and Space, 2007,59(6): 475-497. |
| [19] | HACKL M, MALSERVISI R, HUGENTOBLER U, et al. Estimation of Velocity Uncertainties from GPS Time Series: Examples from the Analysis of the South African TrigNet Network[J]. Journal of Geophysical Research,2011. doi:10.1029/2010JB008142. |
| [20] | FRIEDERICHS T. Analysis of Geodetic Time Series Using Allan Variances[D]. Stuttgart: University of Stuttgart, 2010. |
| [21] | NIU X, CHEN Q, ZHANG Q, et al. Using Allan Variance to Analyze the Error Characteristics of GNSS Positioning[J]. GPS Solutions, 2013,18(2):231-242. |
| [22] | ALLAN W D. Statistics of Atomic Frequency Standards[J]. Proceedings of IEEE, 1966,54(2):221-230. |
| [23] | RILEY W J. Handbook of Frequency Stability Analysis[EB/OL].[2008-07-01].https://safe.nrao.edu/wiki/pub/Main/ToddHunter/nist1065.pdf. |
| [24] | RUTMAN J. Characterization of Phase and Frequency Instabilities in Precision Frequency Sources: Fifteen Years of Progress[J]. Proceedings of IEEE, 1978,66(9):1048-1075. |
| [25] | LI Zhenghang, HUANG Jinsong. GPS Surveying and Data Processing [M]. Wuhan: Wuhan University Press,2010. (李征航,黄劲松.GPS测量与数据处理[M]. 武汉: 武汉大学出版社,2010.) |