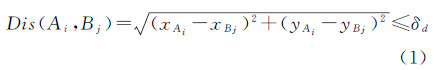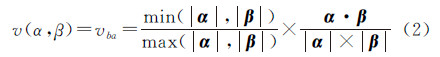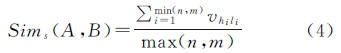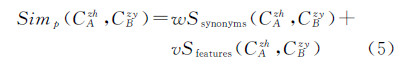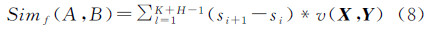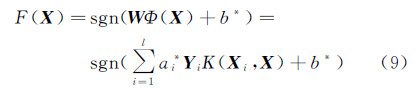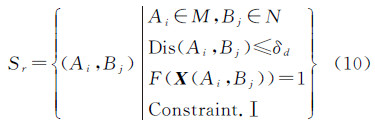2. 江苏省国土资源信息中心, 江苏 南京 210017;
3. 南京师范大学强化培养学院, 江苏 南京 210023;
4. 南京市测绘勘察研究院有限公司, 江苏 南京 210019;
5. 江苏省地理信息资源开发与利用协同创新中心, 江苏 南京 210023
2. Information Center of Jiangsu of Land and Resources, Nanjing 210017, China;
3. Honour School of Nanjing Normal University, Nanjing 210023, China;
4. Nanjing Institute of Surveying, Mapping and Geotechnical Investigation, Co. Ltd, Nanjing 210019, China;
5. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China
1 引 言
地下管线是城市物质流、能量流和信息流的主要通道,是城市重要的基础设施和“生命线”。受管线管理模式及管线空间数据应用目的差异的影响,当前城市管线信息化中普遍存在两种不同类型的管线地理信息系统应用:为城市规划、管理服务的综合地下管线地理信息系统;为管线权属单位运维服务的专业地下管线地理信息系统。近年来,随着“数字城市”建设的推进,两类地下管线地理信息系统作为支撑城市规划、建设和管理的核心信息化应用,其空间数据也日益成为城市空间信息共享资源的重要内容。虽面向城市同一区域内的相同管线对象,两类管线数据却在数据模型和空间定位精度方面差异明显,由此引发的不同类型地下管线数据集成、融合、共享、交换问题在城市管线信息化深入应用中日益突出,并进一步致使城市内建设的各个地下管线信息系统成为“信息孤岛”[1]。因此,如何通过实体匹配的方式识别相同管线间的对应关系成为解决这些问题的关键所在。
同名实体的匹配就是通过分析空间实体相似性识别出不同来源图中表达现实世界同一地物或地物集的过程[2]。空间相似性是空间信息认知的重要内容,实体匹配算法中常用的指标有空间信息指标和属性信息指标[3],通过计算几何、拓扑、语义等方面的空间相似性,作为匹配参考依据。根据选取的相似性因子,分为几何匹配、拓扑匹配和语义匹配,主要的算法有缓冲区法[4, 5]、几何距离法[6, 7]、形状相似性法[8]、语义距离相似性法[9]等,亦有采用多空间相似因子的匹配算法[2]。道路网匹配延续传统空间相似性计算方法,针对匹配数据尺度是否相同,有面向多尺度数据的匹配[4, 8]和单一尺度下的匹配[10, 11]。多尺度下,数据匹配多从弧段角度计算弧段几何距离相似性,单一尺度数据下匹配则多以节点为中心的道路结构相似性作为匹配依据,而基于道路网数据自身特征与空间相似性指标又演化出概率松弛法[12]、蚁群算法[13]等。
地下管线与道路网类似,是典型的“节点-弧段”结构,其空间结构、属性信息和形状特征明显,因而道路网匹配算法对地下管线的匹配具有一定借鉴意义,但与道路数据不同,地下管线数据中节点类型多样且节点分布相对密集,因而从弧段出发运用单一的几何距离衡量管线相似性会存在误差。此外,管线数据中无论是节点还是弧段,其语义信息都要比路网数据复杂。基于此,设计适合管线自身数据特征的空间相似性指标,构建科学、高效的计算模式与匹配算法则是管线数据能否正确匹配的关键。本文以城市地下天然气管线为研究对象,结合管线自身特征从管点匹配角度出发,以地下管线结构、语义、形状等特征的相似性为管点空间特征向量,提出了一种综合性的管线数据匹配算法。
2 两类管线数据差异分析及匹配算法思想两类地下管线数据虽都由其各自的管点(点状设施)与管段(线状设施)地理实体资源组成,但由于数据采集方式和处理标准的不同,两类数据在数据精度、空间结构、属性表达上差异较大。
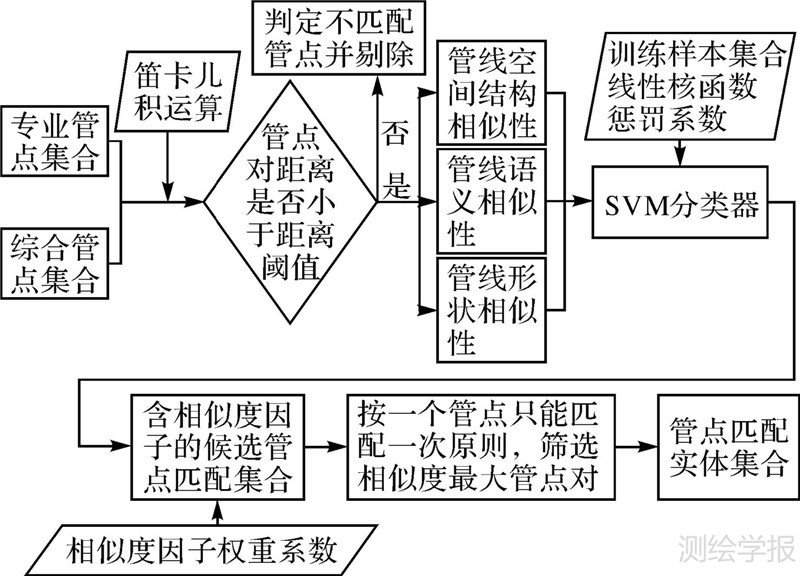
图 1是同一小块区域内天然气管线的空间数据图形表示,其中图 1(a)是综合地下管线,图 1(b)是专业地下管线。图 1(a)中的A2管点和图(b)中的B2管点,从经验判断上同为天然气“弯头”对象,但两个管点的位置坐标明显不同;图 1(a)中类型为“多通”的A3管点,在图 1(b)中对应的B3其类型却为“三通”;图 1(a)中A4管点与图 1(b)B4管点的直连管段数也不相同。考虑到从管段角度出发的矢量数据匹配算法需要顾及管段之间存在着的N∶1、1∶1、1∶0、M∶N等多种复杂对应关系,而采用先匹配管点再匹配管段的算法更符合管线数据匹配的实际情况。以管点为中心的匹配过程中,管点关联的管段及管点本身信息是匹配的重要依据。管点距离可以间接反映管点实体空间相关性,待匹配管点对距离过大,其相关性越低;管点直接关联管段方向、长度信息在局部空间上描述了管线形态和空间结构特征;管点关联的多级管段在方向、形状上反映出管线的形状特征;管点分类及关联管段的属性信息表达了管线语义特征。因而,本文选取管点间距离Dis、管线空间结构相似性Sims、管线语义相似性Simp和管线形状相似性Simf综合评价待匹配管点对间相似性程度,一对管点对(A,B),形成一组管点对相似向量Vector(A,B)=[Dis(A,B)Sims(A,B)Simp(A,B)Simf(A,B)],用于描述管点实体间相似性。具体的匹配算法流程如图 2所示。

|
| 图 1 天然气地下管线空间数据实例 Fig. 1 A case of partial data based on professional pipelines and integrated pipelines |
|
| 图 2 算法流程 Fig. 2 Algorithm flow chart |
考虑到管线数据量庞大,在计算所有因子之前,缩小参与匹配的管点实体集合是有必要的,本文选取距离阈值初步筛选候选匹配实体集进行数据预处理。
设定阈值δd,计算两个管点的空间几何距离,与阈值δd比较。当两点距离小于阈值时,初步判定为同一地物。
假设综合地下管线管点集合为M,专业地下管线管点集合为N,设综合管点Ai∈M,1≤i≤m,坐标为(xAi,yAi);专业管点Bj∈N,1≤j≤n,坐标为(xBj,yBj)。两点间距离Dis(Ai,Bj),距离阈值δd。若Ai与Bj满足式(1),则两管点为匹配实体集初始管点对之一。
通过阈值约束,选取有可能成为匹配管点对的集合,在降低匹配实体数量的同时,为之后的相似度计算奠定基础,得到初始匹配实体集S={(Ai,Bj)Ai∈M,Bj∈N,Dis(Ai,Bj)≤δd}。
在初始匹配集合基础上,计算管线空间结构、语义、形状相似性,采用SVM支持向量机的分类方法筛选待匹配管点集合,之后通过管点唯一匹配原则选取实体集中未匹配管点中相似性最大管点对,最终得到管点匹配实体集。
3 管线空间相似性计算方法 3.1 管线空间结构相似性管线空间结构是指以管点为中心,其直接关联的管段所形成的管线空间分布形态。考虑到管线间的长度与方向的相似程度是衡量两个管线是否相似的重要指标,因而描述管线空间结构的相似程度是将管点关联管段的方向、长度等拓扑信息通过模型转化为直观数字方便比较的过程,其中转换模型方法参照文献[11]中的拓扑相似度计算方法。
设初始匹配实体集中某综合管点A关联的一管段为lAa,起点为A,终点为A′,其中lAa为管点A关联的第a个管段,1≤a≤m,m为A关联管段的个数;与管点A对应的专业管点B关联的一管段为lBb,起点为B,终点为B′,其中lBb代表管点B关联的第b个管段,1≤b≤n,n为B关联管段的个数。设管线长度Length(lBb)<Length(lAa),为比较两管段的相似性,首先需在lAa管段上截取一段与lBb等长的管段,设在AA′管段上的截点为K,连接AK形成向量α,连接BB′形成向量β,则lAa与lBb形成的向量相似度v为
管线间的空间结构相似性计算需要在综合管段集合与专业管段集合中查找最佳匹配的管段。在两管段集合进行笛卡儿积运算的基础上,根据管段间向量相似度值的大小进行查找,其具体计算步骤如下:
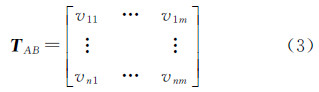
首先,任意两管点关联管段进行笛卡儿积运算,对每对管段进行向量相似性计算,得到n×m的管线向量相似度矩阵TAB
其次,在相似度矩阵T中查找最大值vij,则管段lBi与管段lAj为最相似,同时将矩阵T中第i行,第j列的矩阵值最小化,并记录行列号i、j。
最后,重复上一步骤,直至查找到的相似管段对数达到两管点关联管段数最小值min(n,m)时,停止查找,得到相似性管段行列号集合(h1,l1),(h2,l2),…,(hmin(n,m),lmin(n,m)),hi和li分别是管点B、A关联管段集合中的编号,其中1≤i≤min(n,m)。
由此管线空间结构相似度Sims的计算公式为
3.2 管线语义相似性管线语义是指地下管线数据中概念名称及属性的语言表达。在管线数据中,管点比管段的语义分类完善,为降低语义相似计算复杂度,计算管点间的概念相似性作为管线语义相似性。本体是语义的形式化表达,是衡量本体相似性的有效工具。依据文献[14, 15, 16]等管线地理信息标准,构建包含概念、分类及属性等的管线地理信息本体,其部分本体片段如图 4所示。天然气综合管点主要分为特征点和附属物两类,特征点有多通、弯头、变径(深)点、非普查4类,附属物有阀门井、检修井、伸缩管井、凝水缸、阀门、预留口、出入地、调压箱、调压柜9类。天然气专业管点类型众多,主要分为设备、设施、配件3大类,设备分为阀门、凝水缸、调压柜等8类,设施分为阀门井、调压站、加气站等10类,配件分为三通、阴极保护、信息球等16类。在此基础上,本文基于Rodriguez提出的MD3模型[12],顾及管线数据的特点,将语义距离融入概念名称和概念属性以计算管线语义相似性。

|
| 图 3 天然气专业管点与综合管点本体片段 Fig. 3 The ontology fragment of Integrated and professional pipepoints |
|
| 图 4 测试数据SVM分类结果Kappa系数随惩罚因子变化图 Fig. 4 Kappa coefficient of test-data’s SVM classification- varying with penalty factor |
设综合管线中概念CAzh,专业管线中概念CBzy,则两概念相似度计算公式为
式中,w+v=1;Ssynonyms(CAzh,CBzy)指概念名称相似性;Sfeatures(CAzh,CBzy)概念属性的相似性,其计算依据是Tversky的特征匹配模型[17] 式中,t为synonyms、features;GAzh和GBzy分别为不同t值下概念CAzh和CBzy对应的集合项;GAzh∩GBzy指集合GAzh与集合GBzy的交集,GAzh/GBzy指在集合GAzh中但不在集合GBzy中的项,GBzy/GAzh指在集合GBzy中但不在集合GAzh中的项;|·|用于计算集合的基数;f是根据概念深度计算权重的函数,计算公式如下式 式中,depth(·)是计算概念深度的函数,其值表示概念所在节点到根节点的最短路径长度。 3.3 管线形状相似性管线形状是多管点相连管段形成的路径形态,两管线的形状相似性通过比较两管线中折点集合形成的向量异同获得。选取已知的人工匹配管点对作为参考点,求取当前管点与参考点间的最短路径,形成两条参考路径,作为管线形状相似性计算的参考依据。
选取人工匹配管点对(Ar,Br),Ar为综合管点,Br为经人工判定与Ar匹配的专业管点,则候选匹配实体集中(A,B)到达对应的人工匹配管点的最短路径分别为lAAr和lBBr,以此为基础计算两管线的形状相似性作为衡量管点A与B是否匹配的一个依据。
假设lAAr的折点序列集合为{p1A,p2A,…,pKA},lBBr折点序列集合为p1B,p2B,…,pHB,折点pij坐标为(xpij,ypij),计算每个折点与起点之间的累积距离占总长度的百分比,将折点序列集合转化为百分比序列集合s1A,s2A,…,sKA,s1B,s2B,…,sHB,并将两条折线百分比序列融合排序,得到序列s1,s2,…,sK+H,s∈0,1。设比例s在lAAr上对应的点坐标为(xA(s),yA(s)),在lBBr上对应的点坐标为(xB(s),yB(s)),任意连续两点(xA(si),yA(si))和(xA(si+1),yA(si+1))形成向量X,(xB(si),yB(si))与(xB(si+1),yB(si+1))形成向量Y,则管线lAAr与lBBr的相似度为
4 管点匹配 4.1 基于SVM的管点分类支持向量机的主要思想是使用映射函数Φ( )将n维l个样本向量(Xi,Yi)0<i
式中,sgn( )为符号函数 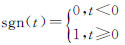 ;W为权重向量;Xi为第i个样本n维向量;Yi为第i个样本的标签;X为训练样本数据;b*为分类阈值;ai*为支持向量机最优解。具体原理及推导公式可参照文献[18, 19]。
;W为权重向量;Xi为第i个样本n维向量;Yi为第i个样本的标签;X为训练样本数据;b*为分类阈值;ai*为支持向量机最优解。具体原理及推导公式可参照文献[18, 19]。
经过管线相似性的计算,对于任意一对在初始匹配集S中的管点对(A,B),可形成基于空间相似性的管点对特征向量X(A,B)=[Sims(A,B)Simp(A,B)Simf(A,B)]。在此基础上,将基于特征向量的匹配问题转化成基于特征向量的分类问题,即将目标管点数据分为“匹配”(用1表示)和“不匹配”(用0表示)两类。在确定管点初始匹配实体集S基础之上,确定SVM支持向量机的核函数参数与惩罚因子C,增加匹配决策函数约束F(X(Ai,Bj))=1,再次缩小匹配实体集,得到集合S′。
4.2 管点唯一匹配原则经SVM分类后获得管点匹配实体集S′,但在S′中依旧存在一部分不匹配的管点对,究其原因是部分管点在距离阈值范围内有多个相似管点,因而产生一个管点对应多个匹配管点的状况。为解决这一现象,增加管点唯一匹配规则。
Constraint.Ⅰ:任意管点对(Ai,Bj)中的管点Ai和Bj,在最终的管点匹配实体集合Sr中只能存在一个。且这一个管点对(Ai,Bj),在待匹配实体集合S′所包含含有Ai或Bj的管点对中总相似度最大。
总相似度Sim(Ai,Bj)=WsSims+WpSimp+WfSimf,其中,Ws、Wp、Wf是衡量实体相似性的权值,Ws、Wp、Wf相似度权值的确定依据式(11)最优线性决策函数权重向量W=[WsWpWf]的求解方法。为了在表达上的简单明确,将权重缩放到[0,1]之间,使其满足Ws+Wp+Wf=1。
最终,添加匹配规则Constraint.Ⅰ,进一步缩小管点匹配实体集合S′,得到最终管点匹配实体集合Sr。
5 实例分析本文采用C#语言、ArcGIS Engine10.0控件以及Matlab等工具实现该算法,选取某市小区部分天然气地下管线数据,对数据进行处理得到该区域管线训练数据和测试数据。训练数据包含天然气专业地下管线三通、变径、调压器等16种点状设备设施752个,管段数为987个;天然气综合地下管线管点数402个,管段数393个。测试数据中天然气专业地下管线,含有三通、变径、放散管、水井等16种点状设备设施共828个,对应的管段数1012个;天然气综合地下管线,共有408个管点,管段475个。采用人工匹配方法,得到训练样本数据中匹配管点247个,测试数据中匹配管点153个。
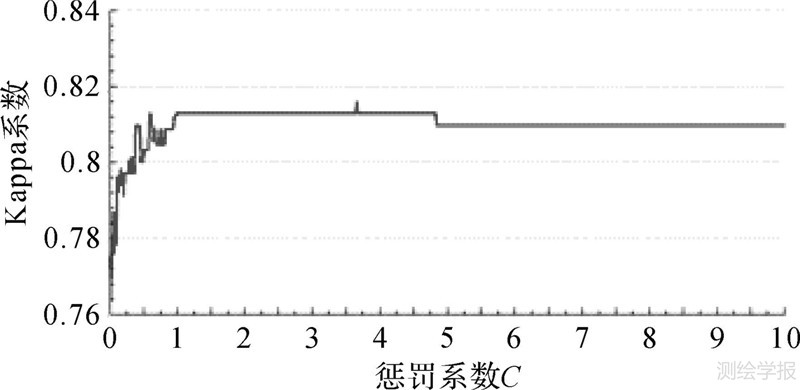
经统计,训练样本数据中247个匹配管点最大间距为12.3 m,在试验中适当放宽距离阈值保证匹配管点在距离范围内的同时,尽量减少综合管点与专业管点笛卡儿积运算产生的管点对集合,本文选取管点距离阈值米δd=13 m。经距离阈值筛选,在管线训练数据中选出583个管点,在管线测试数据中选出838个管点。以线性函数作为SVM支持向量机核函数,计算不同惩罚因子C下SVM分类结果的Kappa系数[20]。以Kappa系数衡量分类结果和人工匹配结果的相似性,Kappa系数越大,其分类效果越好。图 4为测试样本数据分类结果的Kappa系数随惩罚因子变化图。惩罚因子C以0.01为步长,在[0.01,10]区间上计算测试样本数据Kappa系数,当Kappa系数分布在[0.95,4.8]区间时,其Kappa系数达到最大,且分布趋势平稳,值为0.812 9。根据文献[20]所述Kappa系数分布在0.81~0.99之间表示分类效果与人工匹配结果十分相近,SVM分类器分类效果最好。
因而,选取C=1,对阈值筛选出的训练数据的匹配管点实体集合元素缩减为190个。最后按4.1节中管点唯一匹配规则Constraint.Ⅰ,依据权重Ws=0.669 4、Wp=0.141 2、Wf=0.189 4计算出总相似度,再进行集合缩减,最终匹配管点个数为152个。
如表 1所示,随着约束条件的不断增加,匹配管点实体集合中的管点对个数Ns与其中正确匹配管点数Nc逐渐缩减,从最终匹配的管点对结果来看,最终获得实体集合中匹配管点对个数Ns为152个,与人工匹配管点个数Nh=153相比有140个相同,即正确匹配管点数Nc=140。所以在最终获得的匹配管点集合Sr中存在12对错误匹配的管点对,而人工匹配集合中13个管点对不在集合Sr中,即存在未匹配的管点对13个。
| 测试样本数据集合 | 笛卡儿积运算 | 距离阈值约束Dis(Ai,Bj)≤δd=13 m | SVM分类约束F(X(Ai,Bj))=1 | 管点唯一匹配原则Constraint.I |
| 匹配管点实体集合管点对个数Ns | 337 824 | 838 | 190 | 152 |
| 人工匹配管点对个数Nh | 153 | 153 | 153 | 153 |
| 错误删除匹配管点对个数Nn | 0 | 2 | 6 | 5 |
| 匹配管点实体集合中正确匹配数Nc | 153 | 151 | 145 | 140 |
经过对匹配结果中错误匹配和未匹配管点对的查找与分析,得到了产生这两个现象原因。表 2显示造成管点数据匹配错误的原因主要是管点与管段分布密集,管点对的管线空间相似性在该区域范围内最大。在表 3中管点未匹配主要有3个原因:①匹配管点间距离过大,大于阈值距离无法匹配;②管点空间结构上的巨大差异,导致空间相似性向量在SVM支持向量机分类过程中被错误分类;③如表 2所述,由于管点与管段的密集分布,导致关联管段数为2的管点在管线相似性向量上存在多个极其相似的管点对,匹配的管点在管点唯一匹配的原则Constraint.Ⅰ约束下被当作错误匹配管点对剔除,如表 2中的编号1与表 3中的编号4管点对。追究这一问题的根本原因,这是管线数据自身特性所导致的,即综合管线与专业管线在空间形态上既存在非同一区域但分布相似的情况(管线密集分布),又存在同一区域分布差异巨大的情况(探测范围不同)。
| 编号 | 问题管点图 | 管点间距离/m | 空间结构相似度 | 形状相似度 | 语义相似度 | 原因 |
| 1 | 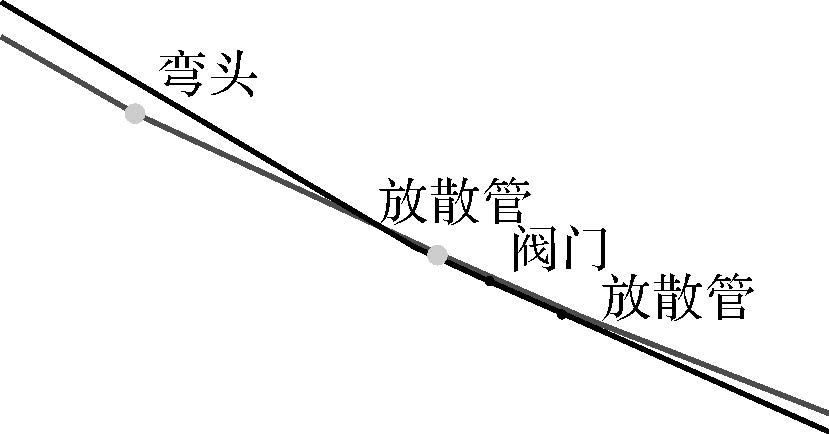 | 5.964 4 | 0.999 9 | 0.984 5 | 0.238 1 | 管点所在管线形态及形状差异小 |
| 2 | 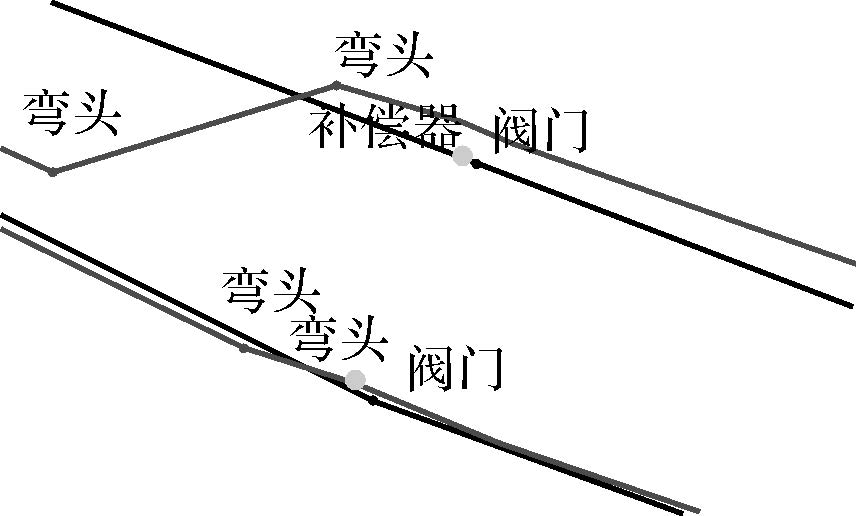 | 4.556 0 | 0.982 0 | 0.982 0 | 0.238 1 | 当管线分布密集且管线形态相似时,会对管点的匹配存在影响 |
| 编号 | 问题管点图 | 管点间距离/m | 空间结构相似度 | 形状相似度 | 语义相似度 | 原因 |
| 1 | 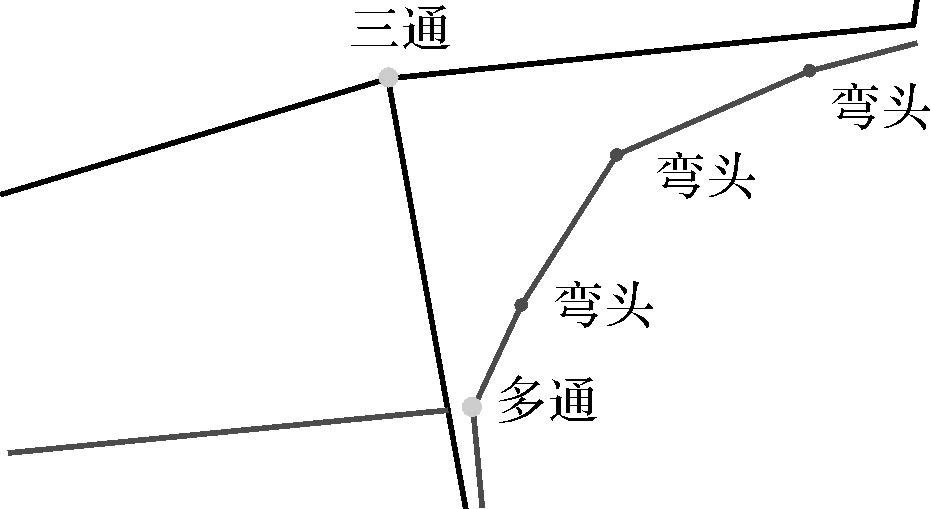 | 7.519 4 | 0.829 8 | 0.984 9 | 0.743 9 | 局部管线空间形态差异巨大 |
| 2 | 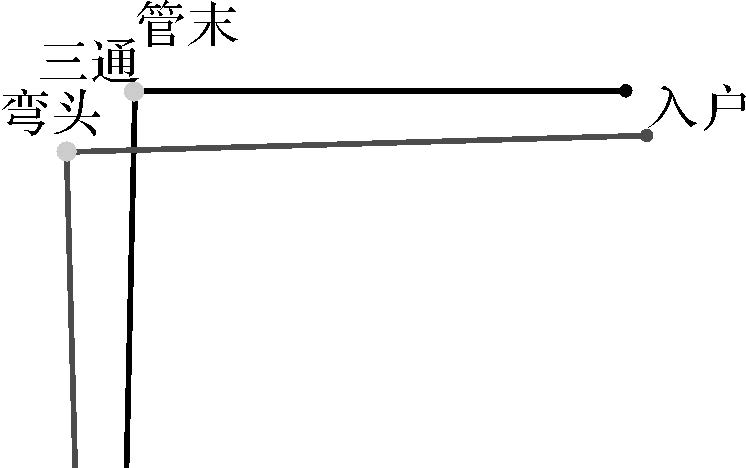 | 0.972 8 | 0.666 2 | 0.983 1 | 0.238 1 | 探测区域不一致,导致管点类型及局部管线形态不一致 |
| 3 | 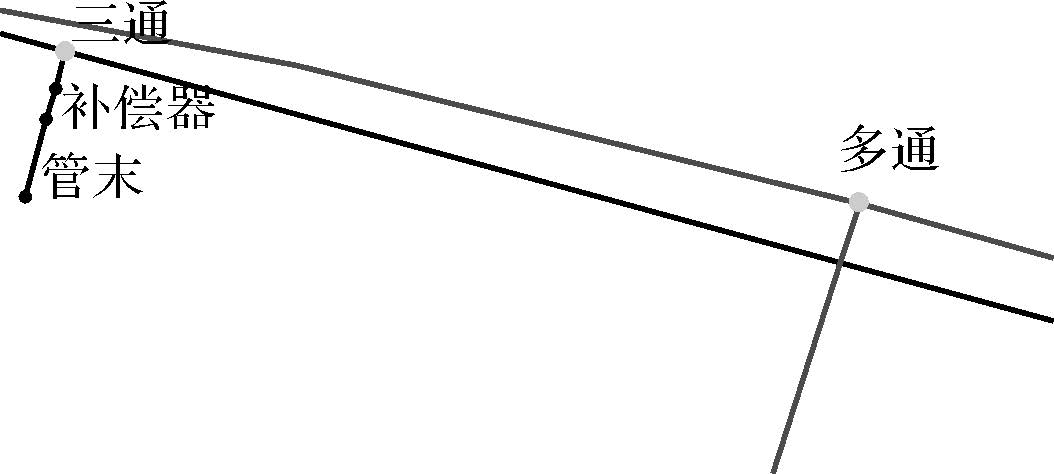 | 13.27 | 0.998 9 | 0.969 9 | 0.743 9 | 两管点距离大于距离阈值 |
| 4 |  | 7.038 4 | 0.997 2 | 0.982 8 | 0.238 0 | 表3编号1的管点对中该“弯头”管点已经匹配 |
如图 5所示,为测试数据中部分管线数据的管点匹配结果图,其中红色实线代表天然气综合地下管线,黑色虚线代表天然气专业地下管线,对于匹配的管点对,使用蓝色实线连接。在该区域内共有46个匹配管点,从图示的匹配效果上来看,该算法在这一区域内可以将天然气综合地下管线与天然气专业地下管线中的大部分管点数据相匹配。从总体匹配角度来看,最终管点对匹配数为152个,其中正确匹配的管点对个数为140个,匹配正确率高达92.105%;与人工匹配的管点数153相比,正确率达到91.503%;本文算法在管点匹配的数量及正确率上都很高,与人工匹配结果近似。从试验结果上来看,本文提出的基于空间相似性的地下管线匹配算法能够有效解决管线数据中的管点匹配问题。
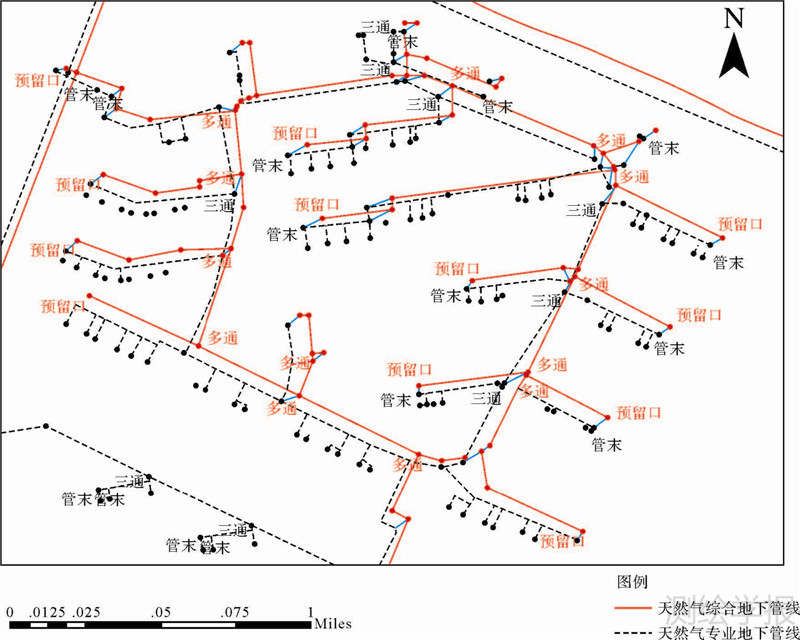
|
| 图 5 测试数据部分管点匹配结果 Fig. 5 A figure of part of matching pipe points in test data |
当前地下管线数据间的多重异构是制约管线数据集成、共享的重要因素,采用本文提出的顾及多空间相似性的地下管线数据匹配方法能够有效解决管线数据中管点数据的匹配问题。
本文选取天然气管线为研究对象,但地下管线数据种类多、管点分类与管线属性也不尽相同,因此,管线语义相似性的计算方法及算法可能会有不同,解决方法则需要进一步研究并建立多种类型一体的地下管线空间本体。从匹配结果上看,管点匹配集在最后的匹配结果中存在部分错误匹配或未匹配的情况,单从管点出发已经难以解决,在后续的管线匹配算法中,可以考虑从管线及管点邻接管线角度进行匹配优化,以提高管线匹配的正确率。此外,以本文算法为基础开发管线数据匹配软件,通过规模化应用,可进一步完善相应的算法成果。
| [1] | ZHANG Shuliang, CHU Zhengwei, HE Yuan, et al. The Analysis of the Differences of Spatial Data on Urban Integrated and Professional Underground Pipeline[J]. Bulletin of Surveying and Mapping, 2013(12): 58-62. (张书亮, 储征伟, 何源, 等. 城市综合与专业地下管线空间数据的差异性分析[J]. 测绘通报, 2013(12): 58-62.) |
| [2] | HAO Yanling, TANG Wenjing, ZHAO Yuxin, et al. Areal Feature Matching Algorithm Based on Spatial Similarity[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 501-506. (郝燕玲, 唐文静, 赵玉新, 等. 基于空间相似性的面实体匹配算法研究[J]. 测绘学报, 2008, 37(4): 501-506.) |
| [3] | COBB M A, CHUNG M J, FOLEY III H, et al. A Rule-Based Approach for the Conflation of Attributed Vector Data[J]. GeoInformatica, 1998, 2(1): 7-35. |
| [4] | HU Yungang, CHEN Jun, ZHAO Renliang, et al. Matching of Roads under Different Scales for Updating Map Data[J]. Geomatics and Information Science of Wuhan University, 2010, 35(4): 451-456. (胡云岗, 陈军, 赵仁亮, 等. 地图数据缩编更新中道路数据匹配方法[J]. 武汉大学学报:信息科学版, 2010, 35(4): 451-456.) |
| [5] | WALTER V, FRITSCH D. Matching Spatial Data Sets: A Statistical Approach[J]. International Journal of Geographical Information Science, 1999, 13(5): 445-473. |
| [6] | MUSTIÈRE S, DEVOGELE T. Matching Networks with Different Levels of Detail[J]. GeoInformatica, 2008, 12(4): 435-453. |
| [7] | CHEN Yumin, GONG Jianya, SHI Wenzhong.A Distance-based Matching Algorithm for Multi-scale Road Networks[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 84-90. (陈玉敏, 龚健雅, 史文中. 多尺度道路网的距离匹配算法研究[J]. 测绘学报, 2007, 36(1): 84-90.) |
| [8] | LUO Lei, YIN Jianping, ZHANG Guomin, et al. Point Matching for Shapes Based on Weighted Neighborhood Relationships[J]. Computer Engineering & Science, 2008, 30(11): 34-37. (罗磊, 殷建平, 张国敏, 等. 基于加权相邻关系的形状轮廓点匹配[J]. 计算机工程与科学, 2008, 30(11): 34-37.) |
| [9] | RODRÍGUEZ M A, EGENHOFER M J. Determining Semantic Similarity among Entity Classes from Different Ontologies[J]. IEEE Transactions on Knowledge and Data Engineering, 2003, 15(2): 442-456. |
| [10] | LUAN Xuechen, YANG Bisheng, LI Qiuping. Pattern-based Node Matching Approach for Road Networks[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 608-614. (栾学晨, 杨必胜, 李秋萍. 基于结构模式的道路网节点匹配方法[J]. 测绘学报, 2013, 42(4): 608-614.) |
| [11] | ZHAO Dongbao, SHENG Yehua. Research on Automatic Matching of Vector Road Networks Based on Global Optimization[J].Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 416-421. (赵东保, 盛业华. 全局寻优的矢量道路网自动匹配方法研究[J]. 测绘学报, 2010, 39(4): 416-421.) |
| [12] | ZHANG Yunfei, YANG Bisheng, LUAN Xuechen. Automated Matching Urban Road Networks Using Probabilistic Relaxation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 933-939. (张云菲, 杨必胜, 栾学晨. 利用概率松弛法的城市路网自动匹配[J]. 测绘学报, 2012, 41(6): 933-939.) |
| [13] | GONG Xianyong, WU Fang, JI Cunwei, et al. Ant Colony Optimization Approach to Road Network Matching[J]. Geomatics and Information Science of Wuhan University, 2014, 39(2): 191-195. (巩现勇, 武芳, 姬存伟, 等. 道路网匹配的蚁群算法求解模型[J]. 武汉大学学报:信息科学版, 2014, 39(2): 191-195.) |
| [14] | YANG Jieming, TANG Dingfu, ZHANG Minglan, et al. GB/T 28590-2012, Classification and Code for Urban Underground Facilities[S]. Beijing: China Standard Publishing House, 2012.(杨洁明, 唐定富, 张明兰, 等. GB/T 28590-2012, 城市地下空间设施分类与代码[S].北京: 中国标准出版社, 2012.) |
| [15] | HONG Libo, ZHOU Fenglin, QU Fubang, et al. CJJ61-2003,Technical Specification for Detecting and Surveying Underground Pipelines and Cables in City[S].Beijing: China Building Industry Press, 2004.(洪立波, 周凤林, 曲福邦, 等. CJJ 61-2003, 城市地下管线探测技术规程[S].北京: 中国建筑工业出版社, 2004.) |
| [16] | NJCH002, Technical Specification for Detecting and Surveying Pipelines and Cables in Nanjing[S]. Nanjing: Nanjing Urban Planning Bureau, 2004. (NJCH002, 南京市管线探测技术规程[S].南京:南京市规划局,2014.) |
| [17] | TVERSKY A. Features of Similarity[J]. Psychological Review, 1977, 84(4): 327-352. |
| [18] | YAN Weiwu, SHAO Huihe. Application of Support Vector Machines and Least Squares Support Vector Machines to Heart Disease Diagnoses[J]. Control and Decision, 2003, 18(3): 358-360. (阎威武, 邵惠鹤. 支持向量机和最小二乘支持向量机的比较及应用研究[J]. 控制与决策, 2003, 18(3): 358-360.) |
| [19] | DINGShifei, QI Bingjuan, TAN Hongyan. An Overview on Theory and Algorithm of Support Vector Machines[J]. Journal of University of Electronic Science and Technology of China, 2011, 40(1): 2-10. (丁世飞, 齐丙娟, 谭红艳. 支持向量机理论与算法研究综述[J]. 电子科技大学学报, 2011, 40(1): 2-10.) |
| [20] | VIERA A J, GARRETT J M. Understanding Interobserver Agreement: The Kappa Statistic[J]. Family Medicine, 2005, 37(5): 360-363. |