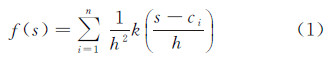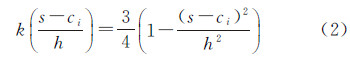2. 武汉大学资源与环境科学学院, 湖北 武汉 430079;
3. 天津大学海洋科学与技术学院, 天津 300072;
4. 华中师范大学城市与环境科学学院, 湖北 武汉 430079
2. School of Resource and Environmental Sciences, Wuhan University, Wuhan 430079, China;
3. School of Marine Science and Technology, Tianjin University, Tianjin 300072 China;
4. College of Urban and Environmental Science, Central China Normal University, Wuhan 430079, China
1 引 言
城市设施兴趣点(point of interest,POI)是当前数字城市领域最易被专业规划部门和普通民众关注的地图对象,它可以描述城市空间中各类工程型与社会性服务设施,蕴含了丰富的人文经济及自然信息。由于诸多类别设施在功能性质上具有较强的关联关系,其POI点在地理空间中也往往表现为聚集形式,即热点(hotspot),例如城市中央商务区内金融设施、信息咨询设施及零售业设施聚集形成的空间热点,以及旅游活动区域中地标建筑、博物馆等文化设施的聚集分布[1]。集成POI热点信息与道路、人类活动等专题信息可以为城市旅游推荐、城市发展规划、商业选址、基础设施布局等领域提供丰富的量化数据资料及决策支持[2, 3, 4]。然而,传统对于POI热点的定义比较模糊,主观性较强,如何界定热点及其空间区位一直是GIS、城市规划等相关学科的难题。
POI分布热点具有比其他区域更高密度的目标群。在城市分析领域,相关研究主要是通过融合空间密度估计、空间自相关技术和等值线方法来界定POI热点的范围。例如,文献[5]基于样方密度估计技术,提出了一种面向位置签到POI数据的城市热点探测方法。文献[6]利用核密度估计方法将兴趣点和兴趣面数据转换成连续的密度表面,以此来评价人类活动在城市空间的分布强度。文献[7]同样是基于该类方法,通过分析密度表面的高值区域来估计POI热点范围。总体上看,以上研究大多是将城市环境视为均质的、各向同性的欧氏空间,缺乏有效的空间度量,从而很难准确、客观地获取城市功能沿交通轴布局的形态与范围[8, 9]。
城市环境中多数人为活动或过程是受限于二维欧氏空间内的网络交通部分,即网络空间,例如快餐点外送、停车场、银行业务及交通事故等。传统基于欧氏距离的空间均质化假设在城市网络现象研究中过于理想化,容易高估城市功能的空间分布聚集程度,影响POI热点范围的形态与大小。针对以上问题,国内外学者提出了一系列基于道路网络的分析模型与方法,例如,文献[8, 10]基于网络路径距离评估城市零售商业需求;文献[11, 12, 13, 14]采用网络Voronoi图划分城市商业等公共设施的市场域;文献[15]通过构建网络Voronoi图来优化多仓库的物流配送路径;文献[16, 17]提出了一种网络空间核密度模型,并获得了令人满意的设施服务分布结果。网络核密度方法顾及了地理学第一定律的区位影响以及考虑了道路网络在城市功能覆盖上的重要作用,它在经济活动空间分布分析、犯罪热点分析等研究中应用广泛。
核密度研究需要将空间划分为基础样方单元(即细小弧段),以便于结果的输出和可视化表达。然而,现有网络核密度研究主要基于数学图的数据模型,采用传统Dijkstra算法计算网络位置上的核密度值[16, 17, 18]。该算法需要频繁比较邻接节点的权重,因此在大量的弧段数据计算应用中,还存在分析效率低、可扩展性不高等问题。
本文提出一种面向城市设施POI数据的网络空间热点分析方法,对热点区域的定性化特征建立了定量化表达模型,并顾及弧段不规则排列的约束以及网络计算的效率问题,给出了一种基于一维栅格参考系统及形态运算的网络核密度计算方法。与传统网络核密度估计方法比较,该方法的效率更高,并且可以较好地表达设施POI分布的线性特征。
2 网络空间核密度估计核密度估计是点模式分析中最常用也最有效的方法之一,该方法的计算结果表现出距离核心越近的区域所受中心辐射值越大的特征,符合城市设施服务对周边位置影响的扩散特点。比较其他密度计算方法(如样方法),核密度估计在表达事故危险性、犯罪分布等空间连续性现象中具有优势[2, 3]。本文根据城市公共设施与被辐射对象的联系主要通过道路进行的事实,应用基于路径距离的网络核密度估计方法进行设施分布热点分析。文献[3]对核密度公式的定义为
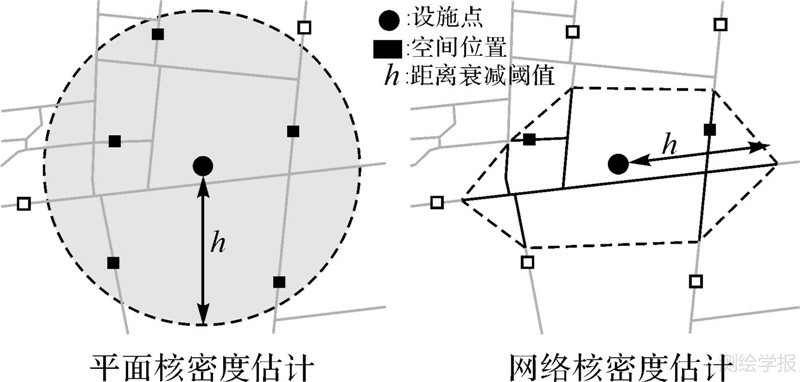
式中,f(s)是位置s处的核密度估计函数;h是路径距离衰减阈值,即带宽;n是与位置s的路径距离小于或等于h的POI点数;k函数选择应用最普遍的4次空间权重方程(式(2))[3] 式(1)中存在两个关键参量,即空间权重函数k与距离衰减阈值h。权重函数虽然有多种定义方式,但是具体的选择对密度分析的影响不大[2, 3],因为它们均基于“距离衰减效应”,即密度值在远离核心要素ci过程中不断降低,直至与核心ci的网络距离达到阈值h时核密度值降为0。核密度分析真正需要注意的是带宽的选择,它的设定往往根据POI数据情况和应用环境而定,可能的影响因素就包括有分析尺度、POI点的离散程度以及功能辐射性质等。带宽覆盖区域属于地理现象的空间影响域,在欧氏空间,“影响域”是圆形二维平面,在网络空间则是扩散的路径集,例如设施POI沿街道扩散所形成的中心服务域,如图 1所示。在实例中,设施周围有5个矩形位置处于平面影响域的范围内,而在网络空间下只有两个,这说明平面核密度估计容易造成网络现象过度集聚的结果。总体来说,相比于平面核密度估计,网络核密度估计在以下两个方面存在显著差异:网络空间取代欧氏空间作为点集的上下文;距离衰减阈值和权重函数计算都是基于最短路径距离而非欧氏直线距离。
|
| 图 1 平面核密度计算与网络核密度计算产生的聚类效果对比 Fig. 1 The comparison of clustering effects with the planar kernel density computation and the network kernel density computation |
核密度分析首先需要离散化目标空间,即建立栅格空间[3]。在栅格空间中,最有效的目标分析与识别方法是形态运算(即膨胀操作)。然而,基于二维栅格结构的形态运算在实际网络分析应用中并不广泛,这主要是受平面剖分方式的限制。在欧氏空间中,平面剖分结构的特点包括:基础单元为网格;邻近运算方向为四方向或八方向。虽然这种剖分结构广泛应用于地貌综合、洪水淹没模拟、人口密度分析及城市扩展分析等表面分析与建模研究,但是它并不便于实现线性空间下的序贯操作。因此,本文提出一种基于路径单元剖分的一维栅格结构,该类栅格在网络分析领域的优势主要体现在3个方面:①二维栅格容易夸大弧段的长度或权重值,产生Z字形的网络抽象形态,而一维栅格可以准确负载弧段上的度量信息;②基于二维栅格的序贯运算需要分析除弧段位置之外的像素信息,而基于一维栅格的运算只需要考虑拓扑连接的像素;③在可视化表达方面,二维栅格考虑整个平面的地理现象分布,而基于一维栅格的密度符号便于表达呈线状分布的热点信息。
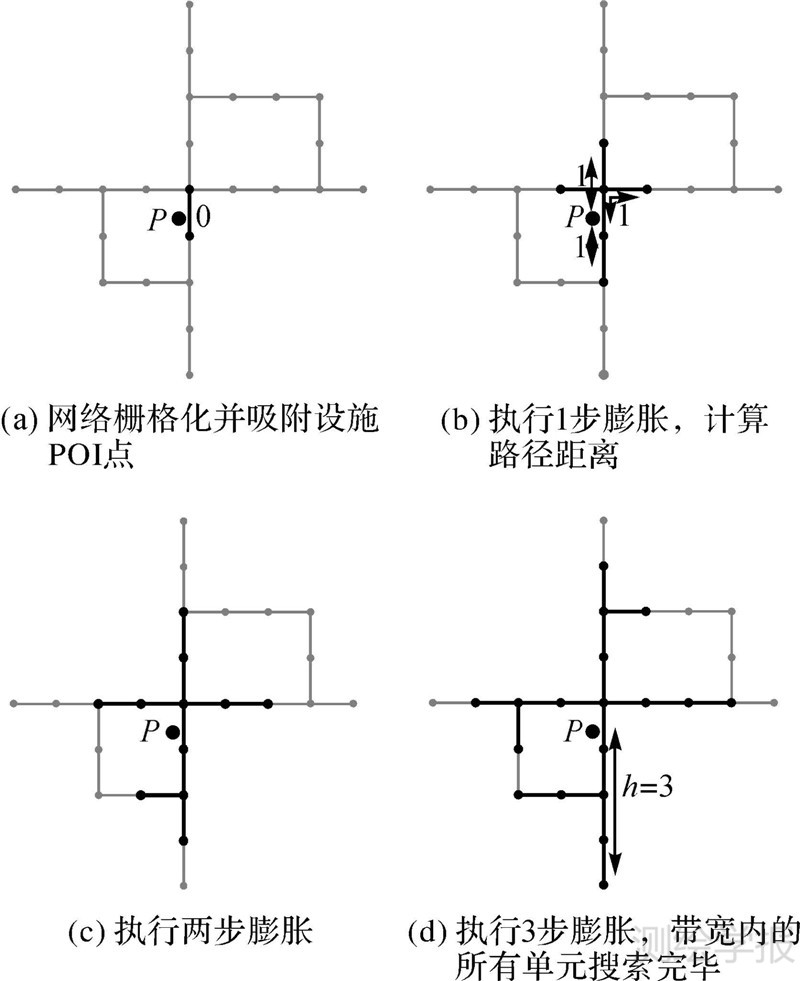
如图 2所示,基于一维栅格的核密度估计方法通过执行网络膨胀运算,来计算线性单元间的路径距离并获取POI在网络各位置上的核密度值。该操作过程类似于水流扩展现象,即形态活跃单元沿着网络上的可通行路径同时向外蔓延,直至到达带宽边界或者到达边的尽头。算法的具体步骤如下:①利用道路交叉点将网络分割成首尾相接的弧段,将所有弧段等分为一定长度l的基础线性单元集,建立线性单元网络拓扑关系;②将POI点映射到最近的线性单元(定义为发生元),记录每个发生元所吸附的点数,将其作为密度计算的权重值;③查询发生元邻接的所有线性单元,定义为活跃单元,建立活跃单元集合C,并记录当前膨胀步数作为发生元与活跃单元间的距离;④对于活跃集C中的每一个元素,基于网络拓扑关系搜索其所有邻接非活跃单元(即未被膨胀算子标记),并加入临时集合C′,将原活跃集合C中各元素移除,记录当前膨胀步数,若小于或等于衰减阈值,则将C′中各元素插入活跃集C;⑤重复执行步骤④,直至膨胀步数达到衰减阈值(图 2中阈值h),计算发生元与带宽范围内各线性单元的路径距离,然后基于式(1)计算各单元的密度估计值。
|
| 图 2 基于一维膨胀运算的网络核密度估计(h为密度衰减阈值,以膨胀步数作为测量标准) Fig. 2 The network kernel density estimation based on the 1D morphological operation (h represents the search bandwidth, measuring in terms of extension steps) |
传统网络核密度算法主要是基于图结构的最短路径树技术(shortest-path tree),其中以文献[18]的研究较为典型,该类算法的基本原理是:从目标位置出发,以弧段为基础单元向外同步膨胀,在每次迭代过程中都需要比较邻接节点的权重来获取最小权重值,进而保证当前路径为全局最短路径。算法的时间复杂度为O(mn+klogk),其中m、n、k分别为POI点的个数、道路弧段的个数及道路交叉点的个数。注意到,在网络核密度计算过程中,网络剖分产生的大量基础弧段会影响该算法的效率;而相比较,本文提出的膨胀计算方法达到了线性时间复杂度,即O(m+n),可避免图搜索算法中每次迭代都需要比较节点权重的耗时操作。
4 试验与分析 4.1 试验数据本文选取深圳市福田区作为研究区域,试验数据包括1∶1000比例尺的道路网数据以及商务设施POI点数据。其中,道路网络由1999条网络弧段组成,商务基础设施包括银行、ATM、保险公司、投资公司、证券公司以及财务咨询公司6个二级类,共有POI点4471个。
单元大小可以影响密度分析结果的详尽性,而搜索半径则会对结果的光滑性产生影响。在试验了多个参数之后,本研究选取10 m的线性单元及600 m的衰减阈值作为最终理想的试验参数。该参数既可保留足够的细节信息,又能较好地反映空间分布的整体特征。
4.2 深圳市金融设施POI的分布密度估计基于本文提出的方法,图 3(a)、(b)分别为深圳市POI在平面空间与街道网络约束下的核密度分布图。观察后发现,传统方法会使空间各位置均获得较高的密度值,密度表层的空间延展特征呈现较理想的二维平滑性,而图 3(b)中核密度估计被约束至道路弧段附近,空间各位置的密度值显著降低,热点分列于城市的主要干道旁。这种线性可视化的形式组合了颜色以及高度视觉变量,能较好地反映城市功能在大尺度下的细部分布特征,可用于网络现象的空间分布模式分析、分布趋势分析以及空间发展预测等应用。

|
| 图 3 设施POI在平面空间与街道网络约束下的核密度分布图 Fig. 3 POI density distribution in the planar space and in the network space |
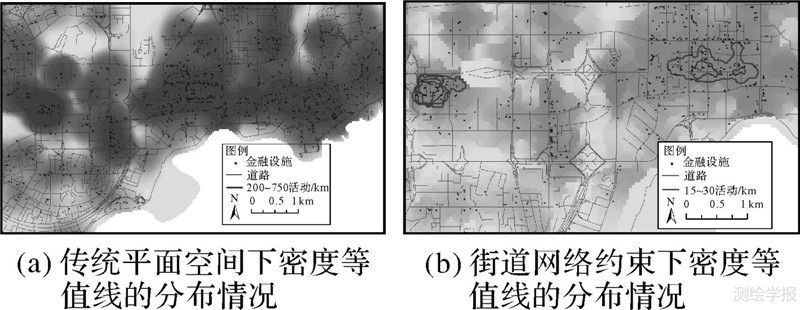
为了能进一步界定深圳市热点范围,在图 3(b)的基础上,将研究区域划分为二维网格空间,利用克吕金插值将网络单元密度值映射到平面空间;然后在带有密度属性的网格表层上,通过生成等值线来分析热点即金融中心的分布范围(图 4)。
|
| 图 4 设施POI功能密度在平面空间与街道网络约束下的等值线分布图 Fig. 4 Isolines of POI density function in the planar space and in the network space |
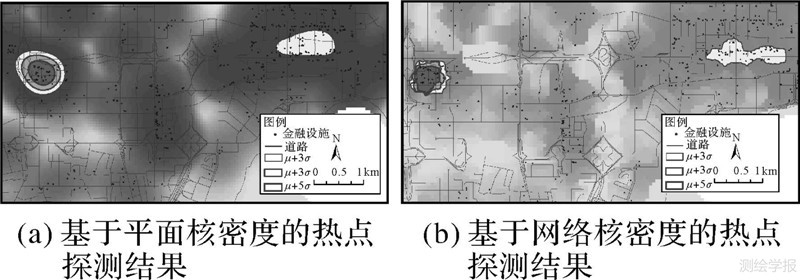
由表 1可见,平面核密度值明显高于网络核密度值,并且图 4(a)中基于欧氏距离的等值线也呈理想化圆弧状,而图 4(b)中,等值线排列于福田区的主干道旁,即深南大道,这种分布模式符合城市商业和商务活动对交通输送的依赖特征[1]。热点是商务功能相对集中的区域,较其他位置,该区域应包括数值总体分布中一定水平的右尾值(即相对高值)。因此如图 5所示,本研究采用标准差值对密度表面做更进一步地专题分类,以便深入地分析热点的可能分布范围。标准差能反映一个数据集的离散程度,根据正态分布,99%水平的数值分布于距平均值小于3个标准差之内的数值范围。如图 5所示,取不同水平的尾值会产生集聚程度不同的热点区域,标准差值越大(即3σ、4σ、5σ),最终界定的范围越小,结果也将越接近于城市功能热点“中心”。通过观察,深圳市金融热点主要分布于福田中心区以及罗湖-上步中心区,深圳市总体规划明确的南北向景观轴(中轴线)及东西向(深南大道)交通轴构成的“十字”轴,成为该热点清晰的“脊梁”[19]。
| 核密度估计方法 | 密度最小值(活动/km2) | 密度最大值(活动/km2) | 密度平均值μ(活动/km2) | 密度标准差σ(活动/km2) |
| 平面核密度 | 0 | 775 | 88 | 115 |
| 网络核密度 | 0 | 34 | 3 | 5 |
|
| 注:μ表示平均值,σ表示一个标准差。 图 5 密度值大于3个标准差的热点分布范围 Fig. 5 The delimitation of hotspot using the value of 3 standard deviation of density function |
在城市规划过程中,金融设施的空间分布热点探测可以为相关管理部门的决策分析提供依据,例如城市的基准地价评估。管理者根据城市空间中各区域的金融热点,修正基准地价的发布,使其更符合实际的用地情况和商业需求。本文采用深圳市政府部门发布的商业用地基准地价数据(如图 6)[20],对图 5中的热点探测结果作进一步的对比分析。如表 2所示,基于平面核密度的热点面积虽然要大于网络核密度的界定结果,但是其热点区域的平均商业地价水平要小于网络约束的地价,可见,本文提出的方法在金融中心分析和地价评估中非常有效,反映出当前深圳市不同地块的商业经济发展水平。
| (3个标准差) | ||
| (3 standard deviation) | ||
| 分析方法 | 热点面积/km2 | 平均商业基准地价/(元/m2) |
| 平面核密度 | 0.608 | 7 053.8 |
| 网络核密度 | 0.352 | 7 462.6 |
本文选择现有Okabe算法作为比较对象[18],通过选择不同的带宽以及POI数目作为参量,评价结果如图 7所示。由图 7可知,随着带宽或POI数目的增大,本文算法计算网络核密度所用时间保持线性增长,仅有微弱的增长趋势;而Okabe算法所用时间则成指数型增长,主要原因如下:Okabe算法基于Dijkstra路径计算,从初始位置向周围网络扩展时,每次迭代都需要比较邻接节点的权重,然后选择最小权重的节点作为最近点;而本文采用形态膨胀方式,不需要比较邻接节点的权重,只需要执行线性的检索操作,随着数据规模的增大,本文算法的效率优势将越明显。

|
| 图 7 比较膨胀算法与基于图的Okabe算法 Fig. 7 The comparison between the expansion algorithm and the graph-based Okabe algorithm |
城市设施POI数据涵盖了各类职能设施的位置信息与关联的属性信息,关于热点分布形态与范围的研究可为城市规划、导航、地理信息查询等应用提供丰富的高阶地理知识。本文顾及城市空间通达、连接是沿着街道路径的事实,将传统核密度估计约束至街道网络空间,基于路径距离探测与分析POI热点的空间分布。与传统的热点分析方法相比,本研究提出的约束型方法可以更细致地模拟人类活动在城市空间中沿街道实施的过程,热点分析结果也能更好地体现公共交通对当代城市功能分布的塑造作用。基于一维形态算子设计,本文提出的网络核密度计算算法比原有方法具有更好的效率与实用性。需要进一步研究不同交通环境下POI热点的分布差异,以及不同性质设施(文化设施、餐饮设施等)在城市空间下的分布依赖性。
| [1] | XU Xueqiang, ZHOU Yixing, NING Yuemin. Urban Geography [M]. Beijing: Higher Education Press, 1997. (许学强, 周一星, 宁越敏. 城市地理学[M]. 北京: 高等教育出版社, 1997.) |
| [2] | BAILEY T C, GATRELL A C. Interactive Spatial Data Analysis[M]. Harlow: Longman, 1995. |
| [3] | SCHABENBERGER O, GOTWAY C A. Statistical Methods for Spatial Data Analysis [M]. Boca Raton: Chapman & Hall/CRC, 2005. |
| [4] | CHEN Fei, DU Daosheng. Application of the Integration of Spatial Statistical Analysis with GIS to the Analysis of Regional Economy[J]. Geomatics and Information Science of Wuhan University, 2002, 27(4): 391-396. (陈斐, 杜道生. 空间统计分析与GIS在区域经济分析中的应用[J]. 武汉大学学报: 信息科学版, 2002, 27(4): 391-396.) |
| [5] | HU Qingwu, WANG Ming, LI Qingquan. Urban Hotspot and Commercial Area Exploration with Check-in Data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(3): 314-321. (胡庆武, 王明, 李清泉. 利用位置签到数据探索城市热点与商圈[J]. 测绘学报, 2014, 43(3): 314-321.) |
| [6] | THURSTAIN-GOODWIN M, UNWIN D. Defining and Delineating the Central Areas of Towns for Statistical Monitoring Using Continuous Surface Representations[J]. Transactions in GIS, 2000, 4(4): 305-317. |
| [7] | BORRUSO G, PORCEDDU A. A Tale of Two Cities: Density Analysis of CBD on Two Midsize Urban Areas in Northeastern Italy[M]//MURGANTE B, BORRUSO G, LAPUCCI A. Geocomputation and Urban Planning. Berlin Heidelberg: Springer, 2009: 37-56. |
| [8] | OKABE A, OKUNUKI K. A Computational Method for Estimating the Demand of Retail Stores on a Street Network and Its Implementation in GIS[J]. Transactions in GIS, 2001, 5(3): 209-220. |
| [9] | YAMADA I, THILL J C. Local Indicators of Network-Constrained Clusters in Spatial Point Patterns[J]. Geographical Analysis, 2007, 39(3): 268-292. |
| [10] | XIE Shunping, FENG Xuezhi, WANG Jiechen, et al. Radiation Domain of Commercial Centers in Nanjing Based on Analysis of Road Network Weighted Voronoi Diagram[J]. Acta Geographica Sinica, 2009, 64(12): 1467-1476. (谢顺平, 冯学智, 王结臣, 等. 基于网络加权Voronoi图分析的南京市商业中心辐射域研究[J]. 地理学报, 2009, 64(12): 1467-1476.) |
| [11] | WANG Xinsheng, YU Ruilin, JIANG Youhua. Delimitating the Store Market Field Based on the Metric of the City-block Distance[J]. Geographical Research, 2008, 27(1): 85-92. (王新生, 余瑞林, 姜友华. 基于道路网络的商业网点市场域分析[J]. 地理研究, 2008, 27(1): 85-92.) |
| [12] | XIE Shunping, FENG Xuezhi, LU Wei. Algorithm for Constructing Voronoi Area Diagram Based on Road Network Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 88-94. (谢顺平, 冯学智, 鲁伟. 基于道路网络分析的Voronoi面域图构建算法[J]. 测绘学报, 2010, 39(1): 88-94.) |
| [13] | XIE Shunping, FENG Xuezhi, DU Jinkang. Maximal Covering Spatial Optimization Based on Network Voronoi Diagrams Heuristic and Swarm Intelligence[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(6): 778-784. (谢顺平, 冯学智, 都金康. 基于网络Voronoi图启发式和群智能的最大覆盖空间优化[J]. 测绘学报, 2011, 40(6): 778-784.) |
| [14] | AI Tinghua, YU Wenhao. Algorithm for Constructing Network Voronoi Diagram Based on Flow Extension Ideas[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(5): 760-766. (艾廷华, 禹文豪. 水流扩展思想的网络空间Voronoi图生成[J]. 测绘学报, 2013, 42(5): 760-766.) |
| [15] | TU Wei, LI Qingquan, FANG Zhixiang. Large Scale Multi-depot Logistics Routing Optimization Based on Network Voronoi Diagram[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1075-1082, 1091. (涂伟, 李清泉, 方志祥. 基于网络Voronoi图的大规模多仓库物流配送路径优化[J]. 测绘学报, 2014, 43(10): 1075-1082, 1091.) |
| [16] | BORRUSO G. Network Density Estimation: Analysis of Point Patterns over a Network[M]//Gervasi O, Gavrilova M L, Kumar V, et al. Lecture Notes in Computer Science: Computational Science and Its Applications-ICCSA 2005. Berlin Heidelberg: Springer, 2005, 3482: 126-132. |
| [17] | BORRUSO G. Network Density Estimation: A GIS Approach for Analysing Point Patterns in a Network Space[J]. Transactions in GIS, 2008, 12(3): 377-402. |
| [18] | OKABE A, SATOH T, SUGIHARA K. A Kernel Density Estimation Method for Networks, Its Computational Method and a GIS-based Tool[J]. International Journal of Geographical Information Science, 2009, 23(1): 7-32. |
| [19] | Urban Planning Land and Resources Commission of Shenzhen Municipality. The Comprehensive Plan of Shenzhen City (2010-2020).[2014-10-01] . http://www.szpl.gov.cn/xxgk/csgh/csztgh/201009/t20100929_60694.htm. (深圳市规划和国土资源委员会. 深圳市城市总体规划(2010-2020).[2014-10-01] . http://www.szpl.gov.cn/xxgk/csgh/csztgh/201009/t20100929_60694.htm.) |
| [20] | Urban Planning Land and Resources Commission of Shenzhen Municipality, The Standard Land Price of Shenzhen City (2013).[2015-01-13] http://www.szpl.gov.cn/xxgk/tzgg/othersgg/201301/t20130111_78391.html. (深圳市规划和国土资源委员会. 深圳市基准地价(2013).[2015-01-13] . http://www.szpl.gov.cn/xxgk/tzgg/othersgg/201301/t20130111_78391.html.) |