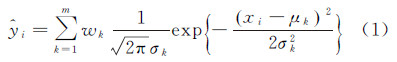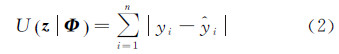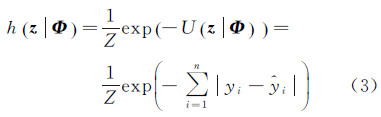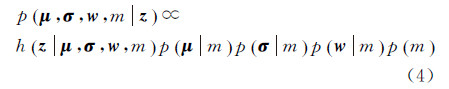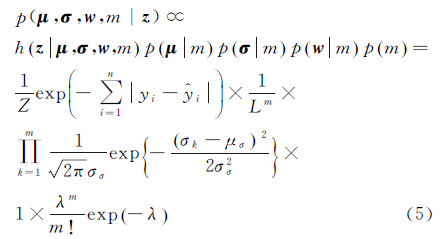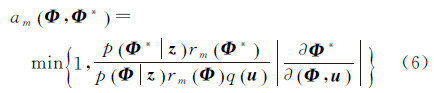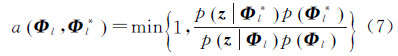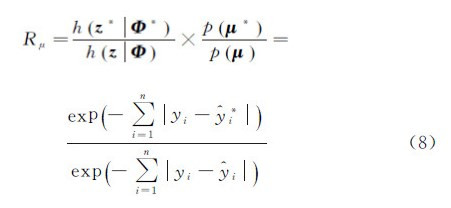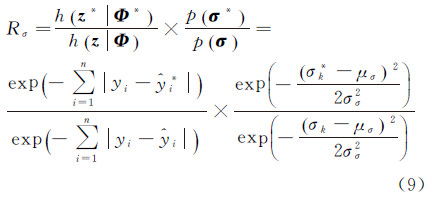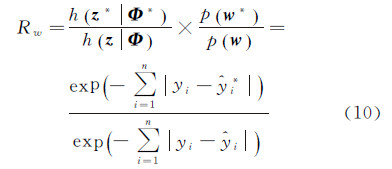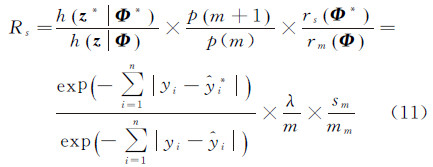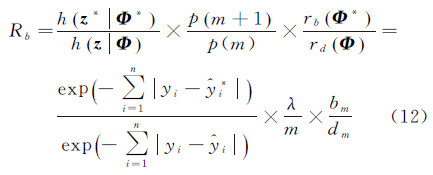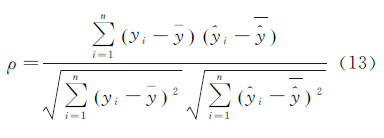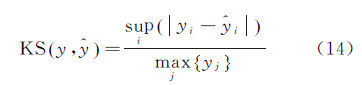1 引 言
与传统激光雷达(light detection and ranging,LiDAR)系统记录点云数据不同,全波形LiDAR系统能够以波形的形式记录一定高程范围内不同高程点上的后向散射能量[1, 2]。记录的波形信息可以提供一定范围(光斑)内的地表高程信息,以及不同高程点上反射能量。根据不同高程点反射能量的大小,能够检测出激光光束传播过程中目标垂直方向(高程方向)的分布情况[3, 4]。根据获取数据时激光束照射在地面光斑的大小,全波形LiDAR系统可分为大光斑系统和小光斑系统。大光斑LiDAR系统的光斑直径一般为8~70 m,脉冲发射频率为40~500 Hz,光斑之间间距在170 m左右,光斑分布稀疏;小光斑LiDAR系统的光斑直径一般为0.3~1 m,脉冲发射频率为40~500 kHz,光斑间的间距小于1 m,光斑分布密集[5]。目前,常用的配有全波形数字化仪的LiDAR系统包括NASA机载的LVIS(laser vegetation imaging sensor)系统[6, 7]、SLICER(scanning LiDAR imager of canopies by echo recover)系统[8, 9]和星载的GLAS(geoscience laser altimeter system)系统[10, 11]等大光斑LiDAR系统;Optech ALTM3100、Leica ALS-70、TopEye Mark Ⅱ、Riegl LMS-Q560以及Falcon Ⅲ等小光斑LiDAR系统[12, 13, 14]。
全波形LiDAR数据记录的是地物在不同高程点上后向散射能量,因此全波形LiDAR数据不仅蕴含地物的高程信息,而且能够反映地物的散射特性。波形分解是获取这些信息的重要手段。波形分解是指用有限一致分布统计模型(Gaussian、Nakagami、Burr等)的组合来拟合原始波形数据。
目前,已经有许多学者对全波形LiDAR数据的分解进行了研究。文献[15]通过雷达方程证明高斯函数可以拟合全波形LiDAR数据,为分解波形数据提供了理论依据。文献[16]提出了基于高斯模型的波形分解方法。该方法虽然能够将原始波形数据分解为若干个高斯分量,但容易陷于局部最优解,无法得到高精度的拟合结果。文献[17]针对波形数据的高斯特性,对原始波形数据进行了分解,该方法虽然提高了拟合精度,但是容易遗漏部分重叠的返回波,分解结果不能充分反映地物沿高程方向的信息。
通过高斯分解,分析高斯分量数、均值和标准差等参数,能够得到地物高程信息和后向散射特性。上述文献中高斯分量数均为给定值,然而由于受地形起伏复杂、回波信号噪声以及地物多次漫反射等诸多因素影响,很难人为确定波形分解数,并且容易遗漏部分重叠的返回波,降低波形拟合精度。因此,为了自动确定波形分解数,获得精确的参数估计值,本文提出了一种基于可变分量高斯混合模型和可逆跳转马尔科夫链蒙特卡洛(reversible jump Markov chain Monte Carlo,RJMCMC)的全波形LiDAR数据分解方法。
2 算法描述给定的全波形LiDAR数据集x={xi;i=1,2,…,n},y={yi;i=1,2,…,n},其中,xi为分布在有效高程L内的采样点,yi为在采样点xi处的反射能量,n为采样点个数。由此,全波形LiDAR数据可进一步表示为:z={(xi,yi);i=1,2,…,n}。一束激光的波形数据为由采样点x作为横坐标,能量值y作为纵坐标形成的点集,如图 1所示。
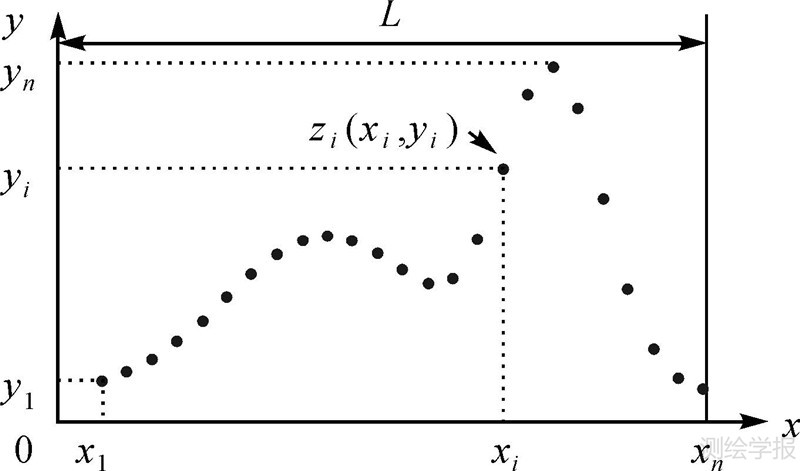
|
| 图 1 波形数据 Fig. 1 Waveform data |
在波形分解过程中,首先假设理想波形为高斯混合模型,用理想波形来拟合实际波形数据;定义能量函数以刻画二者的拟合程度;通过能量函数定义吉布斯分布,表征全波形LiDAR数据的或然率;根据贝叶斯定理构建刻画波形分解的后验概率模型;设计RJMCMC算法模拟该后验概率模型,从而确定波形分解个数及各高斯分量参数,完成波形分解。图 2所示为该算法总体流程,其中,实线框为完成的功能,虚线框为完成功能需要的模型和函数。
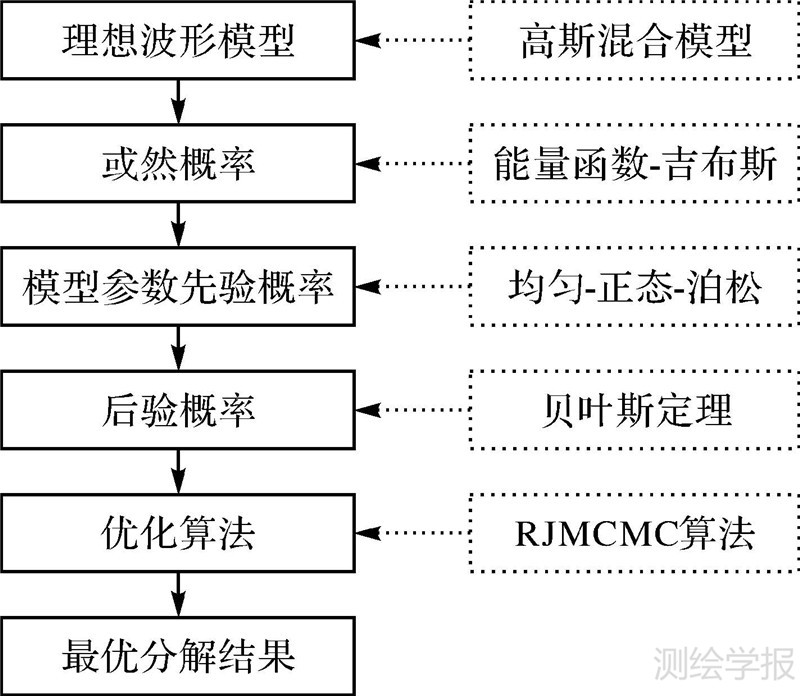
|
| 图 2 波形分解流程 Fig. 2 Waveform |
设理想波形为高斯混合模型,表达为m个高斯函数分量加权和
式中,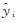 (i=1,2,…,n)为能量yi的理想值;wk为第k个高斯分量的权重,满足
(i=1,2,…,n)为能量yi的理想值;wk为第k个高斯分量的权重,满足 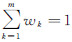 ;μk和σk(k=1,2,…,m)分别代表第k个高斯分量的均值和标准差。
2.2 或然率模型
;μk和σk(k=1,2,…,m)分别代表第k个高斯分量的均值和标准差。
2.2 或然率模型
为了控制理想模型与波形数据拟合程度定义能量函数。设参数集Φ={μ,σ,w,m},其中,μ={μ1,μ2,…,μm};σ={σ1,σ2,…,σm};w={w1,w2,…,wm}。定义控制yi和 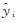 之间差异程度的能量函数为U(z|Φ),由试验分析能量函数用绝对误差和残差二次型的平方根的效果相同,但采用绝对误差可以减少计算量,因此,用绝对误差代替残差二次型的平方根,即
之间差异程度的能量函数为U(z|Φ),由试验分析能量函数用绝对误差和残差二次型的平方根的效果相同,但采用绝对误差可以减少计算量,因此,用绝对误差代替残差二次型的平方根,即
由能量函数U(z|Φ)定义表征波形数据或然率的吉布斯分布h(z|Φ)为
式中,Z为归一化常数。 2.3 后验概率模型为了分解波形,需要构建已知波形数据z条件下高斯分量的位置μ、标准差σ、权重w、个数m的联合后验概率密度函数。根据Bayes定理,已知波形z条件下的后验概率为
式中的先验概率讨论如下:
(1) 高斯分量位置μ。高斯分量的均值μk为对应第k个分解波形最大反射能量的高程,称为该高斯分量的位置。将m个高斯分量的位置按照增序排列为0<μ1<μ2<…<μm<L。假设μk(k=1,2,…,m)服从区间[0,L]上的均匀分布且相互独立,则其联合概率密度函数为
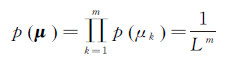
(2) 高斯分量标准差σ。假设各高斯分量的标准差σk(k=1,2,…,m)服从均值和标准差分别为μσ和σσ的正态分布且相互独立,则其联合概率密度函数为
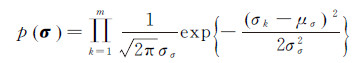
(3) 高斯分量权重w。假设各高斯分量的权重wk(k=1,2,…,m)服从[0,1]上均匀分布并相互独立,则其概率密度函数为
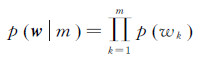
(4) 高斯分量个数m。假设高斯分量的个数m服从均值为λ的泊松分布,则其概率密度函数为 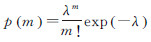 ,其中,2≤m≤kmax,kmax为预先指定的最大高斯分量数。
,其中,2≤m≤kmax,kmax为预先指定的最大高斯分量数。
综上,式(4)的后验概率可重写为
2.4 波形分解波形分解是通过对构建的后验概率模型进行模拟求解,本文采用RJMCMC算法进行后验概率模拟。
2.4.1 RJMCMC算法RJMCMC算法实现参数空间维数改变时,对参数集Φ的相关采样满足概率分布(式(5))。提取候选参数矢量Φ*,根据文献[18],其接受率表示为
式中,u是为确保维度平衡而提出的随机矢量,如状态空间维数增加时,则|Φ*|=|Φ|+|u|;rm(·)为选择移动类型m的概率;式中的Jacobian项,由参数集的改变,即由(Φ,u)→Φ*引起的。当参数空间维数不变时,称为M-H(Metropolis-Hastings)算法,式(6)接受率简化为
式中,Φl为总参数矢量Φ的第l个元素,候选参数Φl*依其相应的概率分布抽取。 2.4.2 基于RJMCMC方法的波形分解采用RJMCMC算法对式(5)后验概率模型进行模拟,为了实现完备采样,设计4种移动操作类型:①更新高斯分量参数;②更新高斯分量权重w;③合并或分裂高斯分量;④生成或删除高斯分量。
2.4.2.1 更新高斯分量参数更新高斯分量参数包括更新高斯分量位置μ和更新高斯分量标准差σ,该操作中参数空间维数没有发生改变,其过程包括:在m个高斯分量中随机抽取一个高斯分量k∈{1,2,…,m},该操作改变该高斯分量位置μk或标准差σk,而保持其他参数不变。候选μk*和σk*分别服从以当前μk和σk为均值,σt和σs为标准差的正态分布。其中σt和σs分别为μk和σk的迭代步长,是预先定义的常数。当σt过大时可以很快遍历整个μk取值范围,但是得到μk的精度较低;当σt过小时能够取到较高精度的μk,但是需要耗费较长时间。同理,σs具有相同的作用。通过试验,当σt和σs分别取50和1时得到的结果比较理想。则改变μ和σ的接受概率分别为:a(μk,μk*)=min{1,Rμ},a(σk,σk*)=min{1,Rσ},其中
2.4.2.2 更新高斯分量权重w在更新高斯分量权重w的操作中,参数空间维数没有发生改变,其过程包括:在m个高斯分量中随机抽取两个高斯分量,假设选取第k和k+1个高斯分量,该操作改变wk和wk+1,保持其他参数不变。随机生成s∈(0,1),则改变高斯分量权重前后需满足平衡条件wk*=(wk+wk+1)s和wk+1*=(wk+wk+1)(1-s)。则改变w的接受概率为:a(wk,wk*)=min{1,Rw},其中
2.4.2.3 合并或分裂高斯分量在合并或分裂高斯分量操作中,高斯分量的个数m发生变化,同时参数空间维数也发生改变。在分裂处理中,首先以等概率选择高斯分量k,将其分裂成两个高斯分量,分别记为k*和(k+1)*,它们的位置、标准差以及权重分别为(μk*,μk+1*)、(σk*,σk+1*)、(wk*,wk+1*)。将μk+1、μk+2、…、μm重新标号为μk+2*、μk+3*、…、μm+1*,σ、w作同样的操作,则参数μ={μ1,μ2,…,μm}、σ={σ1,σ2,…,σm}和w={w1,w2,…,wm}分别变为μ*={μ1,μ2,…,μk*,μk+1*,…,μm+1*}、σ*={σ1,σ2,…,σk*,σk+1*,…,σm+1*}和w*={w1,w2,…,wk*,wk+1*,…,wm+1*}。分裂后,高斯分量的位置μk*和μk+1*均服从以当前μk为均值,σt为标准差的正态分布,其中σt为预先定义的常数;标准差σk*和σk+1*均服从以当前σk为均值,σs为标准差的正态分布,其中σs为预先定义的常数;权重wk*和wk+1*满足平衡条件wk*=wku1和wk+1*=wk(1-u1),u1为保证维度平衡而设置的随机数,u1∈(0,1)。则分裂高斯分量的接受概率为as=min{1,Rs},其中
式中,Jacobian项为1;rs和rm分别为分解高斯分量和合并高斯分量的总概率,rs=sm/2m,rm=mm/2(m+1),其计算方法sm和mm分别为随机选择合并或分裂高斯分量的概率,当m=1时,m1=0,s1=1;当m=mmax时,smmax=0、mm max=1(mmax是m的最大值);当m=2,3,…,mmax-1时,sm=mm=0.5。分解高斯分量的过程包括:在m状态下选择分裂高斯分量,其概率为sm;然后在原有的m个高斯分量中以等概率随机抽取一个高斯分量,如k,其概率为1/m;将对应的第k个高斯分量以等概率(1/2)分离为第k*个高斯分量或第(k+1)*个高斯分量。合并高斯分量是分裂高斯分量的对偶操作。其过程包括:在m+1状态下选择合并高斯分量操作,其概率为mm;然后在原有的m+1个高斯分量中以等概率随机抽取一个高斯分量,其概率为1/m+1,然后在与其相邻的两个高斯分量中随机抽取一个与其合并,其概率为1/2。由于合并高斯分量操作是分裂高斯分量操作的对偶操作,因此其接受概率为:ac=min{1,1/Rs}。
2.4.2.4 生成或删除高斯分量在生成或删除高斯分量操作中,高斯分量数m发生变化,同时参数空间维数也发生改变。对于生成高斯分量操作,首先以等概率选择一个高斯分量k,设新生成的高斯分量的位置、标准差和权重分别为μk+1*、σk+1*和wk+1*。μk+1*服从(μk,μk+1)之间的均匀分布,σk+1*由其服从的先验分布中抽取,权重wk*和wk+1*满足平衡条件wk*=wku2和wk+1*=wk(1-u2),u2为保证维度平衡而设置的随机数,u2∈(0,1),则生成一个高斯分量的接受概率为ab=min{1,Rb},其中
式中,Jacobian项为1;rb=bm/m、rd=dm/m+1,rb和rd分别为生成高斯分量和分解高斯分量的总概率,其计算方法为bm和dm的选取和前面的sm和cm相同。生成高斯分量的过程包括在m状态下选择生成操作,其概率为bm;在原有的m个高斯分量中以等概率随机抽取一个高斯分量k,设生成的高斯分量标号为(k+1)*,然后将μk+1、μk+2、…、μm重新标号为μk+2*、μk+3*、…、μm+1*,其概率为1/m。删除高斯分量是生成高斯分量的对偶操作,其过程包括:在m+1状态下选择删除操作,其概率为dm;在原有m+1个高斯分量中以等概率随机抽取一个高斯分量k,并删除该高斯分量,然后将位置μk+1、μk+2、…、μm+1重新标号为μk*、μk+1*、…、μm*,其概率为1/m+1。由于删除高斯分量操作是生成高斯分量操作的对偶操作,因此其接受概率为ad=min{1,1/Rb}。
3 试验与分析 3.1 试验数据试验数据采用ICESat-GLAS测高数据,来源于美国冰雪中心(national snow and ice data center,NSIDC)(http://nsidc.org/data/icesat/)获取,数据采集时间为2003年10月05日至2005年10月23日。GLAS系统为首个极地轨道星载大光斑LiDAR系统,每秒发射40次激光脉冲,每个激光脉冲在地面上形成直径约为70 m的光斑,光斑之间的间隔为170 m。每个光斑对应一个波形,每个波形有544个采样点。每个数据采集时间段对应一个操作周期。L1A和L2A操作周期的波形数据采样点间隔为1 ns(15 cm),有效高程范围为81.6 m。从L2B操作周期以后,对波形进行了压缩处理,前151个采样点间隔增加到4 ns(60 cm),有效高程范围增加到150 m[19, 20]。ICESat-GLAS共提供了15种标准数据产品(GLA01-GLA15),用户可以根据不同需求和目的选择相应的标准数据产品。试验数据采用33版本的GLA01和GLA14两种标准数据产品。其中GLA01中记录了光斑号、时间、脉冲强度、经纬度等信息,GLA14中记录高程、大地经纬度、回波振幅等地表高度信息[21]。
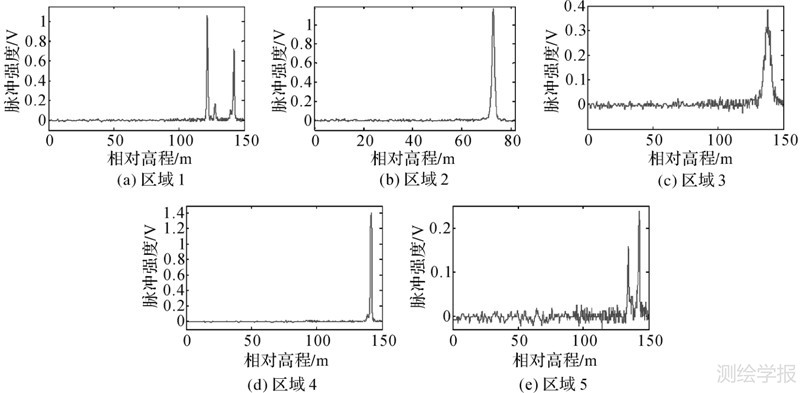
本文的研究区针对城市区域,图 3所示为研究区的遥感影像和ICESat-GLAS光斑分布,图 3(a)中由上至下4条线分别为2004年5月20日、2005年5月22日、2005年10月23日和2003年10月05日的卫星轨迹。由遥感图像可以看出,该城区主要地物为道路、建筑物、广场、公园、矿区等。本文选择了小区、广场、公园、郊区、矿区等几个具有代表性的区域进行研究,图 3(b)-(f)分别为选择5个典型区域的遥感影像,圆圈内为光斑所覆盖的范围。图 4为5个研究区域对应的ICESat-GLAS原始波形数据,表 1为5个研究区域的数据信息。

|
| 图 3 研究区遥感影像及ICESat-GLAS光斑的分布 Fig. 3 Remote sensing image of study area and distribution for ICESat-GLAS shots |
|
| 图 4 GLAS原始波形 Fig. 4 GLAS raw waveform |
| 参数 | 区域1 | 区域2 | 区域3 | 区域4 | 区域5 |
| time | 2004-05-20 | 2003-10-05 | 2004-05-20 | 2005-10-23 | 2005-05-22 |
| laser operation period | L2C | L2A | L2C | L2D | L3C |
| UINDEX | 227526024 | 134769156 | 227526024 | 452731023 | 386291216 |
| shot | 20 | 16 | 30 | 7 | 30 |
为便于对不同返回波能量进行比较和加权,增强不同波形之间的可比性,需对波形数据进行归一化处理,使能量值落入到[0,1]区间。
为了提高波形拟合的精度,需要对波形数据进行去噪处理。定义噪声阈值为单个回波的4倍标准差,即:ε=4σr,其中,σr为前100个高程点能量值的标准差。当脉冲能量小于阈值时认为是噪声,将其能量视为0。
3.3 试验结果及讨论首先,采用本文提出的算法对5个区域的波形数据进行波形分解试验。图 5为最终分解结果。
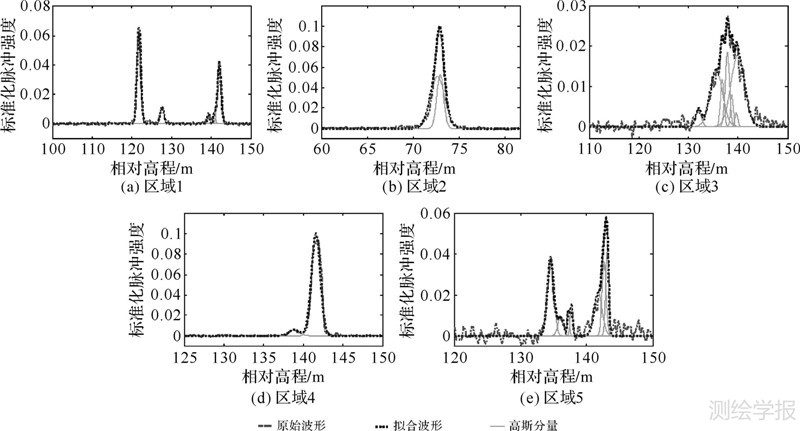
|
| 图 5 分解结果 Fig. 5 Decomposition results |
图 5(a)为区域1波形分解结果,分解成5个高斯分量。根据该区域遥感影像(图 3(b))可以看出该区域主要地物有高低不齐的平顶建筑物,车棚以及树木。为了验证地物覆盖,对实地进行了勘测,并测得其平均高程分别为20、14.5、3和1 m。因此该地区分解的5个高斯分量分别代表高建筑物返回回波、低建筑物返回回波、车棚返回回波、树木返回回波以及地面返回回波。试验得到的地物高程分别为20.3、14.4、2.7和1.2 m。图 5(b)为区域2波形分解结果,分解成两个高斯分量,根据该区域遥感影像(图 3(c))可以看出该区域主要地物为低矮植被,实测高程为0.3 m。因此该区域分解的两个高斯分量分别为低矮植被返回波和地面返回回波。试验得到的植被高程为0.3 m。图 5(c)为区域3波形分解结果,分解成7个高斯分量,根据该区域遥感影像(图 3(d))可以看出该区域垂直方向上主要地物有亭子和较高的植被,实测高程分别为8和4.5 m。因此该地区分解的7个高斯分量分别代表亭子返回回波,中间的几个高斯分量为植被返回回波,最后一个高斯分量为地面返回回波。试验得到亭子和植被的高程分别为8和4.4 m。图 5(d)为区域4波形分解结果,分解成两个高斯分量,根据该区域遥感影像(图 3(e))可以看出该区域主要地物为尖顶的低建筑物,经实地勘测,其高程为3 m。因此该区域分解的两个高斯分量分别为建筑物顶部返回回波和地面返回回波,试验得到建筑物的高程为2.7 m。图 5(e)为区域5波形分解结果,分解成7个高斯分量,根据该区域遥感影像(图 3(f))可以看出该区域垂直方向上主要地物是地面倾斜的矿区,实测高差为8.5 m。因此该地区分解的7个高斯分量分别代表矿区不同高程地面返回回波。试验得到地面倾斜矿区的高差为8.6 m。
通过分解后波形可以看出,低矮植被返回信号能量比较集中,振幅较高,脉冲较窄(图 5(b));较高植被返回信号能量较分散,振幅较低,脉冲较宽(图 5(c));平顶建筑物返回信号能量较大,振幅较高,脉冲较窄(图 5(a));尖顶建筑返回信号能量较小,振幅较低,脉冲较宽(图 5(d);地面倾斜的矿区根据地面倾斜程度的不同返回信号能量、振幅、脉冲的宽度都有所不同(图 5(e)。
从图 5的分解结果可以看出,对于不同地物类型区域的波形数据,由本文算法得到的理想波形都能很好地拟合原始波形数据,并且分解的波形能够与实际地物相对应,能够得到地物沿高程方向的散射特性,说明本文算法具有可行性和有效性。
试验进行了10 000次迭代,在迭代循环过程中,误差很快减小。图 6为5个研究区域10 000次迭代误差变化曲线。由图 6可以发现,前4000次迭代误差有一定波动,在后6000次迭代中误差达到稳态,为了使试验结果更加准确,忽略前4000次的迭代结果,比较后6000次高斯分量个数,并计算其分别出现的概率(表 2为区域1不同高斯分量个数出现的概率),将出现概率最大的高斯分量个数作为最终分解的波形个数。
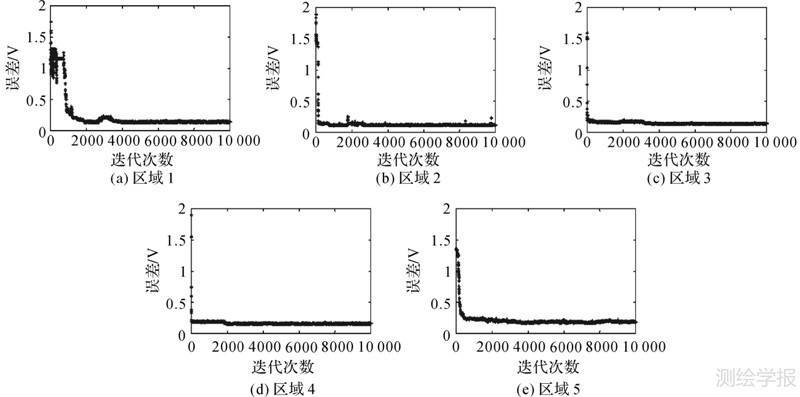
|
| 图 6 10 000次迭代误差变化曲线 Fig. 6 Change in error during 10 000 iterations |
| 高斯分量个数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 概率/(%) | 0 | 4.20 | 4.19 | 20.09 | 30.68 | 19.87 | 12.09 | 6.39 | 2.49 |
该算法基于Matlab 7.12.0 开发,运行环境为Intel Core i5-3470-3.20 GHz-4 G,Window7操作系统。以区域1为例,该区域有544个采样点,一次迭代完成5种移动操作的时间约为0.02 s。因此,完成10 000次迭代总共的操作时间约为4 min。更新高斯分量位置、更新高斯分量标准差、更新高斯分量权重、合并或分裂高斯分量以及生成或删除高斯分量分别占用时间的比例约为:10%、6%、4%、45%以及35%。其中,合并或分裂高斯分量和生成或删除高斯分量两种操作中不仅需要判断是否满足进行该操作的条件,而且还要判断操作后高斯分量的均值、标准差以及权重是否满足条件,因此,需要的操作时间略长。
为了验证本文算法的可靠性和准确性,将本文方法与Matlab提供的CFTOOL高斯拟合方法进行比较。由于CFTOOL高斯拟合方法不能自动确定分解成高斯分量数,所以将本文算法得到的高斯分量数作为该方法高斯分量数,然后将原始波形数据分解为固定数的高斯分量之和。图 7为CFTOOL高斯拟合方法的波形分解结果。表 3分别列出了两种方法得到的5个试验区域高斯分布的均值估计值和标准差估计值。对比两种分解方法结果,本文方法不仅能自动获得高斯分量数,还可以较好地将波形分解,分解的波形能够与不同高程地物相对应,同时得到的高斯曲线能够较好地拟合原始波形。CFTOOL高斯拟合方法不能自动获得高斯分量数,虽然分解波形能较好地拟合原始波形,但未能分解出与不同高程地物对应的波形分量,如区域1的第3个高斯分量标准差估计和区域2的第2个高斯分量标准差估计值过大,振幅接近于平值,并且对部分波形未能拟合,特别是有细微能量变化的波形,如区域3的第1个脉冲和区域4的第1个脉冲,区域5的第2个脉冲。因此,CFTOOL高斯拟合方法分解的波形不能与地物相对应,无法反映地物沿高程方向的散射特性,其原因在于CFTOOL高斯拟合方法没有对分解波形的参数进行约束,因此出现标准差估计值较大等情况。
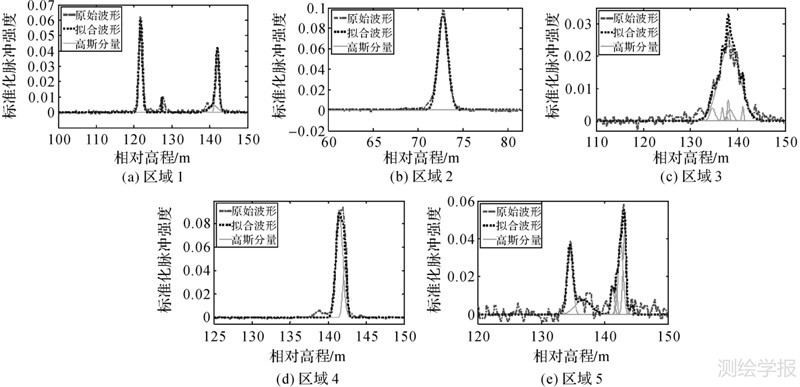
|
| 图 7 CFTOOL方法分解结果 Fig. 7 Decomposition results from CFTOOL |
| 高斯分量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| 区域1 | 均值 | 本文方法 CFTOOL方法 | 121.8121.8 | 127.7127.4 | 139.4127.7 | 140.9141.0 | 142.1142.1 | - | - |
| 标准差 | 本文方法 CFTOOL方法 | 0.482 70.638 1 | 0.470 90.021 3 | 0.233 41×105 | 0.255 81.639 5 | 0.458 60.590 1 | - | - | |
| 区域2 | 均值 | 本文方法 CFTOOL方法 | 72.6 69.6 | 72.9 72.8 | - | - | - | - | - |
| 标准差 | 本文方法 CFTOOL方法 | 0.78920.7739 | 0.3719802.35 | - | - | - | - | - | |
| 区域3 | 均值 | 本文方法 CFTOOL方法 | 132.0134.7 | 135.6136.8 | 136.8137.7 | 137.9138.0 | 138.8138.2 | 139.7139.7 | 140.0140.0 |
| 标准差 | 本文方法 CFTOOL方法 | 0.553 40.784 4 | 1.263 90.296 0 | 0.353 10.197 0 | 0.429 80.312 2 | 0.255 03.058 5 | 0.288 60.844 1 | 1.379 00.249 6 | |
| 区域4 | 均值 | 本文方法 CFTOOL方法 | 138.9141.5 | 141.6142.2 | - | - | - | - | - |
| 标准差 | 本文方法 CFTOOL方法 | 0.671 40.621 0 | 0.558 50.355 2 | - | - | - | - | - | |
| 区域5 | 均值 | 本文方法 CFTOOL方法 | 134.6134.5 | 136.1136.6 | 137.3141.2 | 137.7141.8 | 141.8142.5 | 142.7143.1 | 143.1144.3 |
| 标准差 | 本文方法 CFTOOL方法 | 0.479 10.610 4 | 0.409 01.752 0 | 0.152 10.376 7 | 0.171 00.223 4 | 0.601 70.526 9 | 0.302 50.355 3 | 0.223 60.371 5 | |
为了对波形分解结果进行定量评价,分别计算每个试验区域原始波形与拟合波形之间的相关系数ρ和KS距离[22],计算公式分别为
式中,yi为原始波形中第i个高程点的能量值;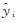 为拟合波形中第i个高程点的能量值;
为拟合波形中第i个高程点的能量值; 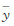 和
和 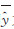 为其分别的均值。相关系数ρ∈[-1,1],是衡量两个随机变量之间线性相关程度的指标,相关系数越大,说明拟合数据与原始数据相关性越强,波形拟合的精度越高。KS∈[0,1],KS距离能够检测出脉冲的丢失以及拟合数据与原始数据之间局部的变化。KS距离越小,说明波形拟合的精度越高。当分解的波形能够准确地拟合原始波形数据时ρ=1,KS=0。
为其分别的均值。相关系数ρ∈[-1,1],是衡量两个随机变量之间线性相关程度的指标,相关系数越大,说明拟合数据与原始数据相关性越强,波形拟合的精度越高。KS∈[0,1],KS距离能够检测出脉冲的丢失以及拟合数据与原始数据之间局部的变化。KS距离越小,说明波形拟合的精度越高。当分解的波形能够准确地拟合原始波形数据时ρ=1,KS=0。
表 4为计算结果,根据计算结果可以看出,得到的相关系数均在0.98以上,KS距离均在0.2以下,说明本文算法具有有效性和准确性。
| 试验区域 | 区域1 | 区域2 | 区域3 | 区域4 | 区域5 |
| 相关系数 | 0.995 5 | 0.989 5 | 0.988 9 | 0.981 6 | 0.988 2 |
| KS距离 | 0.021 3 | 0.197 9 | 0.052 9 | 0.170 0 | 0.132 7 |
本文提出了一种基于可变分量混合高斯模型和RJMCMC的全波形LiDAR数据分解方法,首先假定波形数据服从高斯分布,然后对LiDAR波形数据实现可变个数的分解。本文方法不仅能自动确定波形分解数,同时还可以有效地获取最优的模型参数估计。利用本文算法分别对不同地物类型的区域进行了波形分解试验,并和Matlab中CFTOOL的高斯拟合方法进行了对比,定性和定量的测试结果验证了本文方法的有效性、可靠性和准确性。虽然本文算法能够准确地确定波形分解的个数,实现波形的分解,并且分解的结果能够与地物相对应,同时具有很高的拟合精度,但是对于一些非对称、倾斜或者拖尾的波形,本文的方法还不能非常准确地拟合。在未来的工作中,对如何进一步提高波形拟合精度,使算法更普遍地适用于各种形状的波形,还需要继续从理论上进行研究,如选择其他的随机模型来模拟原始波形数据,使分解的波形更准确地拟合原始波形数据,从而提高波形拟合精度。
| [1] | ZUO Zhiquan,ZHANG Zuxun,ZHANG Jianqing.A High-quality Filtering Method with Adaptive TIN Models for Urban LiDAR Points Based on Priori-knowledge[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 246-251. (左志权, 张祖勋, 张剑清. 知识引导下的城区LiDAR点云高精度三角网渐进滤波方法[J]. 测绘学报, 2012, 41(2): 246-251.) |
| [2] | SUI Lichun, ZHANG Yibin, LIU Yan, et al. Filtering of Airborne LiDAR Point Cloud Data Based on the Adaptive Mathematical Morphology[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 390-396. (隋立春, 张熠斌, 柳艳, 等. 基于改进的数学形态学算法的LiDAR点云数据滤波[J]. 测绘学报, 2010, 39(4): 390-396.) |
| [3] | PARRISH C E, NOWAK R D. Improved Approach to LiDAR Airport Obstruction Surveying Using Full-waveform Data[J]. Journal of Surveying Engineering, 2009, 135(2): 72-78. |
| [4] | SUN G, RANSON K J. Modeling LiDAR Returns from Forest Canopies[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(6): 2617-2626. |
| [5] | MALLET C, BRETAR F. Full-waveform Topographic LiDAR: State-of-the-art[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2009, 64(1): 1-16. |
| [6] | BLAIR J B, RABINE D L, HOFTON M A. The Laser Vegetation Imaging Sensor: A Medium-altitude, Digitisation-only, Airborne Laser Altimeter for Mapping Vegetation and Topography[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1999, 54(2-3): 115-122. |
| [7] | SUN Guoqing, RANSON K J, ZHANG Zhongjun. Forest Vertical Parameters from LiDAR and Multi-angle Imaging Spectrometer Data[J]. Journal of Remote Sensing, 2006, 10(4): 523-530. (孙国清, RANSON K J, 张钟军. 利用激光雷达和多角度频谱成像仪数据估测森林垂直参数[J]. 遥感学报, 2006, 10(4): 523-530.) |
| [8] | PANG Yong, LI Zengyuan, CHEN Erxue, et al. LiDAR Remote Sensing Technology and Its Application in Forestry[J]. Scientia Silvae Sinicae, 2005, 41(3): 129-136. (庞勇, 李增元, 陈尔学, 等. 激光雷达技术及其在林业上的应用[J]. 林业科学, 2005, 41(3): 129-136.) |
| [9] | MEANS J E, ACKER S A, HARDING D J, et al. Use of Large-footprint Scanning Airborne LiDAR to Estimate Forest Stand Characteristics in the Western Cascades of Oregon[J]. Remote Sensing of Environment, 1999, 67(3): 298-308. |
| [10] | BRENNER A C, ZWALLY H J, BENTLEY C R, et al. ATBD V3.0 Derivation of Range and Range Distributions from Laser Pulse Waveform Analysis for Surface Elevations, Roughness, Slope, and Vegetation Heights [J/OL]. http://glas.wff.nasa.gov.2000. |
| [11] | SPAANS K H, RONSE A L A B. Reconstruction of an ICESat Full Waveform by Terrestrial and Airborne Laser Scanning[J]. Earth and Planetary Observation Letters, 2007, 3(20): 1-9. |
| [12] | LI Qi, MA Hongchao. The Study of Point-cloud Production Method Based on Waveform Laser Scanner Data[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 349-354. (李奇, 马洪超. 基于激光雷达波形数据的点云生产[J]. 测绘学报, 2008, 37(3): 349-354.) |
| [13] | WANG Jinhu, LI Chuanrong, ZHOU Mei. Airborne Full-waveform LiDAR Data Processing and Application[J]. Foreign Electronic Measurement Technology, 2012, 31(6): 71-75, 79. (王金虎, 李传荣, 周梅. 机载全波形激光雷达数据处理及其应用[J]. 国外电子测量技术, 2012, 31(6): 71-75, 79.) |
| [14] | HUG C, ULLRICH A, GRIMM A. Litemapper-5600-A Waveform-digitizing LiDAR Terrain and Vegetation Mapping System[J]. International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 2004, 36(8/W2): 24-29. |
| [15] | WAGNER W, ULLRICH A, DUCIC V, et al. Gaussian Decomposition and Calibration of a Novel Small-footprint Full-waveform Digitising Airborne Laser Scanner[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2006, 60(2): 100-112. |
| [16] | HOFTON M A, MINSTER J B, BLAIR J B. Decomposition of Laser Altimeter Waveforms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(4): 1989-1996. |
| [17] | MA Hongchao, LI Qi. Modified EM Algorithm and Its Application to the Decomposition of Laser Scanning Waveform Data[J]. Journal of Remote Sensing, 2009, 13(1): 35-41. (马洪超, 李奇. 改进的EM模型及其在激光雷达全波形数据分解中的应用[J]. 遥感学报, 2009, 13(1): 35-41.) |
| [18] | GREEN P J. Reversible Jump Markov Chain Monte Carlo Computation and Bayesian Model Determination[J]. Biometrika, 1995, 82(4): 711-732. |
| [19] | WEN Hanjiang, CHENG Pengfei. Introduction to Principle of ICESAT/GLAS Laser Altimetry and Its Applications[J]. Science of Surveying and Mapping, 2005, 30(5): 33-35. (文汉江, 程鹏飞. ICESAT/GLAS激光测高原理及其应用[J]. 测绘科学, 2005, 30(5): 33-35.) |
| [20] | SUN G, RANSON K J, KIMES D S, et al. Forest Vertical Structure from GLAS: An Evaluation Using LVIS and SRTM Data[J]. Remote Sensing of Environment, 2008, 112(1): 107-117. |
| [21] | NELSON R, RANSON K J, SUN G, et al. Estimating Siberian Timber Volume Using MODIS and ICESat/GLAS[J]. Remote Sensing of Environment, 2009, 113(3): 691-701. |
| [22] | MALLET C, LAFARGE F, ROUX M, et al. A Marked Point Process for Modeling LiDAR Waveforms[J]. IEEE Transactions on Image Processing, 2010, 19(12): 3204-3221. |