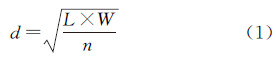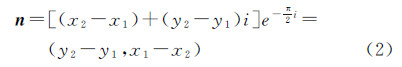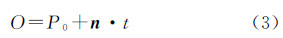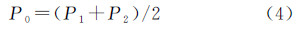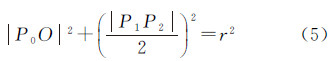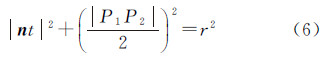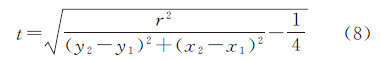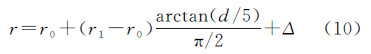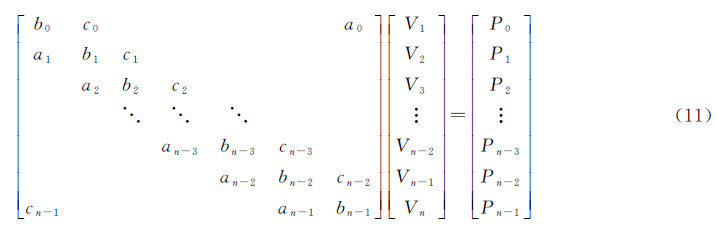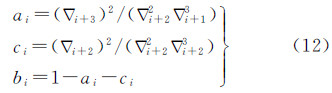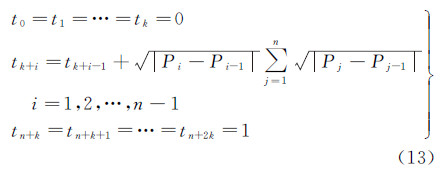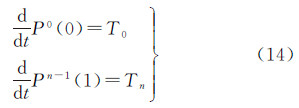2. 北京航空气象研究所, 北京 100085
2. Beijing Aviation Meteorological Institute, Beijing 100085, China
1 引 言
地形表面通常分布着建筑物、植被、车辆和人员等物体,激光扫描获取地形点云后的基础工作之一是把分布在地面上的点(地面点)与分步在其他目标上的点(地物点)进行区分。LiDAR点云滤波的目的就是区分地面点和地物点并滤除地物点得到地面点,这是建立高精度数字地面模型的关键环节。
近年来随着三维激光扫描技术的进步,很多学者对LiDAR点云滤波方法进行了研究并提出了相关算法。根据文献[1]中的总结,可以把现有的滤波方法大致分为以下几类:
(1) 基于坡度变化的方法。经典的坡度变化滤波法[2]设计了两点距离为自变量而最大高度差阈值为因变量的函数,根据两点间实际高差与高差阈值比较区分地面点和地物点。
(2) 三角网渐进加密滤波法。文献[3]首次提出了三角网渐进加密滤波方法,其区分地物点和地面点的依据是当前点与其垂足所在三角形之间的垂直距离和当前点到该三角形3个顶点的连线与该三角形之间的夹角。三角网渐进加密滤波法对森林地区的植被和城区的高大建筑物有较好的滤波效果,因此该方法得到较多关注[4, 5, 6, 7],并应用于商业软件TerraScan中。文献[4]在三角网渐进加密的基础上引入了基于多核处理器的并行计算技术,提高了滤波效率以满足快速成图的应用需求。该方法的缺点是滤波过程中初始网格选择不当容易积累误差并且效率偏低,对于低矮植被和物体的滤除效果比较差。
(3) 基于曲面拟合的方法。最有代表性的是文献[8]中提出的最小二乘逼近法,该方法用最小二乘法拟合曲面,根据点到该曲面的距离分配权值,并根据阈值设计了一个权函数,能够保证地面点权值为1而地物点权值为0,经过多次迭代可以逐渐达到滤波的目的。此外也有研究者用Snake样条[9]和多项式[10, 11]拟合逼近地形表面,此类方法在地形变化平缓的地区效果比较好,但对于大型建筑物往往会误把建筑物顶面错判为地形表面。
(4) 基于数学形态学的方法。文献[12]最早提出了该方法,此后很多学者都在此基础上提出了改进的数学形态学滤波法[13, 14, 15, 16, 17, 18, 19]。该方法把图像处理领域的数学形态学概念进行扩展,形成针对地形点云的腐蚀膨胀过程,构造开运算。其弊端是窗口的大小会直接影响滤波的效果,窗口过小导致滤波对大型建筑物失效,窗口过大会使地面上较大的凸起被错误地滤除。文献[13]在数学形态学开算子的基础上,提出增加一个“带宽”参数以提高其自适应程度。此外对地形进行腐蚀膨胀操作时整个窗口的高程取同一个值,使得地面细节丢失,从而造成地形失真。文献[14]采取分步策略,在数学形态学粗滤波的基础上,引入了Car模型对地形进行了模型化处理,提高了滤波的稳健性。
(5) 其他方法。基于体素的滤波法[20]、利用多次回波特性的滤波方法[21]以及二次滤波法[22]等。
尽管滤波的方法已有多种,但试验对比表明[1, 23],准确高效并且普遍适用的方法仍有待深入研究。
滤波过程会导致两类错误,一类是把本属于地面的点错判为地物点滤除;另一类是把本属于地物上的点错判为地面点保留。文献[1]把这两类错误分别称为Ⅰ型错误和Ⅱ型错误。通常地形表面都是连续缓和变化,少量的Ⅰ型错误并不会导致地形的较大失真;而Ⅱ型错误过多会引起地形的较大误差。因此应该在维持较小Ⅱ型错误的基础上尽量减少Ⅰ型错误的发生。为了改善滤波精度、简化滤波方法并提高滤波效率,本文给出一种改进的滤波算法,其思路是:①沿同一方向等间距逐行扫描点云,获取点序列构成的扫描线,针对每条扫描线,采取半径可变的圆环从面向地心一侧滚过,滚动过程中远离圆环边缘的点通常是地物点可以滤除;②为便于采取B样条拟合地形表面,对每条滤波后的扫描线等间距均匀采样,得到规则分布的地表型值点,在此基础上用均匀B样条曲面拟合地形表面;③遍历原始地形点云中的每一个点,计算其在拟合曲面上的投影高程,并与实际高程比较,根据两者的差值区分地表点和地物点。技术流程如图 1所示。

|
| 图 1 算法流程 Fig. 1 Algorithm flow chart |
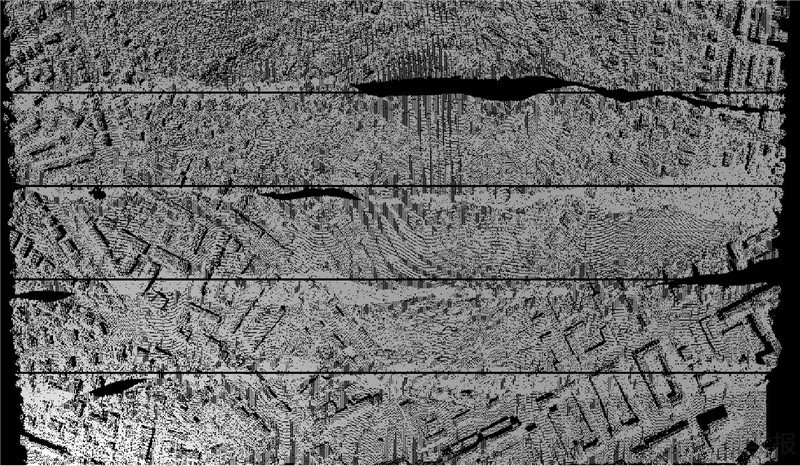
通常情况下地面的变化比较平缓,获取扫描线可以通过设定一组与地面垂直的等间隔平行平面,如图 2所示,然后给定阈值Δd,每一个平面附近到该平面的距离小于给定阈值Δd的点构成该平面位置处的扫描线。阈值Δd可以取作点云平均间距的1/2。点云平均间距d可以通过式(1)计算得到
式中,n为点云中点的数量;L和W分别表示点云所表示地形范围的长和宽。
|
| 图 2 获取扫描线 Fig. 2 Obtain scanning line |
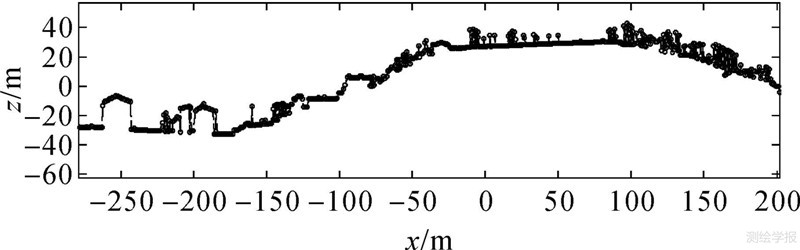
图 3所示为图 2所示地形点云中的一条扫描线,从该扫描线上可以清楚看出地面和植被、建筑等地物。
|
| 图 3 扫描线 Fig. 3 Scanning line |
由于空洞的存在会导致扫描线上出现数据缺失,此时需要连接扫描线上空洞的两端点,以点云平均间距为间隔进行等间距插值,补充缺失的数据点。这使得扫描线滤波得以顺利进行。
扫描线滤波就是要滤除扫描线上的地物点,为此可以从面向地心的一侧,用一个圆环,从扫描线的一端逐点依次滚向另一端,由于建筑物和植被等非地面点从地心一侧观察表现为向上凹陷,因此当圆环半径取值适当时,圆环边缘只能滚过地面点,未被圆环滚过的点被认为是地物点并滤除。
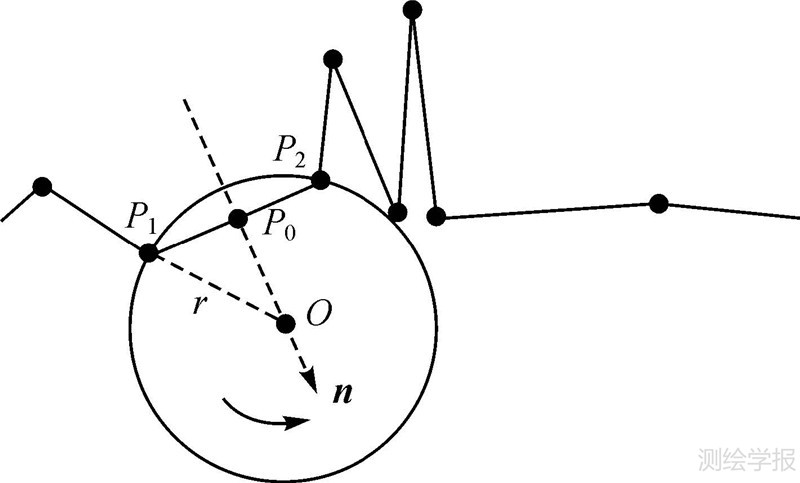
2.2 圆心计算对于任一条扫描线可以任选其一端为起始点,则另一端即为终点,如图 4所示,为了说明问题方便,不妨设扫描线的左端点为起始点,则当圆环从面向地心的一侧从左端起始点滚向右端终点时,圆环实际在作逆时针滚动。
|
| 图 4 圆心计算 Fig. 4 Calculation circle center |
定义1 当前点:由于扫描线上的点序列从起始点到终点有序排列,则圆环滚动过程中任一时刻与圆环边缘相接触的点中最接近终点的一个称为当前点。
定义2 相邻目标点:扫描线上的点序列中,在圆环滚动前进方向上与当前点相邻的下一点称为相邻目标点。
把起始点作为地表点和当前点,圆环滚动过程中依次判断下一个相邻目标点是否被圆环的边缘滚过,直至终点。滚过与否可以通过比较圆环半径和点到圆心的距离来判断。给定圆环半径r,圆心的计算如图 4所示。
假设当前点为P1(x1,y1),滚向相邻目标点P2(x2,y2),可以计算矢量P1P2={x2-x1,y2-y1},把该矢量顺时针旋转90°可得到过P1P2中点P0并指向圆心O的矢量n
因此得过P1P2中点P0并指向圆心O的参数方程由于P0是P1P2的中点,因此有
根据 代入P0和圆心O得 代入P1P2的坐标得圆心O的对应参数
代入参数方程可得圆心坐标
当从P1点滚向P2点时,首先根据式(9)计算圆心,然后判断扫描线上是否存在到该圆心距离小于r的点:如果存在这样的点,说明P2不能被圆环边缘滚过,因此可以确定P2点是地物点,继续取圆环前进方向上与P2点相邻的下一点作为相邻目标点,判断能否从当前点P1滚过;如果不存在这样的点,说明圆环可以滚过P2点,则可以确定P2点是地面点,然后用P2更新P1作为当前点,继续判断,直到圆环滚至终点。
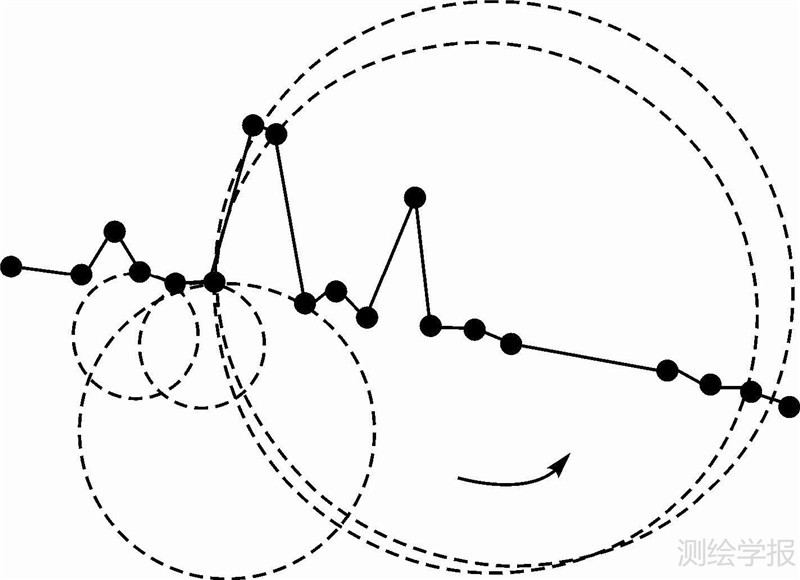
2.3 可变半径对于实际地形,建筑物的尺寸大小不同,圆环半径过大会把凸起的地形滤除,圆环半径过小,会滚过大型建筑物,把部分建筑物表面误判为地面。此外扫描线上相邻点的间距并不均匀,如果采用固定半径,当相邻点距大于圆环直径时,圆环会漏过,表现在计算中是在计算圆心参数时出现复数开方的情况,导致计算中断。因此为避免此类情况发生,可以设计可变半径的圆环,半径根据当前点和相邻目标点之间的距离自动调整。可变半径的圆环滚动如图 5所示。
|
| 图 5 可变半径 Fig. 5 Variable radius |
为保持更多的地面细节,圆环的边缘可以使之具有弹性变形,如同真实地面上具有弹性的轮胎能够正常滚过微小的凹凸地形。
半径的变化范围可根据点云的平均间距和建筑物最大尺寸设定。不妨用r0表示点云的平均间距,作为圆环半径的最小取值,用r1表示建筑物最大尺寸,作为圆环半径的最大取值。当相邻的当前点与相邻目标点之间的距离增大时,为避免出现计算中断情况,半径的变化应该能够较快的增大,然后逐渐稳定在最大半径附近,因此可以设计半径计算公式(10),即
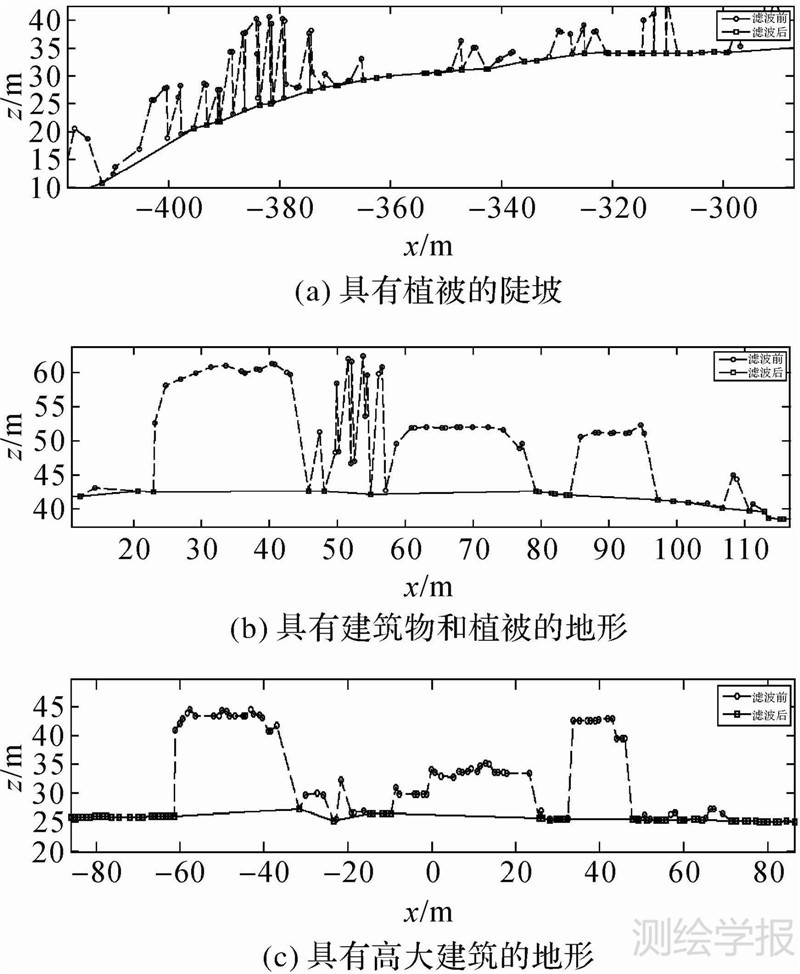
式中,d表示当前点P1与相邻目标点P2之间的距离;Δ表示圆环边缘的弹性变形范围,根据实际情况通常可取0.5甚至更小,即认为点到圆心的距离误差可以控制在0.5 m,这样距离地面小于0.5 m的点可认为是地面微小的起伏造成,被判断为是地面细节予以保留。弹性变形参数Δ固定,当圆环半径r较小时,可以滚过较小的凹凸起伏,保留住更多的地表细节,半径较大时,则滤波结果比较平坦,较小的凹凸起伏会被滤除;圆环半径r固定,当弹性变形参数Δ较大时,可以保留更多细节,较小的Δ会滤掉更多细节。采用上述方法,某地形的扫描线滤波结果如图 6所示。
|
| 图 6 扫描线滤波结果 Fig. 6 Result of scanning line filtering |
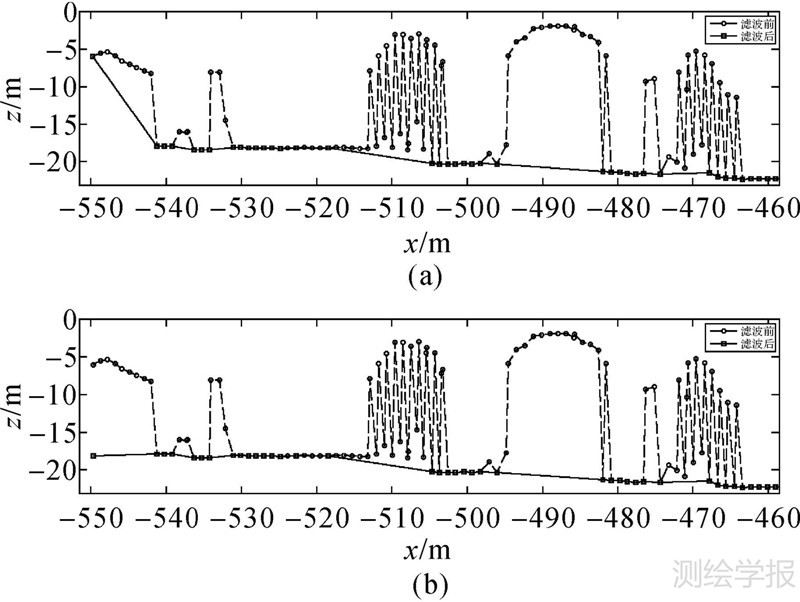
如果地形的边缘刚好是某建筑物或植被的最高点,滚圆法滤波后会出现端点上翘,即把端点处的地物点误判为地面点而犯Ⅱ型错误,如图 7(a)的左端点。此情况需要在端点附近取连续地面点拟合光滑曲线对端点进行插值,因为地形局部起伏不大通常可采用二次多项式插值,插值后如图 7(b)所示,端点回落到地面并避免了Ⅱ型错误。
|
| 图 7 切面线滤波结果 Fig. 7 Result of section line filtering |
通过扫描线滤波,得到光滑的地形扫描线,并且地形扫描线之间间距相等。为了采用均匀有理B样条曲面拟合地形表面,首先要在每条扫描线上等间隔采样获取型值点阵列,型值点是指位于地形表面上的点,即拟合后B样条曲面上的点;其次,为了对原始点云中每个点进行过滤,需要通过型值点阵列反算出拟合B样条曲面的控制点阵列,控制点直接决定了拟合后B样条曲面的形状。最后,把原始点云中每个点的位置坐标(x,y)代入B样条参数曲面,求得点在样条曲面上的投影高程,并与实际高程比较,根据给定的阈值判断并区分地面点和地物点。
假设在等间隔的扫描线上均匀采样得到型值点阵列P={pij,i=1,2,…,m,j=1,2,…,n}。即有m条等间隔扫描线,在每一条扫描线上均匀采样n个点。由型值点阵列反算控制点阵列,可以分别在与地面平行的两个方向上先后进行两次一维反算,通常要两次求解式(11)所示的三对角线性方程组
式中,Pi表示型值点;Vi表示控制点;ai、bi和ci为线性方程组的系数,通过式(12)计算 式中,∇表示节点矢量梯度,并且∇i=ti+1-ti,ti表示节点矢量,可以根据弦长参数化计算 式中,k表示曲线或曲面的阶次。B样条曲面的相关计算细节可以参考文献[24]。由于地形曲面不封闭,对于非周期曲线,控制点数比方程数多2,可补充切失边界条件如式(14)
即两端点的切矢量的值给定分别为T0和Tn,可以由两端型值点计算。反算得到均匀有理B样条曲面的控制点阵列,可以计算点云中任一点在样条曲面上的投影,采取二维德布尔快速算法[24]计算该点在B样条曲面上的投影点并计算其高程hij,比较投影点高程hij与点的实际高程zij,如果小于规定的阈值Δ,即满足|hij-zij|<Δ,该点为地面点予以保留,否则为地物点应该滤除。阈值大小体现了地面允许的凹凸起伏程度,通常可以取0.5 m。阈值小,滤波后地形较光滑,过小则容易犯Ⅰ型错误;阈值大,允许地面的起伏大,保留地面细节多,过大则容易犯Ⅱ型错误。
4 试验与结果分析 4.1 试验数据为了验证本文算法的有效性,本文采取ISPRS公布的数据进行滤波试验,其中3个具有典型地貌特征的地形见表 1。
| 地形 | 范围/(m×m) | 点数量 | 地貌特征 |
| 1 | 1096×695 | 1 365 906 | 城区、陡坡、山坡,山腰分布建筑物和花草树木等植被 |
| 2 | 524×384 | 376 959 | 大型建筑、不规则建筑和桥梁 |
| 3 | 1598×1228 | 628 251 | 郊区、陡坡、花草树木和采石场以及河流形成的数据空洞 |
试验中采用的计算机配置为CPU 2.0 GHz,内存2GB。3个典型地形滤波结果如图 8所示。图 8(a)、图 8(c)、图 8(e)为滤波前地形,图 8(b)、图 8(d)、图 8(f)分别为其对应的滤波后地形,图 8(a)和图 8(c)是城市地形,图 8(e)为林区地形。对图 8(a)、图 8(c)、图 8(e) 3个地形滤波的时间消耗分别为17.3、3.2和13.2 s,可见具有较高的时间效率。

|
| 图 8 滤波结果 Fig. 8 Results of filtering |
从图 8中对不同地形的滤波结果看,疏密程度不同的地表植被和各种形状的建筑物基本被滤除,同时保留了地形特征和地面细节。
4.3 试验结果定量分析为便于对滤波算法进行定量分析,文献[1]提出了3个指标:Ⅰ型误差、Ⅱ型误差和总误差,计算方法为
Ⅰ型误差=误判为地物的地面点数/地面点数
Ⅱ型误差=误判为地面的地物点数/地物点数
总误差=总的误判点数/总点数
采用ISPRS标准地形对算法进行测试,限于篇幅本文仅列出3个典型地形测试结果,如图 9所示。

|
| 图 9 滤波结果 Fig. 9 Results of filtering |
图 9(a)为覆盖植被和建筑物的陡坡,图 9(c)为密集的建筑物地形,图 9(e)为变化频繁的长地物地形。3个地形的滤波误差如下表 2-4所示。
| (%) | |||||||
| 误差 | Elmqvist | Roggero | Brovelli | Axelsson | Sithole | Pfeifer | 本文方法 |
| Ⅰ型 | 23.63 | 57.88 | 69.41 | 56.22 | 60.40 | 71.86 | 21.26 |
| Ⅱ型 | 4.31 | 3.63 | 2.13 | 1.83 | 5.49 | 0.65 | 1.41 |
| 总误差 | 27.94 | 35.06 | 40.91 | 33.34 | 37.39 | 42.01 | 12.91 |
| (%) | |||||||
| 误差 | Elmqvist | Roggero | Brovelli | Axelsson | Sithole | Pfeifer | 本文方法 |
| Ⅰ型 | 23.63 | 13.09 | 41.66 | 9.68 | 17.67 | 15.78 | 7.83 |
| Ⅱ型 | 4.31 | 2.81 | 1.17 | 0.95 | 0.72 | 0.60 | 0.52 |
| 总误差 | 27.94 | 8.13 | 22.02 | 5.47 | 9.49 | 8.46 | 4.07 |
| (%) | |||||||
| 误差 | Elmqvist | Roggero | Brovelli | Axelsson | Sithole | Pfeifer | 本文方法 |
| Ⅰ型 | 4.3 | 13.37 | 20.40 | 4.68 | 12.18 | 8.02 | 4.26 |
| Ⅱ型 | 1.98 | 0.26 | 0.25 | 0.26 | 0.15 | 0.24 | 0.16 |
| 总误差 | 3.68 | 4.30 | 6.38 | 1.62 | 3.85 | 2.64 | 1.47 |
试验表明,对于不同特征的地形,本文算法通用性好并且滤波误差更小,从表 2-4可以看出与传统方法相比滤波精度提高了1~5倍。此外传统方法需要迭代,例如Pfeifer提出的层次法、Axelsson提出的三角网渐进加密法、Brovelli方法以及可变窗口的数学形态学方法等。迭代的方法最坏情况下其时间复杂度为O(n2),导致算法效率不高。本文算法不仅避免了迭代,而且通过获取扫描线转化为一维计算,其算法时间复杂度为O(n)。
5 结 论本文提出了一种基于可变半径圆环和B样条拟合的地形点云滤波方法,该方法首先从地形表面面向地心的一侧以可变半径的滚圆法对等间隔的地形扫描线滤波,获得光滑的地形表面采样阵列,然后针对采样阵列,采用均匀有理B样条曲面进行拟合,计算原始地形点云中每个点在拟合曲面上的投影点高程,并与实际高程比较,如果在给定阈值范围内,则被认为是地面点并保留,否则被认为是地物点并滤除。最后采取ISPRS标准数据进行试验,验证了本文算法的有效性和通用性,同时也验证了本文算法的执行速度和滤波精度。
| [1] | SITHOLE G,VOSSELMAN G.Experimental Comparison of Filter Algorithms for Bare-Earth Extraction from Airborne Laser Scanning Point Clouds[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2004, 59(1-2): 85-101. |
| [2] | VOSSELMAN G.Slope Based Filtering of Laser Altimetry Data[J]. International Archives of Photogrammetry and Remote Sensing, 2000, 33(PartB 3/2): 935-942. |
| [3] | AXELSSON P. DEM Generation from Laser Scanner Data Using Adaptive TIN Models[J]. International Archives of the Photogrammetry and Remote Sensing, 1999, 33(B4/1): 110-117. |
| [4] | KANG Xiaochen, LIU Jiping, LIN Xiangguo. Parallel Filter of Progressive TIN Densification for Airborne LiDAR Point Cloud Using Multi-core CPU[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 331-336. (亢晓琛, 刘纪平, 林祥国. 多核处理器的机载激光雷达点云并行三角网渐进加密滤波方法[J]. 测绘学报, 2013, 42(3): 331-336.) |
| [5] | LEE H S, YOUNAN N H. DTM Extraction of LiDAR Returns via Adaptive Processing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(9): 2063-2069. |
| [6] | WU Congcong, LU Xiaoping, LI Guoli, et al. Research on Filtering Algorithm for LiDAR Data Based on TIN[J]. Bulletin of Surveying and Mapping, 2013(3): 32-35. (吴丛丛, 卢小平, 李国利, 等. 基于TIN的LiDAR数据滤波算法研究[J]. 测绘通报, 2013(3): 32-35.) |
| [7] | SUI Lichun, ZHANG Yibin, ZHANG Shuo, et al. Filtering of Airborne LiDAR Point Cloud Data Based on Progressive TIN[J]. Geomatics and Information Science of Wuhan University, 2011, 36(10): 1159-1163. (隋立春, 张熠斌, 张硕, 等. 基于渐进三角网的机载LiDAR点云数据滤波[J]. 武汉大学学报: 信息科学版, 2011, 36(10): 1159-1163.) |
| [8] | KRAUS K,PFEIFER N.Determination of Terrain Models in Wooded Areas with Airborne Laser Scanner Data[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 1998, 53(4): 193-203. |
| [9] | ELMQVIST M, Jungert E, Persson L Å, et al. Terrain Modelling and Analysis Using Laser Scanner Data[J]. International Archives of the Photogrammetry and Remote Sensing, 2001, 34(3/W4): 219-224. |
| [10] | BROVELLI M A, CANNATA M. Digital Terrain Model Reconstruction in Urban Areas from Airborne Laser Scanning Data: the Method and the Example of the Town of Pavia (Northern Italy)[J]. International Archives of the Photogrammetry and Remote Sensing, 2002. 34(2): 43-48. |
| [11] | SHANG Dashuai, LI Hengming, ZHAO Xi. A Filtering Method Based on Surface Constraint for Point Cloud Data[J]. Radar Science and Technology, 2013, 11(4): 413-418. (尚大帅, 黎恒明, 赵羲. 一种基于曲面约束的点云数据滤波方法[J]. 雷达科学与技术, 2013, 11(4): 413-418.) |
| [12] | KILIAN J, HAALA N, ENGLICH M. Capture and Evaluation of Airborne Laser Scanner Data[J]. International Archives of the Photogrammetry and Remote Sensing, 1996, 31(B3): 383-88. |
| [13] | SUI Lichun, ZHANG Yibin, LIU Yan, et al. Filtering of Airborn LiDAR Point Cloud Data Based on the Adaptive Mathematical Morphology[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 390-396. (隋立春, 张熠斌, 柳艳, 等. 基于改进的数学形态学算法的LiDAR点云数据滤波[J]. 测绘学报, 2010, 39(4): 390-396.) |
| [14] | SUI Lichun, YANG Yun. Filtering of Airborne LiDAR Point Cloud Data Based on car(p, q) Model and Mathematical Morphology[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 219-224. (隋立春, 杨耘. 基于car(p, q)模型和数学形态学理论的LiDAR点云数据滤波[J]. 测绘学报, 2012, 41(2): 219-224.) |
| [15] | ZHANG Keqi, CHEN Shuching, WHITMAN D, et al. A Progressive Morphological Filter for Removing Nonground Measurements from Airborne LiDAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(4): 872-882. |
| [16] | CHEN Qi, GONG Peng, BALDOCCHI D, et al. Filtering Airborne Laser Scanning Data with Morphological Methods[J]. Photogrammetric Engineering and Remote Sensing, 2007, 73(2): 175-185. |
| [17] | SUN Meiling, LI Yongshu, CHEN Qiang, et al. A Progressive Morphological Filtering Method for Airborne LiDAR Point Cloud Based on Scan Line[J]. Opto-Electronic Engineering, 2013, 40(11): 71-75. (孙美玲, 李永树, 陈强, 等. 基于扫描线的渐进式形态学机载LiDAR点云滤波[J]. 光电工程, 2013, 40(11): 71-75.) |
| [18] | SHEN Jing, LIU Jiping, LIN Xiangguo. Airborne LiDAR Data Filtering by Morphological Reconstruction Method[J]. Geomatics and Information Science of Wuhan University, 2011, 36(2): 167-170, 175. (沈晶, 刘纪平, 林祥国. 用形态学重建方法进行机载LiDAR数据滤波[J]. 武汉大学学报: 信息科学版, 2011, 36(2): 167-170, 175.) |
| [19] | LI Yong, WU Huayi. Filtering Airborne LiDAR Data Based on Morphological Gradient[J]. Journal of Remote Sensing, 2008, 12(4): 633-639. (李勇, 吴华意. 基于形态学梯度的机载激光扫描数据滤波方法[J]. 遥感学报, 2008, 12(4): 633-639.) |
| [20] | TANG Feifei, LIU Jingnan, ZHANG Xiaohong, et al. A Voxel-based Filtering Algorithm For DTM Data Extraction in Forest Areas[J]. Journal of Beijing Forestry University, 2009, 31(1): 55-59. (唐菲菲, 刘经南, 张小红, 等. 基于体素的森林地区机载LiDAR数据DTM提取[J]. 北京林业大学学报, 2009, 31(1): 55-59.) |
| [21] | ZHANG Xiaohong. Airborne LiDAR Points Cloud Classification Based on Difference of Twice Return Pulse Heights[J]. Science of Surveying and Mapping, 2006, 31(4): 48-50. (张小红. 利用机载LiIDAR双次回波高程之差分类激光脚点[J]. 测绘科学, 2006, 31(4): 48-50.) |
| [22] | WAN Jianhua, HUANG Ronggang, ZHOU Hang, et al. A Secondary Filter Method of LiDAR Point Cloud Based on Curvature Statistics[J]. Journal of China University of Petroleum, 2013, 37(1): 56-60. (万剑华, 黄荣刚, 周行, 等. 基于曲率统计的LiDAR点云二次滤波方法[J]. 中国石油大学学报: 自然科学版, 2013, 37(1): 56-60.) |
| [23] | HUANG Xianfeng, LI Hui, WANG Xiao, et al. Filter Algorithms of Airborne LiDAR Data: Review and Prospects[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(5): 466-469. (黄先锋, 李卉, 王潇, 等. 机载LiDAR数据滤波方法评述[J]. 测绘学报, 2009, 38(5): 466-469.) |
| [24] | SHI Fazhong. CAGD & NURBS[M]. 2nd ed. Beijing: Higher Education Press, 2013. (施法中. 计算机辅助几何设计与非均匀有理B样条[M]. 第2版. 北京: 高等教育出版社, 2013.) |