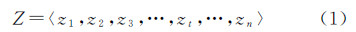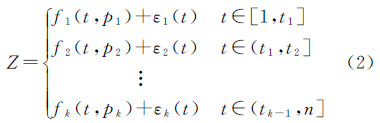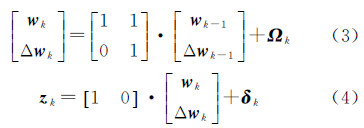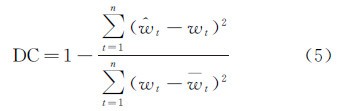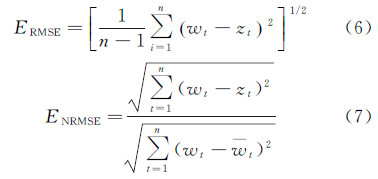2. 江西师范大学鄱阳湖湿地与流域研究教育部重点实验室, 江西 南昌 330000;
3. 香港中文大学太空与地球信息科学研究所, 香港 999077;
4. 西南交通大学地球科学与环境工程学院, 四川 成都 611756;
5. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉 430079;
6. 成都理工大学地球科学学院, 四川 成都 610059
2. Key Laboratory of Poyang Lake Wetland and Watershed Research, Ministry of Education, Jiangxi Normal University, Nanchang 330000, China;
3. Institute of Space and Earth Information Science, The Chinese University of Hong Kong, Hong Kong 999077, China;
4. Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, Chengdu 611756, China;
5. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
6. College of Earth Sciences, Chengdu University of Technology, Chengdu 610059
1 引 言
实时水位观测数据是洪水预报、水库调度和防汛指挥决策的重要基础资料，其质量直接影响后续防洪抢险辅助决策的可靠性。由于自动水文气象站受环境、噪声、仪器故障等的影响，因此实时水位观测数据流噪声和数据异常问题突出。快速高效地发现与剔除观测数据中的错误和异常数据，实现水位观测数据流的动态数据质量控制，是进一步提升多源传感器信息在突发事件应急响应和环境监测高效分析等方面实时应用能力的关键[1, 2, 3, 4]。
由于监测参数随时间不断变化，特别是水文过程的多阶段演化过程复杂、高时变空变特征突出，因此，作为水文过程演变状态的表征，实时水位观测数据的多样性、快速性和时变性等特点突出。时变性和多样性不但体现在观测数据值方面，更重要的是体现在观测数据的复杂变化特征和模式方面。在传感器动态观测数据模式发生变化后，数据清洗过程所采用的数据估计模型需进行相应调整，否则数据估计模型将难以对后续持续到达的传感器动态观测数据进行准确估计[5, 6]。因此，及时感知和发现观测数据中蕴藏的复杂变化特征和模式，对于指导和支撑传感器动态观测数据清洗具有重要意义。然而目前传感数据流的清洗方法，多采用单一静态估计模型对传感器动态观测数据进行估计，并未考虑不同环境下动态观测数据特征和模式的变化；当在极端情况发生时，数据估计模型对动态观测数据的变化不敏感，静态估计模型参数难以根据动态观测数据的复杂变化特征进行及时调整和更新，从而导致较大的数据估计误差，这已成为在线观测数据清洗的关键瓶颈[7]。
随着传感器技术的发展，传感器观测数据流在线滤波成为热点，国内外出现了大量传感器观测数据流在线清洗方法[8, 9, 10]，主要包括冗余法、基于规则的清洗方法和贝叶斯滤波法等。其中，贝叶斯滤波泛指一类以贝叶斯定理为基础的滤波技术，包括卡尔曼滤波、高斯滤波、粒子滤波等[6, 11, 12, 13, 14]。卡尔曼滤波理论由于在线估计时间短、存储量小等特点决定了该技术适合于实时处理和计算，因而在观测数据流估计中得到了最为广泛的应用[15, 16, 17, 18]。卡尔曼滤波是一种包含噪声的递归估计算法，通过持续预测与更新的过程，实现动态系统状态的估计。该类方法无须记录历史观测数据，只需获取上一时刻动态系统状态的估计值和当前时刻的系统观测值即可计算获取当前时刻的系统估计值。传统卡尔曼滤波方法多采用单一静态的估计模型对动态观测数据值进行估计[5]，且该类算法严格依赖精确的估计模型和噪声统计[19]。然而，实际水位等水文要素均为非线性动态系统，受外界环境变化影响，水文要素的状态转移函数通常是动态、不确定的，估计模型较难确定[7]。特别是发生极端天气事件时，水位观测数据流变化快速且复杂，单一静态估计模型对动态系统描述能力有限，其估计模型难以根据观测数据流的模式变化进行动态调整和更新，滤波会出现滞后现象，从而导致较高的误报率，因此如何动态描述系统时变特征，以此驱动和约束数据流估计模型的动态更新是解决上述问题的关键。
针对上述问题，本文提出一种水文变化语义约束的动态水位观测数据流在线卡尔曼滤波方法：在分析和理解动态水位观测数据时空变化规律的基础上，构建动态水位观测数据与水文过程时空变化特征高层语义之间的映射关系，在滤波过程中以水文变化语义知识约束卡尔曼滤波参数的动态调整，最后利用不同降雨情境下的水位观测数据流对本算法进行了测试。
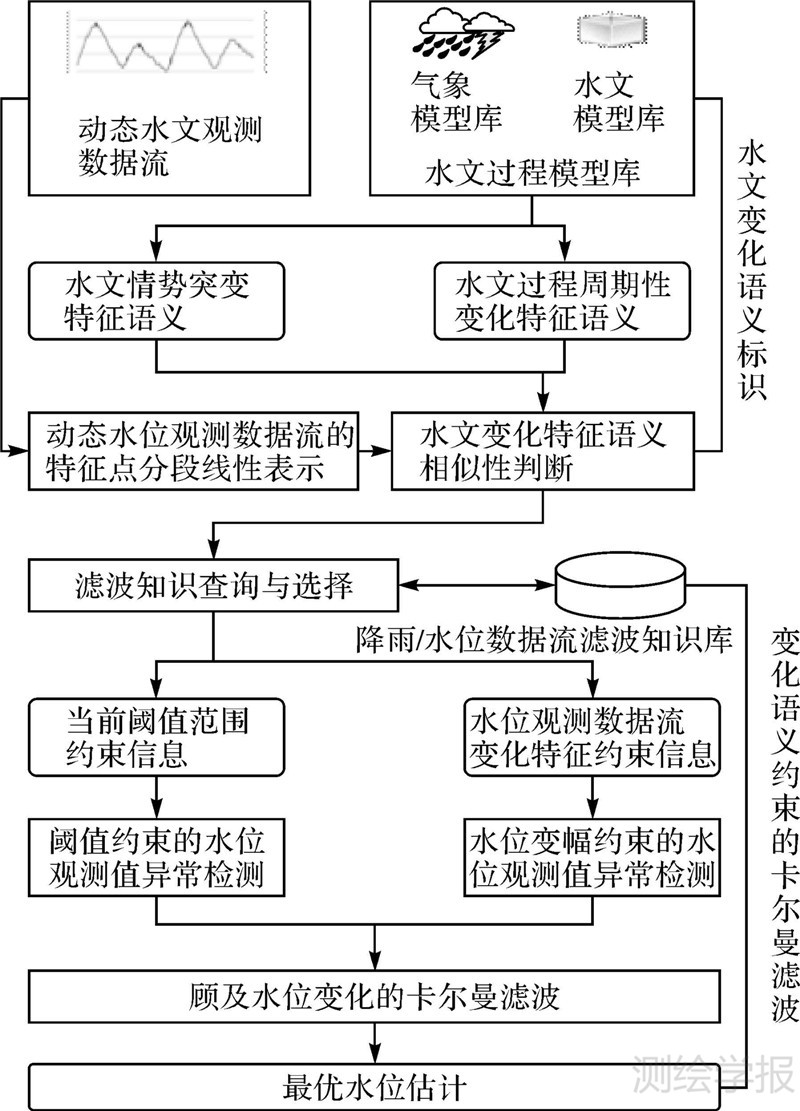
2 变化语义约束的实时水位观测数据在线卡尔曼滤波算法如图 1所示，水文变化语义标识和变化语义约束的在线卡尔曼滤波是本方法的两个关键步骤。在水文变化语义标识阶段，首先要根据历史观测数据和已有的水文过程模型，对动态水位观测数据流的不同变化特征进行语义描述和分类表达，以建立理解和分析动态水位观测数据流变化特征的基础。动态水位观测数据流中的水文变化主要包括两大类，一类是稳定环境下的周期性水文变化特征，一类是降雨、决堤等突发情况下的不规则水文突变特征。在实时水位观测数据流的动态接入过程中，通过对实时水位数据流进行特征点分段线性表示和水位变化特征的语义相似性判断，实现水位观测数据流的语义标识。在数据流在线滤波阶段，根据实时水位数据流的语义标注信息，通过水文变化语义相似性计算和语义关联分析，从动态维护的水文过程模型知识库检索获取适应于当前数据变化特征的水文变化语义约束信息。水文变化语义约束信息具体描述了不同外界条件下动态观测数据值的阈值范围及数据变化幅度约束信息。基于动态获取的水文变化语义约束信息，即可实现阈值约束和变幅约束的异常值检测与剔除，以及卡尔曼滤波模型参数的自适应调整。
|
| 图 1 语义约束的观测数据在线滤波方法框架图 Fig. 1 The framework of the proposed method |
如何对实时水位数据流变化特征进行语义标识，是后续进行滤波参数动态更新的基础。本文的语义标识过程是：首先对实时水位观测数据流进行特征点分段线性表示；其次对每段数据流子段进行变化模式的量化；最后将量化后的数据流变化特征与水文过程模型库中所定义的水文变化特征进行语义相似性度量，从而实现水位观测数据流变化模式的语义标识。其中，水位观测数据流特征点分段线性表示以及水位变化特征量化的关键定义详细描述如下。
2.1.1 实时水位观测数据流(定义1)令Z代表实时水位观测数据流，其中zt代表时间戳t时刻的水位观测值，则某采样时间段n内的实时水位观测数据流可表示为
2.1.2 动态水文观测数据流变化模式的特征点(定义2)
设动态水位观测数据流Z=〈z1,z2,z3,z4,…,zn〉，其局部特征点定义如下：对于∀zk，zk-1，zk，zk+1∈Z，若满足以下任意条件，则称zk为该变化模式的一个局部极值点或特征点，①zk-1≤zk且zk≥zk+1；②zk-1≥zk且zk≤zk+1。
2.1.3 动态水位观测数据流变化模式的特征点分段线性表示(定义3)设动态观测数据流Z=〈z1,z2,z3,z4,…,zn〉，其线性分段模式表示为
式中，pk代表动态观测数据流在时间区间[tk-1,tk]的两个端点，这两个端点为该时间区间的起点和终点，且该时间区间内有且仅有的两个特征点；fk(t,pk)为表示[tk-1,tk]两个端点内子模式的线性函数；εk(t)是该段变化数据流与其变化模式之间的差值。
局部极值特征点分段线性表示是对水位变化模式的定量描述，是进行变化模式语义标识的基础。为了定量评价每个特征点分段线性表示的模式段的变化特征，每个变化模式段的线性表示函数fk的信息熵En(fk)(由于是线性函数，所以其斜率等可用于表示信息熵)，具体定义见定义4。
2.1.4 动态水文观测数据流的局部波动程度因子(定义4)对于En(fk)的计算，本文定义了一个简单度量数据流局部波动程度因子BL(bending level)，定义为
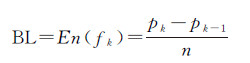
结合历史自动气象水文站观测数据，本文对不同降雨事件下水位观测数据流变化模式进行了分析，并根据BL实际取值对水位观测数据流变化特征进行了量化和分类，具体见表 1。
| 水位观测数据流变化类型 | 变化模式语义编码Base_Z | 基模式判别准则Description_Z |
| 水位无明显升降变化 | z(0) | BL≈0 |
| 水位平缓上升 | z(+) | 0.1%·Δz≤BL<10%·Δz,zt＞zt-1 |
| 水位平缓下降 | z(-) | 0.1%·Δz≤BL<10%·Δz,zt＜zt-1 |
| 水位陡升 | z(++) | 10%·Δz≤BL,zt＜zt-1 |
| 水位陡降 | z(--) | 10%·Δz≤BL,zt＞zt-1 |
| 注：Δz为水位观测数据变幅。 | ||
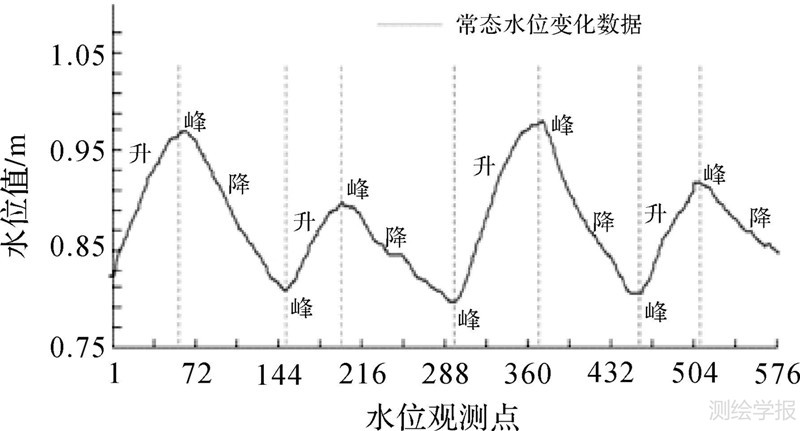
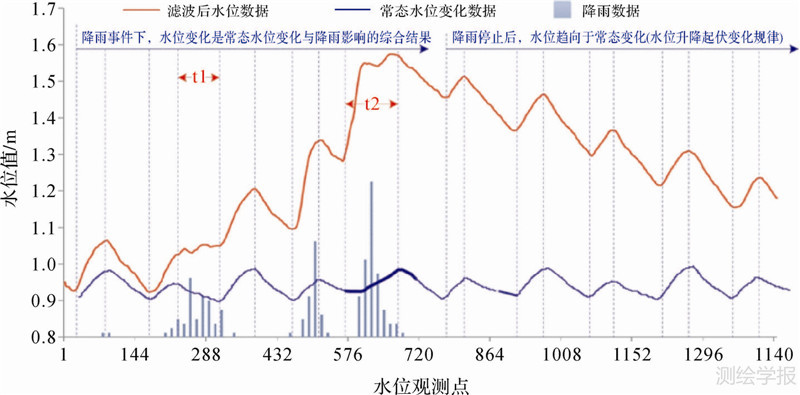
本文假定水位变化是周期性水位升降变化及降雨引起的水位升降变化的综合结果。在进行实时水位观测数据流的变化模式语义标识时，需在常态水位变化模式控制下，约束判断未能匹配的连续观测点是否为可疑点。实时水位观测数据流语义标识流程可以概要描述为：对连续观测点组成的轨迹进行特征点分段线性表示，其次对每段数据流子段进行变化模式的量化，并将量化后的变化特征与模型库中定义的水文变化特征进行语义相似性度量，判断其是否与某一变化特征相似。相似性度量成功的轨迹就可标识为对应的变化语义；若相似性度量不成功，则将该段观测点标记为可疑点Ei。其中，笔者基于所在研究团队的已有研究基础，即“时空变化显式表达的GIS三域模型”，进行水文变化的显式语义表达以及水文过程模型库的建立，详细介绍可参考文献[1, 2, 21]。常态无降水时，水位升降及峰现变化规律(如图 2所示，水位以升z(+)-峰值-降z(-)-峰值z(+)的模式规律变化)，在常态变化模式下，对于水位上升模式时出现的水位下降点则标记为可疑点，反之亦然。降水时，水位变化整体上仍部分服从常态模式的变化规律(详见图 5的分析)，降雨情况下的水位变化是常态变化与降雨影响的综合结果。因此，对于常态水位变化模式对应水位“升”模式，且又存在外界降雨时，此时水位变化应为“升”模式，观测值中若出现水位“降”模式，则需标记为异常值。对于常态水位变化模式对应水位“降”模式，且又存在外界降雨时，此时水位的“升”或“降”模式，均有可能出现，因此这种情况下的水位值需进行进一步的卡尔曼估计。此处，常态变化模式可理解为除降水影响以外、导致水位周期性稳定上升或下降现象的外界影响总和。
|
| 图 2 黄姑塘水位站常态水位变化模式(2 d，576个点) Fig. 2 Normal change patterns of the real-time water level data stream obtained at Huanggutang station |
|
| 图 5 黄姑塘水位站降雨情况下实测水位数据滤波效果分析 Fig. 5 Filtering results analysis of the real-time water level data stream obtained at Huanggutang station |
利用卡尔曼滤波算法对实时水位观测数据流校正的过程，首先必须依赖于状态方程和观测方程的建立。本文假定水位变化均是渐变(即水位变化幅度与降水强度相关)，则tk时刻的水位值wk可以描述为tk-1时刻的水位值wk-1加上相邻时刻的水位变化值Δwk，即：wk=wk-1+Δwk。另外，由于水位量测方程较为简单，可认为水位的观测误差系列服从独立的正态分布。根据上述假设和推导，以水位和水位变化值为状态向量，顾及水位变化特征的卡尔曼滤波状态方程和观测方程构造为
式中，wk和Δwk分别为tk时刻的状态向量，即水位和水位变化的预估值；zk为tk时刻的水位观测向量；Ωk和δk分别为tk时刻的动态预测噪声和观测噪声；预测与观测误差的协方差矩阵分别为Qk和Rk。方程(2)为状态方程；方程(3)描述了状态向量wk与观测向量zk之间的关系，称为观测方程。本研究中Ωk和δk为相互独立的正态白噪声，E[Ωk]=0，E[δk]=0。
卡尔曼滤波方程中相关参数初始值对滤波结果也有一定程度影响，特别是卡尔曼状态方程和观测方程不合理的情况下，相关矩阵的初值对于后续模拟结果影响较大。传统的卡尔曼滤波算法应用于实际的水位观测数据流滤波时，有几个问题需注意：①Qk和Rk需已知；②若Qk和Rk估计偏差较大，则E[Ωk]≠0，而实际中要比较精确地估计Qk和Rk较为困难。传统方法并未考虑观测数据变化特征的滤波递推模型用于实时水位预估容易引起预报值发散(或偏离真值)。对于非降雨下的水位观测数据，实时水位观测数据流变化是稳定的(图 2)，预测噪声Ωk和观测噪声δk可认为是平稳的随机过程。对于降雨情况下的水位，水位变化是受动态降雨影响等外界环境影响的非平稳随机过程，其预测噪声Ωk和观测噪声δk也同样是非平稳的随机过程。为了降低本算法对Qk和Rk的敏感度，使卡尔曼滤波效果不受Qk和Rk的影响，本文以少量水位观测样本预估Qk和Rk的初值。滤波过程中，本方法中的滤波模型会根据估计误差情况，自适应调整估计系统的相关参数，使其受不同降雨情况下的水位变幅信息约束控制，实时适应水位观测数据流中数据模型变化的情况，从而实现较高的精度估计。采用多次样本试验证明，本算法对初始状态向量和其误差协方差矩阵初值的依赖性及敏感性较低，初值可任意设置，随着滤波过程的继续，本算法中相关参数会逐渐收敛。
3 试验与分析本节首先介绍试验数据，其次分析与评价不同降雨事件下的滤波结果，最后和其他方法进行比较分析。
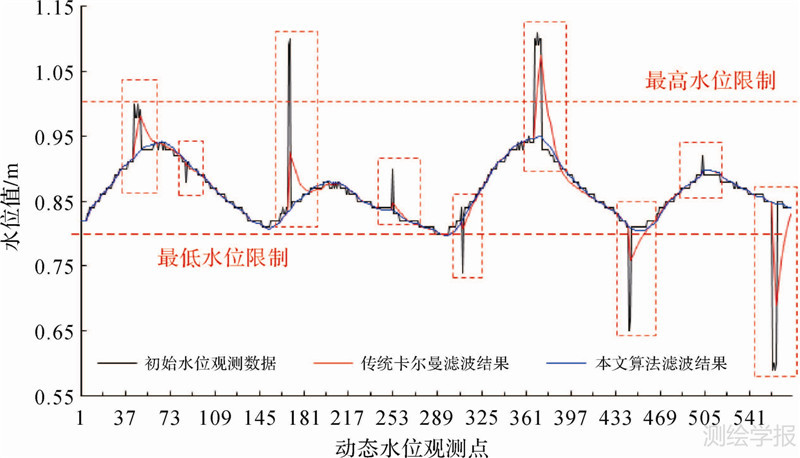
3.1 试验数据试验数据来自平湖市水文站监测系统实际得到的实时水位观测数据。为了全面验证本算法的性能，试验选用不同降雨情境下的水位观测数据流，选用的水位观测数据流变化剧烈且频繁。试验数据选择黄姑塘水文站两个降雨情景下的实时水位观测数据，具体如图 3黑实线所示(无降雨情景)以及图 4黑实线所示(无降雨-暴雨情景)的水位观测数据流。该数据为5 min的采样频率，其中无降雨情景下的测试数据包括576个水位观测点；无降雨-暴雨情景下的观测数据包括1440个水位观测点。
|
| 图 3 黄姑塘水位站无降雨情况下实测水位数据滤波效果(2014-06-09-2014-06-10) Fig. 3 Filtering results of the real time observational water level data stream obtained at Huanggutang station with no precipitation (2014-06-09-2014-06-10) |
|
| 图 4 黄姑塘水位站降雨情况下实测水位数据滤波效果(2014-06-25-2014-06-29) Fig. 4 Filtering results of the real time observational water level data stream obtained at Huanggutang station under rainfall weather (2014-06-25-2014-06-29) |
采用本文算法对上述水位观测数据进行滤波处理所得到的结果如图 3和图 4蓝色实线所示，传统无变化语义约束的卡尔曼滤波结果为图中红色实线所示。为了对滤波结果进行评估，结合国家发布的《水文情报预报规范》中的相关规定，本文选取了确定性系数(determinacy coefficient,DC)以及几个常见的估计评价指标对其精度进行评价，具体如下。
(1) 确定性系数。这是常用来评价洪水预报过程与实测过程之间吻合程度的重要指标，取值范围在0~1之间，取值越接近1，说明预估效果越好，计算公式为
式中，wt为水位实测真值；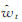
为卡尔曼滤波器的水位预估值； 
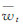为水位实测真值的均值。
(2) 传统评价指标，包括均方根误差(ERMSE)、规范化均方根误差(ENRMSE)等，计算公式为
式中：zt为水位实测值；wt为卡尔曼滤波器的水位预估值；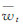
为水位实测值的均值。ERMSE反映估计值 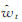相对于观测值zt的平均相对偏离程度。ENRMSE是估计值 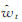相对于观测值zt的平均偏离程度的规范化。本文算法与传统卡尔曼滤波算法的估计精度和效率比较见表 2。
| 方法 | 数据1 | 数据2 | ||||||
| 滤波总时间／s | DC | ERMSE | ENRMSE | 滤波总时间／s | DC | ERMSE | ENRMSE | |
| 传统方法 | 0.005 4 | 0.617 | 0.023 | 0.463 | 0.0231 | 0.951 | 0.015 | 0.073 |
| 本文方法 | 0.003 7 | 0.985 | 0.005 | 0.117 | 0.017 2 | 0.999 | 0.007 | 0.035 |
| 改善程度/(%) | 31.48 | 59.64 | 78.26 | 74.73 | 25.54 | 5.05 | 53.33 | 52.05 |
由表 2可以看出，相对于传统的卡尔曼数据流滤波方法，本文的方法具有较低的计算复杂度，在估计时间上，两组试验数据分别降低了31.48%和25.54%；在估计精度上(DC、均方根误差和规范化均方根误差)有了较大程度的改善。因此本文提出的数据流估计方法在估计精度和估计效率等方面，都具有较强的优势。
另外，由结果可知，对于不同情况下的水位实测数据，本文的算法能够很好地发现和剔除阈值范围内的独立或连续的噪点以及阈值范围内但水位变化特征异常的独立或连续异常水位。特别的，本文中水位观测数据流变化主要是常态变化和降雨影响的综合结果，这也是本文进行变化语义约束滤波的理论支撑。常态水位变化如图 2所示，水位以升-峰值-降-峰值模式规律变化，由图 5所示的实际水位观测数据的滤波结果可知，降雨停止后，水位变化趋向于常态，水位升降以及峰现时间皆与常态水位变化同步。因此，对于无降水情况下，违背相应水位变化规律的水位观测值(例如，变化模式上水位本该上升时，却出现了水位降低，反之亦然)即为水位异常值。对于降水下的水位观测数据，其变化模式是降水和常态变化的综合结果，即水位观测数据流变化整体上仍与升-峰值-降-峰值模式吻合，但滤波时的水位变化约束规则仍需根据降雨情况自适应调整。例如，由于降雨影响(如t1段和t2段)，t1段常态变化模式为降，但由于有降水影响，因此出现水位上升现象；t2段由于突发性暴雨，水位出现陡增现象，此时的滤波规则特别是变幅约束需对应调整。
4 结 论作为水文过程演变状态的表征，实时水位观测数据流复杂时变特征突出，克服传统传感器观测数据滤波方法适应性差的问题，是当前数据清洗技术亟须攻克的核心瓶颈问题。本文提出了一种水文变化语义约束的实时水位观测数据在线清洗方法，通过建立实时水位数据的变化特征及其与水文过程动态演变规律之间的高层语义映射关系，对该水文变化语义约束进行滤波，实现滤波参数的自适应调整。试验结果表明，与传统卡尔曼滤波算法相比，本方法处理两组试验数据的耗时分别降低了31.48%和25.54%、DC系数分别提高了59.64%和5.05%，估算精度和效率均有了较大程度的提高。
洪涝过程复杂，具有动态不确定性，本文定义的水文变化模式分类是在有限的数据流模式基础上进行的，并未综合全面考虑不同复杂环境下的所有水文变化特征。因此，下一步将研究语义感知的水文变化发现方法，实现动态水文观测数据流变化特征的自动发现与感知。
| [1] | DING Yulin, FAN Yida, DU Zhiqiang, et al. An Integrated Geospatial Information Service System for Disaster Management in China[J]. International Journal of Digital Earth,2015, 8(11): 918-945. |
| [2] | DING Yulin, ZHU Qing, LIN Hui. An Integrated Virtual Geographic Environmental Simulation Framework: A Case Study of Flood Disaster Simulation[J]. Geo-spatial Information Science,2014, 17(4): 190-200. |
| [3] | DING Yulin, DU Zhiqiang, ZHU Qing, et al. Adaptive Water Level Correction Algorithm for Flooding Analysis[J]. Acta Geodaetica et Cartographica Sinica,2013, 42(4): 546-553. (丁雨淋, 杜志强, 朱庆, 等. 洪水淹没分析中的自适应逐点水位修正算法[J]. 测绘学报,2013, 42(4): 546-553.) |
| [4] | SUI D, GOODCHILD M. The Convergence of GIS and Social Media: Challenges for GIScience[J]. International Journal of Geographical Information Science,2011, 25(11): 1737-1748. |
| [5] | O'REILLY C, GLUHAK A, IMRAN M A, et al. Anomaly Detection in Wireless Sensor Networks in a Non-stationary Environment[J]. IEEE Communications Surveys & Tutorials, 2014, 16(3): 1413-1432. |
| [6] | SMITH D, TIMMS G, De SOUZA P, et al. A Bayesian Framework for the Automated Online Assessment of Sensor Data Quality[J]. Sensors,2012, 12(7): 9476-9501. |
| [7] | RASSAM M A, MAAROF M A, ZAINAL A. Adaptive and Online Data Anomaly Detection for Wireless Sensor Systems[J]. Knowledge-based Systems,2014, 60: 44-57. |
| [8] | CHANDOLA V, BANERJEE A, KUMAR V. Anomaly Detection: A Survey[J]. ACM Computing Surveys,2009, 41(3): 15. |
| [9] | HILL D J. Automated Bayesian Quality Control of Streaming Rain Gauge Data[J]. Environmental Modelling & Software,2013, 40: 289-301. |
| [10] | PATCHA A, PARK J M. An Overview of Anomaly Detection Techniques: Existing Solutions and Latest Technological Trends[J]. Computer Networks,2007, 51(12): 3448-3470. |
| [11] | LIU Hancong, SHAH S, JIANG Wei. On-line Outlier Detection and Data Cleaning[J]. Computers &Chemical Engineering,2004, 28(9): 1635-1647. |
| [12] | INGLEBY B, HUDDLESTON M. Quality Control of Ocean Temperature and Salinity Profiles-historical and Real-time Data[J]. Journal of Marine Systems,2007, 65(1-4): 158-175. |
| [13] | GELMAN A, CARLIN J B, STERN H S, et al. Bayesian Data Analysis[M]. 3rd ed. Boca Raton: Chapman and Hall/CRC press, 2013. |
| [14] | TROYANSKAYA O G, DOLINSKI K, OWEN A B, et al. A Bayesian Framework for Combining Heterogeneous Data Sources for Gene Function Prediction (In Saccharomyces Cerevisiae)[C]//Proceedings of the National Academy of Sciences of the United States of America,2003, 100(14): 8348-8353. |
| [15] | KANO M,NAKAGAWA Y. Data-based Process Monitoring, Process Control, and Quality Improvement: Recent Developments and Applications in Steel Industry[J]. Computers & Chemical Engineering,2008, 32(1-2): 12-24. |
| [16] | LIU Fanming,QIAN Dong, GUO Jing. Terrain Estimation Algorithm Based on Kalman Filter and Its Simulation Research[J]. Acta Geodaetica et Cartographica Sinica,2011, 40(1): 45-51. (刘繁明, 钱东, 郭静. 基于卡尔曼滤波的地形反演方法及其仿真研究[J]. 测绘学报,2011, 40(1): 45-51.) |
| [17] | LIU Guolin, HAO Huadong, YAN Man, et al. Phase Unwrapping Algorithm by Using Kalman Filter Based on Topographic Factors[J]. Acta Geodaetica et Cartographica Sinica,2011, 40(3): 283-288. (刘国林, 郝华东, 闫满, 等. 顾及地形因素的卡尔曼滤波相位解缠算法[J]. 测绘学报,2011, 40(3): 283-288.) |
| [18] | LI Lihua, PENG Junhuan. Multiple Kalman Filters Model with Shaping Filter GPS Real-time Deformation Analysis[J]. Transactions of Nonferrous Metals Society of China,2014, 24(11): 3674-3681. |
| [19] | YAN Xiaozhen, LUO Qinghua. Dynamic Sensor Data Stream Estimation Method Based on Kalman Filtering[J]. Chinese Journal of Scientific Instrument,2013, 34(8): 1847-1854. (焉晓贞, 罗清华. 基于卡尔曼滤波的动态传感数据流估计方法[J]. 仪器仪表学报,2013, 34(8): 1847-1854.) |
| [20] | XU Weiping, ZHU Qing, ZHANG Yeting, et al. Real-time GIS and its Application in Indoor Fire Disaster[C]//International Archives of the Photogrammetry,Remote Sensing and Spatial Information Sciences. Istanbul: [s.n.],2013, XL-2/W2: 121-127. |