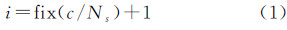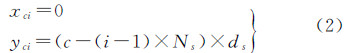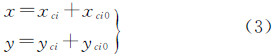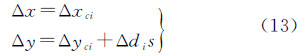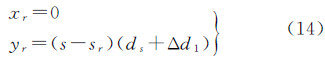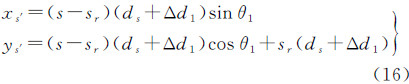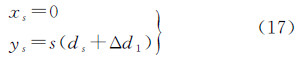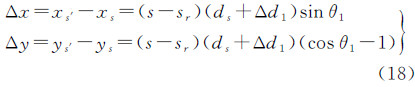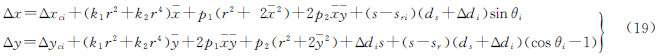1 引言
随着光学卫星遥感的发展,传统线阵CCD相机已不能满足航天光学遥感的需求,时间延迟积分电荷耦合器件(TDI CCD)拼接相机正取而代之,成为主流星载光学传感器。TDI CCD拼接相机的技术革新主要体现在“TDI CCD”与“CCD拼接”两方面,TDI CCD用于保证成像系统轻小型化和足够的曝光量;CCD拼接技术用于保证足够的地面覆盖宽度。
当前实用的CCD拼接方案有两种:一种为光学拼接方案[1],如资源三号卫星三线阵相机,该方案通过分光棱镜形成一对光程相等的共轭面,将透射面和反射面处的多片CCD首尾搭接实现连续的像面;另一种为交错拼接方案[2],该方案将多个CCD在焦平面上交错成两行排列,形成不连续的像面,如CBERS-02B卫星高分相机、天绘一号(TH-1)卫星高分相机。此外,QuickBird、WorldView-2、LandSat-8等典型光学卫星也均搭载了多CCD拼接相机,如图 1所示。

|
| 图 1 典型多CCD拼接相机示意组图 Fig. 1 Set of diagrams of push-broom camera using multi-CCDs |
TDI CCD拼接相机严格几何模型构建及优化的相关研究可提高多片CCD影像的有(无)控定位精度,为后续多片拼接等处理工作提供了良好的几何基础,具有较高的研究价值。为实现该类影像的高精度几何定位,国内外学者开展了诸多研究。
严格几何模型构建方面,文献[10, 11, 12]对多片CCD拼接的Pleiades卫星高分相机及其影像产品进行了介绍,构建了传感器产品的严格几何模型;文献[13]给出了星载线阵传感器严格成像模型的一般形式,并针对SPOT5 HRS/HRG、ALOS/PRISM等典型光学传感器分别给出了具体的严格成像模型;文献[14, 15]提出了一种通用线推扫传感器几何模型并利用SPOT 5、QuickBird、ALOS/PRISM等卫星影像对其模型进行了验证;文献[4, 16]以3片TDI CCD交错拼接的 CBERS-02B/02C卫星高分相机为原型,构建了单片TDI CCD影像的严格几何模型并对内视场拼接方法进行了深入研究;文献[17]采用虚拟CCD线阵重成像技术实现CCD分片影像拼接进而构建资源三号(ZY-3)测绘卫星成像几何模型;文献[18]提出了ZY-3三线阵影像传感器校正产品的生成方法并构建其严格几何模型;文献[19]对光学卫星线推扫相机几何模型构建的研究进展进行了综述。
在几何模型优化方面,分别构建内外误差补偿模型并对其进行整体求解的方法在本景或相邻景影像内能取得一定效果,但受内外参数相关性的影响,求解出的参数并不具备推广应用性[20];分别构建内外误差补偿模型并采用先外后内、分步求解的方法,可得到具备推广应用潜力的内部误差参数[21];常用的外部误差描述方法有姿态角常差、姿态角系统误差、侧视角常差等[22, 23, 24, 25];常用的内部误差模型有探元指向角模型[26]和物理内畸变模型[27],探元指向角模型可综合描述各类内部误差但参数不具备物理意义,物理内畸变模型构建过程复杂但各参数对应明确的畸变因子,具有明确的物理含义。
本文以8片TDI CCD交错拼接的TH-1高分相机为原型,基于成像瞬间多片CCD共享一套外方位元素的特点构建该类相机的“整体几何模型”。以整体几何模型为基础,构建TDI CCD拼接相机的内外误差补偿模型,并采用先外后内、分步求解的解算方法克服参数间的相关性,实现几何模型的合理优化。
2 TDI CCD交错拼接相机推扫成像特点TDI CCD交错拼接相机焦平面的主要特点为:沿轨方向多片TDI CCD成两行平行交错排列,垂轨方向相邻TDI CCD之间具有少量重叠探元。TDI CCD是一种面阵结构线阵输出的探测器件,通过时间延迟积分技术提高曝光量,推扫成像时几何上仍满足线中心投影原理。
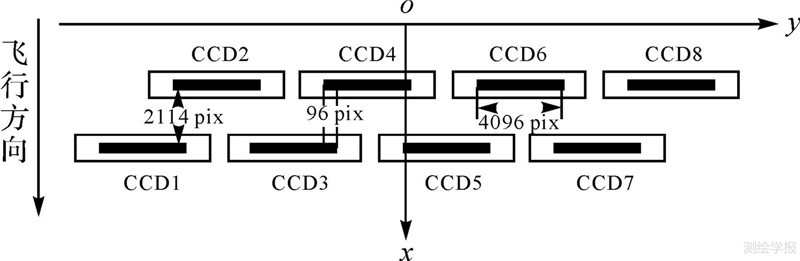
先后成功发射并投入使用的TH-1的01星、02星上均搭载了2 m分辨率的高分相机、5 m分辨率的LMCCD三线阵相机和10 m分辨率的多光谱相机。其中,2 m分辨率高分相机采用8片交错拼接的TDI CCD作为探测器件(每片TDI CCD长度方向有4096个探元),8片TDI CCD元件随封装盒一起,相互之间错开一定距离,分两行平行地交错排列在焦平面上,相邻TDI CCD元件之间重叠96个探元,如图 2所示。TH-1卫星及其高分相机的主要参数如表 1所示。
|
| 图 2 TH-1高分相机焦面示意图 Fig. 2 Diagram of TH-1 HR camera focal plane |
| TH-1卫星 | 发射时间 | 01星:2010-08-2402星:2012-05-06 |
| 发射地点 | 酒泉卫星发射中心 | |
| 轨道高度/km | 500 | |
| 轨道倾角/(°) | 97.4 | |
| 高分相机 | 相机类型 | 8片TDI CCD交错拼接 |
| 成像方式 | 推扫 | |
| 器件总长度/像素 | 8×4096 | |
| 地面分辨率/m | 2 |
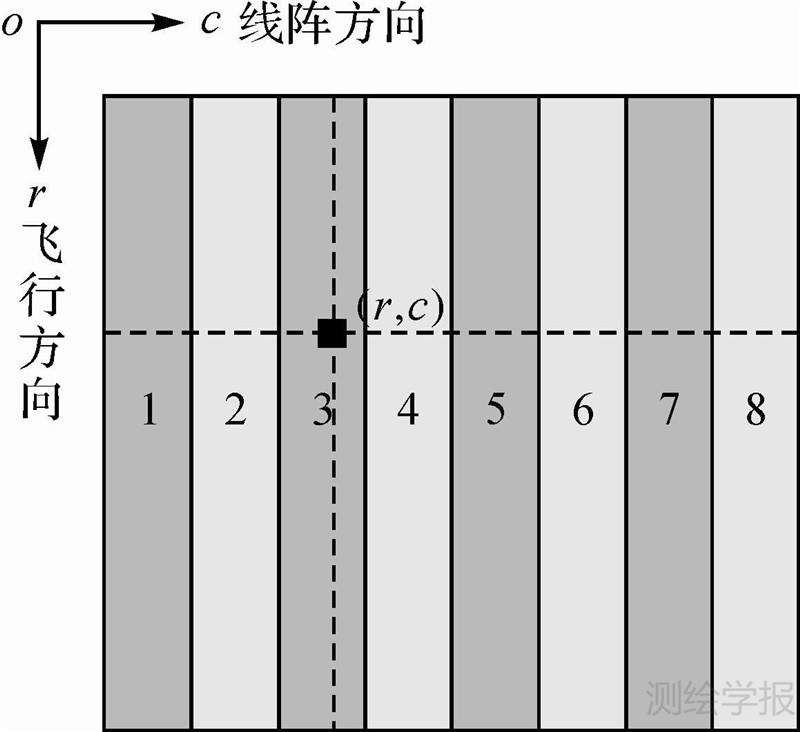
以TH-1高分相机为例对TDI CCD交错拼接推扫相机的成像特点进行介绍。在每一成像瞬间,8片CCD的地面投影覆盖仅为8个扫描行,如图 3(a)所示;但随着卫星平台的向前飞行,8片CCD连续推扫成像,最终获取8个分片图像,8个分片图像对应的地面投影覆盖如图 3(b)所示。将分片图像按成像时间(行号)对齐并存储在一个矩阵中可得到一幅整体图像,本文称之为原始整体图像,如图 4所示。本文严格几何模型的构建及优化都是基于原始整体图像进行的。

|
| 图 3 瞬间及推扫成像地面投影覆盖 Fig. 3 Projection area of instantaneous imaging and push-broom imaging |
|
| 图 4 原始整体图像 Fig. 4 Original integral image |
内定向是根据像点在原始整体图像坐标系下的行列号(r,c),确定相应CCD探元在相机坐标系下光线指向的过程。多片TDI CCD交错拼接相机特殊的焦面构造使得其内定向过程与传统线阵CCD相机有较大不同,本文设计的内定向步骤如下:
(1) 计算CCD分片编号i。根据原始整体图像坐标系o-rc下像点坐标(r,c)的列坐标c,按式(1)判断该点由第几片CCD成像,即确定i的值(i=1,2,…,8)
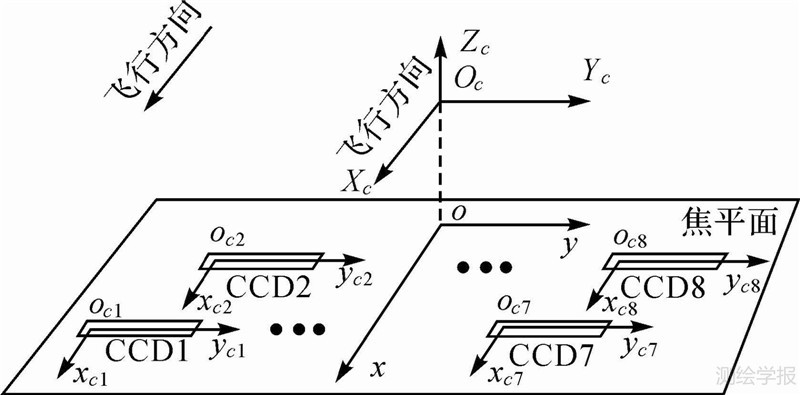
式中,fix表示截尾取整;Ns为单片CCD的长度,单位为像元。(2) 构建单片CCD坐标系oci-xciyci。以各单片CCD左侧第一个像元中心为原点,沿飞行方向为xci轴,沿线阵方向为yci轴,以毫米为单位,在焦平面内构建分片CCD坐标系oci-xciyci,如图 5所示,Oc-XcYcZc代表相机坐标系,o-xy代表焦平面坐标系。
|
| 图 5 分片CCD坐标系 Fig. 5 Coordinate system of individual CCD |
(3) 原始整体图像坐标系o-rc到单片CCD坐标系oci-xciyci的转换。根据像点在原始图像坐标系下的坐标(r,c)计算对应探元在单片CCD坐标系下坐标(xci,yci)的公式为
式中,ds为以毫米为单位的CCD探元尺寸。(4) 单片CCD坐标系oci-xciyci到相机坐标系o-xcyczc的转换。根据各单片CCD在焦平面的安置位置参数(xci0,yci0)完成单片CCD坐标系oci-xciyci到焦平面坐标系o-xy的转换,如式(3)所示(此时为理想状态,不考虑各种畸变)。根据焦平面坐标配合相机焦距f,即可得到该像点在相机坐标系下的坐标(x,y,-f)
(5) 根据式(4)计算相机坐标系下的视线向量u1
2.2 外定向TDI CCD交错拼接相机采用推扫方式成像,其外定向过程与传统单线阵CCD推扫相机相类似。TH-1卫星定轨结果是其GPS天线相位中心在CGCS2000坐标系下的位置,频率为1 Hz,定姿结果是星敏感器坐标系在J2000坐标系下的姿态四元数,频率为2 Hz。外定向的主要步骤如下:
(1) 行时计算。卫星时间测量系统并不对每条影像行的成像时刻进行记录,而是每隔一定时间记录一组关于时间的观测量。该观测量由扫描行行号、星务时刻、行积分时间等组成,根据该观测量可计算出每一行影像的成像时刻[4]。
(2) 轨道参数内插。采用拉格朗日插值对轨道参数进行内插,任意时刻t的轨道参数可用时间上最邻近的n个轨道参数值(XGPSj,YGPSj,ZGPSj),j∈[1,n]进行内插得到
式中,(XGPS,YGPS,ZGPS)为内插出的t时刻轨道参数;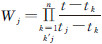 。一般n取8时可满足精度要求,本文取n=8。
。一般n取8时可满足精度要求,本文取n=8。
(3) 四元数姿态参数内插。四元数是形如q=q0+q1i+q2j+q3k的超复数,q0、q1、q2、q3为任意实数,i、j、k为虚数单位,i2=j2=k2=-1。采用球面线性内插方式对姿态四元数进行内插[28]。
2.3 严格几何模型根据两条视线u′1与u2共线构建严格几何模型。
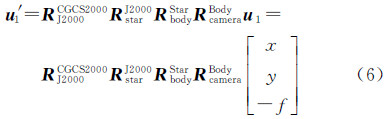
(1) u′1为根据相机坐标系下的视线向量u1经过一系列旋转得到的CGCS2000坐标系下的视线向量
式中,RcameraBody、RbodyStar、RstarJ2000、RJ2000CGCS2000依次为高分相机坐标系到卫星本体坐标系、卫星本体坐标系到星敏坐标系、星敏坐标系到J2000坐标系、J2000坐标系到CGCS2000坐标系的旋转矩阵。(2) u2为CGCS2000坐标系下地面点坐标(X,Y,Z)与相机投影中心坐标(Xs,Ys,Zs)之差得到的视线向量
根据GPS相位中心位置(XGPS,YGPS,ZGPS)和相机投影中心与GPS相位中心的位置偏移,计算相机投影中心的位置(Xs,Ys,Zs)
式中,(DX,DY,DZ)与(dx,dy,dz)分别为CGCS2000坐标系下、卫星本体坐标系下相机投影中心与GPS相位中心的位置偏移。(3) 视线向量u′1与u2共线的数学描述为
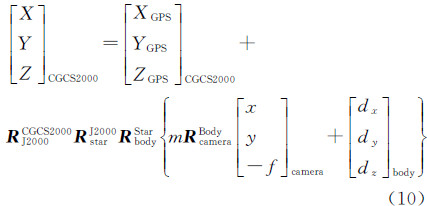
式中,m为比例因子。(4) 将式(8)代入式(7),式(6)、式(7)代入式(9),可得TH-1高分相机严格几何模型
式中,(x,y,-f)根据3.1节的内定向过程计算,其余各参数物理意义上文中均已介绍。 3 严格几何模型的优化 3.1 外部误差补偿模型与发射前相比,卫星入轨后相机安置矩阵、星敏安置矩阵、GPS偏心差等参数都将会发生变化,并且星上测得的姿轨参数会也会含有系统误差,本文将上述误差统称为外部误差。引入偏置矩阵Roff(正交旋转矩阵)对外部误差统一补偿[27],外部误差补偿后的几何模型为
3.2 内部误差补偿模型将相机的光学畸变、主距变化、主点偏移,CCD的平移、旋转、缩放等因素引起的误差统称为内部误差。在构建TDI CCD交错拼接相机内部误差补偿模型时应参考以下准则:
(1) TDI CCD分片共享一套光学系统,因此光学畸变、主点偏移、主距变化等与光学系统相关的畸变因子对多片TDI CCD而言是共用的。
(2) 各TDI CCD阵列之间相互独立,因此CCD的平移、旋转、缩放等与CCD阵列相关的畸变因子对多片TDI CCD而言需分别建模。
(3) 对像点偏移影响规律一致的畸变参数可进行合并处理。
以8片交错拼接的TH-1高分相机为例进行具体分析:
(1) 相机的光学畸变。对光学畸变引起的像点偏移(Δx,Δy)统一建模为
式中,k1、k2为径向畸变参数;p1、p2为偏心畸变参数;(x,y)为焦平面坐标系下的像点坐标;r为辐射距。(2) 相机的主点偏移、主距变化,CCD的平移、缩放。对可合并的畸变参数进行合并处理,其中主点偏移可并入各分片CCD的平移,主距变化在焦平面x方向引起的像点偏移可并入x方向的CCD平移,主距变化在y方向产生的像点偏移可并入y方向CCD尺度缩放(探元尺寸变化)产生的像点偏移,最终上述各因素引起的像点偏移(Δx,Δy)
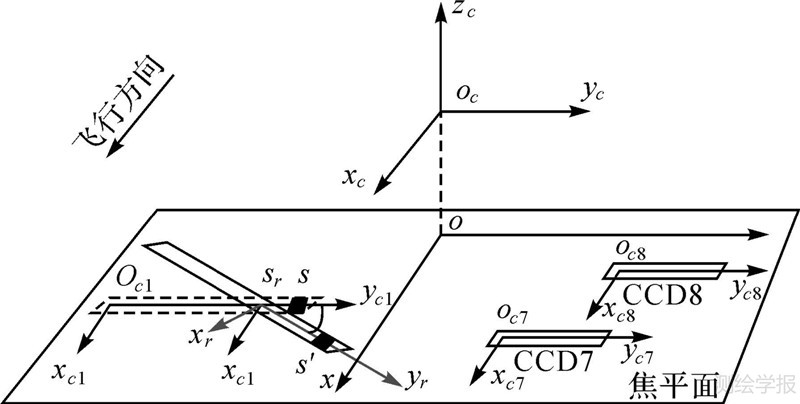
式中,(Δxci,Δyci)为各分片CCD的平移;Δdi为各分片CCD的探元尺寸变化因子,i=1,2,…,8,代表CCD分片编号;s为各分片从左至右的探元编号。(3) CCD的旋转。以CCD1为例对旋转误差进行说明,如图 6所示。假定CCD1绕其第sr个探元旋转了θ1角,s与s′分别代表旋转前后的同一探元,则s′在坐标系sr-xryr下的坐标为
式中,ds为探元尺寸;Δd1为分片CCD1探元尺寸变化因子。
|
| 图 6 CCD旋转示意图 Fig. 6 Diagram of CCD rotation |
s′在坐标系sr-xc1yc1的坐标为
s′在分片坐标系oc1-xc1yc1的坐标为
s在分片坐标系oc1-xc1yc1的坐标为
则由CCD旋转引起的像点偏移(Δx,Δy)为 综合式(12)、式(13)和式(18)可得TH-1高分相机各类内部误差引起的综合像点偏移(Δx,Δy)(内部误差补偿模型)为上述内部误差补偿模型中8片CCD共用的参数有4个,即k1、k2、p1、p2;各片CCD独用的参数有5个,即Δxci、Δyci、Δdi、θi、sri,则总的待求解内部误差补偿参数共4+5×8=44个。
3.3 先外后内、分步求解的解算流程克服参数间强相关性的常见处理方法有两种[29]:一种是在平差解算过程中将各待求参数视为虚拟观测值并根据先验知识赋予一定权值,另一种是采用分步解算的策略。本文采用先外后内、分步求解的解算流程[26]:①将相机内部参数视为“真值”,对外部误差补偿参数进行求解;②将外部误差补偿后的外定向参数视为“真值”,对内部误差补偿参数进行求解;③循环执行步骤①和步骤②,当两类参数的值趋于稳定时停止计算。
4 试验与分析 4.1 试验设计为验证本文方法的正确性和有效性,设计以下5组试验。
(1) 直接定位试验。内定向参数采用相机设计值,外定向参数采用原始姿轨数据,进行直接定位试验,目的是验证所构建严格几何模型的正确性。
(2) 外部误差补偿定位试验。内定向参数采用相机设计值,基于少量控制点对外部误差补偿后进行定位试验,目的是验证外部误差补偿方案的有效性。
(3) 内部误差补偿定位试验。基于卫星影像与嵩山试验区高精度DOM、DEM匹配量测获取的密集控制点,采用先外后内、分步求解的流程解算相机内部误差补偿参数,对相机内部参数进行更新;利用更新后的相机内部参数和原始姿轨数据,进行定位试验,目的是验证内部误差补偿方案的有效性。
(4) 内部、外部误差补偿定位试验。采用更新后的相机内部参数、配合少量控制点对外部误差补偿后进行定位试验,目的是验证内部误差、外部误差均补偿时可达到的定位精度。
(5) 内部误差补偿参数应用于其他多景影像试验。将求解出的内部误差补偿参数应用于不同成像时间的其他多景影像进行定位试验,目的是测试相机内部几何状态的稳定性并进一步验证所求解内部误差补偿参数的有效性。
4.2 试验数据试验数据包括:①两景嵩山试验区TH-1高分相机原始影像,该区域地面高程范围为4~1445 m,均匀布设51个厘米级GPS野外实测平高控制点;②两景新乡试验区TH-1高分相机原始影像,该区域地面高程范围为5~838 m,均匀布设12个厘米级GPS野外实测平高控制点;③嵩山数字检校场比例尺为1∶5000的DOM和DEM。影像信息见表 2(落在相邻CCD重叠区内的控制点将“一分为二”,最终4景影像上实际的控制点数目分别为13、13、53、51),控制点分布情况见图 7。
| 覆盖区域 | 影像 | 成像时间 | 野外实测控制点数 |
| 新乡 | 134-1 | 2010-11-28 | 13 |
| 134-2 | 2010-12-20 | 13 | |
| 嵩山 | 135-1 | 2010-11-28 | 53 |
| 135-2 | 2010-12-20 | 51 |

|
| 图 7 控制点分布示意图 Fig. 7 Distributions of GCPs |
利用原始姿轨数据及相机设计参数,基于本文严格几何模型进行直接定位试验,所有野外实测控制点均作为检查点进行直接定位精度评估(表 3),试验结果验证了所构建严格几何模型的正确性。
| 影像编号 | 控制点个数 | 检查点个数 | 最大残差/m | 中误差/m | ||||
| X | Y | Z | X | Y | Z | |||
| 134-1 | 0 | 13 | 35.457 | 9.676 | 23.365 | 26.042 | 5.661 | 20.582 |
| 134-2 | 0 | 13 | 43.562 | 24.574 | 47.122 | 32.906 | 19.918 | 44.147 |
| 135-1 | 0 | 53 | 36.693 | 9.151 | 25.599 | 25.406 | 4.685 | 19.649 |
| 135-2 | 0 | 51 | 50.015 | 26.334 | 57.530 | 36.047 | 21.022 | 48.240 |
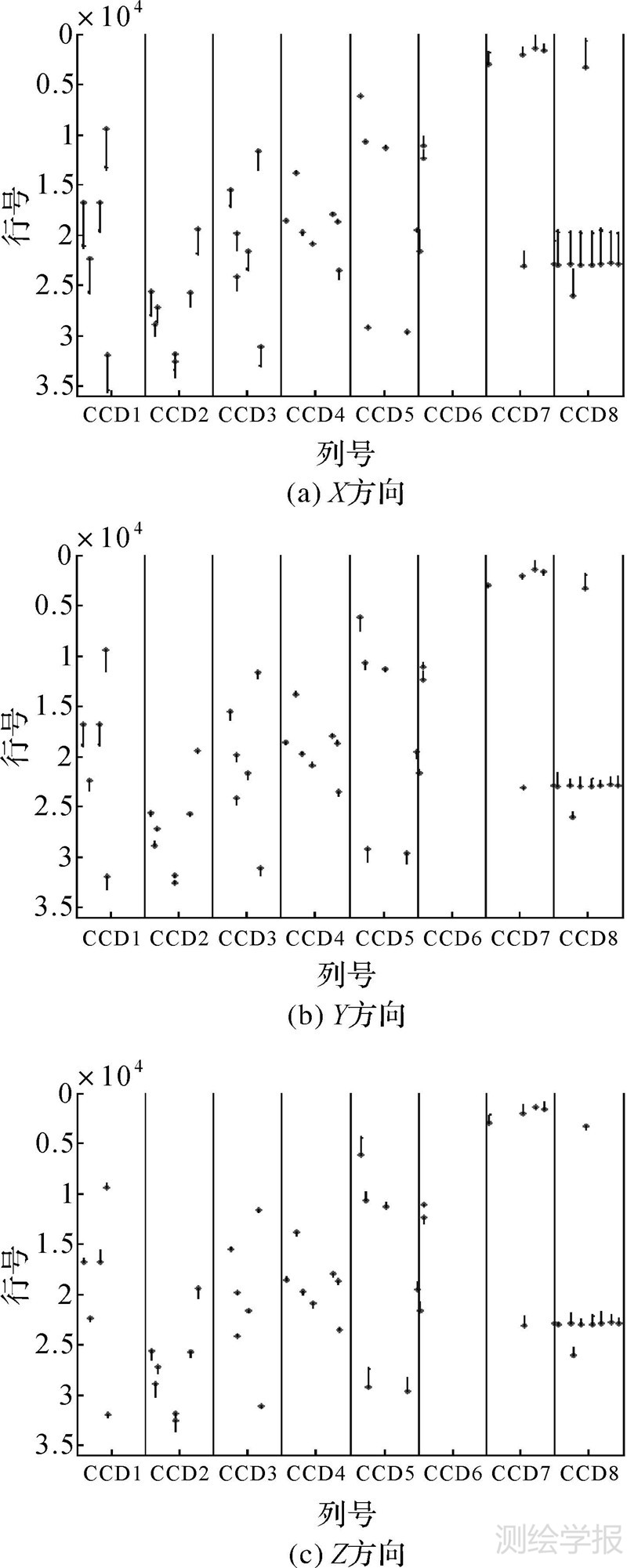
内参数仍采用相机设计值,各景图像利用“四角布设”的4个野外实测控制点按3.1节描述方法进行外部误差补偿定位试验。表 4为8片CCD整体定位精度统计结果。为分析经外部误差补偿后8片CCD各自范围内检查点的残差情况,将野外实测检查点的定位残差(以米为单位,后同)按各分片CCD范围进行展示(以135-1景为例),如图 8所示。
| 影像编号 | 控制点个数 | 检查点个数 | 最大残差/m | 中误差/m | ||||
| X | Y | Z | X | Y | Z | |||
| 134-1 | 4 | 9 | 14.928 | 8.169 | 2.412 | 8.613 | 3.831 | 1.426 |
| 134-2 | 4 | 9 | 17.744 | 8.504 | 3.552 | 10.256 | 4.053 | 2.043 |
| 135-1 | 4 | 49 | 14.989 | 7.119 | 6.171 | 7.197 | 2.934 | 2.618 |
| 135-2 | 4 | 47 | 14.275 | 9.259 | 8.717 | 7.280 | 3.717 | 3.068 |
|
| 图 8 外部误差补偿后各分片CCD残差分布 Fig. 8 Residuals after exterior error compensation |
表 4表明与直接定位相比,外部误差补偿定位可显著提升影像定位精度;但同时图 8表明,经外部误差补偿,CCD1-CCD8各分片影像仍含有不同的残余系统误差。
产生上述结果的原因为外部误差补偿只能消除多片CCD共享的外定向参数中的系统误差及可能存在的多片CCD共享的内部误差,而各片CCD各不相同的内部误差并不能得到补偿。
4.5 内部误差补偿定位试验以嵩山试验区高精度DOM和DEM为参考数据,通过卫星影像与DOM子像素级匹配获得密集控制点[27],根据3.2节的模型,进行内部误差补偿定位试验。为抑制高频误差对内部误差补偿参数求解的影响,匹配在应在短条带区域内进行;本文在长度为500行的短条带内进行控制点匹配量测。该匹配过程对参考影像的时效性和地面覆盖范围有较高要求:参考影像和待补偿卫星影像之间的地物变化不能过大,否则将影响匹配点数和精度;参考影像的地面覆盖范围要足够大,以保证覆盖卫星影像的成像范围。经匹配,嵩山试验区135-1影像获得均匀分布控制点10 686个,135-2影像获得均匀分布控制点10 402个。根据3.2节模型,分别解算出135-1和135-2两组内部误差补偿参数。
利用更新后的相机内部参数和原始姿轨数据,进行定位试验,试验结果见表 5;将所有检查点的定位残差按各分片CCD范围进行展示(以135-1景为例),如图 9所示。
| 影像编号 | 控制点个数 | 检查点个数 | 最大残差/m | 中误差/m | ||||
| X | Y | Z | X | Y | Z | |||
| 135-1 | 0 | 53 | 27.945 | 7.221 | 24.354 | 25.521 | 4.159 | 19.843 |
| 135-2 | 0 | 51 | 41.818 | 24.901 | 55.057 | 36.991 | 20.572 | 48.561 |

|
| 图 9 内部误差补偿后各分片CCD残差分布 Fig. 9 Residuals after interior error compensation |
表 5表明与直接定位相比,经内部误差补偿影像定位精度并未显著提升,但同时图 9表明,经内部误差补偿,CCD1-CCD8各分片影像的不同残余误差得以剔除,片间定位精度一致性得到明显改善。
产生上述结果的原因为内部误差补偿使得各片CCD各不相同的内部误差得以补偿,从而保证了各分片CCD影像片间定位精度的一致性,但由于作为定位误差主要因素的外部误差未能得到补偿,导致定位精度并未显著提升。
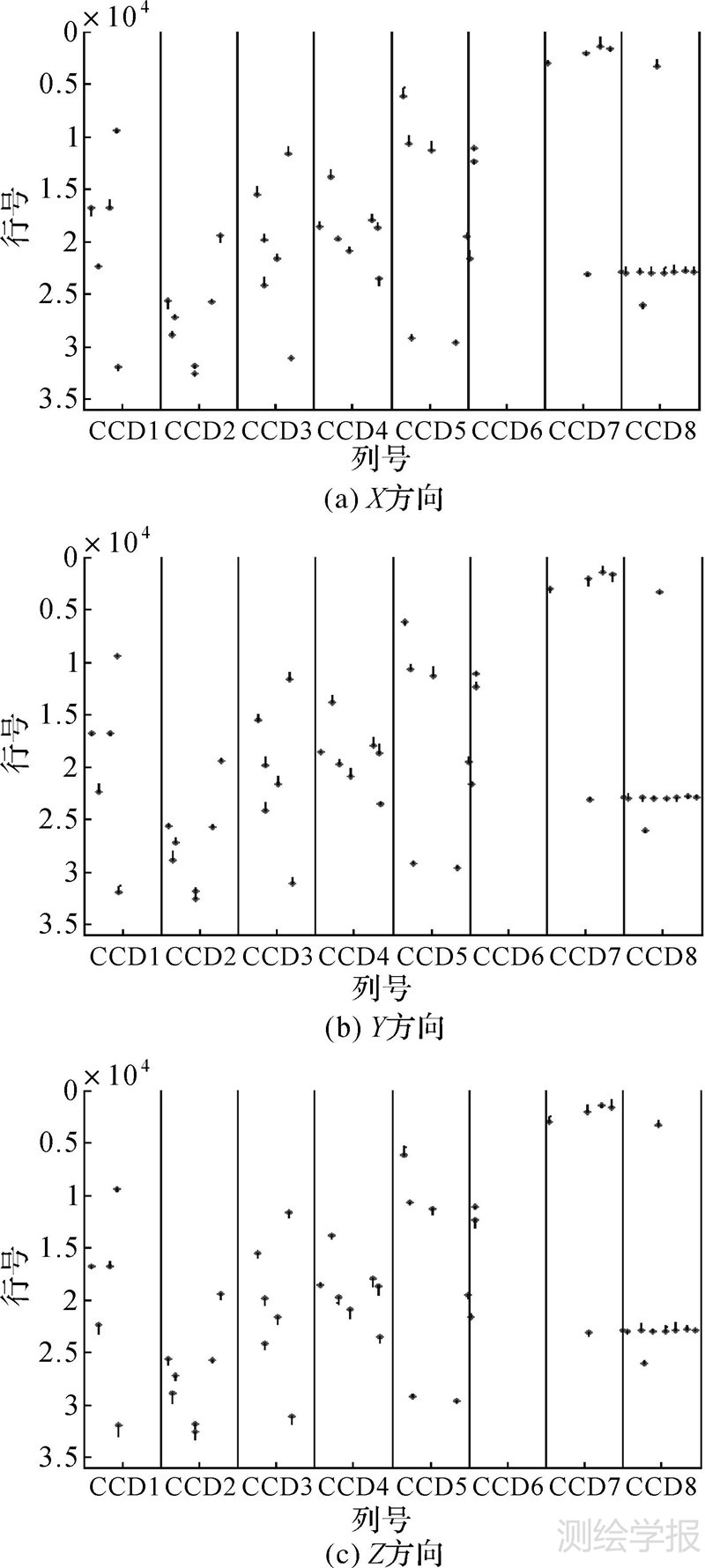
4.6 内部、外部误差补偿定位试验基于更新后的相机内部参数,各景影像采用与4.4节完全相同的四角布设的4个野外实测控制点对外部误差再次补偿后进行定位试验,试验结果如表 6所示。经过内部、外部误差补偿后,8片CCD各自范围内的野外实测检查点残差分布图如图 10所示(以135-1景影像为例)。
| 影像编号 | 控制点个数 | 检查点个数 | 最大残差/m | 中误差/m | ||||
| X | Y | Z | X | Y | Z | |||
| 135-1 | 4 | 49 | 3.066 | 3.069 | 3.445 | 1.737 | 1.630 | 1.926 |
| 135-2 | 4 | 47 | 4.074 | 3.578 | 3.680 | 1.999 | 1.820 | 2.065 |
将表 6与表 4进行对比可发现,与仅进行外部误差补偿相比,内部、外部误差均补偿后影像定位精度进一步提升,野外检查点在X、Y、Z方向的残差中误差均小于等于2 m。
图 10与图 8、图 9对比表明,经过内部、外部误差补偿后,CCD1-CCD8各分片影像不同的残余误差被有效剔除,片间定位精度具备了一致性,且影像定位精度显著提升。
|
| 图 10 内、外部误差补偿后各分片CCD残差分布 Fig. 10 Residuals after exterior and interior error compensation |
将135-1和135-2求解出的两组相机内部畸变参数应用于一定时间段内的其他多景影像进行定位试验验证,结果如表 7所示。
| 应用方法 | 控制点个数 | 检查点个数 | 最大残差/m | 中误差/m | ||||
| X | Y | Z | X | Y | Z | |||
| 135-1→134-1 | 4 | 9 | 3.239 | 2.632 | 3.485 | 1.606 | 1.470 | 1.811 |
| 135-1→134-2 | 4 | 9 | 3.391 | 1.942 | 3.023 | 2.106 | 1.263 | 1.877 |
| 135-1→135-2 | 4 | 47 | 3.368 | 2.949 | 3.478 | 1.933 | 1.631 | 1.989 |
| 135-2→134-1 | 4 | 9 | 3.219 | 2.962 | 3.433 | 1.510 | 1.555 | 1.888 |
| 135-2→134-2 | 4 | 9 | 3.125 | 2.232 | 2.897 | 2.087 | 1.240 | 1.764 |
| 135-2→135-1 | 4 | 49 | 3.179 | 3.505 | 3.531 | 1.808 | 1.907 | 2.114 |
表 7表明:①将135-1景影像计算出的内部误差补偿参数应用于当天的134-1景、相隔22 d的134-2景和135-2景影像时,取得了与135-1本景验证时相当的定位精度,野外实测检查点在X、Y、Z方向的残差中误差均小于等于2 m;②将135-2景影像计算出的内部误差补偿参数应用于当天的134-2景、相隔22 d的134-1景和135-1景影像时,取得了与135-2本景验证时相当的定位精度,野外实测检查点在X、Y、Z方向的残差中误差均小于等于2 m。
上述结果还表明在本文试验影像所覆盖的22 d内,TH-1高分相机内部几何状态稳定,且该结果进一步验证了本文计算出的内部畸变参数的有效性。
5 结论通过对TDI CCD交错拼接推扫相机的严格几何模型构建及优化方法的研究,可得出以下结论:
(1) 本文构建的整体几何模型可严格描述TDI CCD交错拼接推扫相机的原始成像几何,基于整体几何模型设计的内外误差补偿模型和先外后、内分步求解的解算方法正确有效。
(2) 基于少量控制点和本文外部误差补偿方案可有效剔除相机安置、姿轨测量等外部误差,显著提升影像定位精度。
(3) 基于DOM匹配量测得到的密集控制点和本文内部误差补偿方案可有效剔除光学系统畸变、CCD阵列畸变等内部误差,可显著改善分片CCD影像定位精度的一致性。
(4) 本文计算出的内部畸变参数应用于间隔22 d的其他多景影像时,也达到了与本景验证时同样的定位精度,表明本文采用的几何模型优化方法可计算出稳定有效的内部畸变参数,同时本文试验结果一定程度上也验证了TH-1高分相机内部几何状态的稳定性。
| [1] | LI Zhaohui, WANG Zhaoxun, WU Keyong. Optical Assembly of CCD Focal Plane for Space Camera[J]. Optics and Precision Engineering, 2000, 8(3): 213-216. (李朝辉, 王肇勋, 武克用. 空间相机CCD焦平面的光学拼接[J]. 光学精密工程, 2000, 8(3): 213-216.) |
| [2] | ZHANG Xingxiang,REN Jianyue.Mechanical Interleaving Assembly of TDICCD Focal Plane[J]. Acta Optica Sinica, 2006, 26(5): 740-745. (张星祥, 任建岳. TDICCD焦平面的机械交错拼接[J]. 光学学报, 2006, 26(5): 740-745.) |
| [3] | JACOBSEN K. Calibration of Optical Satellite Sensors[EB/OL]. [2014-02-28].http://www.isprs.org/proceedings/papers/CalSatJac_Jacobsen.pdf. |
| [4] | HU Fen. Research on Inner FOV Stitching Theories and Algorithms for Sub-images of Three Non-collinear TDI CCD Chips[D]. Wuhan: Wuhan University, 2010: 34-36. (胡芬. 三片非共线TDI CCD成像数据内视场拼接理论与算法研究[D]. 武汉: 武汉大学, 2010: 34-36.) |
| [5] | ASTRIUM. SPOT6 & SPOT7 Imagery User Guide[EB/OL]. [2014-04-01]. http://www.astrium-geo.com/en/. |
| [6] | IRONSA J R, DWYER J L, BARSI J A. The Next LandSat Satellite: The LandSat Data Continuity Mission[J]. Remote Sensing of Environment, 2012, 122: 11-21. |
| [7] | ZHANG Guo, JIANG Yonghua, LI Deren, et al. In-orbit Geometric Calibration and Validation of ZY-3 Linear Array Sensors[J]. The Photogrammetric Record, 2014, 29(145): 68-88. |
| [8] | MCEWEN A S, ELIASON E M, BERGSTROM J W, et al. Mars Reconnaissance Orbiter's High Resolution Imaging Science Experiment (HiRISE)[J]. Journal of Geophysical Research, 2007, 112(E5): 1-40. |
| [9] | UPDIKE T. Radiometric Use of WorldView-2 Imagery, Technical Note (2010), DigitalGlobe, 1601 Dry Creek Drive Suite 260 Longmont, Colorado, USA, 80503[EB/OL]. [2014-02-28].http://www.digitalglobe.com/resources/technical-information/. |
| [10] | DE LUSSY F, KUBIK P, GRESLOU D, et al. Pleiades-HR Image System Products and Quality Pleiades-HR Image System Products and Geometric Accuracy[C]//Proceedings of the ISPRS International Conference. [s.l.]: ISPRS, 2005: 100-103. |
| [11] | ASTRIUM. Pléiades Imagery User Guide[EB/OL]. http://www.satimagingcorp.com//User_Guide_Pleiades.pdf. |
| [12] | DE LUSSY F, GRESLOU D, DECHOZ C, et al. Pleiades HR in Flight Geometrical Calibration: Location and Mapping of the Focal Plane[C]//The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2012 XXII ISPRS Congress. Melbourne:[s.n.], 2012, XXXIX-B1: 519-523. |
| [13] | WANG Tao, ZHANG Yan, ZHANG Yongsheng, et al. Construction and Validation of Rigorous Imaging Model for High-resolution Remote Sensing Satellites[J]. Journal of Remote Sensing, 2013, 17(5): 1087-1102. (王涛, 张艳, 张永生, 等. 高分辨率遥感卫星传感器严格成像模型的建立及验证[J]. 遥感学报, 2013, 17(5): 1087-1102.) |
| [14] | WESER T, ROTTENSTEINER F, WILLNEFF J, et al. A Generic Pushbroom Sensor Model for High-resolution Satellite Imagery Applied to SPOT5, QuickBird and ALOS Data Sets[C]//The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Science, Vol. XXXVI, Part B1. Beijing: [s.n.], 2008:723-729. |
| [15] | WESER T, ROTTENSTEINER F, WILLNEFF J, et al. Development and Testing of a Generic Sensor Model for Pushbroom Satellite Imagery[J]. The Photogrammetric Record, 2008, 23(123): 255-274. |
| [16] | PAN Jun, HU Fen, WANG Mi, et al. An Inner FOV Stitching Method for Non-collinear TDI CCD Images[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43 (11): 1165-1173. (潘俊, 胡芬, 王密, 等. 一种非共线TDI CCD成像数据内视场拼接方法[J]. 测绘学报, 2014, 43(11): 1165-1173.) |
| [17] | TANG Xinming, ZHANG Guo, ZHU Xiaoyong, et al. Triple Linear-array Imaging Geometry Model of ZiYuan-3 Surveying Satellite and Its Validation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 191-198. (唐新明, 张过, 祝小勇, 等. 资源三号测绘卫星三线阵成像几何模型构建与精度初步验证[J]. 测绘学报, 2012, 41(2): 191-198.) |
| [18] | PAN Hongbo, ZHANG Guo, TANG Xinming, et al. The Geometrical Model of Sensor Corrected Products for ZY-3 Satellite[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 516-522. (潘红播, 张过, 唐新明, 等. 资源三号测绘卫星传感器校正产品几何模型[J]. 测绘学报, 2013, 42(4): 516-522.) |
| [19] | POLI D, TOUTIN T. Review of Developments in Geometric Modelling for High Resolution Satellite Pushbroom Sensors[J]. The Photogrammetric Record, 2012, 27(137): 58-73. |
| [20] | WESER T, ROTTENSTEINER F, WILLNEFF J, et al. An Improved Pushbroom Scanner Model for Precise Georeferencing of ALOS PRISM Imagery[C]//The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. Beijing: [s.n.], 2008, XXXVII(B1): 739-744. |
| [21] | WANG Mi, YANG Bo, HU Fen, et al. On-orbit Geometric Calibration Model and Its Applications for High-resolution Optical Satellite Imagery[J]. Remote Sensing, 2014, 6(5): 4391-4408. |
| [22] | YUAN Xiuxiao, WANG Taoyang. Block Adjustment for CBERS-02B Satellite Images[J]. Journal of Remote Sensing, 2012, 16(2): 310-324. (袁修孝, 汪韬阳. CBERS-02B卫星遥感影像的区域网平差[J]. 遥感学报, 2012, 16(2): 310-324.) |
| [23] | YUAN Xiuxiao, YU Junpeng. Calibration of Constant Angular Error for High Resolution Remotely Sensed Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(1): 36-41. (袁修孝, 余俊鹏. 高分辨率卫星遥感影像的姿态角常差检校[J]. 测绘学报, 2008, 37(1): 36-41.) |
| [24] | YUAN Xiuxiao, YU Xiang. Calibration of Angular Systematic Errors for High Resolution Satellite Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 385-392. (袁修孝, 余翔. 高分辨率卫星遥感影像姿态角系统误差检校[J]. 测绘学报, 2012, 41(3): 385-392.) |
| [25] | FAN Dazhao, LIU Chubin, WANG Tao, et al. Building & Validation of Rigorous Geometric Model of ALOS PRISM Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(5): 569-574, 581. (范大昭, 刘楚斌, 王涛, 等. ALOS卫星PRISM影像严格几何模型的构建与验证[J]. 测绘学报, 2011, 40(5): 569-574, 581.) |
| [26] | YANG Bo, WANG Mi. On-orbit Geometric Calibration Method of ZY-1 02C Panchromatic Camera[J]. Journal of Remote Sensing, 2013, 17(5): 1175-1190. (杨博, 王密. 资源一号02C卫星全色相机在轨几何定标方法[J]. 遥感学报, 2013, 17(5): 1175-1190.) |
| [27] | JIANG Yonghua, ZHANG Guo, TANG Xinming, et al. High Accuracy Geometric Calibration of ZY-3 Three-line Image[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 523-529. (蒋永华, 张过, 唐新明, 等. 资源三号测绘卫星三线阵影像高精度几何检校[J]. 测绘学报, 2013, 42(4): 523-529.) |
| [28] | GONG Hui. A Study on Positioning Theory of Line-array CCD Imagery Based on Quaterni-on[D]. Zhengzhou: Information Engineering University, 2008: 6-9. (龚辉. 基于四元数的线阵CCD影像定位技术研究[D]. 郑州: 信息工程大学, 2008: 6-9.) |
| [29] | GUO Haitao, ZHANG Baoming, GUI Qingming. Application of Generalized Ridge Estimate to Computing the Exterior Orientation Elements of Satellite Linear Array Scanner Imagery[J]. Geomatics and Information Science of Wuhan University, 2003, 28(4): 444-447. (郭海涛, 张保明, 归庆明. 广义岭估计在解算单线阵CCD卫星影像外方位元素中的应用[J]. 武汉大学学报: 信息科学版, 2003, 28(4): 444-447.) |