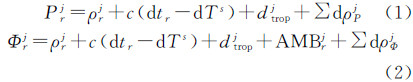2.德国地学研究中心, 波茨坦 14473
2. German Research Centre for Geosciences(GFZ), Potsdam 14473, Germany
1 引言
GPS精密单点定位技术(precise point positioning,PPP)由于无须自己架设地面基准站,不受作业距离的限制,机动灵活,单机作业,使用成本低,可直接获得与国际地球参考框架(ITRF)一致的高精度测站坐标的优势,被广泛应用于低轨卫星的精密定轨、GPS气象、海陆空不同载体的高精度动态和静态定位、精密授时、GPS地震学、地球板块运动与动力学研究等诸多地学研究及工程应用领域[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]。但是,单GPS系统精密单点定位技术仍然存在诸多不足,使得在某些领域的应用受到了限制,如较长的收敛时间导致其无法在实时快速定位领域得到应用。单GPS系统在一定区域内可见卫星数的有限,使其在城市、山区等遮挡严重的复杂环境中无法获得高精度定位结果。目前,随着各国各地区卫星导航系统的蓬勃发展,过去单一的GPS系统时代正逐步转变为多系统并存且兼容的全球性卫星导航系统(global navigation satellite systems,GNSS)时代[11],其4大卫星导航定位系统(美国的GPS系统、俄罗斯的GLONASS系统、中国的北斗系统和欧盟的Gailieo系统)的在轨卫星数已达74颗。更多的可见卫星数,使得山区、城市等可见卫星数较少的区域定位服务能力大大提高;新的信号结构将提高抗干扰能力和降低多路径的影响;多频卫星信号,也将为模糊度固定和电离层高阶项误差的消除提供新途径。因此,多系统融合的GNSS精密单点定位已成为当前GNSS精密定位技术发展的重要趋势。目前,已有学者研究表明:多系统组合PPP可以有效提高定位精度和收敛速度,但是这些研究主要以GPS-GLONASS组合、GPS-BeiDou组合、GPS-Gailieo等双系统组合为主[10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21],对4系统融合的PPP定位研究较少。4大卫星导航定位系统的相继建成与完善以及IGS也提供相应的精密星历、精密钟差等产品,为4系统融合PPP的提供了条件。基于此,本文重点对4系统融合的PPP进行研究,分析了在不同高度角下4系统融合PPP静态解、动态解结果,分析了其定位精度、收敛时间以及定位稳定性,并与单系统和双系统组合的PPP结果进行了比较。
2 Multi-GNSS PPP定位模型及处理策略 2.1 基本观测方程对于一个双频GNSS接收机,在传统的精密单点定位算法中,一般采用无电离层组合的观测值来消除电离层延迟一阶项的影响,其观测方程如下
式中,j代表卫星号;r代表测站;ρrj为测站r到卫星j之间的几何距离;Prj为消电离层的组合伪距观测值;Φr,ij为消电离层的组合载波相位观测值(距离);AMBrj为整周模糊度(距离),在无电离层组合观测方程中,该值不具有整数特性;c为真空中的光速;dTs为卫星钟差;dtr为接收机钟差;dtropj为对流层延迟误差;∑dρPj、∑dρΦj分别为伪距和载波相位观测值的其他各项误差之和。在传统单GNSS定位模型的基础上,综合考虑系统间时间偏差和频间偏差的影响,可以得到如下多系统PPP的观测方程
式中,G、R、E、C分别代表GPS、GLONASS、Galileo和BeiDou卫星;ISBEr、ISBCr分别是GALILEO、BeiDou相对于GPS的系统间偏差;Rk中的k代表GLONASS卫星的频率号;ISBrj,Rk是GLONASS卫星相对于GPS的系统间偏差。值得注意的是,GLONASS的系统间偏差ISBrj,Rk是与测站i和卫星j相关的,而北斗和伽利略的ISBrE、ISBrC是与卫星无关的,这是因为GLONASS采用频分多址(frequency division multiple access,FDMA)的信号结构,导致每颗卫星存在的频率偏差延迟均不一致;其余符号与式(1)和式(2)中类似。 2.2 数据处理策略本文观测模型采用无电离层组合的多系统PPP模型,参数估计方法使用扩展卡尔曼滤波EKF,待估计的参数包括接收机位置、天顶对流层延迟、接收机钟差、系统偏差等,其中,接收机的位置参数(x,y,z)分别进行静态和动态处理;模糊度、静态坐标、系统偏差参数作为常量进行估计;接收机钟差、动态坐标当作白噪声进行处理;对流层延迟湿分量采用随机游走过程模拟。滤波过程中,依据动态模型将前一历元状态向量预测到当前历元。在测量更新过程中利用观测信息求解状态向量及其方差协方差。所需要的精密轨道、精密钟差等精密产品均由IGS各分析中心提供。卫星端和接收机端天线相位中心偏移(PCO)和天线相位中心变化(PCV)使用IGS提供的ANTEX文件改正。但由于目前IGS只提供了粗略的BDS卫星端PCO改正,尚无机构或组织提供BDS卫星端PCV以及接收机端的PCO与PCV信息,因此无法进行精确的PCO及PCV改正。其他详细的数据处理策略如表 1所示。
| 类别 | 参数 | 模型 |
| 观测值 | 观测量 | GPS+GLONASS+Galileo+BeiDou(74颗卫星)相位观测值和伪距观测值 |
| 信号 | GPS:L1/L2;GLONASS:L1/L2;Galileo:E1/E5a;BeiDou:B1/B2; | |
| 采样率 | 30 s | |
| 先验约束 | P1:1.0 m;L1:0.01周 | |
| 截止角 | 7° | |
| 观测值加权 | p=1,e >30°;p =2sin e,e ≤30°;ppseudo:pphase=1∶10 000 | |
| 误差改正 | 相位缠绕 | 模型改正 |
| 相位中心偏差 | IGS_08模型(考虑PCO、PCV改正) | |
| 相对论效应 | 模型改正 | |
| 卫星轨道 | MGEX精密轨道(采样间隔5 min) | |
| 卫星钟差 | MGEX精密钟差(采样间隔30 s) | |
| 电离层延迟 | 无电离层组合消除一阶项延迟 | |
| 对流层延迟干分量 | 模型改正 | |
| 参数估计 | 接收机坐标 | 估计(静态和动态) |
| 接收机钟差 | 估计,白噪声(每个历元估计一次) | |
| 对流层延迟湿分量 | 随机游走 | |
| ISB | 估计,GPS作为参考 | |
| 模糊度 | 估计 |
试验数据选取了全球多系统定位服务实验网(the multi-GNSS experiment,MGEX)及中国北斗实验观测网(BeiDou experimental tracking network,BETN)部分测站2014年6月1日至2014年6月30日总计30 d的观测数据,数据采样率30 s。本文分别对单系统(单GPS、单GLONASS、单BeiDou、单Galileo,简写为G、R、C、E)、多系统组合(GPS+GLONASS、GPS+BeiDou、GPS+Galileo、GPS+GLONASS+BeiDou+Galileo,简写为GR、GC、GE、GREC)共8种模式,评估其不同模式下的PPP定位性能(静态精度、动态精度、收敛性性、不同高度角下定位性能)。
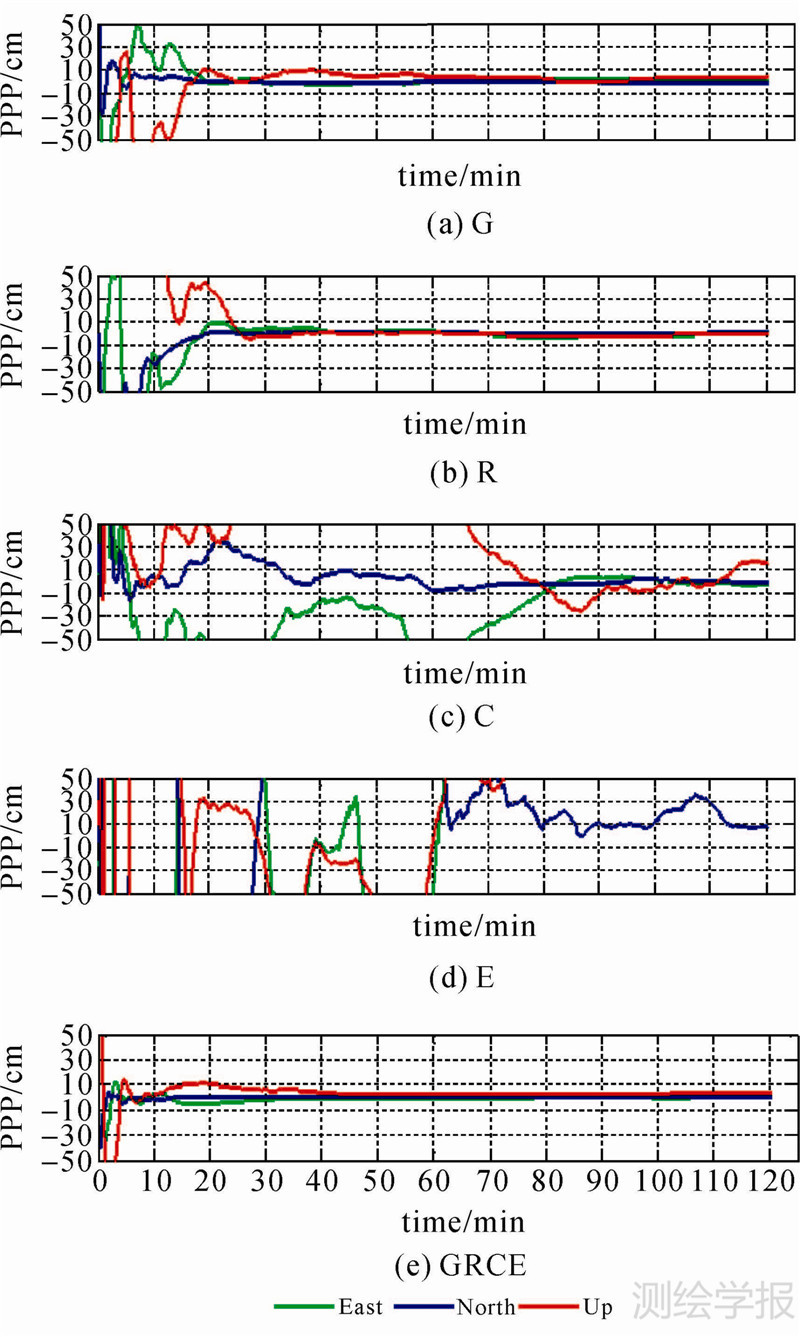
3.2 静态PPP试验图 1为以GMSD测站为例的静态PPP解算结果,其子图(a)、(b)、(c)、(d)、(e)分别为G、R、C、E、GREC的定位结果。为了便于比较不同系统及组合的定位收敛速度,图中仅显示了2014年6月1日前2 h的结果,其中绿色、蓝色、红色的线分别代表东方向(East)、北方向(North)、天顶方向(UP)。图 2给出了静态PPP时段解(时段分为10 min、15 min、30 min、1 h、2 h、4 h、6 h、12 h)的精度,特别注意的是BeiDou和GLONASS在10 min的时候其RMS已超过30 cm,图上为了显示清楚,图 2将10 min时RMS值超过30 cm的结果取值为30 cm。图中圆圈、上三角、正方形、星号、五角星、下三角分别代表GPS、GLONASS、BeiDou、GR、GC、GREC的时段解RMS值,从左到右的3幅子图分别为E、N、U 3个方向。
|
| 图 1 2014年6月1日GMSD测站(30.55°N,131.01°E)不同系统及组合的PPP静态解结果 Fig. 1 Static PPP solutions of single-system, dual-system and four-system modes at station GMSD (30.55°N,131.01°E),on June 1,2014. |
|
| 图 2 不同时段长度解的静态PPP定位精度及收敛速度(10 min、15 min、30 min、1 h、2 h、4 h、6 h、12 h) Fig. 2 RMS values of static PPP solutions with different session lengths (10 min、15 min、30 min、1 h、2 h、4 h、6 h and 12 h) in single-,dual-and four-system modes. |
由图 1可以看出,在测站GMSD的单系统定位中,由于GPS和GLONASS卫星系统在轨卫星数较多,定位精度和收敛速度要优于BeiDou和Galileo,其结果在20~30 min左右可收敛在10 cm以内;由于BeiDou和Galileo卫星数较少,其定位结果较差,特别是Galileo在大多数情况下无法完成连续PPP定位,2 h内只有N方向定位精度收敛到30 cm以内,而其他方向则远大于50 cm。而BeiDou系统的定位结果在80 min以后,其结果才能达到10 cm左右。由图 1(e)可以看出,多系统融合后,能有效加快PPP的收敛速度,其GREC收敛时间仅需要10 min左右,而且其定位结果的稳定性也有一定幅度的提高,但高程方向相对于平面方向无论是单系统还是多系统仍然存在较大的偏差。
由图 2的结果可以看出,组合后的PPP定位结果在很短的时间便能达到较高的定位精度,如GREC的10 min时段解RMS值E、N、U方向便达到了11.35、4.82、12.36 cm,30 min左右各方向RMS值就可以收敛到5 cm,而单GNSS的结果要想达到同样的精度需要1 h左右。图中由于Galileo卫星数较少,较多情况下没有足够的可见卫星,所以并未给出其结果。在双系统组合中(GR、GC),对单系统定位结果也有较为明显的提高,和4系统组合一样,其收敛时间显著缩短,约1 h左右其RMS值可以收敛到2~3 cm。
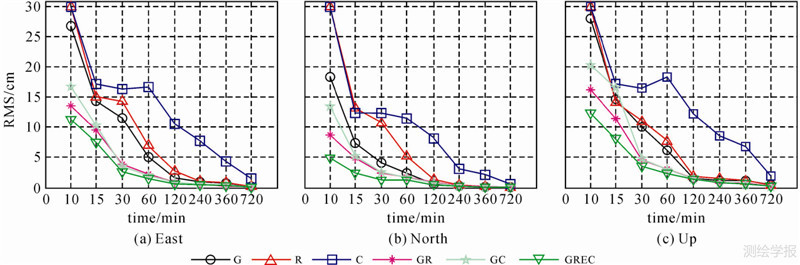
3.3 动态PPP试验同样采用3.1节介绍的数据处理策略和试验数据进行处理,对各测站进行动态PPP定位并对其结果的RMS值进行统计。图 3给出了部分测站(CHDU、SIGP、ABMF、BRST、CUT0、LMMF、NNOR、GMSD)动态PPP定位结果的统计RMS值。图 3(a)、(b)中(CHDU、SIGP)为仅有BeiDou和GPS数据的双系统测站,所以图中给出了单GPS、单BeiDou、GPS和BeiDou组合(GC)3种模式N、E、U方向的RMS结果,其中蓝色、绿色、红色分别为G、C、GC。后6幅子图为其他多系统测站不同系统组合动态PPP的统计RMS值。由图 3可以看出,组合后的结果要优于单GNSS的结果,特别是四系统的组合能显著提高定位精度,但是由于单GNSS本身能够达到较高的定位精度(高度角为7°时),所以其多系统组合对水平方向的改善比较有限,但是对于高程方向却有非常显著的改善。
|
| 图 3 部分测站PPP动态解定位误差的RMS值统计结果 Fig. 3 Daily RMS values of single-system, dual-system and four-system kinematic PPP solutions |
图 4给出了以GMSD测站为例,在不同卫星高度角下(左图为10°、右图为40°)单GPS与GREC组合的定位结果(其中,红色为GPS、绿色为GREC),其中图 4(a)、(b)、(c)分别为E、N、U方向单GPS与GREC组合的定位结果;图 4(d)为不同时刻单GPS与GREC的可见卫星数。从图 4中可以看出,高度角对单系统影响较大,而对多系统组合影响较小。当高度角为40°时,多系统融合仍然可以得到高精度的定位结果,而且其定位结果的稳定性也要优于单系统。随着高度角的增加,单系统的可见卫星数迅速减少,而多系统组合时从高度角10°到40°时可见卫星数一直保持在10颗以上,这也是多系统融合定位结果的稳定性和精度要优于单系统的原因。值得注意的是,当截止高度角被选取的较高时,天顶方向的位置分量和ZTD的可分离性将越来越差,导致多系统对高程方向的贡献比较有限,但是当单系统卫星数不足时,多系统仍然能够体现出它的优势。
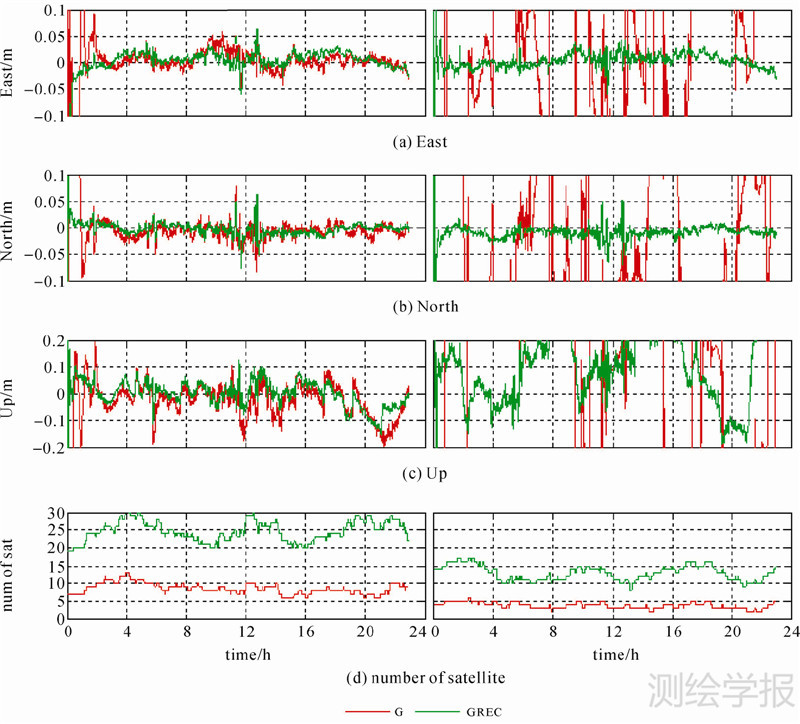
|
| 图 4 测站GMSD单系统与多系统组合在不同高度角下的PPP定位精度及其可见卫星数 Fig. 4 Comparisons of PPP results in single- and multi-system modes under different cut-off elevation angles (10° and 40°) at station GMSD and the corresponding satellite numbers and PDOP values |
本文基于MGEX网的大量实测数据,主要从定位精度和收敛速度两个方面,研究分析了单系统、双系统和4系统融合PPP动态/静态定位性能,以及在不同高度角下单系统和不同系统组合的PPP定位精度和收敛性。得到以下结论:
(1) 在单系统观测几何构型不理想的地方,多系统融合的PPP动态与静态定位结果的精度要明显优于单系统,而且其解的稳定度也有较好的提高。在收敛速度方面,多系统融合的静态PPP时段解收敛速度相对于单系统也提高较为明显,如以GMSD测站为例,同样获得10 cm左右的定位精度,单GPS需要1 h左右而多系统融合则只需要30 min左右即可。
(2) 在不同高度角情况下,单系统定位性能会随截止高度角的增加而迅速变差,特别是截止高度角大于30°时,其定位结果可靠性较低。而多系统融合后,截止高度角为40°时,其动态定位水平精度仍然可以达到厘米级,且其解较为稳定。这对于GNSS在山区、城区以及遮挡较为严重的区域有非常重要的应用价值。
(3) 多系统融合由于其可见卫星数的增加,信号质量的提高,不仅能够有效提高定位导航的能力(精度更高、稳定性更高、城市和山区等特殊地区的连续定位),而且可为大气探测、地壳形变监测等提供更有效的技术手段,如提高形变监测的能力,提高电离层、对流层提取的精度,以及解决单系统目前进行大气探测时空间分辨率低的问题等。
致谢:感谢IGS提供多系统精密轨道和钟差产品以及IGSMGEX提供多系统观测数据。
| [1] | GAO Yang, SHEN Xiaobing.Improving Ambiguity Convergence in Carrier Phase-based Precise Point Positioning[C]//Proceedings of the 14th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS2001). Salt Lake City:Salt Palace Convention Center, 2001:1532-1539. |
| [2] | CHEN Wu, HU Congwei, LI Zhihua, et al. Kinematic GPS Precise Point Positioning for Sea Level Monitoring with GPS Buoy[J]. Journal of Global Positioning Systems, 2004, 3(1-2): 302-307. |
| [3] | ZHANG Xiaohong, ANDERSEN O B. Surface Ice Flow Velocity and Tide Retrieval of the Amery Ice Shelf Using Precise Point Positioning[J]. Journal of Geodesy, 2006, 80(4): 171-176. |
| [4] | BISNATH S, GAO Yang. Current State of Precise Point Positioning and Future Prospects and Limitations[M]//SIDERIS M G.Observing Our Changing Earth. Berlin: Springer, 2007, 133: 615-623. |
| [5] | ZHANG Xiaohong, LIU Jingnan, FORSBERG R. Application of Precise Point Positioning in Airborne Survey[J]. Geomatics and Information Science of Wuhan University, 2006, 31(1): 19-22, 46. (张小红, 刘经南, FORSBERG R. 基于精密单点定位技术的航空测量应用实践[J]. 武汉大学学报: 信息科学版, 2006, 31(1): 19-22, 46.) |
| [6] | YUAN Xiuxiao, FU Jianhong, LOU Yidong. GPS-supported Aerotriangulation Based on GPS Precise Point Positioning[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(3): 251-255. (袁修孝, 付建红, 楼益栋. 基于精密单点定位技术的GPS辅助空中三角测量[J]. 测绘学报, 2007, 36(3): 251-255.) |
| [7] | ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Precise Point Positioning Algorithm Based on Original Dual-frequency GPS Code and Carrier-phase Observations and Its Application[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 478-483. (张宝成, 欧吉坤, 袁运斌, 等. 基于GPS双频原始观测值的精密单点定位算法及应用[J]. 测绘学报, 2010, 39(5): 478-483.) |
| [8] | ZHANG Xiaohong, HE Xiyang, LI Xingxing. Analysis of Undifferenced Kinematic POD for LEOs Using Trip[J]. Geomatics and Information Science of Wuhan University, 2010, 35(11): 1327-1330. (张小红, 何锡扬, 李星星. Trip软件非差几何法精密定轨精度分析[J]. 武汉大学学报: 信息科学版, 2010, 35(11): 1327-1330.) |
| [9] | ZHANG Baocheng, OU Jikun, YUAN Yunbin, et al. Calibration of Slant Total Electron Content and Satellite-receiver's Differential Code Biases with Uncombined Precise Point Positioning Technique[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(4): 447-453. (张宝成, 欧吉坤, 袁运斌, 等. 利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J]. 测绘学报, 2011, 40(4): 447-453.) |
| [10] | SHI Chuang, ZHAO Qile, LI Min, et al. Precise Orbit Determination of BeiDou Satellites with Precise Positioning[J]. Science China Earth Sciences, 2012, 55(7): 1079-1086. (施闯, 赵齐乐, 李敏, 等. 北斗卫星导航系统的精密定轨与定位研究[J]. 中国科学: 地球科学, 2012, 42(6): 854-861.) |
| [11] | MONTENBRUCK O, STEIGENBERGER P, KHACHIKYAN R,et al. IGS-MGEX: Preparing the Ground for Multi-constellation GNSS Science[J]. Inside GNSS, 2014, 9:42-49. |
| [12] | PÍRIZ R, CALLE D, MOZO P,et al.Orbits and Clocks for GLONASS Precise-point-positioning[C]//Proceedings of the 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2009). Savannah:Savannah International Convention Center, 2009: 2415-2424. |
| [13] | MELGARD T, VIGEN E, DE JONG K, et al.G2: the First Real-time GPS and GLONASS Precise Orbit and Clock Service[C]//Proceedings of the 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2009). Savannah: Savannah International Convention Center, 2009: 1885-1891. |
| [14] | MELGARD T, VIGENE, ØRPEN O, et al. Pulling in All Signals PPP with GPS and GLONASS: The New G2[J]. GPS World, 2010, 21(3): 28. |
| [15] | DACH R, LUTZS,MEINDLM, et al. Combining the Observations from Different GNSS[C]//EUREF 2010 Symposium. Gävle:Bundesamtfür Kartographie und Geodäsie,2010. |
| [16] | ZHANG Xiaohong, GUO Fei, LI Xingxing, et al. Study onPrecise Point Positioning Based on Combined GPS and GLONASS[J]. Geomatics and Information Science of Wuhan University,2010, 35(1): 9-12. (张小红, 郭斐, 李星星, 等. GPS/GLONASS组合精密单点定位研究[J]. 武汉大学学报: 信息科学版,2010, 35(1): 9-12) |
| [17] | LI Pan, ZHANG Xiaohong. Integrating GPS withGLONASS to Accelerate Convergence and Initialization Times of Precise Point Positioning[J].GPS Solutions, 2014, 18(3): 461-471. |
| [18] | CAI Changsheng,GAO Yang. Modeling and Assessment of Combined GPS-GLONASS Precise Point Positioning[J]. GPS Solutions, 2013, 17(2): 223-236. |
| [19] | CHEN Junping, XIAO Pei, ZHANG Yize, et al. GPS-GLONASS System Bias Estimation and Application in GPS-GLONASS Combined Positioning[C]//SUN Jiadong, JIAO Wenhai, WU Haitao,et al. Lecture Notes in Electrical Engineering: China Satellite Navigation Conference (CSNC) 2013 Proceedings, 2013, 244: 323-333. |
| [20] | ZHANG Xiaohong, ZUO Xiang, LI Pan, et al. ConvergenceTime and Positioning Accuracy Comparison between BDS and GPS Precise Point Positioning[J]. Acta Geodaeticaet Cartographica Sinica, 2015, 44(3): 250-256. (张小红, 左翔, 李盼, 等. BDS/GPS精密单点定位收敛时间与定位精度的比较[J]. 测绘学报, 2015, 44(3): 250-256.) |
| [21] | CHEN Junping, ZHANG Yize, WANG Jungang, et al. A Simplified and Unified Model of Multi-GNSS Precise Point Positioning[J]. Advances in Space Research, 2015, 55(1): 125-134. |