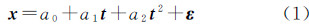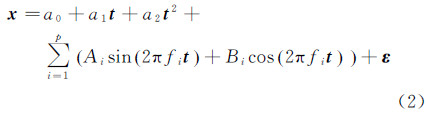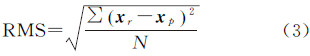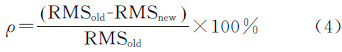1 引言
对卫星钟进行精确建模和预报是卫星导航的基础。通过高精度的卫星钟差建模与预报,不仅可以提高导航电文所发播的钟差参数的可靠性和准确性,而且可以支持实时精密单点定位等新应用的开展,还能为卫星自主导航提供时间基准[1]。
目前,北斗采用星地双向无线电时间比对以及多星定轨联合解算卫星轨道和钟差两种技术手段获取卫星钟差。其中,前者主要用于北斗系统运控方进行高精度的星地时间同步,是我国北斗区别于其他GNSS系统的一大特点,其数据目前尚未公开;后者则广泛应用于国际GNSS服务组织(IGS)卫星轨道和钟差产品的解算中,为基于GNSS的研究提供了公开、免费和可靠的数据源。
卫星钟差建模一般采用多项式来进行拟合[2, 3]。但是,在多星定轨解算轨道和卫星钟差的过程中,轨道误差和钟差相互耦合,使得卫星钟差结果存在着周期波动,导致多项式模型的拟合精度仍不够精确。因此,卫星钟差周期波动的性质及其内在的物理机制一直是研究的热点。目前,在国际GNSS服务组织(IGS)的全球监测网数据支持下,国内外学者对GPS、GLONASS以及Galileo卫星钟差的周期波动规律进行了比较充分的研究。文献[3, 4, 5]的研究表明,GPS、GLONASS和Galileo卫星钟差都具有周期项;文献[6]对GPS SVN62卫星的周期波动规律进行了研究,得出了一些有益的结论;文献[7]通过改进Galileo光压模型减弱了卫星钟差周期波动的振幅。文献[8, 9, 10]提出了附加周期项的多项式钟差预报模型,文献[11]研究了基于谱分析方法来评价IGS精密卫星钟差产品的理论。但是,目前还未见到有公开发表的研究北斗卫星钟差周期性及其应用的相关文献。
我国北斗卫星钟差数据的周期性研究主要受限于卫星钟差数据的数量和质量。随着北斗全球跟踪网络的进一步拓展和完善,武汉大学GNSS中心等一些机构开始发布北斗多星定轨解算的卫星轨道和钟差产品,为研究多星定轨条件下的北斗卫星钟差性质以及改善卫星钟差建模提供了数据基础[12, 13, 14, 15, 16, 17, 18, 19, 20]。另外,北斗多星定轨解算的卫星钟差存在不连续[18]和粗差现象,需要针对北斗卫星钟差数据中断个粗差进行预处理。
本文将基于北斗观测网多星定轨生成的卫星钟差产品,利用适用于间断数据的谱分析方法,对多星定轨条件下的北斗卫星钟差数据进行周期项提取,并利用周期项改进后的钟差预报模型评估24 h以内的预报精度。
2 数据间断条件下的谱分析方法受限于北斗系统尚不完善的地基全球观测网,多星定轨解算的北斗卫星钟差存在不连续现象[17]。此外,由于人为操作以及环境因素等影响,卫星钟差存在着粗差。为了准确的得到卫星钟差周期波动规律,需要对北斗卫星钟差数据进行预处理。
首先基于中位数(median absolute deviation,MAD)的抗差估计探测粗差方法对卫星钟差数据进行粗差剔除[21, 22, 23],再基于多项式模型去除趋势项,对得到的残差进行快速傅里叶变换(FFT),从而获取卫星钟差序列的频谱及其主要周期项。主要步骤如下:
步骤 1:数据预处理。获取北斗卫星钟差,首先将钟差数据进行一次差分转换为频率数据,基于每天的卫星钟的频率数据序列进行粗差剔除。
步骤2:去除趋势项。对每天的卫星钟差数据进行二次多项式拟合,并对滤除该趋势项后的拟合残差进行拼接,得到长期的残差序列。
步骤3:傅里叶变换。对于残差序列进行快速傅里叶变换,得到卫星钟差序列的频谱图。
需要注意的是,常规的粗差剔除和傅里叶变换都是基于等间隔连续数据进行的。针对多星定轨条件下北斗卫星钟差存在大量间断的情况,必须予以特殊处理。
(1) 在步骤1粗差剔除中,仅考虑连续数据段作为粗差探测的样本,然后将所有的粗差点和数据缺失点的卫星钟差都置为0。
(2) 在步骤2中仅对每天的非0数据进行拟合,求取其残差,且将钟差为0处的残差直接设置为0。
通过傅里叶变换获取得到卫星钟差序列的频谱图,提取其主频率,即可分析卫星钟差的周期性波动特性及其主周期,并用于改进常规的钟差二次多项式模型。
3 改进的钟差预报模型最常用的卫星钟差预报模型为多项式模型,针对卫星钟差序列{x},其卫星钟差模型为
式中,a0、a1、a2分别为钟差、钟速以及钟加速;ε为残差。利用最小二乘法可以求解出多项式模型的3个未知参数。若顾及卫星钟差的周期性波动,对多项式模型进行周期项改正,则改进后的卫星钟差模型为
式中,fi为卫星钟差序列的第i个主频项;Ai和Bi为该主频项所对应的系数。对历史钟差序列进行拟合,求解出上式中的未知参数,从而建立改进的卫星钟差预报模型。采用均方根误差作为卫星钟差预报精度的评价指标,即
式中,xr与xp为预报时间序列中卫星钟差实测值及其预报值;N为预报序列的长度。为了比较改进前后模型预报精度的定量关系,定义模型改进率ρ
式中,RMSold和RMSnew分别为改进前后模型的预报均方根误差。 4 算例与分析 4.1 北斗卫星钟差数据质量分析武汉大学GNSS中心基于IGS-MGEX(IGS multi-GNSS experiment),采用多星定轨的方法对北斗事后精密轨道和钟差产品进行了解算[17, 18]。
利用武汉大学GNSS中心的事后卫星钟差产品,对北斗星钟进行了数据质量统计。选用的数据时间段总长度为340 d,即2013年1月1日至2013年12月7日(MJD 56 293—56 633),采样间隔为5 min。
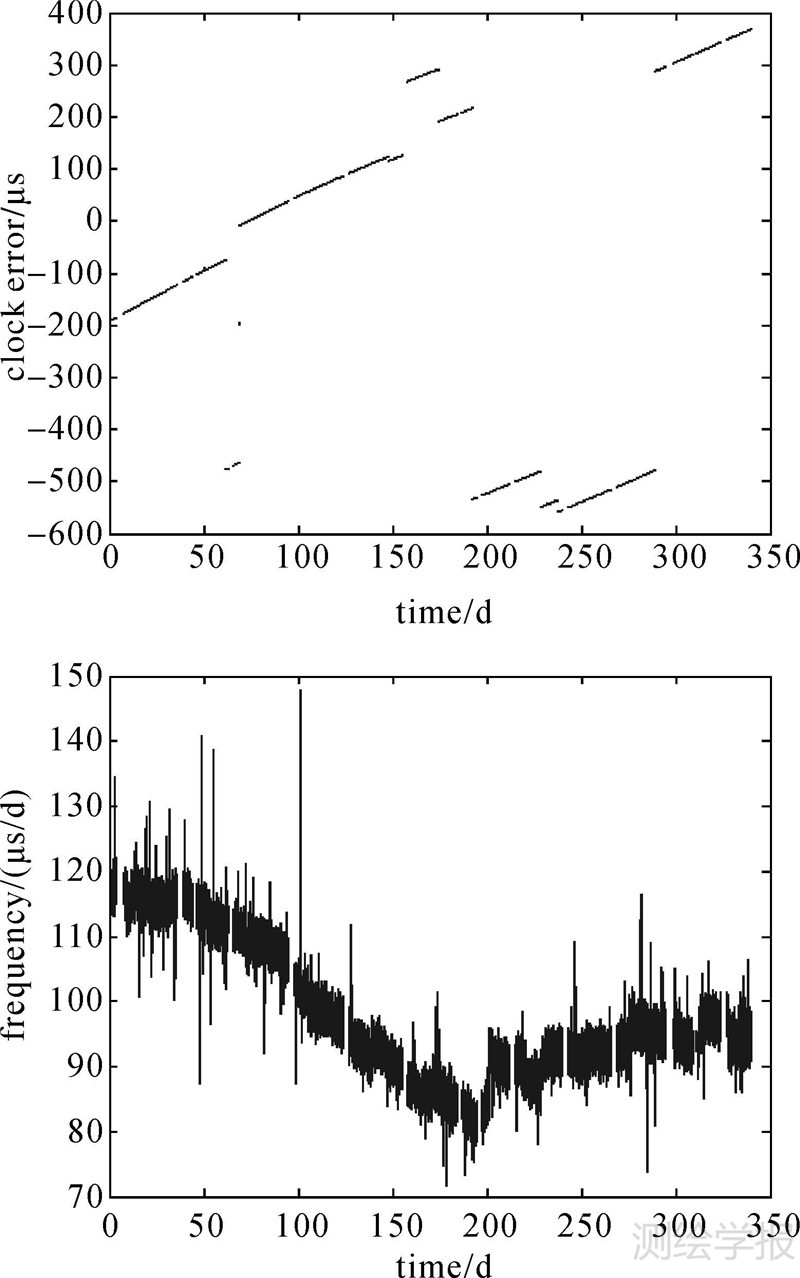
图 1分别为北斗C01卫星340 d内的钟差和频率数据。可以看出,虽然GEO卫星全天可视,该时段内C01卫星钟差仍然有频繁的跳频/跳相,而且还存在一些比较明显的数据间断和粗差异常。
|
| 图 1 340 d内北斗C01卫星钟差和频率变化(MJD56 293—56 633) Fig. 1 BeiDou C01 satellite clock error and frequency variations in 340 days(MJD 56 293—56 633) |
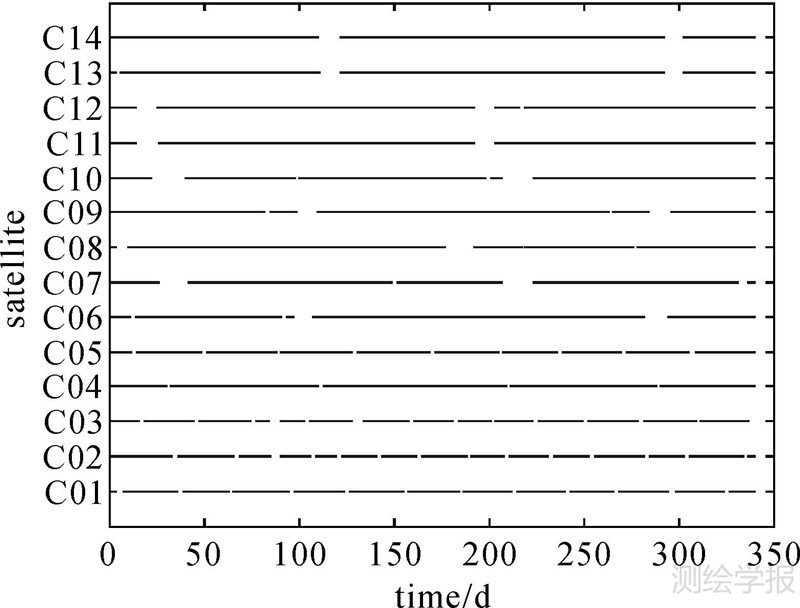
图 2给出了该时段内北斗3类卫星的钟差数据间断统计。数据统计表明,北斗卫星钟差具有某种原因不详的周期性间断。GEO卫星(C01—C05)钟差每隔28 d会出现4 d左右的周期性间断;IGSO卫星(C06—C10)每隔110 d会出现15 d左右的周期性间断;MEO卫星(C11—C14)每隔100 d会出现10 d左右的周期性间断。此外,3类卫星数据均有随机的短期间断现象。
|
| 图 2 北斗卫星钟差在MJD56 293—56 633时段的数据缺失情况 Fig. 2 Data gaps of BeiDou satellite clock error in MJD (56 293—56 633) |
表 1对每个卫星钟差数据的缺失率进行了统计。3类卫星的数据缺失率都在20%以下,MEO卫星的数据缺失显然多于GEO和IGSO卫星。此外,为了研究BDS各卫星钟差的精度,表 1中还给出了二次多项式拟合的残差标准差的平均值。可以看出,钟差精度基本上在同一量级,其中MEO卫星的钟差精度整体上高于GEO/IGSO卫星。
| 卫星类型 | 编号 | 数据缺失率/(%) | 平均精度值/m |
| GEO | C01 | 11.23 | 0.17 |
| C02 | 13.55 | 0.70 | |
| C03 | 1.30 | 0.23 | |
| C04 | 3.80 | 0.16 | |
| C05 | 8.36 | 0.25 | |
| IGSO | C06 | 9.50 | 0.29 |
| C07 | 12.44 | 0.17 | |
| C08 | 5.91 | 0.55 | |
| C09 | 8.60 | 0.12 | |
| C10 | 12.10 | 0.18 | |
| MEO | C11 | 10.47 | 0.09 |
| C12 | 10.94 | 0.09 | |
| C13 | 16.10 | 0.13 | |
| C14 | 15.31 | 0.08 |
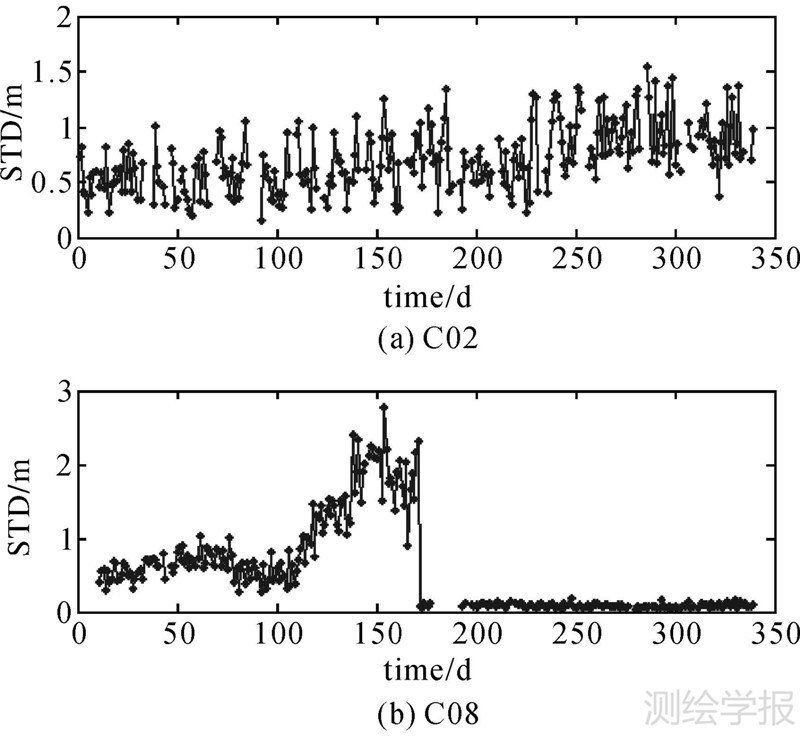
图 3进一步列出了钟差精度最差的C02和C08的卫星钟差精度的变化情况。C02的钟差精度相对一致,表明可能是卫星钟自身性能原因,而C08则在2013年195 d前后明显不一致,且原因未知。在后文的C08谱分析中,剔除了2013年前200 d数据,以免影响谱分析结果。
|
| 图 3 C02和C08卫星钟差精度变化 Fig. 3 Precision variations of C02 and C08 clock products |
卫星钟差数据间断的主要原因是:①BDS全球监测网络的监测站分布不均匀,观测数据缺失;②广播星历缺失,导致该时段不能参与多星定轨;③卫星轨道机动或卫星钟切换等。在前两种间断不会导致轨道和钟差的精度不一致;第3种情况发生的时段相对于近一年的时段所占比例小或者概率低,这里暂未考虑。
4.2 数据间断条件下的谱分析验证为了验证本文谱分析方法对间断卫星钟差数据的适用性,基于IGS提供的GPS事后卫星钟差对该方法进行了验证。选用的数据为GPS PRN02卫星在2012年6月10日至2013年5月16日(MJD 56 088—56 428)共计约340 d的卫星钟差,采样间隔为5 min。根据北斗卫星钟差的数据缺失规律,在GPS卫星钟差数据的基础上人为设置数据间断,包括:①短时的随机间断,考虑到北斗卫星钟差包含较多的短时间断,在GPS卫星钟差数据中设置了50次长度为0~3 h的随机间断;②长持续时间的周期性间断。根据北斗3类卫星不同的周期性间断规律,在GPS卫星钟差的基础上人为的设置周期性长时间数据间断,即每隔28 d加入4 d的周期性间断。
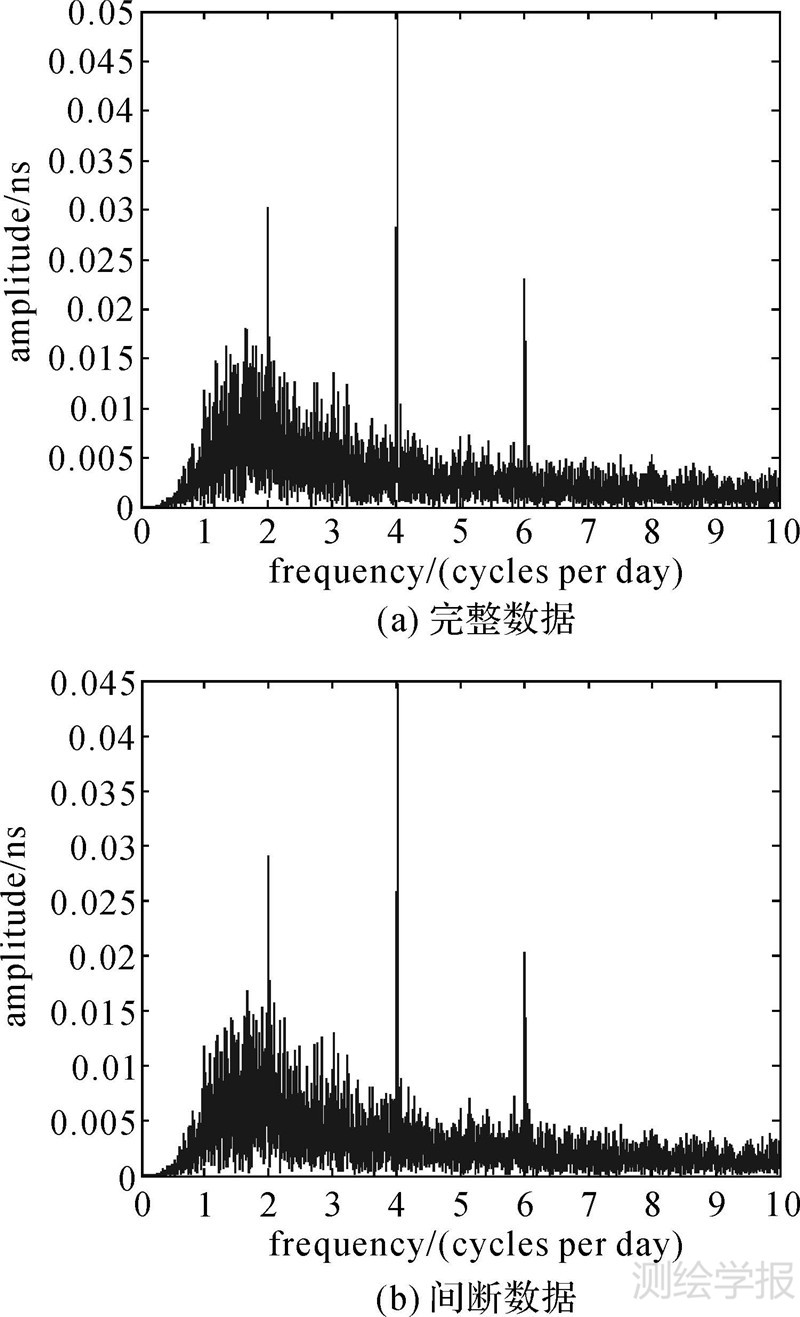
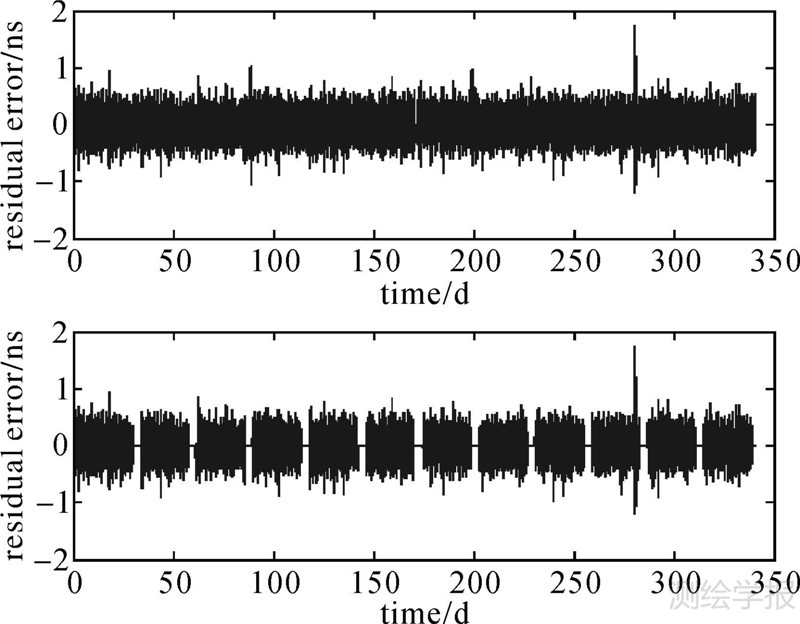
对间断前后卫星钟差的谱分析结果表明,在数据缺失情况下的谱分析仍能够提取准确的主频项。图 4所示为GPS卫星钟差有无间断数据情况下的谱分析结果对比,图 5是两种情况下解算得到的残差对比图,其中间断数据部分的残差被置为0。
|
| 图 4 GPS PRN02实测钟差和人为数据间断条件下谱分析结果 Fig. 4 Spectral analysis of GPS PRN02’s original clock error and clock error with artificial gaps |
|
| 图 5 GPS PRN02卫星实测钟差和人为数据间断条件下解算得到的残差 Fig. 5 GPS PRN02’s residual error with original clock error and clock error with artificial gaps |
表 2列出了该GPS卫星钟差序列在有无间断数据情况下谱分析提取的主频率结果。显然,在这种数据间断设置情况下,谱分析方法仍能给出PRN02卫星的3个最大的周期项,其主频率依次为2.004、4.012和6.014,与文献[4]中的结论基本一致,验证了本文谱分析方法对于间断数据的有效性。需要注意的是,由于文献[4]所给出的GPS卫星钟差的周期变化为对整个GPS星座进行平均的结果,因此和本文单星相比存在一定差异。
| 实测数据 | 间断数据 | ||
| 主频率/cpd | 振幅/ns | 主频率/cpd | 振幅/ns |
| 2.004 | 0.030 | 2.004 | 0.025 |
| 4.012 | 0.049 | 4.012 | 0.044 |
| 6.014 | 0.023 | 6.014 | 0.020 |
| cpd—cycles per day. | |||
此外,注意到数据间断导致各主频项的振幅整体上均略有减小,虽然不至于影响提取主频率,但是在应用中对数据缺失率还是应有所限制。
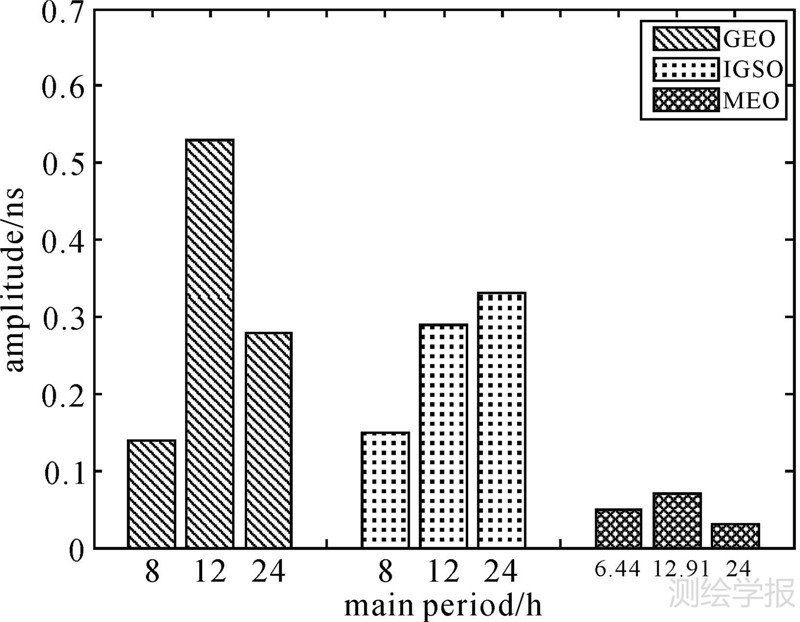
4.3 北斗卫星钟差的周期波动规律基于数据间断条件下的谱分析方法,对北斗卫星钟差数据进行了分析。为了反映北斗卫星钟差周期性波动的普遍规律,对同类型卫星的频谱进行了平均,并分别提取了3类卫星的主周期项,结果如图 6和表 3所示。从谱分析的结果可以看出:
|
| 图 6 北斗卫星钟差主周期及其振幅 Fig. 6 Main periods and amplitudes of BeiDou satellite clock error |
| 卫星类型 | 轨道周期 | 数据主周期项 | 振幅/ns |
| GEO | 23 h 56 min | 12 h | 0.53 |
| 24 h | 0.28 | ||
| 8 h | 0.14 | ||
| IGSO | 23 h 56 min | 24 h | 0.33 |
| 12 h | 0.29 | ||
| 8 h | 0.15 | ||
| MEO | 12 h 53 min | 12 h 55 min | 0.07 |
| 6 h 26 min | 0.05 | ||
| 24 h | 0.03 |
(1) 北斗3类卫星钟差都具有明显的周期项。其中,GEO卫星钟差主周期依次为12、24和8 h;而IGSO主周期依次为24、12和8 h;MEO卫星钟差的主周期项依次为12.91、6.44和24 h。其中前两个主周期分别近似为1倍和1/2倍轨道周期,表明多星定轨同时解算卫星轨道和钟差的过程中,部分轨道误差被卫星钟差所吸收。
(2) GEO和IGSO卫星钟差各周期项的振幅要比MEO的对应项大一个量级。从图 6可以看出,MEO卫星钟差振幅在亚纳秒级,这可能是因为MEO定轨精度高于GEO/IGSO,从而轨道中未被建模的误差项较小,因此卫星钟差中周期项的振幅较小。此外,MEO数据缺失较多也会造成振幅能量的一定损失。
(3) 3类卫星钟差都具有的24 h的主周期。除了与轨道周期的耦合外,表明星载钟的在轨性能可能与卫星平台的昼夜温差变化有密切联系。因此,北斗卫星的力学建模尤其是光压模型可能存在未被充分建模的系统偏差,这也是需要进一步验证和改进的工作方向。
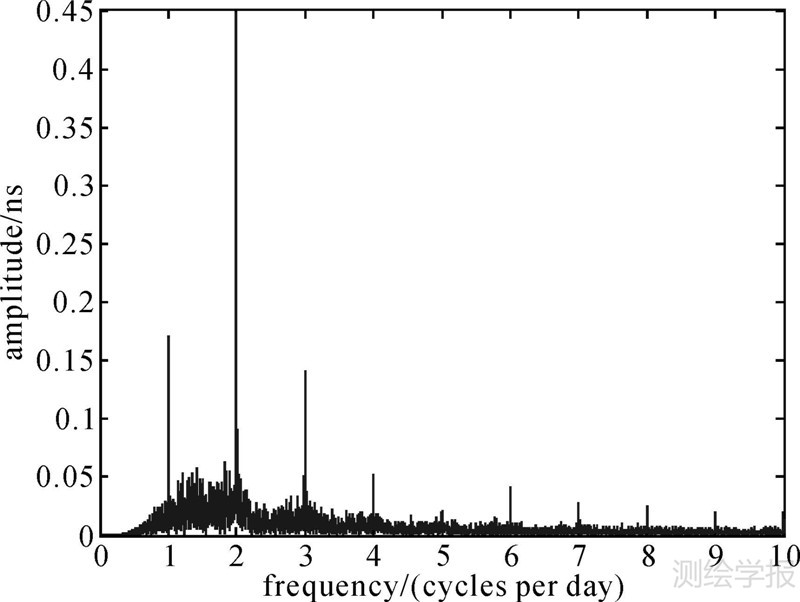
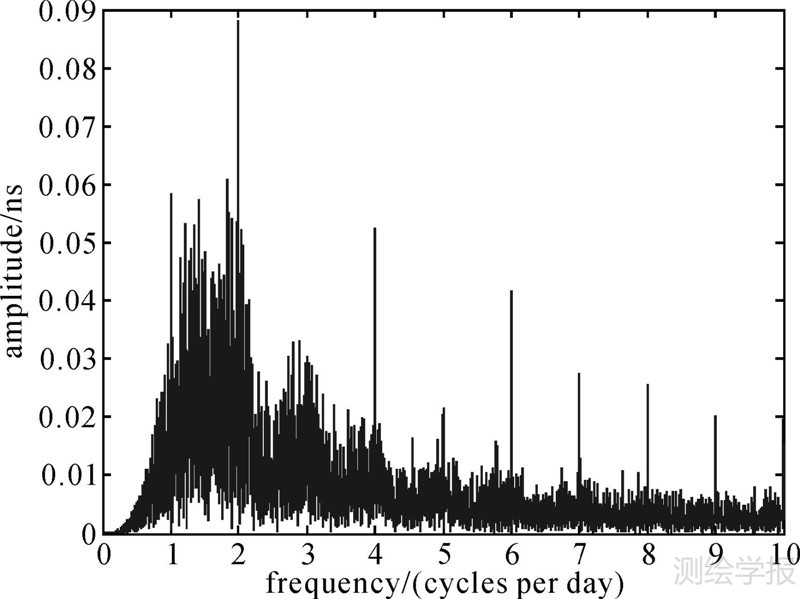
图 7和图 8列出了C01卫星钟差去除3个主周期前后的残差谱分析。可以看出,去除3个主周期后还有12 h附近的周期项(f=2.004),但是其振幅小于0.1 ns,这说明了本文建模的合理性。
|
| 图 7 C01卫星钟差谱分析结果 Fig. 7 Spectral analysis of C01 satellite clock error |
|
| 图 8 C01卫星钟差去除3个主周期项后的谱分析结果 Fig. 8 Spectral analysis of C01 clock error after extract three main periods |
对周期性波动显著的GEO和IGSO卫星进行卫星钟差模型改进。考虑到本文选用的卫星钟差最长主周期为24 h,重点对多项式模型和改进模型24 h以内的短期预报进行研究。鉴于3类卫星的钟差精度基本上为同一量级,但是MEO卫星钟差周期项振幅比GEO和IGSO的小一个数量级,且MEO的数据间断相对频繁,这里暂不考虑MEO卫星。
选取北斗星座的2颗GEO卫星(C01、C05)和2颗IGSO卫星(C06、C09)的30 d卫星钟差数据,时段为2013年2月27日至3月29日(MJD 56 350—56 380)。该时段内卫星钟差数据缺失相对较少,有利于钟差模型的精度评定。
分别考察以下3种卫星钟差拟合和预报模型:
(1) 二次多项式模型。
(2) 改进模型Ⅰ,二次多项式+2个主周期项。
(3) 改进模型Ⅱ,二次多项式+3个主周期项。
拟合数据均为1 d,分别考察2、12和24 h的钟差预报精度。共有1 d-2 h约348组,1 d-12 h约58组,1 d-1 d约29组,对各组预报精度进行统计。
表 4给出了3种卫星钟差模型预报精度的对比结果。统计表明:
| 预报方案 | 卫星编号 | 二次多项式模型/ns | 改进模型Ⅰ/ns | 改进模型Ⅱ/ns | 改进模型Ⅰ模型改进率/(%) |
| 1 d-2 h 预报 | C01 | 1.12 | 0.66 | 0.73 | 41.25 |
| C05 | 1.60 | 0.95 | 1.15 | 40.67 | |
| C06 | 0.97 | 0.77 | 0.73 | 19.99 | |
| C09 | 0.99 | 0.52 | 0.52 | 47.66 | |
| 1 d-12 h预报 | C01 | 4.03 | 3.75 | 5.01 | 7.09 |
| C05 | 5.98 | 4.12 | 5.24 | 31.10 | |
| C06 | 14.7 | 6.42 | 6.67 | 56.31 | |
| C09 | 3.56 | 2.99 | 2.77 | 15.94 | |
| 1 d-24 h预报 | C01 | 9.1 | 7.9 | 8.5 | 13.19 |
| C05 | 14.2 | 11.5 | 11.7 | 19.01 | |
| C06 | 28.1 | 14.6 | 12.8 | 48.04 | |
| C09 | 5.8 | 4.9 | 5.7 | 15.52 |
(1) 引进2个主要周期项改正能够明显提高卫星钟差短期预报精度。由3种模型的预报均方根误差可知,两种改进模型的预报精度都优于二次多项式模型。当增加两个主周期项时,预报2~24 h的平均改进幅度可达20%~40%,这也从预报的角度验证了多星定轨中北斗卫星钟差周期性变化的存在。但是注意到,若继续增加周期项,改进幅度没有增加,反而会出现明显减小。
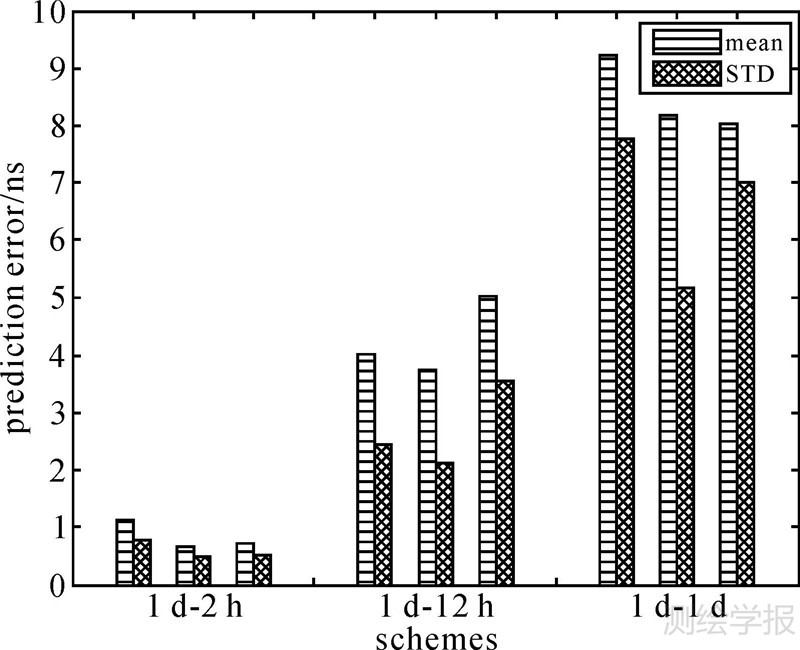
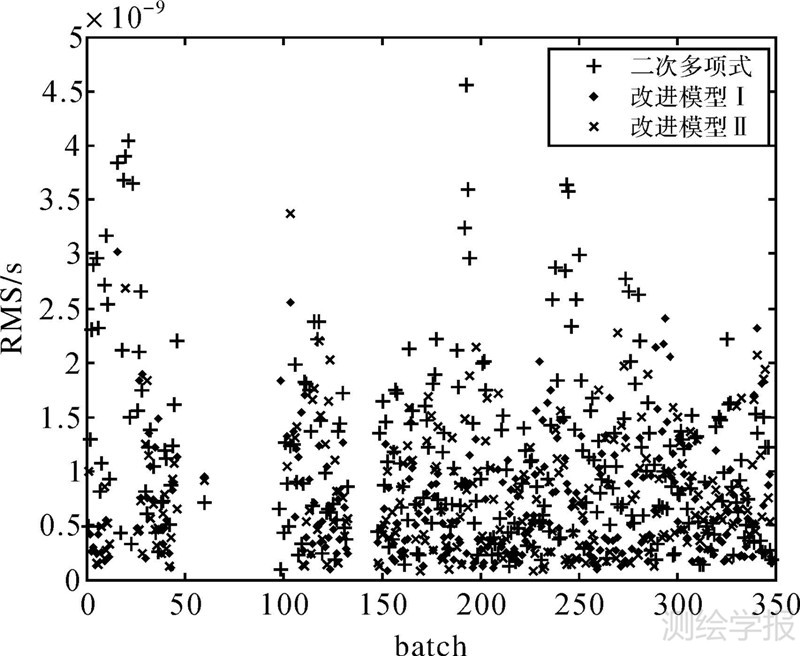
(2) 引进钟差周期项改正还提高了卫星钟差预报的稳定性。图 9和图 10对比给出了C01卫星3种钟差预报方案的预报精度,改进模型Ⅰ的预报精度要优于二次多项式模型,且标准差要小于其他两种模型,对其余卫星的分析也能得到类似结论。这说明3种模型中改进模型Ⅰ最为稳定,能更好地描述卫星周期波动规律。
|
| 图 9 C01卫星钟差预报精度及其标准差 Fig. 9 C01 satellite clock error prediction accuracy and its standard deviation |
|
| 图 10 C01卫星3种模型24 h-2 h的预报精度对比 Fig. 10 Comparison of C01 satellite clock error prediction accuracy in the 24 h-2 h scheme |
需要说明的是,这里仅考虑了1 d的拟合长度。试验表明,在一定条件下,适当增大拟合资料的长度可以提高二次多项式模型和改进模型的钟差预报精度。但是最佳拟合长度的规律性较差,限于篇幅这里不再列出。事实上,北斗星载原子钟的性能指标、轨道空间环境和在轨工作时间等的差异,将会影响到这种统一改进模型的适用性和预报精度的一致性。由于预报模型中二次多项式的主导作用,无论是多项式模型还是改进模型,预报误差都随着时间积累,因此,在考虑是否对二次多项式模型进行周期项改正时,一定要根据各方面的因素予以综合考虑,如卫星钟特性、钟差拟合时长以及预报时长、周期项的选取等。
5 结论采用适用于间断数据的谱分析方法,对多星定轨条件下的北斗卫星钟差的周期波动规律进行了研究。结果表明:
(1) 北斗3类卫星钟差都具有比较明显的周期波动。GEO 3个主周期依次为12、24和8 h;IGSO 3个主周期依次为24、12和8 h;而MEO卫星3个主周期依次为12.91、6.44和24 h。但是,MEO卫星的主周期项的振幅比GEO和IGSO的小一个数量级,在亚纳秒级。
(2) 顾及周期项的改进二次多项式钟差预报模型,能够显著提高北斗GEO/IGSO卫星钟差预报的精度。当增加2个主周期项时,预报2~24 h的平均改进幅度可达20%~40%。
由于目前使用的武汉大学GNSS中心提供的北斗卫星钟差数据并不完整,数据质量仍有待提高。此外,本文的处理方法对BDS每一种类型卫星的谱分析结果进行了平均,以发现其共性规律。事实上仍然存在一些有差异的卫星数据,其3个周期项的大小规律与本文给出的规律可能并不完全一致,因此对谱分析和预报精度的评价有一定的影响。下一步将深入研究北斗卫星钟差周期的性质及其内在机制,提高北斗卫星钟差建模和预报的精度。
致谢:感谢武汉大学GNSS中心提供数据支持。
| [1] | GUO Hairong. Study on the Analysis Theories and Algorithms of the Time and Frequency Characterization for Atomic Clocks of Navigation Satellites[D]. Zhengzhou: Information Engineering University, 2006. (郭海荣. 导航卫星原子钟时频特性分析理论与方法研究[D]. 郑州: 信息工程大学, 2006.) |
| [2] | GUO Hairong, YANG Yuanxi, HE Haibo, et al. Determination of Covariance Matrix of Kalman Filter Used for Time Prediction of Atomic Clocks of Navigation Satellites[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 146-150. (郭海荣, 杨元喜, 何海波, 等. 导航卫星原子钟Kalman滤波中噪声方差-协方差的确定[J]. 测绘学报, 2010, 39(2): 146-150.) |
| [3] | HUANG Guanwen. Research on Algorithm for Precise Clock Offset and Quality Evaluation of GNSS Satellite Clock[D]. Xi'an: Chang'an University, 2012. (黄观文. GNSS星载原子钟质量评价及精密钟差算法研究[D]. 西安: 长安大学, 2012.) |
| [4] | SENIOR K L, RAY J R, BEARD R L. Characterization of Periodic Variations in the GPS Satellite Clocks[J]. GPS Solutions, 2008, 12(3): 211-225. |
| [5] | WALLER P, GONZALEZ F, HAHN J, et al. In-orbit Performance Assessment of Giove Clocks[R]. Noordwijk: European Space Agency Noordwijk, 2008. |
| [6] | MONTENBRUCK O,HUGENTOBLER U, DACH R, et al. Apparent Clock Variations of the Block IIF-1 (SVN62) GPS Satellite[J]. GPS Solutions, 2012, 16(3): 303-313. |
| [7] | MONTENBRUCK O, STEIGENBERGER P, HUGENTOBLER U. Enhanced Solar Radiation Pressure Modeling for Galileo Satellites[J]. Journal of Geodesy, 2015, 89(3): 283-297. |
| [8] | BROEDERBAUER V,OPITZ M,WEBER R.Automated Quasi-realtime Prediction of GNSS Clock Corrections[J]. Geophysical Research Abstracts, 2007, 9: 02964. |
| [9] | ZHENG Zuoya, DANG Yaming, LU Xiushan, et al. Prediction Model with Periodic Item and Its Application to the Prediction of GPS Satellite Clock Bias[J]. Acta Astronomica Sinica, 2010, 51(1): 95-102. (郑作亚, 党亚民, 卢秀山, 等. 附有周期项的预报模型及其在GPS卫星钟差预报中的应用研究[J]. 天文学报, 2010, 51(1): 95-102.) |
| [10] | HEO Y J, CHO J, HEO M B. Improving Prediction Accuracy of GPS Satellite Clocks with Periodic Variation Behaviour[J]. Measurement Science and Technology, 2010, 21(7): 073001. |
| [11] | HUANG Guanwen, ZHANG Qin, XU Guochang, et al. IGS Precise Satellite Clock Model Fitting and Its Precision by Using Spectral Analysis Method[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5): 496-499. (黄观文, 张勤, 许国昌, 等. 基于频谱分析的IGS精密星历卫星钟差精度分析研究[J]. 武汉大学学报: 信息科学版, 2008, 33(5): 496-499.) |
| [12] | YANG Yuanxi. Progress, Contribution and Challenges of Compass/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-6. (杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1): 1-6.) |
| [13] | LIU Weiping, HAO Jinming, LI Jianwen, et al. Multi-GNSS Joint Precise Orbit Determination of BeiDou Navigation Satellite System[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(11): 1132-1138. (刘伟平, 郝金明, 李建文, 等. 多GNSS融合的北斗卫星精密定轨[J]. 测绘学报, 2014, 43(11): 1132-1138.) |
| [14] | MONTENBRUCK O, STEIGENBERGER P, KHACHIKYAN R, et al. IGS-MGEX: Preparing the Ground for Multi-constellation GNSS Science[C]//Proceedings of the 4th International Colloquium on Scientific and Fundamental Aspects of the Galileo System. Prague: ESA, 2013. |
| [15] | YANG Yuanxi, LI Jinlong, WANG Aibing, et al. Preliminary Assessment of the Navigation and Positioning Performance of BeiDou Regional Navigation Satellite System[J]. Science China Earth Sciences, 2014, 57(1): 144-152. |
| [16] | ZHOU Shanshi, HU Xiaogong, WU Bin, et al. Orbit Determination and Time Synchronization for a GEO/IGSO Satellite Navigation Constellation with Regional Tracking Network[J]. Science China Physics, Mechanics and Astronomy, 2011, 54(6): 1089-1097. |
| [17] | ZHAO Qile, GUO Jing, LI Min, et al. Initial Results of Precise Orbit and Clock Determination for Compass Navigation Satellite System[J]. Journal of Geodesy, 2013, 87(5): 475-486. |
| [18] | DENG Z, ZHAO Q, SPRINGER T, et al. Orbit and Clock Determination——BeiDou[C]//Proceedings of IGS Workshop. Pasadena: IGS, 2014. |
| [19] | MAO Yue, DU Yu, SONG Xiaoyong, et al. GEO and IGSO Joint Precise Orbit Determination[J]. Science China Physics, Mechanics and Astronomy, 2011, 54(6): 1009-1013. |
| [20] | STEIGENBERGER P, HUGENTOBLER U, HAUSCHILD A, et al. Orbit and Clock Analysis of Compass GEO and IGSO Satellites[J]. Journal of Geodesy, 2013, 87(6): 515-525. |
| [21] | RILEY W J. User Manual: Stable32 Frequency Stability Analysis Version 1.5.0[M]. Beaufort, SC: Hamilton Technical Services, 2007. |
| [22] | RILEY W J. Frequency Jump Detection in Stable32[M]. Beaufort, SC: Hamilton Technical Services, 2008. |
| [23] | BARTOCCINI U, BARCHI G, NUNZI E. Methods and Tools for Frequency Jump Detection[C]//Proceedings of IEEE International Workshop on Advanced Methods for Uncertainty Estimation in Measurement, 2009. Bucharest: IEEE, 2009: 109-112. |