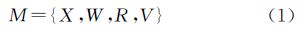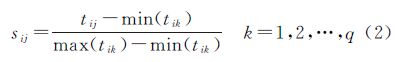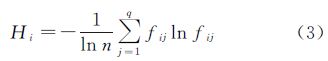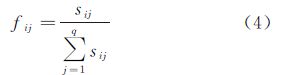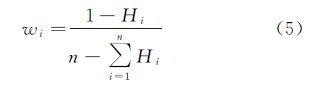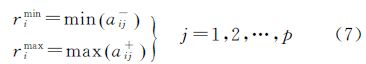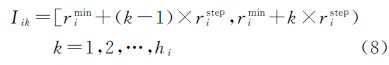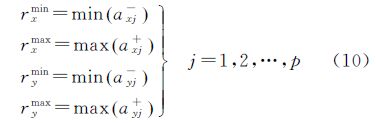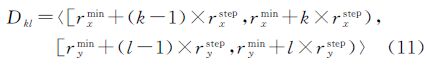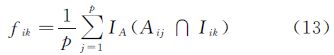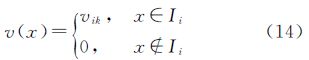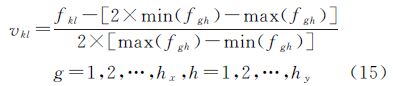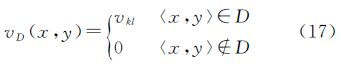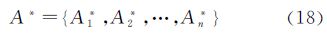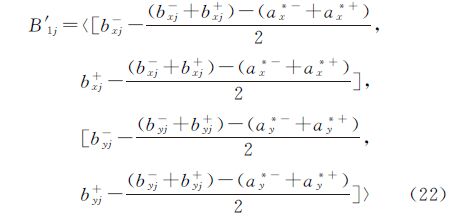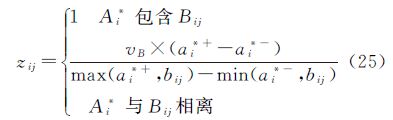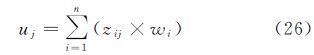2. 四川省应急测绘与防灾减灾工程技术研究中心,四川 成都 610041;
3. 成都理工大学地学空间信息技术国土资源部重点实验室,四川 成都 610059;
4. 高速铁路运营安全空间信息技术国家地方联合工程实验室,四川 成都 611756;
5. 西南交通大学地球科学与环境工程学院,四川 成都 611756
2. Sichuan Engineering Research Center for Emergency Mapping & Disaster Reduction, Chengdu 610041, China;
3. Key Laboratory of Geoscience Spatial Information Technology, Ministry of Land and Resources of the P. R. China, Chengdu 610059, China;
4. State-Province Joint Engineering Laboratory of Spatial Information Technology of High-Speed Rail Safety, Chengdu 611756, China;
5. Faculty of Geosciences and Enviromental Engineering, Southwest Jiaotong University, Chengdu 611756, ChinaAbstract
1 引 言
随着对地观测技术的发展,遥感数据呈现出明显的“大数据”特征:遥感数据日益多元化,不同成像方式、不同波段和分辨率的数据并存;遥感影像数据量显著增加,呈指数级增长;数据获取的速度加快,更新周期缩短,时效性越来越强[1]。然而,在资源和用户不断增加的同时,也出现了“信息过载”和“搜索迷失”问题[2]。现有的遥感信息共享平台大多提供搜索界面,由用户输入关注区域、产品类型、需求时间等条件,返回满足要求的遥感数据搜索结果,再由用户浏览下载所需数据。这样的数据服务方式存在被动性、同一性缺点,既不能主动推荐数据,也难以提供个性化的搜索结果。随着空间信息应用的深入,“为最需要的人、在最适宜的时间和地点、提供最适宜的服务”的智能化服务方式成为日益迫切的需求[3]。只有当用户的兴趣、偏好和访问模式等用户信息可以很好地被系统“理解”时,才可能满足多样化、跨领域的遥感信息需求,实现从“人找信息”发展到“信息找人”的智能阶段,这将大大降低用户使用遥感信息解决实际问题的难度,提高遥感信息资源的利用率。
智能服务的一般过程可以概括为:收集与用户相关的数据;根据收集到的数据推断出用户的兴趣;对满足用户兴趣的信息进行主动推荐。当前淘宝、Amazon等电子商务网站会根据以往的购物和浏览记录提供相应的产品推荐列表,即对用户行为进行分析后对用户的兴趣偏好进行建模,继而将其可能感兴趣的商品资源推荐过去。从推荐方法上分,可以分为基于网络的推荐方法与基于内容的推荐方法[2, 4, 5, 6]。基于网络的推荐方法核心思想是首先利用用户的历史信息计算用户之间的相似性,然后利用与目标用户相似性较高的邻居对其他产品的评价来预测目标用户对特定产品的喜好程度,系统根据这一喜好程度对目标用户进行推荐。在产品数量相对稳定的系统中,基于网络的推荐方法是很有效的,例如Amazon的书籍推荐系统[7]。但是对于遥感信息这类每天数据量都在急剧增加的系统,这种方法是不适用的。基于内容的推荐系统,是通过历史数据获取用户兴趣,然后比较用户兴趣与待分发产品的相似度,并直接向用户推荐与其兴趣最相似的产品,其核心在于获取产品内容与用户兴趣特征的关联规则。但是,在面对多源、多时相与多分辨率遥感信息时不可避免地受到用户兴趣特征获取的约束,自动提取遥感信息的内容特征具有技术上的困难,使得相关应用受到了很大限制。近年来,空间信息服务的智能化成为网络化信息服务的前沿焦点[8, 9, 10, 11, 12]。文献[11]采用区间数表达具有区间覆盖特征的经度、纬度、时间、波谱等属性的用户检索特征,较好地解决了用户兴趣在遥感信息各属性上特征分布的表达问题,但仍存在空间范围定位不够准确、效用度估计存在偏差等不足。文献[12]在文献[11]的基础上扩展,引入权值衰减函数和用户信息反馈等动态化因素,使模型能够随着时间推移进行修正。
本文针对遥感信息核心元数据的区间覆盖特性,引入区间数学的方法建立用户模型,描述用户兴趣在遥感信息核心元数据上的分布特征。实例分析表明,本文方法能够自动获取用户兴趣并进行遥感信息的主动推荐。
2 遥感信息用户建模方法用户建模是发现并获取与用户需求、兴趣相关的知识的过程,其结果是产生一个表示用户特有背景知识或需求、兴趣的用户模型[4]。用户模型是智能服务的主要知识源,其捕捉用户真实偏好的能力在很大程度上决定了推荐的成功与否。
向量空间模型是目前较流行的用户模型表示方法。该方法将用户模型表示成一个n维特征向量,向量的每一维由一个关键词及其权重组成,表示了用户是否对某个概念感兴趣以及感兴趣的程度[13, 14]。本文以遥感信息的元数据作为用户模型的元素项,考虑到遥感信息的部分核心元数据(例如空间范围、波谱范围等)具有覆盖特征,不宜通过一个数值,而需要通过一个范围来描述,因此引入区间数学的方法加以描述。在文献[12]四元组模型的基础上加以改进,模型结构如式(1)所示
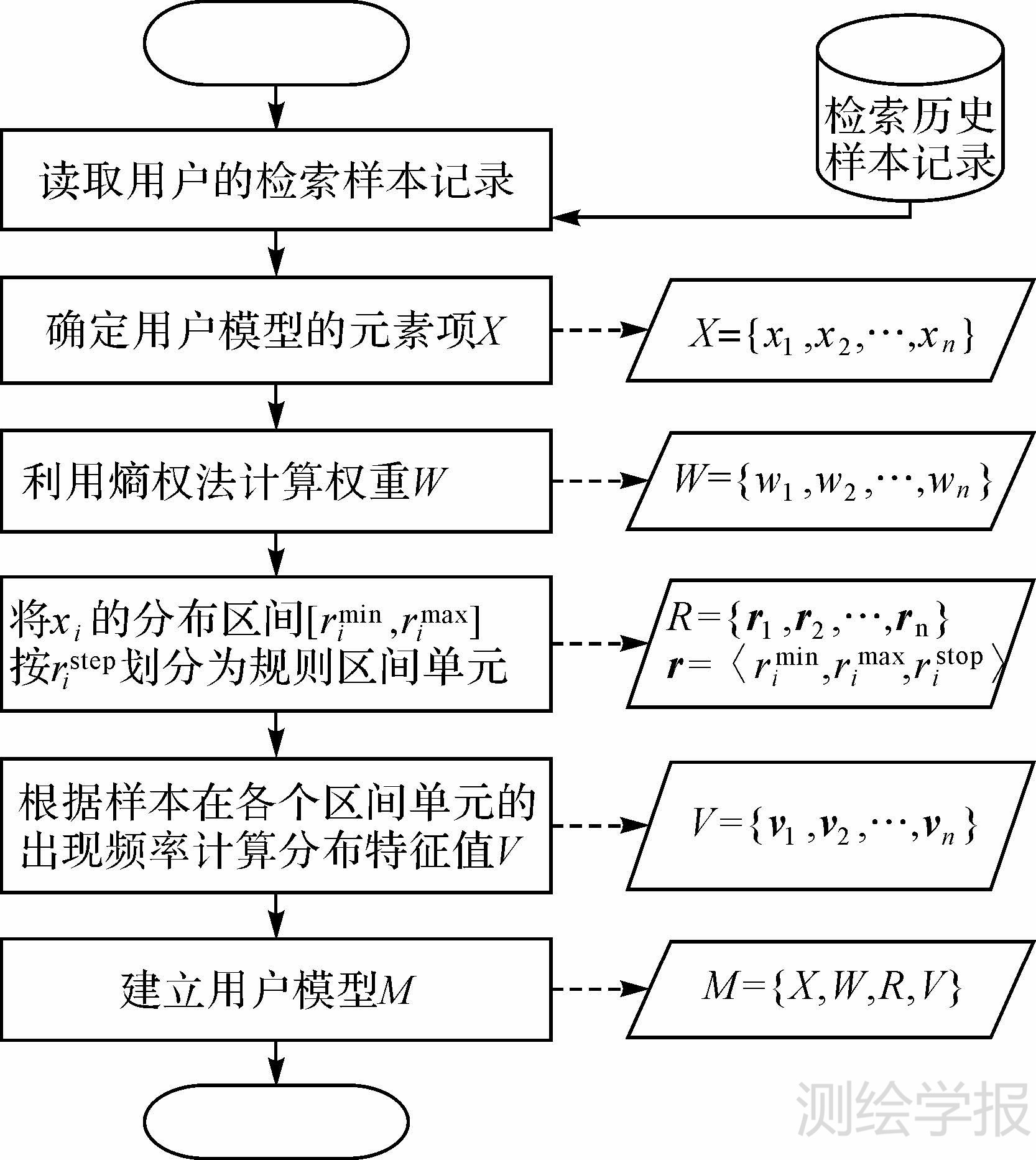
式中,X={x1,x2,…,xi,…,xn},元素项xi为遥感信息元数据项;W={w1,w2,…,wi,…,wn},wi为xi的权值;R={r1,r2,…,rn},ri=〈rimin,rimax,ristep〉,描述xi的分布范围和步长;V={v1,v2,…,vn},vi为反映用户兴趣在xi的分布特征向量或者矩阵。遥感信息用户建模流程如图 1所示。
|
| 图 1 用户建模流程图 Fig. 1 User profiling flowchart |
遥感信息用户兴趣隐藏于检索记录中,检索频率越高的元素项对于用户兴趣的贡献就越大,反之则越小。本文用权重wi来描述不同元素项xi之间的相对重要性,反映不同元素项对用户兴趣的贡献。确定权重的方法有两类:主观赋权法和客观赋权法。熵权法是一种客观赋权法,按照信息论基本原理,如果指标的信息熵越小,则该指标所提供的信息量越大[15]。本文在权重的确定中引入了信息熵概念,将用户对不同元素项的检索次数作为信息熵指标,直接根据指标原始信息通过统计的方法获得权重。
根据检索历史,将用户在过去一段时间内的检索记录分为q组,每一组包含若干条检索记录。分别统计每一组内对元素项xi的检索次数,并且用一个矩阵(tij)n×q记录。计算权重的步骤如下:
(1) 数据标准化处理
式中,sij为用户第j组检索记录中对元素项xi检索次数的标准化值;tij表示第j组检索记录中对元素项xi的检索次数; min(tik)和max(tik)分别为q组检索记录中元素项xi被检索次数的最小值和最大值。
(2) 计算各个元素项xi的信息熵Hi
(3) 由信息熵Hi计算各元素项的权重wi
2.2 元素项的分布范围与步长
本文选择空间范围、时间范围、波谱范围和空间分辨率范围4个核心元数据作为用户模型的元素项,依次对应x1、x2、x3、x4。考虑到不同元素项xi具有各自的区间覆盖特性,其分布范围与步长R的表示方法也不同,具体分3种情况处理:
(1) 对于时间范围x2、波谱范围x3与空间分辨率范围x4,用户常采用范围来表达检索需求,因此可用一维区间数Aij=[aij-,aij+]来记录用户的第j个检索记录在元素项xi上的检索样本值,aij-、aij+分别为检索样本值Aij的下限和上限,其中,i=2,3,4,j=1,2,…,p,p为检索记录的个数。令Ii表示包含所有p个检索样本值的最小区间
取步长ristep将区间Ii均匀分割成大小相等的子区间,当ristep取最大值时,则称步长ristep将Ii划分hi个一维区间单元Iik
式(8)满足以下两个条件:
① rimin+hi×ristep=rimax。
② 对于任一检索样本值Aij=[aij-,aij+],均存在唯一的s和t,满足rimin+s×ristep=aij-,rimin+t×ristep=aij+。
(2) 对于具有二维覆盖特性的元素项空间范围x1,用户的p个检索样本值可用二维区间数来表示,即A1j=〈[axj-,axj+],[ayj-,ayj+]〉,j=1,2,…,p。其中,axj-、axj+分别为第j个样本经度范围的下限和上限;ayj-、ayj+分别为第j个样本纬度范围的下限和上限。令D表示包含所有p个检索样本值的最小二维区间,则
式中,Dx表示包含所有p个检索样本经度范围的最小区间;rxmin和rxmax分别为Dx的下限和上限;Dy表示包含所有p个检索样本纬度范围的最小区间;rymin和rymax分别为Dy的下限和上限
取步长rxstep将Dx沿经度方向均匀分割,rystep将Dy沿纬度方向均匀分割,当rxstep和rystep都取最大值时,则称步长rxstep和rystep将空间范围元素项x1的取值区间D划分为若干个二维区间单元Dkl
式中,k=1,2,…,hx(hx为沿经度方向分割Dx得到的单元个数);l=1,2,…,hy(hy为沿纬度方向分割Dy得到的单元个数)。
(3) 对于搜索条件不具备区间形式的元素项,为了统一描述,可用上下限相等的一维区间数(退化为普通实数)来记录检索样本值的范围,其分布范围和步长的确定与波谱范围等一维区间元素项一致。
2.3 元素项的分布特征值对于同一元素项而言,那些被检索频率高的区间也比频率低的区间凝聚了更多的用户兴趣,例如相比只检索过一两次的地区,用户反复检索的地区必然是用户更感兴趣的地区。
在文本检索领域中,常采用TF-IDF技术根据关键词-频率来表达关键字在文档检索中的重要程度,词频越高,重要性就越大,反之则越低。借鉴这一思想,步长划分得到的区间单元在用户检索样本中出现的频率也能反映用户的兴趣,出现频率越高的区间单元,凝聚的用户兴趣也就越高,反之则越小。因此,遥感信息用户模型利用分布范围和步长R及其分布特征向量V来描述用户兴趣在不同区间上的分布特征。即对区间单元的出现频率进行线性变换,将这种出现频率映射到合理的取值范围,使得分布特征值对不同区间单元的重要程度具有较好的区分能力[11]。
(1) 对于采用一维区间数表示的元素项时间范围x2、波谱范围x3和空间分辨率范围x4,元素项xi(i=2,3,4)各区间单元Iik(k=1,2,…,hi)的分布特征值vik的计算方法如式(12)所示
式中,fik表示元素项xi的第k个区间单元Iik在p个检索记录中的出现频率,计算方法如式(13)所示
式中,Aij为第j个检索记录元素项xi的样本值;Iik为第k个区间单元;IA(·)为示性函数;当Aij∩Iik非空时为1,空集时为0。
区间单元Iik对应的分布特征值vik越大,意味着Iik在用户检索记录中出现越频繁,本文定义一维分布特征函数v(x)描述分布特征值随区间的分布
(2) 对于采用二维区间数表示的元素项空间范围x1,二维区间单元Dkl的分布特征值vkl的计算方法见式(15)
式中,fkl表示二维区间单元Dkl在p个检索记录中的出现概率,计算方法如式(16)所示
式中,A1j为第j个检索记录的空间范围样本值;Dkl为第k个经度区间单元和第l个纬度区间单元共同确定的二维区间单元;ID(·)为示性函数;当A1j∩Dkl非空时为1,空集时为0。
本文定义分布特征函数vD(x,y)描述分布特征值随二维区间的分布,如式(17)所示
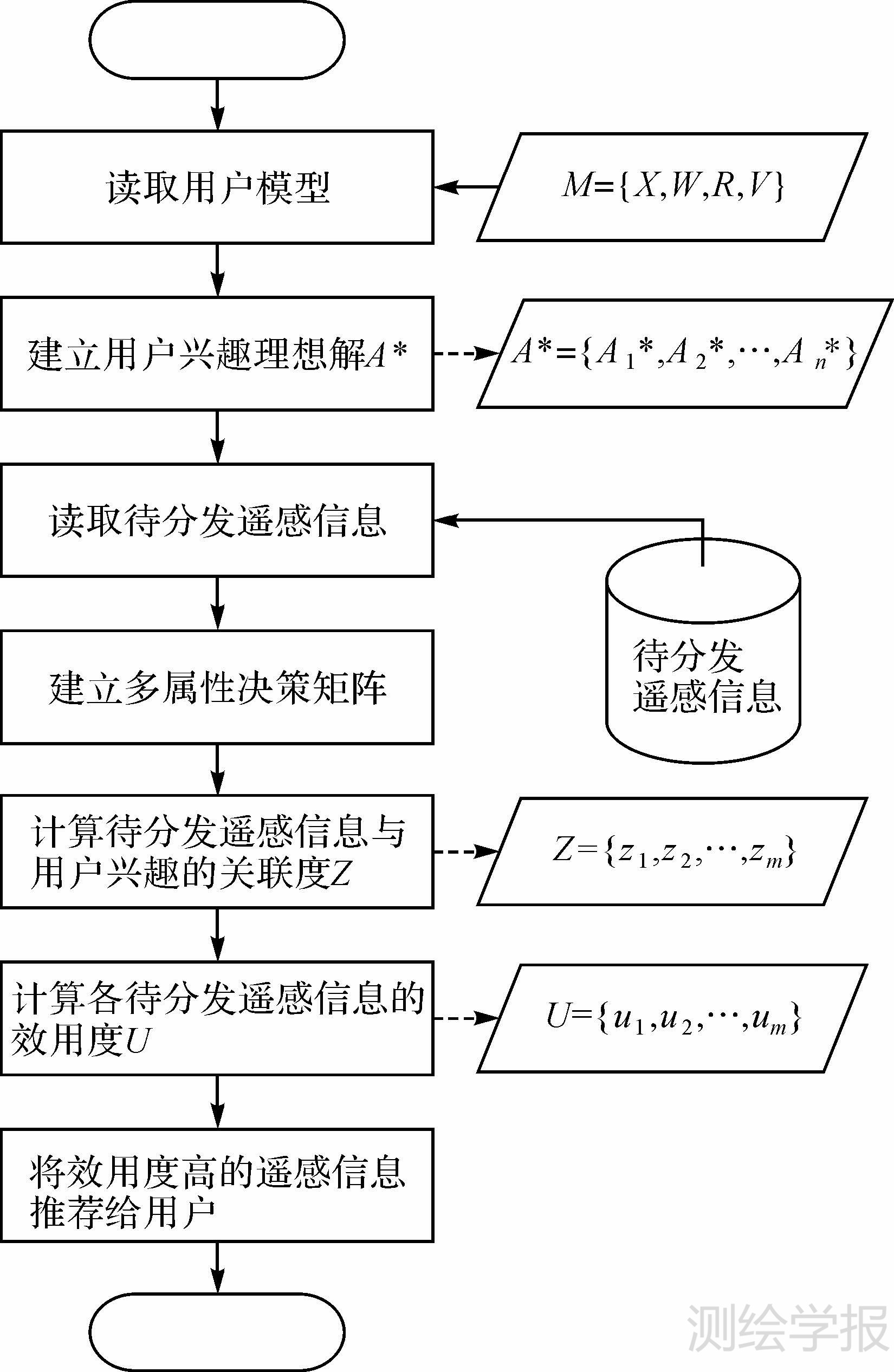
3 用户模型驱动的遥感信息主动推荐方法根据用户兴趣进行遥感信息的个性化、主动推荐,是实现智能服务的核心。本文提出了用户模型驱动的遥感信息主动推荐方法,首先从用户模型获取满足用户兴趣的理想解;接着,构造了多属性决策矩阵将待分发遥感信息的主动推荐问题转化为多属性决策问题;然后,设计了关联函数定量计算待分发信息在各个元素项上对理想解的满足程度;最后,计算各待分发信息的效用度,从而实现了基于用户兴趣的遥感信息主动推荐。用户模型驱动的主动推荐方法流程图如图 2所示。
|
| 图 2 遥感信息推荐流程图 Fig. 2 Remote sensing information recommendation flowchart |
所谓理想解是指设想的最优解(方案)[16]。基于上述用户模型,在n个元素项上都具有最大分布特征值的区间单元所组成的集合构成理想解A*
式中,Ai*为元素项xi理想解对应的区间单元的集合,即
(1) A1*=〈[ax*-,ax*+],[ay*-,ay*+]〉,当且仅当vD([ax*-,ax*+],[ay*-,ay*+])=max(vkl);k=1,2,…,hx;l=1,2,…,hy;
(2) Ai*=[ai*-,ai*+],当且仅当v(Ai*)=max(vik);k=1,2,…,hi。
3.2 建立决策矩阵如果将待分发的遥感信息集B={B1,B2,…,Bm}作为备选方案集,将Bj的各元素项X={x1,x2,x3,x4}作为决策属性集,Bij为第j个待分发遥感信息在元素项xi的值,矩阵(Bij)n×m表示备选方案集B关于决策属性集X的决策矩阵,则遥感信息的主动推荐问题可以转化为多属性决策问题,即从备选方案集中选择满意解(满足用户兴趣的遥感信息集)的过程。
3.3 关联函数在可拓学中,采用关联函数来刻画论域中的元素具有某种性质的程度i[17],本文定义关联函数来评价待分发遥感信息在各元素项xi上对用户兴趣的满足程度。常用的相似度衡量标准有距离和夹角余弦[6],文献[11, 12]均采用距离标准,但是这两类标准更适合于衡量点之间的相似度。空间范围和波谱范围等属性本身具有覆盖特性,因此衡量其是否满足用户兴趣的标准在于是否包含或者重叠了感兴趣的范围,而不是距离上的接近。本文针对覆盖特性,分析了元素项xi的理想解A*与待分发信息Bj的区间范围Bij之间的拓扑关系,设计了关联函数。
3.3.1 波谱范围元素项的关联函数对于一维区间,待分发信息Bj波谱范围所在区间B3j与理想解A3*之间存在6种拓扑关系:相离、叠加、相等、相接、包含于和包含。对B3j进行线性变换,目的是将B3j的中心平移至A3*所在区间的中心,如式(19)所示
式中,a3*-和a3*+分别为A3*的下限和上限;b3j-和b3j+分别为B3j的下限和上限;B′3j为B3j经线性变换后产生的新的一维区间。
变换后的B′3j与A3*之间存在3种拓扑关系:相等、包含、包含于。变换前后拓扑关系的变化共有12种可能情形,见表 1。
| 变换后 | 变换前 | |||||
| 相离 | 叠加 | 相等 | 相接 | 包含于 | 包含 | |
| 相离 | N/A | N/A | N/A | N/A | N/A | N/A |
| 叠加 | N/A | N/A | N/A | N/A | N/A | N/A |
| 相等 | 存在 | 存在 | 存在 | 存在 | N/A | N/A |
| 相接 | N/A | N/A | N/A | N/A | N/A | N/A |
| 包含于 | 存在 | 存在 | N/A | 存在 | 存在 | N/A |
| 包含 | 存在 | 存在 | N/A | 存在 | N/A | 存在 |
| 注:N/A表示不会出现的情形。 | ||||||
设计波谱范围的关联函数如式(20)所示
式中,z3j代表B3j与A3*的关联度,Interest(A3*)、Interest(B3j)、Interest(B′3j)分别为A3*的兴趣度、B3j的兴趣度和B′3j的兴趣度。对于一维区间[a,b],凝聚在[a,b]上的兴趣度是对分布在区间[a,b]上的分布特征函数v(x)作定积分,如式(21)所示
3.3.2 空间范围元素项的关联函数
传统的可拓学是建立在一个维度上,而由经纬度描述的空间范围存在于二维空间,其复杂性呈指数增长。将空间范围理想解所在的二维区间称为A1*,第j个待分发信息空间范围所在的二维区间称为B1j,参考九交模型1[18],则A*与B1j之间的拓扑关系共存在36种不同的情形,见表 2。
| 纬度 | 经度 | |||||
| 相离 | 叠加 | 相等 | 相接 | 包含于 | 包含 | |
| 相离 | 相离 | 相离 | 相离 | 相离 | 相离 | 相离 |
| 叠加 | 相离 | 叠加 | 叠加 | 相接 | 叠加 | 叠加 |
| 相等 | 相离 | 叠加 | 相等 | 相接 | 被覆盖 | 覆盖 |
| 相接 | 相离 | 相接 | 相接 | 相接 | 相接 | 相接 |
| 包含于 | 相离 | 叠加 | 被覆盖 | 相接 | 包含于 | 叠加 |
| 包含 | 相离 | 叠加 | 覆盖 | 相接 | 叠加 | 包含 |
对二维区间B1j进行线性变换,目的是将B1j的中心平移至A1*的中心,如式(22)所示
式中,B′1j为线性变换后产生的新的二维区间;ax*-和ax*+分别为A1*经度范围的下限和上限;ay*-和ay*+分别为A1*纬度范围的下限和上限;bxj-和bxj+分别为B1j经度范围的下限和上限;byj-和byj+分别为B1j纬度范围的下限和上限。A1*与变换后的B′1j之间的拓扑关系存在9种可能的情形,见表 3。
| 纬度 | 经度 | |||||
| 相离 | 叠加 | 相等 | 相接 | 包含于 | 包含 | |
| 相离 | N/A | N/A | N/A | N/A | N/A | N/A |
| 叠加 | N/A | N/A | N/A | N/A | N/A | N/A |
| 相等 | N/A | N/A | 相等 | N/A | 被覆盖 | 覆盖 |
| 相接 | N/A | N/A | N/A | N/A | N/A | N/A |
| 包含于 | N/A | N/A | 被覆盖 | N/A | 包含于 | 叠加 |
| 包含 | N/A | N/A | 覆盖 | N/A | 叠加 | 包含 |
根据变换前后B1j、B′1j与A1*的拓扑关系,设计关联函数如式(23)所示
式中,z1j代表B1j与A1*的关联度;Interest(A1*)、Interest(B1j)、Interest(B′1j)分别为A1*、B1j和B′1j的兴趣度。对于二维区间〈[a,b],[c,d]〉,凝聚在〈[a,b],[c,d]〉上的兴趣度是对分布在〈[a,b],[c,d]〉上的分布特征函数作定积分,如式(24)所示
3.3.3 时间范围与空间分辨率元素项的关联函数与波谱范围类似,用户在对时间和空间分辨率进行检索时,常采用区间数来表达需求范围。但是由于遥感成像几乎是瞬时完成的,因此待分发信息的时间元素项更适合作为一个点来处理。空间分辨率亦是如此。对于这两类元素项,其理想解与待分发信息只存在两种关系,即包含和相离。在相离的情况下,与理想解的距离越小,则对用户兴趣的满足程度越大。因此这两类元素项的关联函数不同于上述情况,如式(25)所示
式中,zij代表Bij与理想解Ai*的关联度;bij同时为Bij的下限和上限(此时区间退化为一个实数);vB为Bij所落入区间单元的分布特征值。
3.4 多属性决策支持的效用度计算从决策理论的角度来看,效用度指备选方案与理想解的相对贴近程度,效用度越大则该方案越接近理想解,越能满足用户的兴趣[19, 20]。因此,可以通过计算效用度来定量评价待分发信息对用户兴趣的满足程度,备选方案Bj的效用度uj即为各个元素项关联度zij的加权和,计算方法如式(26)所示
式中,zij为Bij与理想解Ai*的关联度;wi为元素项xi的权重。 4 实例分析
为了便于对比分析,本文 选择文献[11, 12]中的检索记录生成用户模型,包含5项元数据项:经度范围、纬度范围、时间范围、波谱范围和空间分辨率范围,检索总次数15次。收集到的检索记录样本值如下。
(1) 地理经度范围(东经,单位为度):{[100.00,110.00],[101.00,108.00],[101.00,106.00],[101.00,104.00],[102.00,104.00],[102.50,104.00],[101.50,104.00],[102.00,104.00],[102.50,104.00],[101.50,104.00],[101.00,104.00]}
(2)地理纬度范围(北纬,单位为度):{[28.00,34.00],[28.00,33.00],[29.00,32.00],[29.00,32.00],[30.00,32.00],[30.50,32.00],[30.00,32.00],[31.00,32.00],[31.00,32.00],[31.00,32.00],[31.00,32.00]}
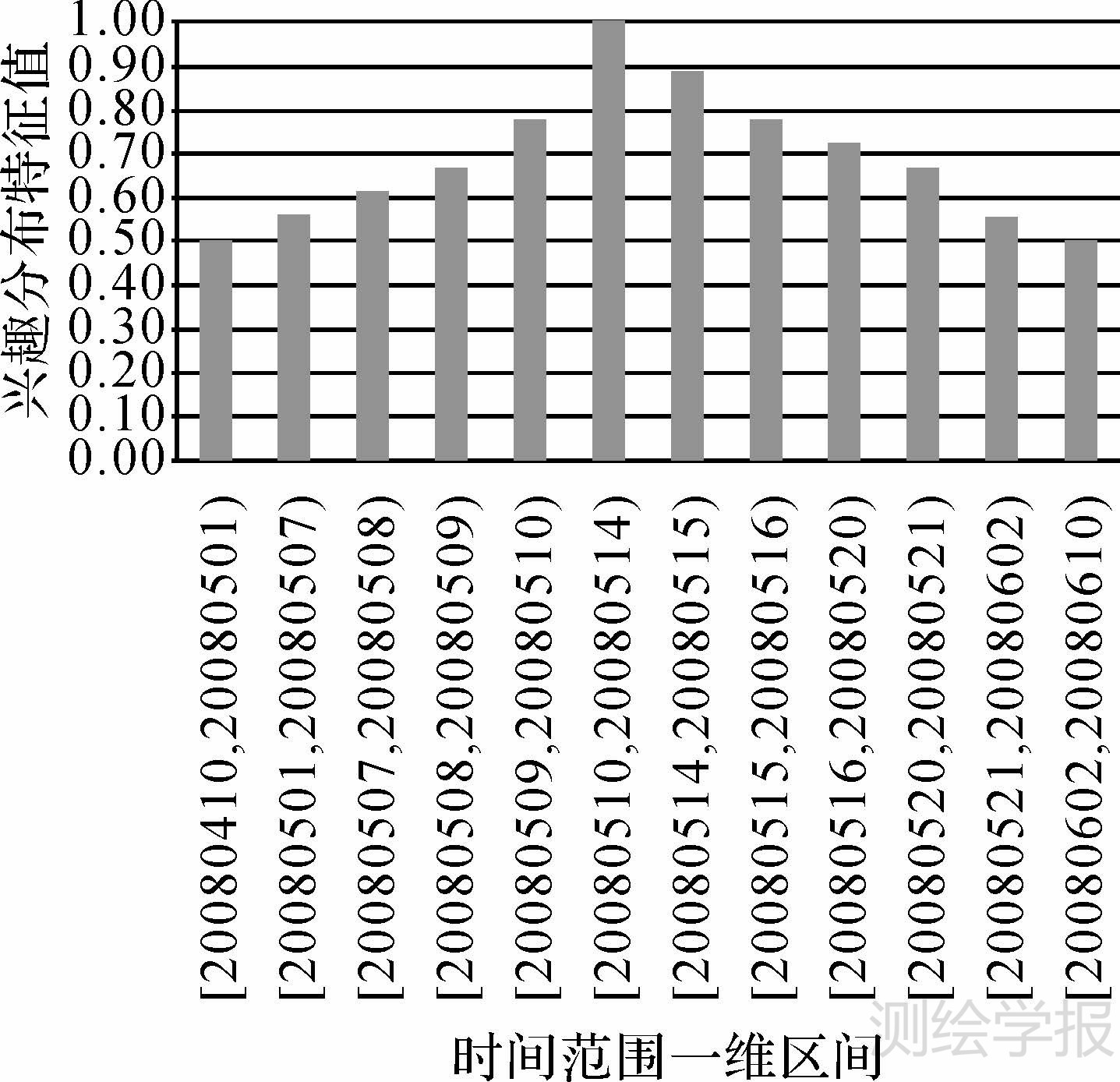
(3)时间范围(格式:年年年年月月日日):{[20080410, 20080514],[20080510, 20080515],[20080509, 20080509],[20080509, 20080509],[20080510, 20080510],[20080507, 20080507],[20080510, 20080510],[20080508, 20080508],[20080501, 20080501],[20080510, 20080510]}
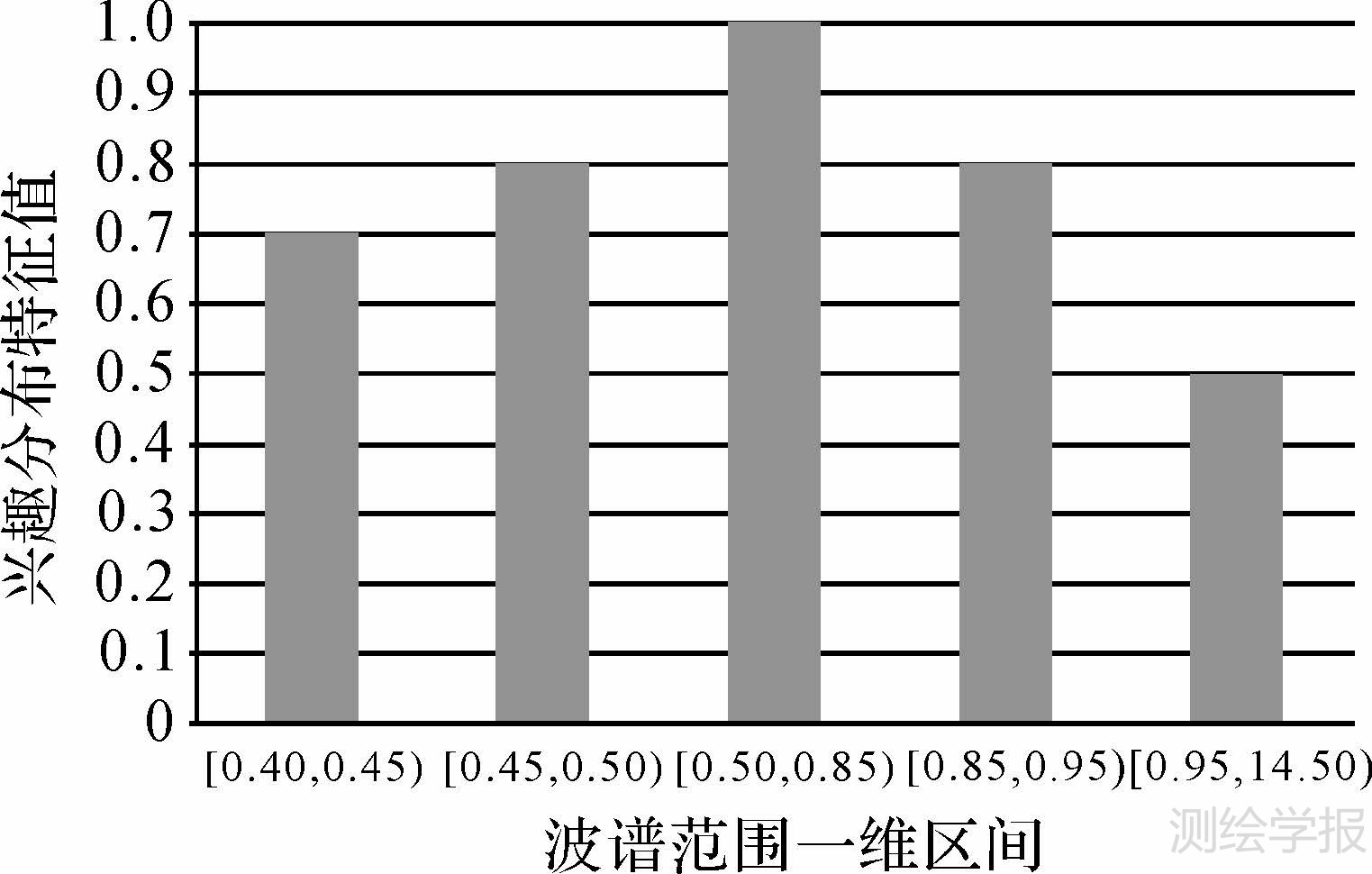
(4)波谱范围(单位μm):{[0.40,14.50],[0.45,0.90],[0.50,0.80],[0.50,0.80],[0.40,0.90],[0.40,14.50],[0.40,0.90]}
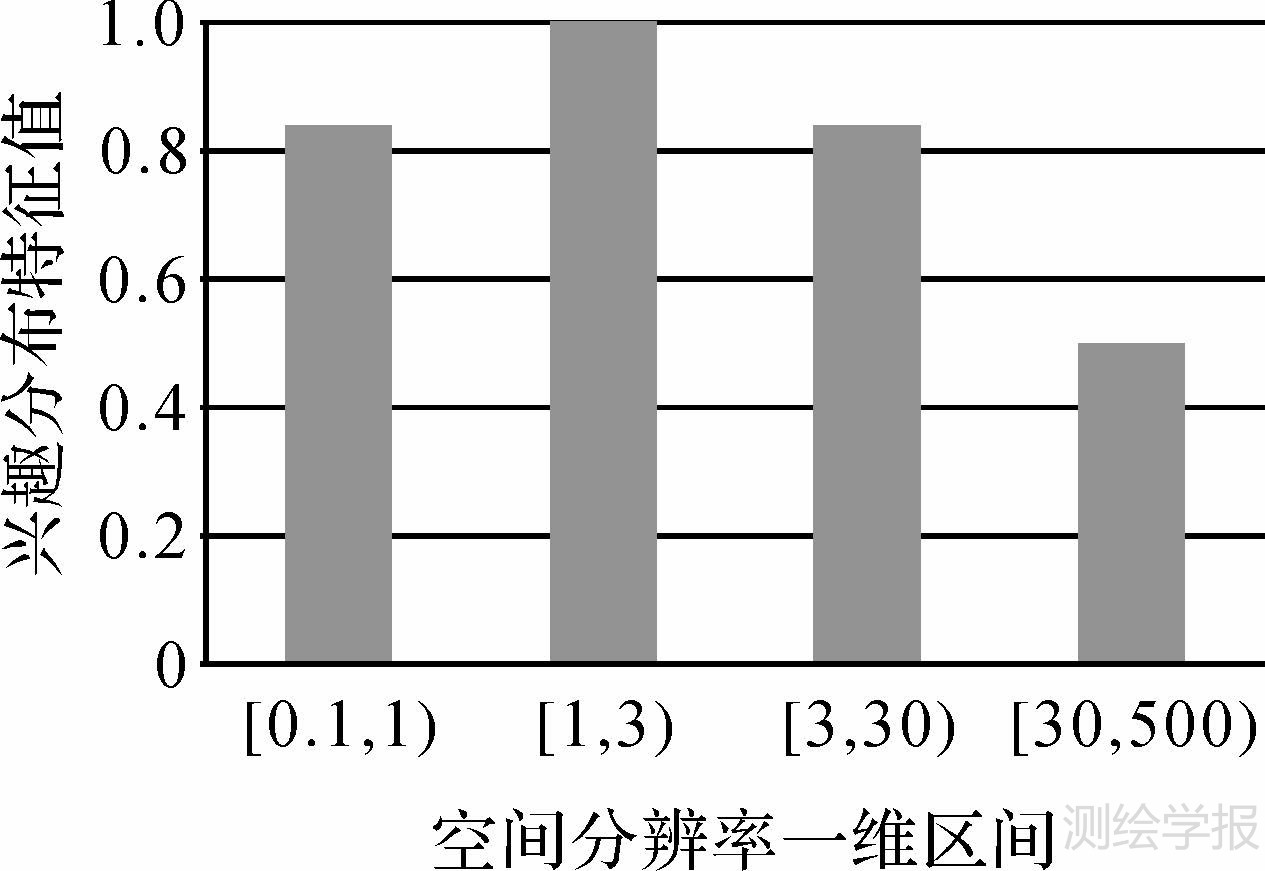
(5)空间分辨率范围(单位m):{[0.1,30.0],[0.1,10.0],[10.0,10.0],[0.1,3.0],[1.0,2.5],[0.1,30.0],[0.1,10.0],[30.0,500.0],[0.1,30.0]}
经纬度范围的最小二维区间D=〈[100.00,110.00],[28.00,34.00]〉,经度方向取最大步长rxstep=0.50,则沿经度方向均匀分割为20个区间单元,纬度方向取最大步长rystep=0.50,则沿纬度方向均匀分割为12个区间单元。现将经纬度综合考虑,则共划分240个二维区间单元,其特征值分布如图 3所示。时间范围元素项x2的最小区间I2=2[20080410, 20080410],取最大步长rstep=1,则I2均匀分割为61个区间单元,其分布特征值如图 4所示。波谱范围元素项x3的最小区间I3=[0.40,14.50],取最大步长r3step=0.05,则I3均匀分割为282个区间单元,其分布特征值如图 5所示。空间分辨率范围元素项x4的最小区间I4=[0.1,500.0],取最大步长r4step=0.10,则I4均匀分割为4999个区间单元,其分布特征值如图 6所示。

|
| 图 3 空间范围的用户兴趣特征分布 Fig. 3 User interest feature distribution of spatial range |
|
| 图 4 时间范围的用户兴趣特征分布 Fig. 4 User interest feature distribution of time range |
|
| 图 5 波谱范围的用户兴趣特征分布 Fig. 5 User interest feature distribution of spectral range |
|
| 图 6 空间分辨率范围的用户兴趣特征分布 Fig. 6 User interest feature distribution of resolutionrange |
取各元素项上具有最大的分布特征值的区间单元构成的集合,得到理想解A*={〈[102.5,104.5],[31.0,32.5]〉,[20080510, 20080510],[0.5,0.85],[1, 3]}
模拟生成近一段时间用户对各元素项的检索次数如表 4所示,然后根据2.1节的熵权法得到用户模型各元素项的权值,将该结果与文献[11, 12]中的元素项权值对比如表 5所示。
| 序号 | 空间范围 | 时间范围 | 波谱范围 | 空间分辨率 | 总样本数 |
| 1 | 11 | 10 | 7 | 9 | 15 |
| 2 | 16 | 12 | 9 | 11 | 18 |
| 3 | 10 | 9 | 7 | 8 | 14 |
| 4 | 20 | 16 | 12 | 15 | 25 |
| 5 | 18 | 12 | 10 | 12 | 20 |
| 6 | 21 | 15 | 11 | 15 | 24 |
| 7 | 16 | 10 | 8 | 9 | 16 |
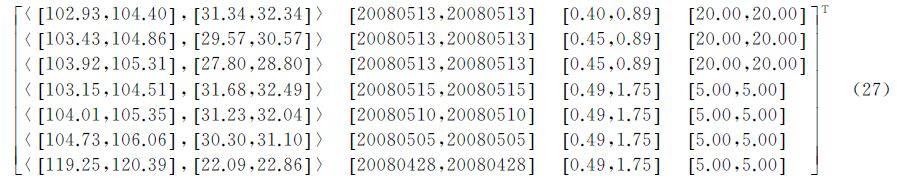
选择文献[11, 12]中方案1—方案7的试验数据作为备选方案集,{x1,x2,x3,x4}作为决策属性集,建立决策矩阵如式(27)所示。
利用3.3定义的关联函数计算各元素项的关联度及各备选方案的效用度如表 6所示。
决策方案的排序为:方案1>方案5>方案4>方案2>方案3>方案6>方案7。若设置阈值为0.5,则满足用户兴趣的待分发数据集为{方案1,方案2,方案3,方案4,方案5}。对比发现,本文所得的7个方案的效用度排序与文献[11, 12]的结果大体一致,但相较于其他两种模型,本模型中各方案的效用度均存在不同程度的变化,原因主要有以下几点:①本文利用熵权法根据用户近期的检索行为数据求解元素项的权值,权值会随时间推移发生变化,提高了用户模型的时效性;②相较于其他两种模型,空间范围的权重有所增加,这是由于本文将经度和纬度综合起来作为一个整体考虑,文献[11, 12]将经度和纬度作为两个独立的元素项会降低效用度的计算结果的准确性,比如某些在二维空间上根本不相交的空间范围,其在经度或纬度上的分量却可能是相交或相等的,相比而言,本方法更符合遥感信息在空间上的二维覆盖特征;③本文将关联度引入模型的构建中,从一维和二维空间上分析了不同元素项的覆盖区间与理想解之间的拓扑关系,其反映各方案优劣程度的准确性更高。
5 结 论遥感信息多源、多时相、多分辨率的特点使得用户兴趣特征的获取与描述存在困难,目前仍然欠缺主动、个性化、准确的遥感信息服务方法。建立用户模型是发现和获取与用户兴趣相关的知识的过程,是实现智能服务的基础。本文在现有遥感信息用户模型的基础上加以改进,根据用户近期的检索历史记录采用熵权法确定权重,提高了模型的时效性。本文提出了用户模型驱动的遥感信息主动推荐方法,通过构建决策矩阵将主动推荐问题转化为多属性决策问题;引入了关联度、兴趣度和效用度等概念用于描述待分发信息对用户兴趣的满足程度;通过分析待分发信息与理想解覆盖区间之间的拓扑关系,探索性地建立了关联函数定量计算关联度。试验表明,本文方法能够从用户的检索记录中获取用户的兴趣特征,提高了遥感信息智能服务的准确度。
本文只针对4项核心元数据进行了分析,今后将继续根据其他元数据(如传感器、轨道号、产品级别、数据质量等)研究用户兴趣的建模和评价方法。此外,关联函数还有待于进一步优化。以空间分辨率为例,由于低分辨率的影像可由高分辨率影像重采样而来,因此分辨率高于理想解的遥感信息的关联度应大于分辨率低于理想解的遥感信息的关联度。这就要求在设计关联函数时,除了考虑区间覆盖的拓扑关系外,还应该与实际应用相关联,才能不断提升遥感信息服务的智能化水平。
| [1] | LI Deren, ZHANG Liangpei, XIA Guisong. Automatic Analysis and Mining of Remote Sensing Big Data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12):1211-1216.(李德仁,张良培,夏桂松. 遥感大数据自动分析与数据挖掘[J]. 测绘学报, 2014, 43(12):1211-1216). |
| [2] | XU Hailing, WU Xiao, LI Xiaodong, et al. Comparison Study of Internet Recommendation System[J]. Journal of Software, 2009, 20(2):350-362.(许海玲,吴潇,李晓东,等. 互联网推荐系统比较研究[J]. 软件学报, 2009, 20(2):350-362). |
| [3] | LIU Lin, LI Deren, LI Wanwu, et al. Thoughts on Smarter Planet from the View of Geomatics[J]. Geomatics and Information Science of Wuhan University, 2012, 37(10):1248-1251.(柳林,李德仁,李万武,等. 从地球空间信息学的角度对智慧地球的若干思考[J]. 武汉大学学报:信息科学版, 2012, 37(10):1248-1251). |
| [4] | WU Lihua, LIU Lu. User Profiling for Personalized Recommending Systems:A Review[J]. Journal of the China Society for Scientific and Technical Information, 2006, 25(1):55-62.(吴丽花,刘鲁. 个性化推荐系统用户建模技术综述[J]. 情报学报, 2006, 25(1):55-62). |
| [5] | ZENG Chun, XING Chunxiao, ZHOU Lizhu. A Survey of Personalization Technology[J]. Journal of Software, 2002, 13(10):1952-1961.(曾春,邢春晓,周立柱. 个性化服务技术综述[J]. 软件学报, 2002, 13(10):1952-1961). |
| [6] | LIU Jianguo, ZHOU Tao, WANG Binghong. Progress of the Personalized Recommendation Systems[J]. Progress of Nature and Science, 2009, 19(1):1-15.(刘建国,周涛,汪秉宏. 个性化推荐系统的研究进展[J]. 自然科学进展, 2009, 19(1):1-15). |
| [7] | LINDEN G, SMITH B, YORK J. Amazon. com Recommendations:Item-to-item Collaborative Filtering[J]. IEEE Internet Computing, 2003, 7(1):76-80. |
| [8] | WANG Zegen, HUA Yixin. Research on Technology of Active Spatial Information Service[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(4):379-384, 389.(王泽根,华一新. 主动空间信息服务技术研究[J]. 测绘学报, 2006, 35(4):379-384, 389). |
| [9] | MOU Naixia, LIU Wenbao, ZHANG Lingxian, et al. Personalized Recommendations on Spatial Information Services[J]. Science of Surveying and Mapping, 2011, 36(3):104-106.(牟乃夏,刘文宝,张灵先,等. 空间信息服务的个性化问题[J]. 测绘科学, 2011, 36(3):104-106). |
| [10] | XIA Yu, ZHU Xinyan. Intelligent Spatial Information Delivery Decision-making by Using Interval Analysis[J]. Geomatics and Information Science of Wuhan University, 2013, 38(9):1103-1107.(夏宇,朱欣焰. 利用区间分析的空间信息智能分发决策[J]. 武汉大学学报:信息科学版, 2013, 38(9):1103-1107). |
| [11] | XIA Yu. The User Profile Model for Intelligent Delivery of Spatial Information[D]. Wuhan:Wuhan University, 2009.(夏宇. 面向空间信息智能分发的用户偏好模型研究[D]. 武汉:武汉大学, 2009.) |
| [12] | LI Xinguang, FAN Minghu, DU Wu. Research on Dynamic User Profile Model for Intelligent Distribution of Spatial Information[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(5):646-654.(李新广,范明虎,杜武. 面向空间信息智能分发的动态化用户偏好模型研究[J]. 测绘学报, 2011, 40(5):646-654). |
| [13] | HAWALAH A, FASLI M. Utilizing Contextual Ontological User Profiles for Personalized Recommendations[J]. Expert Systems with Applications, 2014, 41(10):4777-4797. |
| [14] | HAWALAH A, FASLI M. Dynamic User Profiles for Web Personalisation[J]. Expert Systems with Applications, 2015, 42(5):2547-2569. |
| [15] | COVER T M, THOMAS J A. Elements of Information Theory[M]. New York:Wiley-Interscience, 2006. |
| [16] | GIOVE S. Interval TOPSIS for Multicriteria Decision Making[C]//MARINARO M, TAGLIAFERRI R.Proceedings of the 13th Italian Workshop on Neural Nets-Revised Papers. Lecture Notes in Computer Science. Berlin:Springer,2002:56-63. |
| [17] | CAI Wen. Extension Theory and Its Application[J]. Chinese Science Bulletin, 1999, 44(17):1538-1548.(蔡文. 可拓论及其应用[J]. 科学通报, 1999, 44(7):673-681). |
| [18] | EGENHOFER M J. Deriving the Composition of Binary Topological Relations[J]. Journal of Visual Languages and Computing, 1994, 5(2):133-149. |
| [19] | YOONK P. System Selection by Multiple Attribute Decision Making[D]. Manhattan:Kansas State University, 1980. |
| [20] | TZENG G H, HUANG J J. Multiple Attributes Decision Making:Methods and Applications[M]. Boca Raton:CRC Press, 2011. |