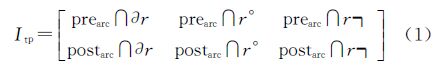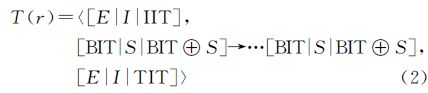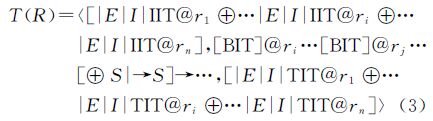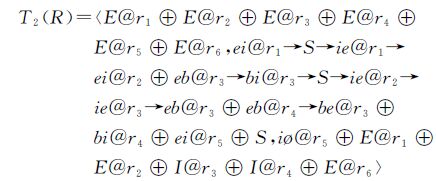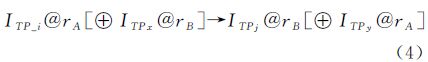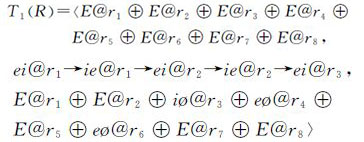2. 武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉 430079;
3. 地球空间信息技术协同创新中心,湖北 武汉 430079
2. State Key Laboratory of Information Engineering in Surveying Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
3. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, ChinaAbstract
1 引 言
伴随着各种定位技术的日趋成熟,以及移动终端的广泛应用,使得海量规模的移动对象的时空数据以轨迹的形式保存下来,给国内外学者提供了一个深入探索移动行为的契机,更拓展了全新的技术应用和服务领域[1]。近年来,众多学者围绕轨迹数据的组织管理[2, 3, 4, 5, 6]、索引查询[7, 8]和分析挖掘[9, 10, 11, 12, 13, 14, 15]等方面进行了大量研究,并取得了丰硕的成果。其中在轨迹数据组织方面比较典型的有, 文献[2, 3, 4]基于已有空间模块类型组织轨迹的点串数据,研制了一系列的轨迹数据库(如DOMINO[2]、SECONDO[3]和TrajStore[4]);文献[5]针对轨迹变化,基于Reeb图研究了轨迹数据的组织框架;文献[6]面向路网中移动数据,通过改进Douglas-Peucker算法实现了轨迹数据的高效压缩组织。
轨迹是对象在地理空间中移动过程的记录,其数据表现为携带对象位置与时间信息的离散时空点P(x,y,t)序列(例如P1→P2→P3→…)。从其空间特征出发,它在地理空间中的投影是有向线,称为轨迹线。显然,线-面拓扑关系方面的研究直接与本文密切相关。拓扑学在描绘轨迹移动相关的地理事件特性的认知中扮演者相当重要的角色[16, 17]。为了表达拓扑关系,文献[18]基于点集拓扑提出的9交模型区分出了19种线-面拓扑关系;文献[19]提出改进的9交模型能描述26种有向线与单区域间的拓扑关系;文献[20]基于Voronoi提出的空间代数区分出了拓扑关系中包括6种基本的线-面关系;文献[21]提出了线面目标间拓扑关系的层次表达方法,结合相应的图例,可以精确描述复合的线-面拓扑关系;文献[22]提出的组合描述可以得到97种线-面拓扑关系;文献[23-25]基于目标整体交-差和欧拉数提出的拓扑关系模型覆盖了19种线面拓扑关系;文献[26]通过引入节点度,进一步研究了线-面拓扑关系细分方法,总结出21种有意义的线-面单元交线类型。
回归到轨迹的本质,轨迹并不是简单的有向线,而是对象在空间中的移动过程记录,包含了对象在整个移动过程中的时间信息、位置信息以及特定的行为或移动模式。合理的组织和描述这些重要信息对于后续更进一步研究移动对象至关重要,比如游客轨迹中的停留行为对于行程规划的研究是至关重要的信息。当前轨迹描述或直接对原始的GPS点位序列数据进行组织(如前文所述),或以特定的语义标签描述特定环境中的移动对象轨迹(如文献[26]以兴趣点为节点和移动方式为弧段描述路网移动对象的轨迹),较少考虑从拓扑角度来研究对象轨迹的移动过程,更缺少轨迹相对于区域的拓扑过程研究。轨迹-区域的拓扑过程描述可以直观地反映出轨迹相对区域时空拓扑关系,以及移动对象的行为语义(如起始、终止、停留等),且不受特定环境限制,即路网中的移动(如车辆在路网中的移动)和自由空间移动的轨迹(如台风的移动)。此外,轨迹相对于多区域的拓扑过程尚未有研究涉及,而实际场景中移动对象轨迹往往游走于地理空间上多个区域之间。具体到应用的层面,轨迹-区域移动过程研究少涉及对于轨迹-区域拓扑过程查询分析方面的支持。
完整的时空拓扑过程模型不仅要从空间层面上描述对象轨迹与区域之间存在的线/面拓扑关系,还应当覆盖对象在其移动过程中附带语义的行为。轨迹相对于区域的移动过程中发生的起始点、终止点、交叠点和停留点所表达的语义对于研究轨迹-区域时空关系方面是至关重要的,本文将其统称为关键点。本文从拓扑角度出发,基于关键点来探讨轨迹与区域地理要素(面状)之间的时空过程,采用分解组合策略,将轨迹与地理要素之间的复杂拓扑过程分解为若干个局部拓扑关系,以基于点集拓扑的交叠模型判定拓扑语义,发掘不同区分能力的拓扑不变量;然后基于轨迹数据的时间特征与行为语义,结合STOP-MOVE的语义结构,设计轨迹-区域语义关联模型得到切合人们思维习惯的轨迹相对区域的全局拓扑过程表达,进而将该拓扑过程表达框架从轨迹-单区域的拓扑过程表达推广至轨迹-多区域的拓扑过程表达。
2 基于关键点的轨迹-区域拓扑过程模型 2.1 轨迹-区域关键点本文研究提取了轨迹移动过程中4类具有较强语义的行为:起始、终止、停留和交叠。在此基础上,以这些行为对应的关键点构建模型综合描述轨迹相对区域移动的拓扑过程。
显然,起始与终止分别对应轨迹的起点与终点。停留行为则指对象在地理空间中移动时,其轨迹数据采样点的空间位置分布在某一空间点的小邻域内超过某一给定的时间阈值。轨迹上发生停留行为的点称为停留点。而交叠行为指轨迹经过区域边界某点时,在该点邻域内轨迹线段与区域边界之间的局部拓扑关系发生改变。轨迹上发生交叠行为的关键点称为交叠点。下文首先将从轨迹-区域交叠点展开描述。
2.2 轨迹-区域交叠类型本节首先基于点集拓扑理论[16, 17],以轨迹线与区域(r)的3个拓扑分量(边界r,内部r°和外部r┑)的几何交叠形态来描述和区分轨迹与区域对象之间的局部拓扑关系。
定义1:交叠点(intersection point)。二维空间内,如果存在轨迹线与区域边界的一个公共点P,在以该点为中心,半径为ε(ε足够小且大于0)的邻域内,连接点P两端的轨迹线弧段不同时属于该区域边界时,则称P点为轨迹与区域的一个交叠点。
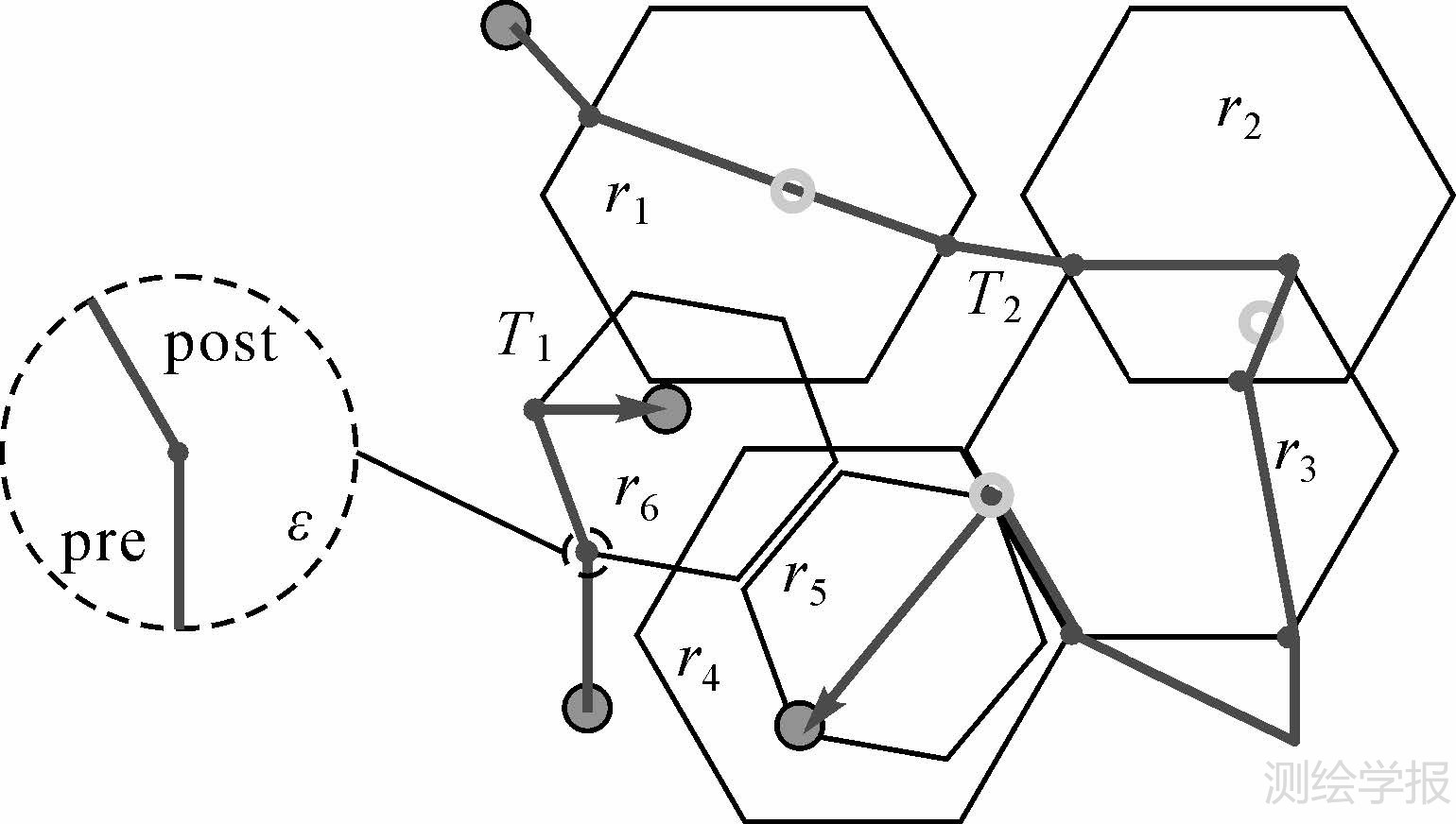
如图 1所示,邻域内沿时间轴方向进入交叠点的弧段称为交叠前弧段(pre_arc),离开交叠点的弧段称为交叠后弧段(post_arc)。本文将交叠点限定为0维交点,而轨迹线与区域边界一维交叠情况将被视作为在时间轴上的两个相邻交叠点。
|
| 图 1 轨迹-区域时空拓扑过程 Fig. 1 The topological process between trajectories and regions |
定义2:交叠类型Itp(intersection type)。在交叠点邻域中,交叠前弧段和交叠后弧段与区域3个拓扑分量组成的矩阵描述的轨迹与区域在该点处的局部拓扑特征。
交叠类型是轨迹与区域要素空间关系中的一个拓扑不变量。交叠类型矩阵的一般表达式为
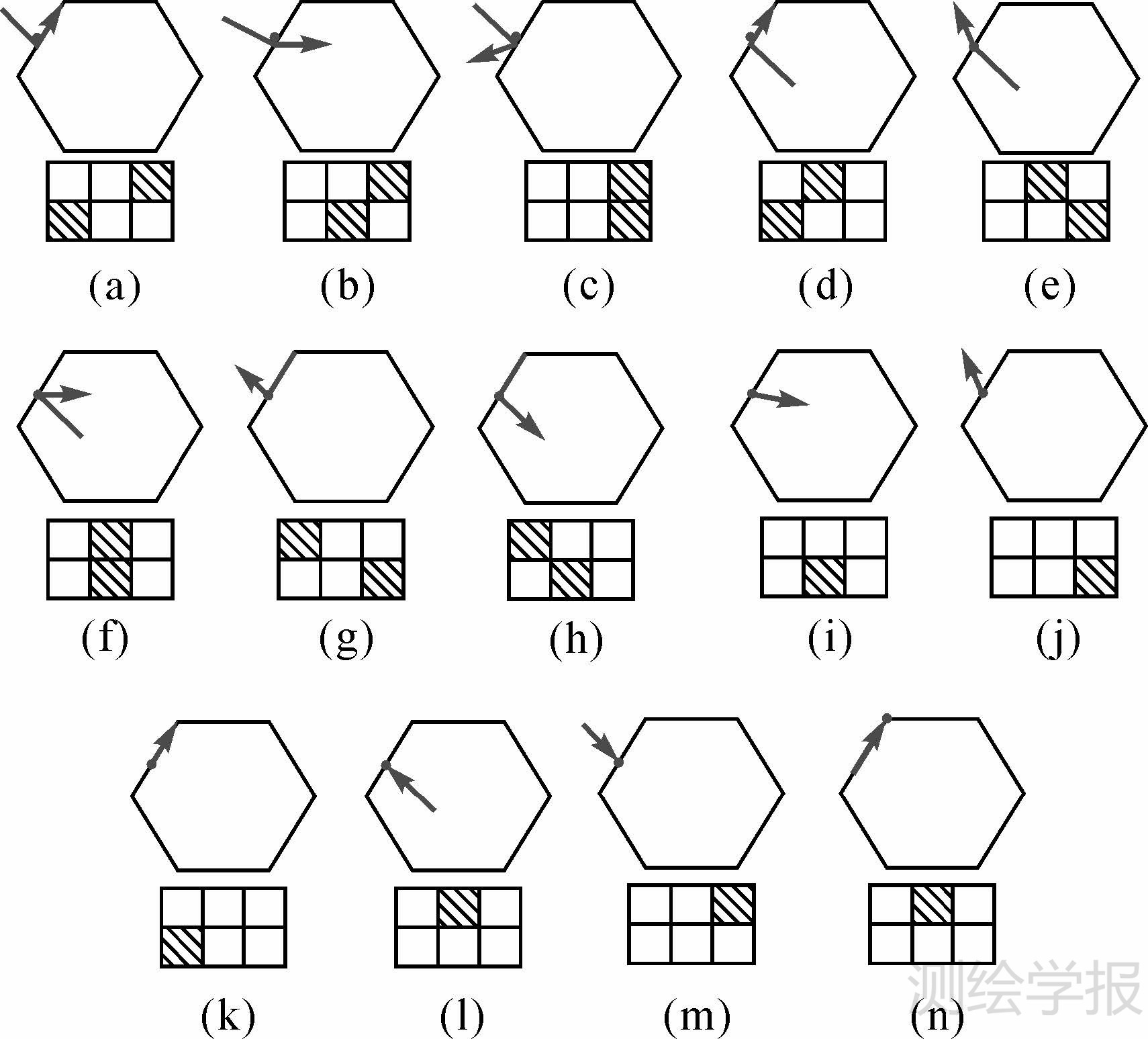
为了更直观表达,本文以3×2的方块矩阵图形表达对应于交叠类型矩阵中的元素[17],通过枚举验证所有可能组合的合理性,得到如图 2所示的14种不同的交叠类型。考虑到特定场景中交叠点的进入和离开弧段可能存在空值,则可将14种交叠类型划分为3类:基本交叠(basic intersection type,BIT),见图 2(a)-(h);起点交叠(initial intersection type,IIT),见图 2(i)-(k);终点交叠(terminal intersection type,TIT),见图 2(l)-(n)。
|
| 图 2 交叠类型 Fig. 2 Types of intersetion |
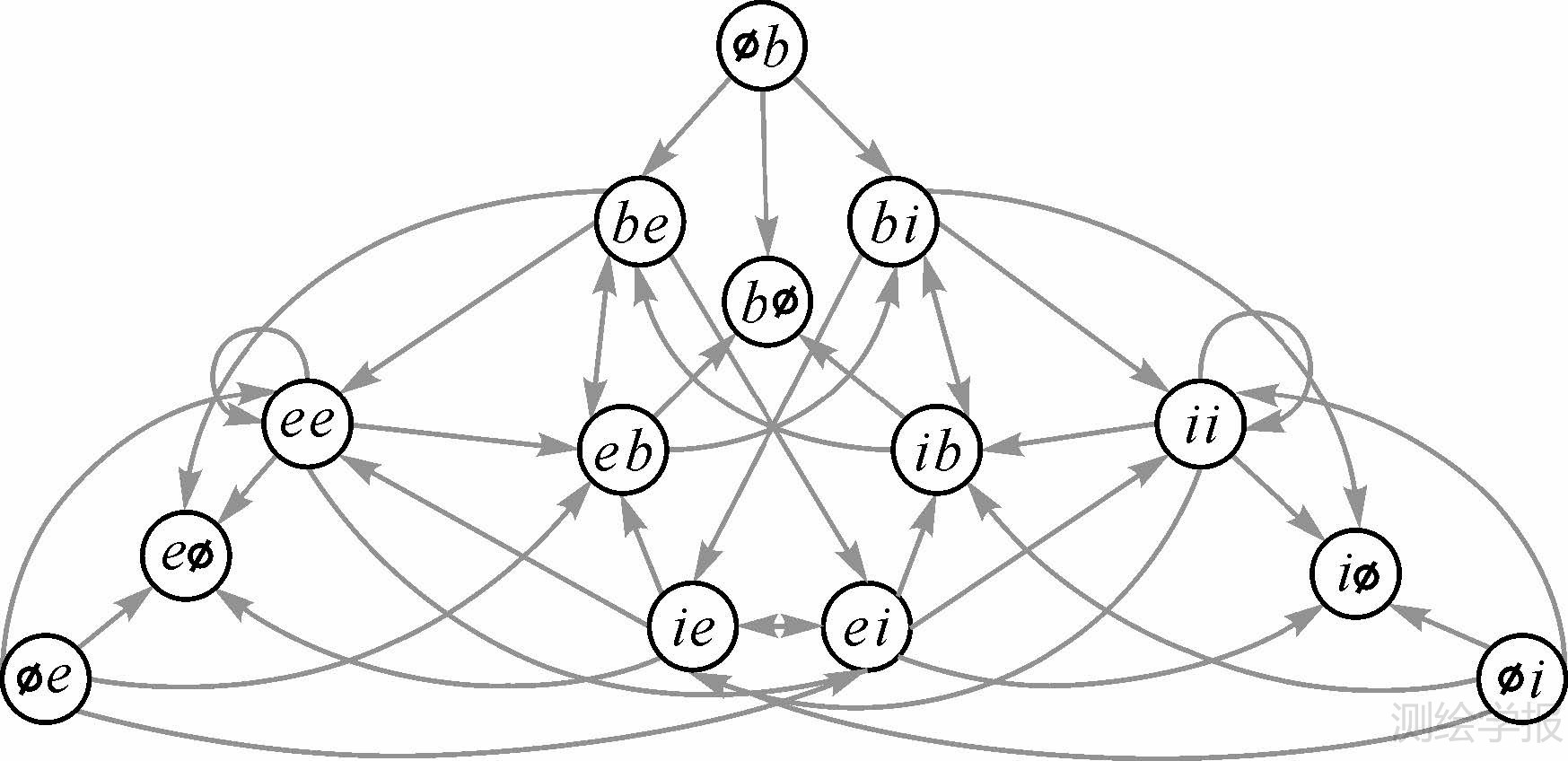
为简化表述,本文在交叠类型矩阵的基础上采用字符编码描述,弧段与区域3个拓扑分量的空交集记为Ø;非空交集分别记为:b(边界),i(内部)和e(外部)。这14种交叠类型在时间轴上存在42组概念邻居关系,组成了如图 3所示的概念邻域图。
|
| 图 3 交叠类型概念领域图 Fig. 3 Conceptual neighborhood diagram of intersection types |
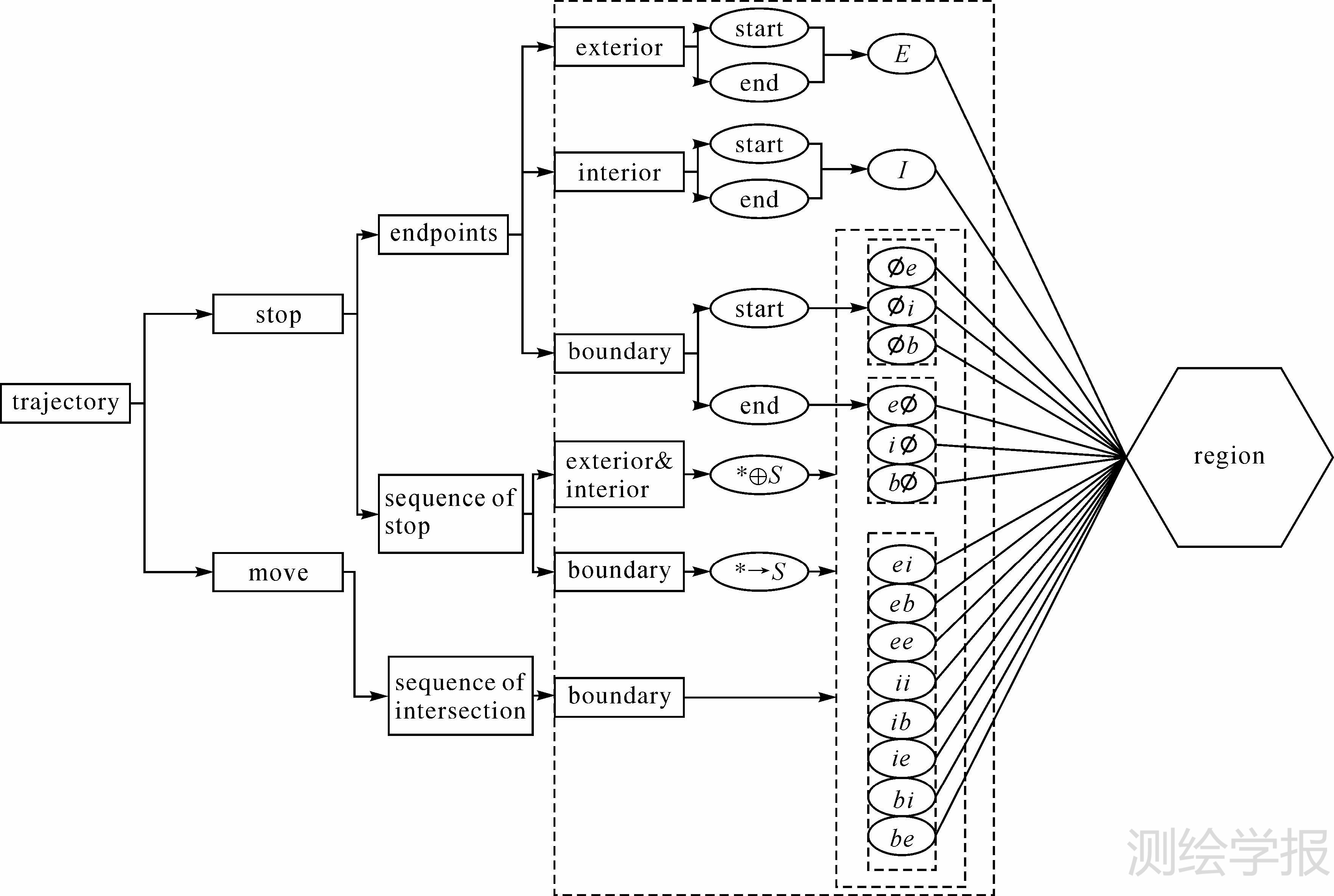
轨迹并非简单的有向线段,单纯的交叠关系并不能完全客观描述轨迹在真实地理环境中的移动状态。作者综合考虑轨迹拓扑关系与轨迹行为语义,从移动对象相对于区域的移动轨迹中提取反映轨迹-区域拓扑过程的关键点,构造轨迹中的STOP-MOVE语义对象,映射交叠序列,沿时间轴建立轨迹关键点与区域要素的语义关联模型,如图 4所示。实际场景中,一个关键点可能同时描述交叠与停留、交叠与起始或交叠与终止的轨迹语义行为。
|
| 图 4 轨迹-区域语义关联模型 Fig. 4 Semantic model between trajectories and regions |
模型中,“⊕”是语义区隔符,用于区隔关键点与区域要素之间所属的多个拓扑语义描述;“→”是关键点区隔符,用于区隔时间轴上不同的关键点。进而将轨迹-区域语义关联模型进行编码可以得到轨迹相对于单个区域的拓扑过程的三元组表达
式中,首项[E|I|IIT]与末项[E|I|TIT],即轨迹的起点和终点分别标记其与区域之间可能的拓扑关系;中间项,描述轨迹与区域之间的交叠以及停留语义。该编码中,必有首末两项,对应轨迹必有起点与终点;中间项可以为空,对应轨迹可能未与区域发生过交叠,或者轨迹过程中未发生停留行为等。由此,图 1中示例轨迹T1相对区域r6的拓扑过程可表达为:T1(r6)=〈E,eb→bi,I〉。模型中结合交叠类型的概念领域关系,通过沿时间轴顺序组合各种交叠类型(基本交叠、起点交叠和终点交叠)可以覆盖现有研究中常见的各类线/面空间关系和拓扑过程。例如,图 1中轨迹T1对于的区域r6的行为,表示为先外部进入区域边界(eb),再从区域边界进入到区域内部(bi)。依此类推,更多复杂的线面拓扑关系都能通过本模型表达。
3 轨迹的时空关系推导 3.1 多区域的时空拓扑关系描述在真实的场景中轨迹的移动过程可能会同时或者陆续遭遇多个区域要素。轨迹-区域语义关联模型沿轨迹T移动方向考查其与区域集合R中要素的局部语义关系集,先以轨迹与区域要素发生语义行为的关键点切分轨迹线段,然后再按时序组合一对多的语义关系的单元描述,从而得到轨迹对多个区域的拓扑过程编码一般表达式
式中,T(R)是轨迹T相对于区域集合R的拓扑过程描述;ri为R集合中的某个区域;@为区域关联符,与其前项的交叠类型和后项的交叠参与区域共同组成一次局部交叠描述;S为轨迹停留点(与stop序列对应)。需要指出的是,该模型在首尾两项分别针对轨迹的起始与终止两个关键点处,显式申明其相对于所有感兴趣区域的交叠类型,据此在后续的解析中(比如,提取其中某个区域的拓扑过程描述)可以不必通过附加的计算即可从中获取轨迹起止关键点相对于任意目标区域的拓扑关系,避免出现提取之后信息不完备的情况。由此,图 1中轨迹T2相对区域集合R(R={r1,r2,r3,r4,r5,r6})的拓扑过程描述为3.2 区域间的拓扑关系与轨迹移动模式
本质上区域之间的拓扑关系在空间和时间上约束了轨迹相对于区域的移动模式,表现在模型上为区域拓扑关系对于交叠行为的约束。本文通过解读模型中交叠序列上相接交叠中两次交叠行为特征,考查连续两个交叠点之间的概念邻居关系和相接交叠中隐藏的区域拓扑信息对轨迹移动模式的约束。
定义3:相接交叠。二维空间内,如果轨迹线上沿时间轴方向存在两个不同点先后与至少两个不同区域发生交叠,则称这两个交叠点为相接交叠。
交叠点在空间中可能同时与多个区域(本文着重考查两个区域,两个以上的区域可以在此基础上进行推导得出,限于篇幅不展开阐述)发生交叠,因此,研究相接交叠时还要考虑公共交叠点的存在。基于前文所述的“轨迹-区域交叠类型”,每个相接交叠都可以分解成n个交叠类型的组合,即为1-n的对应关系。
由此,可以得出相接交叠的一般表达式
式中,[]内的交叠关系为该交叠点在公共边界时,与其他区域发生的交叠关系。
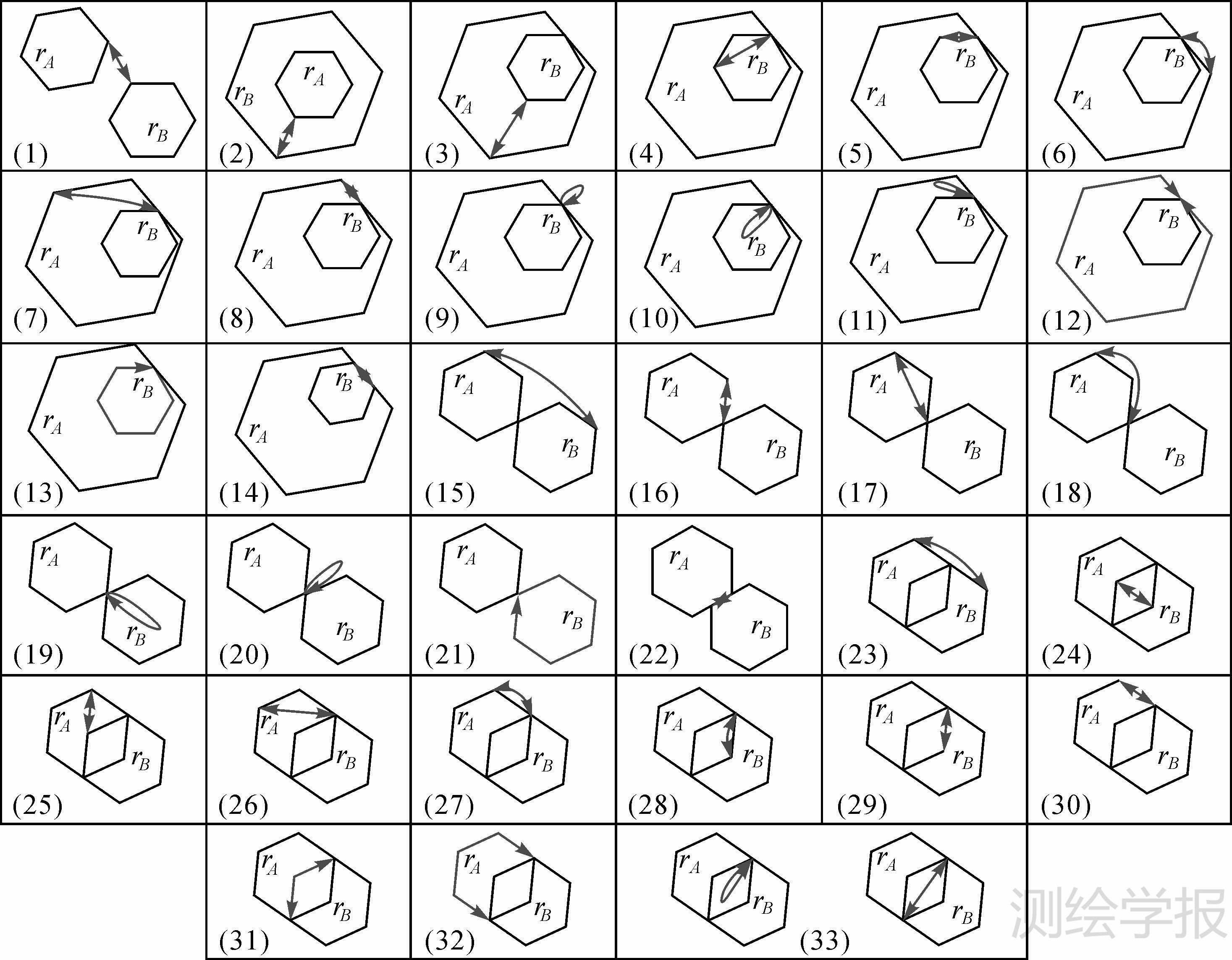
本文经过验证后得到如图 5所示的33种不同的相接交叠。
|
| 图 5 两区域拓扑关系对相接交叠的约束 Fig. 5 Contiguous intersections between two regions |
(1) 两个区域外相离时,相接交叠只表现出一种移动模式:“?e@rA→e?@ rB”,见图 5(1)(“?”表示可取任意合理字(限于篇幅本文不列出所有表达式)。
(2) 两个区域内相离时,相接交叠表现的移动模式有两种:“?i@rA→e?@rB”和“?i@rB→e?@ rA”,见图 5(2)。
(3) 两个区域内相切时,相接交叠表现的移动模式依据轨迹与区域公共边的关系,可分为公共弧段未经过公共边(图 5(3)),公共弧段一次经过公共边,见图 5(4)-(8),以及公共弧段两次经过公共边(图 5(9)-(14))。
(4) 两个区域外相切时,相接交叠表现的移动模式依据轨迹与区域公共边的关系,可分为(轨迹从rA到rB与从rB到rA的相接交叠是对称的):公共弧段未经过公共边(图 5(15)),公共弧段一次经过公共边(图 5(16)-(18)),以及公共弧段两次经过公共边(图 5(19)-(22))。
(5) 两区域相交时,相接交叠表现的移动模式依据轨迹与区域公共边的关系,可分为(轨迹从rA到rB与从rB到rA的相接交叠是对称的):公共弧段未经过公共边(图 5(23)-(25)),公共弧段一次经过公共边(图 5(26)-(30)),以及公共弧段两次经过公共边(图 5(31)-(33))。
(6) 两区域重叠时,轨迹相接交叠相对于rA到rB所表现的移动模式所受约束类似单区域情况下交叠类型概念邻域的约束(例如,两区域重叠时相接交叠不可能出现ie@rA→ie@rB的情况等)。
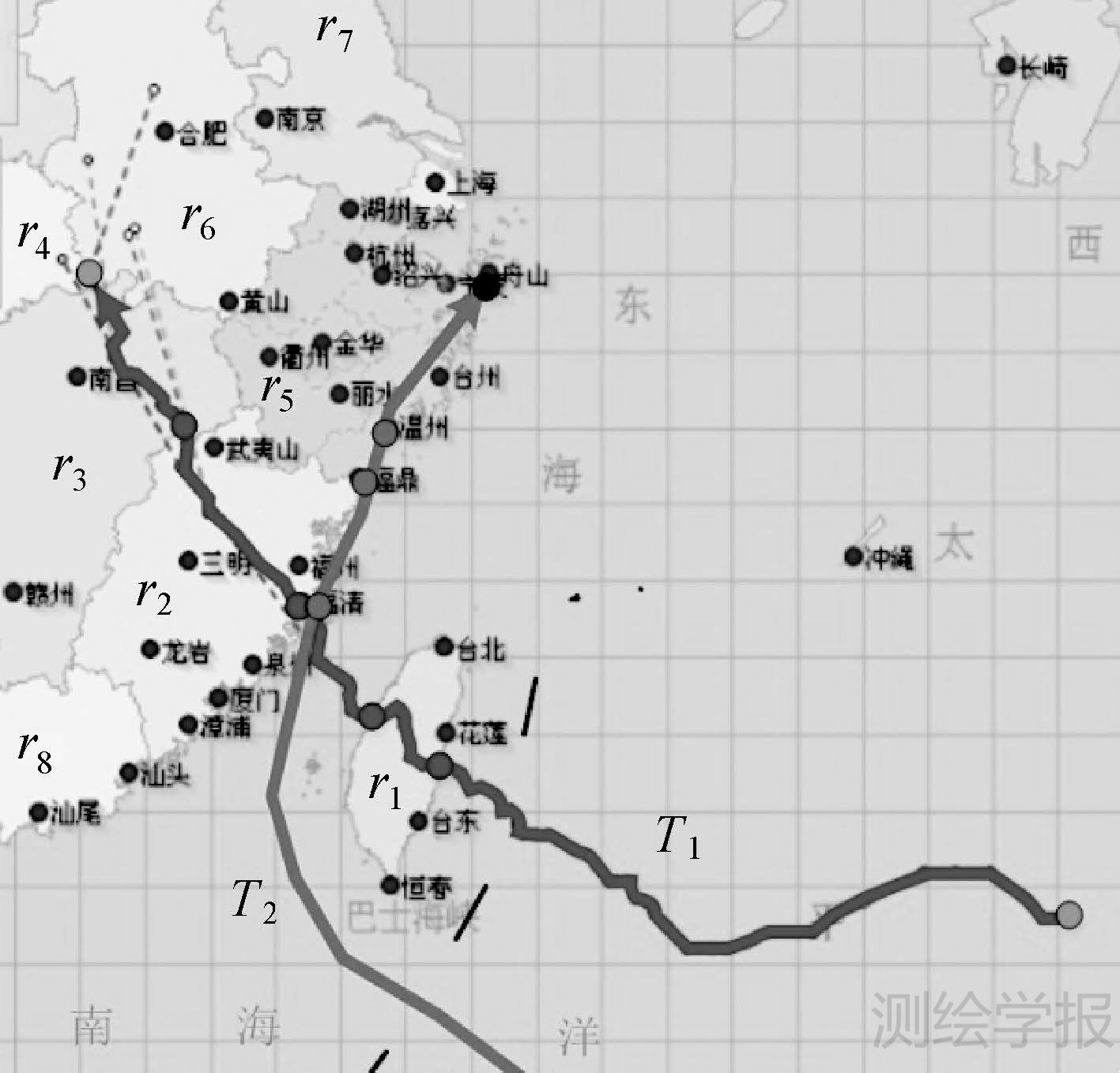
4 模型应用示例根据台风的原始移动轨迹数据,基于轨迹-区域拓扑过程模型,可以完整描述其相对过境区域之间的拓扑过程,不但可以提取台风行进的移动特征,同时还能为进一步的分析与挖掘提供支持。图 6为2008年8月台风“凤凰”与2001年1月的台风“飞燕”在中国东南沿海一带的移动路径图。
|
| 图 6 台风轨迹移动 Fig. 6 Movements of typhoon trajectories |
以“凤凰”为例,T1与中国东南部各地区之间的模型描述为
从其模型描述可以解读拓扑过程的完整信息:起于所有陆地区域之外的太平洋(E@r1⊕E@r2⊕E@r3⊕E@r4⊕E@r5⊕E@r6⊕E@r7⊕E@r8);依次穿过r1、r2两个区域,从r2、r3的共同边界进入r3区域(ei@r1→ie@r1→ei@r2→ie@r2→ei@r3);在r3中继续移动,最后在区域r3、r4和r6的边界交点处终止(E@r1⊕E@r2⊕i@r3⊕e@r4⊕E@r5⊕e@r6⊕E@r7⊕E@r8)。
5 结 论本文从空间拓扑关系出发,提出了一种基于关键点的轨迹-区域拓扑过程模型。该模型通过轨迹的起关键点,表达轨迹移动过程中所固有的拓扑不变量及语义信息。首先基于交叠关键点提出轨迹-区域交叠类型描述,以交叠类型矩阵分析确定了14种交叠类型,并采用字符编码表达,从局部拓扑关系开始讨论,进而依据交叠类型在单-多区域情况下的组合约束,设计轨迹-区域关联语义模型,导出切合人们思维习惯的符号化描述,直观表达轨迹-区域的全局拓扑过程,并在此表达框架上按一定约束完成复杂轨迹的时空推导。本文提出的面向关键点的轨迹-区域拓扑过程模型相对于其他模型,具有以下3个特点:
(1) 以起始点、终止点、交叠点以及停留点等作为轨迹-区域拓扑过程的关键点,从拓扑角度对其进行语义描述,以表达轨迹相对于区域的随时间演变的语义拓扑关系。
(2) 轨迹对于区域而言,其关键点表达的拓扑特征仅在局部范围内有效,据此,引入关键点邻域概念,在此基础上建立邻域内的交叠类型矩阵,并进行简单直观地编码表达,例如,eb@r3表示轨迹从外部进入区域r3的边界,且沿着边界方向移动。
(3) 在关键点编码的基础上,提出了轨迹-区域拓扑过程模型,不仅可以有效表达轨迹相对于单个区域以及多个区域间各种复杂的拓扑过程,还能反映区域间的拓扑关系对于轨迹在区域间移动模式的约束。
本文后续的研究工作将研究从原始轨迹数据中提取空间拓扑关系和停留点的算法,计算生成轨迹-区域拓扑过程模型,并考虑基于本文模型分析挖掘轨迹-区域拓扑移动过程的模式。
| [1] | ZHENG Yu, ZHOU Xiaofang. Computing with Spatial Trajectories[M]. New York:Springer, 2011. |
| [2] | WOLFSON O, SISTLA P, XU Bo, et al. Tracking Moving Objects Using Database Technology in DOMINO[C]//Proceedings of the 4th Workshop on Next Generation Information Technologies and Systems(NGITS).Zikhron-Yaakov, Israel:[s.n.], 1999:112-119. |
| [3] | GVTING R H, BEHR T, ALMEIDA V, et al. SECONDO:An Extensible DBMS Architecture and Prototype[J]. Collaborative Design, 2004:439-450. |
| [4] | CUDRÉ-MAUROUX P, WU E, MADDEN S. Trajstore:An Adaptive Storage System for Very Large Trajectory Data Sets[C]//ICDE Conference.[S.l.]:IEEE, 2010:109-120. |
| [5] | BUCHIN K, BUCHIN M, VAN KREVELD M, et al. Trajectory Grouping Structure[C]//DEHNE F,SOLIS-OBA R, SACK J R. Proceedings of the 13th International Symposium WADS. Berlin:Springer, 2013:219-230. |
| [6] | POPAI S, ZEITOUNI K, ORIA V, et al. Spatio-temporal Compression of Trajectories in Road Networks[J]. Geoinformatica,2015, 9(1):117-145. |
| [7] | VIEIRA M R, BAKALOV P, TSOTRAS V J. Querying Trajectories Using Flexible Patterns[C]//Proceedings of the 13th International Conference on Extending Database Technology.New York:ACM, 2010:406-417. |
| [8] | FRENTZOS E, GRATSIAS K, THEODORIDIS Y. Index-based Most Similar Trajectory Search[C]//Proceedings of the IEEE International Conference on Data Engineering.Istanbul:IEEE, 2007:816-825. |
| [9] | ZHENG Kai, ZHENG Yu, YUAN N J, et al. On Discovery of Gathering Patterns from Trajectories[C]//Proceedings of the IEEE International Conference on Data Engineering.Washington, D.C.:IEEE, 2013. |
| [10] | CAO Xin, CONG Gao, JENSEN C S. Mining Significant Semantic Locations from GPS Data[J]. Proceedings of the VLDB Endowment,2010, 3(1-2):1009-1020. |
| [11] | HADJIELEFTHERIOU M, KOLLIOS G, GUNOPULOSD, et al. On-line Discovery of Dense Areas in Spatio-temporal Databases[C]//HADZILACOST, MANOLOPOULOS Y, RODDICK J, et al. Advances in Spatial and Temporal Databases.Berlin:Springer,2003:306-324. |
| [12] | LEE J G, HAN Jiawei, LI Xiaolei. Trajectory Outlier Detection:A Partition and Detect Framework[C]//Proceedings of the IEEE International Conference on Data Engineering.Cancun, Mexico:IEEE, 2008:140-149. |
| [13] | QUDDUS M A,OCHIENG W Y, NOLAND R B. Current Map-matching Algorithms for Transport Applications:State-of-the-art and Future Research Directions[J]. Transportation Research Part C:Emerging Technologies, 2007, 15(5):312-328. |
| [14] | SPACCAPIETRA S, PARENT C, DAMIANI M L, et al. A Conceptual View on Trajectories[J]. Data & Knowledge Engineering,2008, 65(1):126-146. |
| [15] | YING J J C, LEE W C, WENG T C, et al. Semantic Trajectory Mining for Location Prediction[C]//Proceedings of the 19th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Chicago:ACM,2011:34-43. |
| [16] | KLIPPELA. Spatial Information Theory Meets Spatial Thinking:Is Topology the Rosetta Stone of Spatio-temporal Cognition?[J]. Annals of the Association of American Geographers,2012, 102(6):1310-1328. |
| [17] | EGENHOFER M J, FRANZOSA R D. Point-set Topological Spatial Relations[J]. International Journal of Geographical Information Systems,1991, 5(2):161-174. |
| [18] | KURATAY. Three-valued 9-intersection for Deriving Possible Topological Relations from Incomplete Observations[M]//SESTER M, BERNARD L, PAELKE V.Advances in GIS Science.Berlin:Springer,2009:289-308. |
| [19] | KURATAY. 9+-intersection Calculi for Spatial Reasoning on the Topological Relations between Heterogeneous Objects[C]//Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems. San Jose, CA:ACM, 2010:390-393. |
| [20] | LI Zhilin, ZHAO Renliang, CHEN Jun. A Voronoi-based Spatial Algebra for Spatial Relations[J]. Progress in Natural Science,2002, 12(7):528-536. |
| [21] | DENG Min, MA Hangying. The Hierarchical Representation of Topological Relations between a Line and an Area[J]. Acta Geodaetica et Cartographica Sinica,2008, 37(4):507-520.(邓敏,马杭英. 线与面目标间拓扑关系的层次表达方法[J]. 测绘学报,2008, 37(4):507-520). |
| [22] | GUO Qingsheng, CHEN Yujian, LIU Hao. Combinational Reasoning of Spatial Topological Relations between a Line and an Area[J]. Geomatics and Information Science of Wuhan University,2005, 30(6):529-532.(郭庆胜,陈宇箭,刘浩. 线与面的空间拓扑关系组合推理[J]. 武汉大学学报:信息科学版,2005, 30(6):529-532). |
| [23] | ZHOU Xiaoguang, CHEN Jun, LI Zhilin, et al. Computation of Topological Relations between Cadastral Objects Based on Euler-number[J]. Acta Geodaetica et Cartographica Sinica,2006, 35(3):293-298.(周晓光,陈军,李志林,等. 基于欧拉数的地籍拓扑关系计算[J]. 测绘学报,2006, 35(3):293-298). |
| [24] | ZHOU Xiaoguang, CHEN Jun, ZHAN FB, et al. A Euler Number-based Topological Computation Model for Land Parcel Database Updating[J]. International Journal of Geographical Information Science,2013, 27(10):1983-2005. |
| [25] | ZHOU Xiaoguang, CHEN Fei, CHEN Jun. A Node-degree Based Line/Region Topological Relationship Refinement Model and Its Applications[J]. Acta Geodaetica et Cartographica Sinica,2015, 44(4):445-452.(周晓光,陈斐,陈军. 引入结点度的线面拓扑关系细分方法与应用[J]. 测绘学报,2015, 44(8):445-452). |
| [26] | SESTERM, FEUERHAKE U, KUNTZSCH C, et al. Revealing Underlying Structure and Behaviour form Movement Data[J]. Künstliche Intelligenz,2012, 26(3):223-231. |
| [27] | EGENHOFER M J, MARK D M. Modeling Conceptual Neighborhoods of Topological Line-region Relations[J]. International Journal of Geographical Information Systems,1995, 9(5):555-565. |