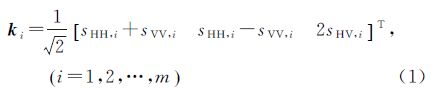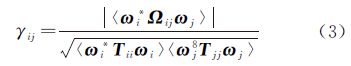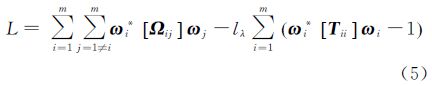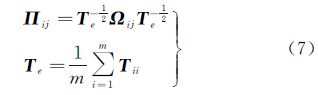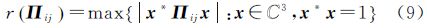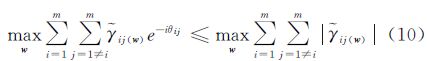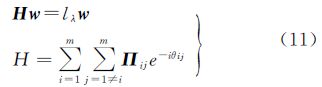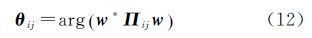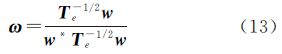2. 中国测绘科学研究院,北京 100830
2. Chinese Academy of Surveying and Mapping, Beijing 100830, ChinaAbstract
1 引 言
单极化干涉SAR处理中,默认配准后的像元具有相同的散射中心,但实际上每个像元所记录的是一个分辨单元内的平均散射信息,因此无法反映某一特定散射中心的实际高度[1]。极化最优相干技术可以提取一种最接近点散射体的散射机理,减少一个像元内因散射中心高度差引起的去相关,从而获得最优的干涉图。该技术常被用作植被参数反演[2, 3, 4]。常用的最优相干算法有奇异值分解(singular value decomposition,SVD)方法[5]和数值半径(numerical radius,NR)方法[6]。此外,多极化数据也被用来提高相位解缠精度[7]。
多基线极化最优相干技术将极化最优相干技术扩展到多基线数据中[8, 9, 10],在全局条件下寻找最优的干涉相位,统一同一景影像在不同干涉图中的散射中心,从而提高干涉相位精度。多基线极化最优相干技术有两种方法:多散射机理(multiple scattering mechanisms,MSM)方法和同散射机理(equal scattering mechanisms,ESM)方法。这些方法应用于差分干涉SAR (differential interferometric SAR,DInSAR)技术[11, 12]和永久散射体(persistent scatterer,PS)技术[13]中,可以比单极化条件下多获取数倍的候选点。将多基线极化最优相干技术和多基线干涉SAR技术相结合可以进一步提高DEM质量[14]。
本文方法是联合多景全极化影像,通过整体解算以保持每景影像在不同的干涉图中相同的散射中心,从而达到统一各干涉图散射中心的目的。由于每景影像的散射中心得以确定,因此降低了因散射中心不一致带来的相位误差,也提高了后续多基线干涉SAR高程反演的精度。
2 多基线极化最优相干技术利用传统的单基线极化最优相干方法处理多基线极化干涉SAR影像时,每次处理两景影像,获得一幅最优干涉图。而利用多基线最优相干方法处理时,可以同时处理所有数据,一次获得全部的最优干涉图。
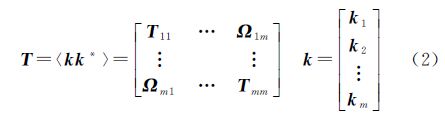
假设有m景全极化SLC数据,经过两两组合生成n=C2m幅干涉图如图 1(a)排列,纵坐标为主影像编号,横坐标为副影像编号。本文认为Ii,j和Ij,i为相同的干涉图,为表示方便,用Ii,j1≤i<j≤m表示第i景为主影像和第j景为副影像形成的干涉图。此时目标T在每一景全极化SLC数据中的散射机理如图 1(b)所示,ωi,j为单位复矢量,表示第i景影像在Ii,j中呈现的散射机理;ωj,i表示第j景影像在Ii,j中呈现的散射机理。最终导致目标T在每幅干涉图中对应的散射中心不一致,如图 2(a)所示。

|
| 图 1 多基线极化最优相干中干涉图和散射机理示意图 Fig. 1 Interferograms and scattering mechanisms in multibaseline PolInSAR coherence optimization |
多基线极化最优相干技术,综合全部的全极化SLC数据,使每一景影像在其所有涉及的干涉图中保持相同的散射机理,如图 1(c)所示,此时目标T在所有干涉图中对应的散射中心一致,如图 2(b)所示。

|
| 图 2 两两最优相干和全局最优相干的散射中心对比 Fig. 2 Comparison of scattering centers between single baseline and multibaseline PolInSAR coherence optimization |
与任意两景影像的单基线最优相干相比,全局最优相干获得的干涉图统一了每一景影像在不同干涉图中的散射中心。虽然一定程度上降低了相干性,但是基于全部可用的信息估计干涉相位,拥有更高的相位精度和可靠性。因此,利用全局最优相干获得的最优干涉图进行多基线干涉SAR高程反演具有更高的高程精度。
2.1 多基线极化最优相干准则多基线极化最优相干技术由于是在全局条件下获得全部最优干涉图,因此与单基线相比,其最优化准则需要包含全部相干信息。
对于每一景全极化SLC数据,按照Pauli基定义散射矢量
式中,sHH,i、sVV,i和sHV,i表示第i景影像HH通道、HV通道和VV通道的数据。此时的多基线极化相干矩阵为< 式中,〈·〉表示多视处理;*表示共轭转置;Tii=kik*i,包含极化信息;Ωij=kik*j,包含基线相关的极化和干涉信息。定义相干系数为
定义最优化函数作为全局最优化准则
通过对不同的散射机理,即ωi,进行组合,使式(4)达到最大值,从而完成最优相干的过程。
2.2 MSM多基线极化最优相干算法MSM方法是SVD方法在多基线条件下的拓展,认为不同影像的同名点对应不同的散射机理,即ωi≠ωj。为了获取式(4)的最大值,引入拉格朗日乘数lλ,定义拉格朗日方程
令式(5)的偏导数为0等价于广义特征值问题
求解出最大的特征值,其平方根即为相干系数。利用ωi计算最优相干系数和对应各基线的干涉相位。
2.3 ESM多基线极化最优相干算法ESM方法是NR方法在多基线条件下的拓展,认为不同影像的同名点对应相同的散射机理,即ωi=ωj=ω。定义矩阵Πij及其对应的复相干系数ij和数值半径rΠij
式中,C3表示三维复数域。为了去除相干系数取模的运算,引入相移量θij∈-π,π,θji=-θij,满足如下不等式
式中,为相干系数的复数形式。式(10)中,不等式右侧的最大值确定,左侧部分的最大值取决于相移量θij。当相移量与最优相干条件下的干涉相位相等时,式(10)为等式。ESM算法无法直接计算最优相干相位和对应的散射矢量,需要迭代计算。最优的散射矢量通过求解厄米特矩阵H的最大特征值及其对应的特征向量获得
计算最优的相移量
将式(12)的结果代入式(11)中重新计算最优散射矢量,迭代计算直至满足要求。
相移量初值通过求解矩阵Πij的迹得出,θij=argtraceΠij,并令λ=0。将相移量初值代入式(11),并与式(12)一起迭代计算。直到两次的lλ差值小于给定的小数ε,即lλmax-λ≤ε,停止迭代,并计算最优的散射矢量
2.4 MSM方法与ESM方法的比较
理论上,由于任意两次数据的获取条件存在差异,MSM方法的不同散射机理假设更接近客观事实,并且在一定程度上MSM方法具有更好的相位分辨率。
ESM方法由于强制限定了相同的散射机理,从而降低了对噪声的敏感度。但是受限于必须有相似的相干矩阵,因此当散射机理发生较大变化时,此方法不适用。
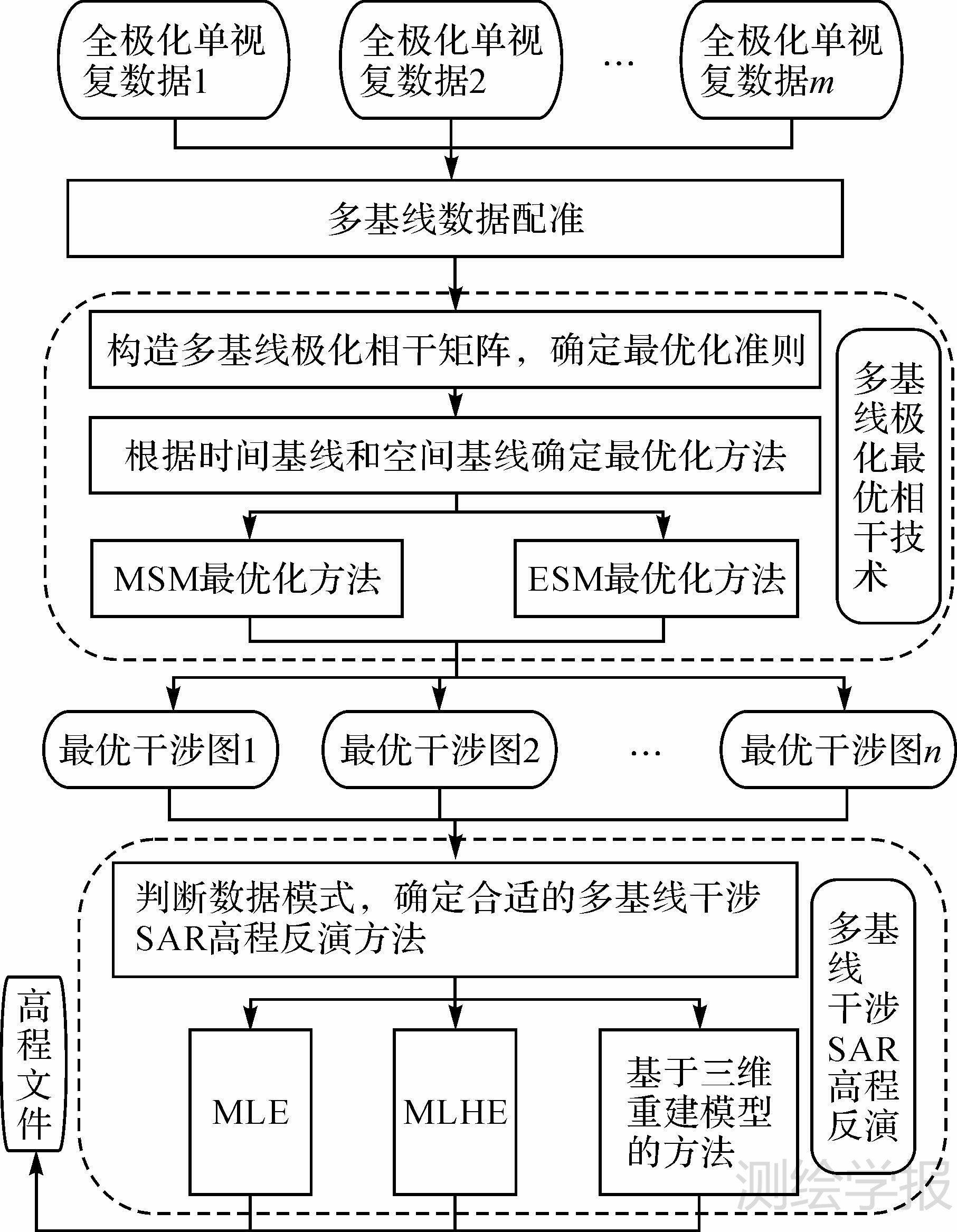
3 试验与分析3.1 多基线极化干涉SAR高程反演技术流程本文进行的基线极化干涉SAR高程反演方法分为两步,如图 3所示。
|
| 图 3 多基线极化干涉SAR高程反演流程 Fig. 3 Flow diagram of multi-baseline polarimetric InSAR elevation inversion |
首先进行多基线极化最优相干处理。在多基线全极化数据配准的基础上,按照Pauli基定义的散射矢量表示形式,构建多基线极化相干矩阵,确定最优化准则。根据时间基线和空间基线的长度选择采用MSM方法或ESM方法,再进行整体最优化估计,确定每一景影像的散射中心,获得各组干涉数据的最优干涉图。
由于本文方法面向多基线数据,因此,单基线的最优相干技术被认为是非全局的方法。
其次进行多基线干涉SAR高程计算。目前多基线干涉SAR高程反演方法主要分为估计干涉相位[15, 16, 17, 18]和计算高程[19, 20, 21, 22, 23, 24]两类。根据数据本身的特点选择合适的多基线高程反演方法。
本文共进行两个试验。在极化最优相干步骤,分别选择单极化、单基线极化最优相干方法和多基线极化最优相干方法。在多基线高程反演步骤,在第1个试验中选择最大似然估计(maximum likelihood estimation,MLE)方法[15],第2个试验选择基于三维重建模型(three-dimensional reconstruction mode,3DRe)的方法[25]进行多基线的高程反演试验。
3.2 国产机载X-SAR数据试验本试验采用工作在组合模式下的国产X-SAR机载双天线系统在海南获取的数据进行试验。雷达载波频率为9.6 GHz,垂直于航迹方向上基线长度为1.22 m。组合模式的工作方式是:假设载机的两副天线分别为A天线和B天线,在某一时刻,A天线发射信号,A、B两副天线均接收信号;在下一时刻B天线发射信号,A、B两付天线均接收信号。共计获取4景影像,按照信号发射、接收的顺序,将影像命名为AA、AB、BA和BB。
由于影像AB和BA的信号从发射到接收的路程是一致的,因此仅选择AA、BA和BB进行多基线干涉处理。图 4(a)、(b)和(c)分别为AA、BA和BB的Pauli基合成影像。由于干涉图intAA,BB的绝对干涉相位是intAA,BA和intBA,BB的两倍,因此可以将数据等效为基线长度为1∶2的多基线数据,适合MLE方法处理。数据处理中采用MLE方法进行相位估计,在极化方法上分别选择HH极化、SVD方法、MSM方法和ESM方法。数据处理结果如图 5所示,图中平面坐标为影像行列号。

|
| 图 4 Pauli影像及检查点分布 Fig. 4 Pauli images of experimental area and distribution of check points |

|
| 图 5 基于MLE多基线极化干涉SAR高程反演试验高程图 Fig. 5 Height map of multi-baseline polarimetric InSAR elevation inversion using MLE method |
表 1为不同极化最优相干方法获得结果的比较。从图 5中各方法获得的高程结果可以看出:
| 极化最优相干方法 | 噪声水平 | 强散射体处 | 高程精度 |
| HH极化方式 | 高 | 较明显 | 较低 |
| SVD方法 | 较低 | 较明显 | 较高 |
| MSM方法 | 较低 | 明显 | 低 |
| ESM方法 | 低 | 不明显 | 高 |
(1) 在影像最下端的空地为停放飞机的停机坪,飞机和建筑物在影像中表现为强散射体。MSM方法获得的相位存在较大误差,高程有较多错误值,SVD方法有所减轻,ESM方法不明显,单极化方法此处亦存在部分异常值。多基线方法由于融合了多组基线的数据,降低了由此带来的误差的影响,使得结果看起来更为光滑。停机坪本身为平地,SVD方法获得的结果较为粗糙,近似存在随机噪声,MLE_SVD结果有一定程度改善,ESM和MSM方法结果较好,其中ESM方法更为“平整”一些。
(2) 停机坪旁边的建筑物(图 6),MSM方法的结果中,该建筑物处高程值略高于周围,但是并不明显;SVD方法,此处虽高于周围但存在少量异常值;ESM方法结果较好;单极化方法则存在大量噪声,结果不明显。

|
| 图 6 停机坪附近结果 Fig. 6 Results of tarmac |
(3) 道路方面,SVD方法中的道路高程值明显低于周围,MSM方法和ESM方法在道路处高程略低。
选取检查点如图 4(d)所示,其精度结果如表 2所示。
| 方法 | C1 | C2 | C3 | C4 | C5 | 中误差 |
| MLE_HH | 5.11 | 11.10 | 1.99 | 6.63 | -2.06 | 6.35 |
| MLE_SVD | -5.58 | 2.00 | 1.44 | -3.96 | -8.65 | 5.06 |
| MLE_MSM | -9.01 | 1.87 | 1.13 | -5.12 | -10.95 | 6.81 |
| MLE_ESM | -5.04 | 5.86 | 1.99 | -1.13 | -6.38 | 4.60 |
从表 2中可以看出,ESM方法获得的高程精度最高,SVD方法次之,单极化方法和MSM方法获得的结果精度最低。
总体而言,无论是对噪声的削弱、强散射体干扰的抑制还是在检查点处的精度,MLE_ESM方法具有较好的效果和最高的精度。
3.3 ESAR系统数据试验试验采用德国宇航局(Deutsches Zentrum für Luft-und Raumfahrt,DLR)的E-SAR机载L波段SAR系统3次飞临同一地区获取的全极化数据,其相关系统参数如表 3所示。
| 参数 | 数值 |
| 载波频率/GHz | 1.3 |
| 极化状态 | HH、HV、VH、VV |
| 侧视方向 | 左侧视 |
| 飞行高度/m | 3670 |
| 方位向采样间隔/m | 0.49 |
| 距离向采样间隔/m | 1.50 |
| 视角/(°) | 42 |
| 地面平均高程/m | 600 |
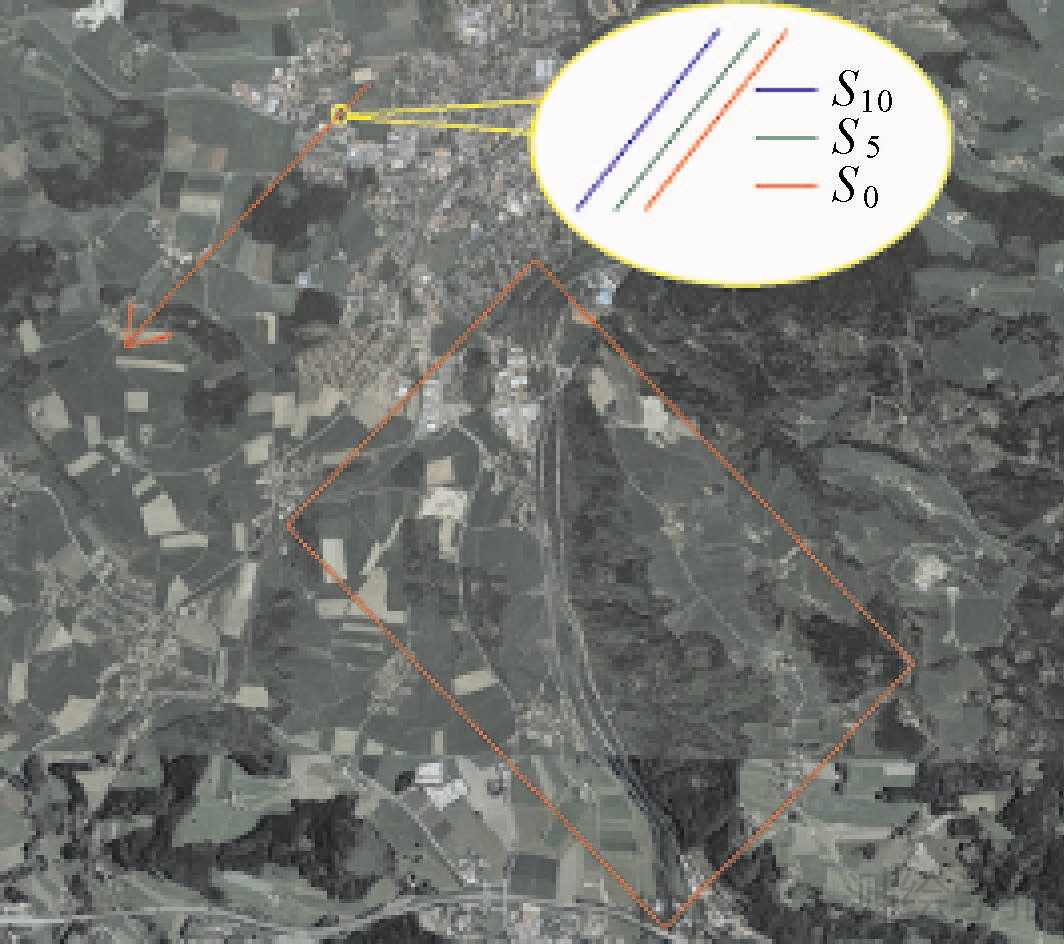
试验区位于Traustein小镇,包含树林、低矮草地和裸地。试验区光学影像如图 7所示,图中红色矩形区域为SAR影像覆盖的地面范围,红色箭头为飞行航线,椭圆内红色、绿色和蓝色表示3次航迹的相对关系,分别命名为S0、S5和S10,对应图 8(a)、(b)和(c)的影像。航线S0和S5空间间隔约为4.5 m,时间间隔约10 min;S5和S10空间间隔约为5.3 m,时间间隔约10 min。
|
| 图 7 试验区光学影像图 Fig. 7 Optical image of experimental area |

|
| 图 8 试验区Pauli影像 Fig. 8 Pauli images of experimental area |
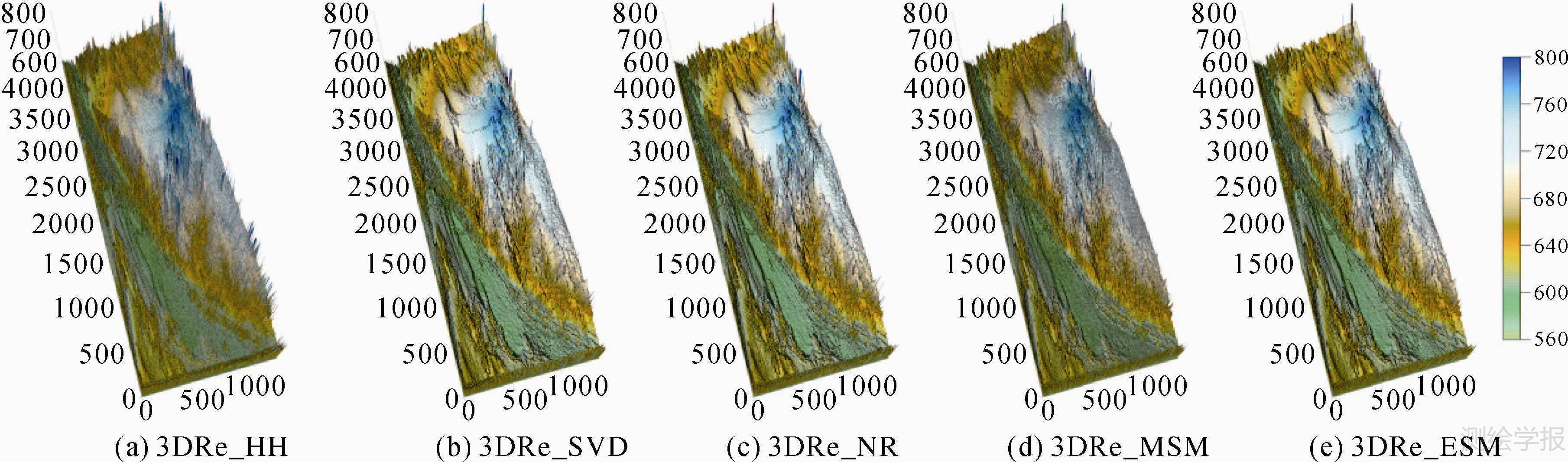
3景全极化数据共计组合为3组干涉数据,分别为 S0_S5、S0_S10和S5_S10。图 9为ESM方法获得的3幅干涉条纹图。数据处理中,在极化方法上分别选择HH极化、SVD方法、NR方法、MSM方法和ESM方法,在高程反演方法上选择3DRe多基线高程反演方法,获得的高程如图 10所示,图中平面坐标为影像行列号。

|
| 图 9 试验区干涉条纹图 Fig. 9 Interferograms of experimental area |
|
| 图 10 E-SAR数据获取的高程图 Fig. 10 Height map of the data obtained by E-SAR |
处理方法中,SVD和MSM同为基于不同散射机理的假设,而NR和ESM同为基于相同散射机理的假设。通过高程反演结果可以看出:
(1) 经过极化最优相干处理的结果,不管是两两极化最优相干还是全局最优相干,与单极化数据相比明显降低了噪声,获得高程更加平滑。图 10中,(a)为单极化干涉数据高程反演结果,其余为全极化干涉数据高程反演结果,单极化结果明显包含大量噪声。
(2) 在同散射机理假设的方法中,ESM方法优于NR方法。由于本试验中各景影像获取的时间间隔(最长20 min)和空间基线(最长10 m)均较短,很好地符合了同散射机理的假设,同时ESM方法的保证散射中心一致的优势更有利于处理多基线数据。
(3) 在不同散射机理假设的方法中,SVD方法优于MSM方法。由于MSM方法对噪声比较敏感,使得其对应的多基线结果反而劣于两两极化最优相干的结果。
(4) 在多基线极化最优相干中,ESM方法优于MSM方法。主要得益于ESM方法对噪声抑制作用,ESM方法获得的高程图 更加平滑。
(5) 上述结论对不同的多基线高程反演方法均适用。
4 结 论本文提出了面向多基线干涉SAR高程反演的全局最优相干方法,统一了进行多基线干涉SAR高程反演时各干涉图的相位中心,提高了干涉相位的精度和可靠性。通过大量试验得出如下结论:
ESM方法对噪声具有良好的抑制作用,即使是对强散射的目标,依然具有较高的相位精度,同时ESM方法保证了散射中心的一致,提高了多基线干涉SAR高程反演的精度。
MSM方法理论上更有优势,也能保证了散射中心的一致,但是其对噪声比较敏感,在处理过程中会放大噪声带来的误差。
但是本文试验中各景影像获取的时间间隔较短,试验1几乎同时获取,试验2时间间隔最大20 min。在如此短的时间内目标没有发生较大改变,试验数据比较接近同散射机理假设。下一步工作,应研究长时间基线条件下、目标散射机理发生较大改变时DEM的提取。
| [1] | WU Yirong, HONG Wen, WANG Yanping. The Current Status and Implications of Polarimetric SAR Interferometry[J]. Journal of Electronics & Information Technology, 2007, 29(5):1258-1263.(吴一戎,洪文,王彦平. 极化干涉SAR的研究现状与启示[J]. 电子与信息学报, 2007, 29(5):1258-1263). |
| [2] | SHI Lei. Vegetation Height and Underlying Ground Altitude Estimation Based on Multi-baseline PolInSAR Images[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(3):330-330.(史磊. 多基线PolInSAR植被高度与植被下地形估计[J]. 测绘学报, 2014, 43(3):330-330). |
| [3] | ZHU Jianjun, XIE Qinghua, ZUO Tingying, et al. Criterion of Complex Least Squares Adjustment and Its Application in Tree Height Inversion with PolInSAR Data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(1):45-51.(朱建军,解清华,左廷英,等. 复数域最小二乘平差及其在PolInSAR植被高反演中的应用[J]. 测绘学报, 2014, 43(1):45-51). |
| [4] | FU Haiqiang, ZHU Jianjun, WANG Changcheng, et al. Polarimetric SAR Interferometry Vegetation Height Inversion Method of Complex Least Squares Adjustment[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10):1061-1067.(付海强,朱建军,汪长城,等. 极化干涉SAR植被高反演复数最小二乘平差法[J]. 测绘学报, 2014, 43(10):1061-1067). |
| [5] | CLOUDE S R, PAPATHANASSIOU K P. Polarimetric SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(5):1551-1565. |
| [6] | COLIN E, TITIN-SCHNAIDER C, TABBARA W. An Interferometric Coherence Optimization Method in Radar Polarimetry for High-resolution Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(1):167-175. |
| [7] | HE Chu, SHI Bo, JIANG Houjun, et al. A Combined Multi-polarimetric InSAR Phase Unwrapping Algorithm Based on Conditional Random Fields[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6):838-845.(何楚,石博,蒋厚军,等. 条件随机场的多极化InSAR联合相位解缠算法[J]. 测绘学报, 2013, 42(6):838-845). |
| [8] | REIGBER A, NEUMANN M, ERTEN E, et al. Multi-baseline Polarimetrically Optimised Phases and Scattering Mechanisms for InSAR Applications[C]//IEEE International Geoscience and Remote Sensing Symposium. Barcelona:IEEE, 2007:2620-2623. |
| [9] | NEUMANN M, FERRO-FAMIL L, REIGBER A. Multibaseline PolInSAR Coherence Modelling and Optimization[C]//Proceeding of the IEEE International Geoscience and Remote Sensing Symposium. Barcelona:IEEE, 2007:2624-2627. |
| [10] | NEUMANN M, FERRO-FAMIL L, REIGBER A. Multibaseline Polarimetric SAR Interferometry Coherence Optimization[J]. IEEE Geoscience and Remote Sensing Letters, 2008, 5(1):93-97. |
| [11] | ALIPOUR S, TIAMPO K F, SAMSONOV S, et al. Multibaseline PolInSAR Using RADARSAT-2 Quad-pol Data:Improvements in Interferometric Phase Analysis[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(6):1280-1284. |
| [12] | IGLESIAS R, MONELLS D, FABREGAS X, et al. Phase Quality Optimization in Polarimetric Differential SAR Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(5):2875-2888. |
| [13] | NAVARRO-SANCHEZ V D, LOPEZ-SANCHEZ J M, FERRO-FAMIL L. Polarimetric Approaches for Persistent Scatterers Interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(3):1667-1676. |
| [14] | LU Lijun,ZHANG Jixian,HUA Fenfen,et al. Multi-mode PolInSAR Experiments Using Airborne X-band SAR System in China[J]. International Journal of Remote Sensing, 2014, 35(5):1625-1639. |
| [15] | LOMBARDINI F. Absolute Phase Retrieval in a Three-element Synthetic Aperture Radar Interferometer[C]//Proceedings of the CIE International Conference of Radar. Beijing:IEEE, 1996:309-312. |
| [16] | ZHANG Qiuling, WANG Yanfei. Improving the Interferometric Phase Accuracy of Distributed Satellites InSAR System with Multibaseline Data Fusion[J]. Journal of Electronics & Information Technology, 2006, 28(11):2011-2014.(张秋玲,王岩飞. 利用多基线数据融合提高分布式卫星InSAR系统的干涉相位精度[J]. 电子与信息学报, 2006, 28(11):2011-2014). |
| [17] | YUAN Zhihui, DENG Yunkai, LI Fei, et al. Multichannel InSAR DEM Reconstruction through Improved Closed-form Robust Chinese Remainder Theorem[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(6):1314-1318. |
| [18] | LI Zhenfang, BAO Zheng, LI Hai, et al. Image Autocoregistration and InSAR Interferogram Estimation Using Joint Subspace Projection[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(2):288-297. |
| [19] | PASCAZIO V, SCHIRINZI G. Estimation of Terrain Elevation by Multifrequency Interferometric Wide Band SAR Data[J]. IEEE Signal Processing Letters, 2001, 8(1):7-9. |
| [20] | FERRAIUOLO G, PASCAZIO V. A Bayesian Approach Based on Modified Markov Random Fields for Microwave Tomography[C]//Proceedings of the IEEE International Geoscience and Remote Sensing Symposium. Toronto, Ontario:IEEE, 2002, 6:3393-3395. |
| [21] | FERRAIUOLO G, PASCAZIO V, SCHIRINZI G. Maximum a Posteriori Estimation of Height Profiles in InSAR Imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2004, 1(2):66-70. |
| [22] | PASCAZIO V, SCHIRINZI G. Multifrequency InSAR Height Reconstruction through Maximum Likelihood Estimation of Local Planes Parameters[J]. IEEE Transactions on Image Processing, 2002, 11(12):1478-1489. |
| [23] | SHABOU A, TUPIN F. A Markovian Approach for DEM Estimation from Multiple InSAR Data with Atmospheric Contributions[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(4):764-768. |
| [24] | YUAN Zhihui, DENG Yunkai, LI Fei, et al. Improved Multichannel InSAR Height Reconstruction Method Based on Maximum Likelihood Estimation[J]. Journal of Electronics & Information Technology, 2013, 35(9):2161-2167.(袁志辉,邓云凯,李飞,等. 改进的基于最大似然估计的多通道InSAR高程重建方法[J]. 电子与信息学报, 2013, 35(9):2161-2167). |
| [25] | HUA Fenfen, ZHANG Jixian, HUANG Guoman, et al. Multi-baseline InSAR Elevation Inversion Method Based on Rigorous Model[J]. Journal of Nanjing University of Science and Technology, 2014, 38(6):726-732.(花奋奋,张继贤,黄国满,等. 基于严密模型的多基线InSAR高程反演方法[J]. 南京理工大学学报:自然科学版, 2014, 38(6):726-732). |