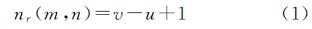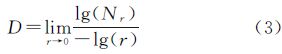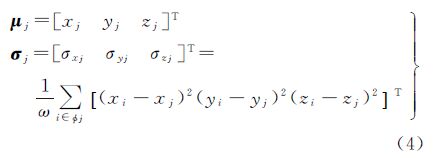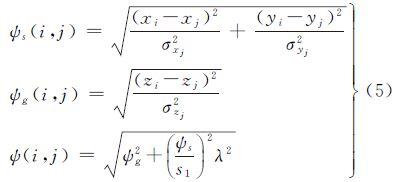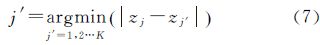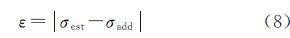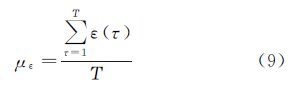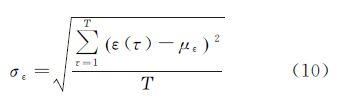2. 悉尼大学信息科技学院,新南威尔士 悉尼2006
2. School of Information Technologies, University of Sydney, Sydney 2006, AustraliaAbstract
1 引 言
在遥感图像的获取过程中,难免会引入各种类型的噪声。根据表现形式,可将噪声分为周期噪声和随机噪声。周期噪声可以通过技术手段有效去除[1],而随机噪声则无法彻底消除。如何准确估计遥感图像中随机噪声的强度一直是研究的热点与难点。准确的噪声估计结果可以为图像的后续处理工作提供先验参数,如图像去噪[2]、图像分割[3]、图像分类[4]、目标识别[5]等。
根据噪声与图像信号的相关性,可以将遥感图像中的噪声分为加性噪声和乘性噪声。对于光学遥感图像中的噪声,一般认为是与图像信号不相关的加性噪声[6, 7];而雷达图像中存在的斑点噪声,则通常认为是与图像信号相关的乘性噪声[8, 9, 10]。本文主要研究光学遥感图像中加性噪声强度的估计,一般将其模拟为零均值的高斯白噪声,而噪声的标准差即作为衡量噪声强度的标准。基于该噪声模型,目前已有多种噪声估计算法[6, 7, 11, 12, 13, 14, 15, 16, 17, 18, 19]。根据不同算法中使用的主要技术,可将已有算法分为图像滤波、变换域和图像块划分3类。其中,图像滤波算法[7, 11]一般利用高通滤波器对图像进行滤波处理,将原图像与滤波后图像的差值图像作为纯噪声图像,以此进行噪声估计。变换域的算法主要包括奇异值分解域[12]和小波变换域[13],利用图像奇异值的尾部数据或者小波分解后高频对角子带的小波系数进行图像噪声估计。图像块划分的算法[6, 14, 15, 16, 17, 18, 19]通常首先将图像分为若干矩形图像块,利用不同技术进行平滑(不包含图像结构信息)图像块选取。该类算法认为在平滑图像块中灰度值的变化完全由噪声引起,并据此估计图像中噪声的强度。
在上述算法中,基于图像块划分的噪声估计算法因原理简单、运算效率和准确性较高而得到广泛应用。然而,传统的图像块划分的算法在处理纹理复杂的图像时,往往难以将图像信息和噪声有效区分,导致噪声估计出现较大偏差。如图 1所示,图 1(a)为宽度为s1的水平条纹图像,采用传统的图像块划分方法将图像分为s1×s1大小的图像块;图 1(b)中所有划分的图像块均为平滑图像块。若将图 1(a)旋转45°,得到如图 1(d)所示的倾斜条纹图像,采用传统分块方法得到如图 1(e)所示的分块结果。显然,所有图像块均包含两种灰度值,均不是平滑图像块。此时,无论采用何种平滑图像块选取算法,也无法得到准确的结果。

|
| 图 1 本文自适应图像块划分与传统的规则矩形图像块划分方法比较 Fig. 1 Comparison between the conventional and the proposed adaptive image block division algorithm |
为了解决传统图像块划分的噪声估计算法的不足,本文跳出规则矩形图像块划分的思路,提出一种自适应于图像局部信息的图像块划分算法,并创新性地将其应用于遥感图像噪声估计。如图 1(c)所示,同样采用初始大小为s1×s1的自适应图像块对水平条纹图像进行分块,本文分块结果与传统分块结果一致。而对于倾斜条纹图像,本文中提出的自适应图像块划分结果如图 1(f)所示。
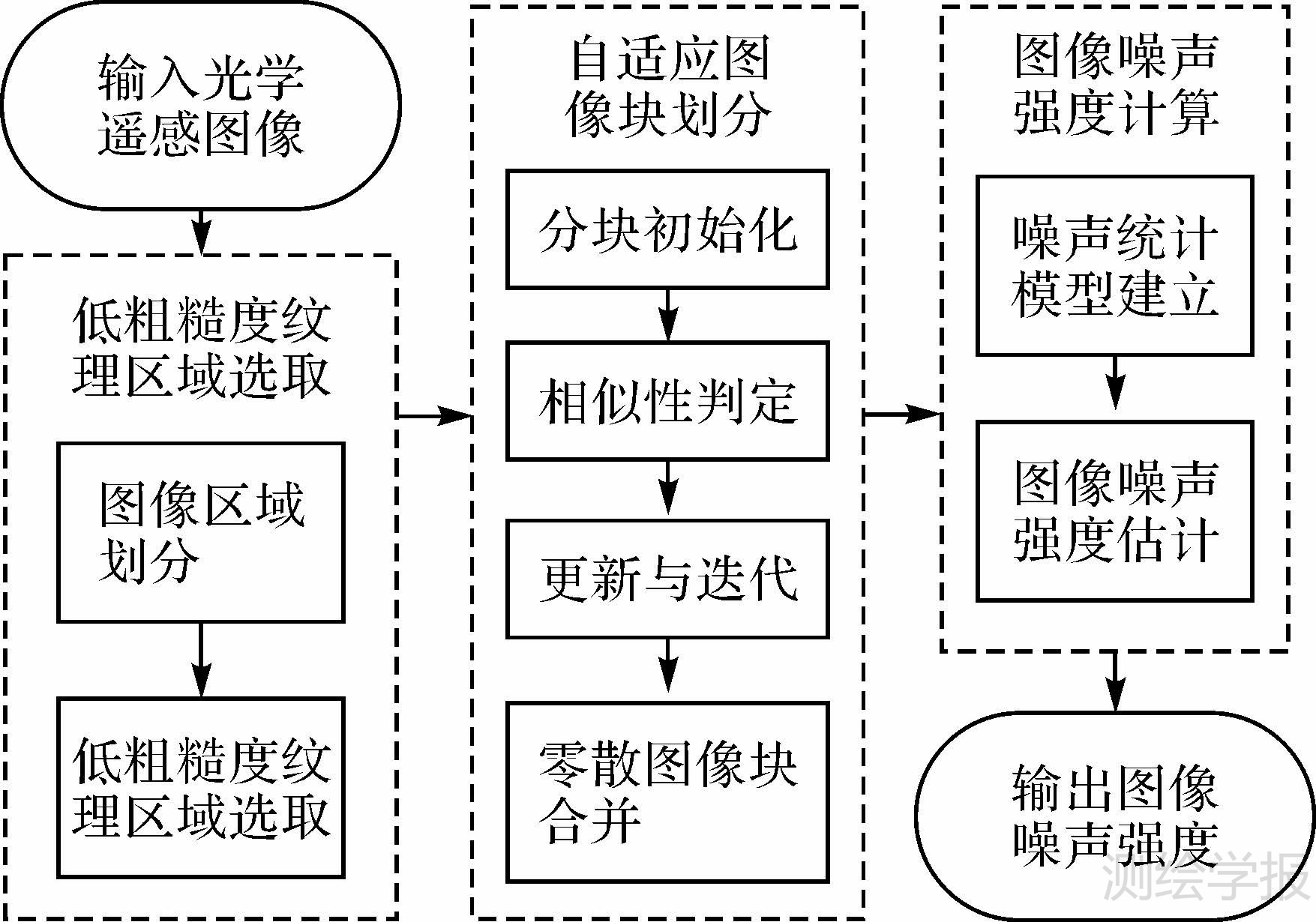
2 本文方法本文方法主要分为3个步骤,如图 2中流程图所示:①低粗糙度纹理区域选取;②自适应图像块划分;③图像噪声强度计算。
|
| 图 2 本文方法流程图 Fig. 2 Flow chart of the proposed method |
遥感图像的纹理特征是图像的重要空间结构信息,而分形理论常用于遥感图像的纹理分析[20, 21, 22]。通常,遥感图像中纹理的粗糙度因地物类型而各不相同,分形维数则能够很好地表征纹理粗糙度。分形维数较小的区域,对应图像中纹理粗糙度较低,图像相对平滑。据此,本文中首先将图像划分为若干连续不重叠的图像区域,大小为S×S的矩形块。对于每一个图像区域,采用差分盒计数法[23]计算该图像区域的分形维数,并将其中分形维数较小的图像区域用于后续的自适应图像块划分及噪声计算。
对于一个S×S大小的图像区域,将其划分成L×L的均匀网格,L为度量图像的尺度,令r=L/S。在每个网格上放置一列L×L×h大小的盒子,盒子的高度h=L×G/S,其中,·表示向下取整,G为总的灰度级。假设在第(m,n)个网格中灰度值最大和最小的像素点分别落在第v和第u个盒子中,则覆盖该网格所需盒子数nr(m,n)为
而覆盖整个图像区域所需盒子数Nr为
由此,可计算出该图像区域的分形维数D为
选取不同的度量尺度L,计算相应的Nr值,通过最小二乘线性回归即可求出分形维数D,进而利用分形维数对图像中低粗糙度纹理区域进行选取。如图 3所示,图 3(a)为一幅资源三号卫星图像,图像左上方纹理较为粗糙,而右下方纹理相对平滑。利用本文方法在此图像中选取100个20像素×20像素大小的低粗糙度纹理区域,如图 3(b)所示,选取结果验证了本文所提算法的有效性。

|
| 图 3 低粗糙度纹理区域选取结果 Fig. 3 Selection results of the weak textured image regions |
对于每一个选取出的低粗糙度纹理区域,将其划分成若干自适应于图像局部信息的图像块。文献[24]中曾提出一种类似的图像聚类算法SLIC(simple linear iterative clustering),作为图像分割和分类的预处理。但该方法对噪声较为敏感,在处理含噪图像时会出现错误的图像块划分。本文在此方法的基础上,引入一种新的相似性度量准则及零散图像块合并策略,使得在面对加性噪声严重的光学遥感图像时依然能够很好地进行自适应图像块划分。本文提出的自适应图像块划分算法共包括以下4个步骤:
(1) 分块初始化。
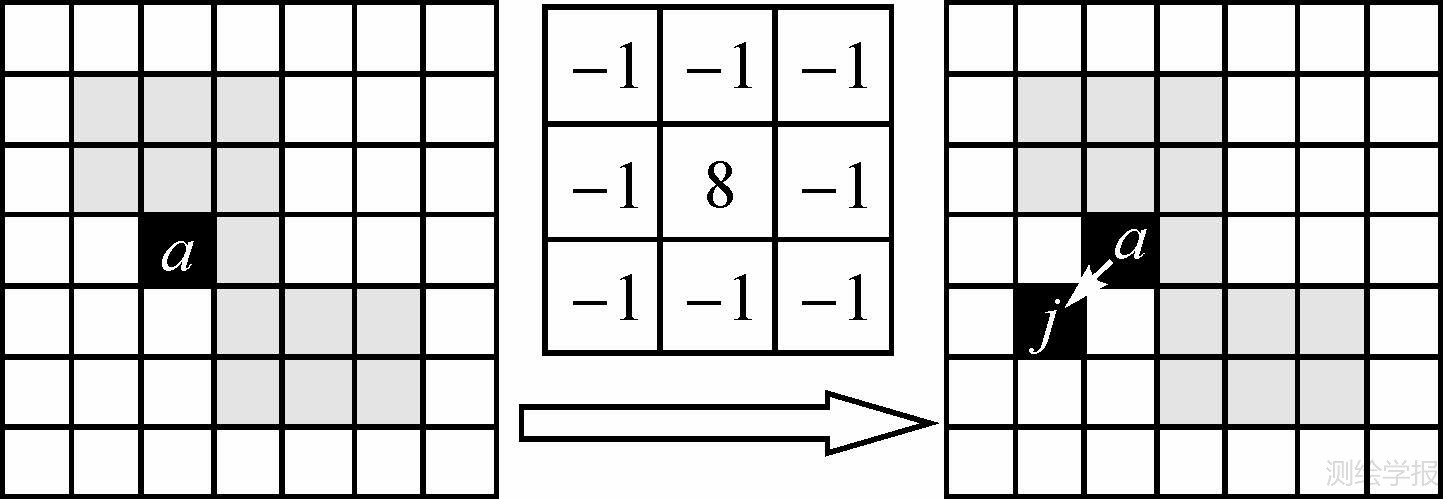
对于大小为S×S的低粗糙度纹理区域,若将其划分成初始化大小为s1×s1的图像块,则自适应图像块个数M≈S2/s21,其中·表示四舍五入取整。首先将M个初始图像块中心点平均分布在图像上。为了避免初始点处于图像中的边缘信息上,本文采用一个滤波窗口将初始点移至其3×3邻域内梯度最低处。如图 4所示,点a为平均分布的初始点,位于图像边缘之上,而经过调整后初始点移动到处于平滑区域的j点。本文中采用图像空间坐标和灰度值对应的均值向量μj和标准差向量σj对任一图像块中心点j进行初始化
式中,xj、yj和zj分别代表了初始图像块中心点j的横坐标、纵坐标和灰度值;ϕj表示属于图像块j的像素点集合,在初始化时即是以j为中心的s1×s1范围内的像素点;ω则为其对应的像素点个数。
|
| 图 4 图像块初始中心点调整示意图 Fig. 4 Adjustment of the initial centers |
(2) 相似性判定。为了能够在自适应图像块划分时有效地区分噪声和图像信息,本文结合了图像的空间信息和灰度信息,提出一种新的相似性度量标准ψ(i,j),并据此将每个像素点分配到最相似的图像块中。本文方法中相似性度量标准ψ(i,j)通过式(5)进行计算
式中,ψs(i,j)和ψg(i,j)分别表示像素点i和图像块中心点j之间的空间相似性和灰度相似性度量;参数λ用来调整空间相似性和灰度相似性的权重。为了提高算法的效率,每个初始图像块只在其中心点的2s1×2s1范围内进行相似点的搜索。
(3) 更新与迭代。根据本文的相似性判定准则将图像像素点分配至各个图像块后,新的图像块中心点根据式(6)进行更新
式中,ϕ′j表示更新后图像块中像素点集合;ω′为其中像素点个数;μ′j和σ′j是更新后图像块像素点在空间相似性和灰度相似性上的均值向量和标准差向量。按照步骤(2)和步骤(3)将图像中相似像素点的分配和中心点的更新不断重复,直到每个自适应图像块不再变化。
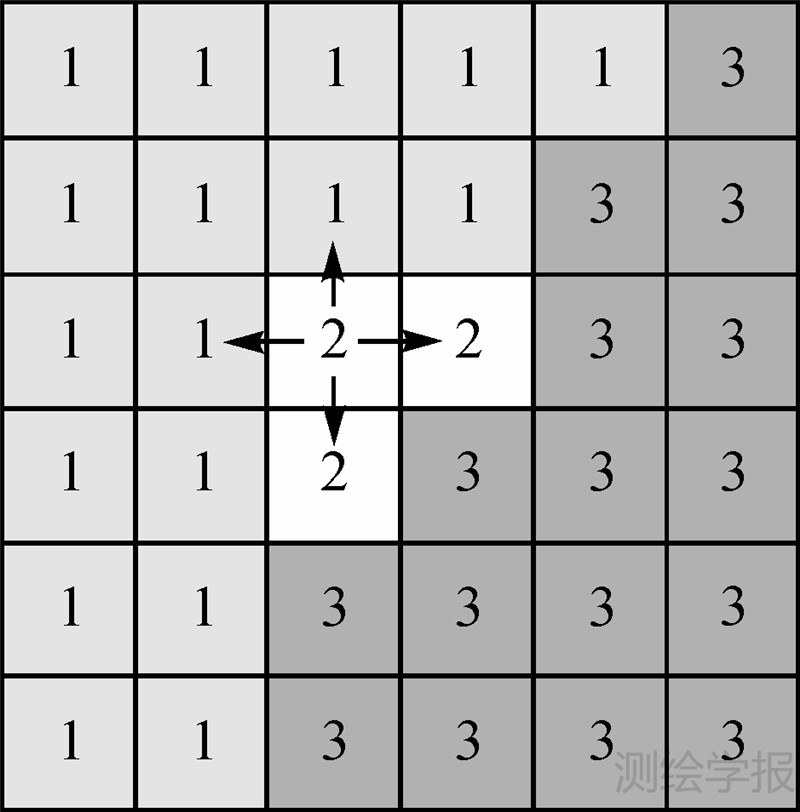
(4) 零散图像块合并。经过上述3个步骤,初步完成了自适应图像块的划分。但此时图像中存在一些零散的图像块,如图 5中自适应图像块2,只包含3个像素点,需要将其合并到相邻的图像块中。根据试验效果,若划分后某自适应图像块中像素点个数小于初始化图像块中像素点个数的25%,则认定该自适应图像块为零散图像块。对于图 5中的零散图像块2,在四邻域连通方向上寻找到与其相邻的自适应图像块,如图 5中的图像块1和块3,并依据图像块的平均灰度相似性进行合并。对于零散图像块j,通过式(7)将其合并至图像块j′
式中,图像块j′是与j空间相邻的图像块;K为相邻图像块的个数。至此,自适应图像块划分完成。
|
| 图 5 零散图像块合并示意图 Fig. 5 Mergence of the fragmentary image blocks |
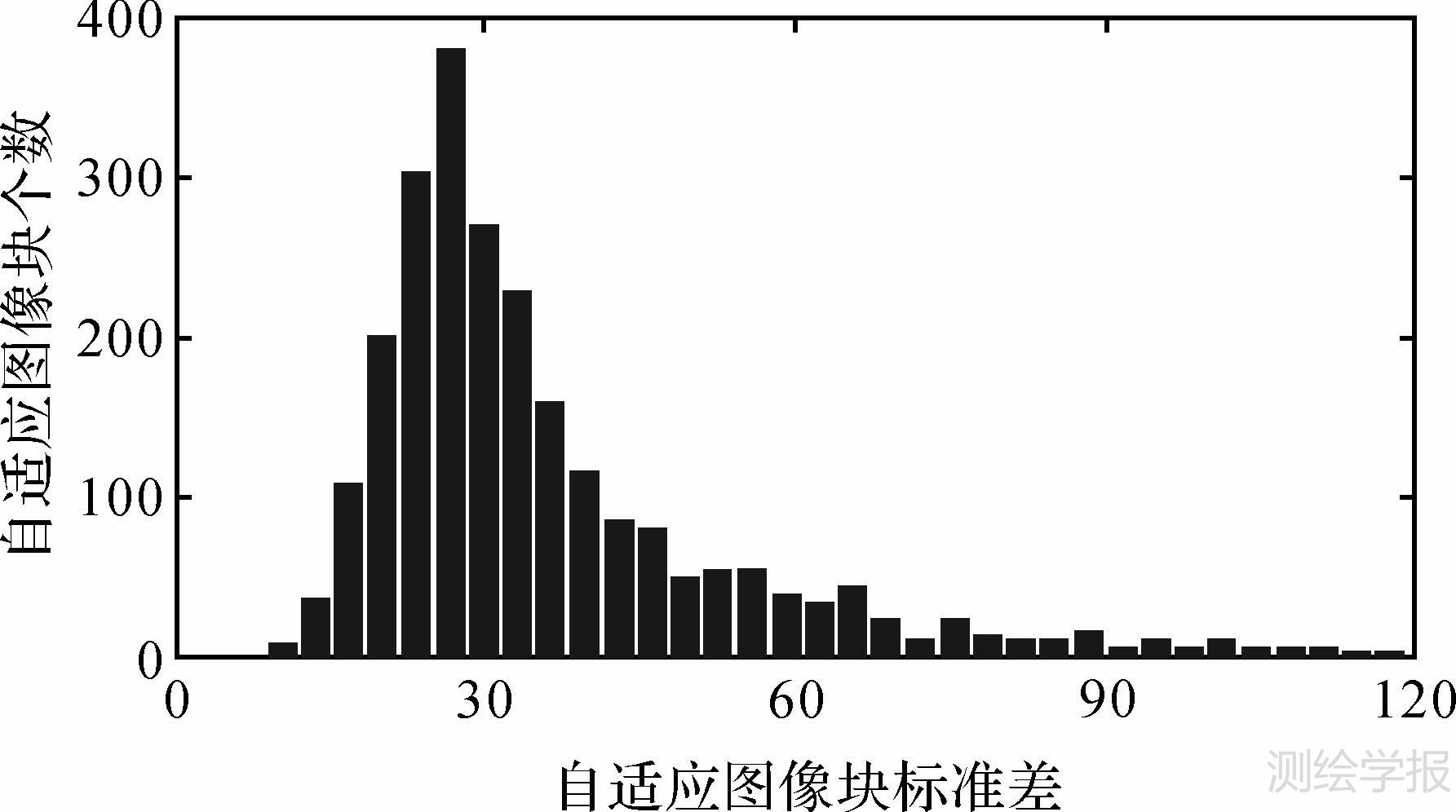
根据自适应图像块划分结果,本文采用直方图统计模型[6]进行噪声强度估计。在图像低粗糙度纹理区域中进行自适应图像块划分,其中平滑图像块通常占据很高的比例,而平滑图像块对应的标准差即为图像噪声的标准差。据此,本文首先计算出所有低粗糙度纹理区域中自适应图像块的标准差,在最小值和最大值之间建立若干等间隔的区间,按照各个自适应图像块的标准差值将其列入相应区间,如图 6所示,包含自适应图像块最多的区间对应标准差的平均值即为图像中噪声的标准差。然而,在采用直方图统计模型进行噪声估计时,通常会出现对于低噪声强纹理图像产生过估计,或者对于高噪声弱纹理图像产生欠估计。通过准确地设置直方图统计模型的横轴范围和等间隔区间划分数目可以在一定程度上解决这一问题,提高图像噪声估计的精度。如何更好地设置直方图统计模型的参数,本文将在3.2.2 节中进行详细讨论。
|
| 图 6 利用统计特性进行图像噪声强度计算 Fig. 6 Calculation of the image noise level by using the statistical property |
采用本文自适应图像块划分算法和SLIC算法分别对噪声强度较小和噪声强度较大的光学遥感图像进行自适应图像块划分,试验结果如图 7和图 8所示。其中图 7(a)为信噪比较高的资源三号卫星图像,图 7(d)为加入标准差为30的噪声后的图像;图 8(a)为AVIRIS高光谱遥感数据的第65波段图像,图像中噪声较小;而图 8(d)为第112波段图像,图像中噪声较为严重。根据试验结果可知,在处理噪声较小的图像时,采用本文算法和SLIC算法均能较好地进行自适应图像块划分;而当图像中噪声比较严重时,本文算法可以有效地排除噪声干扰,所划分的图像块依然能够准确地自适应于图像的局部信息,如图 7(e)和图 8(e)所示。然而,SLIC算法在处理噪声比较严重的图像时容易受到噪声的干扰,不能准确地贴合图像中边缘纹理等结构信息,如图 7(f)和图 8(f)所示。

|
| 图 7 本文算法与SLIC算法对于原始资源三号卫星图像和加入噪声后图像进行自适应图像块划分的结果对比 Fig. 7 Comparison of the adaptive image block division results between the proposed method and SLIC with the original ZY-3 satellite image and the image with noise added |

|
| 图 8 资源三号卫星图像 Fig. 8 ZY-3 satellite images |
在试验部分,本文采用资源三号卫星图像对本文方法的准确性和稳定性进行定量分析。资源三号卫星是我国首颗民用高分辨率光学传输型立体测图卫星,于2012年1月9日成功发射。试验中使用图像如图 9所示,图 9(a)和(b)是在同一幅大场景卫星图像中截取而得,图像大小均为512×512像素。其中,图 9(a)对应的图像纹理结构相对简单,图像整体比较平滑;而图 9(b)则图像细节信息丰富,图像整体比较复杂。选取图 9(a)和(b)是为了测试本文方法在处理不同复杂程度光学遥感图像时的稳健性。

|
| 图 9 本文算法与SLIC算法对于不同噪声强度的AVIRIS图像进行自适应图像块划分的结果对比 Fig. 9 Comparison of the adaptive image block division results between the proposed method and SLIC with AVIRIS images with different noise levels |
为了对算法性能进行定量评估,笔者在试验图像中加入已知标准差的高斯白噪声。参考文献[12—15],假设原图像中噪声可以忽略,则噪声估计的误差ε可通过式(8)计算
式中,σest为估计噪声的标准差;σadd为加入噪声的标准差。为了保证试验结论的可靠性,本文中对每幅试验图像进行多次重复试验,依据式(9)和式(10)计算噪声估计误差的均值με和标准差σε,并以此作为衡量算法准确性和稳定性的标准
式中,Τ为重复试验的次数,本文试验中Τ=100。 3.2.2 本文方法的参数设置
结合试验效果和运算效率,在试验中将本文方法所涉及参数设置如下:
(1) 低粗糙度纹理区域选取时采用20像素×20像素大小的图像区域,选取的所有低粗糙度纹理区域中像素总数占整幅图像像素总数的10%~20%。为了更加准确地对不同复杂程度的光学遥感图像进行噪声估计,当图像场景较为复杂时,应选取较少的低粗糙度纹理区域;而当图像场景较为简单时,则应选取较多的低粗糙度纹理区域。本文试验图像大小为512×512像素,在试验中选取100个20×20像素大小的低粗糙度纹理区域。
(2) 采用直方图统计模型进行图像噪声标准差计算时,需要设置直方图的横轴范围和等间隔区间划分数目。在文献[6]中,考虑到个别图像块内部边缘纹理信息极其丰富,这部分图像块对应的标准差极大,因此将直方图的横轴范围设置为图像块标准差的最小值到所有图像块标准差平均值的1.2倍。而本文已经在之前步骤中进行了低粗糙度纹理区域选取,边缘纹理信息极为丰富的图像块已被排除在外,因此本文中直接采用图像块对应标准差的最小值和最大值作为直方图统计模型的横轴范围。此外,等间隔区间划分数目同样会影响噪声估计的精度:若区间划分过密,将有很大一部分平滑图像块不能用于噪声的计算;而区间划分过于稀疏又会导致在噪声统计时引入包含图像结构信息的图像块,使得噪声估计结果出现较大偏差。根据试验效果,在处理大小为200×200像素至1000×1000像素的光学遥感图像时,笔者建议等间隔区间划分数目在40~60范围内进行设置。当图像尺寸较小时,应采用较少的等间隔区间划分数目;反之,应采用较多的等间隔区间划分数目。当图像尺寸在此范围之外时,如果图像尺寸过小,参与直方图统计的图像块会很少,本文方法的准确性会降低;如果图像尺寸过大,则会大幅度增加算法的运行时间,此时可以在整幅图像中截取一块大小适中的图像进行噪声估计。对于本文试验中采用的大小为512×512像素的光学遥感图像,笔者将等间隔区间划分数目设置为50。
(3) 在自适应图像块划分时,需要设定用于调整灰度相似性和空间相似性的权重λ。如图 10所示,对于图 7(a)中的图像进行自适应图像块划分,若参数λ设置较小,则自适应图像块划分时灰度相似性占主导地位,此时图像块极不规则,且易受噪声干扰,划分结果如图 10(a)所示;相反,若λ较大,则空间相似性占主导地位,此时图像块近似规则矩形,不能很好地自适应于图像的局部信息,如图 10(c)所示。根据试验结果,当λ∈[5, 10]时,本文算法能够很好地进行自适应图像块划分。当图像场景较为复杂时,应采用较小的λ值,使得所划分的自适应图像块更加贴合图像中的边缘纹理等结构信息;而当图像场景比较简单时,应选取较大的λ值。在本文试验中,将λ值设置为7,如图 10(b)所示,所划分的自适应图像块形状相对规则且能很好地自适应于图像局部信息。

|
| 图 10 采用不同权重参数λ时自适应图像块划分结果 Fig. 10 Adaptive image block division results with various λ |
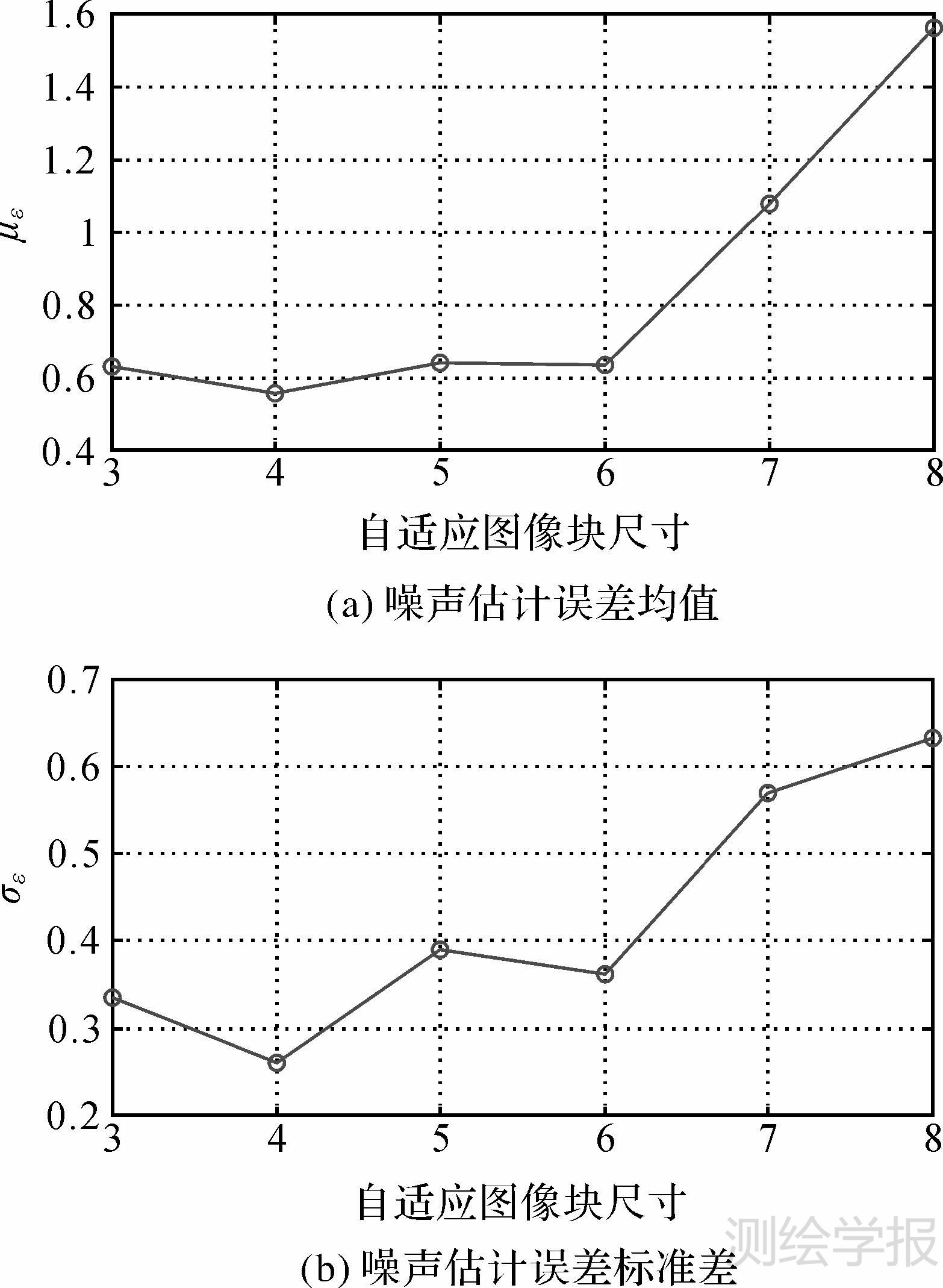
(4) 在自适应图像块划分时,初始图像块尺寸s的选取对噪声估计结果影响较大。若自适应图像块选取过小,将不能很好地反映噪声的统计特性;若自适应图像块选取过大,则难以保证大多数图像块内部的平滑性,使得噪声估计结果偏大。本文利用图 9(b)进行试验,在图像中加入标准差为10的高斯白噪声,并采用初始图像块大小分别为s=3、4、5、6、7、8的自适应图像块进行噪声估计,噪声估计误差的均值和标准差如图 11所示。由图 11可以看出,当图像块尺寸s∈[3, 6]时,噪声估计误差的均值和标准差都较低,且在s=4时,取得最好的试验结果;当s大于6时,自适应图像块中图像纹理信息增多,噪声估计误差的均值和标准差明显升高,算法的准确性和稳定性均有所下降。结合试验结果,本文中将自适应图像块初始化大小设置为4×4像素。
|
| 图 11 采用不同初始图像块尺寸的噪声估计结果 Fig. 11 Noise estimation results with various initial image block size |
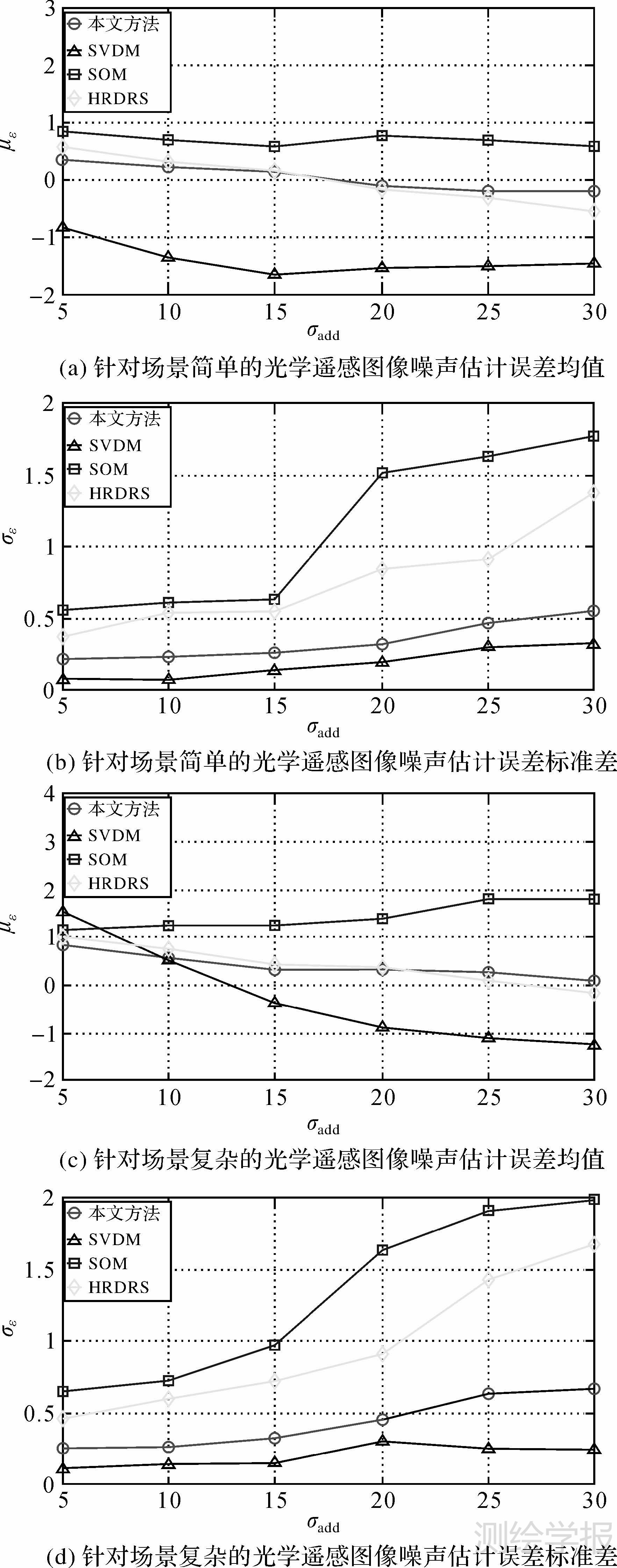
为了验证在处理不同复杂程度及不同噪声强度的光学遥感图像时本文方法的准确性和稳定性,在图 9(a)和(b)中分别加入噪声标准差σadd=5,10,15,20,25,30的高斯白噪声。采用本文方法、SVDM (singular value decomposition method)[12]、SOM (structure-oriented method)[14]、以及HRDRS (homogeneous region division and residuals statistics)[19]等4种噪声估计方法分别对加入不同强度噪声的图像进行试验。其中,SVDM为基于图像奇异值域的噪声估计方法;SOM为基于传统的规则矩形图像块划分的噪声估计方法;而HRDRS方法在规则图像块划分的基础上,利用平滑图像块内部相邻像素点之间的强相关性进行噪声估计。在试验时,用于比较的3种噪声估计方法所需参数均按照其各自论文中的建议值进行设置,试验结果如图 12所示。
|
| 图 12 针对不同复杂程度及不同噪声强度的光学遥感图像,本文方法与已有方法的性能比较 Fig. 12 Comparison between the proposed and the existing methods when dealing with optical remote sensing images with various complexities and different noise levels |
根据图 12(a)中试验结果可知,在针对场景较为简单的光学遥感图像进行噪声估计时,本文方法的准确性最高。而另外3种方法中,HRDRS方法的噪声估计精度与本文方法最为接近,但是相比于本文方法,HRDRS在针对噪声较弱和较强的图像进行噪声估计时分别产生了比较严重的过估计和欠估计。SOM方法的噪声估计精度不如HRDRS方法,且噪声估计值大于真实值。而SVDM方法的准确性在所有4个方法中最低,利用该方法计算得到的噪声估计值远小于真实值。
由图 12(c)可知,在针对场景较为复杂的光学遥感图像进行噪声估计时,由于图像边缘纹理等结构信息的增加,本文方法的噪声估计精度有所下降,但相比于其他3种方法,本文方法的准确性依然最高。HRDRS方法的精度与本文方法最接近。而SOM方法在处理场景复杂的图像时不能有效地区分噪声和图像结构信息,噪声的估计值远大于真实值。此外,SVDM方法的噪声估计精度随着噪声强度的增加而大幅降低,同时依然出现了较为严重的欠估计现象。
根据图 12(b)和(d)可以看出,在处理场景较为简单和场景较为复杂的光学遥感图像时,SVDM方法的稳定性最高,本文方法次之。HRDRS和SOM方法的稳定性较差,且随着噪声强度的增加,这两种方法的稳定性下降明显。
综上所述,本文方法能够较好地适用于不同复杂程度、不同噪声强度的光学遥感图像的噪声估计。值得注意的是,为了更加合理地与其他3种噪声估计方法进行比较,在本文试验中处理场景简单和场景复杂的图像时采用了相同的参数设置。在实际应用时,可以根据3.2.2 节本文方法参数设置的建议,针对光学遥感图像对应的地物分布的复杂程度进行参数调整,能够进一步提高本文噪声估计方法的性能。
4 讨 论本文主要针对光学遥感图像中存在的加性高斯白噪声,提出了一种准确的噪声强度估计方法。本文中提出的低粗糙度纹理区域选取和自适应图像块划分的思想,在经过改进后,同样可以有效地应用于雷达图像中乘性噪声的估计。
文献[8]中提出了一种散点拟合法SPM(scatter plot method),该方法可以用于估计雷达图像中的乘性噪声。首先,将雷达图像划分为若干规则的矩形图像块;然后以所有平滑图像块对应的均值的平方为横轴,方差为纵轴,绘制散点图;最后对图中散点进行直线拟合,其中拟合直线对应的斜率即为乘性噪声的方差。在该方法中,平滑图像块的选取极为重要。笔者在SPM方法的基础上,引入了本文中提出的低粗糙度纹理区域选取和自适应图像块划分的思想:首先选取出图像中的低粗糙度纹理区域,然后在低粗糙度纹理区域中进行自适应图像块划分,最后利用所划分的自适应图像块进行散点图的绘制和拟合,从而估计图像中乘性噪声的强度,文中称之为“改进方法”。为了验证改进方法的有效性,笔者采用雷达图像进行了相关试验。
试验中采用的雷达图像为TerraSAR-X图像数据,如图 13所示。其中,图 13(a)、(b)截取于同一幅图像,图 13(a)对应的地物场景较为简单,图 13(b)对应的地物场景相对复杂。首先,分别采用SPM方法和改进方法对图 13(a)进行噪声估计,试验结果如图 14所示。需要指出的是,本文中提出的自适应图像块划分算法是在SLIC算法的基础上,引入了新的相似性度量标准,该相似性度量标准针对图像中存在加性高斯白噪声的情况下能够更加有效地区分噪声值和图像信号值。而雷达图像中的噪声主要为乘性斑点噪声,针对该类型噪声,文献[25]在SLIC算法的基础上,通过引入像素灰度值比距离测度PIRD(pixel intensity ratio distance),提出了一种适用于存在斑点噪声的雷达图像的自适应图像块划分算法,称之为PILS(pixel intensityand location similarity)算法。在该试验中,笔者采用PILS算法进行自适应图像块划分。

|
| 图 13 TerraSAR-X图像 Fig. 13 TerraSAR-X images |
图 14(a)和(b)分别对应SPM和改进方法的噪声估计试验结果。采用最小二乘法LSM(least square method)对图中散点进行拟合,如图中拟合直线所示。其中,图 14(a)和(b)中拟合直线对应的斜率分别为0.065和0.063,即图像中乘性噪声的方差。可以看出,对于地物场景比较简单的图像,采用SPM方法和改进方法所获取的乘性噪声方差是非常接近的。

|
| 图 14 SPM方法和改进方法对于图 13(a)的噪声估计试验结果 Fig. 14 Noise estimation results on Fig. 13(a) with SPM and the improved method |
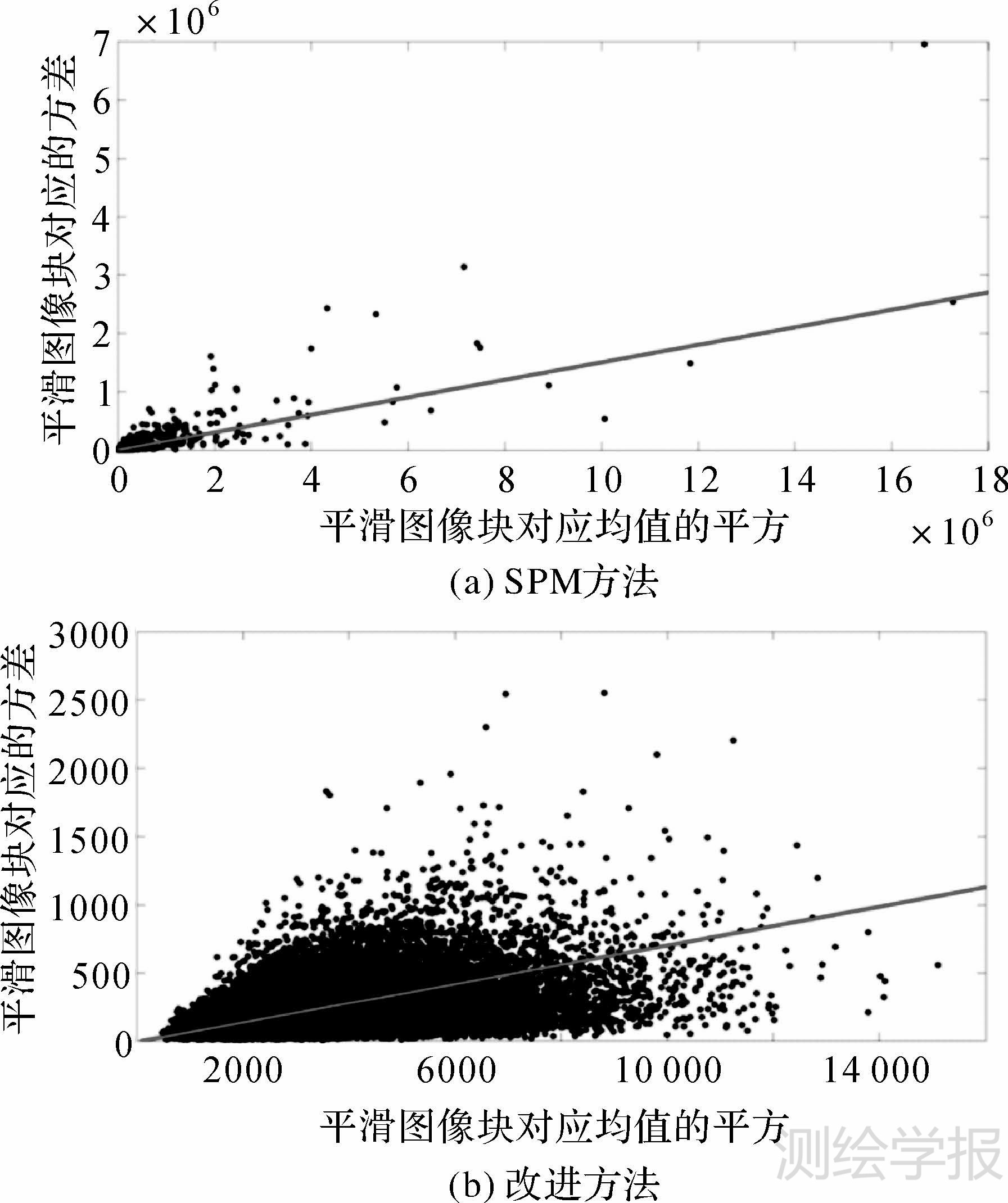
采用SPM方法和改进方法对地物场景相对复杂的图 13(b)进行噪声估计,试验结果如图 15所示。其中,图 15(a)和(b)中的散点拟合直线对应的斜率分别为0.150和0.071。与图 14中的试验结果相比,SPM方法的噪声估计值偏差较大,而改进方法的试验结果偏差较小。由图 15(a)不难看出,由于图像中存在较多的边缘和纹理,SPM方法中很多划分的图像块并不是平滑图像块,因此在散点图中出现了较多的异常点,影响了噪声估计的准确性。需要指出的是,虽然在处理地物场景较为复杂的图像时改进方法比SPM方法更加准确,但是与图 14中的试验结果相比,采用改进方法对图 13(b)进行噪声估计的结果依然偏大。这是因为即使通过低粗糙度纹理区域选取和自适应图像块划分后,所得到的图像块也不完全是平滑图像块。在针对加性高斯白噪声估计时,笔者采用了直方图统计模型进一步选取出最平滑的一部分自适应图像块。在针对存在乘性斑点噪声的雷达图像中,同样有很多方法可以进一步进行最平滑图像块的选取,如文献[26]中的方法等。在该试验中,笔者旨在验证将本文提出的低粗糙度纹理区域选取和自适应图像块划分的思想引入到雷达图像乘性斑点噪声估计方法中的有效性。
|
| 图 15 SPM方法和改进方法对于图 13(b)的噪声估计试验结果 Fig. 15 Noise estimation results on Fig. 13(b) with SPM and the improved method |
本文提出了一种基于分形理论和自适应图像块划分的光学遥感图像噪声估计方法。与目前已有的基于图像块划分的噪声估计方法不同,本文提出的算法,结合基于分形理论的低粗糙度纹理区域选取以及基于直方图统计模型的图像噪声标准差计算,该方法可以针对不同复杂程度、不同噪声强度的光学遥感图像进行全自动的噪声强度估计。同时,本文中的低粗糙度纹理区域选取和自适应图像块划分的思想,在经过改进后,可以有效应用于雷达图像中乘性噪声的估计。需要指出的是,本文方法中需要通过迭代运算来进行自适应图像块划分,尽管已缩小了相似像素点的搜索区域,但相比传统的规则图像块划分算法依然效率较低。如何在保证本文方法准确性和稳定性的基础上提高算法效率,将是下一步研究的重点。
| [1] | WATANABE J, HOSAKA T, HAMAMOTO T. Sensor-Pattern-Noise Map Reconstruction in Source Camera Identification for Size-reduced Images[J]. IEICE Transactions on Information and Systems, 2013, 96(8):1882-1885. |
| [2] | TAO Ke, ZHU Jianjun. A Hybrid Indicator for Determining the Best Decomposition Scale of Wavelet De-noising[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5):749-755.(陶珂,朱建军. 多指标融合的小波去噪最佳分解尺度选择方法[J]. 测绘学报, 2012, 41(5):749-755). |
| [3] | SHARON A, MEIRAV G, ACHI B, et al. Image Segmentation by Probabilistic Bottom-up Aggregation and Cue Integration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(2):315-327. |
| [4] | YANG Honglei, PENG Junhuan, LI Shuhui, et al. Log-principal Component Transformation Based EM Algorithm for Remote Sensing Classification[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4):378-382.(杨红磊,彭军还,李淑慧,等. 基于对数-主成分变换的EM算法用于遥感影像分类[J]. 测绘学报, 2010, 39(4):378-382). |
| [5] | IWEN M A, TEWFIK A H. Adaptive Strategies for Target Detection and Localization in Noisy Environments[J]. IEEE Transactions on Signal Processing, 2012, 60(5):2344-2353. |
| [6] | GAO B C. An Operational Method for Estimating Signal to Noise Ratios from Data Acquired with Imaging Spectrometers[J]. Remote Sensing of Environment, 1993, 43(1):23-33. |
| [7] | CORNER B R, NARAYANAN R M, REICHENBACH S E. Noise Estimation in Remote Sensing Imagery Using Data Masking[J]. International Journal of Remote Sensing, 2003, 24(4):689-702. |
| [8] | LEE J S, HOPPEL K. Noise Modeling and Estimation of Remotely Sensed Images[C]//IEEE International Geoscience and Remote Sensing Symposium.Vancouver:IEEE, 1989:1005-1008. |
| [9] | LEE J S, HOPPEL K, MANGO S A. Unsupervised Estimation of Speckle Noise in Radar Images[J]. International Journal of Imaging Systems and Technology, 1992, 4(4):298-305. |
| [10] | XU Bin, CUI Yi, ZHOU Guangyi, et al. Unsupervised Speckle Level Estimation of SAR Images Using Texture Analysis and AR Model[J]. IEICE Transactions on Communications, 2014, E97-B(3):691-698. |
| [11] | IMMERKER J. Fast Noise Variance Estimation[J]. Computer Vision and Image Understanding, 1996, 64(2):300-302. |
| [12] | LIU Wei, LIN Weisi. Additive White Gaussian Noise Level Estimation in SVD Domain for Images[J]. IEEE Transactions on Image Processing, 2013, 22(3):872-883. |
| [13] | HASHEMI M, BEHESHTI S. Adaptive Noise Variance Estimation in Bayes Shrink[J]. IEEE Signal Processing Letters, 2010, 17(1):12-15. |
| [14] | AMER A, DUBOIS E. Fast and Reliable Structure-oriented Video Noise Estimation[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2005, 15(1):113-118. |
| [15] | FU Peng, SUN Quansen, JI Zexuan, et al. A New Method for Noise Estimation in Single-band Remote Sensing Images[C]//IEEE International Conference on Fuzzy Systems and Knowledge Discovery.Chongqing:IEEE, 2012:1664-1668. |
| [16] | FU Peng, SUN Quansen, JI Zexuan, et al. A Method of SNR Estimation and Comparison for Remote Sensing Images[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4):559-567.(傅鹏,孙权森,纪则轩,等. 一种遥感图像信噪比评估和度量准则[J]. 测绘学报, 2013, 42(4):559-567). |
| [17] | LIU Xinhao, TANAKA M, OKUTOMI M. Noise Level Estimation Using Weak Textured Patches of a Single Noisy Images[C]//IEEE International Conference on Image Processing.Orlando:IEEE, 2012:665-668. |
| [18] | LIU Xinhao, TANAKA M, OKUTOMI M. Single-image Noise Level Estimation for Blind Denoising[J]. IEEE Transactions on Image Processing, 2013, 22(12):5226-5237. |
| [19] | QIN Bangyong, HONG Bo, ZHANG Zhi, et al. A Generally Applicable Noise-Estimating Method for Remote Sensing Images[J]. Remote Sensing Letters, 2014, 5(5):481-490. |
| [20] | SILVETTI A F, DELRIEUX C A. Quadratic Self-correlation:An Improved Method for Computing Local Fractal Dimension in Remote Sensing Imagery[J]. Computers & Geosciences, 2013, 60:142-155. |
| [21] | SUN W, XU G, GONG P, et al. Fractal Analysis of Remotely Sensed Images:A Review of Methods and Applications[J]. International Journal of Remote Sensing, 2006, 27(22):4963-4990. |
| [22] | PENTLAND A P. Fractal-based Description of Natural Scenes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1984, PAMI-6(6):661-674. |
| [23] | SARKAR N, CHAUDHURI B B. An Efficient Approach to Estimate Fractal Dimension of Textured Images[J]. Pattern Recognition, 1992, 25(9):1035-1041. |
| [24] | ACHANTA R, SHAJI A, SMITH K, et al. SLIC Superpixels Compared to State-of-the-art Superpixel Methods[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11):2274-2281. |
| [25] | XIANG Deliang, TANG Tao, ZHAO Lingjun, et al. Superpixel Generating Algorithm Based on Pixel Intensity and Location Similarity for SAR Image Classification[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(6):1414-1418. |
| [26] | AIAZZI B, ALPARONE L, BARONTI S, et al. Coherence Estimation from Multilook Incoherent SAR Imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(11):2531-2539. |