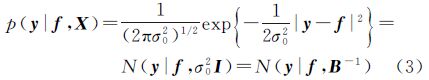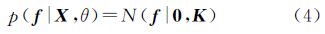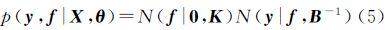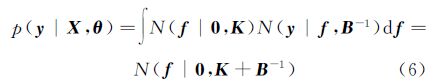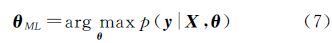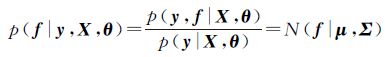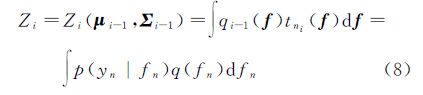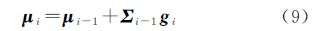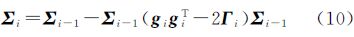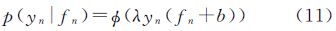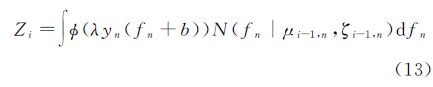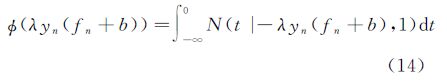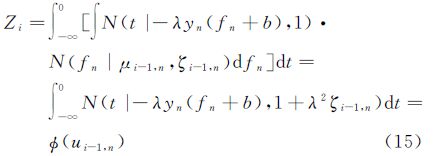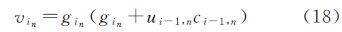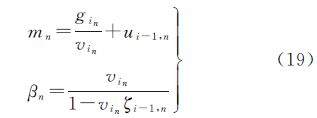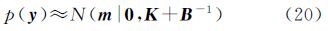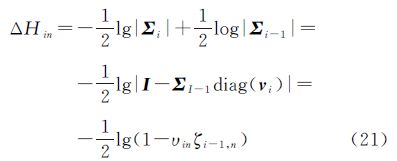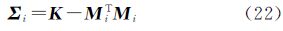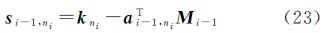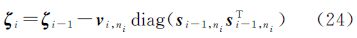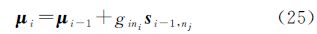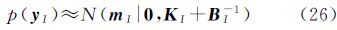1 引 言
20世纪80年代出现的高光谱遥感技术，将图像和光谱相结合，克服了传统光学遥感在地物属性信息精细探测方面的不足[1]。高光谱遥感的优势主要表现为对地观测时能够获取众多连续波段的光谱影像，从而实现对地面目标的精细描述，达到识别地物的目的[2]。
高光谱影像分类是高光谱影像处理与分析以及广泛应用的关键问题和核心技术。然而，高光谱影像数据的高维小样本、波段间的高相关性以及非“线性可分”等特点制约着高光谱影像分类技术的发展与应用。训练样本的不足使得传统统计模式分类中参数估计的可靠性成为一个挑战，容易出现“维数灾难”现象[4]。
为了提高数据处理效率，确保分类精度，通常可采用两种有效策略：一是在分类处理前，对原始高光谱影像数据进行特征降维处理即光谱特征选择与提取[5]；二是采用以支持向量机(support vector machine,SVM)为主的核方法[7]。总体上讲，这两种不同的分类策略在不同的应用场合均取得了较好的成果，其中以SVM为主的核方法越来越成为高光谱影像分类的重点。尽管如此，SVM仍存在一定的不足之处，如核函数必须满足Mercer定理、模型训练时间较长、参数选择较困难、结果不具有概率统计意义以及稀疏性有限等。
针对这些问题，文献[9]在稀疏贝叶斯分类模型的基础上，提出利用相关向量机(relevance vector machine,RVM)进行高光谱影像分类，得到了相对稀疏的、具有概率统计意义的分类结果，但其分类精度仍低于SVM分类器。另外，高斯过程(Gaussian process,GP)[10]是一种几乎与支持向量机(SVM)同时出现的基于核函数的机器学习算法。相较于SVM，高斯过程是在贝叶斯框架下的非参数概率模型，核函数参数可自适应获得，且其输出结果具有一定的概率意义，主要用于数据降维、回归与分类等方面。但其在处理大样本数据时仍存在计算效率低、内存耗费大和稀疏性弱的问题。文献[11]通过最小化KL散度来达到稀疏数据子集选择的目的；文献[12—14]利用信息原理中的贪婪准则来选择训练样本，提出了信息向量机(informative vector machine，IVM)。目前，IVM在手写数字识别[12]、人脸识别[15]和神经活动分类[16]等方面得到一定的应用。
本文在高斯过程回归模型的基础上，利用假定密度滤波算法(assume density filtering,ADF)将分类中的概率噪声模型逼近高斯噪声模型，采用最大化边缘似然函数自适应获得模型参数，通过选择活动子集(active subset)中信息向量的数量来进行模型的训练，达到稀疏的目的，采用一系列的两类IVM分类器组合解决多类分类问题，并将其应用于高光谱影像分类。通过ROSIS高光谱影像分类试验，验证了基于IVM的高光谱影像分类方法的优势。
2 高斯过程回归模型 2.1 高斯过程高斯过程是指一系列随机变量的集合，集合中任意有限数量的随机变量均服从联合高斯分布。简而言之，高斯过程是把多元高斯分布推广到无限多个随机变量的形式，即多元高斯分布由均值向量和协方差矩阵确定，而高斯过程由均值函数和协方差函数确定。
如果一个随机变量的集合x=(x1,x2,…,xN)的联合分布服从均值为μ，协方差矩阵为Σ的高斯分布即x=(x1,x2,…，xN)~N(μ,Σ)，那么将随机变量以函数的形式表示为一个随机过程f(x)，则可以通过随机过程f(x)的均值函数m(x)和协方差函数或核函数k(x,x′)来完全确定高斯过程
式中,m(x)=E(f(x))；k(x,x′)=cov[f(x),f(x′)]。 2.2 高斯过程回归模型
给定一个训练样本集D={xn,yn}n=1N，设输入数据为X=[x1x2…xN]T，输出观察值为y=[y1y2…yN]T，考虑如下的回归模型
式中，ε为噪声；f(x)=wTφ(x)表示隐变量函数，φ(x)为映射函数，f表示f(x)函数的值，由所有样本数据组成的隐变量函数集为f=[f1(x1)f2(x2)…fN(xN)]T。
在回归模型中，一般认为输出观测值是由函数值f和噪声ε组成的，即式(2)的形式。在式(2)中，假设噪声ε是服从0均值，σ20方差的高斯分布，即
y-f(x)=ε~N(0,σ02)
同时假设训练样本服从独立同分布，那么训练样本集的似然函数即y关于f的条件概率密度可间接地用噪声的高斯分布来表示
式中，N(y|fσ20I)表示y是均值为f，协方差矩阵为σ20I的多元高斯分布；B为对角矩阵，其第n个对角元素βn的值为1/σ20。
一般的，隐变量f是一个高斯过程。根据高斯过程的定义，并将其均值函数设为0，则隐变量集f的先验分布可表示为
式中，θ为协方差函数的参数；K为协方差矩阵或核矩阵。
根据贝叶斯公式，隐变量集f和输出观测值y的联合分布可表示为
2.3 参数学习和数据预测
一般情况，高斯过程回归问题可归结为训练和测试两个步骤。训练是指利用训练样本数据根据最大化边缘似然函数进行核参数θ的学习，自适应地选择核参数θ的过程；测试是指当确定核参数θ后，利用测试样本数据集根据后验概率对测试数据的输出进行预测的过程。
(1) 参数学习。通过对式(5)的联合分布进行积分，可得边缘似然函数
最大化似然p(y|X,θ)，得到包含核参数θ的目标函数为
在实际应用中，一般将最大值问题转化为最小值问题进行求解，即将式(7)的最大化边缘似然函数转化为最小化负对数边缘似然函数。
(2) 数据预测。在给定最优核参数θML的条件下，预测的目的就是给定测试数据x，确定隐函数f(x)的分布，即在x处预测f(x)的函数值。
根据贝叶斯公式以及多元高斯分布的性质，联合式(5)和式(6)可得f的后验概率
式中,
。
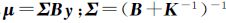同时，根据隐变量f的先验假设和多元高斯分布的性质可得到[ff(x)]的联合分布，在测试数据x处，隐变量f(x)的分布可通过[ff(x)]的联合分布与后验分布的积分求得
式中，
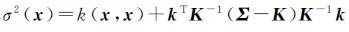为后验协方差函数；
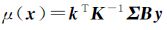为后验均值函数。
高斯过程回归模型的主要优点就是一旦给出了边缘似然p(y|X,θ)，则协方差函数(或核函数)参数θ可通过最大化边缘似然函数估计得到，避免了像SVM、RVM需要通过交叉验证选择核函数参数计算量较大的问题。然而，高斯过程回归模型中的一个重要假设条件是噪声模型必须服从高斯分布，否则，边缘似然函数和后验概率密度都无法通过积分求解。因此，为了能够使高斯过程适用于非高斯噪声模型，学者们在这方面展开了大量的研究工作，提出了一系列的近似逼近方法，比较典型的有变分法[17]、马尔科夫链蒙特卡洛近似法(Markov chain Monte Carlo,MCMC)[18]、拉普拉斯近似法(Laplace approximation,LA)[19]、期望传播法(expectation propagation,EP)[20]和假定密度滤波(assume density filtering,ADF)[11]等。本文采用ADF近似逼近法进行噪声模型的转换。
3 信息向量机3.1 假定概率滤波近似ADF近似法的基本思想是：每次选择一个训练样本数据后，计算改变后的后验概率密度，使其近似服从某一高斯分布，并利用该高斯分布代替后验概率密度。
ADF算法将训练样本数据分为两个集合：一个是活动子集I，表示已经选择的训练样本数据，主要用于计算近似高斯分布；另一个是非活动子集J，表示未被选择的训练样本数据。初始化时，I为空集，而J为所有训练样本数据。假设在选择了第i个训练样本后，近似逼近qi(f)为
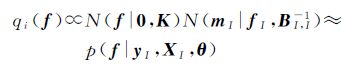式中，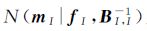
为活动子集I中训练样本数据近似的噪声模型，包含参数mni和βni，该参数可通过顺序序列选择获得。初始近似可表示为q0(f)=t0(f)=N(f|0,K)。
ADF近似真实后验的过程就是从非活动子集J中选择一个训练样本数据ni到活动子集I中，加入ni后的后验分布为
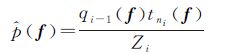式中，Zi为归一化常数约束，其表达式为<
通过最小化qi(f)和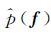
之间的KL散度，可得到新的近似qi(f)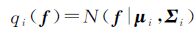
式中,μi和Σi分别为近似qi(f)的均值向量和协方差矩阵，其更新表达式为
式中，
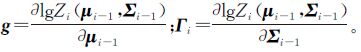
通过上述分析可知，利用ADF算法可将任何噪声模型近似逼近高斯噪声模型，利用高斯过程回归模型进行求解。
3.2 高斯过程分类在高斯过程分类问题中，噪声模型一般不具有高斯分布的形式。因此，需要将高斯过程分类问题转化为回归问题进行求解。本文采用累积高斯函数进行概率转换，得到高斯过程分类的概率噪声模型(probit noise model)为
式中，λ为控制曲线倾斜度的参数;ϕ(z)为累积高斯函数
将式(11)的概率噪声模型代入式(8)可得归一化常数Zi
式中，μi-1,n为均值μi-1的第n个元素；ζi-1,n为协方差阵Σi-1中第n个对角元素；(λyn(fn+b))的表达式为
将式(14)代入式(13)，并交换积分的顺序，可得归一化常数约束为
式中
由此可得如式(9)和式(10)的近似逼近qi(f)中均值向量和协方差矩阵更新公式，其中的参数分别为
式中，gin为gi的第n个元素；γin为Г的第n个对角线元素；vin为对角矩阵(gigTi-2Γi)的第n个对角线元素。
那么近似高斯分布为N(mn|fn,β-1n)，其中mn和βn的表达式为
则分类问题中的边缘似然函数可表示为如下形式
3.3 信息向量机
在ADF近似算法的高斯过程分类中，所有的训练样本数据都被用于确定模型学习的参数，若训练样本总数为N，波段数为d，则在计算核矩阵及其逆的过程中，计算的复杂度为O(N3)；同时，在核参数θ的估计中，需要求边缘似然对θ的梯度，这也将导致O(N3)的计算复杂度和O(N2)的内存耗费。当训练样本数量N较大时，将严重影响计算效率。本文采用文献[12]提出的通过选择活动子集中的信息向量数量来进行模型的训练即信息向量机(IVM)。IVM能够将ADF近似算法的计算复杂度从O(N3)降低到O(d2N)，内存耗费从O(N2)降低到O(dN)；由于d N，因此IVM方法极大地提高了计算效率、降低了内存耗费。
IVM通过最大后验微分熵选择下一个将被包含于活动子集中的训练样本。针对第i个训练样本，近似逼近qi(f)的熵表示为
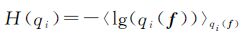式中，〈·〉qi(f)表示在qi(f)分布下的数学期望。根据高斯分布熵的性质，并联合式(10)，可得后验微分熵为
通过最大化式(21)来确定某一训练样本是否被选择包含于活动子集中。
同时，为了保存整个后验协方差矩阵Σi-1，需要O(N2)的内存空间，为了降低大量的内存耗费，需要寻找一个有效的方法来稀疏表示Σi-1。考虑后验协方差矩阵Σi的特殊结构，即Σi可通过原始先验协方差矩阵Σ0=K的连续外积得到
式中，Mi的第k行为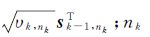
表示包含的第k个训练样本；si-1,ni为Σi-1的第ni列。si-1,nk可根据Mi-1和K计算得到
式中，kni=s0,ni表示K=Σ0的第ni列向量；ai-1,ni表示矩阵Mi-1的第ni个列向量。这样，利用列或行向量来代替矩阵存储于内存中，内存需求将大大降低，变为O((i-1)N)。
另外，由于后验协方差矩阵Σi为对角矩阵，其形式可表示ζi=diag(Σi)，以对角形式表示的更新公式和后验均值向量的更新公式分别为
以上两个更新公式的复杂度为O(N)。因此，通过选择活动子集中一定数量的信息向量以及协方差矩阵的对角化表示这两种策略，能较大程度降低计算效率和内存需求。
算法1：IVM分类中活动子集信息向量数量选择。
步骤1：初始化。设活动子集中信息向量数量为d；m=0；β=0；设ζ0=diag(K)；μ=0；非活动子集为所有训练样本数据J={1,2,…，N}；活动子集为空集I=Ø，S0为空矩阵，i=1,2,…，d，n∈J。
步骤2：当i=1时，遍历所有的训练样本n∈J，根据式(17)计算gin和γin；根据式(21)计算ΔHin。
步骤3：计算最大后验微分熵ni=argmaxn∈JΔHin。
步骤4：根据式(19)更新mn和βn。
步骤5：根据式(23)、式(24)和式(25)计算ζi和μi。
步骤6：扩展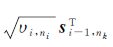
到Mi-1，再根据式(23)更新Mi。
步骤7：将第ni个数据添加到活动子集中，同时在非活动子集中去掉ni个数据点。
步骤8：当i=2,3,…，d时，重复步骤2至步骤7，直到选出d个数据包含于活动子集中。
3.3.2 参数的优化IVM中核函数参数θ可以通过最大化边缘似然函数自适应地获取，这种方法被称为第Ⅱ类型边缘似然最大化(marginal likelihood maximisation，MLM)方法。当噪声模型为非高斯噪声模型时，需要通过ADF算法将其近似高斯分布，得到式(20)形式。IVM算法利用活动子集中的训练样本代替所有训练样本进行高斯近似，可得边缘似然函数为
核函数参数θ包含于KI中，可采用尺度共轭梯度法(scaled conjugate gradient,SCG)[21]最大化式(26)的边缘似然函数即可得到最优的θ。
算法2：IVM参数θ优化。
步骤1：设活动子集中训练样本个数为d，迭代次数为T。
步骤2：当i=1,2,…，T时，通过算法1选择活动子集的训练样本。
步骤3：利用式(26)计算边缘似然函数，通过SCG算法估计核函数参数θ。
4 试验与分析基于SVM和RVM的高光谱影像分类方法是目前研究较多且分类效果较好的分类方法。因此，本文采用SVM、RVM与IVM分类器进行高光谱影像分类性能比较分析。
4.1 试验数据试验数据采用德国宇航中心研制的反射式光学系统成像光谱仪ROSIS成像光谱仪获取的意大利帕维亚城市中心(Pavia center)的高光谱影像，影像大小为1096像素×715像素，空间分辨率1.3 m，原始数据共115个波段，去除较低信噪比的波段后余下102个波段进行试验。影像中包含水、树木等9种地物类型，由波段15、89、52组成的数据立方体如图 1(a)所示，样本分布如图 1(b)所示，采集的样本数量信息如表 1所示。
|
| 图 1 ROSIS影像数据立方体和样本分布 Fig. 1 Data cube and samples distribution of ROSIS imagery |
| 类别 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 名称 | 水体 | 树木 | 草地 | 砖块 | 裸土 | 柏油路面 | 沥青屋顶 | 瓦片屋顶 | 阴影 |
| 数量 | 456 | 488 | 335 | 366 | 581 | 465 | 457 | 404 | 295 |
在核方法中，常用的核函数(或协方差函数)有线性核函数(linear)、径向基核函数(RBF)和多层感知器核函数(multi-layer perceptron，MLP)等。试验过程中，选用这3种核函数进行比较分析，选择最优核函数进行后续分类性能比较试验。为便于比较分析，信息向量的数量d固定，设置为100。Pavia center高光谱数据不同核函数IVM分类的训练时间、测试时间和分类错误率如表 2所示，表中数字加粗部分为3种核函数所得结果的最优值。
| 核函数 | linear | MLP | RBF |
| 训练时间/s | 15.84 | 53.82 | 25.24 |
| 测试时间/s | 1.22 | 1.12 | 1.02 |
| 错误率/(%) | 5.65 | 1.93 | 2.16 |
从表 2的试验结果分析可知：
(1) 线性核函数的模型训练时间最短，但分类错误最高。
(2) MLP核函数的分类错误最低，但模型训练时间最长。
(3) RBF核函数在模型训练时间和分类错误率上都在线性核函数和MLP核函数之间，但分类错误率与MLP相差较小。
(4) 3种核函数的测试时间基本一致且都较短。
因此，综合考虑以上试验结果，本文选择RBF核函数进行后续的活动子集信息向量数量的选择和分类性能比较试验。
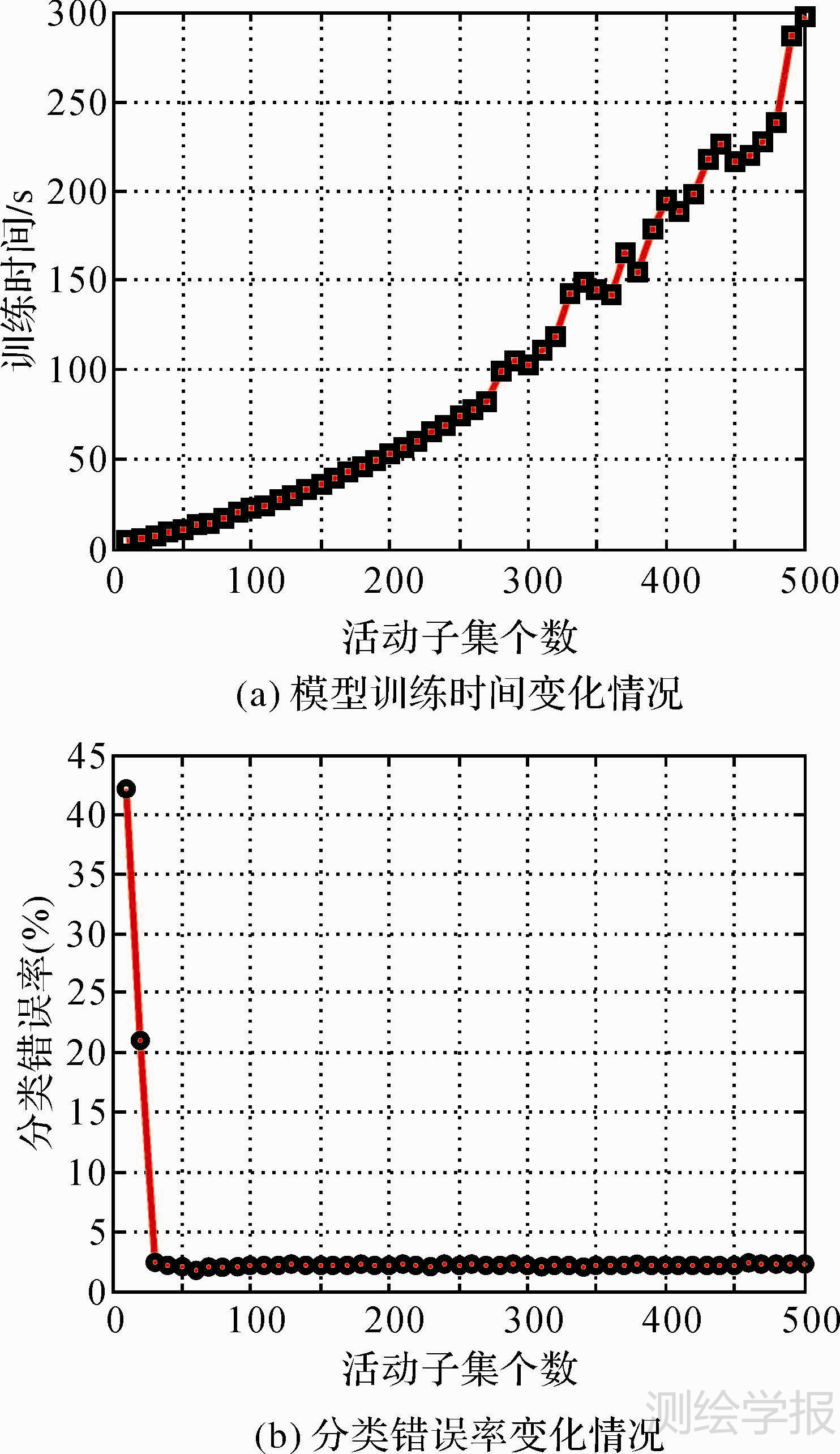
4.3 信息向量数量的选择选择RBF核函数，设置活动子集信息向量数量最大为500个，当样本数量少于500个时，将训练样本数量设置为最大信息向量数量。ROSIS高光谱影像数据不同信息向量数量与模型训练时间和分类错误率如图 2所示。
通过对图 2高光谱影像数据不同信息向量数量条件下的IVM模型训练速度和分类错误率试验结果的综合分析可知，随着信息向量数量的不断增加，模型训练速度急剧增加，分类错误率快速减少，且经过少量的信息向量数量后逐渐趋于平稳，达到最优。
|
| 图 2 ROSIS影像不同信息向量数量IVM分类结果 Fig. 2 IVM classification result with different number of informative vector for ROSIS imagery |
在确定核函数和活动子集中信息向量数量的条件下，通过与SVM、RVM分类试验，比较分析IVM的分类性能。
在SVM和RVM分类器中，惩罚系数和核函数参数的选择一般都是通过交叉验证的方法获取。因此，为了增加试验结果的可比性，需统一设置参数。首先根据不同信息向量数量的试验结果，选择高光谱数据的最优信息向量数量，然后进行高光谱影像的IVM分类，通过最大化边缘似然函数估计得到最优的RBF核函数参数σIVM，再将SVM和RVM的核函数参数设置为σIVM进行分类试验。其中，在进行SVM试验时，通过2-折交叉验证在0.2×i，i={1,2,…，10}范围内选择最优惩罚系数C。SVM分类器采用序列最小优化算法(SMO)进行模型学习[22]，RVM分类器采用快速序列稀疏贝叶斯学习算法(sequential sparse Bayesian learning algorithm，SSBLA)进行模型的学习[9]。SVM、RVM和IVM的多类分类构造策略均采用一对余法。
ROSIS高光谱影像数据的IVM与SVM、RVM分类结果如表 3所示。表中，基向量数量分别表示支持向量、相关向量和信息向量的数量；训练时间表示利用训练样本进行模型学习的时间；测试时间为对测试样本数据进行预测的时间；错误率为错误分类的样本数据占全部测试样本数据的比例。另外，在SVM分类器中，参数σ和训练时间一栏括号中的数字表示最优惩罚系数C以及交叉验证时间。
| 类别 | SVM | RVM | IVM |
| 参数σ | 0.72(1.6) | 0.72 | 0.72 |
| 基向量数量 | 361 | 85 | 50 |
| 训练时间/s | 93.46(241.26) | 65.60 | 18.59 |
| 测试时间/s | 0.18 | 0.09 | 0.98 |
| 错误率/(%) | 4.13 | 3.79 | 1.71 |
ROSIS高光谱影像数据的IVM分类结果如图 3所示。
|
| 图 3 ROSIS影像分类结果比较 Fig. 3 The comparison of ROSIS imagery classification result |
通过以上试验结果分析可得出如下结论：
(1) 高光谱影像SVM、RVM和IVM分类错误率都较低。
(2) 即使在固定核函数参数σ的条件下，SVM交叉验证选择最优惩罚系数的时间也较长。
(3) 在相同核函数参数σ的条件下，IVM分类器的基向量数量少于SVM和RVM，稀疏性更强；IVM模型训练时间更短，效率更高；IVM分类器的分类错误率更低，精度更高。
(4) 高光谱影像数据的IVM分类结果较好，且所分结果地物类别基本接近真实地表覆盖。
5 结束语本文提出了一种基于信息向量机的高光谱影像分类方法。针对分类问题中的概率噪声模型，采用假定概率滤波法近似逼近某一高斯噪声模型，将分类问题转化为高斯回归模型，并通过微分后验熵得分来选择活动子集中信息向量数量进行模型学习，达到稀疏的目的，采用一对余的多类分类处理进行高光谱影像分类处理。通过ROSIS高光谱影像试验表明，IVM分类器基向量数量少、稀疏性强；训练时间短、效率高；分类错误率低、可靠性高。
本文只是将高光谱影像作为一个向量数据的集合，利用其光谱特征进行分类处理。实际上，由于地物分布的连续性和同质性，高光谱影像中还包含如纹理特征、上下文特征和形状结构特征等多种空间信息，如何将这些空间特征信息与光谱特征信息相结合进行分类处理将是下一步研究的重点。
| [1] | YANG Guopeng, YU Xuchu, FENG Wufa, et al. The Development and Application of Hyperspectral RS Technology[J]. Bulletin of Surveying and Mapping, 2008(10):1-4.(杨国鹏，余旭初，冯伍法，等. 高光谱遥感技术的发展与应用现状[J]. 测绘通报, 2008(10):1-4.) |
| [2] | TAN Xiong, YU Xuchu, ZHANG Pengqiang, et al. A Classification Algorithm for Hyperspectral Images Based on Fuzzy Mixed Pixel Decomposition[J]. Journal of Geomatics Science and Technology, 2013, 30(3):279-283.(谭熊，余旭初，张鹏强，等. 一种基于模糊混合像元分解的高光谱影像分类方法[J]. 测绘科学技术学报, 2013, 30(3):279-283.) |
| [3] | YU Xuchu, FENG Wufa, YANG Guopeng, et al. Analysis and Application for Hyerspectral Imagery[M]. Beijing:Science Press, 2013.(余旭初，冯伍法，杨国鹏，等. 高光谱影像分析与应用[M]. 北京:科学出版社, 2013.) |
| [4] | TAN Xiong. Research on Classification Techniques for Hyperspectral Imagery Based on Combined Spectral and Spatial Features[D]. Zhengzhou:Information Engineering University, 2014.(谭熊. 联合光谱和空间特征的高光谱影像分类技术研究[D]. 郑州:信息工程大学, 2014.) |
| [5] | SUN Weiwei. Theory and Methods of Dimensionality Reduction Using Manifold Learning for Hyperspectral Imagery[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(4):439.(孙伟伟. 基于流形学习的高光谱影像降维理论与方法研究[J]. 测绘学报, 2014, 43(4):439.) |
| [6] | SHI Qian, DU Bo, ZHANG Liangpei. A Dimensionality Reduction Method for Hyperspectral Imagery Based on Local Discriminative Tangent Space Alignment[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3):417-420.(石茜，杜博，张良培. 一种基于局部判别正切空间排列的高光谱遥感影像降维方法[J]. 测绘学报, 2012, 41(3):417-420.) |
| [7] | TAN Kun, DU Peijun. Wavelet Support Vector Machines Based on Reproducing Kernel Hilbert Space for Hyperspectral Remote Sensing Image Classification[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2):142-147.(谭琨，杜培军. 基于再生核Hilbert空间的小波核函数支持向量机的高光谱遥感影像分类[J]. 测绘学报, 2011, 40(2):142-147.) |
| [8] | ZHANG Lei, SHAO Zhenfeng, ZHOU Xiran, et al. Semi-supervised Collaborative Classification for Hyperspectral Remote Sensing Image with Combination of Cluster Feature and SVM[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(8):855-861.(张磊，邵振峰，周熙然，等. 聚类特征和SVM组合的高光谱影像半监督协同分类[J]. 测绘学报, 2014, 43(8):855-861.) |
| [9] | YANG Guopeng, YU Xuchu, ZHOU Xin, et al. Research on Relevance Vector Machine for Hyperspectral Imagery Classification[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(6):572-577.(杨国鹏，余旭初，周欣，等. 基于相关向量机的高光谱影像分类研究[J]. 测绘学报, 2010, 39(6):572-577.) |
| [10] | YAO Futian, QIAN Yuntao. Gaussian Process and Its Applications in Hyperspectral Image Classification[J]. CAAI Transactions on Intelligent Systems, 2011, 6(5):396-404.(姚伏天，钱沄涛. 高斯过程及其在高光谱图像分类中的应用[J]. 智能系统学报, 2011, 6(5):396-404.) |
| [11] | CSATÓ L. Gaussian Processes-iterative Sparse Approximations[D]. Aston:Aston University, 2002. |
| [12] | LAWRENCE N D, SEEGER M, HERBRICH R. The Informative Vector Machine:A Practical Probabilistic Alternative to the Support Vector Machine[R]. Sheffield, UK:Technical Report, Department of Computer Science, 2005. |
| [13] | LAWRENCE N D, SEEGER M, HERBRICH R. Fast Sparse Gaussian Process Methods:The Informative Vector Machine[M]//Advances in Neural Information Processing Systems.[S.l.]:MIT Press, 2003:625-632. |
| [14] | LAWRENCE N D, PLATT J C. Learning to Learn with the Informative Vector Machine[C]//Proceedings of the 21st International Conference in Machine Learning. San Francisco:[s.n.], 2004:512-519. |
| [15] | LIU Jianwei, XU Xiang, LUO Xionglin. Face Recognition Based on Orthogonal Locality Preserving Projection and Informative Vector Machine[J]. Computer Engineering, 2010, 36(7):200-202.(刘建伟，徐翔，罗雄麟. 基于OLPP和信息向量机的人脸识别[J]. 计算机工程, 2010, 36(7):200-202.) |
| [16] | XU Xiang, LIU Jianwei, LUO Xionglin. Research on Nerval Activity Classification and Decoding Based on Informative Vector Machine[J]. Computer Engineering, 2010, 36(7):198-199, 202.(徐翔，刘建伟，罗雄麟. 基于信息向量机的神经活动分类和译码研究[J]. 计算机工程, 2010, 36(7):198-199, 202.) |
| [17] | GIBBS M N, MACKAY D J C. Variational Gaussian Process Classifiers[J]. IEEE Transactions on Neural Networks, 2002, 11(6):1458-1464. |
| [18] | NEAL R M. Regression and Classification Using Gaussian Process Priors[J]. Bayesian Statistics, 1998, 6(10):475-501. |
| [19] | WILUAMS C K I, BARBER D. Bayesian Classification with Gaussian Processes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, 20(12):1342-1351. |
| [20] | MINKA T P. A Family of Algorithms for Approximate Bayesian Inference[D]. Cambridge:Massachusetts Institute of Technology, 2001:36-48. |
| [21] | MØLLER M F. A Scaled Conjugate Gradient Algorithm for Fast Supervised Learning[J]. Neural Networks, 1993, 6(4):525-533. |
| [22] | LI Hang. Statistical Learning Method[M]. Beijing:Tsinghua University Press, 2012.(李航. 统计学习方法[M]. 北京:清华大学出版社, 2012.) |