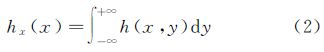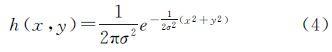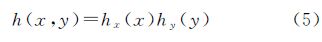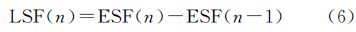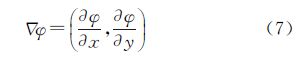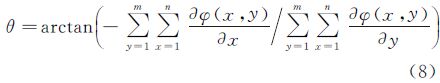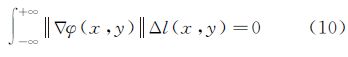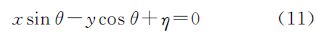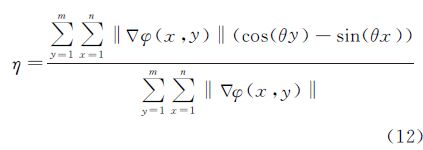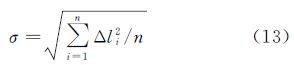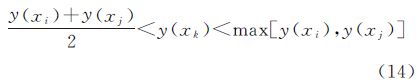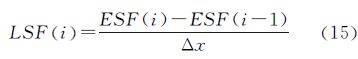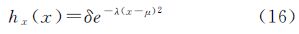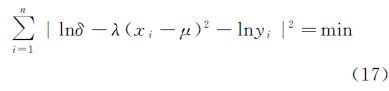1 前 言
光学系统获取自然光信号时,点光源退化为光团的效应称为点扩散函数(point spread function,PSF)[1]。如何从退化的数字图像中准确提取PSF是分析成像指标及进一步提升图像质量所需要解决的重要问题[2]。文献[3]提取CBERS-1卫星影像的PSF进行复原,并对复原后的影像进行分类,获得了良好的分类效果。文献[4]在超分辨率重建过程中利用PSF进行复原,获得了质量更为良好的高分辨率影像。
目前的PSF估算方法主要有点光源响应[5]、刀刃边缘响应、矩形脉冲响应等方法[6]。其中刀刃边缘响应法(刃边法)是目前最为主流、最为有效的方法[2]。然而传统的刀刃法在应用中存在一些限制条件,文献[6]指出传统刀刃法只限于应用在理想刀刃区域(刃边方向与像元排列方向相近,刀刃倾角在8°以内)。文献[2]通过试验分析刀刃倾角与点位偏移量的关系,指出采用刃边法测量PSF时,若铺设靶标则阶跃倾斜角度不宜过大,并选取太阳高度角最大时捕获影像。但实际情况中理想刀刃边缘较少见,而倾斜的刃边却存在亚像素的误差[7]。
文献[8]对传统刃边法测得的PSF进行矫正,获取准确的PSF,但由于其采用离散函数进行推导,忽略了亚像素误差,导致所得PSF仍存在误差。文献[9—12]提出另一种解决办法,根据几何投影的思想调整像元点采样方向以获得准确的样本。该方法克服了刀刃边缘角度的限制,但由于该方法对刃边直线的拟合精度与ESF的拟合精度依赖较高,而这两个过程精度却不理想,仍然可能出现误差。
本文分析了现有刃边法的误差原因,并针对这些问题,提出了一种包括刃边拟合、样本优化及PSF拟合的PSF估计方法,通过准确的刃边拟合得到采样位置精确的样本,用去噪、防走样方法获得采样值精确的样本,并通过对PSF的直接拟合提高了PSF的估计精度。
2 刃边法原理图像的退化过程可以看作是一个线性不变系统。常见的退化模型如式(1)所示[13, 14, 15, 16]。该模型中包括无退化的自然信号f、退化的数字影像φ、点扩散函数h及加性噪声n,*代表卷积运算
刃边法原理如图 1所示,刀刃区域在刀刃梯度方向的二维空间表现为阶跃函数形式,其退化函数为线扩散函数(line spread function,LSF)hx,与PSF关系如下[2]

|
| 图 1 刃边法示意图 Fig. 1 Brief explanation of edge method |
阶跃函数退化后表现为边缘扩散函数(edge spread function,ESF),由式(1)可推知,其与LSF的关系如式(3)所示[17]。
文献[18]根据文献[19]提供的方法进行试验,得出PSF近似服从高斯分布的结论,那么PSF用高斯函数表示下[20, 21, 22]
再根据式(2)及PSF的对称性,可得LSF与PSF关系[23, 24]
3 方法与问题
传统刃边法LSF(式(5))[25]仅适用于ESF采样间隔为一像元单位的理想刀刃区域。
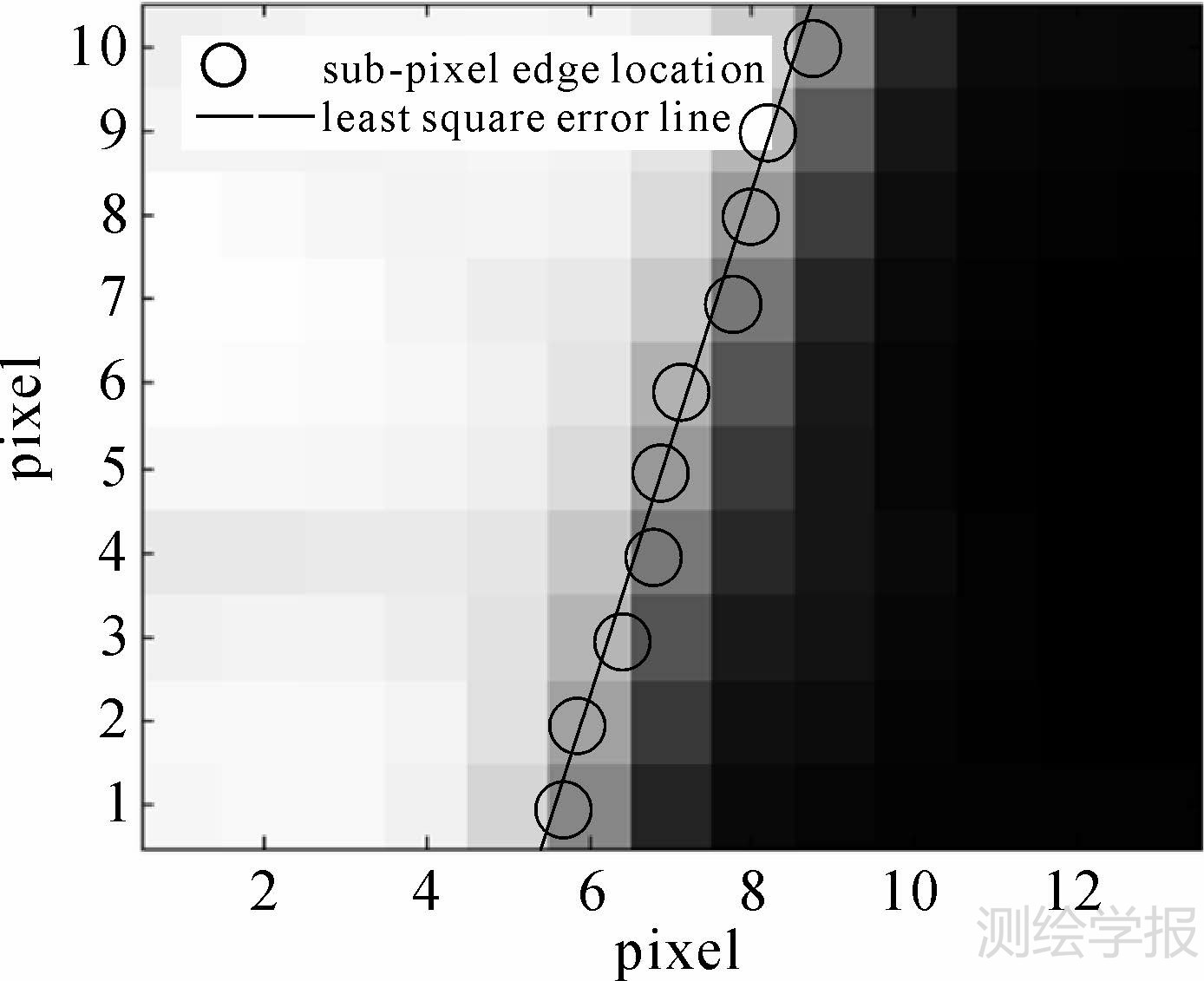
文献[5]给出了对齐拐点的方法以进行倾斜刀刃区域的LSF计算,如图 2所示,计算每行拐点亚像素位置、拟合出刃边直线、对齐拐点进行ESF采样、采用三次样条插值重采样一像元单位间距ESF样本。但ESF采样方向与刀刃梯度方向不一致,样本横坐标被拉伸,必然导致误差[7]。
|
| 图 2 传统刃边法拟合直线 Fig. 2 Line fitting by traditional edge method |
针对这一问题,有两种解决思路:对测得的PSF进行矫正以获取准确的PSF;调整ESF采样方向以获得准确的ESF样本。
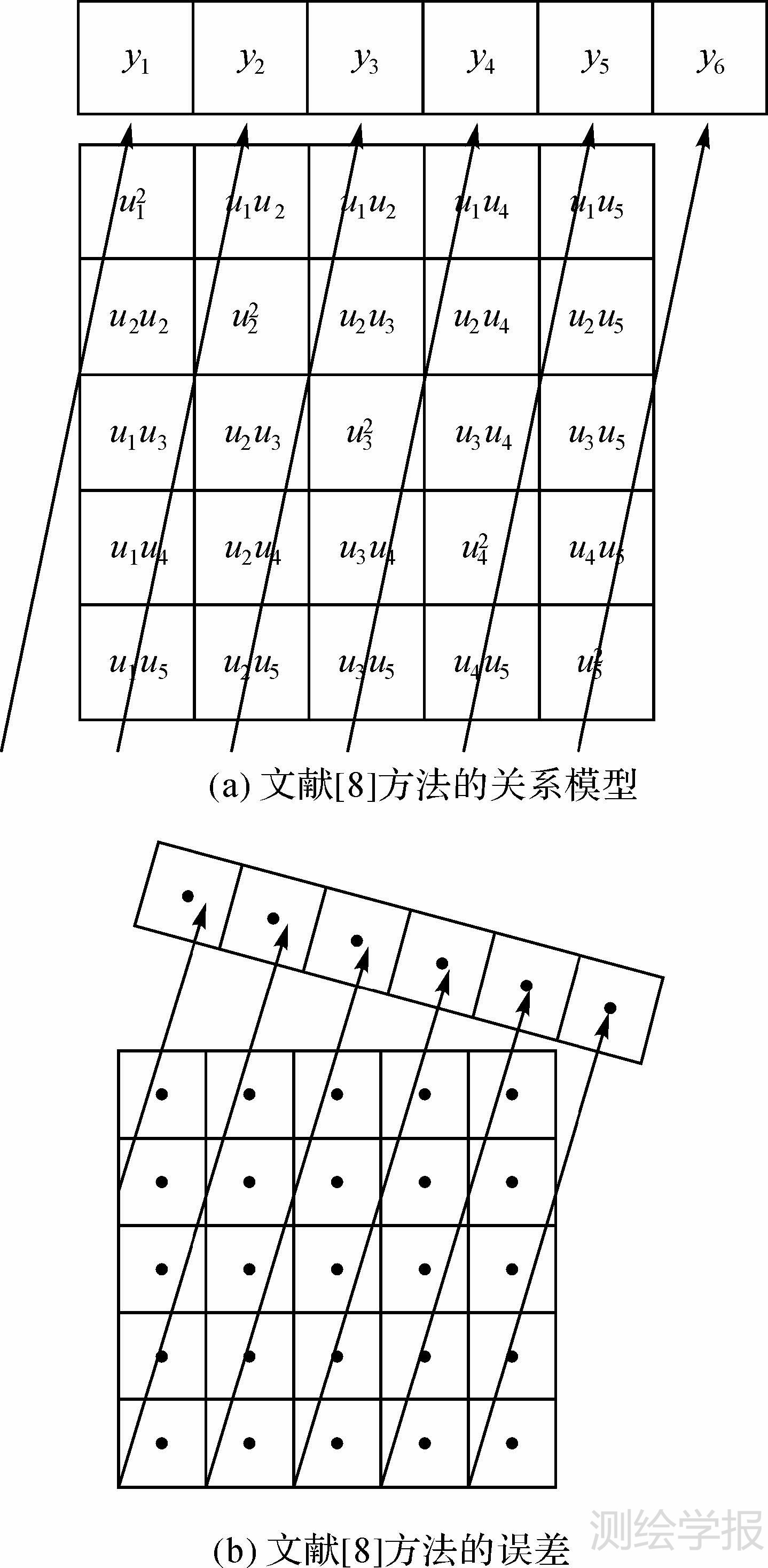
采用第1种思路,文献[8]通过模拟离散卷积过程,构建测量PSF与真实PSF的关系模型,并通过最小二乘法求解真实PSF,关系模型如图 3(a)所示。虽然文献[8]的方法解决了角度误差的问题,但却由于采用离散的模型,产生了亚像素的点位误差,如图 3(b)所示,必然会影响PSF的估计精度。
|
| 图 3 测量PSF与真实PSF关系 Fig. 3 Relation between measured PSF and real PSF |
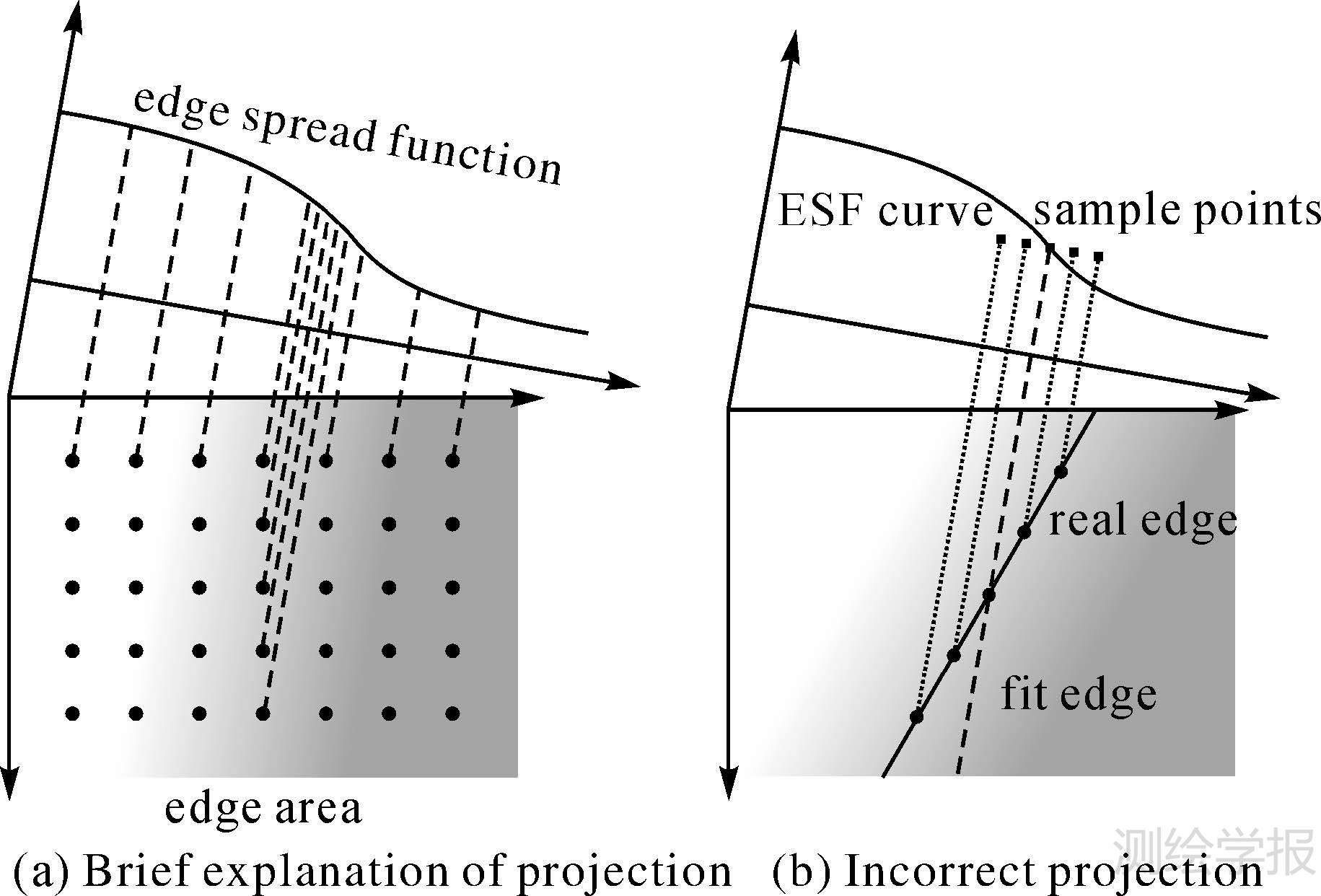
第2种思路就是采用倾斜刃边法(投影法)。该方法根据几何投影的思想,将像元点投影到刃边梯度方向上以获得较为准确的ESF的采样数据,如图 4(a)所示[26]。该方法有效地解决了点位误差与倾角误差的问题,是目前较为有效的PSF估计方法。但该法的精度对刃边直线的拟合精度依赖较大,现有方法常常采用拐点拟合的方法,存在误差。当刃边拟合存在误差时,如图 4(b)所示,在倾角偏差较大时,远离中心行的像元点采样存在递增误差,严重影响刃边直线的拟合精度。
|
| 图 4 倾斜刃边法 Fig. 4 Slant edge method |
由于离散像元点的误差与噪声点的影响,难以获取高质量的LSF样本,因此,目前的刃边法都需要对ESF进行拟合。常用的拟合函数有两种:三次样条插值与近似函数最小二乘拟合[27]。三次样条插值对ESF的拟合精度较低。在倾斜刃边法的应用中,大多采用近似函数最小二乘拟合的方法,拟合函数主要有高次多项式拟合与Fermi函数拟合[28]。高次多项式在固定区间上对ESF的拟合精度较高,但由于其没有固定形状,受ESF样本质量影响较大,稳定性较差。Fermi函数具有固定形状,与ESF形状相似,因此其拟合稳定性较高,但由于两函数自身存在偏差,拟合精度也较低。此外,LSF是ESF的导函数,ESF失之毫厘,LSF却可能谬以千里,对ESF拟合后求LSF极易造成LSF函数变形。
除了采用Fermi函数拟合估计的PSF不需要进行归一化以外,其他方法估计的PSF都需要进行归一化,在归一化的过程中,一个单点的误差会导致全局的误差,致使整体PSF精度下降。
4 高精度估计算法相较而言,倾斜刃边法具有较好的PSF估计效果,但刃边直线拟合与ESF拟合等精度问题仍需解决。在倾斜刃边法基础上,本文算法改进了刃边直线的拟合方法,并通过对ESF样本的优化提高了样本精度,从而得到了可用的LSF样本。由于PSF近似服从高斯分布,因此本算法采用高斯函数拟合LSF得到连续的PSF函数。
4.1 刃边直线拟合与ESF采样基于倾斜刃边法的原理,刀刃角求解的精度对PSF的估计精度至关重要。本文基于梯度与点扩散函数对称性提出一种刃边拟合的方法。为了保证刀刃角的精度,应以刀刃区域整体对刀刃角进行直接拟合。刃边方向与梯度方向垂直,只要求出梯度方向便可得刀刃角。引入边缘检测中的梯度运算,则有
对区域内梯度方向进行线性拟合,可得刀刃角θ
为了方便后续过程,应求出刀刃边缘的直线方程。根据点扩散函数的对称性有
由式(2)、式(3)可得
式中,Δl为点到刃边直线l的距离,存在负值。设l的方程为
则可得
在求取梯度的运算中,2×2的一阶差分算子具有良好的效果,但该算子在横纵方向均会产生0.5像素的偏移量,得出的直线方程后应对其进行校正。获得精确的刃边直线方程后,便可以进行ESF采样。
4.2 ESF样本预处理由于真实影像的无规律性,以及自然环境或设备问题等的影响,得到的ESF样本中往往存在噪声点。与其他采样点相比,这些噪声点明显偏离ESF曲线,视为粗差。因此在PSF的估计之前应先对ESF样本进行预处理,剔除其中的噪声点。
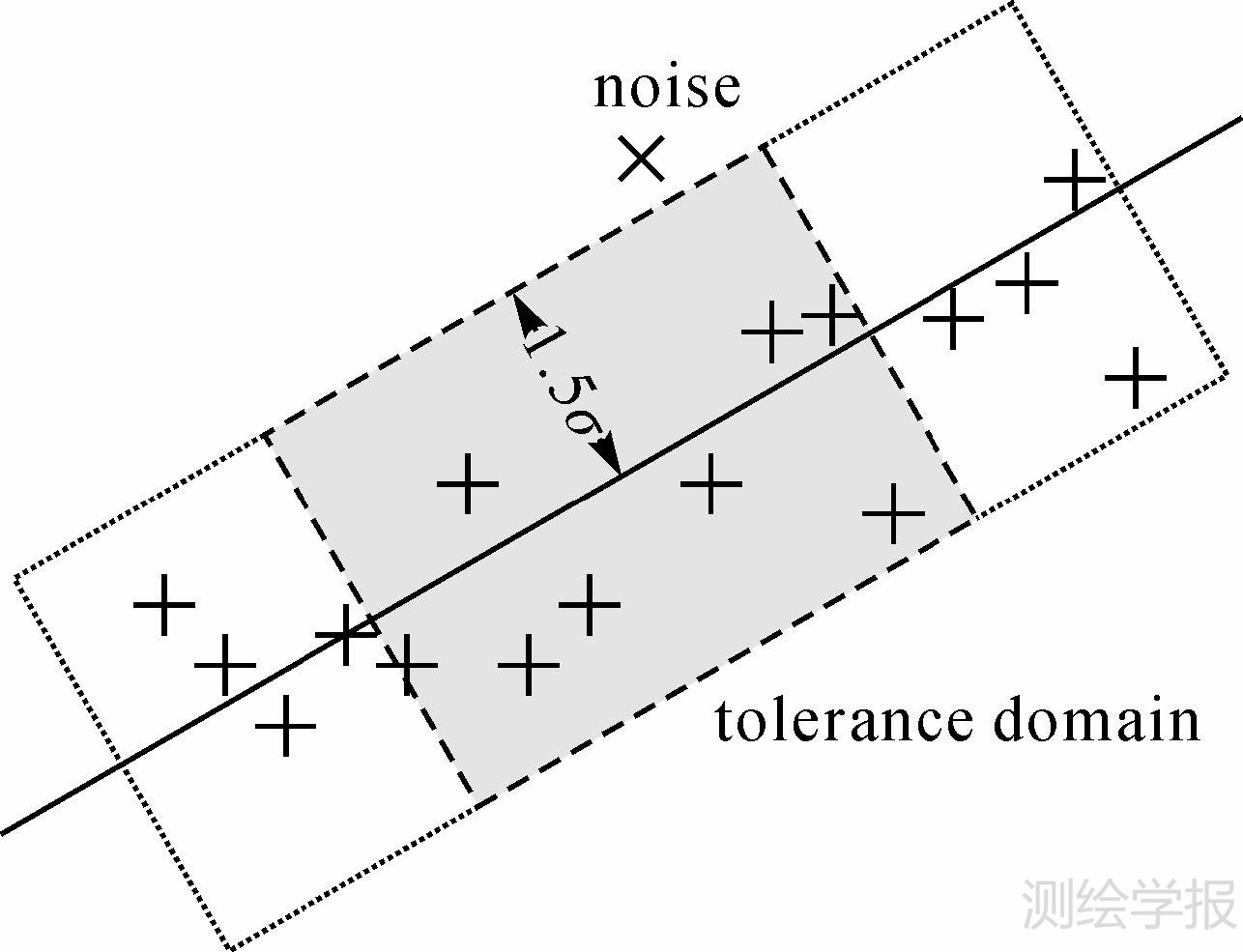
在ESF曲线的一个微小区间上,其形状可以近似看作一条直线。在此区间内拟合出这条直线,以到直线距离为依据在直线两侧构建等距的容忍域,如图 5所示,在容忍域范围以外的采样点即为噪声点。
|
| 图 5 容忍域示意图 Fig. 5 Brief explanation of tolerance domain |
在本研究中,采用最小二乘法对该直线进行拟合,容忍误差为1.5σ。该标准差是以采样点与拟合直线垂直偏差为误差进行计算,如式(13)所示,其中,Δli为第i个采样点到拟合直线的距离
本文提出采样分段扩展方法进行ESF样本噪声的逐段进行检测,具体步骤如下:
(1) 以一像元单位为基准对ESF样本分段,并对每段向两端扩展半像元单位。
(2) 对每段及其扩展区域内的样本进行直线拟合。
(3) 判断每段不包含扩展区域的样本中的噪声点,并剔除。
4.3 ESF分层重采样剔除粗差后的ESF样本在局部范围内仍是不规则的,这样的样本并不适于进行LSF的采样。因此,需要对ESF进行重采样以获取规则等间距的ESF样本。在亚像素重采样中,往往会出现局部曲线走样,该重采样的等距样本是为LSF采样提供采样材料,需要较高的精度,因此应保证ESF曲线形状。依据ESF的单调性及凹凸性,本文提出二分法防变形重采样,对ESF进行分层重采样。
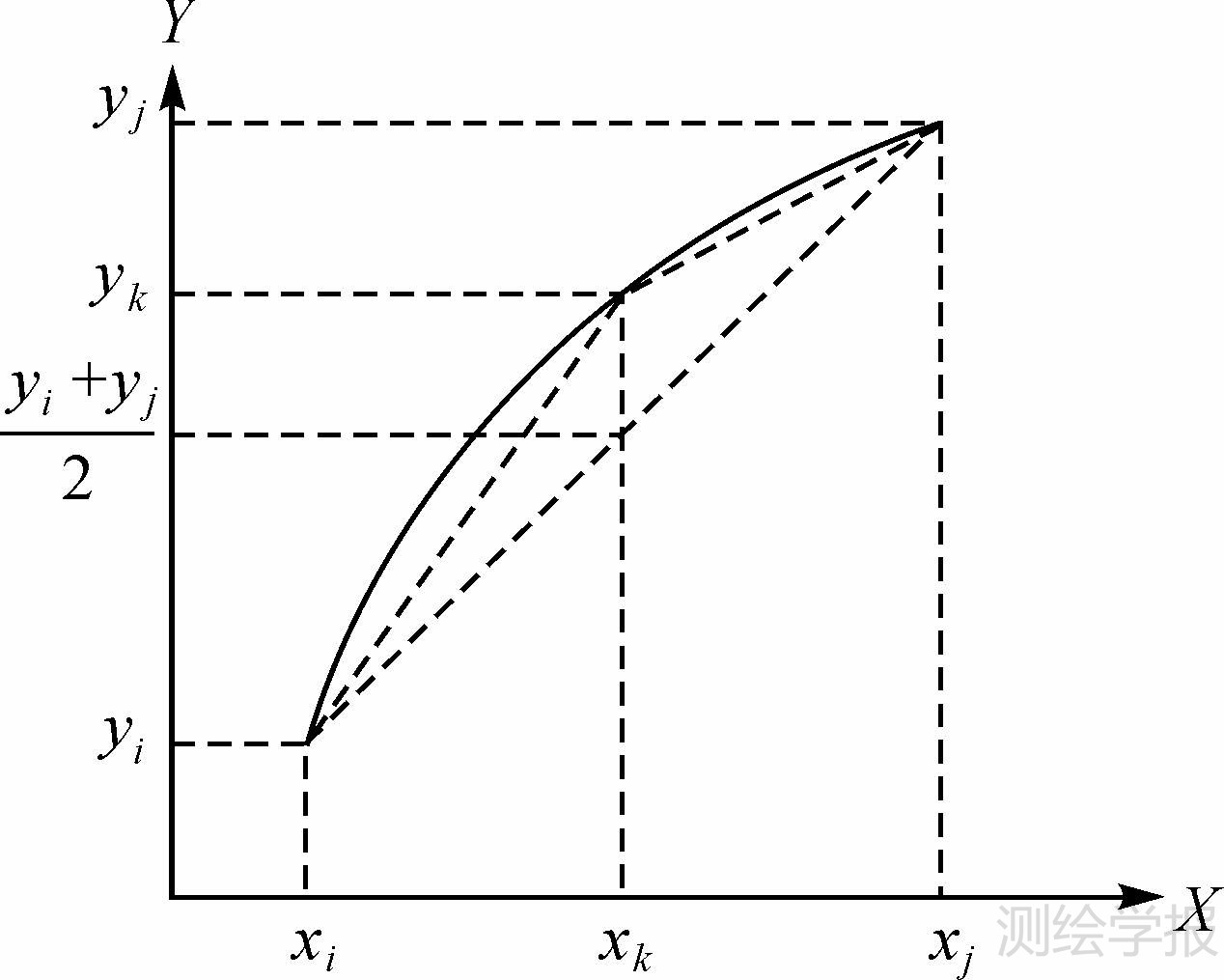
ESF是单调函数,在梯度极值点两侧凹凸性一致,图 6所示为某一单调递增ESF极值点右侧的单位坐标长度的一段曲线。如果该曲线中两端点xi、xj已被插值出,为保持曲线形状,该段曲线中点xk处插值点必然满足下述的ESF防变形判定公式
|
| 图 6 二分法重采样 Fig. 6 Dichotomy resampling |
ESF二分法防变形分层重采样具体步骤如下:
(1) 以梯度极值点为横坐标原点,对ESF进行第1层的整数点插值重采样。
(2) 对已有重采样点的每相邻两点中点进行插值重采样,并依据(ESF防变形判定公式)判定采样点是否变形。
(3) 对变形点采用3.2节中的去噪声方法,以σ为容忍误差,排除原采样点中的噪声点,并重新插值,如果结果仍不满足式(14)则舍弃。
(4) 重复(2)—(3)直至重采样密度满足要求。
在本文中,重采样间距为0.25像素。
4.4 LSF采样与拟合由式(3)可知,LSF样本可通过ESF样本微分获得
所得的LSF样本具有较为正确的曲线形状与相对较高的准确性,便可以对其进行拟合进行较为精确的PSF估计。由于PSF近似服从高斯分布,因此以一维高斯函数对LSF样本进行拟合,拟合模型如式(16)、式(17)所示,加入位移系数μ对LSF的极值点坐标进一步校正以提高PSF估计精度。
依据最小二乘准则,对拟合模型变形后可以建立如下最小二乘问题
LSF样本的质量对于拟合精度有很大影响,虽然通过去噪及防变形重采样可提高LSF的采样精度,但当刀刃区域质量偏低时,也可能产生LSF样本走样或过少的情况。因此在拟合LSF时应对其精度设定阈值,如果拟合精度过低应另寻找合适的刀刃区域进行PSF估计。由于最小二乘问题式(17)中的拟合函数相对简单,本文采Levenberg-Marquardt最优化方法进行求解。该算法具有快速的全局收敛性,并属于“信赖域法”,便于精度阈值的使用。
由式(4)与式(16)可得
根据式(5)便可得到一个连续的二维PSF,且无须再进行归一化处理。
5 试验与讨论为了验证本文方法能否提高PSF的估计精度,设计了两组对比试验对新方法进行评估,并与现有方法进行分析比较。
5.1 模拟试验首先需要检验提出的PSF估计方法对于不同刀刃倾角的刃边区域,不同PSF的适用性,并与现有刃边法进行横向比较。因此笔者设计了如下模拟试验:①采用计算机绘制一幅无退化的刃边图像,并对图像添加白噪声生成噪声刃边图像;②采用高斯函数构造PSF;③对无退化刃边图像和噪声刃边图像卷积获得模拟的退化刃边图像。刃边倾角θ分别采用0、15°、22.5°、30°、45°,高斯函数参数σ分别采用0.5、1.0、1.5,共获得30幅退化刃边图像。
分别采用传统刃边法、文献[8]刃边法、倾斜刃边法(分别采用多项式与Fermi函数拟合ESF,为减少拟合函数对结果的影响,所得结果采用Gauss函数拟合得出最终PSF)与本文方法进行PSF估计。为便于对比,采用估计PSF与真实PSF的峰值信噪比(peak signal to noise ratio,PSNR)来评价估计精度,其中峰值为真实PSF函数的极值,结果见表 1。表中的主数值为带有白噪声的刃边图像,括号中的数值为不带噪声的刃边图像。由PSNR对比,可以看出:
| θ/(°) | σ | 传统刃边法 | 文献[8]方法 | 多项式拟合倾斜刃边法 | Fermi函数拟合刃边法 | 本文方法 | |||||
| 0 | 0.5 | 6.18 | (19.51) | 7.62 | (19.51) | 28.31 | (17.62) | 21.44 | (21.75) | 48.05 | (108.72) |
| 1.0 | 8.06 | (31.57) | 11.01 | (31.57) | 12.67 | (23.39) | 30.02 | (30.03) | 54.76 | (47.57) | |
| 1.5 | 14.90 | (40.92) | 11.04 | (40.92) | 9.72 | (30.57) | 31.46 | (31.45) | 45.75 | (56.41) | |
| 15 | 0.5 | 6.57 | (20.59) | 7.68 | (11.70) | 22.13 | (21.52) | 31.00 | (29.28) | 54.30 | (92.63) |
| 1.0 | 18.17 | (28.16) | 22.25 | (29.78) | 22.82 | (31.60) | 30.93 | (30.35) | 53.96 | (81.99) | |
| 1.5 | 20.10 | (32.32) | 16.64 | (40.25) | 25.75 | (37.39) | 31.52 | (31.48) | 70.17 | (72.85) | |
| 22.5 | 0.5 | 18.92 | (19.46) | 20.60 | (13.43) | 20.54 | (21.51) | 29.53 | (29.26) | 52.41 | (95.59) |
| 1.0 | 20.23 | (24.71) | 18.63 | (31.85) | 26.92 | (33.55) | 31.45 | (30.47) | 39.46 | (71.58) | |
| 1.5 | 26.31 | (25.56) | 15.38 | (28.43) | 23.73 | (38.30) | 30.87 | (31.57) | 47.41 | (66.92) | |
| 30 | 0.5 | 11.38 | (18.03) | 10.38 | (19.93) | 21.51 | (21.51) | 27.30 | (29.27) | 66.28 | (88.87) |
| 1.0 | 6.45 | (21.45) | 9.23 | (35.60) | 24.06 | (33.23) | 28.70 | (31.31) | 40.89 | (63.85) | |
| 1.5 | 15.41 | (11.04) | 3.12 | (8.53) | 23.73 | (44.67) | 27.50 | (29.63) | 37.56 | (60.54) | |
| 45 | 0.5 | 13.61 | (14.40) | 16.21 | (11.00) | 13.70 | (20.02) | 21.74 | (30.55) | 41.17 | (105.36) |
| 1.0 | 13.82 | (15.76) | 19.73 | (34.88) | 16.78 | (32.65) | 25.57 | (31.51) | 44.47 | (84.37) | |
| 1.5 | 11.33 | (16.21) | 14.39 | (22.20) | 21.42 | (28.25) | 23.23 | (27.89) | 72.14 | (74.06) | |
(1) 传统刃边法受刀刃倾角影响严重,θ越接近45°,PSNR越低,精度越差。稳定性低,易受噪声影响。
(2) 文献[8]方法的精度几乎不受刀刃倾角影响,但却严重受制于σ。在σ为1.0时,其表现尚佳,而在σ为0.5与1.5时,其精度大幅降低。稳定性低,易受噪声影响。
(3) 采用多项式拟合ESF的倾斜刃边法不受刀刃倾角影响,而受ESF采样点分布影响:当θ接近22.5°时,其采样点分布较为均匀,精度也较高;当σ较小时,采样数量相对较少,精度也偏低。稳定性较低,有时受噪声影响明显。
(4) 采用Fermi函数拟合ESF的倾斜刃边法,由于其具有固定形状,稳定性较好,几乎不受θ与σ的影响,也不受噪声影响,但精度却不够高。
(5) 相较于其他方法,本文方法具有明显优势。在不同刀刃倾角、不同PSF的刀刃区域中,均能对PSF进行精确地估计,且对噪声图像也能进行较为精确地估计。由于本文方法拟合的PSF曲线与真实PSF基本一致,当θ较小时,真实PSF的峰值较大,从而PSNR值较高。
5.2 ADS40遥感影像试验下一试验继续对本文方法的实用性进行评价。试验数据采用带有辐射条纹靶标的ADS40遥感影像,如图 7所示。图中A、B、C、D 4个方框区域为选取的理想刃边区域,采用传统刃边法对4个刃边区域的PSF进行测量,并用高斯函数进行拟合,取平均值作为PSF的参考值,参考值的高斯函数参数σ为0.867 3。

|
| 图 7 ADS40影像中的刃边区域选取 Fig. 7 Selection of edge areas in ADS40 |
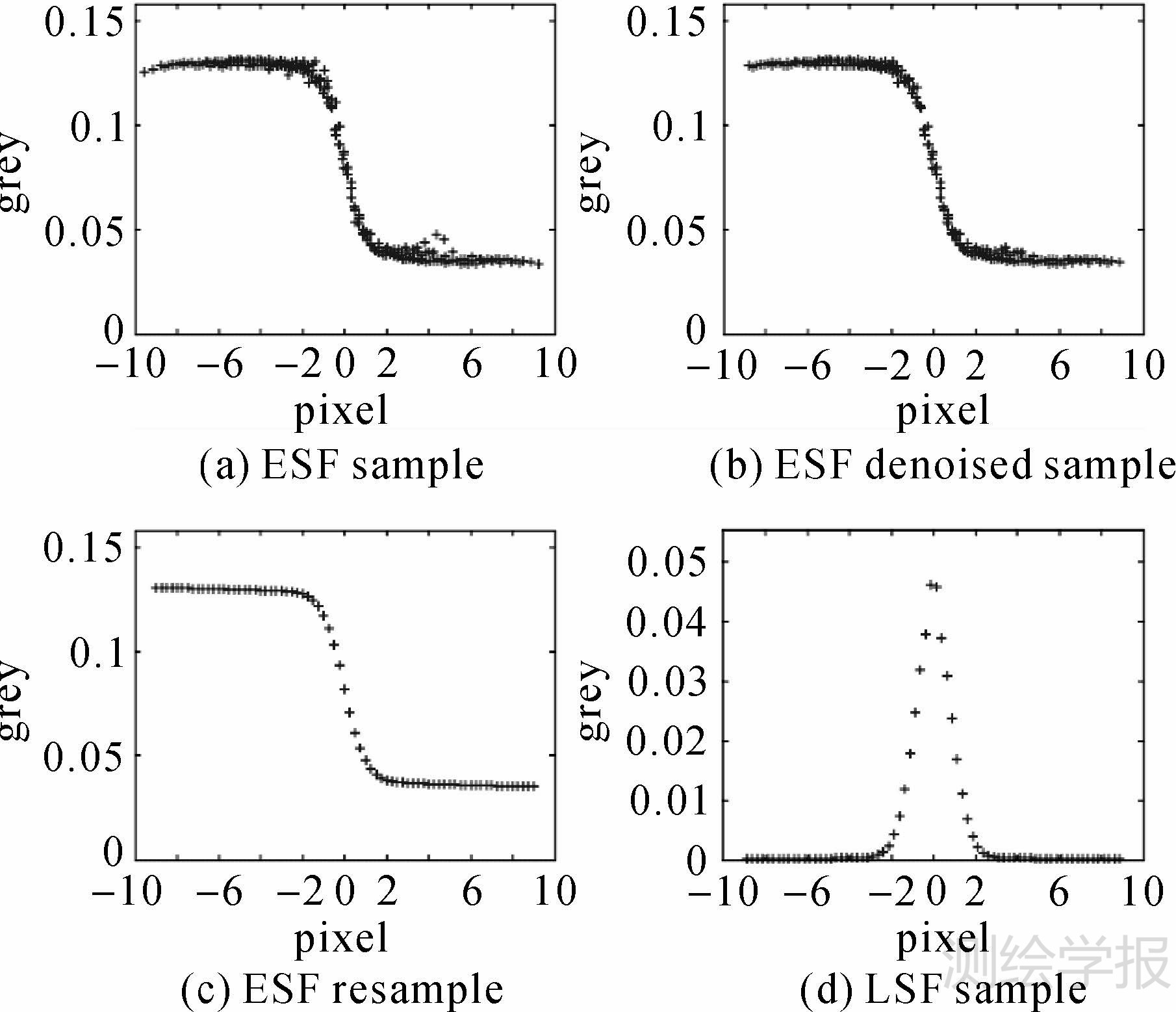
选取图 7中E方框内的倾斜刃边区域为试验区域,经测量,其刀刃倾角约为22°25′10″。采用本文方法对该刃边区域进行PSF估计,其中ESF采样、ESF去噪、ESF重采样、LSF采样结果如图 8所示。由图 8可知,本文的采样方法能够有效地去除噪声防止ESF曲线变形,得到良好的LSF样本。
|
| 图 8 采样过程 Fig. 8 Sampling |
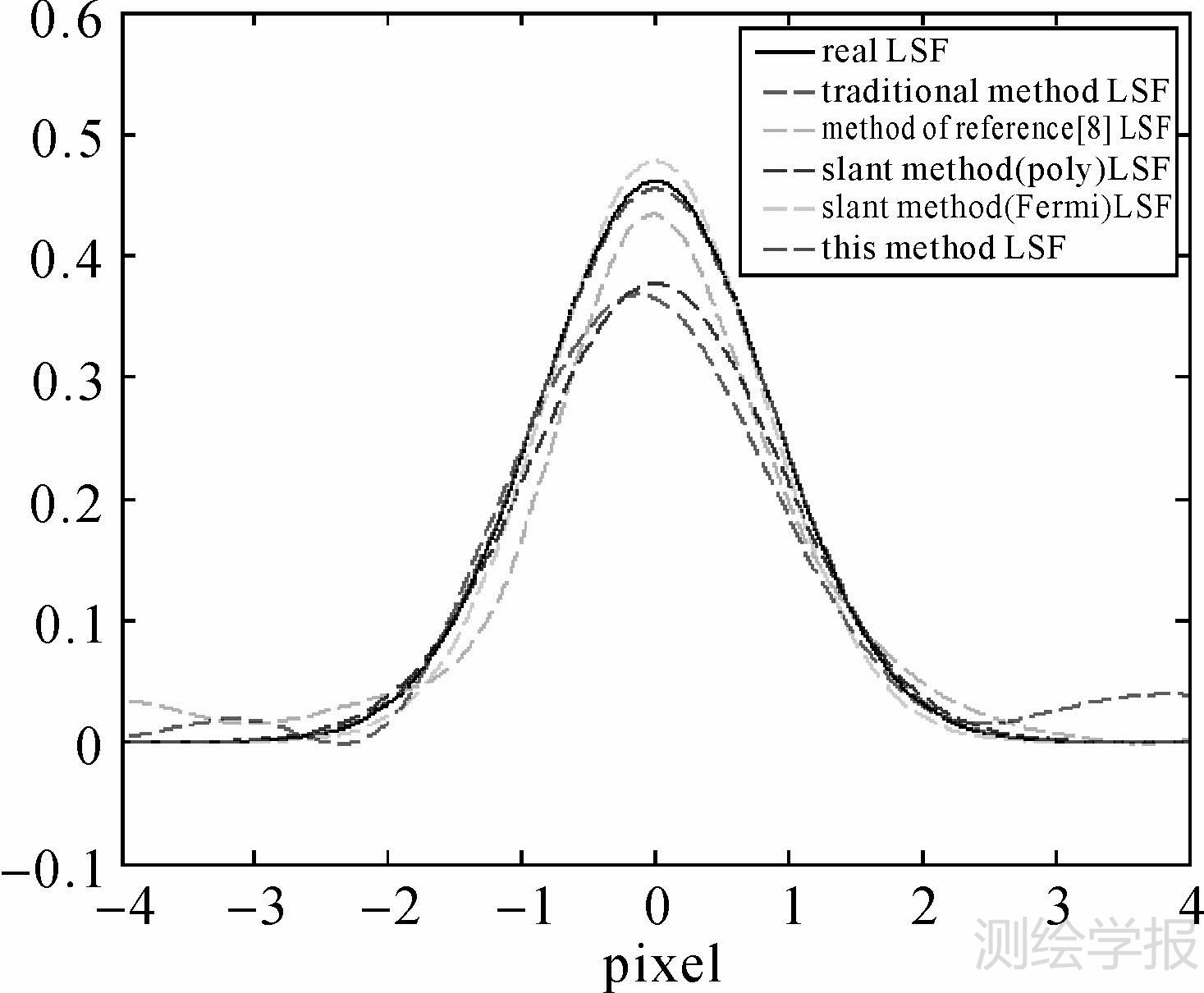
分别采用传统刃边法、文献[8]方法、倾斜刃边法对同一刃边进行估计。为减小拟合函数影响,倾斜刃边法均采用Gauss函数对最终结果进行拟合。为了便于比较,对采用各种方法估计的PSF以及参考PSF拟合成曲线进行对比,如图 9所示。同时计算各种方法估计的PSF与真实值得相关系数(coefficient of correlation,CORRCOEF)、中误差(mean square error,MSE)、峰值信噪比,如表 2所示。
|
| 图 9 LSF估值曲线对比 Fig. 9 Comparison of estimated LSF curves |
从图 9可以看出,由于刃边区域灰度不够平滑,传统刃边法、文献[8]方法与采用多项式拟合的倾斜刃边法表现不佳,采用Fermi函数拟合的倾斜刃边法表现比较稳定,但精度仍存在偏差。相比于其他方法,本文方法估计的PSF几乎与真实PSF吻合,具有明显的精度优势。
在表 2中,各种方法估计的PSF,其相关系数与中误差均较好,但峰值信噪比却具有明显不同,参照图 9可知,PSNR能够正确反映各个方法PSF的估计精度;本文方法精度明显优于现有算法,MSE极小,而PSNR可以达到为其他算法的两倍以上。
根据试验结果可知,与现有刃边法相比,本文方法影像的PSF估计精度有明显提高。与其他刃边法一样,本方法的估计精度也会受到刃边区域质量的影响,但是其稳定性高于前者。这个试验中PSF的估计精度要低于模拟试验,这是因为模拟图像中的刀刃区域是比较完美的,但是实际的图像中的色差,噪声是无法避免的,而且真实的PSF近似于高斯函数,但是也会有细小出入,这些都会影响到PSF最终的估计精度。
6 结 论本文基于刃边法提出了一种高精度的PSF估计算法,该方法可较为精确地估计图像的PSF,可应用于图像恢复。该算法通过对ESF样本的预处理去除噪声点以及防变形重采样得到了更高质量的ESF样本,进而得到较为精确的LSF样本,并直接对LSF进行拟合,从而提高PSF的估计精度。
从试验中可知,本文方法无论在精度还是稳定性上都要高于传统刀刃法与倾斜刀刃法。这一方法可广泛应用于遥感图像的预处理过程中,尤其对超分辨率重建具有重要意义。但是,还有一些问题有待解决。首先,由于图像上的灰度是离散的,必然会影响PSF的估计精度,具体表现在模拟试验中本文方法精度的无规律微波动。其次,本方法通过对ESF样本去噪及防变形重采样一定程度上减弱了刀刃区域质量的影响,但ESF样本质量问题仍然对PSF估计精度有很大影响。此外,本方法的拟合样本并非直接采样得到的,而是通过ESF加工获得的,这也在一定程度上影响了本方法的精度。
| [1] | PARKER J R. Algorithms for Image Processing and Computer Vision[M]. 2nd ed.New York:Wiley, 2010:251-283. |
| [2] | GUO Lingling, WU Zepeng, ZHANG Liguo, et al. A Precise Method to Measure the On-orbit Point Spread Function of Remote Sensors[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(3):284-289.(郭玲玲,吴泽鹏,张立国,等. 遥感相机在轨点扩散函数高精度测量方法[J]. 测绘学报, 2014, 43(3):284-289.) |
| [3] | HE Jing, CHENG Xinwen, YAO Yuan. Image Restoration with MTF of CBERS-1 No.2 Satellite and the Result Evaluation[J]. Science of Surveying and Mapping, 2007, 32(2):108-110.(何静,程新文,姚远. CBERS-1卫星02号星图像MTF复原及其结果分析评价[J]. 测绘科学, 2007, 32(2):108-110.) |
| [4] | ZHANG Xiaolin, HE Xiaohai, LI Tao, et al. The Image Sequence Blind Super-resolution Algorithm Based on Slanted-edge Method[J]. Journal of Sichuan University:Engineering Science Edition, 2013, 45(Sup):84-89.(张晓林,何小海,李滔,等. 基于刃边法的序列图像盲超分辨率重建算法[J]. 四川大学学报:工程科学版, 2013, 45(Sup):84-89.) |
| [5] | LEGERD, DUFFAUTJ, ROBINETF. MTF Measurement Using Spotlight[C]//International Geoscience and Remote Sensing Symposium.Pasadena, CA:IEEE, 1994, 4:2010-2012. |
| [6] | CHOIT. IKONOS Satellite on Orbit Modulation Transfer Function(MTF) Measurement Using Edge and Pulse Method[D]. Brookings:South Dakota State University, 2002. |
| [7] | ZANDHUIS J A, PYCOCKD, QUIGLEY S F, et al. Sub-pixel Non-parametric PSF Estimation for Image Enhancement[J]. IEE Proceedings Vision, Image and Signal Processing, 1997, 144(5):285-292. |
| [8] | QIN Rongjun, GONG Jianya. A Robust Method of Calculating Point Spread Function from Knife-edge without Angular Constraint in Remote Sensing Images[J]. Journal of Remote Sensing, 2011, 15(5):895-907.(秦荣君,龚健雅. 不受刀刃边缘倾角约束的遥感影像点扩散函数稳健计算方法[J]. 遥感学报, 2011, 15(5):895-907.) |
| [9] | SAMEI E, RANGER N T, DOBBINS J T, et al. Intercomparison of Methods for Image Quality Characterization I:Modulation Transfer Function[J]. Medical Physics, 2006, 33(5):1454-1465. |
| [10] | ESTRIBEAU M, MAGNAN P. Fast MTF Measurement of COMS Imagers at the Chip Level Suing ISO 12233 Slanted-edge Methodology[C]//Proceedings of SPIE Sensors, Systems, and Next-generation Satellites.Maspalomas. Canary Islands:SPIE, 2004, 5570:557-567. |
| [11] | HWANG H, CHOI YW, KWAK S, et al. MTF Assessment of High Resolution Satellite Images Using ISO 12233 Slanted-edge Method[C]//Proceedings of SPIE Image and Signal Processing for Remote Sensing.Cardiff, Wales:SPIE, 2008, 7109:710905. |
| [12] | HSIEH S H, CHEN C H, TSENG Y W. Adaptive Edge Enhancement Based on Anisotropic Image Interpolation[C]//Proceedings of the 8th World Congress on Intelligent Control and Automation(WCICA). Jinan:IEEE, 2010:3286-3290. |
| [13] | GUO Lingling, WU Zepeng, ZHANG Liguo, et al. Multichannel Blind Deconvolution Based on Orbit Estimation of Point Spread Function for Space Optical Remote Sensor[J]. Acta Optica Sinica, 2013, 33(4):0428001.(郭玲玲,吴泽鹏,张立国,等. 基于多通道盲反卷积的空间光学遥感器在轨点扩展函数估算[J]. 光学学报, 2013, 33(4):0428001.) |
| [14] | XU Yuanjing, WANG Qiaojue, SHEN Huanfeng, et al. A Remote Sensing Image Restoration Method Based on Estimation and Regularization Model[J]. Journal of Geomatics, 2010, 35(6):7-9.(徐源璟,汪俏珏,沈焕锋,等. 基于刃边法与正则化方法的遥感影像复原[J]. 测绘信息与工程, 2010, 35(6):7-9.) |
| [15] | XIE Dingjie, LI Tiecheng, FENG Huajun, et al. Image Restoration of Cassegrain Optical Remote Sensing System[J]. Acta Optica Sinica, 2001, 31(6):0611004.(谢丁杰,李铁成,冯华君,等. 卡塞格林光学遥感系统的图像复原[J]. 光学学报, 2001, 31(6):0611004.) |
| [16] | WANG Tianhui, LI Shengyang, LI Xuzhi. Blur Estimation and Restoration of Remote Sensing Images Using a Reference Image[J]. Journal of Remote Sensing, 2010, 14(3):460-467.(王天慧,李盛阳,李绪志. 利用参考图像的遥感图像模糊估计与恢复[J]. 遥感学报, 2010, 14(3):460-467.) |
| [17] | LI Tiecheng, TAO Xiaoping, FENG Huajun, et al. Modulation Transfer Function Calculation and Image Restoration Based on Slanted-edge Method[J]. Acta Optica Sinica, 2010, 30(10):2891-2897.(李铁成,陶小平,冯华君,等. 基于倾斜刃边法的调制传递函数计算及图像复原[J]. 光学学报, 2010, 30(10):2891-2897.) |
| [18] | CAPEL D. Image Mosaicing and Super-resolution[M]. London:Springer, 2004. |
| [19] | REICHENBACH SE, PARK SK, NARAYANSWAMY R. Characterizing Digital Image Acquisition Devices[J]. Optical Engineering, 1991, 30(2):170-177. |
| [20] | QIN Fengqing, JUN Min, GUO Hongrong. A Blind Image Restoration Method Based on PSF Estimation[C]//WRI World Congress on Software Engineering. Xiamen:IEEE, 2009, 2:173-176. |
| [21] | YANG Lihong, REN Jianyue. Remote Sensing Image Restoration Using Estimated Point Spread Function[C]//IEEE International Conference on Information Networking and Automation(ICINA). Kunming:IEEE, 2010, 1:48-52. |
| [22] | YANG Lihong,ZHANG Xingxiang, REN Jianyue. Adaptive Wiener Filtering with Gaussian Fitted Point Spread Function in Image Restoration[C]//Proceedings of IEEE the 2nd International Conference on Software Engineering and Service Science(ICSESS). Beijing:IEEE, 2011:890-894. |
| [23] | HUANG Haile, ZHU Leiming, PENG Yu, et al. Research on MTF of Space Camera Based on an Edge Method[J]. Optics & Optoelectronic Technology, 2013, 11(2):71-73.(黄海乐,朱雷鸣,彭宇,等. 刃边法检测空间相机MTF的方法研究[J]. 光学与光电技术, 2013, 11(2):71-73.) |
| [24] | QIN Rongjun, GONG Jianya, FAN Chong. Multi-frame Image Super-resolution Based on Kinfe-edges[C]//Proceedings of 2010 IEEE 10th International Conference on Signal Processing. New York:IEEE, 2010:972-975. |
| [25] | WANG Qiaojue, XU Yuanjing, YUAN Qiangqiang, et al. Restoration of CBERS-02B Remote Sensing Image Based on Knife-edge PSF Estimation and Regularization Reconstruction Model[C]//2011 4th International Conference on Intelligent Computation Technology and Automation. Shenzhen:IEEE, 2011, 2:687-690. |
| [26] | [JP+6]SAMEI E, RANGER N T, DOBBINS J T, et al. Intercomparison of Methods for Image Quality Characterization I:Modulation Transfer Function[J]. Medical Physics, 2006, 33(5):1454-1465. |
| [27] | ZHU Jin, PAN Yu, XU Tao, et al. The Algorithm for Computing MTF of Remote Sensing Image in Mid-lowSpatial Resolution and with Curve Edge[J]. Remote Sensing Information, 2009(3):3-6.(朱近,潘瑜,徐涛,等. 基于弯曲刃边的中低分辨率遥感影像MTF计算方法[J]. 遥感信息, 2009(3):3-6.) |
| [28] | DONG Jianting, CHEN Wei, SHI Manli. Implementation of MTF Real-time Test with Knife-edge Method[J]. Computer Measurement & Control, 2013, 21(2):349-351.(董建婷,陈伟,史漫丽. 基于刃边法的MTF实时测试技术实现[J]. 计算机测量与控制, 2013, 21(2):349-351.) |