2. 武汉大学地球空间环境与大地测量教育部重点实验室，湖北 武汉 430079
2. Key Laboratory of Geospace Environment and Geodesy Ministry of Education, Wuhan University, Wuhan 430079, ChinaAbstract
1 引 言
GOCE卫星于2009年3月17日发射成功，其采用高低卫星跟踪卫星测量技术和重力梯度测量技术相结合的模式，目标是确定1~2 cm的全球大地水准面和10-5 m/s2的全球重力异常，同时空间分辨率达到100 km。为实现此目标，GOCE首次搭载了高精度的重力梯度仪[1]。该梯度仪具有高精度高灵敏度特性，存在固有误差，同时需要稳定的观测环境。由于离心加速度的确定存在误差，并且受到GOCE运行过程中仪器与卫星组合误差、卫星平台误差的影响，GOCE重力梯度观测值(后文简称观测值)不仅含有随机噪声，还包含有色噪声[2]。在对观测值进行预处理时，对其进行时变重力场改正、粗差探测与修复之后，还需要对其进行外部校准[3]，为恢复高精度静态全球重力场提供可靠的梯度数据。
重力梯度的外部校准[4]是指为了使观测值不受系统误差(如比例因子和偏差)的影响而利用独立数据对其进行的校准，通过与独立数据比较，估计观测值中存在的尺度因子、偏差、漂移等参数。这方面得到国外学者的深入研究，文献[5]对利用GPS数据校准GOCE卫星重力梯度的原理作了相关研究；文献[3—4，6—8]研究了利用地面重力数据对GOCE梯度数据进行外部校准的理论与方法，并作了数值模拟计算；文献[9]提出利用加速度数据和恒星敏感器数据获得梯度仪校准参数的方法。国内学者也对GOCE数据的预处理作了大量探讨，文献[10]将移动开窗检验法应用在GOCE数据的粗差探测中并验证了其有效性；文献[11]详细讨论了利用地球重力场模型、GOCE卫星跟踪卫星数据、地面重力数据对GOCE重力梯度进行外部校准的方法；文献[12—13]对利用地球重力场模型和地面重力数据校准GOCE重力梯度的方法进行了数值模拟计算，取得了良好效果；文献[3—4,8,14]研究了利用重力场模型对梯度数据校准的理论与方法，并利用EIGEN-5C重力场模型、GPS数据、地面重力数据分别对实测GOCE梯度数据进行校准分析，得到的比例因子的平均值均接近于1，在利用EIGEN-5C模型校准时每周校准一次，并且对观测值进行了高通滤波，仅保留频率大于0.005 Hz的信号，因此滤波后的观测值中不存在偏差，分析了Vxx、Vyy、Vzz分量比例因子的稳定性，其标准差分别是8×10-4、8×10-4、5×10-4。
本文研究了利用重力场模型对GOCE梯度观测值进行外部校准的理论与方法，在没有对观测值进行高通滤波的情况下对其进行校准，并详细分析了相同模型不同阶次、同阶次不同模型以及是否估计漂移参数对比例因子、偏差参数及校准观测值的影响。
2 基于参考重力场模型校准重力梯度的原理考虑到梯度观测值的误差特性，基于先验重力场模型的校准模型可以表示为如下形式[4]
式中，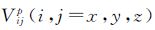
是t时刻利用先验重力场模型计算的GOCE沿轨重力梯度；Vij是t时刻待校准的观测值；s是比例因子；b是偏差；d是漂移；ω=2πt/T，t是时间，T是平均轨道周期；ak、bk是与轨道旋转频率有关的系数，k表示每圈k次的频率(k-cpr，cycle per revolution)；e是观测噪声及其他未模型化的误差。三角函数项表示由于GOCE轨道的周期性变化导致观测值存在的k-cpr特性。需要指出，Vpij本应为经过时变改正的真实静态重力场信号，但不可能知道真实的静态重力场，因此利用已有的重力模型计算其近似值。
本文仅对Vxx、Vyy、Vzz分量进行校准，利用上式基于最优线性无偏估计即可求出外部校准参数s、b、d、ak、bk。
3 数值计算与分析在模拟GOCE沿轨引力梯度张量观测值时，采用的先验重力场模型有EIGEN-5C[15]、EGM2008[16]、GGM03S[17]、GO_CONS_GCF_2_TIM_R3[18](简称GOTIM3)、ITG-Grace 2010s[19]。GOTIM3是仅仅基于GOCE实测数据反演得到的卫星重力场模型，因此采用该模型分析校准结果对先验模型的依赖性。本文采用的其他数据均由ESA[20, 21]发布，包括梯度仪坐标系下的重力梯度数据EGG_GGT (gravity gradient tensor)，重力梯度坐标系相对于惯性坐标系的姿态数据EGG_IAQ (inertial attitude quaternions)，精密科学轨道数据SST_PSO_2 (precise science orbits)。校准前对观测值进行时变重力场改正，并进行粗差探测与修复。数据周期从2009年11月至2010年6月，采样率1 s。模拟沿轨梯度时EIGEN-5C与EGM2008模型取至250阶，其他模型采用最高阶次。校准周期为1 d，即1 d计算一组校准参数；选择k=1，即仅考虑每圈1次对应频率的影响。
3.1 是否考虑漂移项对校准结果的影响分析首先分析校准模型中漂移对校准参数、校准观测值及其差异的影响。利用250阶的EIGEN-5C模型对GOCE梯度数据进行校准，得到了是否考虑漂移项的两组校准参数和校准观测值。表 1给出了比例因子的统计特性，表中“是”表示校准时考虑了漂移项，“否”表示忽略漂移项。从表 1可以看出，如果不考虑漂移，Vxx、Vzz分量的比例因子变化很小，Vyy分量的比例因子变化则比较明显。考虑漂移项，Vyy分量比例因子的稳定性为5.6×10-4，但如果不考虑漂移项，稳定性则为8.4×10-3。
| 分量 | 平均值 | 标准差 | 最小值 | 最大值 | ||||
| 是 | 否 | 是 | 否 | 是 | 否 | 是 | 否 | |
| Vxx | 0.999 6 | 0.999 6 | 5.0×10-4 | 5.3×10-4 | 0.997 9 | 0.997 8 | 1.001 2 | 1.001 3 |
| Vyy | 1.000 3 | 0.987 5 | 5.6×10-4 | 8.4×10-3 | 0.998 1 | 0.910 2 | 1.001 7 | 1.001 3 |
| Vzz | 1.000 5 | 1.000 5 | 3.2×10-4 | 3.2×10-4 | 0.999 6 | 0.999 1 | 1.002 0 | 1.001 4 |
为了进一步分析漂移对校准的影响，表 2给出了校准后观测值的差异。从表 2可以看出，漂移对校准观测值有很大影响：Vyy分量达到0.4 E(1 E=10-9/s2)，Vxx分量大约20 mE(1 mE=10-3 E)，Vzz分量小于10 mE。结合表 1中比例因子稳定性的差异，在利用先验重力场模型以1 d为周期对GOCE重力梯度观测值进行外部校准时，校准模型中需要考虑漂移。本文接下来的校准都考虑了漂移。
| mE | ||||
| 分量 | 平均值 | 标准差 | 最小值 | 最大值 |
| Vxx | 7.6×10-11 | 24.1 | -86.0 | 86.1 |
| Vyy | 2.8×10-9 | 429.9 | -1 026.0 | 990.8 |
| Vzz | 7.0×10-11 | 6.8 | -31.4 | 31.4 |
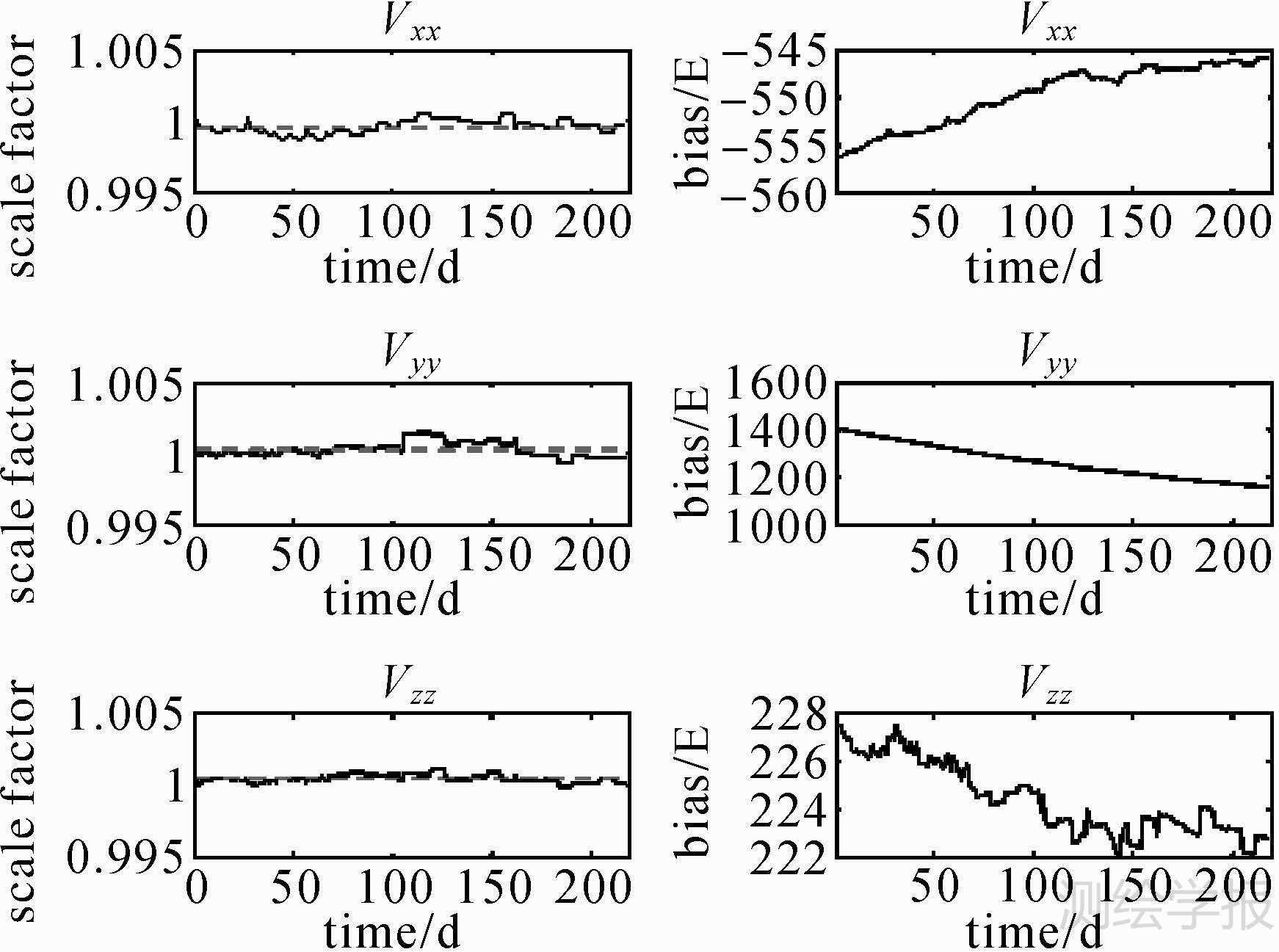
利用250阶次EIGEN-5C模型进行校准求得的校准参数如图 1所示。图 1分别是Vxx、Vyy、Vzz分量的比例因子和偏差变化图。左边3幅图的实线反映了比例因子每天的变化特性，虚线表示比例因子的平均值。从图中可以看出Vxx、Vyy分量的比例因子变化幅度较大，而Vzz分量变化相对较小。Vxx、Vyy分量的偏差呈明显的线性变化，而Vzz分量的偏差虽然呈跳跃性的变化，但也存在线性变化的趋势。这种线性变化的特点说明梯度观测值存在明显的与时间相关的漂移，也说明在一定时间周期内对观测值进行校准，需要考虑漂移的影响。
|
| 图 1 EIGEN-5C模型校准得到的比例因子和偏差 Fig. 1 Scale factors and bias calculated by the external calibration using EIGEN-5C up to 250 degree |
比例因子的统计信息见表 1。从表中可以看出Vxx、Vyy、Vzz分量比例因子的标准差分别为5.0×10-4、5.6×10-4、3.2×10-4，这说明外部校准以10-4的精度确定了比例因子，优于文献[14]中比例因子的稳定性。梯度观测值中低频信号强于高频信号，并且低频信号变化幅度较小，这导致比例因子更加稳定，因此认为本文与文献[14]中比例因子的差异是本文没有对梯度观测值进行高通滤波造成的，此外本文与文献[14]采用的校准周期也不相同，这也导致了两者结果不完全一致。为了进一步分析比例因子的特点，表 3给出了以1周为周期校准得到的比例因子统计信息，从表 3中可以发现，在以1周为校准周期时，比例因子的标准差更小，但与以1 d为周期校准得到比例因子非常接近，这说明GOCE比例因子变化很小，梯度仪运行非常稳定。
| 分量 | 平均值 | 标准差 | 最小值 | 最大值 |
| Vxx | 0.999 6 | 4.5×10-4 | 0.998 9 | 1.000 5 |
| Vyy | 1.000 3 | 5.1×10-4 | 0.999 4 | 1.001 5 |
| Vzz | 1. 0005 | 2.7×10-4 | 1.000 0 | 1.001 2 |
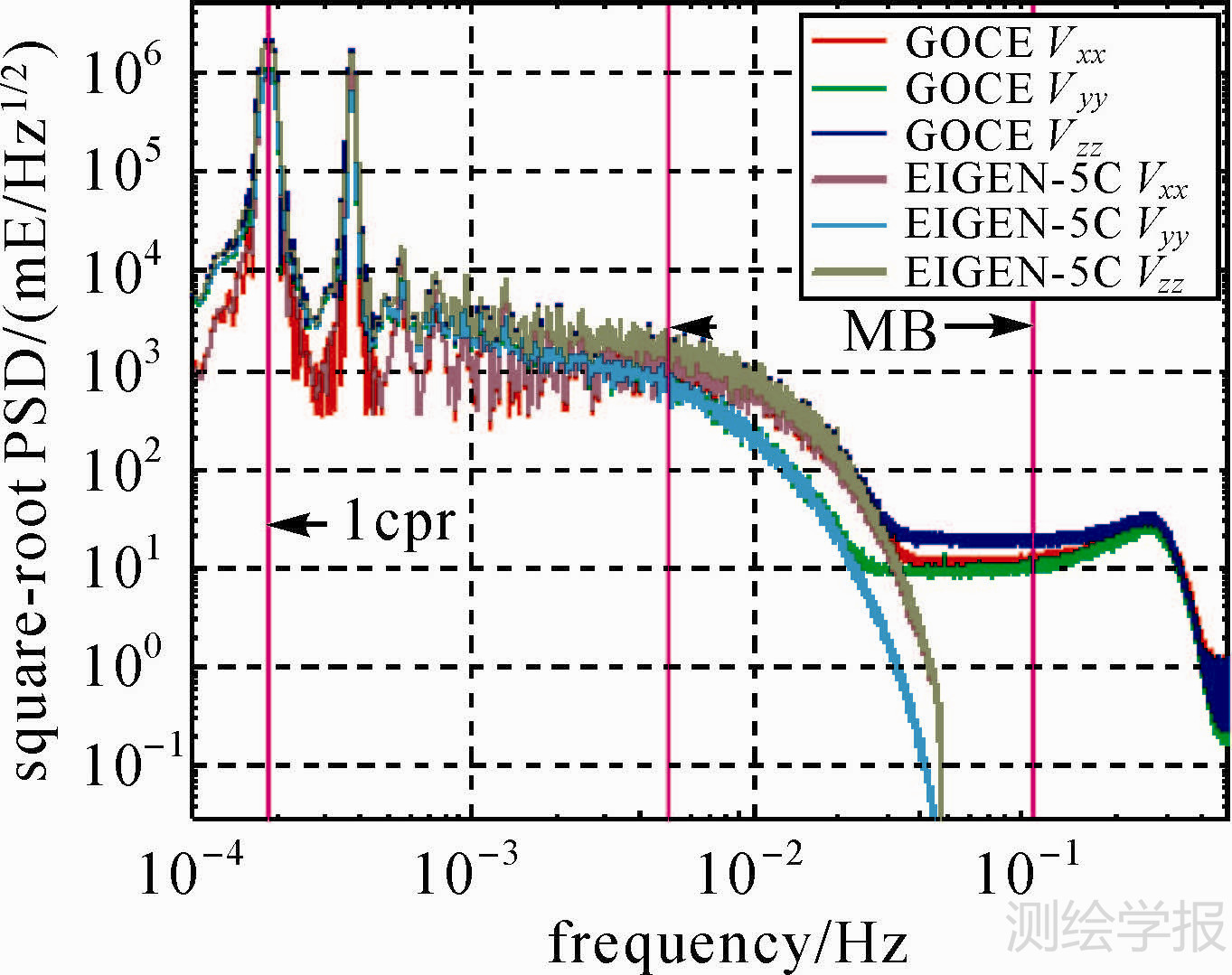
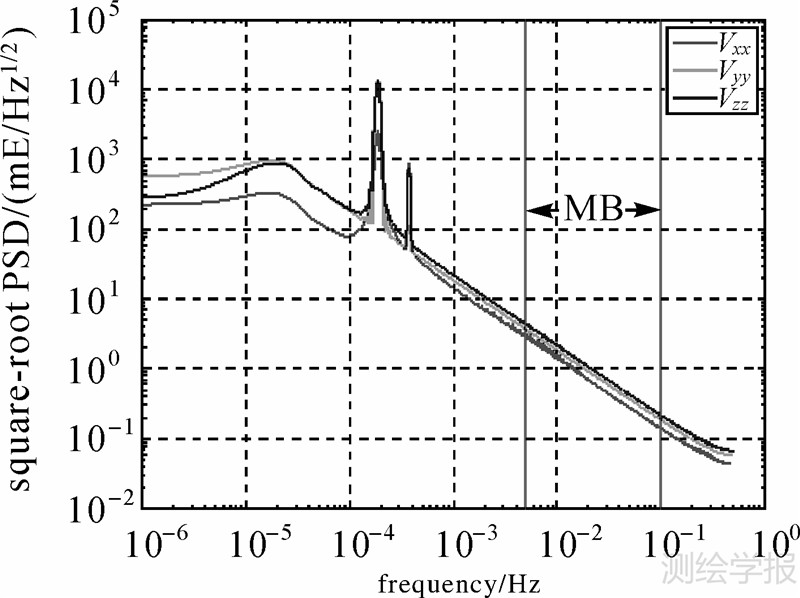
在分析校准观测值的影响之前，首先分析观测值在观测频带内的误差水平和特点。图 2给出了GOCE和EIGEN-5C模型引力梯度张量对角分量的功率谱密度(power spectral density，PSD)。这里假设EIGEN-5C模型代表真实静态重力场信号，GOCE的实测信号则包含了真实的静态重力场信号和观测噪声。从图 2中可以看出，在0.005~0.03 Hz范围内，GOCE与EIGEN-5C模型的信号非常接近，并随着频率的增加逐渐减小，在0.03~0.1 Hz频带内EIGEN-5C模型信号迅速减小，而实测信号则基本保持不变。如果将模型信号看作是真值，则从0.04 Hz频率开始实测信号中误差信号占优，根据仪器在观测频带内应该满足白噪声的特点[22]，从0.04 Hz开始实测信号的大小可以代表观测频带内误差的水平，从图 2可以看出，在0.04~0.1 Hz范围内，Vxx、Vyy分量的噪声大约为10 mE，而Vzz分量为20 mE，这与文献[23]中Vxx、Vyy、Vzz分量的噪声量级一致。
|
| 图 2 GOCE重力梯度值的PSD1/2 Fig. 2 PSD1/2 of GOCE gravitational gradients |
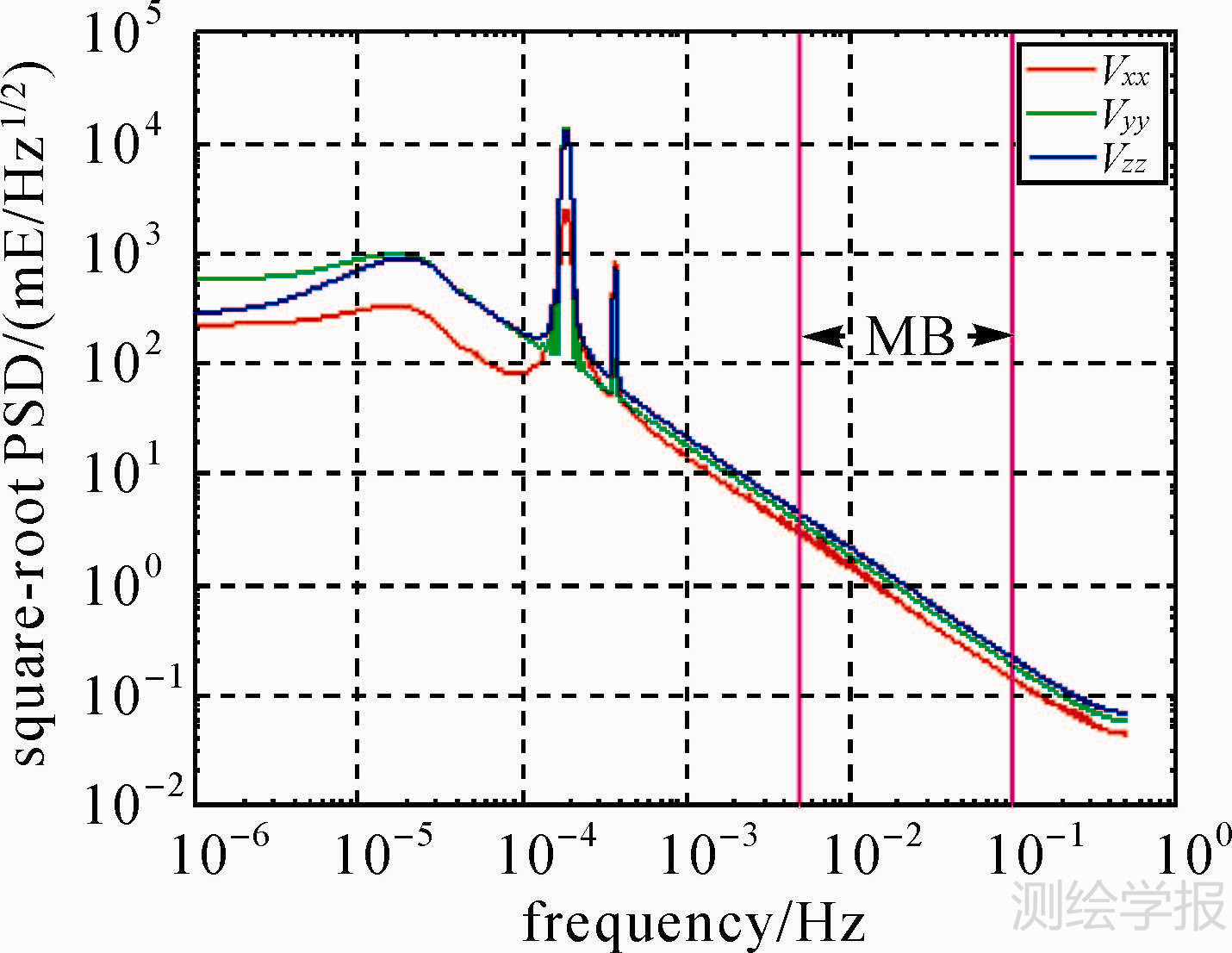
图 3给出了校准前后GOCE梯度值差异的PSD。从图中可以发现差异的PSD主要分布在低频(3×10-5Hz)部分；当频率大于3×10-5Hz时，随着频率的增加，差异越来越小。在0.005 Hz处，差异为3 mE，远远小于图 2中信号的强度，随着频率的增加，差异呈指数递减。比较图 2和图 3可以发现，校准过程对GOCE梯度值在观测频带内的信号影响很小，因此校准后的观测值可用于恢复中高频的重力场信号。
|
| 图 3 GOCE重力梯度值与EIGEN-5C校准观测值差异的PSD1/2 Fig. 3 PSD1/2 of the difference between original and calibrated GOCE gravitational gradients using EIGEN-5C |
为了分析不同阶次的先验重力场模型对校准结果的影响，分析了100、120、150、200阶EIGEN-5C模型的校准结果与250阶EIGEN-5C模型校准结果的差异。表 4给出了不同阶次比例因子的标准差。比较表 4和表 1可以发现：不同阶次比例因子的标准差差异很小，120阶与250阶比例因子的标准差相同。
| 分量 | 阶次 | ||||
| 100 | 120 | 150 | 200 | ||
| Vxx | 5.0×10-4 | 5.0×10-4 | 5.0×10-4 | 5.0×10-4 | |
| Vyy | 5.7×10-4 | 5.6×10-4 | 5.6×10-4 | 5.6×10-4 | |
| Vzz | 3.4×10-4 | 3.2×10-4 | 3.2×10-4 | 3.2×10-4 | |
为进一步分析不同阶次的重力场模型对校准结果的影响，表 5给出了不同阶次与250阶校准观测值差异的统计信息。从表 5中可以看出：不同阶次重力场模型的校准观测值存在差异，但当模型高于150阶时，差异远小于上文分析得到的GOCE卫星梯度仪的观测噪声。因此，当模型高于150阶时，不同阶次的重力场模型校准结果之间的差异很小。
| 分量 | 阶次 | ||||
| 100 | 120 | 150 | 200 | ||
| Vxx | 0.026 | 0.006 | 8×10-4 | 7×10-5 | |
| Vyy | 0.476 | 0.189 | 5×10-2 | 7×10-3 | |
| Vzz | 0.480 | 0.190 | 5×10-2 | 7×10-3 | |
本节分析了不同重力场模型对校准结果的影响。把250阶EIGEN-5C模型校准结果作为标准，比较分析ITG-Grace2010s、EGM2008、GGM03S、GOTIM3模型校准结果与其差异。研究发现不同重力场模型校准得到的比例因子与EIGEN-5C模型比例因子差异很小，甚至完全相同，如用GOTIM3模型校准得到的Vxx、Vyy、Vzz分量比例因子的标准差为5.0×10-4、5.6×10-4、3.2×10-4。表 6给出了不同模型校准观测值的差异，可以发现不同模型校准观测值的差异比GOCE观测精度低两个数量级。
| 分量 | 阶次 | ||||
| EGM2008 | GOTIM3 | GGM03S | ITG-Grace2010s | ||
| Vxx | 0.001 8 | 0.002 2 | 0.032 1 | 0.031 3 | |
| Vyy | 0.134 9 | 0.122 1 | 0.161 6 | 0.096 0 | |
| Vzz | 0.136 2 | 0.123 7 | 0.173 3 | 0.114 1 | |
图 4给出了GOTIM3模型的校准观测值与GOCE梯度值差异的PSD。可以发现图 4与图 3非常相似，这再次表明校准过程对GOCE梯度值在观测频带内的信号影响很小，并且校准后的观测值可用于恢复中高频的重力场信号。实际上ITG-Grace2010s、EGM2008、GGM03S模型的校准观测值与GOCE梯度值差异的PSD也与图 3非常相似，这说明先验模型对校准结果的影响很小。
|
| 图 4 GOCE重力梯度值与GOTIM3校准观测值差异的PSD1/2 Fig. 4 PSD1/2 of the difference between original and calibrated GOCE gravitational gradients using GOTIM3 |
本文采用EIGEN-5C、EGM2008、GOTIM3、GGM03S、ITG-Grace2010s等重力场模型对GOCE重力梯度观测值进行的对角线分量进行校准分析。主要结论如下：
(1) 采用250阶的EIGEN-5C模型，以1 d为周期对Vxx、Vyy、Vzz观测值校准，得到比例因子的标准差分别为5.0×10-4、5.6×10-4、3.2×10-4，略小于文献[14]中的标准差，这可能是因为本文未采用滤波技术移除观测值的低频信号。
(2) 不同重力场模型校准观测值之间的差异较小，重力场模型对校准结果的影响很小。
(3) 在以1 d为周期对观测值校准时，漂移对校准参数校准后的观测值有很大影响，校准模型中需要考虑漂移。
(4) 校准参数和校准后的观测值主要决定于模型的中低阶(频)信号，对高阶(>150)信号不敏感；同时校准过程对GOCE梯度值在观测频带内的信号影响很小，校准后的观测值可用于恢复中高频的重力场信号。
| [1] | ESA.Gravity Field and Steady-state Ocean Circulation Mission[R]. Reports for Mission Selection of the Four Candidate Earth Explorer Core Missions.[S.l.]:ESA Publications Division, 1999. |
| [2] | ESA RESEARCH FELLOW. GOCE Gradiometer Calibration and Level 1b Data Processing[R]. Noordwijk, The Netherlands. ESA Working Paper EWP-2384, 2011. |
| [3] | BOUMAN J, RISPENS S, GRUBER T, et al. Preprocessing of Gravity Gradients at the GOCE High-level Processing Facility[J]. Journal of Geodesy, 2009, 83(7):659-678. |
| [4] | BOUMAN J, KOOP R, TSCHERNING C C, et al. Calibration of GOCE SGG Data Using High-low SST, Terrestrial Gravity Data and Global Gravity Field Models[J]. Journal of Geodesy, 2004, 78(1-2):124-137. |
| [5] | VISSER P N A M. GOCE Gradiometer Validation by GPS[J]. Advances in Space Research, 2007, 39(10):1630-1637. |
| [6] | ARABELOS D, TSCHERNING C C. Calibration of Satellite Gradiometer Data Aided by Ground Gravity Data[J]. Journal of Geodesy, 1998, 72(11):617-625. |
| [7] | ARABELOS D N, TSCHERNING C C, VEICHERTS M. External Calibration of GOCE SGG Data with Terrestrial Gravity Data:A Simulation Study[M]//TREGONING P, RIZOS C. Dynamic Planet. Berlin Heidelberg:Springer,2007:337-344. |
| [8] | BOUMAN J, KOOP R, HAAGMANS R, et al. Calibration and Validation of GOCE Gravity Gradients[M]//SANSF. A Window on the Future of Geodesy. Berlin Heidelberg:Springer,2005:265-270. |
| [9] | SIEMES C, HAAGMANS R, KERN M, et al. Monitoring GOCE Gradiometer Calibration Parameters Using Accelerometer and Star Sensor Data:Methodology and First Results[J]. Journal of Geodesy, 2012, 86(8):629-645. |
| [10] | XU Tianhe, HE Kaifei. Outlier Snooping Based on the Test Statistic of Moving Windows and Its Applications in GOCE Data Preprocessing[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(5):391-396.(徐天河，贺凯飞. 移动开窗检验法及其在GOCE数据粗差探测中的应用[J]. 测绘学报, 2009, 38(5):391-396.) |
| [11] | LUO Zhicai, WU Yunlong, ZHONG Bo, et al. Pre-processing of the GOCE Satellite Gravity Gradiometry Data[J]. Geomatics and Information Science of Wuhan University, 2009, 34(10):1163-1167.(罗志才，吴云龙，钟波，等. GOCE卫星重力梯度测量数据的预处理[J]. 武汉大学学报:信息科学版, 2009, 34(10):1163-1167.) |
| [12] | WU Yunlong. Study on Pre-processing of GOCE Satellite Gravity Gradiometry Data[D]. Wuhan:School of Geodesy and Geomatics, Wuhan University, 2010.(吴云龙. GOCE卫星重力梯度测量数据的预处理研究[D]. 武汉:武汉大学测绘学院, 2010) |
| [13] | WU Yunlong, LI Hui, LIU Ziwei, et al. External Calibration of Gravity Gradient Measurement Based on Global Gravity Models[J]. Journal of Geodesy and Geodynamics, 2010, 30(S2):10-13, 26.(吴云龙，李辉，刘子维，等. 基于地球重力场模型的重力梯度测量数据外部校准[J]. 大地测量与地球动力学, 2010, 30(S2):10-13, 26.) |
| [14] | BOUMAN J, FIOROT S, FUCHS M, et al. GOCE Gravitational Gradients along the Orbit[J]. Journal of Geodesy, 2011, 85(11):791-805. |
| [15] | FÖRSTE C, FLECHTNER F, SCHMIDT R, et al. EIGEN-GL05C——A New Global Combined High-resolution GRACE-based Gravity Field Model of the GFZ-GRGS Cooperation[J/OL]. Geophysical Research Abstracts, 2008, 10:SRef-ID:1607-7962/gra/EGU2008-A-03426. |
| [16] | PAVLIS N K, HOLMES S A, KENYON S C, et al. The Development and Evaluation of the Earth Gravitational Model 2008(EGM2008)[J]. Journal of Geophysical Research:Solid Earth, 2012, 117(B4):B04406. |
| [17] | TAPLEY B, RIES J, BETTADPUR S, et al. The GGM03 Mean Earth Gravity Model from GRACE[C]//American Geophysical Union, Fall Meeting Abstracts, 2007, G42A-03. |
| [18] | PAIL R, BRUINSMA S, MIGLIACCIO F, et al. First GOCE Gravity Field Models Derived by Three Different Approaches[J]. Journal of Geodesy, 2011, 85(11):819-843. |
| [19] | MAYER-GüRR T, KURTENBACH E, EICKER A. ITG-Grace2010 Gravity Field Model[EB/OL].[2010-10-20]. http://www.igg.uni-bonn.de/apmg/index.php?id=itg-grace2010. SERCO/DATAMAT CONSORTIUM. GOCE L1BProductsUser Handbook[R]. Technical Note, GOCE PDGS Team, GOCE-GSEG-EOPG-TN-06-0137, 2008. |
| [20] | EGG-C. GOCE Level 2 Product Data Handbook[R]. GOCE High Level Processing Facility, GO-MA-HPF-GS-0110, 2010. |
| [21] | CESARE S. Performance Requirements and Budgets for the Gradiometric Mission[R]. Technical Report, Thales Alenia Space. GO-TN-AI-0027, 2008. |
| [22] | RUMMEL R, YI Weiyong, STUMMER C. GOCE Gravitational Gradiometry[J]. Journal of Geodesy, 2011, 85(11):777-790. |