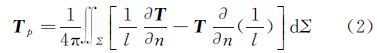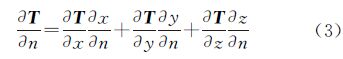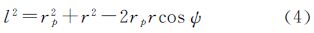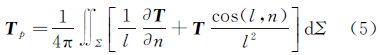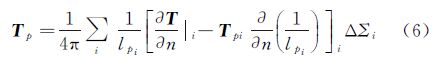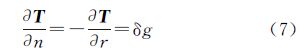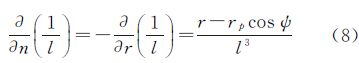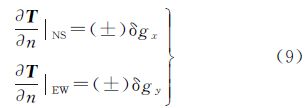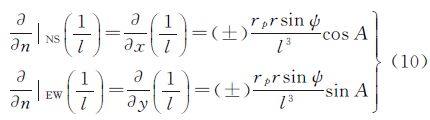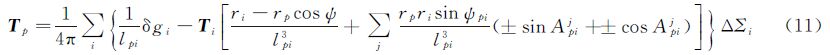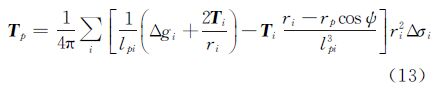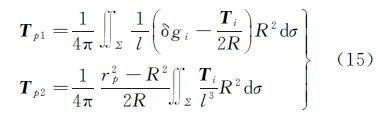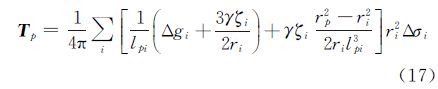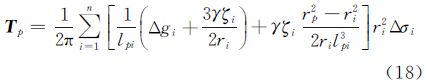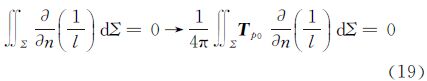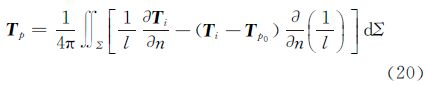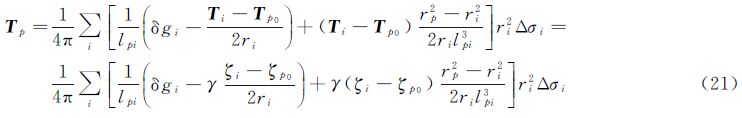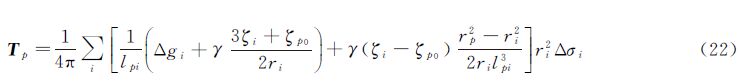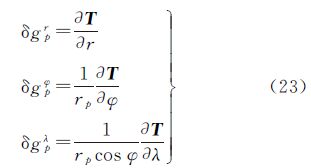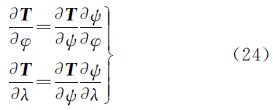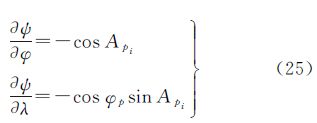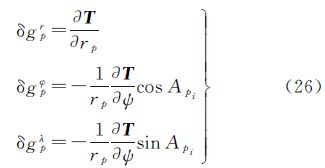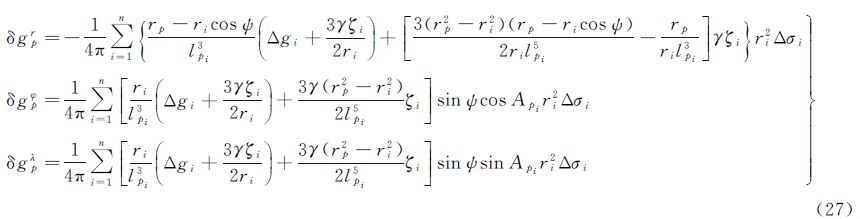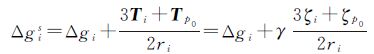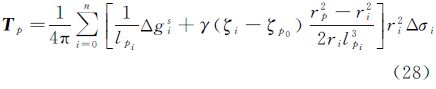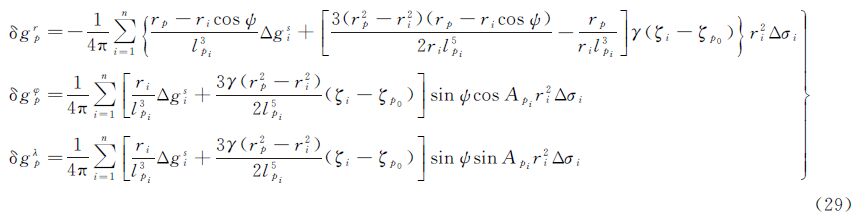1 扰动重力位的地面边值问题
确定地球外部重力场和大地水准面是大地测量学的主要任务之一[1, 2, 3, 4, 5]。确定地球外部重力场和大地水准面的斯托克斯理论需要将地面观测的重力异常归算至大地水准面[6]，再采用调和函数球面边值的解式(如Stokes公式)求得大地水准面及其外部的扰动重力位[7, 8]。归算将涉及对大地水准面至地面的质量迁移，对大地水准面产生间接影响，而且由于归算对质量进行了调整，改变了外部扰动重力场，因此归算到大地水准面上的重力异常用以确定外部扰动重力位会导致结果的歪曲[9, 10]。
直接以地面重力异常为边值的Molodensky问题从理论上避免了归算的困难，成为近代外部重力场研究的理论基石[11]。然而，由于地球表面的复杂性，给这一问题的求解带来极大难度。Molodensky基于基本积分方程的小参数解法得到地面扰动位的级数解式[12, 13]。文献[10]提出将地面重力异常解析地延拓到一点的水准面上，再采用球面的Stokes积分得到地面扰动位，其结果同样是级数的形式。文献[15]也研究得到类似的级数解。文献[16]则提出将地面重力异常调和地延拓到一个内部球面上，再由球面边值问题解逼近外部扰动位，其调和延拓需要求解Poisson积分方程。尽管这些理论解的途径有所不同，但在一定前提下它们是等价的。虽然经过线性化和地球椭球作球近似后的所谓简单Molodensky问题的研究已得到几近完美的理论结果，但它们的实现仍具有相当大的困难[17]。由于受到数据和高阶项计算稳定性的限制，目前在实际上通常只能考虑到一阶项[10]。
对于确定地球外部扰动重力场问题，上述解在应用上受到一定的限制。像Molodenky解通常应用于地面，Moritz的解析延拓解和Bjeharmmar解虽然可以拓展到外部空中，但边值的延拓仍是一个较复杂的过程[10]。本文侧重于应用的需要，讨论直接由地面边值确定外部扰动位的方法。
2 地面边值问题的格林公式表示确定地球外部扰动重力位T归结为下面的边值问题[18]
式中，
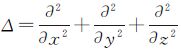为Laplace算子；B代表某一泛函算子；f为已知泛函。
由位理论知，T作为调和函数可以由格林第三恒等式表示为[19]
式中，l是计算点p至地面Σ上面元dΣ的空间距离；n是相对于调和空间的边界面外法线方向。取局部北东天坐标系，求法线方向导数得[20]
根据位理论，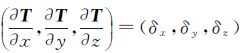
为扰动重力矢量，
为法线的方向余弦，因此可知，
即为扰动重力在法线方向的分量，如图 1。
|
| 图 1 内法线方向示意图 Fig. 1 Schematic diagram of inner normal direction |
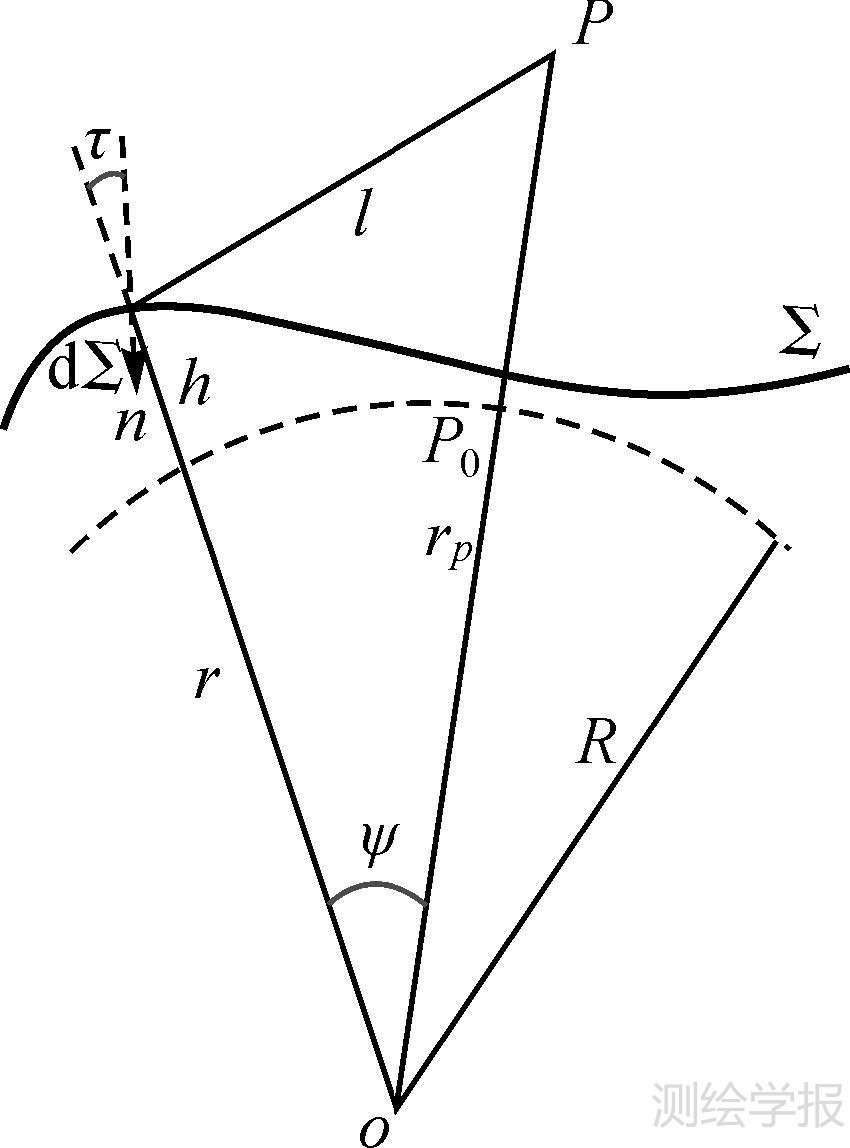
对于所谓的简单Molodensky问题，即将地球椭球近似为球面时，上述各元素的几何关系见图 2。由距离公式
式中，l为P点与dΣ单元处的距离；rp为P点的球心距离；r为dΣ单元处的球心距离；ψ为P点到dΣ单元处的极距，求导可得n
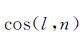，因此可得
|
| 图 2 球近似下各元素的几何关系 Fig. 2 Geometric relations among the elements under the condition of the ball approximation |
应用格林公式可以在实际地球表面上计算外部扰动位。其条件是需要同时具有地面上的扰动位和扰动重力矢量的观测值。这在实际应用中是有困难的。一方面，所需的边值条件很难满足。另一方面地球表面非常复杂，这就使得在地表起伏较大地区该式中的法线方向变化剧烈，其计算相当困难。尽管如此，格林公式提供了不需作任何边值的归算或延拓而以地球自然表面上的边值条件确定外部扰动重力场的唯一可能的解析形式。
3 基于格网数字地形面的扰动重力位边值问题解式在实际应用中，地面通常是采用格网化的数字形式表示的。在这些格网单元中，其高度取作一个常数，因此这些格网显示的只是一个个平面单元。而在重力场实际数据处理过程中，由于观测数据是离散的，不可能达到地面边值的连续分布，通常将离散的观测数据(如重力异常)处理成不同规格的格网平均值，它们可视为相应于平面格网地形面上的值。另外，在重力计算时，也是根据精度要求选取最优的积分半径和格网大小，而非采用越小越好的格网选择策略。所以在实际上面临的是由不同平面格网单元组合的地球表面的边值问题。这种数字格网地形面是与实际地球表面最接近且为应用上必然的形式。在此情况下，格林公式形式的简化有助于其应用的实现。
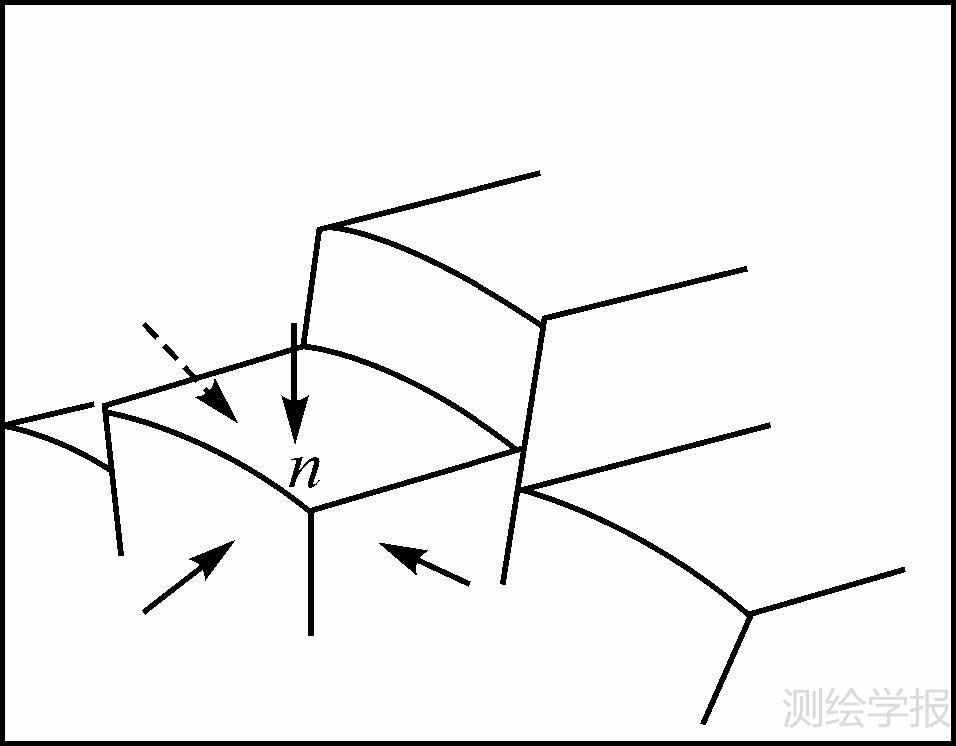
设地形表面由经纬度方向微小格网构成，每一个格网为高程是常数的球面体单元(如图 3所示)，该格网中的边值元素为一定值，得到离散的格林积分为
|
| 图 3 格网数字地形面示意图 Fig. 3 Schematic diagram of gridded digital terrain surface |
在每一格网单元中，对于朝上的格网顶面积，被积元素为
对于四周的侧面积
式中，δgx、δgy是该格网点扰动重力的两个水平分量；A是该格网点至计算点P的方位角。
注意到，法线方向n都是指向网格内的(如图 3所示)，当该格网点处于地形高处的情况下，相对的两个侧面积扰动重力分量取相反的符号，其积分是抵消的，对于在地形持续升高或降低的地区，格网通常有1—2个单向的侧面积需要计算。考虑到在重力计算情况下，格网间的起伏(平均坡度)通常小于5％，即使重力水平分量与垂直分量数值大小相当(一般后者要大于前者)，其积分贡献也较小，故可忽略侧面积的扰动重力水平分量，得到
同样的，对于两个相对的侧面积因方位角相差180°，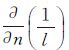
的取值符号相反，因此式(11)中最后一项取值为零。即使对于单个侧面积其贡献也较小，故为简化计算亦可忽略。得
根据重力异常与扰动重力的关系，式(12)也可表示成重力异常的形式
由式(4)的关系，式(11)还可表示成
在式(14)中，需要有地面扰动位和重力异常(或扰动重力垂直分量)两个边值条件。它是由一个重力异常(或扰动重力垂直分量)的单层位和扰动位的Poisson核的位两部分组成。可以证明，在球面情况下，它们分别是这两种边值问题的解，即
可见，格林积分在球面情况下即退变成两个单边值问题解之和。
目前的边值问题理论多是研究以重力异常为单一边值条件，地面扰动位通常是作为要取得的结果。但对于确定外部扰动重力场而言，为了能应用格林公式直接由地面的边值求取外部扰动重力场，需要有地面扰动位作为边值条件，为此要用到已有的地面扰动位的结果。
因为扰动位与高程异常有以下关系
式中，γ是正常重力；ζ是高程异常。故可将式(14)中的扰动位替代为高程异常
式(17)可由地面重力异常和高程异常直接确定外部扰动位，而不需要经过延拓或归算。注意到，根据格林公式的性质，该公式适用于地面外部的空间，如果计算点位于地面Σ上时，其公式应表示为
格林公式在从空间到层面上是不连续的，另外，应用式(16)求取外部扰动位，要用到地面高程异常。目前我国地面高程异常亦取得较好的精度(东部地区优于10 cm，西部地区优于30 cm)，可以作为格林公式中的已知地面元素。但对式(17)分析可见，含高程异常项的是Poisson积分核函数，它对于计算点附近的高程异常的精度要求较高。假如平均重力异常的精度为3 mGal(1 mGal=10-5m/s2)，对于1 km高度的计算点，则要求积分范围10 km以内的高程异常要优于30 cm的精度才能与平均异常精度匹配。当高度增加或减小时，这个范围要求作相应扩大或减小。为了降低对高程异常的精度要求，需要对格林积分式作以下改进。
由位理论知，当p点位于地面外部时有
则式(2)可表示成
式中，p0点是计算点沿向径至地面上的点。可以证明，该式在空间和地面上都是适用的，据此，式(14)变为
或
上述改进公式的作用在于：因为采用了相对于p0点的高程异常差作为输入数据，它消除了高程异常的系统性误差(包含高程基准的系统差)和长波长的误差。特别对于距离p0较近的点，高程异常差可以消除许多公共性误差，这些误差在高程异常误差中占很大比重，从而可以保证计算对高程异常数据的精度要求。另外，p0点附近高程异常在原格林积分中贡献占优，特别是计算点接近地面时积分强奇异。而在改进的格林积分中，由于p0点附近高程异常差接近于零，降低了积分的奇异性，以精度更高的重力异常起主要作用。另外注意到，经过改化的格林公式不仅适用于外部空间，同时也适用于地面，即从地面到外部是连续的。而原始格林公式在外部至地面的极限是不同的(相差1/2，这是由于单层位的导数在层面上的极限不连续)。
4 由地面边值确定扰动重力场元地球外部扰动重力矢量通常采用沿球心向径、纬度和经度3个方向的分量表示。它们与扰动位有以下关系[12]
其中对经、纬度方向的导数为
根据球面关系，可得
式中，A是计算点p至流动面元的方位角。得到
将式(17)代入式(26)，有
式(27)就是利用未改进的格林公式以地面重力异常和高程异常求取外部扰动重力三分量的计算公式。
令
并代入式(22)，扰动位则表示为
代入式(26)则表示为
利用式(29)，即可由地面上的重力异常和相对p0的高程异常差计算地面或空间一点的扰动重力矢量的3个分量。
5 试验计算分析下面进行两个模拟计算。试验1验证了边界面为球面时改进的格林公式和Stokes公式的等效性，试验2验证了在实际地形面为边界面的情况下格林积分公式优于Stokes公式。
5.1 改进的格林公式与Stokes公式的等效性验证采用2160阶EGM2008地球重力场模型模拟区域21°N—31°N，109°N—119°N，大地高为0的分辨率为2′×2′的重力异常和高程异常网格数据。空中数据用EGM2008模型模拟区域23.5°N—28.5°N，111.5°E—116.5°E，高度为3000 m，分辨率为2′×2′的150×150格网扰动重力三分量，将其作为“真值”检验格林积分计算外部扰动重力的质量(见表 1)。利用格林公式选取积分半径为2.5°采用移去恢复法计算外部扰动重力(见表 2)。
| mGal | ||||
| 扰动重力分量 | 最大差值 | 最小差值 | 平均值 | 标准差 |
| 径向分量 | 13.429 8 | -8.732 1 | 0.030 3 | 2.123 1 |
| 经度方向分量 | 0.579 1 | 0.498 5 | 0.000 2 | 0.098 8 |
| 纬度方向分量 | 0.991 6 | -1.007 6 | 0.002 | 0.208 4 |
| mGal | ||||
| 扰动重力分量 | 最大差值 | 最小差值 | 平均值 | 标准差 |
| 径向分量 | 0.420 3 | -0.532 6 | -0.001 3 | 0.084 2 |
| 经度方向分量 | 0.579 1 | -0.501 1 | 0.000 2 | 0.098 8 |
| 纬度方向分量 | 0.991 4 | -1.007 6 | 0.002 0 | 0.208 4 |
可以看出利用改进的格林公式大大地提高了径向分量的精度。利用Stokes公式计算相同区域相同高度的扰动重力三分量，结果如表 3所示。
| mGal | ||||
| 扰动重力分量 | 最大差值 | 最小差值 | 平均值 | 标准差 |
| 径向分量 | 1.336 0 | -0.761 5 | 0.002 5 | 0.210 1 |
| 经度方向分量 | 0.154 8 | -0.158 8 | 0.001 8 | 0.049 4 |
| 纬度方向分量 | 0.355 2 | -0.314 2 | 0.002 3 | 0.112 3 |
采用同样的地面重力数据分别利用Stokes公式和改进的格林公式计算同样范围的1500 m高度的扰动重力三分量得到的结果如表 4、表 5所示。
| mGal | ||||
| 扰动重力分量 | 最大差值 | 最小差值 | 平均值 | 标准差 |
| 径向分量 | 4.376 2 | -8.767 4 | -0.008 9 | 1.311 4 |
| 经度方向分量 | 6.118 2 | -6.109 9 | -0.002 | 1.074 5 |
| 纬度方向分量 | 6.243 9 | -5.711 4 | -0.003 3 | 1.049 8 |
| mGal | ||||
| 扰动重力分量 | 最大差值 | 最小差值 | 平均值 | 标准差 |
| 径向分量 | 3.771 4 | -7.612 3 | -0.005 1 | 1.109 9 |
| 经度方向分量 | 5.334 9 | -5.274 2 | 0.001 | 0.937 4 |
| 纬度方向分量 | 5.727 3 | -5.283 2 | -0.001 7 | 0.966 5 |
为了检验格林公式在实际地形面上的计算效果，选取了采用2160阶EGM2008地球重力场模型模拟区域32°N—36°N，108°E—114°E，分辨率为2′×2′的重力异常和高程异常网格数据。高程信息采用实际的高程，分辨率为2′×2′。试验区高程的统计信息：最大值2 463.5 m、最小值55 m、平均值686 m、标准差459.6 m。同样采用2160阶EGM2008模型计算的距离地面1500 m高度的扰动重力三分量作为“真值”检验改进格林公式以及Stokes公式的计算精度(见表 6、表 7)。
| mGal | ||||
| 扰动重力分量 | 最大差值 | 最小差值 | 平均值 | 标准差 |
| 径向分量 | 18.311 6 | -16.160 1 | 0.032 3 | 4.178 7 |
| 经度方向分量 | 9.292 7 | -10.799 3 | 0.028 4 | 2.243 8 |
| 纬度方向分量 | 9.067 | -7.655 2 | 0.019 3 | 2.312 1 |
| mGal | ||||
| 扰动重力分量 | 最大差值 | 最小差值 | 平均值 | 标准差 |
| 径向分量 | 4.750 8 | -5.586 5 | 0.005 4 | 1.333 9 |
| 经度方向分量 | 7.590 3 | -8.691 1 | 0.021 6 | 1.839 6 |
| 纬度方向分量 | 9.943 1 | -11.142 3 | 0.042 6 | 2.506 4 |
可以看出在实际的地形区，在径向方向改进的格林公式计算的精度要大大优于Stokes公式，水平方向分量精度与Stokes公式相当。结果表明以实际地形面为边界面求解外部扰动重力，改进的格林公式相比Stokes公式结果较好。
为了检验不同积分半径、不同计算高度对于改进的格林积分公式求解外部扰动重力三分量结果的影响，分别以1°、30′、20′为积分半径计算3000 m高度扰动重力三分量，结果统计如表 8—表 10所示。
| mGal | ||||
| 扰动重力分量 | 最大差值 | 最小差值 | 平均值 | 标准差 |
| 径向分量 | 5.843 2 | -7.222 6 | 0.022 8 | 1.783 6 |
| 经度方向分量 | 0.918 4 | -1.349 4 | 0.000 7 | 0.291 6 |
| 纬度方向分量 | 1.298 8 | -1.289 7 | 0.041 5 | 0.274 1 |
| mGal | ||||
| 扰动重力分量 | 最大差值 | 最小差值 | 平均值 | 标准差 |
| 径向分量 | 3.514 9 | -4.626 1 | 0.022 7 | 1.104 2 |
| 经度方向分量 | 1.104 1 | -1.056 2 | 0.006 4 | 0.212 1 |
| 纬度方向分量 | 1.678 2 | -1.384 2 | 0.037 2 | 0.334 0 |
| mGal | ||||
| 扰动重力分量 | 最大差值 | 最小差值 | 平均值 | 标准差 |
| 径向分量 | 1.739 2 | -2.215 7 | 0.036 5 | 0.511 7 |
| 经度方向分量 | 0.694 5 | -0.762 9 | 0.001 | 0.133 3 |
| 纬度方向分量 | 1.673 2 | -1.413 4 | -0.029 1 | 0.363 6 |
根据以上数据可以看出应用改进的格林公式计算扰动重力三分量可以取得比较理想的结果，在1°的积分半径内，随着积分半径的增大，改进的格林公式计算扰动重力径向分量的精度得到了提高。这是由于在1°的范围内，地面点与空中点具有一定的相关性，因此随着半径的增大，精度也就相应地提高。
6 结 论格林公式提供了以地面作为边界确定外部扰动位的解析表达，它要求有地面扰动位及扰动重力矢量边值条件。本文应用格林公式，以格网数值地形面为边界面，忽略较小的垂直面积上的扰动重力水平分量积分，推导出以扰动重力垂直分量(或重力异常)和高程异常差直接求取扰动重力场元的公式，该结果规避了Molodenky问题经典解法需要进行地面数据的延拓和级数解的形式。这不仅减少了延拓过程的巨大工作量，也避免了延拓产生的不适定性误差。核函数简单，易于计算，为确定地球外部重力场提供了一种思路。
| [1] | SJÖBERG L E. On the Discrete Boundary Value Problem of Physical Geodesy with Harmonic Reduction to an Internal Sphere[R]. Stockholm:Royal Institute of Technology, 1975. |
| [2] | WANG Zhengtao, DANG Yamin, CHAO Dingbo.Theory and Methodology of Ultra-high-degree Geopotential Model Determination[M]. Beijing:Surveying and Mapping Press, 2011.(王正涛，党亚民，晁定波. 超高阶地球重力位模型的确定的理论与方法[M]. 北京:测绘出版社, 2011.) |
| [3] | CHENG Luying. General Kernel Functions Based on Integral Transformation among Different Disturbing Potential Elements[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(2):203-210.(程芦颖. 不同扰动位泛函间的积分变换广义核函数[J]. 测绘学报, 2013, 42(2):203-210.) |
| [4] | SEEBER G. Satellite Geodesy[M]. 2nd ed. Berlin:Walter de Gruyter, 2003. |
| [5] | LIN Miao, DENKER H, MüLLER J. Regional Gravity Field Modeling Using Free-positional Point Masses[J]. Studia Geophysica et Geodaetica, 2014, 58(2):206-227. |
| [6] | XU Houze,LU Zhonglian. Earth's Gravity Feld and Geoid in China[M]. Beijing:The People's Liberation Army Press, 1997.(许厚泽，陆仲连. 中国地球重力场与大地水准面[M]. 北京:解放军出版社, 1997.) |
| [7] | STOKES G G. On the Variation of Gravity on the Surface of the Earth[J]. Transactions of the Cambridge Philosophical Society, 1849, 8(5):672-695. |
| [8] | DENKER H,Regional Gravity Field Modeling:Theory and Practical Results[M]//XU Guochang. Sciences of Geodesy-Ⅱ. Berlin Heidelbreg:Springer Verlag, 2013:185-291. |
| [9] | HEISKANEN W A, MORITZ H. Physical Geodesy[M]. LU Fukang, HU Guoli trans. Beijing:Surveying and Mapping Press, 1979.(海斯卡涅W A, 莫里斯H. 物理大地测量学[M]. 卢福康，胡国理，译. 北京:测绘出版社, 1979.) |
| [10] | MORITZ H. Advance Physical Geodesy[M]. London:Abacus Press, 1980. |
| [11] | HOFMANN-WELLENHOF B, MORIZE H. Physical Geodesy[M]. Heidelberg:Springer, 2005. |
| [12] | MOLODENSKY M S, EREMEEV V F, YOURKINA M I. Methods for Study of the External Gravitational Field and Figure of the Earth. Works of Central Research Institute of Geodesy. Aerial Photography and Cartography[M]. Moscow:Geodetic Literature Press, 1960. |
| [13] | MOLODENSKY M S, EREMEEV V F, YOURKINA M I. An Evaluation of Accuracy of Stokes' Series and of Some Attempts to Improve His Theory[J]. Bulletin Géodésique, 1962, 63(1):19-37. |
| [14] | SUNKEL H. Point Mass Models and the Anomalous Gravitational Field of the Earth:Report No.328[R]. Columbus:Ohio State University, 1981. |
| [15] | KATSAMBALOS K E. Simulation Studies on the Computation of the Gravity Vector in Space from Surface Data Considering the Topography of the Earth:Report No.323[R]. Columbus:Ohio State University, 1981. |
| [16] | BJERHAMMAR A. A New Theroy of Geodetic Gravity[M]. Stockholm:Tekniska Hogskolan, 1964. |
| [17] | FORSBERG R. A Study of Terrain Reductions, Density Anomalies, and Geophysical Inversion Methods in Gravity Field Modelling:Report No.355[R]. Columbus:Ohio State University, 1984. |
| [18] | JIANG Tao, LI Jiancheng, DANG Yamin, et al. Regional Gravity Field Modeling Based on Rectangular Harmonic Analysis[J]. Science China:Earth Sciences, 2014, 57(7):1637-1644. |
| [19] | LU Zhonglian. Theory and Method of Earth's Gravity[M]. Beijing:The People's Liberation Army Press, 1996.(陆仲连. 地球重力场理论与方法[M]. 北京:解放军出版社, 1996.) |
| [20] | LU Zhonglian, WU Xiaoping, DING Xingbin, et al. Ballistic Missile Gravity[M]. Beijing:The Ba Yi Press, 1993.(陆仲连，吴晓平，丁行斌，等. 弹道导弹重力学[M]. 北京:八一出版社, 1993.) |