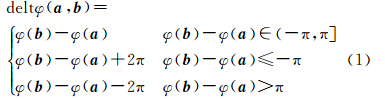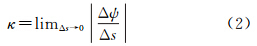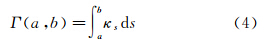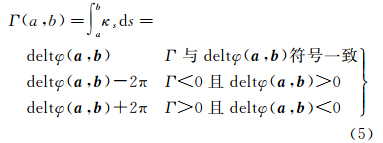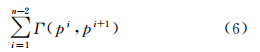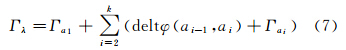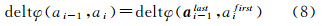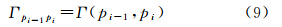2. 深圳大学土木工程学院空间信息智能感知与服务深圳市重点实验室,广东 深圳 518060;
3. 武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉 430079;
4. 深圳市规划国土发展研究中心,广东 深圳 518034
2. Shenzhen Key Laboratory of Spatial Smart Sensing and Services, College of Civil Engineering, Shenzhen University, Shenzhen 518060, China;
3. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
4. Shenzhen Urban Planning & Land Resource Research Center(P& LRC), Shenzhen 518034, China
1 引 言
近年来,在智能交通领域中,GPS浮动车已经成为一种交通、出行信息采集的重要手段。随着互联网大数据时代的到来,地理信息服务需求明显增强,交通、出行等信息同时也成为地理信息数据的重要组成部分[1, 2]。地图匹配方法则是在海量GPS浮动车轨迹中实现地理信息数据挖掘的一项关键技术。然而,浮动车上配置的GPS设备往往是导航型GPS接收机,其定位精度并不高;而且,浮动车的数目一般较多,为避免数据量过大,浮动车的GPS采样间隔往往较长(通常为20~100 s)。在交通地理信息数据处理中,GPS浮动车数据是一系列相对于数字化道路中心线有一定偏离的离散轨迹点。因此,需要对这些轨迹数据实施地图匹配以恢复其在道路网络中的真实行驶路径。
在传统的车载导航中,GPS定位的采样间隔(1 s)相对较短,其所采用的地图匹配算法通过GPS轨迹点的特征[3]以及与航位推算数据的融合,实际上可以达到比较高的匹配正确性与稳定性[4, 5]。与车载导航的地图匹配类似,浮动车地图匹配算法也主要采用GPS轨迹点的几何、拓扑等特性来实施轨迹与道路的匹配。与车载导航中的轨迹数据不同的是,浮动车轨迹数据的采样间隔较大,在两相邻轨迹点之间所缺失的信息较多。因而,需要根据两相邻轨迹点所具有的几何、拓扑等特性在道路网络中作关联性分析来实施地图匹配。现有的浮动车地图匹配方法主要通过下面这些方法来恢复在相邻轨迹点之间损失的路径信息:隐马尔科夫匹配方法通过距离约束建立隐马尔科夫模型来恢复浮动车轨迹在时间序列上最可能的路径[6];时空匹配方法(ST-matching method,ST)通过路网空间距离、拓扑关系及轨迹时间/速度限制来实施轨迹点之间的这种关联性路径恢复[7]。浮动车地图匹配的其他变体方法也往往是基于浮动车轨迹点的方向、距离等初等几何拓扑特征作为路径恢复的一个主要约束条件[8, 9, 10, 11, 12]。从现有浮动车的地图匹配方法来看,其单点匹配主要采用距离、方向等几何特征来约束,其相邻轨迹点之间的关联匹配则主要采用道路拓扑关系来约束。然而,目前互联网大数据时代,各种地理信息服务采用的路网模型往往是针对导航的较为精细的数据模型[13, 14](比如双线路、辅路、匝道等的数字化表达),并且道路网络在一些区域的形式较为复杂[13, 15, 16]。现有浮动车地图匹配方法在道路网络复杂的位置实施地图匹配时,由于具有近似特征的备选道路路段较多,在将轨迹点匹配到道路路段的过程中难以作出正确判决。这种复杂路网的精细数据模型导致在相对较大的时间间隔下,浮动车轨迹数据的地图匹配结果存在正确率并不高,不同情形下匹配正确率并不稳定等问题。
本文提出一种曲率积分约束的GPS浮动车地图匹配方法,主要实现方式为:先分别计算GPS轨迹的相邻轨迹点之间的曲率积分值和相邻轨迹点对应的候选路段对之间的路径的曲率积分值,然后通过这两个曲率积分值之间的相似程度来约束浮动车的地图匹配。
2 曲率的相关概念及其计算 2.1 曲线曲率的相关概念
定义1 在投影平面P中,假设向量a相对于正北方向按顺时针方向旋转所成的角度为向量a的方位角φ(a),其取值范围为[0,2π)。
定义2 两个向量的旋转夹角deltφ(a,b)为b相对于a按顺时针方向旋转所成的角度,旋转角范围定义在(-π,π],逆时针为负值,顺时针为正值。
平面P上两个向量a和b,则可以采用式(1)计算它们之间的旋转夹角
式(1)给出了两个向量旋转夹角与其方位角之间的计算关系。
定义3 假设γ=γ(s):(α,β)→R2为一条以弧长为参数的二维平面光滑曲线,那么,可以定义X=γ(s)点处的曲率[17]为
式中,ψ(s)为曲线在X点的切向量T(s)的角度值;Δψ为ψ(s)的增量;Δs为弧长增量。曲率描述了曲线上切向量T(s)对弧长s的转动速率,也就是说,它描述了曲线在该点的弯曲程度。
定义4 假设γ=γ(s):(α,β)→R2为以弧长为参数的一条二维平面光滑曲线,相对曲率[18]为
平面曲线的相对曲率定向,在曲线上某点X,沿s增加的方向,曲线在X前方的轨迹在切向量左侧则ks<0,在右侧κs>0。在地图投影平面上一般为左手系,定义1、定义2实际上给出的是一种左手坐标系的定义方法,因此,在这里也是采用左手系来定义κs的正负方向。
定义5 假设γ=γ(s):(α,β)→R2为以弧长为参数的一条二维平面光滑曲线γγ,曲线γ上a、b两点,且有a,b∈(α,β),a<b则a、b之间的曲率积分值为
曲率积分Γ(a,b描述的是切向量T(s)从γ(a)处出发沿曲线γ转动到γ(b)处所转动的角度。曲率是曲线的一个内蕴几何量,在GPS轨迹点的地图匹配中,前后两轨迹点之间的曲率积分值给出了曲线在两点之间的这种内蕴几何量的累积值,其度量的是运动轨迹在某一时间段内轨迹曲线的累积弯曲程度。本文将其作为地图匹配的特征之一。
2.2 曲率积分的计算
假设γ:(α,β)→R2为二维平面曲线γ上有两点a,b∈(α,β),a<b,假设a、b两点处的切向量为a和b,且在a、b之间的曲率积分值的取值在(-2π,2π)之间,则曲率积分值Γ可用切向量的方向角φ按式(5)计算
式中,deltφ(a,b)为曲线在a、b处的切向量的旋转夹角。这里给出了二维平面上取值在(-2π,2π)之间的曲线曲率积分值的计算方法,由式(1)、式(5)可以将二维平面上曲线上两点之间的曲率积分值用其两点的切向量方位角计算出来。2.2.1 曲率积分值的计算
假设曲线γ在计算机中被离散表示为n个点的序列〈p0p1…pn〉,序列中相邻前后两点之间向量为pi-1pi(1≤i≤n)。曲率以及曲率积分是在连续曲线上定义的,而在计算机中对连续的曲线(如道路的弧段)做了离散数字化处理,笔者用n个点中前后相邻的两个点形成的向量来近似估算该位置的切向量。因此,在这种局部范围内,曲线γ数字化的前后两点之间的相对曲率κs方向不改变,并且其切向量的旋转远小于2π,这样,根据式(5),被离散化后的曲率积分值可采用式(6)近似计算
式中,点pi处的切向量用向量pi-1pi来近似,每段的Γ值采用式(5)计算。3 曲率积分约束的地图匹配方法 3.1 地图匹配方法框架
地图匹配是在道路网络所嵌入的地图平面中完成,而地图一般是在投影平面P上绘制,这里仅仅考虑GPS定位给出的投影平面坐标(x,y)。将道路网络看作一个有向图G(V,A),这里V为顶点集,代表道路网络中路段端点及道路交叉口,A为弧段集,代表道路网络中的路段。将每个弧段α∈A的非负长度值l作为其权重值。
浮动车的地图匹配实际上是已知GPS采样得到的浮动车轨迹T以及道路网络G(V,A),在图G中找到与真实轨迹ζ最近似的匹配路径λ,如图 1所示。
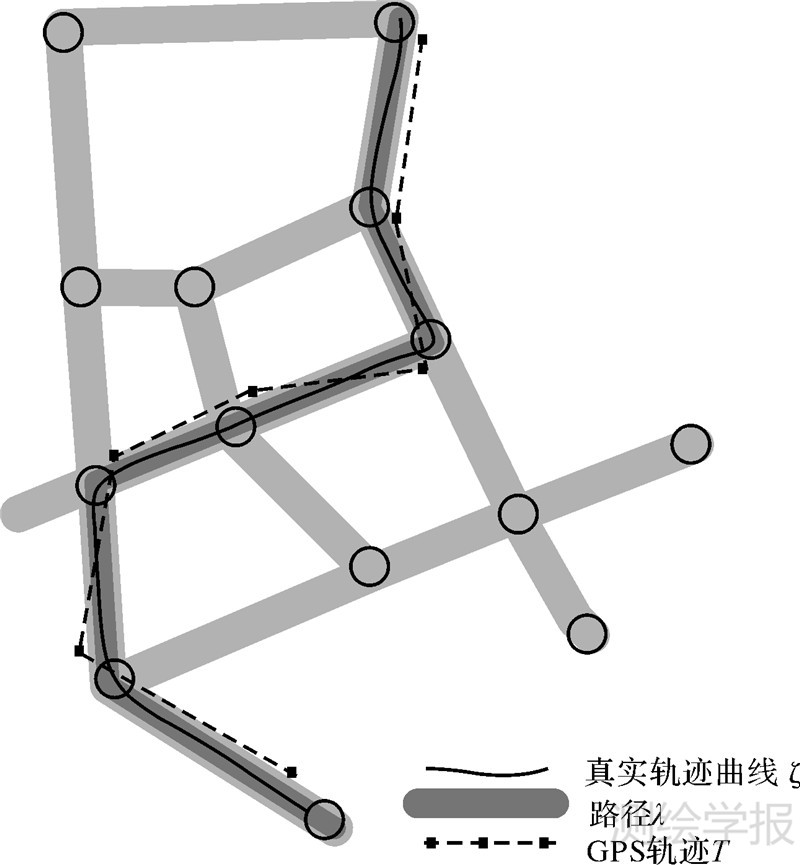 |
| 图 1 浮动车轨迹点、真实轨迹及路径 Fig. 1 Floating car track points,real trajectory and path |
浮动车的地图匹配问题实际上就是根据GPS采样得到的不连续的点坐标序列T在道路网络G中找到与T具有最大相似度的路径λ。由于T是浮动车真实轨迹ζ采样得到的,因此仅仅在采样点处保留了部分特征。地图匹配实际上就是要根据T中所保留的这部分特征在图G中找到与之具有最大相似度的路径λ。也即,浮动车地图匹配问题也就是在平面道路网络G中所有可能的路径中寻找与GPS轨迹T具有的特征相似度最高的一条路径。这实际上是一个最优化问题。给定某种特征度量F,假设路径λ的特征度量与GPS轨迹T的特征度量之间的相似度为S(FT,Fλ),则浮动车的地图匹配问题即为在G中所有可能的路径中找到使得ArgmaxλS(FT,Fλ)成立的路径λ。
在整个地图匹配中采用的特征主要分为单个轨迹点的几何特征和前后轨迹点之间的关联特征。因此,求解地图匹配问题的总体框架主要为以下步骤。
(1) 根据单个轨迹点的位置和方向等单点特征,对每个轨迹点在路网中找到与之具有一定单点相似度的若干候选道路弧段。
(2) 根据相邻轨迹点之间的几何、拓扑的关联特征,在相邻轨迹点的候选弧段对之间找到具有一定关联相似度的子路径(最终的匹配路径是多条子路径首尾相接所组成)。
(3) 上一步形成的子路径组合而成的所有可能路径中,搜索出相似度S(FT,Fλ)最大的路径λ。
在目前的浮动车地图匹配方法中,相似度S(FT,Fλ)的定义方式中未考虑对于轨迹曲线弯曲程度的直接度量。真实轨迹曲线ζ在相邻采样点之间的曲率积分值实际上就是曲线在相邻采样点之间的一种弯曲度量。从整体上来看,浮动车真实轨迹曲线ζ的累积弯曲特征还是较好地保留在了采样后的GPS轨迹T中,如图 1所示。本文的浮动车匹配方法就是基于前述匹配方法框架,利用保留在GPS轨迹T中的相邻轨迹点之间的这种曲率积分值来约束完成地图匹配。
3.2 地图匹配的计算实现
3.1节中已经给出了浮动车的地图匹配方法的基本框架,本节说明在此框架下如何实现曲率积分约束的地图匹配方法。目前的地图匹配方法中关于方向特征的比较计算往往是单个轨迹点的速度方向与单个候选路段之间方向角的比较[9, 11]。与此不同的是,本文方法主要是在计算相邻轨迹点的关联相似度时采用了曲率积分值来做约束。浮动车的GPS轨迹点实际上是车辆运动轨迹曲线的采样点,相邻两个采样点能够包含的曲线特征信息不多,而在此两点之间的曲线曲率积分值给出的是这一段曲线的累积弯曲特征。相邻GPS轨迹点的匹配候选路段对之间的路径的曲率积分值应该与GPS轨迹在相邻GPS轨迹点之间的曲率积分之间具有最大相似度。因此,本文的匹配方法是先通过计算GPS轨迹T上相邻两点之间曲率积分估值,然后根据此估值来约束道路网络中的路径搜索匹配。本文地图匹配方法主要是对3.1节给出的框架的详细实现。本节中首先给出本文地图匹配方法中的曲率积分计算方法,然后给出基于此的详细地图匹配实现步骤。
3.2.1 地图匹配中的曲率积分近似计算
地图匹配中主要需要计算GPS轨迹中相邻点之间的曲率积分值和它们对应的候选匹配路段对之间的路径的曲率积分值。本文先给出计算中用到的数学符号说明,然后分别说明如何计算路网中的路径的曲率积分以及相邻轨迹点之间的曲率积分。
浮动车行驶在道路网络中,其行驶路径λ应该具有与真实轨迹曲线一样的几何拓扑特征。假设路径λ是由弧段序列ai=(vi-1,vi)(1≤i≤k)组成,而在计算机中道路弧段ai由一序列离散的形状点pshpj(1≤j≤q)来表示,其中ai的第一个形状点和最后一个形状点坐标与节点vi-1和vi的坐标重合,即pshp0=vi-1,pshpq=vi。将路径λ上的曲率积分值的计算分成道路弧段内部和道路弧段之间的计算这两部分,即
式中,Γai为路径λ上一条道路弧段ai起点到终点的曲率积分值,其值可以由道路弧段的离散点(即形状点)根据式(6)得到。deltφ(ai-1,ai)为路径中相邻弧段的旋转夹角,其计算公式为 式中,ai-1last、aifirst分别为路径λ上前后相邻弧段的前一弧段ai-1的最后一个形状向量和后一弧段ai的第一个形状向量。GPS轨迹中相邻两个轨迹点pi-1和pi之间的曲率积分,将pi-2pi-1作为pi-1处的近似切向量,将pipi+1作为pi处的近似切向量,一般情况下采样相邻的GPS轨迹点不绕圈(即曲率积分值在(-2π,2π)之间变化),因此可以用式(9)估算其曲率积分值
式中,pi-2为pi-1前一个轨迹点,pi+1为pi后一个轨迹点。再根据式(5)计算其曲率积分估值。3.2.2 曲率积分约束的地图匹配实现
3.2.2 .1 单点相似度的实现
在3.1节匹配框架的步骤(1)中主要采用GPS轨迹点的位置作为单点匹配特征,以GPS点到候选路段之间的距离作为单点相似度量。设定距离阈值对于每个GPS轨迹点可以得到该距离阈值范围内的一个候选弧段集,在此集合中距离越近的弧段就具有越高的相似度。
3.2.2 .2关联相似度的计算实现
在3.1节匹配计算框架的步骤(2)中,主要是计算相邻的两GPS轨迹点与其所对应的候选路段对之间的关联相似度Stopo。本文的匹配方法中Stopo主要由长度相似度Srange与弯曲相似度Scurve求和来实现,其步骤如下。
(i) 相邻两个轨迹点的关联特征计算。关联特征1,根据前后两轨迹点的速度及两点之间的间隔时间估算它们之间的行驶距离lrange;
关联特征2,根据式(9)估算轨迹曲线在两相邻轨迹点之间的曲率积分值Γestm。
(ii) 相邻轨迹点所对应的候选路段对之间的路径搜索。一般认为在浮动车采样点时间间隔内行驶最短路径,因此两相邻轨迹点之间的关联路径搜索主要是计算出一对候选道路弧段aji和aj′i+1之间的最短路径sp[19]并计算sp的长度lsp及曲率积分积sp。这里候选弧段aji为GPS轨迹中第i个轨迹点的候选路段集中的第j个弧段,候选弧段aj′i+1为相邻的第i+1个轨迹点的候选路段集中的第j′个弧段。
(iii) 候选路段对的关联特征计算。候选路段对的关联特征主要是候选路段对之间的可能路径的长度特征和弯曲特征。长度特征直接由步骤(2)确定的路径长度lsp得到,弯曲特征根据公式(7)计算该路径的曲率积分Γsp得到。
(iv) 关联相似度。可能匹配路径的长度相似度Srange:根据步骤(i)、步骤(ii)中得到的lsp、lrange,计算两者的绝对值|lsp-lrange|来确定其相似度Srange。
可能匹配路径的弯曲程度相似度Scurve:根据步骤(i)、步骤(ii)中得到的Γestm、Γsp,计算|Γsp-Γestm|来确定弯曲程度相似度Scurve。
3.2.2.3 全局搜索策略
在3.1节地图匹配框架中的步骤(3)中采用有向无环图实现最大相似度路径搜索,每个轨迹点的候选路段构成图的节点,相邻轨迹点之间的候选路段对之间最短路径作为有向无环图的边,将相邻轨迹点之间的候选路段对的关联相似度以及其所含两个候选路段的单点相似度之和作为有向无环图的边的权重。用有向无环图的拓扑序算法来搜索最长路径[7],该路径对应的匹配道路弧段集即为GPS轨迹的地图匹配结果。
3.2.3 相似度的函数
3.2.2节中的相似度的计算实际上就是将比较值通过一定函数映射到一个权重值范围,即可以将单点相似度中介绍的距离值以及关联相似度中介绍的长度及曲率积分的两个比较差值通过函数映射到一个权重范围上[20]。本文相似度的映射对于距离和长度差值采用幂函数,对于曲率积分采用三角函数,这3种相似度的权重范围均在1~10之间。
4 试验 4.1 试验数据
本文采用两组浮动车GPS轨迹数据集作为地图匹配方法的试验数据,这些轨迹数据中主要包含浮动车辆的经纬度、采样时刻、速度等属性信息。
数据集1为深圳市出租车浮动车数据。这里,出租车浮动车数据为随机选择的10辆出租车GPS轨迹数据(见图 2)。每辆出租车选择不同数目的连续采样GPS轨迹点来参与地图匹配(见表 1)。出租车的GPS采样间隔为30 s(2014年3月22日采集)。
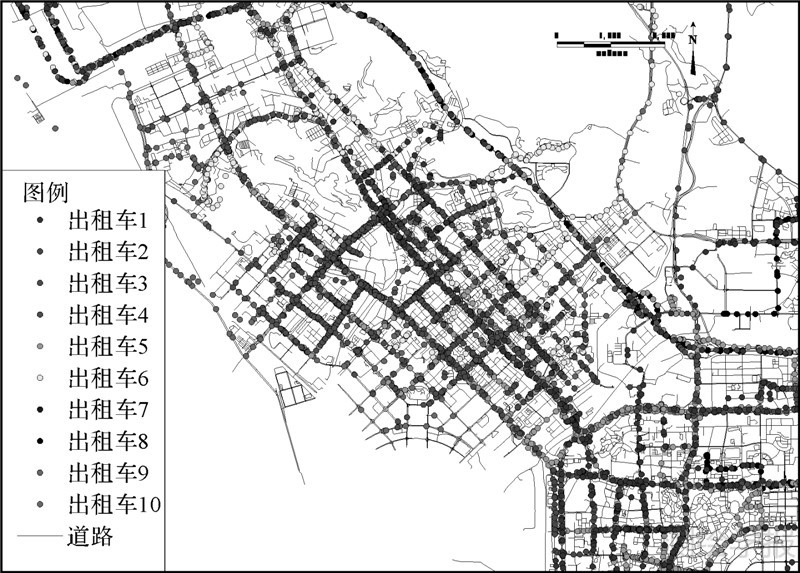 |
| 图 2 试验数据集1数据示例 Fig. 2 Samples of data set 1 for experiments |
| 出租车编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 轨迹点数目 | 80 | 116 | 190 | 228 | 297 | 340 | 372 | 410 | 455 | 522 |
数据集2为深圳市公交车浮动车数据。该数据集为两辆公交车分别在两条路线上按原始采样间隔(20 s)连续采集得到的GPS轨迹数据(2012年2月1日)。其中,公交车路线为两种不同固定路线,一种为在甲、乙两目的地之间往返,一种为环线行驶,本文的公交车路线分别选择这两种类型公交线路。所选择的公交线路为A(深圳公交B829,运营时间为6:30—22:15)和B(深圳公交707线路,运营时间为6:00—23:00),如图 3所示。其所经过的道路主要有广深公路、西乡立交、西乡大道等。基于原始采样间隔GPS轨迹数据进一步抽稀得到40 s、60 s、80 s及100 s间隔的公交车GPS轨迹数据。
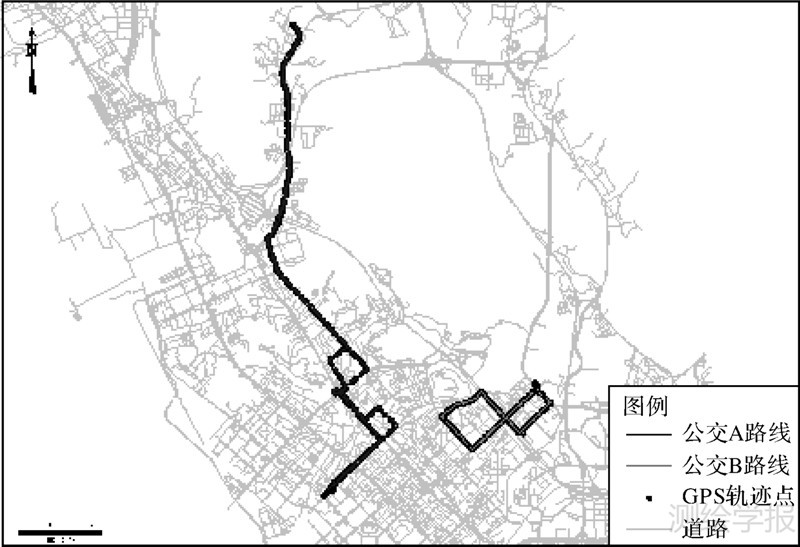 |
| 图 3 试验数据集2数据示例 Fig. 3 Samples of data set 2 for experiments |
两个数据集中的GPS轨迹数据基本都通过了城市中典型的较复杂道路,比如城市快速路、立交匝道、主辅路等。
4.2 试验及其结果
本文试验主要将曲率积分约束的匹配方法与ST算法比较。ST算法主要全面地考虑了多种匹配限制条件并得到相对比较好的匹配效果[7]。该方法在轨迹的单点匹配时采用距离,在相邻点之间的关联匹配时采用道路拓扑及速度来实施匹配限制。该方法是目前文献引用率较高且比较经典的一种低频GPS浮动车地图匹配方法。曲率积分约束的匹配方法即为本文前面所详细论述的匹配方法,此方法除了在单点时采用距离特征,在关联匹配时采用道路拓扑特征之外,还采用了相邻轨迹点之间的轨迹弯曲程度来约束关联匹配。试验采用两种不同的浮动车匹配算法分别针对4.1节介绍的两组浮动车GPS轨迹数据来实施。对于数据集1,在固定采样间隔下不同车辆、不同轨迹点数目分别实施两种地图匹配方法。对于数据集2,不同匹配方法针对不同采样间隔总共实施了20次的轨迹匹配试验。
本文试验主要考察两种不同的方法对于不同浮动车GPS轨迹数据集其匹配结果的正确性及稳定性。为此,本文定义轨迹匹配的错误率与错误程度(长度)两个指标来衡量。每次地图匹配试验的错误率为该次匹配的错误匹配轨迹点数目与轨迹点总数目之比,即
该指标给出了浮动车地图匹配的错误率,错误率越大表明正确匹配的轨迹点越少,匹配方法效果越差。错误程度(长度)为错误匹配轨迹点处错误匹配的路径与正确路径的长度比,本文试验中一次轨迹匹配中的错误程度(长度)采用所有错误匹配点处该值的平均值,即 式中,Nerr为错误匹配点数。该值反映了浮动车轨迹地图匹配结果错误的地方在长度上平均偏离正确路径的程度。该值衡量了匹配结果与正确路径的一种符合程度。该值越大,则匹配结果符合正确路径的程度越差。图 4给出了本文方法与ST方法在数据集1上匹配错误率的柱状比较分析图。整体上来看本文方法的错误率基本都在5%以内,有两项数据甚至达到了1%以下。相比较而言,在不同的轨迹数据上ST方法的匹配错误率均大于本文方法的。从本组数据的地图匹配结果来看,本文给出的曲率积分约束的地图匹配方法其匹配结果在正确率上优于经典的ST方法。
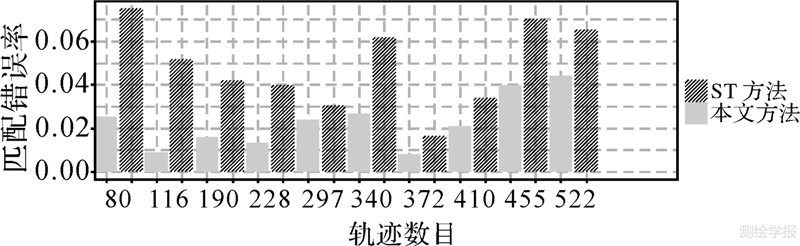 |
| 图 4 数据集1的出租车轨迹地图匹配结果比较 Fig. 4 Map matched results of taxi trajectories in data set 1 |
表 2给出了数据集2中的20次(4组)浮动车轨迹地图匹配试验结果。轨迹匹配试验根据试验方法及试验线路的不同主要分为4组,轨迹编号为”#-#”,这里第1个序号为组号,第2个编号为组内编号。小组编号中,第0、1组为公交线路A的浮动车轨迹数据;2、3组为公交线路B的浮动车轨迹数据;其中0、2组采用曲率的匹配方法,1、3组采用ST算法实施匹配。组内编号反映的是试验中采样间隔的不同,每组内分别测试了20 s、40 s、60 s、80 s、100 s采样间隔下的效果。
| 轨迹组编号 | 时间间隔/s | 总数目 | 路线 | 错误率 | 错误数目 | 错误程度(长度) | 匹配方法 |
| 0-1 | 20 | 459 | A | 0.028 | 13 | 1.16 | 曲率 |
| 0-2 | 40 | 235 | A | 0.009 | 2 | 1.8 | 曲率 |
| 0-3 | 60 | 162 | A | 0.006 | 1 | 0.88 | 曲率 |
| 0-4 | 80 | 70 | A | 0.029 | 2 | 0.88 | 曲率 |
| 0-5 | 100 | 50 | A | 0.06 | 3 | 1.02 | 曲率 |
| 1-1 | 20 | 459 | A | 0.061 | 28 | 1.38 | ST |
| 1-2 | 40 | 235 | A | 0.089 | 21 | 3.6 | ST |
| 1-3 | 60 | 162 | A | 0.111 | 18 | 2.5 | ST |
| 1-4 | 80 | 70 | A | 0.2 | 14 | 3.76 | ST |
| 1-5 | 100 | 50 | A | 0.24 | 12 | 3.4 | ST |
| 2-1 | 20 | 1070 | B | 0.007 | 8 | 1.42 | 曲率 |
| 2-2 | 40 | 583 | B | 0 | 0 | 0 | 曲率 |
| 2-3 | 60 | 379 | B | 0.02 | 5 | 1.16 | 曲率 |
| 2-4 | 80 | 258 | B | 0.03 | 7 | 1.44 | 曲率 |
| 2-5 | 100 | 111 | B | 0.06 | 7 | 1.21 | 曲率 |
| 3-1 | 20 | 1070 | B | 0.02 | 24 | 1.5 | ST |
| 3-2 | 40 | 583 | B | 0.04 | 24 | 2.96 | ST |
| 3-3 | 60 | 379 | B | 0.087 | 33 | 4.23 | ST |
| 3-4 | 80 | 258 | B | 0.085 | 22 | 3.64 | ST |
| 3-5 | 100 | 111 | B | 0.17 | 19 | 5.76 | ST |
图 5给出了数据集2中两种方法在两个错误指标上的试验结果比较。图中横轴为浮动车GPS轨迹采样间隔,纵轴为错误率,曲线拟合出了错误率随着采样时间而变化的曲线。图 4为公交路线A上浮动车轨迹匹配的试验结果,图 5为公交线路B上的浮动车轨迹匹配的试验结果。图中曲线上每个结果点的半径大小正比于其错误程度Elen的大小。总体上看,两种匹配方法随着采样间隔的变大,错误率均呈上升趋势。在两种不同行驶线路上ST方法在不同采样间隔下的错误率均高于本文方法。图 5中,在采样间隔变大的情况下,本文方法的错误率上升较缓慢,这说明将浮动车轨迹曲线的曲率特征用来约束地图匹配可以抑制随着采样间隔变大而产生的部分错误。但是,由于采样间隔变大轨迹点中的信息损失掉得越来越多,因此总体上看错误率仍是呈上升趋势。
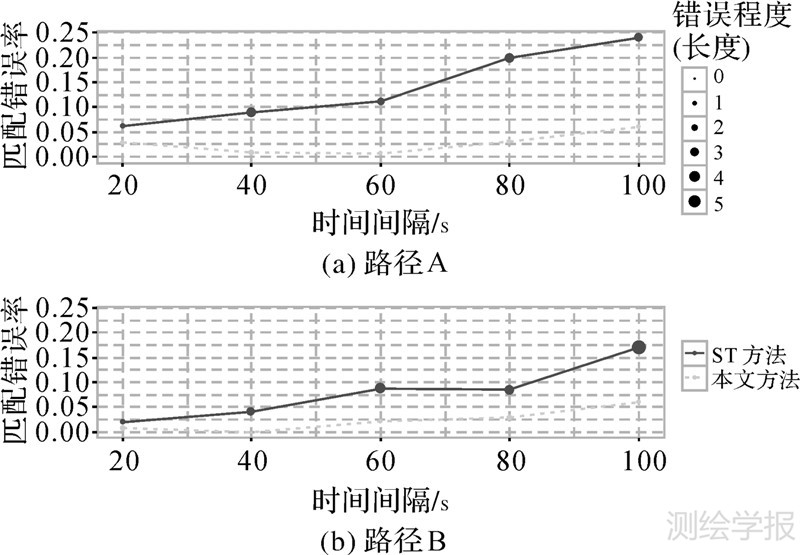 |
| 图 5 不同匹配方法错误指标比较 Fig. 5 Comparison of error indicators for different map-matching methods |
图 6将上述公交路线A和B的结果指标在一张图上绘出。阴影部分拟合出了不同方法在两种固定路线上错误率变动幅度的缓冲范围。从图中可以看出在不同的行驶路线中以及不同采样间隔下两种匹配方法错误率的波动幅度。图 6结果表明,相比较于经典的ST方法,采用曲率约束的地图匹配方法在不同情况下其错误率变化的幅度较小,其匹配结果错误率在不同情况下的变化具有一定的稳定性。
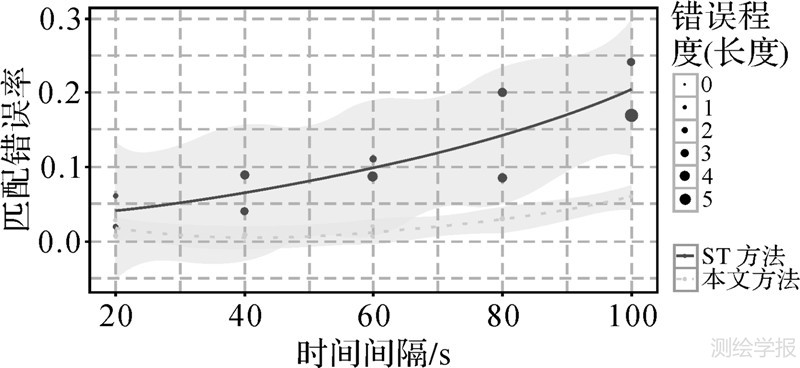 |
| 图 6 不同匹配方法错误趋势比较 Fig. 6 Comparison of error trends for different map-matching methods |
图 7给出了数据集2上两种不同匹配方法的错误程度比较。从图 7中可以看出整体上具有曲率约束的匹配结果错误程度好于ST方法的。曲率约束采用了衡量轨迹曲线弯曲程度的特征,因此不会产生弯曲形状上和真实路径相差太大的匹配结果,从而抑制了一些长度上极大偏离正确轨迹路径的匹配结果的发生。
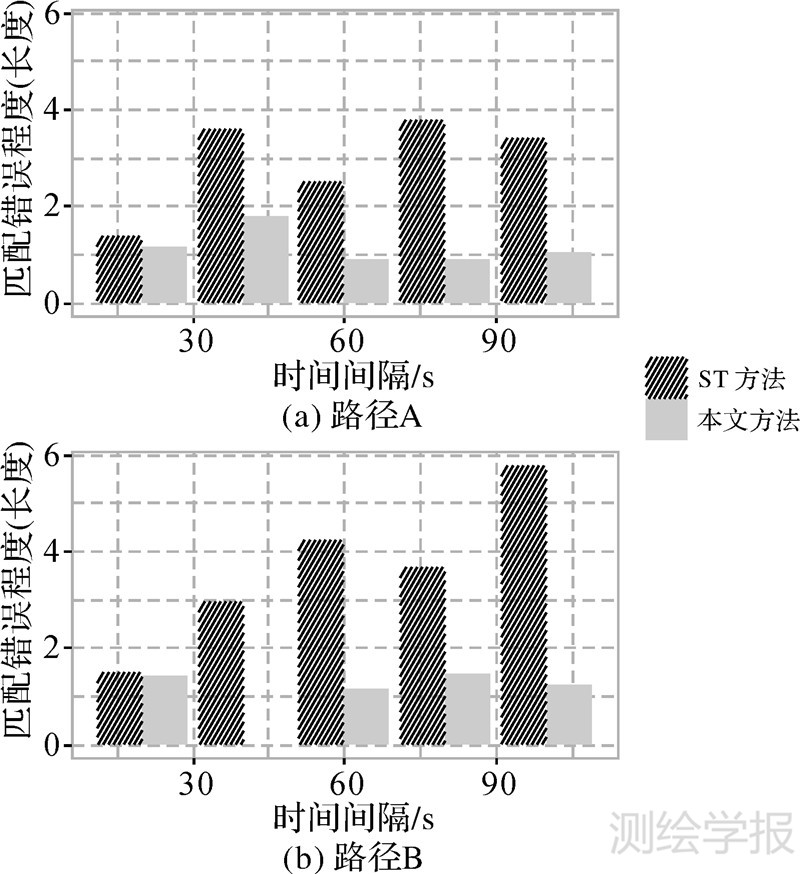 |
| 图 7 不同匹配方法错误程度比较 Fig. 7 Comparison of error levels for different map-matching methods |
本文试验中的ST方法基本包含了传统浮动车地图匹配中采用的一些几何、拓扑特征[7]。本文提出的浮动车地图匹配方法主要是利用曲率积分值直接描述两个相邻轨迹点之间的轨迹曲线的弯曲程度,这种弯曲程度相比较于传统匹配方法中使用的几何拓扑特征更加直接的描述了轨迹在路网中的弯曲程度。前面的4.2节的试验结果表明了这种对弯曲程度的直接度量在路网数据中实施地图匹配是更加有效的。图 8给出了一个本文方法匹配结果与ST方法匹配结果差异比较。图中在轨迹点2处两种匹配方法的匹配结果产生了差异。在该位置处本文方法将轨迹点2匹配到直行道路上,而ST方法将轨迹点2匹配至右转弯道上。ST方法主要采用距离、道路拓扑(网络距离)及速度约束来实现地图匹配,而轨迹2位置处,道路拓扑关系上从右转弯道弯回直行道路的道路网络距离与直行道路的网络距离差别不大;直行道路和弯道的等级一致,且都在路口,其行驶速度近似;然而在欧氏空间距离近似程度上,轨迹点2由于GPS定位误差,其位置非常接近于右转弯道,ST方法在地图匹配中综合考虑这3方面的约束条件,由于网络拓扑以及速度上直行和右转弯道差别不大,而在欧氏距离上轨迹点2明显更接近于右转弯道,因此其结果最终匹配到右转弯道上。而本文方法,引入曲率积分的约束作用后,其积分估值在轨迹点2处接近于直线的积分值,而从直行道路到右转弯道的路径曲率积分接近90°,这种差异弱化了轨迹点2在空间距离上接近于右转弯道的作用,在整体优化策略下,使得轨迹点2最终匹配到了直行道路上。图 8中轨迹点2的道路匹配情形比较具有代表性。我国各城市经济快速发展,道路更新速度很快,各种道路结构比较复杂;同时,当前地理信息服务中的路网模型趋向于更加精细化的表达。因此,在当前的交通道路数据中,车道、匝道等在复杂道路环境中往往表达为单独的数字化曲线,这就导致地图匹配在同等相似度的约束下相近似的候选道路路段增多,匹配的正确率会下降。图 8结果表明,在包含右转匝道的复杂路口处,本文的方法通过曲率积分的约束,可以得到正确的地图匹配结果。
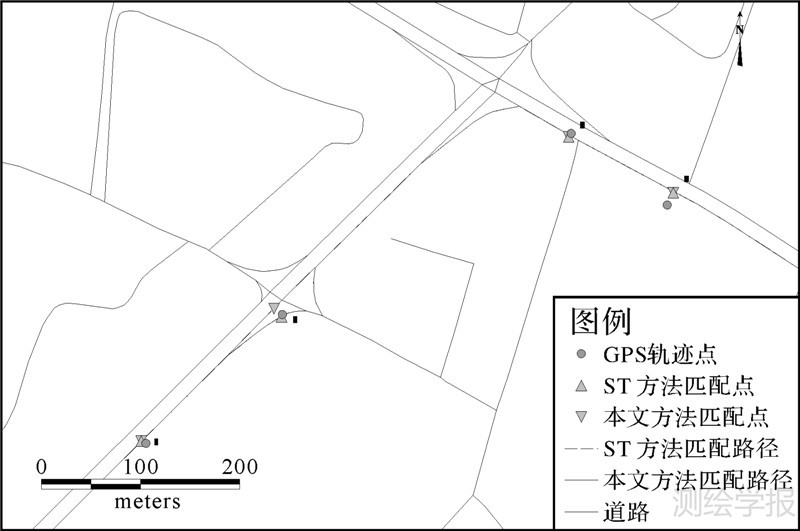 |
| 图 8 不同方法匹配结果的比较示例 Fig. 8 Comparison example for map-matching results of different methods |
另外,随着浮动车采样间隔的增加,相邻轨迹点之间的轨迹位置信息会损失得越来越多。本文匹配方法采用距离、道路拓扑、累积弯曲程度等特征来实施地图匹配可以帮助在信息不完整的GPS轨迹中恢复路径信息并实施地图匹配。图 5和图 6中,可以看到采样间隔增加导致错误匹配率的上升,在100 s的采样间隔以内,曲率积分的约束还是抑制了由于信息损失而导致的错误率上升。曲率积分给出的是两相邻轨迹点之间累积的弯曲程度并不是在一点处的瞬时弯曲值。在本文试验的采样间隔以内总体上比较正确地估计了两点之间的累积弯曲程度,对错误率上升起到抑制作用。但是随着采样间隔增加到大于100 s,GPS轨迹损失的信息将会导致关联匹配中的恢复路径计算(比如,计算相邻轨迹点在道路网络中行驶最短路径,计算相邻两轨迹点之间累积弯曲度)变得不可靠,从而错误率变大。因此在更大采样间隔下更加有效地实现正确的浮动车地图匹配是未来工作的一个方向。
5 结 论
本文给出了一种曲率积分值约束下的GPS浮动车地图匹配方法。曲率度量了平面曲线在一点处瞬时弯曲程度,曲率积分则度量了平面曲线在一段曲线上的累积弯曲程度。本文以曲率积分对于轨迹曲线的这种度量作为浮动车轨迹中相邻点之间的前后关联特征来实施地图匹配。通过两组不同试验数据的比较分析表明,这种基于曲率特征约束的浮动车地图匹配方法在不同类型行驶路线以及不同采样时间间隔下可以提高匹配正确性及匹配稳定性。本文方法比较适用于采样间隔在100 s以内的低频GPS轨迹数据。本文方法的结果可应用于海量低频GPS轨迹数据挖掘及交通出行分析等方面。
| [1] | LI Qingquan, LI Deren. Big Data GIS[J]. Geomatics and Information Science of Wuhan University, 2014, 39(6): 641-644, 666. (李清泉, 李德仁. 大数据GIS[J]. 武汉大学学报: 信息科学版, 2014, 39(6): 641-644, 666.) |
| [2] | LU Feng, ZHANG Hengcai. Big Data and Generalized GIS[J]. Geomatics and Information Science of Wuhan University, 2014, 39(6): 645-654. (陆锋, 张恒才. 大数据与广义GIS[J]. 武汉大学学报: 信息科学版, 2014, 39(6): 645-654.) |
| [3] | GREENFELD J S. Matching GPS Observations to Locations on a Digital Map[C]//Transportation Research Board 81st Annual Meeting.Washington D. C.:[s.n.], 2002. |
| [4] | LI Liang, QUDDUS M, ZHAO Lin. High Accuracy Tightly-coupled Integrity Monitoring Algorithm for Map-matching[J]. Transportation Research Part C: Emerging Technologies, 2013, 36: 13-26. |
| [5] | SU Jie, ZHOU Dongfang, YUE Chunsheng. Real-time Map-matching Algorithm in GPS Navigation System for Vehicles[J]. Acta Geodaetica et Cartographica Sinica, 2010, 30(3): 252-256. (苏洁, 周东方, 岳春生. GPS车辆导航中的实时地图匹配算法[J]. 测绘学报, 2001, 30(3): 252-256.) |
| [6] | NEWSON P, KRUMM J. Hidden Markov Map Matching Through Noise and Sparseness[C]//Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems.Seattle, Washington:ACM, 2009: 336-343. |
| [7] | LOU Yin, ZHANG Chengyang, ZHENG Yu, et al. Map-Matching for Low-Sampling-Rate GPS Trajectories[C]//Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems.Seattle, Washington, ACM,2009: 352-361. |
| [8] | BRAKATSOULAS S, PFOSER D, SALAS R, et al. On Map-Matching Vehicle Tracking Data[C]//Proceedings of the 31st International Conference on Very Large Databases. VLDB Endowment,2005: 853-864. |
| [9] | WANG Meiling, CHENG Lin. Study on Map-matching Algorithm for Floating Car[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(1): 133-138. (王美玲, 程林. 浮动车地图匹配算法研究[J]. 测绘学报, 2012, 41(1): 133-138.) |
| [10] | LI Qingquan, HUANG Lian. A Map Matching Algorithm for GPS Tracking Data[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 207-212. (李清泉, 黄练. 基于GPS轨迹数据的地图匹配算法[J]. 测绘学报, 2010, 39(2): 207-212.) |
| [11] | ZHANG Wei, XU Jianmin, LIN Mianfeng. Map Matching Algorithm of Large Scale Probe Vehicle Data[J]. Journal of Transportation Systems Engineering and Information Technology, 2007, 7(2): 39-45. (章威, 徐建闽, 林绵峰. 基于大规模浮动车数据的地图匹配算法[J]. 交通运输系统工程与信息, 2007, 7(2): 39-45.) |
| [12] | LI Qingquan, HU Bo, YUE Yang. Flowing Car Data Map-matching Based on Constrained Shortest Path Algorithm[J]. Geomatics and Information Science of Wuhan University, 2013, 38(7): 805-808. (李清泉, 胡波, 乐阳. 一种基于约束的最短路径低频浮动车数据地图匹配算法[J]. 武汉大学学报: 信息科学版, 2013, 38(7): 805-808.) |
| [13] | ZHENG Nianbo, LU Feng, LI Qingquan. Dynamic Multi-scale Road Network Data Model for Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(4): 428-434. (郑年波, 陆锋, 李清泉. 面向导航的动态多尺度路网数据模型[J]. 测绘学报, 2010, 39(4): 428-434.) |
| [14] | LI Qingquan, XU Jinghai, ZHENG Nianbo, et al. Function Based Navigation Data Model[J]. Geomatics and Information Science of Wuhan University, 2007, 32(3): 266-270. (李清泉, 徐敬海, 郑年波, 等. 基于功能的导航数据模型[J]. 武汉大学学报: 信息科学版, 2007, 32(3): 266-270.) |
| [15] | ZHANG Yun, LI Qingquan, CAO Xiaohang, et al. An Algorithm for Detecting the Geometric Difference between the Road Networks[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4): 521-525. (张韵, 李清泉, 曹晓航, 等. 一种道路网信息几何差异检测算法[J]. 测绘学报, 2008, 37(4): 521-525.) |
| [16] | ZHENG Nianbo, LU Feng. Improved Navigation Road Network Data Model and Its Organization Method[J]. China Journal of Highway and Transport, 2011, 24(2): 96-102. (郑年波, 陆锋. 导航路网数据改进模型及其组织方法[J]. 中国公路学报, 2011, 24(2): 96-102.) |
| [17] | MEI Xiangming, HUANG Jingzhi. Differential Geometry[M]. 4th ed. Beijing: Higher Education Press, 2008. (梅向明, 黄敬之. 微分几何[M]. 第四版. 北京: 高等教育出版社, 2008.) |
| [18] | MENG Daoji, LIANG Ke. Differential Geometry[M]. Beijing: Science Press, 2002. (孟道骥, 梁科. 微分几何[M]. 北京: 科学出版社, 2002.) |
| [19] | DIJKSTRA E W. A Note on Two Problems in Connexion with Graphs[J]. Numerische Mathematik, 1959, 1(1): 269-271. |
| [20] | QUDDUS M A. High Integrity Map Matching Algorithms for Advanced Transport Telematics Applications[D]. London:Imperial College London Department of Civil and Environmental Engineering, 2006." |