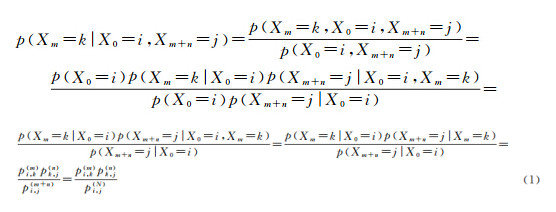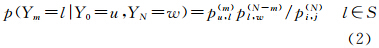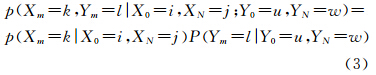2. 武汉大学中国南极测绘研究中心,湖北 武汉 430072
2. Chinese Antarctic Center of Surveying and Mapping, Wuhan University, Wuhan 430072, China
移动对象生成的轨迹由典型的基于离散时间观测的位置样本点组成,在两个相邻样本点之间移动对象在任意时刻所处的位置是不确定的[1]。这种不确定的位置的全体或并集,在经典时间地理中通过时空棱柱体来描述[2, 3, 4, 5, 6]。时空棱柱体在交通网络空间退化为位于交通网上的垂直切面[7, 8, 9, 10]。这些时空体并不区分移动对象位于不同位置的可能性的差异,即认为移动对象在可达范围内呈均匀分布。然而,根据地理学第一定理[11],在初始时刻ts位于起点的移动对象,在时刻ts+Δt位于起点附近的可能性会很大[9];或者,在结束时刻te位于止点的移动对象,在时刻te-Δt位于止点附近的可能性会很大。这意味着,在时刻t∈[ts,te]移动对象分布在不同可达位置的可能性不总是均匀的。
为了能定量描述移动对象在空间分布上的非均一性,文献[12]提出了模糊时空体但尚未研制分析工具,文献[13]给出了概率时间地理的概念[13]。随后,时间地理的概率建模算法不断被提出与发展。文献[9, 14]采用截断正态表达移动对象的空间概率分布,其方差随最大移动速度(vmax)的增大而缺乏收敛性。文献[15—16]采用截断布朗桥表达移动对象的空间概率分布,但布朗桥的方差与现实速度vmax无关,因而难以直接模拟现实的时间地理。基于此,本文提出基于马尔科夫链的概率时间地理算法,其方差一方面随现实速度vmax的变化而变化,从而能表达vmax与移动对象空间概率分布的相关性,另一方面随vmax的增大而趋于稳定,从而保持与中心极限定理的一致性。
1 研究背景 1.1 经典时间地理
现实地理世界的运动轨迹通常是连续的(图 1(a)),而在时空数据库[17, 18, 19, 20]中往往被抽样成离散的点(图 1(b))。在采用序列离散的样本点表达移动轨迹时,会造成移动对象位于两相邻样本点之间位置的缺失,这在样本点足够密集时通过空间插值可以进行弥补。然而,能完全填补这一缺失的模型,是经典时间地理的潜在路径区域(potential path area,PPA)[21],它是移动对象位于两相邻样本点之间的所有可达位置(图 1(c))。
 |
| 图 1 地理与时间地理 Fig. 1 Geography and time geography |
在时刻ts位于起始样本点s的移动对象,以最大速度vmax在时刻te到达下一个样本点e的运动,是一个定向的移动过程。在假设地理空间为均质的经典时间地理中,定向移动在时间[0,T=te-ts]内的可达位置是一个PPA:以s、e为焦点以a=vmaxT/2为半长轴的椭圆;在时刻t∈[0,T]的可达位置则为平面时空棱柱体(planar space-time prisms)[16]或棱镜(图 2(a)),即这样两个圆的交集:一个是以s为中心以rs=vmaxt为半径的圆,另一个是以e为中心以re=vmax(T-t)为半径的圆。其中,两圆的交点构成了椭圆。
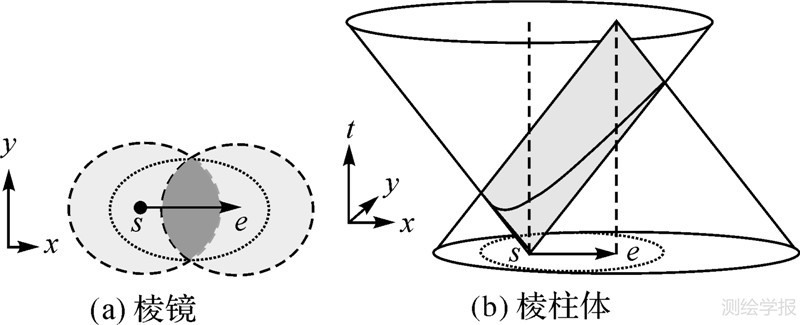 |
| 图 2 棱镜与棱柱体 Fig. 2 Diamond and its space-time prism |
在x-y-t空间,上述两个圆可形成两个反向的圆锥体(图 2(b)):圆锥中轴线与其母线的夹角的正切函数就是vmax[9]。两圆锥体的交集是一个时空棱柱体,它在时刻t就退化为一棱镜,在平面x-y的投影就是PPA。
1.2 概率时间地理
概率时间地理认为移动对象在任意时刻以一定的概率值分布在可达范围[9, 14],而且同一位置的概率值会随时间推移而发生变化。这种基于概率定量化扩展的时空体称概率时空体,包括概率圆锥体[14](图 3(a))和概率棱柱体[9](图 3(b))。
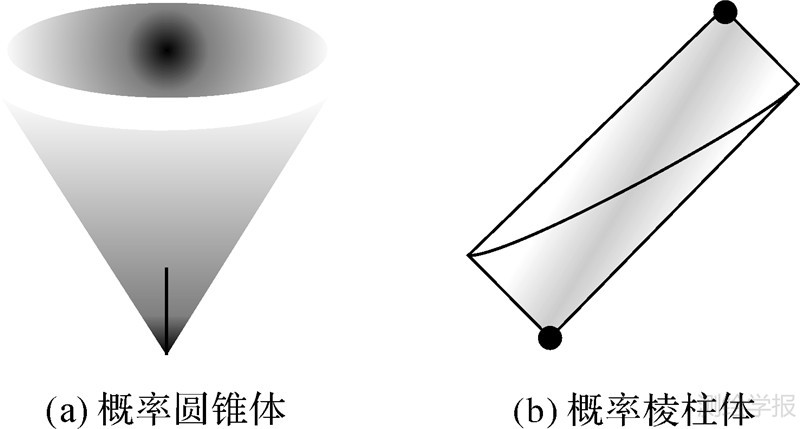 |
| 图 3 概率时间地理 Fig. 3 Probabilistic time geography |
移动对象的随机运动可采用随机走进行模拟。简单的随机走可定义为[26]:设一质点在数轴上随机游动,每隔一单位时间Δt移动一次,每次只能向左或向右移动一个格点(相邻格点长度为Δx),或原地不动,相应的概率为p、q和r,且各次移动相互独立。在随机分析中,随机走是布朗运动、马尔科夫链的定义基础,因而也是概率时间地理的理论基础。
文献[9, 14]认为移动对象在任一时刻t的概率分布可采用正态描述:数学期望μ(t)=2pct/Tp,其中c为半焦距;标准差定义为棱镜最小边界盒的宽度、高度的1/6,有σx2(t=T/2)=(vmaxT-2c)2/36,σy2(t=T/2)=[vmaxT2-4c2]/36。这种方差由于随着vmax的变化而变化(vmax决定棱镜大小),因而具有应用针对性(即同一定向移动在vmax值不同的条件下具有差异化的方差及其概率分布),但随着vmax的增大而呈指数发散[15]。
在随机走中,当步长Δx固定时,Δt=Δx/vmax会随vmax的增大而减小,相应地在时刻t的步数则增大。当vmax或步数足够大,根据中心极限定理随机走近似服从正态分布,相应的数学期望和方差都趋于稳定。布朗运动就属于此类,定向的布朗运动被称为布朗桥[26]。文献[15]直接采用布朗桥模拟定向移动:数学期望μ(t)=2ct/T;方差σ2(t)=C2t(T-t)/T(C为布朗系数)。这种方差由于与vmax无关(只与时间有关),因而具有极端的稳定性(即同一定向移动在vmax值不同的条件下具有相同的概率特性与分布),也就不具有应用的针对性。文献[16]在布朗桥方差公式中新增了乘数项vmax-v2,其中v=2c/T,目的是让修正后的方差公式具有应用针对性。然而,修改后的方差也随vmax的增大而呈指数发散。
2 基于马尔科夫链的概率时间地理原理
马尔科夫链的概率特性由其已知状态、转移矩阵与转移步次等参数决定,因而建立这些参数与定向移动的已知条件(s,e,T,vmax)的映射是利用马尔科夫链计算定向移动概率分布的基础。
2.1 平面空间的马尔科夫链 2.1.1 马尔科夫链
在随机走定义基础上,设质点移动到状态-z或z后,下一次移动必返回到-z+1或z-1,即p-z,-z+1=1,pz,z-1=1,以Xn表示质点经n次移动后所处的格点位置,则{Xn,n≥0}是带反射壁-z和z的马尔科夫链[26]:
(1)位移Xn=Δx(ζ1+ζ2+…+ζn),式中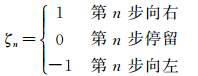
(2)状态空间S={-z,-z+1,…,z-1,z}⊂{-n,-n+1,…,n-1,n}z≤n
(3)初始状态 0
(4)转移概率  2.1.2 中间关于两边的马尔科夫链
2.1.2 中间关于两边的马尔科夫链
马尔科夫链是一种已知起点状态X0=i的正向条件概率。当又知止点状态XN=j时,马尔科夫链就转化为了中间关于两边的双向马尔科夫链p(Xm=k|X0=i,Xm+n=j),它表达了定向移动的空间概率分布,其中m,n∈Z+,i,j,k∈S,m+n=N。
式中,m≥0。由式(1)与C-K方程可知,双向马尔科夫链的概率特性也取决于它的已知状态、转移矩阵与转移步次。类似的,Y维马尔科夫链为平面空间(x,y)上的马尔科夫链可视为X维和Y维马尔科夫链的独立联合,即
2.2 定向移动到马尔科夫链的映射 2.2.1 到转移步次的映射
由物理试验可得,当vmax越大时,移动一步的时间消耗也就越小,每次移动Δx也越小[26],因此可以假设Δx=1/vmax。针对不同的应用,可考虑常数修正因子。
定向移动位于起、止点的时刻分别为0和T,对应于马尔科夫链的第0步和第N步,N=[vmaxT/Δx]。这样,对于任意时刻t∈[0,T],一方面由于vmax与步数N有关,而N根据式(1)又与马尔科夫链的概率特性有关,因此马尔科夫链能表达不同vmax的移动对象在概率特性(如方差等)方面的差异;另一方面当vmax→∞时N→∞,根据中心极限定理马尔科夫链趋于正态分布,其数字特征也趋于稳定。
2.2.2 到状态空间的映射
定向移动在总时间T内的潜在区域PPA是一长半轴为a=vmaxN/2、c=|se|/2、b= 的椭圆,假设椭圆的中心点位于原点,长轴位于X轴。
的椭圆,假设椭圆的中心点位于原点,长轴位于X轴。
(1) 状态空间。在X轴上作随机走的质点总位于[-a,a]内,因而其状态空间Sx={-[a/Δx],-[a/Δx]+1,…,[a/Δx]-1,[a/Δx]},长度Lx=[2a/Δx+1]。类似的,Y轴上的质点总位于[-b,b]内,其状态空间Sy={-[b/Δx],-[b/Δx]+1,…,[b/Δx]-1,[b/Δx]},长度Ly=[2b/Δx+1]。显然,Sx的反射壁为-[a/Δx]和[a/Δx];Sy的反射壁为-[b/Δx]和[b/Δx]。当Δx=1时,X和Y维状态空间及反射壁如图 4所示。
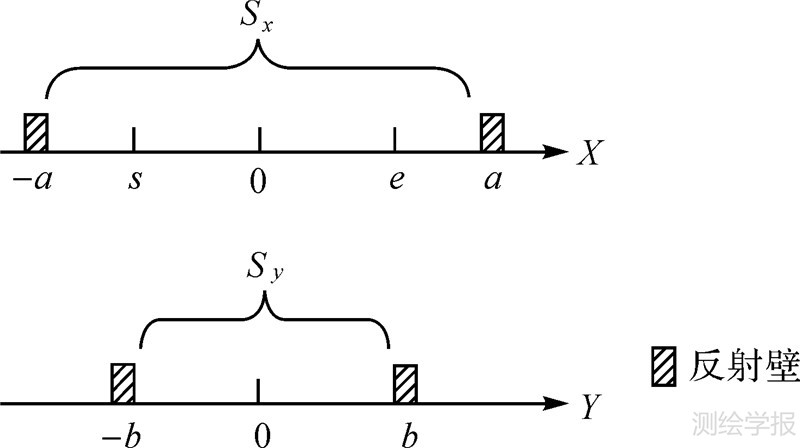 |
| 图 4 状态空间及其反射壁 Fig. 4 State space and its reflective walls |
(2) 初始与结束状态。移动对象在t=0时位于起点s(-c,0),对应于马尔科夫链的初始状态X0=i=-[c/Δx]、Y0=u=0;在t=T时位于止点e(c,0),对应于马尔科夫链的结束状态XN=j=[c/Δx]、YN=w=0。
2.2.3 到转移矩阵的映射
定向移动是一种带起、止点约束的随机走,因而可以假设移动对象在X轴上每次向左或向右移动的概率相等(如p=0.5,q=0.5),原地不动的概率为0(r=0)。这样,根据X轴上的状态空间Sx,可构建大小为Lx的一步转移概率矩阵P

2.3 基于马尔科夫链的概率时间地理算法
通过建立定向移动与马尔科夫链的映射关系,利用双向马尔科夫链模型,能计算定向移动的概率分布云(图 5)。
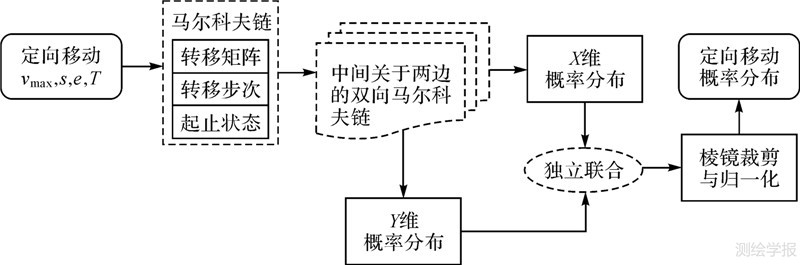 |
| 图 5 算法流程 Fig. 5 Algorithm Flowchart |
首先,根据定向移动与马尔科夫链的映射关系,将定向移动的已知条件(s,e,T,vmax)转换为马尔科夫链的参数(步长、状态空间、转移矩阵等)。
然后,利用式(3)的双向马尔科夫链模型,计算X、Y维空间的概率分布,并通过联合形成平面空间的概率分布云。
最后,通过棱镜进行裁剪及其归一化,形成定向移动的概率分布。
3 例 子
为了验证基于马尔科夫链的概率时间地理原理,在Matlab软件中进行了实例分析。选择的实例是:移动对象在第0 s时位于起点s(-10 m,0 m)且在第20 s时位于止点e(10m,0 m);vmax=2m/s,步长Δx=1/vmaxm;转移概率p=q=0.5、r=0。
3.1 定向移动概率分布云
由定向移动的已知条件(s,e,T,vmax)可获得PPA椭圆(c=10m,a=20 m,b=17.320 5m)。在此基础上,根据步长Δx可获得马尔科夫链状态空间,初始与结束状态,以及总步数。
(1) 状态空间:X维的状态空间Sx={-40 m,-39 m,…,40 m},Y维的状态空间Sy={-34 m,-33 m,…,34 m}。
(2) 初始与结束状态:X维的初始与结束状态{X0=-10m,XN=10 m},Y维的初始与结束状态{Y0=0 m,YN=0 m}。
(3) 总步数:N=[vmaxT/Δx]=80。
(4) 一步转移矩阵:根据状态空间Sx、Sy的大小Lx=81、Ly=69,随机走向左、停留、向右的概率(p=0.5,r=0,q=0.5),能分别建立在X维与在Y维的一步转移矩阵。
依据X维的双向条件马尔科夫链(式(1)),能连续计算移动对象在任意时刻t位于X维的概率分布。类似的,利用式(2)也可获得Y维的概率分布。通过X、Y维概率分布的独立联合,能获得移动对象在任意时刻t分布在二维平面空间上的概率,再经过基于t时刻的棱镜的裁剪和归一化处理即形成定向移动的概率分布。图 6(a)、图 6(b)和图 6(c)分别是在t=5 s、10 s、15 s时基于离散空间的概率分布。
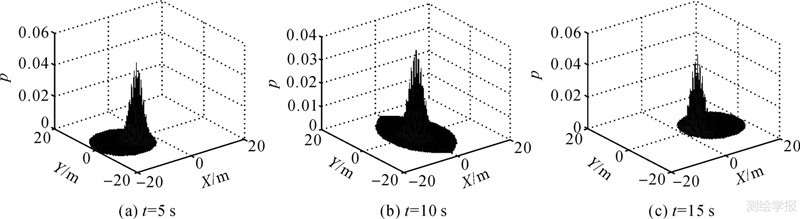 |
| 图 6 不同时刻的概率分布云 Fig. 6 The probability distributions at different times |
由于是在离散空间构建的概率分布,因此图中的概率密度云呈离散的非连续性,其中X、Y轴表示平面的地理空间,Z轴表示概率值。图 6(b)是移动过程在中间时刻(t=10s)的概率分布,棱镜及其概率值关于X、Y轴对称;图6(a)、图 6(c)分别是在t=5s、15 s时刻的概率分布,棱镜及其上分布的概率云只关于X轴对称;由于5 s、15 s分别与10 s等距,因此图 6(a)、图 6(c)的概率云关于Y轴对称。
3.2 数字特征及其变化趋势
根据离散空间的边缘概率分布定义,可将定向移动的概率分布云分解为X-维边缘分布与Y-维边缘分布。在数学期望方面,Y-维边缘分布的期望是一条端点分别为(第0次,0 m)、(第80次,0 m)的直线(图 7(a));X-维边缘分布的期望是一条端点分别为(第0次,-10 m)、(第80次,10 m)的近似直线。因此,马尔科夫链算法的数学期望同布朗桥算法的数学期望μ(t)=2ct/T一致。在方差方面,X-维边缘分布与Y-维边缘分布的方差均呈抛物线型,且在第0、80次的方差均为0(图 7(b))。布朗桥的方差也具有这一抛物线型特征,只是布朗桥的方差与vmax无关。由图可知,定向移动的数学期望、方差均关于中间时刻对称,这从机理上解释了图 6(a)、图 6(c)的概率云关于Y轴对称的原因。
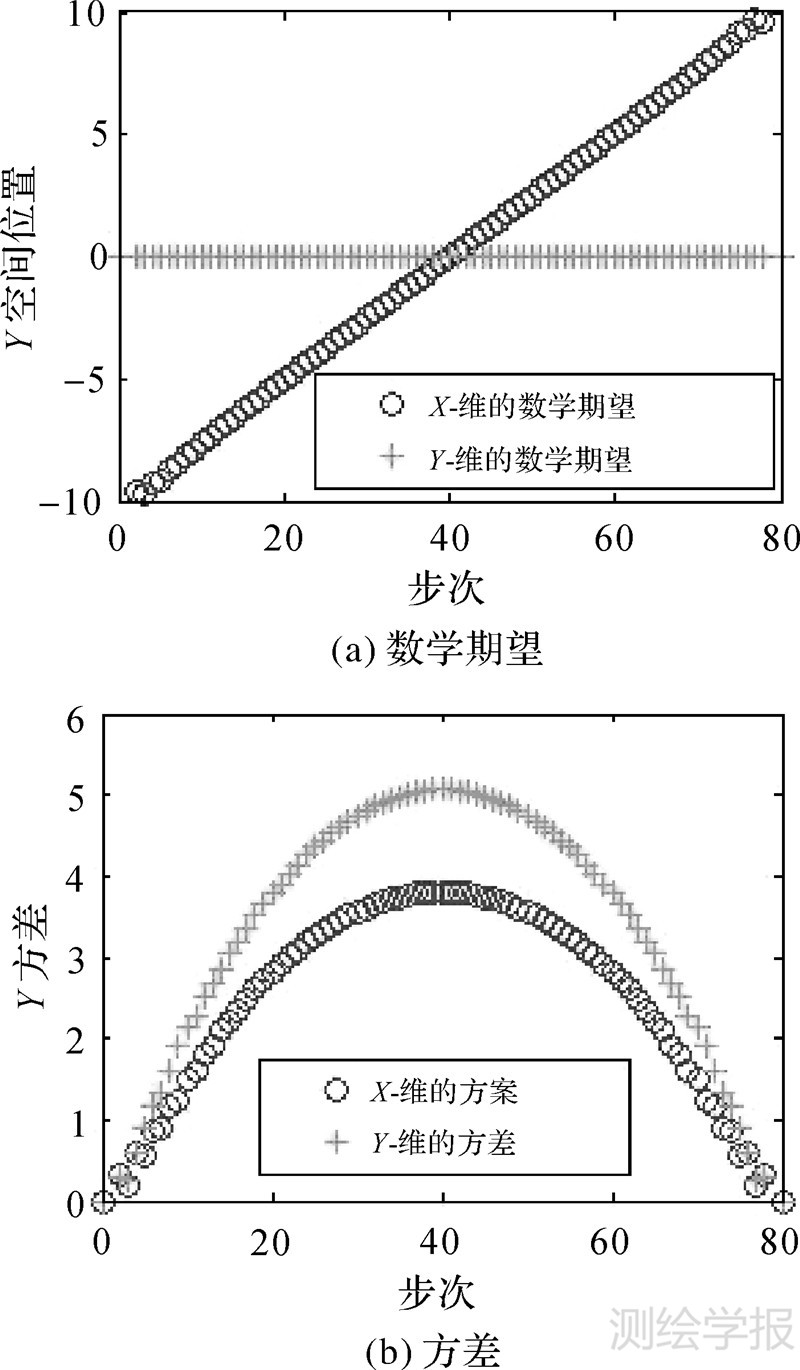 |
| 图 7 边缘概率分布的数学期望与方差 Fig. 7 The mathematical expectation and variance of the marginal probability distribution |
对于同一时刻t=T/2,定向移动基于马尔科夫链的数字特性随着vmax的增大(如vmax=[1.45,1.95,2.45,2.95,3.45,3.95,4.45,4.95,5.45,5.95,6.45]),具有稳定性:①在数学期望方面,X-维、Y-维的期望值都位于中心点处(0,0)(图 8(a));②在方差方面,X-维、Y-维的方差都趋于稳定(图 8(b))。
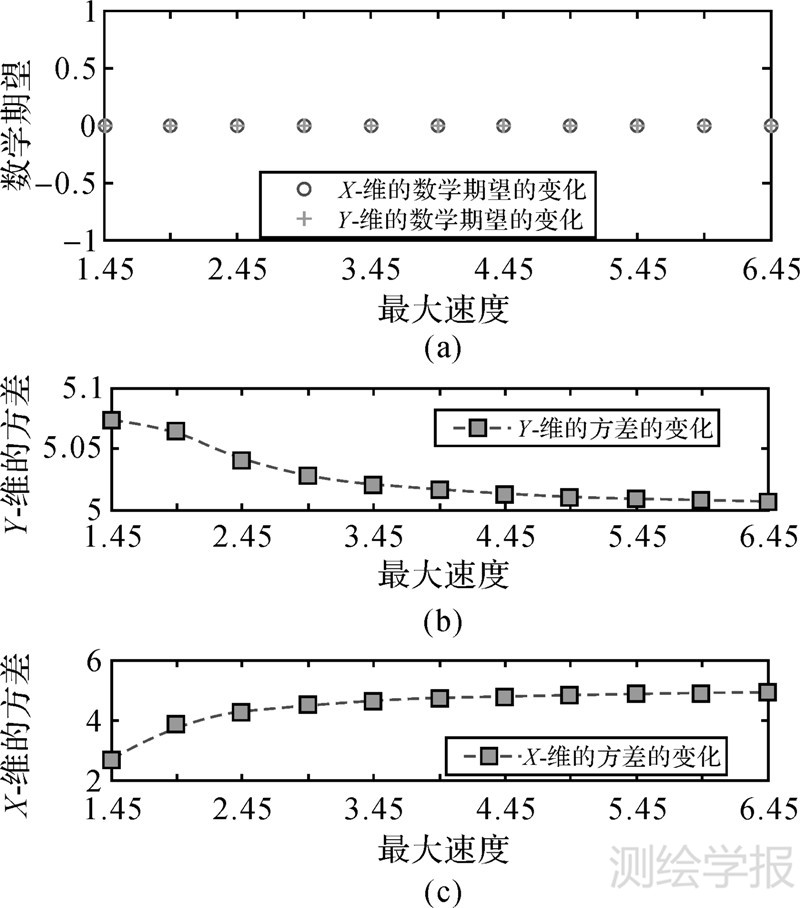 |
| 图 8 数学期望和方差随最大速度增大而稳定 Fig. 8 expectation and variance stabilizing with the increase of the maximum speed |
双向马尔科夫链和布朗桥都由随机走推理而来,这为两种算法的数学期望、方差在形态方面的共性提供了理论依据。然而,随机走的步长Δx在两种算法中的定义不同,从而造成两种概型的方差不同:①在布朗桥中被定义为无穷小(Δx→0),因而其方差自然与Δx无关;②在双向马尔科夫链中可定义为有限的(Δx=1/vmax),本文构建了这种有限值的Δx与马尔科夫链概率分布云之间的映射关系,其方差与Δx有关,这为概率时间地理差异化描述不同步长Δx的定向移动提供了基础。当Δx→0时,布朗桥可视为双向马尔科夫链的极限,这意味着,当Δx=1/vmax→0,或vmax→+∞时,双向马尔科夫链的方差具有收敛性或趋于稳定,这也为图 8(b)的变化规律提供了理论支撑。
4 小 结
随着时间地理的定量化发展,概率时间地理已经引起关注。基于不同概率模型的概率时间地理所表现出的概率特性(如方差等)不同,已有的概率时间地理的方差随vmax的增大要么发散要么不变,在稳定性和应用针对性方面难以调和。基于此,本文引入了能模拟定向移动过程的双向条件马尔科夫链,试验表明其方差在vmax增大时具有针对性和稳定性,即方差对不同vmax的移动对象具有差异性,这种差异性会随vmax的增大而逐渐减小并最终形成稳定的方差。在理论上,马尔科夫链也适合描述交通网空间的定向移动,下一步将本文提出的概率时间地理原理扩展至交通网,以分析定向移动在交通网空间的概率分布云。
| [1] | KUIJPERS B, OTHMAN W. Modeling Uncertainty of Moving Objects on Road Networks via Space-time Prisms[J]. International Journal of Geographical Information Science, 2009, 23(9): 1095-1117. |
| [2] | HÄGERSTRAND T. What about People in Regional Science?[J]. Papers of the Regional Science Association, 1970, 24(1): 6-21. |
| [3] | LIN Guangfa, HUANG Yongsheng. Probe into the Application of GIS in Time-geography[J]. Human Geography, 2002, 17(5): 69-72. (林广发, 黄永胜. GIS在时间地理学中的应用初探[J]. 人文地理, 2002, 17(5): 69-72.) |
| [4] | SHAO Lixia, HE Zongyi. Destination Choice Based on Space-time Prisms and Attracting Ratios of Different Activity Opportunity Establishments[J]. Geomatics and Information Science of Wuhan University, 2007, 32(6): 481-484. (邵黎霞, 何宗宜. 基于时空棱镜和活动场所吸引率的目的地选择研究[J]. 武汉大学学报: 信息科学版, 2007, 32(6): 481-484.) |
| [5] | CHAI Yanwei, ZHAO Ying. Recent Development in Time Geography[J]. Scientia Geographica Sinica, 2009, 29(4): 593-600. (柴彦威, 赵莹. 时间地理学研究最新进展[J]. 地理科学, 2009, 29(4): 593-600.) |
| [6] | DELAFONTAINE M, NEUTENS T, VAN DE WEGHE N. Modelling Potential Movement in Constrained Travel Environments Using Rough Space-time Prisms[J]. International Journal of Geographical Information Science, 2011, 25(9): 1389-1411. |
| [7] | KWAN M P, HONG X D. Network-based Constraints-oriented Choice Set Formation Using GIS[J]. Journal of Geographical Systems, 1998, 5(2): 139-162. |
| [8] | DOWNS J A, HORNER M W. Probabilistic Potential Path Trees for Visualizing and Analyzing Vehicle Tracking Data[J]. Journal of Transport Geography, 2012, 23: 72-80. |
| [9] | WINTER S, YIN Zhangcai. Directed Movements in Probabilistic Time Geography[J]. International Journal of Geographical Information Science, 2010, 24(9): 1349-1365. |
| [10] | MILLER H J. Modeling Accessibility Using Space-time Prism Concepts within Geographical Information Systems[J]. International Journal of Geographical Information Systems, 1991, 5(3): 287-301. |
| [11] | TOBLER W R. A Computer Movie Simulating Urban Growth in the Detroit Region[J]. Economic Geography, 1970, 46(S): 234-240. |
| [12] | NEUTENS T, WITLOX F, VAN DE WEGHE N, et al. Space-time Opportunities for Multiple Agents: A Constrained-based Approach[J]. International Journal of Geographical Information Science, 2007, 21(10): 1061-1076. |
| [13] | WINTER S. Towards a Probabilistic Time Geography[C]//Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Bellevue, WA: ACM Press, 2009: 528-531. |
| [14] | WINTER S, YIN Zhangcai. The Elements of Probabilistic time Geography[J]. Geoinformatica, 2011, 15(3): 417-434. |
| [15] | YIN Zhangcai, HE Xiaorong, ZHANG Xiaopan, et al. Probability Model of Directed Movements Based on Brownian Bridge[J]. Journal of Geomatics Science and Technology, 2012, 29(6): 397-400. (尹章才, 何晓蓉, 张晓盼, 等. 基于布朗桥概率模型的定向移动[J]. 测绘科学技术学报, 2012, 29(6): 397-400.) |
| [16] | SONG Ying, MILLER H J. Simulating Visit Probability Distributions within Planar Space-time Prisms[J]. International Journal of Geographical Information Science, 2014. 28(1): 104-125. |
| [17] | XUE Cunjin, ZHOU Chenghu, SU Fenzhen, et al. Research on Process-oriented Spatio-temporal Data Model[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 95-101. (薛存金, 周成虎, 苏奋振, 等. 面向过程的时空数据模型研究[J]. 测绘学报, 2010, 39(1): 95-101.) |
| [18] | XIA Kai, LIU Renyi, LIU Nan, et al. Research of Forestry Spatio-temporal Data Model in Sequence States[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(3): 433-439. (夏凯, 刘仁义, 刘南, 等. 序列状态的林业资源时空数据模型研究[J]. 测绘学报, 2013, 42(3): 433-439.) |
| [19] | GONG Jianya, LI Xiaolong, WU Huayi. Spatiotemporal Data Model for Real-time GIS[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(3): 226-232. (龚健雅, 李小龙, 吴华意. 实时GIS时空数据模型[J]. 测绘学报, 2014, 43(3): 226-232.) |
| [20] | MA Linbing, ZHANG Xinchang. Research on Full-period Query Oriented Moving Objects Spatio-temporal Data Model[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(2): 207-211. (马林兵, 张新长. 面向全时段查询的移动对象时空数据模型研究[J]. 测绘学报, 2008, 37(2): 207-211.) |
| [21] | MILLER H J. A Measurement Theory for Time Geography[J]. Geographical Analysis, 2005, 37(1): 17-45. |
| [22] | SHAW S L, YU Hongbo. A GIS-based Time-geographic Approach of Studying Individual Activities and Interactions in a Hybrid Physical-virtual Space[J]. Journal of Transport Geography, 2009, 17(2): 141-149. |
| [23] | FARBER S, NEUTENS T, MILLER H J, et al. The Social[JP] Interaction Potential of Metropolitan Regions: A Time-geographic Measurement Approach Using Joint Accessibility[JP][J]. Annals of the Association of American Geographers, 2013, 103(3): 483-504. |
| [24] | O'SULLIVAN D, MORRISON A, SHEARER J. Using Desktop GIS for the Investigation of Accessibility by Public Transport: an Isochrone Approach[J]. International [JP]Journal of Geographical Information Science, 2000, 14(1): 85-104. |
| [25] | MILLER H J, BRIDWELL S A. A Field-based Theory for Time Geography[J]. Annals of the Association of American Geographers, 2009, 99(1): 49-75. |
| [26] | LIN Yuanlie. Applied Stochastic Processes[M]. Beijing: Tsinghua University Press, 2002. (林元烈. 应用随机过程[M]. 北京: 清华大学出版社, 2002.)" |