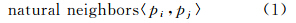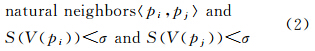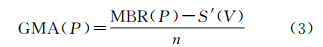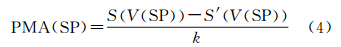1 引 言
点目标多尺度聚类是空间数据知识发现的重要技术之一[1],其采用准确的相似性测度计算点目标间的邻近程度,进而自适应地解译与评估不同空间尺度下目标的分布特征与模式。然而,空间多尺度聚类有两方面特殊性:①线面目标的存在易造成点目标间的不通视或不通达现象[2],直接以欧氏距离判断点目标远近易发生聚类模式混交;②点目标聚散性具有显著的多尺度特征,不同的空间幅度范围内发现不同聚类粒度所遵循的规律与体现的特征不尽相同,单一相似度阈值难以随空间尺度变化准确地划分点目标[3]。
针对前者,已有研究将线面目标视为障碍,增加了障碍约束下点目标真实距离的判别和计算,典型算法有:①直接距离法,根据点与线面特征点的连线计算绕行障碍的最小距离,COD-CLARANS[4]、DBCluC[5]、OETTC-MEANS-CLASA[6]、DBCOD[7]、OBS-UK-means[8]等,不规则线面目标的约减易造成几何特征丢失且计算复杂;②栅格距离法,二值化矢量数据,并运用数学形态学算子进行二值图像的降噪和融合聚类[9, 10],但限于矢栅转换时的精度损失;③邻近判断法,采用简单、规律且平铺的几何结构剖分空间并获取目标的邻近关系和几何特征来实现聚类,基于Delaunay三角网的AUTOCLUST+及其改进算法[11, 12, 13]、基于Voronoi图的聚类算法[14, 15],但从符合人类空间认知的角度而言,Voronoi剖分比Delaunay剖分更为清晰。而对于后者,聚类尺度特殊性的识别需要构建类融合的多尺度模型来实现,常见算法有基于尺度空间理论的聚类[3, 16, 17]、以邻近关系判别的AMOEBA层次聚类[18]、多尺度谱聚类[19]、基于径向基函数网络的多核划分[20]等,但以上算法皆需预定义多尺度阈值,难以实现聚类尺度的自适应收敛。
纵观现有算法的优缺点,本文提出了考虑线面分布的点目标多尺度聚类方法(multi-scale spatial clustering,MSSC),鉴于Voronoi图对点目标邻近关系的准确表达及剖分的直观完整[21],通过生成点线面目标的全要素Voronoi图,提取点线面的邻近关系及计算Voronoi势力范围;进而计算点集的类内平均面积作为面积阈值,将互为自然邻居且其Voronoi图面积小于阈值的点进行融合实现聚类;同时,在不同空间尺度下算法自适应地计算各子类的面积阈值,使得聚类粒度由粗到细划分,并于尺度稳定时收敛。MSSC算法无须自定义参数,可识别异常值并发现任意形态的类。
2 Voronoi剖分下的点目标聚散特征表达
空间实体以点线面的形式存储于空间数据库中,当考虑线面目标约束下的点目标聚类时,必须准确识别3种要素间的空间关系。Voronoi图是一种基于场(field-based)的空间数据模型,是对二维空间的不重叠铺盖,本文通过提取线面要素边界的几何特征点与点目标合并生成Voronoi图,并将同一要素的特征点Voronoi图进行合并,得到全要素Voronoi图,进而以“邻近关系”与“势力范围”两项衡量标准来识别线面目标阻隔下的点目标聚集分布特征。
2.1 邻近关系
线面的阻隔使得点目标的聚集不仅是直线距离的靠近,还必须考虑位置是否邻近。如图 1(a)所示,点目标A与B被线要素阻隔,二者的实际距离需要绕线而测,较为遥远,常规的以直线距离计算远近的方法不能正确判断点目标的接近程度,与空间认知相悖。MSSC算法以Voronoi图判断目标间邻近关系,根据文献[22]提出了Voronoi邻近关系的定义,若两个空间目标具有相同的Voronoi边,则它们构成邻近关系,互为自然邻居(natural neighbors)。
定义1:设点目标集合P={p1,p2,…,pn}⊂R2,pi,∀pj∈P,且i≠j,记pi的Voronoi区域为V(pi),pj的Voronoi区域为V(pj),若存在V(pi)∩V(pj)≠ ,则称目标pi与pj是自然邻居,存在邻近关系
,则称目标pi与pj是自然邻居,存在邻近关系
由定义可得,图 1(b)中Ⅰ与Ⅱ是自然邻居,表达为natural neighbors〈Ⅰ,Ⅱ〉,而A与B、Ⅱ与Ⅲ无公共边,非邻近关系,可见Voronoi图的邻近关系能较好地识别空间障碍的存在。
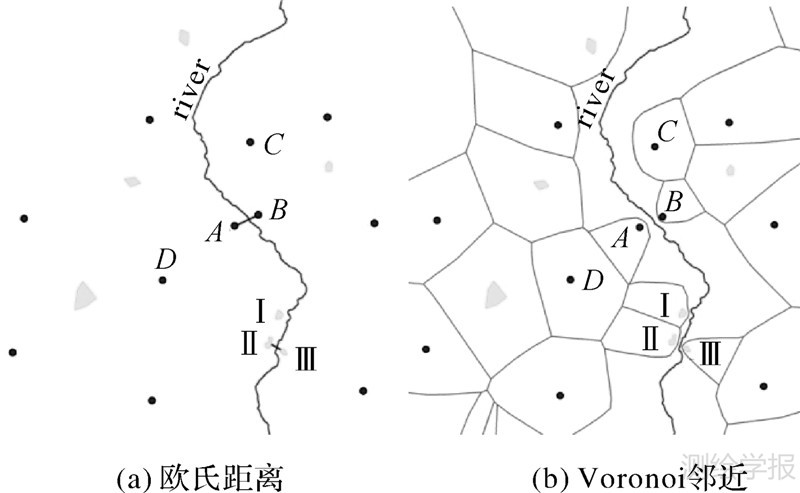 |
| 图 1 空间目标分布的邻近程度测算 Fig. 1 Calculate adjacency of spatial objects distribution |
2.2 势力范围
由Voronoi图几何特性可知,点目标生成的Voronoi图所覆盖的二维平面范围称为势力范围(influence region,IR)[21],随着生长源(点目标)的不均匀分布,Voronoi图的势力范围亦发生变化,具体表现在生长源分布密集的区域,生成的Voronoi势力范围相对较小,反之,分布稀疏的区域,生成的Voronoi势力范围相对较大(见图 2),由此可得,Voronoi势力范围是表征其生长源聚集程度的标准之一。
综合以上两项标准,MSSC算法以点目标Voronoi图的邻近特性和势力范围共同判别点目标间的聚散特性,其中,Voronoi势力范围以Voronoi多边形面积进行量化,并通过定义面积标度值来判断Voronoi多边形的生长源是否聚集,则记该面积标度值为面积阈值σ,即:当两个相邻Voronoi多边形面积均小于面积阈值σ时,其生长源具有聚集性。
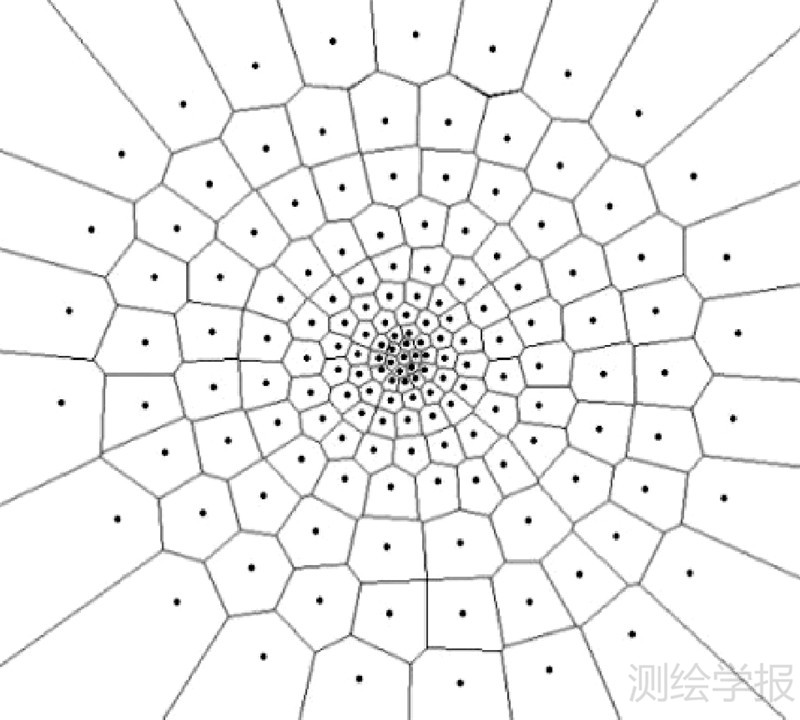 |
| 图 2 Voronoi图表征的生长源分布特征 Fig. 1 Distribution characteristics of generators are expressed by Voronoi diagram |
准则:设点目标集合P={p1,p2,…,pn}⊂R2,pi,∀pj∈P,且i≠j,记pi的Voronoi区域为V(pi),pj的Voronoi区域为V(pj),S(V(pi))、S(V(pj))分别为V(pi)和V(pj)的面积,若
成立,则点pi和pj具有聚集性,可划分为同一类。3 单一尺度的点目标聚类
MSSC算法中,σ值的选取决定了聚类的尺度,记:Smax、Smin分别是集合P的Voronoi多边形面积的最大值和最小值,则σ的取值情况为:当σ≤Smin,所有点目标各自成类;当σ≥Smax,所有点目标合为一类;当Smin<σ<Smax,点目标随σ值的变化实现多尺度的聚类,σ值越小,聚类粒度越细,类内归属信息越精确,但类间相似性越强;σ值越大,聚类粒度越粗,类间差异性越强,类内的相似性越低。
单一尺度下的点目标聚类选取固定的σ值,并根据准则1进行聚散性判断。输入全要素Voronoi图层VoronoiLayer,包含_Shape(目标几何信息)、_geoLyrName(特征点所属线面目标的图层名)、_geoLyrType(特征点所属目标的几何类型——点\线\面)、_geoFID(特征点所属线面目标的标识码),以及_geoArea(Voronoi面积)字段;输出图层ClustersLayer在VoronoiLayer基础上新增了_clusterID(类ID);_isCluster(记录点目标是否被分类)字段,具体算法如下。
算法1:Clustering{
(1) 初始化类编号clusterNum←1,isBoundaryFirst←True表示类的边界点首次被遍历,新建临时栈pStack←Null。
(2) 遍历VoronoiLayer图层中的Voronoi多边形,以k次遍历为例,若vk._geoLyrType=Point,说明该Voronoi区域是点目标生成,将其压入栈中,pStack←vk。
(3) 当栈非空,pStack=┐ ,出栈vj,若vj._isCluster=False,则:
,出栈vj,若vj._isCluster=False,则:
1) 若vj._geoLyrType=Point &&vj._geoArea≤σ,根据定义1,找到vj的自然邻居集合,并将该集合中_isCluster属性为False的Voronoi多边形压入栈pStack,vj._clusterID←clusterNum,vj._isCluster←True,isBoundaryFirst←False;
2) 若vj._geoLyrType≠Point &&vj._geoArea≤σ,根据定义1,找到vj的自然邻居集合,并将该集合中_isCluster属性为False的Voronoi多边形压入栈pStack,vj._isCluster←True,isBoundaryFirst←False;
3) 若vj._geoLyrType=Point &&vj._geoArea>σ&&isBoundaryFirst=False,则vj._clusterID←clusterNum,vj._isCluster←True;
4) 若以上条件皆不满足,Continue。
(4) clusterNum++,转至[2],第k次遍历结束。
(5) 直至遍历VoronoiLayer图层中所有对象,算法结束。}
ClustersLayer图层_clusterID字段值表示聚类的结果,同一_clusterID值的Voronoi多边形为同类,代表其生长源亦属同类。
4 多尺度点目标聚类
空间数据的分布具有相对尺度特征,在不同尺度上体现不同的数量级,尺度的大小亦与空间覆盖范围成正比,即感兴趣点的范围越小,相应的空间尺度越小,划分粒度越细,最小尺度下,每个点目标各自成类;反之亦然[20]。
4.1 多尺度下的Voronoi聚类
不同空间尺度下的Voronoi剖分对类(cluster)的判别标准不一致,如图 3所示,图(a)中空间尺度较大,Voronoi剖分的粒度较粗;随着空间尺度减小,图(b)在图(a)尺度聚类的基础上进行再聚类,细分图(a)中的每个子类(sub-clusters);同样,更小空间尺度的图(c)继续对图(b)中的子类再聚类,得到细粒度的聚类。由此可见,尺度变化实现了聚类粒度的逐层细分,并以Voronoi多边形边界划分类,揭示了更为全面的空间聚集规律。
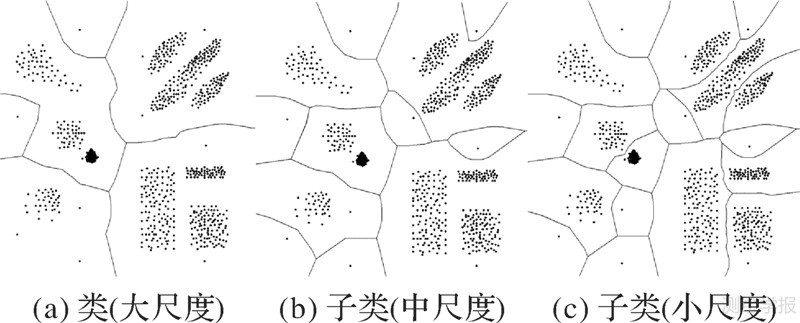 |
| 图 3 不同尺度下点目标粒度的Voronoi划分 Fig. 3 Points granularity is divided by Voronoi in different scales |
假设理想状况下,空间点目标集合P均匀分布,则以P为生长源构建的Voronoi图中所有Voronoi多边形的面积均相等,反之,当点目标位置分布存在空间异质性时,根据势力范围特性,其构建的Voronoi多边形面积大小随点目标的聚散特征呈规律变化。MSSC算法逐一计算不同类内点目标均匀分布时的面积阈值σ作为参考,并与其真实情况下非匀质分布时生成的Voronoi多边形面积进行比较,以判断点目标的聚散性。
面积阈值σ的计算根据初聚类与再聚类分为以下两种:
设点目标集合P={p1,p2,…,pn}R2,由集合P为生长源的Voronoi图集合V(P)={v1(p1),v2(p2),…,vn(pn)}⊂R2的面积为S(V)={s1(v1),s2(v2),…,sn(vn)},线面障碍集合O={o1,o2,…,om}⊂R2,由集合O为生长源的Voronoi图集合V′(O)={v′1(o1),v′2(o2),…,v′m(om)}⊂R2的面积为S′(V)={s′1(v′1),s′2(v′2),…,s′m(v′m)}。
定义2:全局平均面积(global mean area,GMA):假设理想状况下,所有点目标P均匀分布,则点目标势力范围的平均值称为全局平均面积GMA,其等于P的最小外包矩形MBR(P)减去O的Voronoi面积S′(V)之差,再除以点的个数
定义3:局部平均面积(partial mean area,PMA):设SP为P中一子类集合,SP={sp1,sp2,…,spk}⊂R2,假设子类中点均匀分布,则子类中点的势力范围的平均值称为局部平均面积PMA,其等于子类中点的Voronoi面积与子类中线面障碍的面积之差,再除以子类中点的数量
值得注意的是,σ取值主要是用于控制聚类的粒度,σ取值偏大时,不属于同类的点目标会被划分为一类;而σ取值偏小时,本属于同类的点目标会被划分开;σ分别取最大值、最小值时,点目标会全部融合成一类,或每个点目标独立成一类,显然是与聚类算法发现点目标典型聚集模式的初衷相悖,这就要求σ在合适的尺度收敛。此外,同一尺度下σ取值应根据不同子类的聚集模式自适应计算,非唯一值。针对以上两点需求,MSSC算法通过对σ值的处理实现多尺度聚类。
4.3 多尺度聚类的收敛条件
MSSC算法以面积阈值σ控制聚类的粒度,以σ值的变化趋势判断空间多尺度的收敛条件。主要表现为:σ的计算取决于类内点目标生成的Voronoi图的平均面积,即σ=PMA。根据点目标的Voronoi分布特征,当类内点目标非均匀分布时,聚集程度高的点目标生成的Voronoi图面积小于σ,即将该子目标划分为新的子类,在下一尺度计算新子类的PMA,继续聚类;当类内点目标均匀分布,无聚集趋势时,每个点目标生成的Voronoi图面积均大于或等于σ,保持原有分类,下一尺度计算该类的PMA时,值保持不变。由此可以判断:两个相邻尺度下σ值保持不变时,聚类停止,算法尺度收敛。
记空间尺度Λ={λ1,λ2,…,λm,…},可看作聚类的层数,不同尺度下,面积阈值集合Σ={σ1[],σ2[],…,σm[],…},子类集合SubCluster={SC[1][],SC[2][],…,SC[m][],…},对应的子类个数K={k1,k2,…,km,…},ki为大于等于1的任意整数,当相邻两个尺度下,若任一类的面积阈值保持不变,表示类内点目标已均匀分布,即不再产生子类,则聚类终止,MSSC算法的收敛条件为
文中字母黑体加粗与“[]”皆表示集合,尺度收敛过程如下:
(1) 初聚类时,λ1=1,σ1为点目标P的全局平均面积GMA(P),取唯一值,根据算法1进行聚类,得到子类集合SC[1][]={SC[1][1],…,SC[1][k1]};
(2) 再聚类时,λ2=2,先计算子类SC[1][]集合中每个子类的局部平均面积,即σ2[]={PMA(SC[1][1]),…,PMA(SC[1][k1])},若σ1≠σ2[],根据算法1分别进行SC[1][]子类集合中各子类的再聚类,得到子类集合SC[2][]={SC[2][1],…,SC[2][k2]};
(3) 继续再聚类至m尺度,λm=m,计算子类SC[m-1][]集合中每个子类的局部平均面积,即σm[]={PMA(SC[m-1][1]),…,PMA(SC[m-1][km-1])},若σm[]≠σm-1[],根据算法1分别进行SC[m-1][]子类集合中各子类的再聚类,得到子类集合SC[m][]={SC[m][1],…,SC[m][km]},重复过程(3);若σm[]=σm-1[],算法结束,λm-1为点集P聚类的最小尺度。
算法2Multi-Scale Spatial Clustering {
(1) 初始化变量isFirstClustering←True,表示为初聚类。
1) 若isFirstClustering=True,σ值为所有点目标的全局平均面积,σ1=GMA(P),执行算法1,isFirstClustering←False。
2) 若isFirstClustering=False,以尺度λm为例,σm[]为λm-1尺度下得到的各个子类局部平均面积的集合,若σm[]≠σm-1[],对每个子类执行算法1;若σm[]=σm-1[],说明σ已收敛,算法结束,点集P聚类的最小尺度为m-1。}
4.4 MSSC算法的时间复杂度
纵观MSSC算法结构,构建全要素Voronoi的时间复杂度为O(nlognn),n为特征点的个数;算法1的时间复杂度为O(n);算法2中多尺度聚类的是对类的逐层细分,其结构类似于二叉树,当聚类最小尺度为m时,时间复杂度为O(mlogm)。综合考虑MSSC算法的时间复杂度为O(nlogn)+O(n)+O(mlogm),但一般情况下,m远远小于n,则MSSC算法的时间复杂度为O(nlogn)。
5 试验与讨论
试验采用真实数据与模拟数据对MSSC算法的可行性、稳定性进行验证与讨论。
5.1 MSSC算法的可行性
选取典型高原湖泊星云湖上游支流区域作为研究区,空间数据集为Gauss-Kruger投影,西安80参心坐标系,1∶10 000比例尺。在研究区范围内,提取河流、湖泊分别作为线、面目标约束,并按50 m间隔对等高线抽样生成点目标数据(见图 4),从单一尺度综合线面目标聚类与多尺度聚类的自适应收敛考虑,并对比已有聚类算法进行验证。
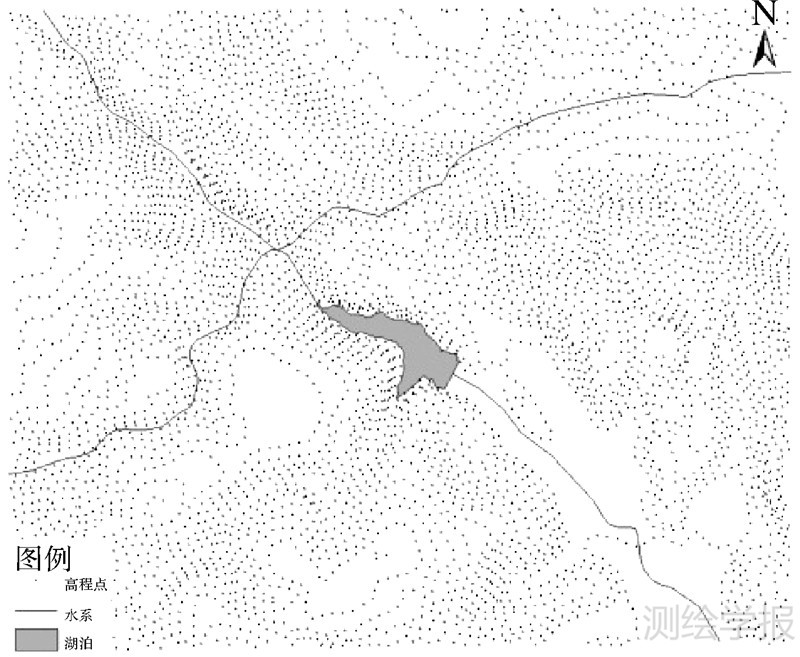 |
| 图 4 研究区空间数据 Fig. 4 Spatial data of research region |
单一尺度综合线面目标聚类。试验选取点目标的最粗聚类粒度作为衡量标准,采用聚类算法k-means[23]、k-medoids[24]、CLARANS[1]以及BIRCH[25]对高程点目标聚类,当预设最终聚类数目k=1(最小值),所有点目标被划分为一类,难以顾及线面目标对空间点集的约束。而客观世界中高程点被河流与湖泊划分,MSSC算法通过构建全要素Voronoi图判断点线面目标间的邻近关系(见图 5),取点目标Voronoi面积的最大值作为面积阈值(σ=80 181.24 m2)进行聚类,将点目标自动划分为4类(见图 6),以不同形状和颜色的点集表征不同的类别,准确识别了线面目标对点目标聚类的划分。
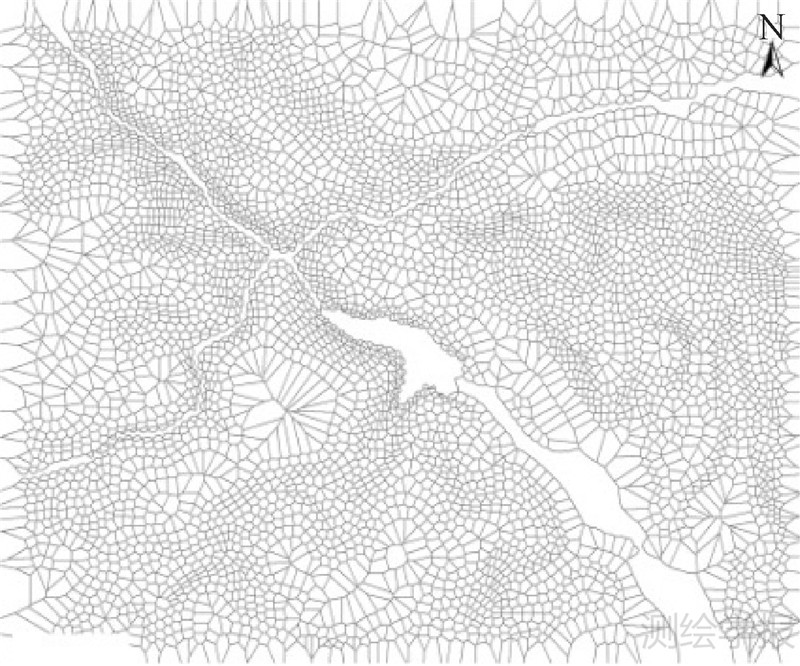 |
| 图 5 全要素Voronoi图 Fig. 5 Voronoi diagram with all features |
 |
| 图 6 综合线面特征聚类 Fig. 6 Clustering with lines and polygons |
多尺度聚类的自适应收敛。现有多尺度聚类算法对尺度的控制范围过大,尺度变化从每个点目标单独成类至所有点目标合为一类,难以准确预定义能够识别点目标典型聚集模式的适合尺度,主观性强。试验采用MSSC算法对研究区点目标聚类,算法在λ=9时收敛,发现79类有聚集趋势的点目标集群,但为说明尺度收敛过程,选取11个空间尺度、4个典型聚类进行分析。图 7中4条折线分别表示4个典型类在11个空间尺度下的面积阈值变化情况,图 8为4个典型类在λ=1,5,9时的聚类情况。
 |
| 图 7 面积阈值与空间尺度的关系 Fig. 7 The relationship between area threshold and spatial scale |
就整体而言,λ= 1时,σ=取全局平均面积GMA(3 142.232 3 m2),λ= 2,3,…,11时,σ=根据子类中点目标的不同分布计算不同子类的局部平均面积,σ==PMA,σ=值随空间尺度的减小而逐渐减小,并在特定的空间尺度之后保持不变。具体而言,Cluster 1、Cluster 2、Cluster 3、Cluster 4的σ=值分别在λ= 9、λ= 7、λ= 6、λ= 6之后恒定,σ=值不变表示聚类粒度不再改变,类的数量不再增加,聚类结束,即验证了算法在两个相邻空间尺度下σ=值不变时达到收敛。
综合以上验证,算法针对真实数据的处理是有效且可行的。另从线面约束形态上看,MSSC算法能精确识别不规则形态的线面目标,不受多边形凹凸的限制,优于通过简化线面目标进而测算点目标绕行障碍物距离来判断点目标聚类的COD-CLARANS[4]、DBCluC[5]等算法;从聚类形态而言,MSSC算法聚类粒度随空间尺度的减小而细化,可以识别分布相对密集且任意形态的点目标集群(见图 8)。
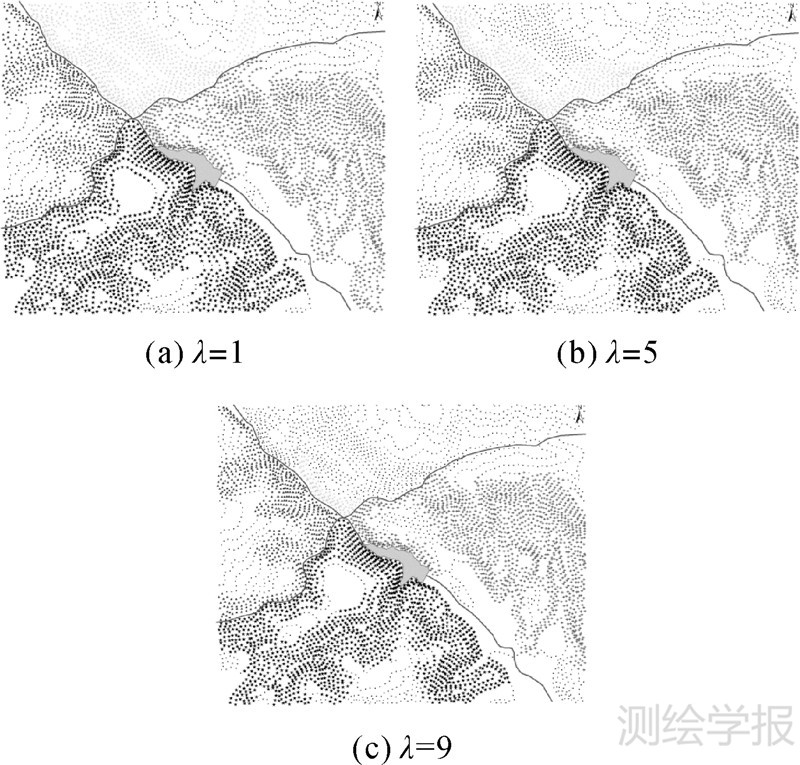 |
| 图 8 不同空间尺度下的MSSC算法聚类结果 Fig. 8 Clustering result of MSSC algorithm in different spatial scales |
聚类算法的稳定性要求算法对空间异常值(噪声)的存在不敏感。二维空间数据聚类中的异常值主要表征为受聚类中心影响较小,不具有聚集趋势的空间点目标[18],而稳定的聚类算法需要能够识别异常值且聚类结果不受异常值影响。
试验在真实高程点数据集外围8个方向加入不具有聚集趋势的8个异常数据点,采用MSSC算法在σ=80 181.24 m2时进行聚类(见图 9),结果显示:8个异常点因远离高程点,使得其生成的Voronoi图面积远远大于具有聚集趋势的高程点生成的Voronoi图面积,且当异常点数目远小于高程点数目时,异常点的Voronoi图面积远大于高程点集的Voronoi图面积的平均值,MSSC算法将Voronoi面积小于σ的点目标进行聚类,大于σ被单独识别,判断为异常值,对比图 6,异常值对高程点目标的聚类不产生影响。
 |
| 图 9 异常值的识别 Fig. 9 Distinguish outliers from points |
MSSC算法利用全要素Voronoi剖分准确地识别了空间点线面目标的邻近关系,对河流、湖泊、建筑物等具有阻碍点目标空间连续性的障碍物的处理符合人类的空间认知习惯;根据点目标分布特征自适应地计算σ值,以其数值控制聚类的粒度,以其变化规律控制尺度的收敛,能够发现空间点目标的典型聚集模式;聚类过程中对异常值处理稳健,无须自定义参数。
MSSC算法适用于发现客观世界中表征地形、气候、经济、人口等位置分布的离散数据点聚集模式,进而解译隐含规律。结合试验对高程点的聚散特征分析,被聚类的高程点表征了地形起伏较大的区域,尺度收敛的速率亦体现了空间数据分布异质性的强弱,相关问题亟待进行下一步实证分析研究。
| [1] | NG R T, HAN J W. Efficient and Effective Clustering Methods for Spatial Data Mining[C]//Proceedings of the 20th VLDB Conference. Santiago, Chile:[s.n.], 1994: 144-155. |
| [2] | ESTIVILL-CASTROV, LEEI. AUTOCLUST+: Automatic Clustering of Point-data Sets in the Presence of Obstacles[C]//Proceedings of the 1st International Workshop on Temporal, Spatial and Spatio-temporal Data Mining. Berlin: Springer-Verlag, 2001: 133-146. |
| [3] | LEUNG Y, ZHANGJ S, XUZ B. Clustering by Scale-space Filtering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(12): 1396-1410. |
| [4] | TUNG A K H, HOU J, Han J W. Spatial Clustering in the Presence of Obstacles[C]//Proceedings of the 17th International Conference on Data Engineering. Heidelberg: IEEE, 2001: 359-367. |
| [5] | ZAIANE O R, LEE C H. Clustering Spatial Data when Facing Physical Constraints[C]//Proceedings of the 2002 IEEE International Conference on Data Mining. Maebashi City, Japan:IEEE, 2002: 737-740. |
| [6] | FAN B. A Hybrid Spatial Data Clustering Method for Site Selection: The Data Driven Approach of GIS Mining[J]. Expert Systems with Applications, 2009, 36(2): 3923-3936. |
| [7] | YANG Yang, SUN Zhiwei, ZHAO Zheng. Density-based Spatial Clustering Method with Obstacle Constraints[J]. Computer Applications, 2007, 27(7): 1688-1691. (杨杨, 孙志伟, 赵政. 一种处理障碍约束的基于密度的空间聚类算法[J]. 计算机应用, 2007, 27(7): 1688-1691.) |
| [8] | CAO Keyan, WANG Guoren, HAN Donghong, et al. Clustering Algorithm of Uncertain Data in Obstacle Space[J]. Journal of Frontiers of Computer Science and Technology, 2012, 6(12): 1087-1097. (曹科研, 王国仁, 韩东红, 等. 障碍空间中不确定数据聚类算法[J]. 计算机科学与探索, 2012, 6(12): 1087-1097.) |
| [9] | WANG Min, ZHOU Chenghu, PEI Tao, et al. MSCMO: A Scale Space Clustering Algorithm Based on Mathematical Morphology Operators[J]. Journal of Remote Sensing, 2004, 8(1): 45-50.(汪闽, 周成虎, 裴韬, 等. MSCMO: 基于数学形态学算子的尺度空间聚类方法[J]. 遥感学报, 2004, 8(1): 45-50.) |
| [10] | KONG Juan, XU Futian, XUE Qingfeng. Clustering Algorithm Based on Mathematical Morphology in the Presence of Obstacles[J]. Computer Knowledge and Technology, 2008, 4(9): 2923-2925. (孔娟, 徐夫田, 薛庆峰. 基于数学形态学的带障碍约束的空间聚类算法研究[J]. 电脑知识与技术, 2008, 4(9): 2923-2925.) |
| [11] | ESTIVILL-CASTROV, LEEI. Clustering with Obstacles for Geographical Data Mining[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2004, 59(1-2): 21-34. |
| [12] | SHI Yan, LIU Qiliang, DENG Min, et al. A Novel Spatial Clustering Method with Spatial Obstacles[J]. Geomatics and Information Science of Wuhan University, 2012, 37(1): 96-100. (石岩, 刘启亮, 邓敏, 等. 一种顾及障碍约束的空间聚类方法[J]. 武汉大学学报: 信息科学版, 2012, 37(1): 96-100.) |
| [13] | LIUD Q, NOSOVSKIYG V, SOURINAO. Effective Clustering and Boundary Detection Algorithm Based on Delaunay Triangulation[J]. Pattern Recognition Letters, 2008, 29(9): 1261-1273. |
| [14] | EDLA D R, JANA P K. A Novel Clustering Algorithm Using Voronoi Diagram[C]//Proceedings of the 7th International Conference on Digital Information Management. Macau: IEEE, 2012: 35-40. |
| [15] | XUE Lixia, WANG Linlin, WANG Zuocheng, et al. Spatial Clustering in the Presence of Obstacles Based on Voronoi Diagram[J]. Computer Science, 2007, 34(2): 189-191. (薛丽霞, 汪林林, 王佐成, 等. 基于Voronoi图的有障碍物空间聚类[J]. 计算机科学, 2007, 34(2): 189-191.) |
| [16] | LUO Jiancheng, YEE Leung, ZHOU Chenghu. Scale Space Based Hierarchical Clustering Method and Its Application to Remotely Sensed Data Classification[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(4): 319-324. (骆剑承, 梁怡, 周成虎. 基于尺度空间的分层聚类方法及其在遥感影像分类中的应用[J]. 测绘学报, 1999, 28(4): 319-324.) |
| [17] | CHEN Xiaoyu. A Study of Economic Regionalization Based on Multiscale Spatial Clustering[J]. Journal of Chongqing Normal University:Natural Science, 2011, 28(5): 81-84, 92. (陈小瑜. 基于多尺度空间聚类的经济区域划分研究[J]. 重庆师范大学学报: 自然科学版, 2011, 28(5): 81-84, 92.) |
| [18] | ESTIVILL-CASTROV, LEEI. Amoeba: Hierarchical Clustering Based on Spatial Proximity Using Delaunay Diagram[C]//Proceedings of the 9thInternational Symposium on Spatial Data Handling. [S.l.]: IGU Study Group on Geographical Information Science, 2000: 1-16. |
| [19] | SHI Peibei, GUO Yutang, HU Yujuan, et al.Multiscale Spectral Clustering Algorithm[J]. Computer Engineering and Applications, 2011, 47(8): 128-130. (施培蓓, 郭玉堂, 胡玉娟, 等. 多尺度的谱聚类算法[J]. 计算机工程与应用, 2011, 47(8): 128-130.) |
| [20] | FU Lihua, LI Hongwei, ZHANG Meng, et al. Multi-scale Radial Basis Function Networks with Multiple Kernels[J]. Journal of Huazhong University of Science & Technology:Nature Science Edition, 2010, 38(1): 39-42. (付丽华, 李宏伟, 张猛, 等. 带多个核函数的多尺度径向基函数网络[J]. 华中科技大学学报: 自然科学版, 2010, 38(1): 39-42.) |
| [21] | CHEN Jun. Voronoi Dynamic Spatial Data Model[M]. Beijing: Surveying and Mapping Press, 2002. (陈军. Voronoi动态空间数据模型[M]. 北京: 测绘出版社, 2002.) |
| [22] | GOLD C M. Dynamic Spatial Data Structures:The Voronoi Approach[C]//Proceedings of the 1992 Canadian Conference on GIS.Ottawa:CIG, 1992: 245-255. |
| [23] | MACQUEEN J. Some Methods for Classification and Analysis of Multivariate Observations[C]//Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability. Berkley:[s.n.],1967: 281-297. |
| [24] | HAN J W, KAMBER M. Data Mining: Concepts and Techniques[M]. Beijing: China Machine Press, 2001. (HAN J W, KAMBER M. 数据挖掘: 概念与技术[M]. 北京: 机械工业出版社, 2001.) |
| [25] | ZHANGT, RAMAKRISHNAN R, LIVNY M. BIRCH: An Efficient Data Clustering Method for Very Large Databases[C]//Proceedings of the 1996 ACM SIGMOD International Conference on Management of Data.New York: ACM, 1996: 103-114." |