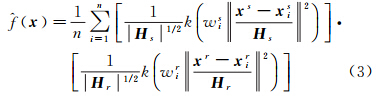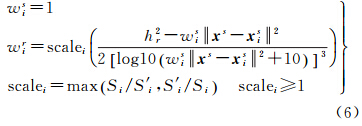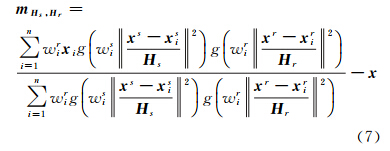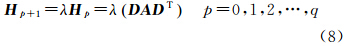2. 武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉 430079
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China
1 引 言
车载全景影像的匹配是研究由移动测量车获取,具有高重叠度全景序列影像间识别同名点的方法,其成果主要应用于街景目标识别与三维重建[1, 2]。目前主要方法为基于相关法(或光流跟踪)的灰度匹配[3, 4]和核线约束的特征匹配[1, 2, 5, 6]。由于车载全景影像具有宽视域和街景地物复杂等特性,对于全景影像的匹配主要存在以下问题:①建筑物等重复性纹理;②序列影像间的同名点存在光照、旋转和尺度等变化特性;③360°的全景地物之间匹配方向的复杂性;④静态和动态地物共存,在道路中间或两侧产生“移动噪声”。因此采用灰度匹配法很难解决上述问题,如受重复性纹理影响,灰度匹配方法的误匹配率很高。虽然特征匹配具有光照、旋转和尺度等不变特性,结合核线几何的约束算法具有一定的稳键性,但仍存在全景核线几何模型无法准确估计问题[7]。
为了提高车载全景特征匹配的稳键性,文献[8]提出了一种光流聚类的特征匹配方法,认为稳定的特征匹配点,其一定领域范围内的特征点也同样具有相关性的特征,而这种相关性在全景序列影像中表现为局部运动结构特征的一致性。在此假设的基础上,利用特征空间中对应的显著图像光流特征为聚类条件,采用非参数化的均值漂移算法求解局部运动一致性的特征点,分SIFT初匹配和光流聚类约束匹配两步实现车载立方体全景序列影像的匹配。但由于核密度估计中的带宽参数是一个固定的经验值,很难适应不同场景间的运动结构在尺度和方向上的变化,影响聚类匹配的准确性。核密度函数的自适应带宽研究,多应用于图像分割和视频跟踪领域,主要方法有基于全局统计和基于局部统计的自适应带宽法[9, 10, 11, 12, 13]。由于采样点包含多种模态时,一般很难计算出全局最优带宽,因此目前主要采用局部自适应带宽计算方法。如文献[14]统计一系列固定带宽中局部模型最稳定的均值和协方差参数,取均值漂移向量模值为最大值时的最小二乘协方差解为最优自适应带宽,但该方法必须知道尺度的取值范围,且增加了计算复杂度。理想的带宽域作用范围应该是正好包括同一类的样本点,但在实际应用中往往简化该过程,如图像分割应用中,文献[15]认为局部自适应带宽反比于局部密度估计的平方根。文献[16]定义一个邻域,采用相关性找到最佳邻域点,将其距离定义为该点的带宽。文献[17]提出了医学图像分割的局部自适应带宽等于k个近邻采样点与样本点特征向量差的一阶范数。视频跟踪应用中,文献[18]提出通过增加一个额外的尺度核,在定义的离散尺度空间中进行均值漂移迭代,从而找到最佳的核带宽。文献[19]采用正负10%的增量分别对核带宽进行修正,取3次跟踪结果中最佳相似度量的带宽为最佳值,但该方法经常会在较小的跟踪窗口中达到局部最大。
综上,局部密度估计每个采样点相对于样本点的带宽,计算方法复杂[14, 15, 16, 17],带宽增量法无法准确估计每个采样点的带宽大小,但计算效率高[18, 19]。本文匹配方法中的自适应带宽计算,综合考虑以上两种方法的优点,主要贡献如下:①建立一种基于SIFT描述特征和运动结构特征的统一匹配框架,利用均值漂移算法求解最优匹配点的运动结构;②分析球全景影像空间域和光流域的相似性分布特征,考虑多维数据间的关系和粗差影响,局部光流特征表现为一种高斯分布下的距离加权过程,定义一种可变带宽的自适应加权核密度函数。考虑均值漂移算法容易陷入局部振荡问题,给出一种种子点选择的简单方法。
2 自适应运动结构特征的车载全景序列影像匹配方法 2.1 光流特征聚类算法
文献[8]将局部光流的相似性运动结构,表达为特征匹配结果在影像空间中的显著光流特征的聚类过程。采用非参数化的均值漂移聚类思想,以SIFT多尺度特征匹配点的位置量和光流矢量,构建影像特征空间的空域和值域,利用特征空间中对应的显著图像光流特征为聚类条件,实现全景序列影像的匹配。在四维空间R4中,给定n个采样点xi,则点xi处的多变量核密度估计器(x)由下式给出
式中,k(x)是归一化的高斯核轮廓函数;h代表空域和值域具有相同的核(带宽)大小;xs、xr分别是二维的特征空域向量和二维的特征值域向量,空域xs由左视影像SIFT特征点的位置坐标定义为(u,v),值域xr由立体影像SIFT匹配点对(u,v)、(u′,v′)的光流矢量,在水平和垂直方向的变化量定义为(du,dv)。因此,采样点x可表达为一个加权的四维特征向量[w1u′w2vw3du′w4dv]。2.2 可变带宽的自适应匹配算法
由于核密度函数的带宽大小决定了均值漂移算法的收敛速度和精度,而且固定权无法准确描述每个采样点在特征空间中的相互作用。分析球全景影像空间域和光流域的相似性分布特征,运动结构相似性度量可采用加权自适应带宽的核密度函数,公式表达如下
式中,wis、wir分别代表空间域和光流域的权函数;Hs、Hr分别代表空间域和光流域的可变带宽矩阵。2.2.1 可变带宽矩阵的定义
文献[20]定义了每个采样点Xi的带宽矩阵为Hi=λDADT,其中λ为窗口大小的尺度因子;D为特征差异矩阵;A为正规化对角矩阵,表达核空间大小。Hi刻画了每个采样点窗口形状和样本点之间的各向异性,但实际上增加了计算量,且该值无法根据局部邻域采样点准确计算。考虑全景影像的特征空间规律,提出一种简易的表达方法,认为物方相邻区域内地物的局部相似性特征,表现为投影到像方的局部空间结构,局部区域内每个采样点均用一个统一的二维带宽矩阵H定义,而其尺度因子λ表达为局部区域的一个可变增量因子,这里暂时不考虑(见2.2.3节); θ表达为局部区域的一个二维旋转矩阵;A表达为核密度函数两个轴的作用域大小,因此H描述了一个局部区域在像方进行仿射变换的过程。通过分析全景影像局部相似性特征的分布形态,就可以近似定义以上参数。
θ表达为局部区域的一个二维旋转矩阵;A表达为核密度函数两个轴的作用域大小,因此H描述了一个局部区域在像方进行仿射变换的过程。通过分析全景影像局部相似性特征的分布形态,就可以近似定义以上参数。
目前主流的车载全景相机,大多由组合式球面相机构成,可生成基于球成像模型的全景序列影像数据。如图 1为连续拍摄的两幅球全景立体影像对,宽高大小为5400像素×2700像素。该影像主要由前后左右4个视图场景组成,相邻序列影像间构成核线几何关系,核点近似落在前后视图的中心位置[3]。采用SIFT特征点提取算法[21],生成球全景影像的特征点(即采样点)。图 2显示了图 1(a)影像1的SIFT特征采样点在空间域的分布,可以看出采样点分布形态与街景地物的分布相关,地物的形态又受球面投影的畸变影响,而畸变的方向近似表现为全景的核线方向,因此采样点主要集中在建筑物场景的中间区域,呈现以中间极点为分割的两个鱼眼形态,局部形态随聚类中心的位置变化,其空间形状也随之变化,并与球全景核线方向一致。由于匹配点间光流方向可近似表达核线方向[7],因此核密度函数的局部空间结构可以描述为与光流方向一致,靠近极点区域,核大小在水平u方向相比垂直v方向压缩严重,中间区域核大小近似相等。
 |
| 图 1 球全景立体影像 Fig. 1 Sphere panoramic stereo images |
 |
| 图 2 球全景影像采样点的空间域分布(数据见图 1(a)) Fig. 2 Spatial domain distribution of sampling point for panoramic image |
空间域方向因子Ds可以通过统计局部区域光流的方向直方图来确定,用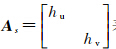 表达空间域(u,v)的核大小,则空域局部带宽Hs可以表达为如下形式
表达空间域(u,v)的核大小,则空域局部带宽Hs可以表达为如下形式
图 3显示了全景序列影像间光流域的空间分布,可以得出以下规律:图 3(a)、(b)为经过粗差处理后的稳健特征匹配结果,横轴u代表图像的列(即水平方向位移),纵轴du、dv分别代表两幅序列图像间光流矢量在水平和垂直方向上的变化量。图 3(a)为u方向上的光流变化量du的分布,可以发现极点处(u=0,2700,5400)是du的变化拐点,du整体变化剧烈(约为-250~300像素);在极点附近,局部窗口(如200像素×200像素)变化幅度在100像素左右,而中间区域非常平缓,一般小于3像素。图 3(b)为u方向上的光流变化量dv的分布,极点处也是dv的变化拐点,但dv整体变化较缓(约为-50~50像素),在极点附近,局部窗口变化幅度在10个像素以内,而中间区域与du规律一致变化较为平缓。图中的零星跳跃点代表在v方向上(即垂直方向位移),有深度变化的前景或后景特征点,但局部窗口内,光流的变化仍然满足上述规律。
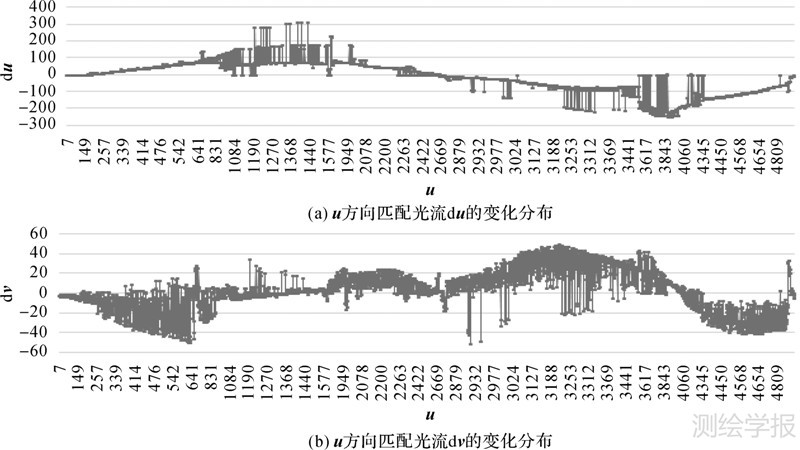 |
| 图 3 全景序列影像间的光流域分析 Fig. 3 The Optical flow domain analysis for panoramic images sequence |
综上,前后视图区域,光流的变化具体表现为du相比dv更剧烈,可以拉伸u方向带宽,形成一个近似垂直方向扁椭圆特征核,通过控制椭圆的两个半轴比率近似表达du和dv光流矢量变化。左右视图区域,du和dv的变化相对稳定,因此可以采用局部圆表达。而核作用域方向上基本保持水平和垂直方向不变,即方向因子D为单位矩阵。车载移动测量系统在数据采集过程中,为保证数据获取的质量,一般测量车沿道路方向匀速运动,且采样间隔短,局部光流矢量的聚类特性并不随着数据而产生太大变化,呈现上述的统一规律,因此定义光流域局部带宽为式(5),其中对角线因子αdu、αdv分别为du、dv方向核大小hr的比例阈值,可以通过统计局部光流矢量幅度直方图确定。
2.2.2 权函数的定义权函数定义的好坏直接影响空间域和光流域的平滑性和边界条件。全景影像的匹配以光流运动结构的相似性占优为主要原则,定义如下选权规则:
(1) 光流相似性约束为主要匹配条件。由于匹配特征的离散性,均值漂移受空间域影响很大,容易陷入局部位置最优,为此设置光流域权值更大。另外该原则可以放大错误光流的差异性,增强聚类对于粗差检测的分离性。
(2) 松弛加权原则。与分割等目的不同,为获得更多的邻域特征来支撑运动结构的一致性特征,需要构建一种松弛的运动一致性邻域扩散方法,通常采用距离加权法。
(3) 尺度一致性原则。像方正确的匹配点表现为物方上的尺度相似性,可有效地避免尺度空间内不稳定匹配点。而匹配点的尺度由物方尺度和相机主距决定,无法准确获得,但我们可以定义尺度的相似性比值因子scalei来近似表达这种一致性。scalei表达为匹配点尺度(Si,S′i)的最大比值,越接近1代表越相似。
综上,分别定义式(3)中空间域和光流域的权函数为如下形式
2.2.3 均值漂移向量求解与终止条件
(1) 均值漂移向量求解。由式(3)-式(6)求解概率密度的最大梯度,其中影子核g(x)=-k′x,可得自适应加权带宽的均值漂移向量为
(2) 均值漂移算法终止条件定义。定义一个统一的尺度因子λ,可变带宽的均值漂移过程采用带宽增量法,由式(4)、式(5)定义第p+1次带宽Hp+1,见式(8)
式中,Hp=0作用域的初始局部采样点由经验值h0定义,采用巴氏距离度量增量前后的概率分布相似性[13]。2.2.4 种子点的定义方法
均值漂移算法中初始聚类中心(即种子点)的选择好坏,将影响算法的收敛性。建立一种简单种子点的待选方法如下:
(1) 以每个采样点为中心,建立一个半径为Rs的搜索圆,根据采样点的平均密度,确定最近邻点数阈值kT
式中,N为采样点总数;A为影像面积;Rs为采样点的邻域半径。(2) 统计每个采样点kT个最近邻点,并计算其到该采样点的欧氏距离,取邻域采样点的平均距离为该采样点的初始密度参数,平均距离越小代表该采样点的密度越大。
(3) 按平均距离从小到大进行排序,作为初始聚类待选种子点的密度参数。
2.3 自适应匹配流程
将灰度特征匹配与运动结构几何特征匹配融合在一个匹配框架中,已知具有一定重叠度的两幅全景影像(I和I′),则本文自适应匹配算法流程如下:
(1) 影像I上提取采样点。采用角点、SIFT等方法在尺度空间提取足够多的初始特征点作为采样点,并建立SIFT描述子。
(2) 构建种子待选点。按2.2.4 节描述方法,取Rs=50构建影像I初始特征点的密度参数。
(3) 初始特征匹配。选择最大密度种子点为中心,影像I、I′上分别取初始带宽h0和2h0的窗口。在影像I′窗口内采用步骤(1)相同方法提取和描述特征点,并进行影像I、I′窗口内特征点的相似性度量。相似性度量方法仍然采用128维特征向量的距离度量,通过设置一个比较宽松的最小距离比值SIFT_ratio1(一般设置为0.6~0.9)获取初始匹配点。
(4) 自适应运动结构特征计算。利用步骤(3)匹配点构建四维特征向量,在初始窗口内统计局部带宽的空间结构因子,利用式(4)、式(5)计算空域和光流域的当前最佳带宽Hp,利用式(6)计算wi,采用式(7)求解均值漂移向量可得最佳均值中心。
(5) 以步骤(4)的最佳均值中心为种子点,按式(8)计算可变带宽Hp+1,重复步骤(3)、(4)。采用巴氏距离度量增量前后匹配点的相似性分布,直到差异性大于某个阈值为止,并标记聚类的特征点。
(6) 在未标记的特征点中,寻找下一个最大密度种子待选点,重复步骤(3)、(4)、(5),并判断是否合并聚类,即聚类中心小于某个阈值合并聚类,直到所有特征点被标记后,程序终止。
(7) 匹配粗差筛选。判断聚类点数小于阈值T的聚类为可能的粗差点,即与邻域运动结构不一致的聚类点。在此基础上反向判断其特征度量,当有一个特征点对应的最小距离比值大于SIFT_ratio2阈值时(一般设置为0.1~0.4),则认定聚类内的点均为粗差点。
3 试验及其结果分析
试验采用拓普康IP-S2车载移动测量系统,获取某城市街景的球全景序列影像,影像数据的采样间隔大约为2m,宽高大小为5400像素×2700像素,主距为3.3mm,像元大小为4.4μm(H)×4.4μm(V)。采用正确匹配点数和正确匹配率指标评价试验结果。算法中涉及的参数,由经验值给出:h0=50、SIFT_ratio2=0.1、hu=hv=hr=h0、λ=1.5、q=4。
3.1 不同内点率下的匹配试验
选择建筑物密集区的两幅球全景立体像对(见图 1),通过控制2.3节步骤(3)中相似性度量的比值参数,可以近似模拟出不同内点率[16]的初始匹配结果。这里设定比值参数SIFT_ratio1为0.6和0.9,分别代表高内点率和低内点率两种情况。固定带宽参数设置为:h=50、100、150、250。
图 1(a)、(b)显示两幅经过球投影的全景拼接影像,可以看出建筑物存在大量的墙面和窗户等重复纹理特征,图 2为影像1提取的24549个初始特征点。特征点在建筑物区域非常密集,但受道路均质特征的影响,特征点较稀疏。图 4为初始特征点对应的密度参数分布图(Rs=50),为了直观地显示种子待选点的密度分布情况,采用Renka Cline三角网内插方法生成密度分布等高线图,其中密度采用16级灰度分类显示,从黑到白代表密度从高到低,无特征区域的密度参数采用内插估计方法仅为显示用。对比图 2和图 4,可以看出本文种子点的初始密度估计还是比较准确的,为增量法可变带宽提供了可靠的初始均值中心,可有效提高算法的收敛性和精度。
 |
| 图 4 种子点密度参数分布图(Rs=50) Fig. 4 The initial feature points and seed point density parameter distribution |
表 1、表 2显示不同内点率下,固定带宽与本文自适应匹配的统计对比结果。表 1为高内点率情况(SIFT_ratio1=0.6)。首先观察固定带宽下的匹配表现,随着带宽的增大,平均聚类方差、匹配点数和正确匹配点数均增大,但正确匹配率在减少。这是因为随着影像1带宽的增大,影像2中的匹配窗口随之按比例放大,可获得更多的匹配点,但也提高了重复性纹理等粗差的概率,因此匹配率下降。本文提出的自适应方法、加权自适应方法在各项指标中均表现较好,总体平衡了正确匹配点数和匹配率之间的关系,在保证较高正确匹配率的基础上,又获得了较高的正确匹配点数。另外匹配精度与聚类阈值T相关,在高内点率情况下,T越小,匹配点数和匹配率更好,而且试验发现本文方法对于T的依赖性相比固定带宽更弱。建议在高内点率情况下T取值范围为1~5,说明在加权自适应匹配中,随着带宽的增大,粗差也随之增大,但通过光流运动结构的加权,提高了寻找正确聚类中心的概率,因此可以很好地控制聚类的精度,达到自适应控制粗差的目的。
| 带宽 | 平均方差 | 初始聚类/ 匹配聚类 | 匹配结果 | ||
| 匹配 点数 | 正确匹配 点数 | 正确 匹配率 | |||
| 50(T=5) | 512.540 | 622/244 | 2626 | 2611 | 0.994 |
| 100(T=5) | 2100.202 | 259/111 | 3054 | 3020 | 0.989 |
| 150(T=5) | 4527.395 | 174/79 | 3158 | 3115 | 0.986 |
| 250(T=5) | 9861.832 | 114/48 | 3217 | 3164 | 0.984 |
| 自适应(T=5) | 2270.157 | 260/92 | 3082 | 3048 | 0.989 |
| 加权自适应(T=5) | 2512.272 | 286/101 | 3065 | 3036 | 0.991 |
| 加权自适应(T=1) | 2512.272 | 286/136 | 3176 | 3147 | 0.991 |
| 带宽 | 平均方差 | 初始聚类/ 匹配聚类 | 匹配结果 | ||
| 匹配 点数 | 正确匹配 点数 | 正确 匹配率 | |||
| 50(T=12) | 142.109 | 3346/140 | 2402 | 2379 | 0.990 |
| 100(T=12) | 374.226 | 2783/103 | 3800 | 3747 | 0.986 |
| 150(T=12) | 686.054 | 2571/73 | 4152 | 4085 | 0.984 |
| 250(T=12) | 1816.470 | 2270/45 | 4431 | 4280 | 0.966 |
| 自适应(T=12) | 279.097 | 2813/86 | 3984 | 3922 | 0.984 |
| 加权自适应(T=12) | 384.470 | 2822/99 | 4034 | 3994 | 0.990 |
| 加权自适应(T=5) | 356.297 | 2822/125 | 4260 | 4176 | 0.980 |
表 2为低内点率情况(SIFT_ratio1=0.9)。可以看出本文自适应匹配的方法,在抗粗差方面表现十分出色,正确匹配点数和匹配率优势非常明显。对比表 1和表 2的统计结果,本文方法正确匹配率并没有受内点率的变化影响,表 1加权自适应法(T=5)为99.1%,表 2加权自适应法(T=12)为99.0%,但在内点率很低的情况下获得了更多的正确匹配点数,正确匹配点数从3036个增加到3994个,多获取了近1000个正确匹配点。由于低内点率下粗差也有可能表现为大聚类的特征,因此应适当增大聚类阈值T,试验表明在低内点率情况下,阈值变化范围以5~12为宜。
图 5为低内点率下的匹配聚类结果(显示为匹配点间的位移矢量线)与影像1叠加显示图。图 5(a)-5(d)显示不同固定带宽下的匹配结果,不同聚类采用颜色区分,即每一种聚类代表其采样点具有局部运动结构的相似性特征。对比红色矩形框标识区域,可以发现随带宽增加每个聚类半径增大,包含了更多的特征点。以“A”标识区域为例(对应影像区域见图 5(e)),在物方为一独立建筑物,但相对于像平面的垂直方向有一点向右倾斜,按深度方向可分为左、中、右3个子区域,各子区域表现为近似共面特征。建筑物在像方的投影,基本位于全景影像左视图的正中心位置,该区域光流运动较为稳定,光流方向近似平行于水平方向,并有轻微向右倾斜,大小随深度不同(3个子区域)有轻微的变化。对比固定带宽匹配结果,可以很明显地看出,带宽过小造成的过分类现象(h=50),有17个聚类。带宽过大造成的过平滑现象(h=250),丢失了精度,仅1个聚类。加权自适应带宽获得4个聚类,在保证精度基础上,较准确地表达了该区域的真实结构特征,而且本文算法中的加权自适应终止条件与运动结构的精度相关,可以根据精度要求来修改自适应条件。图 5(g)和图 5(h)为本文加权自适应匹配前后的聚类结果显示,从“C”标识区域的放大图可以看出低内率下的粗差非常复杂,但本文算法表现了极强的粗差检测能力和算法的稳键性。
 |
| 图 5 固定带宽与自适应匹配结果 Fig. 5 Fixed and adaptive matching results |
3.2 序列数据的匹配试验
本文车载序列影像数据的相机采样间隔为2s,可获取高重叠度的视频影像,相邻重叠度大约在90%。选择50幅全景序列影像,采用两两匹配策略,序列影像间设置5°重叠,仅匹配最大5幅影像,共计190个匹配像对。由于在序列影像上两两匹配,因此基线宽度是变化的,可以验证算法在物方尺度变化情况下的自适应性。试验数据在道路右侧区域纹理较缺乏,建筑物背光且受树木遮挡较严重,部分序列影像见图 6,匹配中的SIFT_ratio1设置为0.8。
 |
| 图 6 部分序列影像 Fig. 6 Part of the sequence images |
图 7、图 8为序列影像的正确匹配率和正确匹配点数的对比结果。图 7(a)、图 8(a)为具有较高重叠度相邻影像间的匹配,由于相邻影像时间间隔最短,重叠度最高,因此局部正确匹配点数量较高,使得影像间的局部运动结构更稳定,可提高均值漂移估计算法的快速收敛和精度,从结果可以看出运动结构相似性匹配方法表现非常出色,正确匹配率均高于88%。固定带宽下的匹配仍然呈现以下现象,带宽越小正确匹配点数越少,但匹配率越高。如h=50时,正确匹配点数大约在1000~2500之内浮动,正确匹配率在91%~99%之间;而本文自适应匹配方法在两方面取得了较好的平衡,正确匹配点数大约在2000~4000,正确匹配率也保持在92%~99%之间。图 7(b)、图 8(b)为较低重叠度的序列影像间匹配(认为物方尺度上有较大的变化),由于低重叠度和尺度的剧烈变化影响,运动结构的相似性下降,因此整体表现不如相邻匹配结果,在最大的5°重叠影像间这种现象尤其明显,最差匹配率为63%。但大部分情况下,本文方法仍表现可观,正确匹配率总体在90%左右浮动,在纹理缺乏区域为80%左右。因此可以看出基于运动结构特征的匹配方法,随着尺度的增大,总体匹配可靠性下降,尤其在纹理缺乏区域,更无法获得足够的邻域相似性匹配点,这种情况下往往需要在后处理中,增加全局的约束条件[7]。
 |
| 图 7 序列影像的正确匹配率对比 Fig. 7 The experiment contrast of correct matching rate |
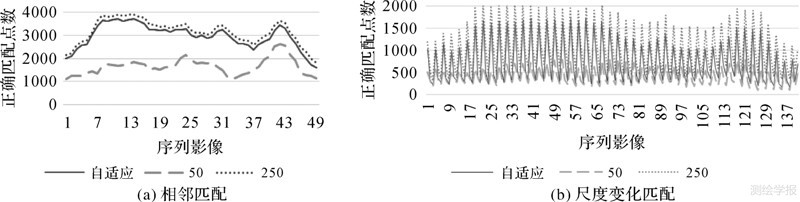 |
| 图 8 序列影像的正确匹配点数对比 Fig. 7 The experiment contrast of correct matching points |
本文研究了一种自适应匹配方法,提出了多尺度的特征度量与运动结构相似性度量相融合的自适应匹配方法,并详细探讨了自适应参数的定义方法。试验表明在内点率变化、物方尺度变化等情况,本文方法可以实现自适应的匹配,提高了匹配的正确点数和匹配率。
基于局部运动结构的一致性假设,要求邻域范围内有足够的特征匹配点。理想情况下应该是均匀且密集分布的,但不适用如下两个条件:一种是独立特征点,由于无法建立其邻域运动结构的支撑度量,这类点往往被孤立;另一种是当重复纹理或运动粗差显现出局部聚类特征情况。因此目前全景自适应匹配的难点仍在于匹配边界的自适应,以及短基线下的运动粗差检测和实时匹配等问题。研究多特征融合的自适应多视匹配方法解决上述问题是今后研究的主要方向。
| [1] | MICUSIK B, KOSECKA J. Piecewise Planar City 3D Modeling from Street View Panoramic Sequences[C]//IEEE Conference on Computer Vision and Pattern Recognition. Miami, FL: IEEE, 2009: 2906-2912. |
| [2] | TORII A, HAVLENA M, PAJDLA T. From Google Street View to 3D City Models[C]//IEEE 12th International Conference on Computer Vision Workshops. Kyoto: IEEE, 2009: 2188-2195. |
| [3] | SATO T, YOKOYA N. Multi-baseline Stereo by Maximizing Total Number of Interest Points[C]//Annual Conference SICE. Takamatsu: IEEE, 2007: 1471-1477. |
| [4] | MATSUHISA R, ONO S, KAWASAKI H, et al. Image-based Ego-motion Estimation Using On-vehicle Omnidirectional Camera[J]. International Journal of Intelligent Transportation Systems Research, 2010, 8(2): 106-117. |
| [5] | SATO T, PAJDLA T, YOKOYA N. Epipolar Geometry Estimation for Wide-baseline Omnidirectional Street View Images[C]//IEEE International Conference on Computer Vision Workshops. Barcelona: IEEE, 2011: 56-63. |
| [6] | JI Shunping, SHI Yun. Image Matching and Bundle Adjustment Using Vehicle-based Panoramic Camera[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(1): 94-100. (季顺平, 史云. 车载全景相机的影像匹配和光束法平差[J]. 测绘学报, 2013, 42(1): 94-100.) |
| [7] | ZHANG Zhengpeng, JIANG Wanshou, ZHANG Jing. A Gross Error Detection Method of Vehicle-borne Cubic Panoramic Image Sequence[J]. Geomatics and Information Science of Wuhan University, 2014, 39(10): 1208-1213. (张正鹏, 江万寿, 张靖. 车载立方体全景影像匹配点的粗差检测方法[J]. 武汉大学学报: 信息科学版, 2014, 39(10): 1208-1213.) |
| [8] | ZHANG Zhengpeng, JIANG Wanshou, ZHANG Jing. An Image Match Method Based on Optical Flow Feature Clustering for Vehicle-borne Panoramic Image Sequence[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(12): 1266-1273. (张正鹏, 江万寿, 张靖. 光流特征聚类的车载全景序列影像匹配方法[J]. 测绘学报, 2014, 43(12): 1266-1273.) |
| [9] | DEVROYE L, LUGOSI G. Variable Kernel Estimates: on the Impossibility of Tuning the Parameters[C]//GINÉ E, MASON D M, WELLNER J A. High Dimensional Probability II. Birkhäuser Boston: Springer, 2000: 405-424. |
| [10] | BERLINET A, BIAU G, ROUVIèRE L. Optimal L1 Bandwidth Selection for Variable Kernel Density Estimates[J]. Statistics & Probability Letters, 2005, 74(2): 116-128. |
| [11] | TURLACH B A. Bandwidth Selection in Kernel Density Estimation: A Review[M]. [S.l.]: Université Catholique De Louvain, 1993. |
| [12] | ZHOU Fangfang, FAN Xiaoping, YE Zhen. Mean Shift Research and Applications[J]. Control and Decision, 2007, 22(8): 841-847. (周芳芳, 樊晓平, 叶榛. 均值漂移算法的研究与应用[J]. 控制与决策, 2007, 22(8): 841-847.) |
| [13] | ZHOU Jiaxiang, ZHU Jianjun, MEI Xiaoming, et al. An Adaptive Mean Shift Segmentation Method of Remote Sensing Images Based on Multi-dimension Features[J]. Geomatics and Information Science of Wuhan University, 2012, 37(4): 419-422, 440. (周家香, 朱建军, 梅小明, 等. 多维特征自适应MeanShift遥感图像分割方法[J]. 武汉大学学报: 信息科学版, 2012, 37(4): 419-422, 440.) |
| [14] | COMANICIU D. An Algorithm for Data-driven Bandwidth Selection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(2): 281-288. |
| [15] | COMANICIU D, RAMESH V, MEER P. The Variable Bandwidth Mean Shift and Data-driven Scale Selection[C]//8th IEEE International Conference on Computer Vision. Vancouver, BC: IEEE, 2001: 438-445. |
| [16] | GILANI S Z A, RAO N I. Data Driven Bandwidth for Medoid Shift Algorithm[C]//MURGANTE B, GERVASI O, IGLESIAS A, et al. Computational Science and Its Applications. Berlin: Springer, 2011: 534-546. |
| [17] | MAYER A, GREENSPAN H. An Adaptive Mean-shift Framework for MRI Brain Segmentation[J]. IEEE Transactions on Medical Imaging, 2009, 28(8): 1238-1250. |
| [18] | COLLINS R T. Mean-shift Blob Tracking through Scale Space[C]//DANIELLE M. IEEE Computer Society Conference on Computer Vision and Pattern Recognition: Vol 2. Baltimore: Victor Graphics, 2003: 234-240. |
| [19] | COMANICIU D, RAMESH V, MEER P. Kernel-based Object Tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(5): 564-575. |
| [20] | WANG Jue, THIESSON B, XU Yingqing, et al. Image and Video Segmentation by Anisotropic Kernel Mean Shift[C]//PAJDLA T, MATAS J. Proceedings of the 8th European Conference on Computer Vision. Berlin: Springer, 2004: 238-249. |
| [21] | LOWE D G. Distinctive Image Features from Scale-invariant Keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. |
| [22] | SUN Deqing, ROTH S, BLACK M J. Secrets of Optical Flow Estimation and Their Principles[C]//IEEE Conference on Computer Vision and Pattern Recognition. San Francisco, CA: IEEE, 2010: 2432-2439." |