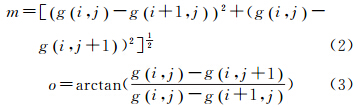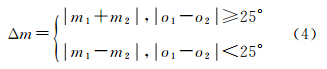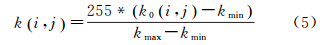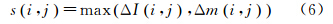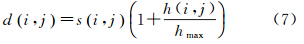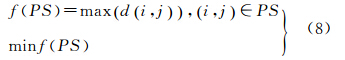2. 国家测绘地理信息局卫星测绘应用中心, 北京 100830
2. Satellite Surveying and Mapping Application Center, NASG, Beijing 100830, China
1 引 言
数字正射影像(DOM)是测绘遥感4D产品的重要组成部分,由于能够直观地表达地形、地貌、地物等丰富信息,使其在地理国情监测、城市规划、应急响应等方面均有重要应用。DOM生产过程中需要将单片纠正后的多幅正射影像拼接成整个区域的正射影像图[1],在单片正射影像间自动智能地找出最优的镶嵌线是DOM生产流程自动化的一个关键步骤。当前很多商业软件自动生成的镶嵌线不能完全避开建筑物等明显地物,仍需要较多人工编辑才能满足生产要求,作业效率比较低。因此,研究镶嵌线智能检测方法对提高DOM产品的生产效率具有重要的意义,是国内外学者研究的热点问题之一。
文献[2]提出利用Dijkstra算法进行搜索,但采用Dijkstra算法有很明显的缺陷,一方面搜索到的镶嵌线可能是经过像素差异值比较大但总像素数比较少的路径,另一方面采用穷举的策略提取镶嵌线,计算量很大。文献[3, 4, 5]以文献[2]方法作为算法原型,采用不同的策略进行优化处理,一定程度上克服了文献[2]方法的不足,但仍然需要迭代搜索。文献[6]为每个镶嵌顶点和每条镶嵌线建立搜索区域并构造每条镶嵌线的搜索图,通过搜索图的最小生成树检测瓶颈值,删除图中权值大于瓶颈值的边以减少Dijkstra算法搜索范围从而减少计算量,但其搜索区域难以确定。文献[7]提出Twin Snakes模型,将RGB空间转换到IHS空间,计算重叠区域对应像素的亮度和梯度差异,通过最小化两条动态轮廓间的能量搜索最佳路径。文献[8, 9]对该算法进行优化但仍会丢失全局最小值区域并在局部或全局最大值处停止。文献[10, 11]提出利用蚁群算法进行正射影像镶嵌线自动选择的方法,以重叠区域像素差异和偏离初始镶嵌线的距离(向心性)为初始信息素值,通过蚁群算法寻找最优镶嵌线,该方法依赖于蚂蚁的数量。文献[12, 13, 14]分别提出利用DSM、LiDAR、道路矢量数据等辅助信息进行搜索,然而一般情况下无法得到此类辅助信息。虽然以上方法各有优点,但依然存在一定的问题,难以完全满足快速生产DOM产品的要求,因此有必要探索一种快速的镶嵌线智能搜索方法。
2 基于最优生成树的镶嵌线智能检测方法 2.1 重叠区域像素差异
使镶嵌线避开建筑、树木等高出地面或色彩差异明显的区域,关键在于使用某种测度较好地表达重叠影像的真实差异。影像亮度差异和梯度信息是最基本的测度。亮度差异ΔIi,j定义为对应像素亮度差的绝对值,即
式中,g1i,j、g2i,j分别为像素i,j在两幅待镶嵌正射影像上重叠区域对应像素的亮度值。对于彩色影像一般转换到IHS色彩空间计算[15]。梯度信息反映影像灰度在水平和垂直方向上的变化[1],计算公式如下式中,m为梯度大小;o为梯度方向。重叠区域梯度差异Δm可按文献[6]计算
式中,m1、m2、o1、o2分别为重叠区域左右影像对应像素的梯度及梯度方向。将重叠区域的灰度差异和梯度差异归一化到[0.255]之间,归一化方法如下
式中,k0i,j、ki,j为归一化前后的影像灰度差异或梯度差异;kmax、kmin分别为影像灰度差异或梯度差异的最大值和最小值。取归一化的灰度差异和梯度差异中较大者作为差异影像对应像素的值si,j 式中,ΔIi,j、Δmi,j为归一化的影像灰度差异和梯度差异。亮度信息使镶嵌线绕开影像色彩差异较大的区域,梯度信息使镶嵌线绕开线状地物[16],如建筑物边缘。最优的镶嵌线应在避开地物的同时,尽量位于由图像区域的几何关系确立的初始镶嵌线[8, 17, 18, 19]附近。因此可以按距离设置一定的权值,则最终差分影像像素值di,j可表示为
式中,hmax为镶嵌线偏离初始镶嵌线的最大距离;hi,j为初始镶嵌线两侧像素到初始镶嵌线的距离。对于8位影像,如di,j计算结果大于255则取值为255。通过计算待镶嵌影像重叠区域的亮度差异和梯度信息构建差分影像,搜索镶嵌线的实质是在差分影像上选择一条避开高亮度区域的最优路径。
2.2 Bottleneck模型
文献[20]定义了最优镶嵌线的Bottleneck模型,使路径上影像像素差异的最大值最小,其数学模型为
式中,PS表示镶嵌线;f(PS)为镶嵌线上差异最大值,即镶嵌效果的测度;minf(PS)表示使f(PS)最小。Bottleneck模型的基本思想是,如果镶嵌线上影像差异较大的部分其两侧目视差异不明显,则镶嵌线上其他部分两侧差异更不明显,因此镶嵌线可以被接受。Fernandez等人采用分治算法进行搜索,其算法复杂、计算量较大。本文以Bottleneck模型为基础,采取最优生成树方法搜索最佳镶嵌线,提高了搜索的效率。
2.3 基于最优生成树智能检测方法 2.3.1 最优生成树
在给定的无向图G=V,E中,u,v代表连接顶点u与顶点v的边(即u,v∈E),而wu,v代表此边的权重,若存在T为E的子集(即TE)且为无循环图,使得
最小,则此T为无向图G的最优(小)生成树[21]。正射影像上的每个像素代表一个固定尺寸的物理单元,通常可认为该单元为一个正方形,其边长即为地面分辨率,因此可将正射影像看作是一个网格图。依据与网格边相邻的两个像素对其赋予权值,则差分影像可视为一个带权无向图。同时,最优生成树的生成准则为每次选择一条具有最小权值的边(或顶点),从而权值小的边被选取,权值大的边被舍弃。因此可以通过求解该带权无向图的最优生成树来搜索最佳镶嵌线。Prim算法与Kruskal算法是寻找最小生成树的经典方法[21],两者都属于贪心法。
2.3.2 最优镶嵌线搜索
根据最优生成树优先选取权值较小的边(顶点)的准则,由差分影像构建的无向图的最优生成树上连接起点和终点的路径满足Bottleneck模型的准则,可视为最佳镶嵌线,路径上最大的权值即为瓶颈值。
对于差分影像,其边的权值定义为相邻的两个像素亮度的和[9](如图 1所示),即
 |
| 图 1 边的权值 Fig. 1 Weight of edges |
在数据结构中,树的每个结点可以有若干个子结点,但只能有唯一的父节点(根节点除外),如图 2。因此,从根结点到某个叶子节点的路径须进行搜索,而从叶子节点到根结点只需依次遍历当前节点的父节点。为提高算法效率,只需记录每个节点的父节点。为此,建立与差分影像顶点对应的“顶点方向图”。图 3(a)中节点上的标记U、D、L、R(分别对应上、下、左、右)表示该顶点的父节点的位置,S表示初始顶点,即根节点。当终点(右下角)加入到最优生成树中,即可逆向遍历出最优镶嵌线(图 3(b))。该方法的优点是回避了迭代搜索过程,显著减少了计算量。
 |
| 图 2 树示意图 Fig. 2 Tree |
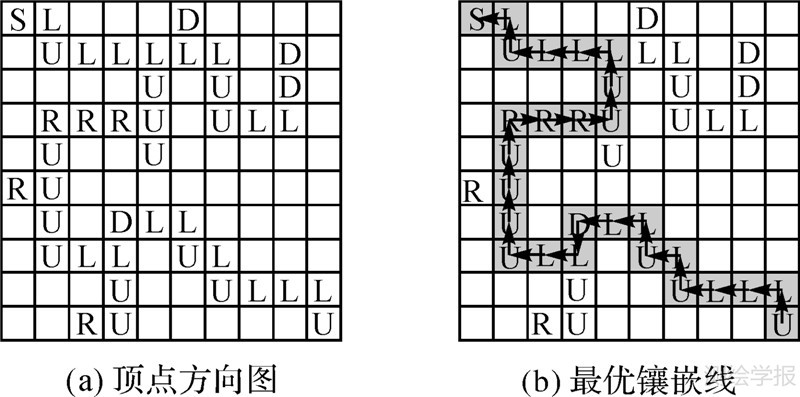 |
| 图 3 最优镶嵌线生成 Fig. 3 Generation of optimal seamline |
对单片正射影像进行镶嵌时,首先生成初始镶嵌网络,可以采用文献[18, 19]提出的顾及重叠的面Voronoi图接缝线网络自动生成方法。然后对初始镶嵌线网络进行智能优化,即找出一条从多边形公共边起始顶点到终止顶点的最佳路径代替该公共边。对于这个问题,相比于Kruskal算法,Prim算法更容易实现,效率也较高。镶嵌线智能检测过程如下:
(1) 以起始顶点为最优生成树的根节点开始搜索,建立备选节点列表,所有与当前最优生成树的根相连的顶点按权值从小到大加入备选节点列表。
(2) 在备选节点列表里取出权值最小的节点,加入到当前最优生成树中,并将与该节点相连的顶点作为备选节点加入到备选节点列表(已处理过的节点不加入)。
(3) 重复步骤(2),直至终止顶点加入最小生成树。
(4) 从终止顶点开始遍历其父节点至根节点,所得到的节点构成的路径即为最优镶嵌线。
一般情况下,影像的重叠区域逐像素建立无向图进行最优生成树搜索所需的内存和计算量均较大,且存在很多不必要的计算。因此,本文采用多级分层的金字塔策略进行优化,首先在最顶层金字塔影像上进行初始搜索,然后根据需要将已搜索到的镶嵌线转换到下一层金字塔影像,并在其邻近的区域采用相同的方法继续搜索。另外,由于镶嵌线上节点过多不利于镶嵌线网络的拓扑关系的构建,有必要对其进行简化,可采用道格拉斯·普克算法[22](Douglas-Peuker algorithm)。
3 试验结果与分析
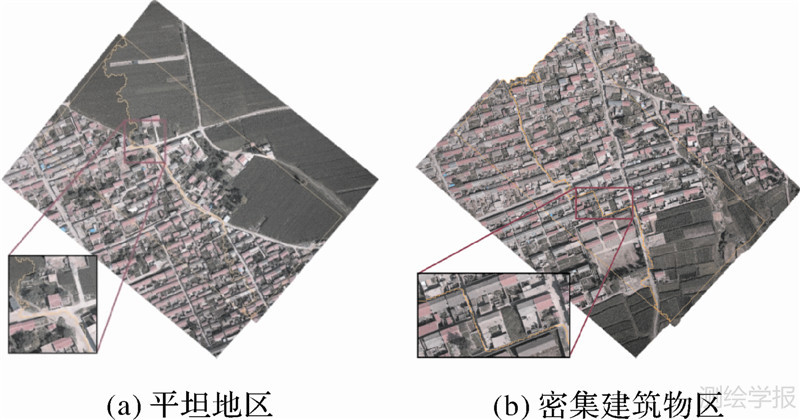
为验证本文算法的可行性,使用Visual C++编程实现了本文提出的正射影像镶嵌线快速智能检测算法,并在Intel(R)Xeon(R)2.66 GHz、16 GB内存、64位Windows 7环境下的台式计算机上进行试验。首先对密集建筑物和平坦地区两种类型的数据进行算法有效性试验,然后将正射影像镶嵌效果与现有算法(OrthoVista 4.6)作出对比分析。 3.1 算法有效性试验
试验影像为Canon 5DMarkⅡ相机拍摄的低空数码影像。图 4(a)、4(b)分别为两种地形区域的两张影像重叠区域的差异影像及生成的镶嵌线,图中亮度较暗的区域为重叠区域。
 |
| 图 4 差异影像 Fig. 4 The difference images |
图 5(a)、5(b)分别为对应区域的镶嵌影像,图中黄色矩形范围内为重叠区域,黄色曲线为镶嵌线。从图中可以看出,本文方法检测到的镶嵌线很好地避开了建筑区域。
 |
| 图 5 镶嵌影像 Fig. 5 Mosaicking images |
表 1列出两区域详细的试验数据统计,从中可以看出,本文所述方法在保证镶嵌线质量的情况下具有很高的效率。
| 重叠区域 大小/像素 | 镶嵌后影像 大小/像素 | 搜索 用时 /s | 镶嵌线效果 | ||||||
| 路径长度/ 像素 | 差异像素数/像素 | 最大值 | 平均值 | ||||||
| 大于50 | 大于100 | 大于150 | |||||||
| 平坦地区 | 5410×5176 | 6806×6488 | 6.6 | 11 565 | 59 | 23 | 9 | 255 | 14.24 |
| 密集建筑物区 | 4760×4452 | 5960×5356 | 1.2 | 8874 | 67 | 12 | 2 | 164 | 11.50 |
| 注:最大值和平均值为差异影像的为归一化的值,并非真实值。 | |||||||||
最优生成树的生成过程是将权值小的边优先加入到生成树中,因此当镶嵌线穿越差异较大的区域时,必然先到达与当前生成树相连的所有小于该区域像素差异的像素。如图 6所示,图中灰色为搜索到的像素,黑色为未搜索过的像素。在图 6(a)平坦地区中,由于镶嵌线的终点落在房屋顶部,镶嵌线要达到终点必须穿越梯度较大的房屋边缘,使得镶嵌线上差异最大值达到255,从而导致差异影像绝大部分结点都在生成树上;在图 6(b)密集建筑物区中,影像下部分属于亮度差异和梯度都很小的庄稼地,因此该区域同样有大部分结点在生成树上。因此,平坦地区的镶嵌线搜索时间明显比密集建筑物区长。另外,即使镶嵌线必须穿过像素差异较大的区域,后续搜索过程中依然会使局部最大值最小化,相比于其他镶嵌线整体迭代替换算法[1, 2, 3, 4, 5, 6, 7, 8, 9, 10],本文方法在镶嵌线搜索效果上更具有优势。
 |
| 图 6 顶点方向图 Fig. 6 Direction of the nodes |
试验1的影像为DMC相机拍摄的常规航空影像。图 7(a)、7(b)分别为本文方法和OrthoVista生成的镶嵌线。本文方法生成的镶嵌线很好地避开了建筑物,而OrthoVista穿过了右边一栋较高的建筑。表 2为两种方法生成的镶嵌线质量与效率的统计数据,本文方法的镶嵌线上差异大于100像素数占路径长度的比例不到1%,大于150的像素数仅为0.3%,用时仅为2.1 s,而OrthoVista则分别达到约7%和5%,用时为17 s。可以看出,本文提出的方法在质量和效率上均取得了较好的效果。
 |
| 图 7 镶嵌影像 Fig. 7 Mosaicking Images |
| 重叠区域 大小/像素 | 镶嵌后影像 大小/像素 | 搜索 用时 /s | 镶嵌线效果 | ||||||
| 路径长度/ 像素 | 差异像素数/像素 | 最大 值 | 平均 值 | ||||||
| >50 (%) | >100 (%) | >150 (%) | |||||||
|
本文方法 OrthoVista | 6329×3003 | 6376×5294 | 2.1 | 11 223 | 168 (1.5) | 78 (0.7) | 30 (0.3) | 243 | 9.67 |
| 17 | 8461 | 823 (9.7) | 576 (6.8) | 393 (4.6) | 255 | 24.58 | |||
| 注:OrthoVista数据为在本文方法生成的差异影像上统计的数据。 | |||||||||
试验2的影像为UCXp相机拍摄的常规航空影像。图 8为某测区利用本文方法和OrthoVista镶嵌9张正射影像的结果对比图。该测区建筑物密集,且存在较多的高层建筑,镶嵌线搜索难度较大。
 |
| 图 8 镶嵌结果比较 Fig. 8 Contrast of Mosaicking Images with OrthoVista |
表 3为两种方法生成的镶嵌线质量与效率的统计数据,表中平均值为单条镶嵌线上像素差异之和与像素总数的比值,总平均值为8条镶嵌线的均值。对比分析表中统计结果,可以看到,两种方法自动生成的镶嵌线局部上有差异,但整体上基本一致,而本文的方法具有更高的搜索效率。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 总平均值 | |||
|
差 异 像 素 数 | 路径长度/ 像素 | (a) | 10 102 | 9165 | 10 401 | 11 823 | 10 669 | 9333 | 11 087 | 11 561 | 10 517.635 |
| (b) | 7278 | 7671 | 7448 | 7156 | 7469 | 7672 | 7645 | 7141 | 7 436.125 | ||
| 搜索用时 /s | (a) | 7.0 | 14.0 | 11.4 | 8.9 | 11.2 | 10.4 | 7.6 | 8.9 | 9.9 | |
| (b) | 120 | 15 | |||||||||
| >50 (%) | (a) | 211 (2.0) | 281 (3.1) | 614 (6.0) | 656 (5.5) | 670 (6.3) | 434 (5.7) | 300 (2.7) | 260 (2.2) | 428.25 (4.1) | |
| (b) | 158 (2.1) | 251 (3.3) | 419 (5.6) | 528 (7.4) | 453 (6.1) | 310 (4.0) | 595 (8.3) | 173 (2.4) | 360.875 (4.8) | ||
| >100 (%) | (a) | 38 (0.4) | 89 (1.0) | 175 (1.7) | 30 (0.3) | 159 (1.5) | 70 (1.9) | 38 (0.3) | 67 (0.6) | 83.25 (1.5) | |
| (b) | 17 (0.2) | 24 (0.3) | 62 (0.8) | 88 (1.2) | 79 (1.1) | 51 (0.7) | 439 (6.1) | 20 (0.3) | 97.5 (0.8) | ||
| >150 (%) | (a) | 11 (0.1) | 31 (0.3) | 5 (0.0) | 2 (0.0) | 4 (0.0) | 10 (1.1) | 6 (0.0) | 6 (0.0) | 9.375 (0.1) | |
| (b) | 1 (0.0) | 13 (0.1) | 16 (0.2) | 11 (0.1) | 6 (0.0) | 8 (0.1) | 185 (2.6) | 7 (0.0) | 30.875 (0.4) | ||
| 平均值 | (a) | 9.50 | 9.75 | 10.61 | 14.44 | 18.56 | 18.81 | 17.90 | 10.21 | 11.6 | |
| (b) | 9.51 | 9.51 | 10.96 | 15.00 | 19.97 | 19.20 | 17.60 | 17.36 | 12.50 | ||
| 注:(a)为本文方法的统计结果;(b)为OrthoVista生成的镶嵌线在相同情况下的统计结果;1-8为图中从上到下镶嵌线的序号。 | |||||||||||
图 9为局部区域的对比结果,其中图 9(a)、图 9(b)为OrthoVista生成的镶嵌线,图 9(c)、图 9(d)为对应区域本文方法生成的镶嵌线。从图中可以看出,本文方法生成的镶嵌线基本避开了较高的建筑物,沿着城市道路或建筑物边缘,效果优于OrthoVista的结果。对该试验区域镶嵌影像总体而言,本文方法自动生成的镶嵌线穿过建筑的次数要少于OrthoVista生成的镶嵌线。
 |
| 图 9 局部镶嵌结果比较 Fig. 9 Contrast of Mosaicking Images in details with OrthoVista |
图 10为城市道路被建筑物遮挡时镶嵌线的通过情况,图 10(a)、图 10(b)为相同区域OrthoVista 和本文方法生成的镶嵌线,图 10(c)为对应区域的差分影像。由于建筑物较高,存在完全遮挡道路的情况,镶嵌线只能在差异相对较小的区域(绿色椭圆区域)通过,因此该区域没有完全避免镶嵌线穿过建筑物。
 |
| 图 10 局部镶嵌结果比较 Fig. 10 Contrast of Mosaicking Images in details with OrthoVista |
本文提出了一种基于最优生成树的正射影像镶嵌线快速智能检测方法,通过影像亮度差异和梯度信息构建差分影像并视其为带权无向图,采用最优生成树生成方法构造无向图各顶点的“顶点方向图”,最后逆序遍历得到最优镶嵌线,回避了常规的迭代搜索过程。该方法检测到的镶嵌线在保证质量的同时具有很高的效率,能够很好地解决正射影像镶嵌过程中镶嵌线的自动选择问题,在建筑物较密集的地区效果更为显著。当初始镶嵌线起点或终点落在建筑物上时,镶嵌线必然会通过建筑,不仅影响镶嵌线的质量,也造成镶嵌线检测效率下降,如何避免这一问题仍需作进一步研究。
| [1] | ZHANG Zuxun, ZHANG Jianqing. Digital Photogrammetry[M]. Wuhan: Wuhan University Press, 1997. (张祖勋, 张剑清. 数字摄影测量学[M]. 武汉: 武汉大学出版社, 1997.) |
| [2] | DAVIS J. Mosaics of Scenes with Moving Objects[C]//IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Santa Barbara: IEEE Computer Society, 1998: 354-360. |
| [3] | CHON J, KIM H. Determination of the Optimal Seam-lines in Image Mosaicking with the Dynamic Programming (DP) on the Converted Cost Space[M]//RUTKOWSKI L, TADEUSIEWICZ R, ZADEH L A, et al. Artificial Intelligence and Soft Computing: Lecture Notes in Computer Science. Berlin: Springer, 2006, 4029: 750-757. |
| [4] | CHON J, KIM H, LIN C. Seam-line Determination for Image Mosaicking: A Technique Minimizing the Maximum Local Mismatch and the Global Cost[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2010, 65(1): 86-92. |
| [5] | YUAN Xiuxiao, ZHONG Can. An Improvement of Minimizing Local Maximum Algorithm on Searching Seam Line for Orthoimage Mosaicking[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(2): 199-204. (袁修孝, 钟灿. 一种改进的正射影像镶嵌线最小化最大搜索算法[J]. 测绘学报, 2012, 41(2): 199-204.) |
| [6] | MILLS S, MCLEOD P. Global Seamline Networks for Orthomosaic Generation via Local Search[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 75: 101-111. |
| [7] | KERSCHNER M. Seamline Detection in Colour Orthoimage Mosaicking by Use of Twin Snakes[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2001, 56(1): 53-64. |
| [8] | WANG Lin, AI Haibin, ZHANG Li. Automated Seamline Detection in Orthophoto Mosaicking Using Improved Snakes[C]//Proceedings of the 2nd International Conference on Information Engineering and Computer Science. Wuhan: IEEE, 2010: 1-4. |
| [9] | AI Haibin, ZHANG Li, WANG Lin. Automatic Mosaicking Method for Large Block of Orthophotos[C]//Proceedings of SPIE 8005, MIPPR 2011: Parallel Processing of Images and Optimization and Medical Imaging Processing.Guilin: SPIE, 2011. |
| [10] | ZHANG Jianqing, SUN Mingwei, ZHANG Zuxun. Automated Seamline Detection for Orthophoto Mosaicking Based on Ant Colony Algorithm[J]. Geomatics and Information Science of Wuhan University, 2009, 34(6): 675-678. (张剑清, 孙明伟, 张祖勋. 基于蚁群算法的正射影像镶嵌线自动选择[J]. 武汉大学学报: 信息科学版, 2009, 34(6): 675-678.) |
| [11] | SUN Mingwei. Research on Key Technology of Automatical and Fast DOM Generation[D]. Wuhan: Wuhan University, 2009. (孙明伟. 正射影像全自动快速制作关键技术研究[D]. 武汉: 武汉大学, 2009.) |
| [12] | ZUO Zhiquan, ZHANG Zuxun, ZHANG Jianqing, et al. Seamlines Intelligent Detection in Large-scale Urban Orthoimage Mosaicking[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(1): 84-89. (左志权, 张祖勋, 张剑清, 等. DSM辅助下城区大比例尺正射影像镶嵌线智能检测[J]. 测绘学报, 2011, 40(1): 84-89.) |
| [13] | SUN Jie, MA Hongchao, TANG Xuan. Optimization of LiDAR System Ortho-image Mosaic Seam-line[J]. Geomatics and Information Science of Wuhan University, 2011, 36(3): 325-328. (孙杰, 马洪超, 汤璇. 机载LiDAR正射影像镶嵌线智能优化研究[J]. 武汉大学学报: 信息科学版, 2011, 36(3): 325-328.) |
| [14] | WAN Youchuan, WANG Dongliang, XIAO Jianhua, et al. Automatic Determination of Seamlines for Aerial Image Mosaicking Based on Vector Roads Alone[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 76: 1-10. |
| [15] | GONZALEZ R C, WOODS R E. Digital Image Processing[M]. RUAN Qiuqi, RUAN Yuzhi, Trans. Beijing: Publishing House of Electronics Industry, 2009. (冈萨雷斯, 伍兹. 数字图像处理[M]. 阮秋琦, 阮宇智, 译. 北京: 电子工业出版社, 2009.) |
| [16] | PAN Jun, WANG Mi. A Seam-line Optimized Method Based on Difference Image and Gradient Image[C]// Proceedings of the 19th International Conference on Geoinformatics. Shanghai: IEEE, 2011: 1-6. |
| [17] | YANG Yi, GAO Yuan, LI Haitao, et al. An Algorithm for Remote Sensing Image Mosaic Based on Valid Area[C]//2011 International Symposium on Image and Data Fusion. Tengchong: IEEE, 2011: 1-4. |
| [18] | PAN Jun, WANG Mi, LI Deren, et al. Automatic Generation of Seamline Network Using Area Voronoi Diagrams with Overlap[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(6): 1737-1744. |
| [19] | PAN Jun. Research on Automatic Color Consistency Processing and Generation of Seamline Network for Aerial Images[D]. Wuhan: Wuhan University, 2008. (潘俊. 自动化的航空影像色彩一致性处理及接缝线网络生成方法研究[D]. 武汉: 武汉大学, 2008.) |
| [20] | FERNANDEZ E, GARFINKEL R, ARBIOL R. Mosaicking of Aerial Photographic Maps via Seams Defined by Bottleneck Shortest Paths[J]. Operations Research, 1998, 46(3): 293-304. |
| [21] | CORMEN T H, LEISERSON C, IVEST R, et al. Introduction to Algorithms[M]. PAN Jingui, GU Tiecheng, LI Chengfa, et al. Trans. Beijing: China Machine Press, 2010. (科曼, 莱瑟森, 李维斯特, 等. 算法导论[M]. 潘金贵, 顾铁成, 李成法, 等译. 北京: 机械工业出版社, 2010.) |
| [22] | DOUGLAS D H, PEUCKER T K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature[J]. The Canadian Cartographer, 1973, 10(2): 112-122." |